The Minimum Target Diameter and the Harvest Age of Oak Natural Secondary Forests in Different Sites Conditions: Case Study in Hunan Province, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site and Data Description
2.2. Site Factors Influencing DBH Growth
2.3. Base Model Selection
2.4. Nonlinear Mixed-Effects Models
2.5. The K-Means Clustering Algorithm
2.6. Model Evaluation
2.7. Quantitative Maturity Age and the Minimum Target Diameter
3. Results
3.1. Importance Analysis of Site Factors
3.2. Base Model Selection and Simulation
3.3. Nonlinear Mixed Models for Different Site Type Combinations
3.4. Clustering of the Site Types and Model Simulation
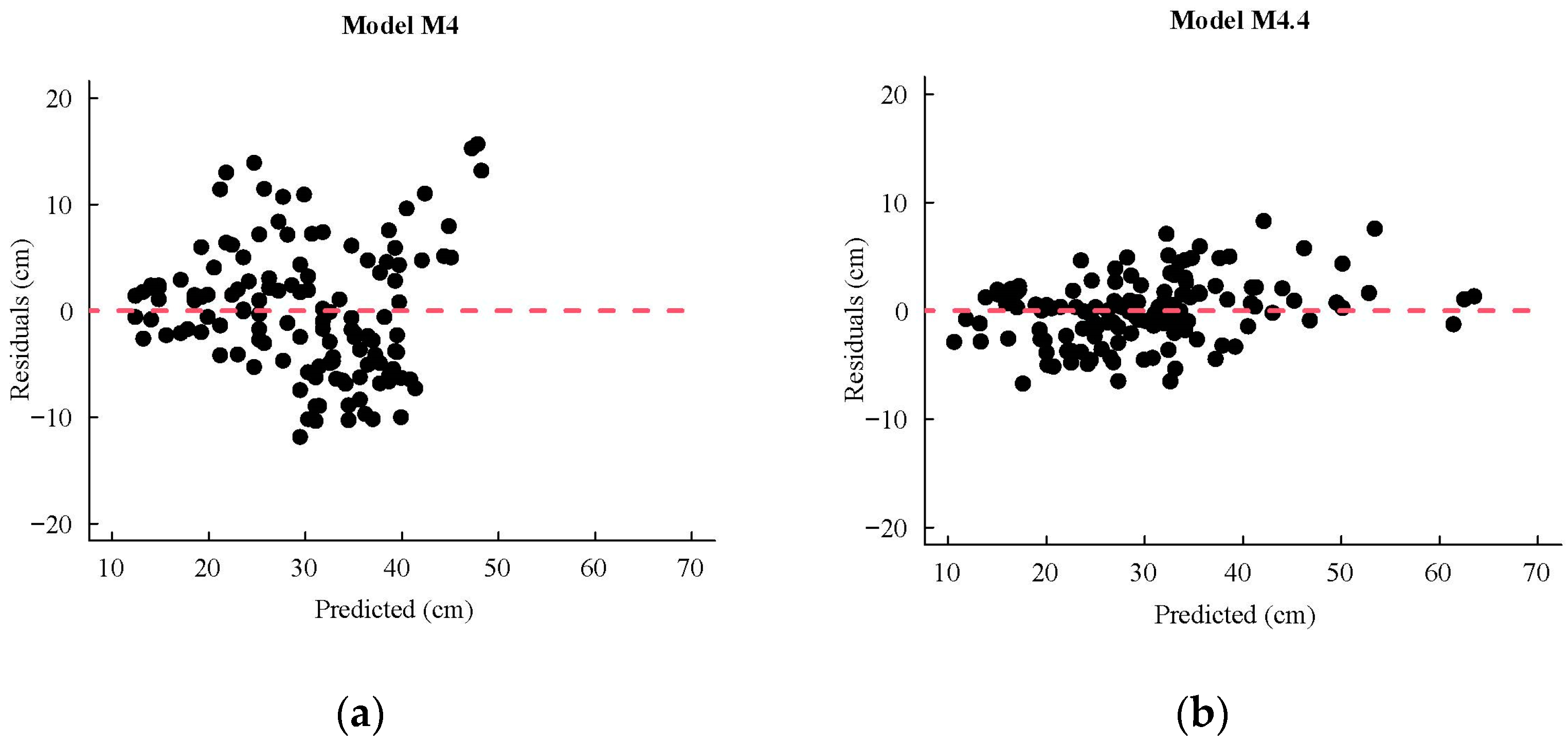
3.5. Model Evaluation
3.6. Harvest Age of Different Target Diameter in Different Sites
3.7. Determination of Quantitative Maturity Age and the Minimum Target Diameter
4. Discussion
4.1. Harvest Age of Different Target Diameters
4.2. The Minimum Target Diameter
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Collado, E.; Piqué, M.; Coello, J.; de-Dios-García, J.; Fuentes, C.; Coll, L. Close-to-Nature Management Effects on Tree Growth and Soil Moisture in Mediterranean Mixed Forests. For. Ecol. Manag. 2023, 549, 121457. [Google Scholar] [CrossRef]
- Brang, P.; Spathelf, P.; Larsen, J.B.; Bauhus, J.; Bončina, A.; Chauvin, C.; Drossler, L.; Garcia-Guemes, C.; Heiri, C.; Kerr, G.; et al. Suitability of Close-to-Nature Silviculture for Adapting Temperate European Forests to Climate Change. Forestry 2014, 87, 492–503. [Google Scholar] [CrossRef]
- Schneider, R.; Franceschini, T.; Duchateau, E.; Bérubé-Deschênes, A.; Dupont-Leduc, L.; Proudfoot, S.; Power, H.; De Coligny, F. Influencing Plantation Stand Structure through Close-to-Nature Silviculture. Eur. J. For. Res. 2021, 140, 567–587. [Google Scholar] [CrossRef]
- O’Hara, K.L. What Is Close-to-Nature Silviculture in a Changing World? For. Int. J. For. Res. 2016, 89, 1–6. [Google Scholar] [CrossRef]
- Van Gossum, P.; Luyssaert, S.; Serbruyns, I.; Mortier, F. Forest Groups as Support to Private Forest Owners in Developing Close-to-Nature Management. For. Policy Econ. 2005, 7, 589–601. [Google Scholar] [CrossRef]
- Gamborg, C.; Larsen, J.B. ‘Back to Nature’—A Sustainable Future for Forestry? For. Ecol. Manag. 2003, 179, 559–571. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, B.; Zhu, Z.; Jia, B.; Xu, W.; Liu, M.; Gao, L.; Gregoire, T.G. The Effects of Crop Tree Thinning Intensity on the Ability of Dominant Tree Species to Sequester Carbon in a Temperate Deciduous Mixed Forest, Northeastern China. For. Ecol. Manag. 2022, 505, 119893. [Google Scholar] [CrossRef]
- Hessenmöller, D.; Bouriaud, O.; Fritzlar, D.; Elsenhans, A.S.; Schulze, E.D. A Silvicultural Strategy for Managing Uneven-Aged Beech-Dominated Forests in Thuringia, Germany: A New Approach to an Old Problem. Scand. J. For. Res. 2018, 33, 668–680. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, S.; Lei, X.; Ning, J.; Wang, Y. Theoretical Basis and Implementation Techniques on Close-to-nature Transformation of Plantations. World For. Res. 2009, 22, 20–27. [Google Scholar]
- Wan, P.; He, R.; Wang, P.; Cao, A. Implementation of Different Forest Management Methods in a Natural Forest: Changes in Soil Microbial Biomass and Enzyme Activities. For. Ecol. Manag. 2022, 520, 120409. [Google Scholar] [CrossRef]
- Geng, Y.; Yue, Q.; Zhang, C.; Zhao, X.; Von Gadow, K. Dynamics and Drivers of Aboveground Biomass Accumulation during Recovery from Selective Harvesting in an Uneven-Aged Forest. Eur. J. For. Res. 2021, 140, 1163–1178. [Google Scholar] [CrossRef]
- Pommerening, A.; Maleki, K.; Haufe, J. Tamm Review: Individual-Based Forest Management or Seeing the Trees for the Forest. For. Ecol. Manag. 2021, 501, 119677. [Google Scholar] [CrossRef]
- Tarp, P.; Buongiorno, J.; Helles, F.; Larsen, J.B.; Meilby, H.; Strange, N. Economics of Converting an Even-Aged Fagus sylvatica Stand to an Uneven-Aged Stand Using Target Diameter Harvesting. Scand. J. For. Res. 2005, 20, 63–74. [Google Scholar] [CrossRef]
- Sterba, H.; Zingg, A. Target Diameter Harvesting Ð a Strategy to Convert Even-Aged Forests. For. Ecol. Manag. 2001, 151, 95–105. [Google Scholar] [CrossRef]
- Schöngart, J. Growth-Oriented Logging (GOL): A New Concept towards Sustainable Forest Management in Central Amazonian Várzea Floodplains. For. Ecol. Manag. 2008, 256, 46–58. [Google Scholar] [CrossRef]
- Sist, P.; Fimbel, R.; Sheil, D.; Nasi, R.; Chevallier, M.-H. Towards Sustainable Management of Mixed Dipterocarp Forests of South-East Asia: Moving beyond Minimum Diameter Cutting Limits. Environ. Conserv. 2003, 30, 364–374. [Google Scholar] [CrossRef]
- Andrade, V.H.F.; Machado, S.d.A.; Figueiredo Filho, A.; Botosso, P.C.; Miranda, B.P.; Schöngart, J. Growth Models for Two Commercial Tree Species in Upland Forests of the Southern Brazilian Amazon. For. Ecol. Manag. 2019, 438, 215–223. [Google Scholar] [CrossRef]
- Roessiger, J.; Ficko, A.; Clasen, C.; Griess, V.C.; Knoke, T. Variability in Growth of Trees in Uneven-Aged Stands Displays the Need for Optimizing Diversified Harvest Diameters. Eur. J. For. Res. 2016, 135, 283–295. [Google Scholar] [CrossRef]
- Zell, J.; Hanewinkel, M.; Seeling, U. Financial Optimisation of Target Diameter Harvest of European Beech (Fagus sylvatica) Considering the Risk of Decrease of Timber Quality Due to Red Heartwood. For. Policy Econ. 2004, 6, 579–593. [Google Scholar] [CrossRef]
- Martins, F.B.; Soares, C.P.B.; Silva, G.F.D. Individual Tree Growth Models for Eucalyptus in Northern Brazil. Sci. Agric. 2014, 71, 212–225. [Google Scholar] [CrossRef]
- Abrantes, K.K.B.; Paiva, L.M.; Almeida, R.G.D.; Urbano, E.; Ferreira, A.D.; Mazucheli, J. Modeling the Individual Height and Volume of Two Integrated Crop-Livestock-Forest Systems of Eucalyptus spp. in the Brazilian Savannah. Acta Sci. Agron. 2019, 41, 42626. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, S. Comparison of Different Methods for Fitting Nonlinear Mixed Forest Models and for Making Predictions. Can. J. For. Res. 2011, 41, 1671–1686. [Google Scholar] [CrossRef]
- Vonesh, E.F.; Chinchilli, V.M. Linear and Nonlinear Models for the Analysis of Repeated Measurements; Marcel Dekker: New York, NY, USA, 1997. [Google Scholar]
- Lhotka, J.M.; Loewenstein, E.F. An Individual-Tree Diameter Growth Model for Managed Uneven-Aged Oak-Shortleaf Pine Stands in the Ozark Highlands of Missouri, USA. For. Ecol. Manag. 2011, 261, 770–778. [Google Scholar] [CrossRef]
- Adame, P.; Hynynen, J.; Cañellas, I.; Del Río, M. Individual-Tree Diameter Growth Model for Rebollo Oak (Quercus pyrenaica Willd.) Coppices. For. Ecol. Manag. 2008, 255, 1011–1022. [Google Scholar] [CrossRef]
- Calegario, N.; Daniels, R.F.; Maestri, R.; Neiva, R. Modeling Dominant Height Growth Based on Nonlinear Mixed-Effects Model: A Clonal Eucalyptus Plantation Case Study. For. Ecol. Manag. 2005, 204, 11–21. [Google Scholar] [CrossRef]
- Uzoh, F.C.C.; Oliver, W.W. Individual Tree Diameter Increment Model for Managed Even-Aged Stands of Ponderosa Pine throughout the Western United States Using a Multilevel Linear Mixed Effects Model. For. Ecol. Manag. 2008, 256, 438–445. [Google Scholar] [CrossRef]
- Subedi, N.; Sharma, M. Individual-Tree Diameter Growth Models for Black Spruce and Jack Pine Plantations in Northern Ontario. For. Ecol. Manag. 2011, 261, 2140–2148. [Google Scholar] [CrossRef]
- Sun, K.; Sun, H.; Lu, G.; Fang, L.; Wan, Z.; Tan, Z. Study on the Effects of Stand Density Management of Chinese Fir Plantation in Northern China. Front. Plant Sci. 2023, 14, 1130299. [Google Scholar] [CrossRef]
- Qu, Y.; Jiang, Y.; Chen, H.; Hu, Y.; Jiang, Y.; Wang, Z.; Chhin, S.; Zhang, J.; Sun, L.; Zhang, X. Does the Peak Time of Stand Leaf Area Equal the Biological Maturity Age of Forests? For. Ecol. Manag. 2023, 538, 120988. [Google Scholar] [CrossRef]
- De Ridder, M.; Van den Bulcke, J.; Van Acker, J.; Beeckman, H. Tree-Ring Analysis of an African Long-Lived Pioneer Species as a Tool for Sustainable Forest Management. For. Ecol. Manag. 2013, 304, 417–426. [Google Scholar] [CrossRef]
- López, L.; Villalba, R.; Bravo, F. Cumulative Diameter Growth and Biological Rotation Age for Seven Tree Species in the Cerrado Biogeographical Province of Bolivia. For. Ecol. Manag. 2013, 292, 49–55. [Google Scholar] [CrossRef]
- State Forestry Administration of China. China Forest Resources Report; China Forestry Publishing House: Beijing, China, 2014.
- He, H.; Zhu, G.; Ma, W.; Liu, F.; Zhang, X. Additivity of Stand Basal Area Predictions in Canopy Stratifications for Natural Oak Forests. For. Ecol. Manag. 2021, 492, 119246. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Meng, J. A Climate-Sensitive Mixed-Effects Tree Recruitment Model for Oaks (Quercus spp.) in Hunan Province, South-Central China. For. Ecol. Manag. 2023, 528, 120631. [Google Scholar] [CrossRef]
- Wang, W.; Chen, X.; Zeng, W.; Wang, J.; Meng, J. Development of a Mixed-Effects Individual-Tree Basal Area Increment Model for Oaks (Quercus spp.) Considering Forest Structural Diversity. Forests 2019, 10, 474. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Lu, J.; Lei, X. Early Effects of Crop Tree Release Tending on Growth of Natural Secondary Quercus mongolica Forest. Sci. Silvae Sin. 2020, 56, 83–92. [Google Scholar]
- Feng, Q.; Chen, C.; Qin, L.; He, Y.; Wang, P.; Duan, Y.; Wang, Y.; He, Y. Effects of Different Management Models on Stand Structure and Plant Diversity of Natural Secondary Forests of Quercus Mongolica. Sci. Silvae Sin. 2018, 54, 12–21. [Google Scholar]
- Li, Y.; Ye, S.; Hui, G.; Hu, Y.; Zhao, Z. Spatial Structure of Timber Harvested According to Structure-Based Forest Management. For. Ecol. Manag. 2014, 322, 106–116. [Google Scholar] [CrossRef]
- Wang, D.; Li, J.; Tang, T. Determining the Optimal Density of Phoebe Bournei Plantations Based on Dynamic Programming under Close-to-Nature Management Measures. Sustainability 2022, 14, 847. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, P.; Shen, H. Competition Intensity Affects Growing Season Nutrient Dynamics in Korean Pine Trees and Their Microhabitat Soil in Mixed Forest. For. Ecol. Manag. 2023, 539, 121018. [Google Scholar] [CrossRef]
- Metz, J.; Seidel, D.; Schall, P.; Scheffer, D.; Schulze, E.-D.; Ammer, C. Crown Modeling by Terrestrial Laser Scanning as an Approach to Assess the Effect of Aboveground Intra- and Interspecific Competition on Tree Growth. For. Ecol. Manag. 2013, 310, 275–288. [Google Scholar] [CrossRef]
- T/CSF 009-2019; Technical Standards on the Close-to-Natural and Multi-Functional Managements of the Natural Oak Forests. Chinese Society of Forestry: Beijing, China, 2019.
- GB/T 38590-2020; Technicalre Gulations for Continuous Forest Inventory. National Forestry and Grassland Administration: Beijing, China, 2020.
- Zhang, W. Forest Site of China; China Science Publishing House: Beijing, China, 1997. [Google Scholar]
- Pearl, R.; Reed, L. On the Rate of Growth of the Population of the United States since 1790 and Its Mathematical Representation. Proc. Natl. Acad. Sci. USA 1920, 6, 275–288. [Google Scholar] [CrossRef] [PubMed]
- Ware, G.O.; Ohki, K.; Moon, L.C. The Mitscherlich Plant Growth Model for Determining Critical Nutrient Deficiency Levels 1. Agron. J. 1982, 74, 88–91. [Google Scholar] [CrossRef]
- Winsor, C.P. The Gompertz Curve as a Growth Curve. Proc. Natl. Acad. Sci. USA 1932, 18, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Schumacher, F. A New Growth Curve and Its Applicability to Timber Yield Studies. J. For. Res. 1939, 37, 819–820. [Google Scholar]
- Zhu, G.; Hu, S.; Chhin, S.; Zhang, X.; He, P. Modelling Site Index of Chinese Fir Plantations Using a Random Effects Model across Regional Site Types in Hunan Province, China. For. Ecol. Manag. 2019, 446, 143–150. [Google Scholar] [CrossRef]
- D’agostino Sr, R.B.; Russell, H.K. Scree Test. In Encyclopedia of Biostatistics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Pinheiro, J.C.; Bates, D.M.; Pinheiro, J.C. Approximations to the Log-Likelihood Function in the Nonlinear Mixed-Effects Model. J. Comput. Graph. Stat. 1995, 4, 12. [Google Scholar]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Ser. B (Methodol.) 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Hang, X. Forest Management, 4th ed.; China Forestry Publishing House: Beijing, China, 2011. [Google Scholar]
- Palahí, M.; Tomé, M.; Pukkala, T.; Trasobares, A.; Montero, G. Site Index Model for Pinus Sylvestris in North-East Spain. For. Ecol. Manag. 2004, 187, 35–47. [Google Scholar] [CrossRef]
- Bravo-Oviedo, A.; del Río, M.; Montero, G. Geographic Variation and Parameter Assessment in Generalized Algebraic Difference Site Index Modelling. For. Ecol. Manag. 2007, 247, 107–119. [Google Scholar] [CrossRef]
- LY/T 2118-2013; Guidelines for Large-Size Timber Cultivation. National Forestry and Grassland Administration: Beijing, China, 2013.
- Buongiorno, J.; Kolbe, A.; Vasievich, M. Economic and Ecological Effects of Diameter-Limit and BDq Management Regimes: Simulation Results for Northern Hardwoods. Silva Fenn. 2000, 34, 223–235. [Google Scholar] [CrossRef]
- Lu, H.; Buongiorno, J. Long- and Short-Term Effects of Alternative Cutting Regimes on Economic Returns and Ecological Diversity in Mixed-Species Forests. For. Ecol. Manag. 1993, 58, 173–192. [Google Scholar] [CrossRef]
- Duncker, P.S.; Barreiro, S.M.; Hengeveld, G.M.; Lind, T.; Mason, W.L.; Ambrozy, S.; Spiecker, H. Classification of Forest Management Approaches: A New Conceptual Framework and Its Applicability to European Forestry. Ecol. Soc. 2012, 17, art51. [Google Scholar] [CrossRef]
- da Silva, R.P.; dos Santos, J.; Tribuzy, E.S.; Chambers, J.Q.; Nakamura, S.; Higuchi, N. Diameter Increment and Growth Patterns for Individual Tree Growing in Central Amazon, Brazil. For. Ecol. Manag. 2002, 166, 295–301. [Google Scholar] [CrossRef]
- Sánchez-González, M.; Tomé, M.; Montero, G. Modelling Height and Diameter Growth of Dominant Cork Oak Trees in Spain. Ann. For. Sci. 2005, 62, 633–643. [Google Scholar] [CrossRef]
- Hein, S.; Dhôte, J.-F. Effect of Species Composition, Stand Density and Site Index on the Basal Area Increment of Oak Trees (Quercus sp.) in Mixed Stands with Beech (Fagus sylvatica L.) in Northern France. Ann. For. Sci. 2006, 63, 457–467. [Google Scholar] [CrossRef]
- Lhotka, J.M. Examining Growth Relationships in Quercus Stands: An Application of Individual-Tree Models Developed from Long-Term Thinning Experiments. For. Ecol. Manag. 2017, 385, 65–77. [Google Scholar] [CrossRef]
- Percel, G.; Parmain, G.; Laroche, F.; Bouget, C. The Larger, the Better? Effects of Delayed Diameter-Limit Cutting on Old-Growth Attributes and Saproxylic Beetle Diversity in Temperate Oak Forests. Eur. J. For. Res. 2018, 137, 237–249. [Google Scholar] [CrossRef]
- Nicolescu, V.-N.; Vor, T.; Mason, W.L.; Bastien, J.-C.; Brus, R.; Henin, J.-M.; Kupka, I.; Lavnyy, V.; La Porta, N.; Mohren, F.; et al. Ecology and Management of Northern Red Oak (Quercus rubra L. syn. Q. borealis F. Michx.) in Europe: A Review. For. Int. J. For. Res. 2020, 93, 481–494. [Google Scholar] [CrossRef]
- Ostrogović Sever, M.Z.; Alberti, G.; Delle Vedove, G.; Marjanović, H. Temporal Evolution of Carbon Stocks, Fluxes and Carbon Balance in Pedunculate Oak Chronosequence under Close-To-Nature Forest Management. Forests 2019, 10, 814. [Google Scholar] [CrossRef]
- Bölöni, J.; Ódor, P.; Ádám, R.; Keeton, W.S.; Aszalós, R. Quantity and Dynamics of Dead Wood in Managed and Unmanaged Dry-Mesic Oak Forests in the Hungarian Carpathians. For. Ecol. Manag. 2017, 399, 120–131. [Google Scholar] [CrossRef]
- Kurtz, W.B.; Garrett, H.E.; Williams, R.A. Young Stands of Scarlet Oak in Missouri Can Be Thinned Profitably. South. J. Appl. For. 1981, 5, 12–16. [Google Scholar] [CrossRef]
- Tkach, V.; Buksha, I.; Slych, O.; Pasternak, V. Optimization of Maturity Age for Coppice Oak Forests within Left-Bank Forest-Steppe in Ukraine. Cent. Eur. For. J. 2021, 67, 181–186. [Google Scholar] [CrossRef]
- Orwig, D.A.; Cogbill, C.V.; Foster, D.R.; O’Keefe, J.F. Variations in Old-Growth Structure and Definitions: Forest Dynamics on Wachusett Mountain, Massachusetts. Ecol. Appl. 2001, 11, 437–452. [Google Scholar] [CrossRef]
- Seydack, A.H.W. An Unconventional Approach to Timber Yield Regulation for Multi-Aged, Multispecies Forests. I. Fundamental Considerations. For. Ecol. Manag. 1995, 77, 139–153. [Google Scholar] [CrossRef]
- Zimmerman, B.L.; Kormos, C.F. Prospects for Sustainable Logging in Tropical Forests. BioScience 2012, 62, 479–487. [Google Scholar]
- Nicolescu, V.N.; Carvalho, J.; Hochbichler, E.; Bruckman, V.; Bruckman, V. Silvicultural Guidelines for European Coppice Forests; Albert Ludwig University Freiburg Printing Press: Freiburg, Germany, 2017. [Google Scholar]
- Laliberté, J.; Pothier, D.; Achim, A. Adjusting Harvest Rules for Red Oak in Selection Cuts of Canadian Northern Hardwood Forests. For. Int. J. For. Res. 2016, 89, 402–411. [Google Scholar] [CrossRef]



| Variables | Min | Max | Mean | STD |
|---|---|---|---|---|
| DBH (cm) | 10.6 | 63.5 | 29.9 | 10.3 |
| H (m) | 9.2 | 28.4 | 16.0 | 3.5 |
| Age (years) | 24 | 155 | 59 | 26 |
| Elevation (m) | 80 | 1638 | 806 | 546 |
| Slope (°) | 11 | 45 | 30 | 9 |
| Soil depth (cm) | 43 | 95 | 72 | 13 |
| Site Factors | Classification Criteria | |||||||
|---|---|---|---|---|---|---|---|---|
| EL | 7 classes by 200 m | |||||||
| SL | <5° | 5°–14° | 15°–24° | 25°–34° | 35°–44° | ≥45° | ||
| SP | Ridge | Upper slope | Middle slope | Lower slope | ||||
| AS | 23°–67° | 68°–112° | 113°–157° | 158°–202° | 203°–247° | 248°–292° | 293°–337° | 338°–22° |
| SD | <40 cm | 40–79 cm | ≥80 cm | |||||
| SOT | Yellow soil | Red soil | Yellow-brown soil | |||||
| Model | Equation Form | Equation Expression | Parameter | Source |
|---|---|---|---|---|
| M1 | Logistic | D = a/[1 + b × exp (−c × Age)] | a, b, c > 0 | [46] |
| M2 | Mitscherlich | D = a × [1 − exp (−b × Age)] | a, b > 0 | [47] |
| M3 | Compertz | D = a × exp [−b × exp (−c × Age)] | a, b, c > 0 | [48] |
| M4 | Schumacher | D = a × exp (−b/Age) | a, b > 0 | [49] |
| Factor | Sum of Squares | Degree of Freedom | Mean Square | F Value | p |
|---|---|---|---|---|---|
| EL | 549.8541 | 6 | 109.9708 | 6.0685 | 0.000020 |
| SL | 551.0830 | 4 | 137.7708 | 7.6026 | 0.000056 |
| SOT | 212.3262 | 2 | 212.3262 | 11.7168 | 0.000884 |
| AS | 282.6399 | 7 | 40.3771 | 2.2281 | 0.037548 |
| SP | 76.6321 | 3 | 25.5440 | 1.4096 | 0.244145 |
| SD | 3.9473 | 1 | 3.9473 | 0.2178 | 0.641672 |
| Model | Parameter Estimates | R2 | MAE | ||
|---|---|---|---|---|---|
| a | b | c | |||
| M1 | 87.7613 | 5.3615 | 0.0169 | 0.6489 | 6.4304 |
| M2 | 74.6164 | 0.0090 | 0.6451 | 6.5053 | |
| M3 | 120.2000 | 2.2550 | 0.0081 | 0.6512 | 6.3998 |
| M4 | 61.8500 | 38.5910 | 0.6599 | 6.2496 | |
| Model | RP | Parameter Estimates | AIC | Log-Likelihood | R2 | |
|---|---|---|---|---|---|---|
| a | b | |||||
| M4 | 61.8500 | 38.5910 | 835.1980 | −414.5990 | 0.6599 | |
| M4.1 | a | 62.5298 | 38.0017 | 768.0842 | −380.0421 | 0.9298 |
| M4.2 | b | 73.8649 | 49.2816 | 764.9466 | −378.4733 | 0.9380 |
| M4.3 | a,b | 65.2385 | 41.3734 | 761.8526 | −375.9263 | 0.9436 |
| Site Type Group | Sample Size | Number of Site Types |
|---|---|---|
| STG1 | 15 | 7 |
| STG2 | 48 | 13 |
| STG3 | 17 | 3 |
| STG4 | 49 | 18 |
| Model | Site Type Group | Parameters and Values | AIC | Log-Likelihood | R2 | |
|---|---|---|---|---|---|---|
| a | b | |||||
| M4.4 | STG1 | 78.9773 | 35.9271 | 693.6620 | −341.8310 | 0.9126 |
| STG2 | 72.6711 | 42.1384 | ||||
| STG3 | 76.5123 | 52.3228 | ||||
| STG4 | 56.8188 | 44.1287 | ||||
| Model | R2 | MAE |
|---|---|---|
| M4 | 0.6454 | 6.3650 |
| M4.1 | 0.8564 | 3.8535 |
| M4.2 | 0.8672 | 3.6992 |
| M4.3 | 0.8729 | 3.6332 |
| M4.4 | 0.9015 | 3.2927 |
| STG | TD (cm) | ||||
|---|---|---|---|---|---|
| 24 | 30 | 40 | 50 | 60 | |
| STG1 | 30 | 37 | 53 | 79 | 131 |
| STG2 | 38 | 48 | 71 | 113 | 220 |
| STG3 | 45 | 56 | 81 | 123 | 215 |
| STG4 | 51 | 69 | 126 | 345 | NA |
| Model | Site Type Group | Peak MAI (cm/year) | MTD (cm) | QMA (Year) |
|---|---|---|---|---|
| M4.4 | STG1 | 0.8087 | 29 | 36 |
| STG2 | 0.6344 | 27 | 42 | |
| STG3 | 0.5380 | 28 | 52 | |
| STG4 | 0.4737 | 21 | 44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, W.; Zhu, G. The Minimum Target Diameter and the Harvest Age of Oak Natural Secondary Forests in Different Sites Conditions: Case Study in Hunan Province, China. Forests 2024, 15, 120. https://doi.org/10.3390/f15010120
You W, Zhu G. The Minimum Target Diameter and the Harvest Age of Oak Natural Secondary Forests in Different Sites Conditions: Case Study in Hunan Province, China. Forests. 2024; 15(1):120. https://doi.org/10.3390/f15010120
Chicago/Turabian StyleYou, Wenbiao, and Guangyu Zhu. 2024. "The Minimum Target Diameter and the Harvest Age of Oak Natural Secondary Forests in Different Sites Conditions: Case Study in Hunan Province, China" Forests 15, no. 1: 120. https://doi.org/10.3390/f15010120
APA StyleYou, W., & Zhu, G. (2024). The Minimum Target Diameter and the Harvest Age of Oak Natural Secondary Forests in Different Sites Conditions: Case Study in Hunan Province, China. Forests, 15(1), 120. https://doi.org/10.3390/f15010120





