Simultaneous Models for the Estimation of Main Forest Parameters Based on Airborne LiDAR Data
Abstract
:1. Introduction
2. Data and Methods
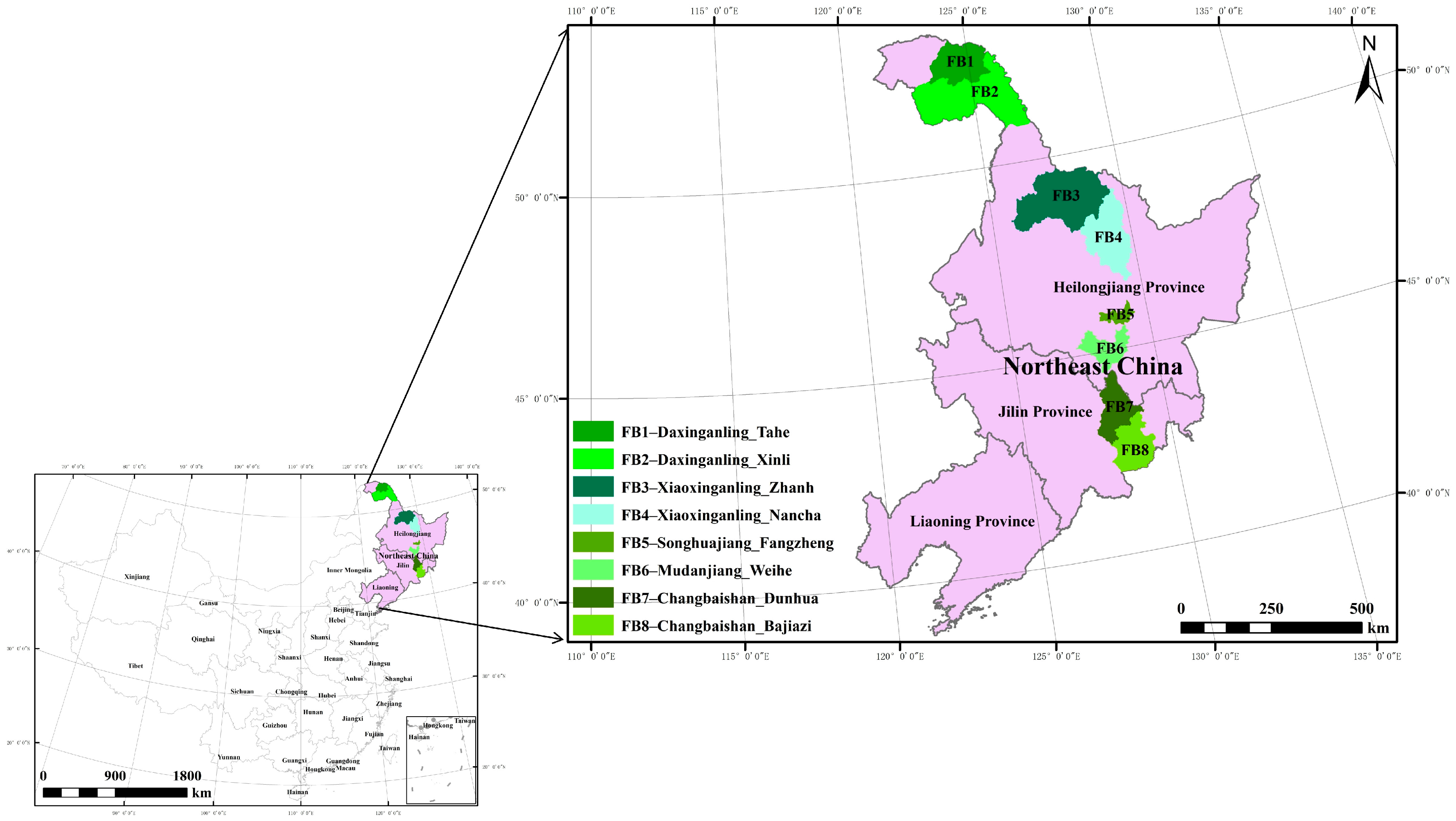
2.1. Study Area
2.2. Data Collection
2.2.1. Field Data
2.2.2. Aerial Data
2.2.3. Data Screening
2.3. Modeling Method
2.3.1. Independent Models
2.3.2. Simultaneous Models
2.3.3. Model Evaluation
3. Results and Analysis
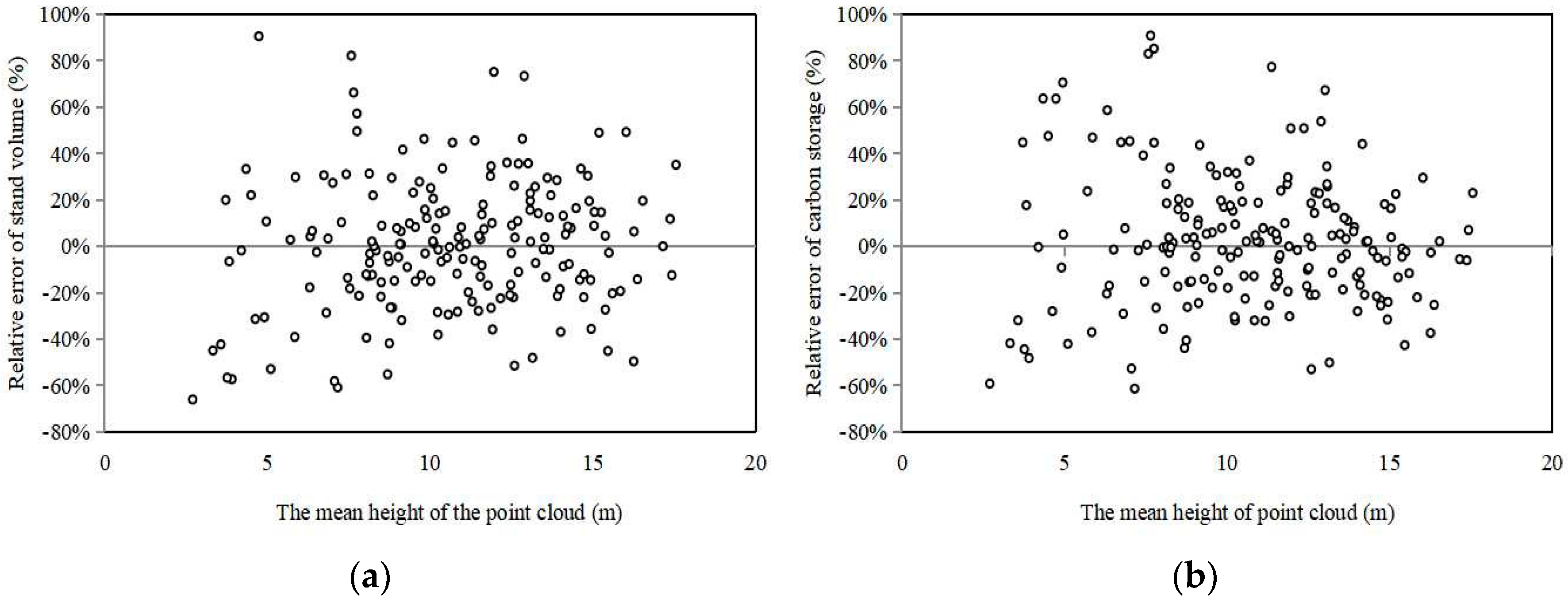
4. Discussion
5. Conclusions
- (1)
- It is technically feasible to estimate the main stand factors, such as the volume, biomass, carbon storage per hectare, mean diameter at breast height, average tree height, mean dominant tree height, number of trees, and basal area per hectare, using the error–in–variable simultaneous equations method based on airborne LiDAR and ground survey sample plot data.
- (2)
- The MPE values of the eight main forest stand factor prediction models for spruce–fir forests in Northeast China were all less than 5%, with the exception of that of the number of trees. The MPSE values reflecting the accuracy of the models for a single unit of population were below 25%, indicating that the accuracy of the established models can meet the requirements of the Technical regulations for inventory for forest management planning and design and can be promoted and applied in practice.
- (3)
- To increase the accuracy of the estimates of the main stand factors, especially the dominant height and tree number per hectare, it is necessary to improve the goodness–of–fit of each model in the simultaneous equations in future studies. One approach is to combine LiDAR data with other remote sensing data to enhance the potential of applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Awange, J.; Kiema, J. Environmental Geoinformatics: Extreme Hydro-Climatic and Food Security Challenges: Exploiting the Big Data; Springer: Cham, Switzerland, 2019; pp. 291–306. [Google Scholar]
- Bolton, D.; Tompalski, P.; Goops, N.; White, J.; Wulder, M.; Hermosilla, T.; Queinnec, M.; Luther, J.; van Lier, O.; Fournier, R.; et al. Optimizing Landsat time series length for regional mapping of LiDAR-derived forest structure. Remote Sens. Environ. 2020, 239, 111645. [Google Scholar] [CrossRef]
- Luther, J.E.; Fournier, R.A.; van Lier, O.R.; Bujold, M. Extending ALS-based mapping of forest attributes with medium resolution satellite and environmental data. Remote Sens. 2019, 11, 1092. [Google Scholar] [CrossRef]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Zald, H.S. Large-area mapping of Canadian boreal forest cover, height, biomass and other structural attributes using Landsat composites and LiDAR plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]
- Pang, Y.; Li, Z.Y.; Chen, B.W.; Liang, X.J. Status and development of space borne LiDAR application in forestry. Aerospace 2019, 36, 20–27. [Google Scholar]
- MacLean, G.A.; Krabill, W.B. Gross merchantable timber volume estimation using an airborne LiDAR System. Can. J. Remote Sens. 1986, 12, 7–18. [Google Scholar] [CrossRef]
- Næsset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
- Holmgren, J.; Nilsson, M.; Olsson, H. Estimation of tree height and stem volume on plots using airborne laser scanning. For. Sci. 2003, 49, 419–428. [Google Scholar] [CrossRef]
- Holmgren, J. Prediction of tree height, basal area and stem volume in forest stands using airborne laser scanning. Scand. J. Forest Res. 2004, 19, 543–553. [Google Scholar] [CrossRef]
- Hollaus, M.; Dorigo, W.; Wagner, W.; Schadauer, K.; Höfle, B.; Maier, B. Operational wide-area stem volume estimation based on airborne laser scanning and national forest inventory data. Int. J. Remote Sens. 2009, 30, 5159–5175. [Google Scholar] [CrossRef]
- Cartus, O.; Kellndorfer, J.; Rombach, M.; Walker, W. Mapping canopy height and growing stock volume using airborne LiDAR, ALOS PALSAR and Landsat ETM+. Remote Sens. 2012, 4, 3320–3345. [Google Scholar] [CrossRef]
- Saarela, S.; Holm, S.; Healey, S.P.; Andersen, H.-E.; Petersson, H.; Prentius, W.; Patterson, P.L.; Næsset, E.; Gregoire, T.G.; Ståhl, G. Generalized hierarchical model-based estimation for aboveground biomass assessment using GEDI and Landsat Data. Remote Sens. 2018, 10, 1832. [Google Scholar] [CrossRef]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Miranda, D. Estimation of stand variables in Pinus Radiata D. Don plantations using different LiDAR pulse densities. Forestry 2012, 85, 281–292. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J. Generalizing predictive models of forest inventory attributes using an area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Maselli, F.; Chiesi, M.; Montaghi, A.; Pranzini, E. Use of ETM+ images to extend stem volume estimates obtained from LiDAR data. ISPRS J. Photogramm. Rem. Sens. 2011, 66, 662–671. [Google Scholar] [CrossRef]
- Hyyppä, J.; Yu, X.; Hyyppä, H.; Vastaranta, M.; Holopainen, M.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Vaaja, M.; Koskinen, J.; et al. Advances in forest inventory using airborne laser scanning. Remote Sens. 2012, 4, 1190–1207. [Google Scholar] [CrossRef]
- Penner, M.; Pitt, D.G.; Woods, M.E. Parametric vs. nonparametric LiDAR models for operational forest inventory in boreal Ontario. Can. J. Remote Sens. 2013, 39, 426–443. [Google Scholar]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Zörner, J.; Dymond, J.R.; Shepherd, J.D.; Wiser, S.K.; Jolly, B. LiDAR-based regional inventory of tall trees-Wellington, New Zealand. Forests 2018, 9, 702. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Slavik, M. 3D point cloud fusion from UAV and TLS to assess temperate managed forest structures. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102917. [Google Scholar] [CrossRef]
- Terryn, L.; Calders, K.; Bartholomeus, H.M.; Bartolo, R.E.; Brede, B.; D’hont, B.; Disney, M.I.; Herold, M.; Lau, A.; Shenkin, A.; et al. Quantifying tropical forest structure through terrestrial and UAV laser scanning fusion in Australian rainforests. Remote Sens. Environ. 2022, 271, 112912. [Google Scholar] [CrossRef]
- Pang, Y.; Li, Z.Y. Inversion of biomass components of the temperate forest using airborne LiDAR Technology in Xiaoxing’an Mountains, Northeastern of China. Chin. J. Plant Ecol. 2012, 36, 1095–1105. [Google Scholar] [CrossRef]
- Cao, L.; Dai, J.S.; Xu, J.X.; Xu, Z.Q.; She, G.H. Optimized extraction of forest parameters in subtropical forests based on airborne small footprint LiDAR technology. J. Beijing For. Univ. 2014, 36, 13–21. [Google Scholar]
- Liu, Q.W.; Tan, B.X.; Hu, K.L.; Fan, X.; Li, Z.Y.; Pang, Y.; Li, S.M. The remote sensing experiment on airborne LiDAR and hyperspectral integrated system for subtropical forest estimation. High Technol. Lett. 2016, 3, 264–274. [Google Scholar]
- Yuan, Y.N.; Pegn, D.L.; Wang, W.; Zeng, W.S. Estimating standing stocks of the typical conifer stands in Northeast China based on airborne LiDAR data. Chin. J. App Ecol. 2021, 32, 836–844. [Google Scholar]
- Zhang, Z.N.; Wang, T.J.; Skidmore, A.K.; Cao, F.L.; She, G.H.; Cao, L. An improved area-based approach for estimating plot-level tree DBH from airborne LiDAR data. For. Ecosyst. 2023, 10, 100089. [Google Scholar] [CrossRef]
- Zeng, W.S.; Sun, X.N.; Wang, L.R.; Wang, W.; Pu, Y. Estimating forest volume, mean height and basal area based on airborne laser scanning data. Forest Ecol. Manag. 2020, 2, 79–86. [Google Scholar]
- Zeng, W.S.; Sun, X.N.; Wang, L.R.; Wang, W.; Pu, Y. Developing aerial stand volume tables based on laser scanning data for forest region of Northeast China. Forest Ecol. Manag. 2021, 1, 147–155. [Google Scholar]
- Zeng, W.S.; Sun, X.N.; Wang, L.R.; Wang, W.; Pu, Y. Development of forest stand volume models based on airborne laser scanning data. Sci. Silvae Sin. 2021, 57, 31–38. [Google Scholar]
- Zhao, P.; Gao, L.; Gao, T. Extracting forest parameters based on stand automatic segmentation algorithm. Sci. Rep. 2020, 10, 1571. [Google Scholar] [CrossRef]
- Li, C.G.; Li, Z. Generalizing predictive models of sub-tropical forest inventory attributes using an area-based approach with airborne LiDAR data. Sci. Silvae Sin. 2021, 57, 23–35. [Google Scholar]
- Zhou, X.B.; Li, C.G.; Dai, H.B.; Yu, Z.; Li, Z.; Su, K. Effects of point cloud density on the estimation accuracy of large-area subtropical forest inventory attributes using airborne LiDAR data. Sci. Silvae Sin. 2023, 59, 23–33. [Google Scholar]
- Dai, H.B.; Li, C.G.; Pang, Y.; Li, C.G. Method for sub-compartment investigation factors setting and information acquisition based on integrated aerial-space-ground forest inventory system. Forest Ecol. Manag. 2021, 1, 180–188. [Google Scholar]
- Zeng, W.S.; Sun, X.N.; Wang, L.R.; Wang, W.; Pu, Y. Developing stand volume, biomass and carbon stock models for ten major forest types in forest region of Northeastern China. J. Beijing For. Univ. 2021, 43, 1–8. [Google Scholar]
- Zeng, W.S.; Tang, S.Z. Bias correction in logarithmic regression and comparison with weighted regression for non-linear models. Sci. Silvae Sin. 2011, 47, 106–113. [Google Scholar]
- LY/T 1353-1999; State Forestry Administration. Tree Volume Table. China Standards Press: Beijing, China, 1999.
- LY/T 2655-2016; State Forestry Administration. Tree Biomass Models and Related Parameters to Carbon Accounting for Abies. China Standards Press: Beijing, China, 2017.
- LY/T 2656-2016; State Forestry Administration. Tree Biomass Models and Related Parameters to Carbon Accounting for Picea. China Standards Press: Beijing, China, 2017.
- Bottalico, F.; Chirici, G.; Giannini, R.; Mele, S.; Mura, M.; Puxeddu, M.; McRoberts, R.E.; Valbuena, R.; Travaglini, D. Modeling Mediterranean forest structure using airborne laser scanning data. Int. J. Appl. Earth Obs. 2017, 57, 145–153. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Buckmaster, G. Validating estimates of merchantable volume from airborne laser scanning (ALS) data using weight scale data forestry chronicle. For. Chron. 2014, 90, 378–385. [Google Scholar] [CrossRef]
- Tompalski, P.; Coops, N.C.; Marshall, P.L.; White, J.C.; Wulder, M.A.; Bailey, T. Combining multi-date airborne laser scanning and digital aerial photogrammetric data for forest growth and yield modelling. Remote Sens. 2018, 10, 347. [Google Scholar] [CrossRef]
- García, M.; Riaño, D.; Chuvieco, E.; Danson, F.M. Estimating biomass carbon stocks for a Mediterranean forest in Central Spain using LiDAR height and intensity data. Remote Sens. Environ. 2010, 114, 816–830. [Google Scholar] [CrossRef]
- Gallagher-Duval, X.; van Lier, O.R.; Fournier, R.A. Estimating Stem Diameter Distributions with Airborne Laser Scanning Metrics and Derived Canopy Surface Texture Metrics. Forests 2023, 14, 287. [Google Scholar] [CrossRef]
- GB/T 26424-2010; State Administration for Market Regulation, National Standardization Administration. Technical Regulations for Inventory for Forest Management Planning and Design. China Standards Press: Beijing, China, 2011.
| Forest Stand Factors | Mean | Min | Max | Standard Deviation (SD) | Coefficient of Variation (CV)/% |
|---|---|---|---|---|---|
| Mean diameter at breast height D (cm) | 16.8 | 7.6 | 30.6 | 4.8 | 28.3 |
| Mean tree height H (m) | 14.13 | 4.59 | 24.85 | 3.93 | 27.8 |
| Mean dominant tree height Hd (m) | 18.71 | 5.15 | 28.23 | 4.10 | 21.9 |
| Number of trees per hectare N (ha−1) | 1097 | 400 | 3133 | 461 | 42.0 |
| Basal area per hectare G (m2/ha) | 23.02 | 1.93 | 45.22 | 9.16 | 39.8 |
| Volume per hectare V (m3/ha) | 185.8 | 5.3 | 491.8 | 100.7 | 54.2 |
| Biomass per hectare B (t/ha) | 140.1 | 6.7 | 326.2 | 67.1 | 47.9 |
| Carbon storage per hectare C (t/ha) | 68.5 | 3.3 | 156.3 | 32.7 | 47.7 |
| Type | Factors | Parameter Estimates | Evaluation Indices | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a0~g0 | a1~f1 | a2~c2 | R2 | SEE | TRE/% | ASE/% | MPE/% | MPSE/% | ||
| Independent model | H | 8.17 | 0.6618 | −0.3226 | 0.696 | 2.19 | 0.07 | 0.33 | 2.21 | 12.55 |
| G | 10.50 | 1.0234 | −0.5259 | 0.699 | 5.07 | −0.03 | −0.21 | 3.15 | 18.86 | |
| V | 65.38 | 1.5221 | −0.8354 | 0.743 | 51.49 | −0.11 | −0.25 | 3.97 | 21.68 | |
| B | 9.330 | 0.7050 | / | 0.888 | 22.63 | −0.15 | 0.86 | 2.31 | 10.99 | |
| C | 0.4886 | / | / | 0.899 | 10.40 | −0.09 | 0.91 | 2.17 | 10.54 | |
| D | 1.780 | 0.8491 | / | 0.695 | 2.64 | 0.07 | 0.34 | 2.25 | 12.03 | |
| Hd | 7.34 | 0.8048 | / | 0.596 | 2.62 | 0.00 | −0.17 | 2.00 | 12.39 | |
| N | / | / | / | 0.115 | 442 | 2.83 | 5.90 | 5.77 | 31.24 | |
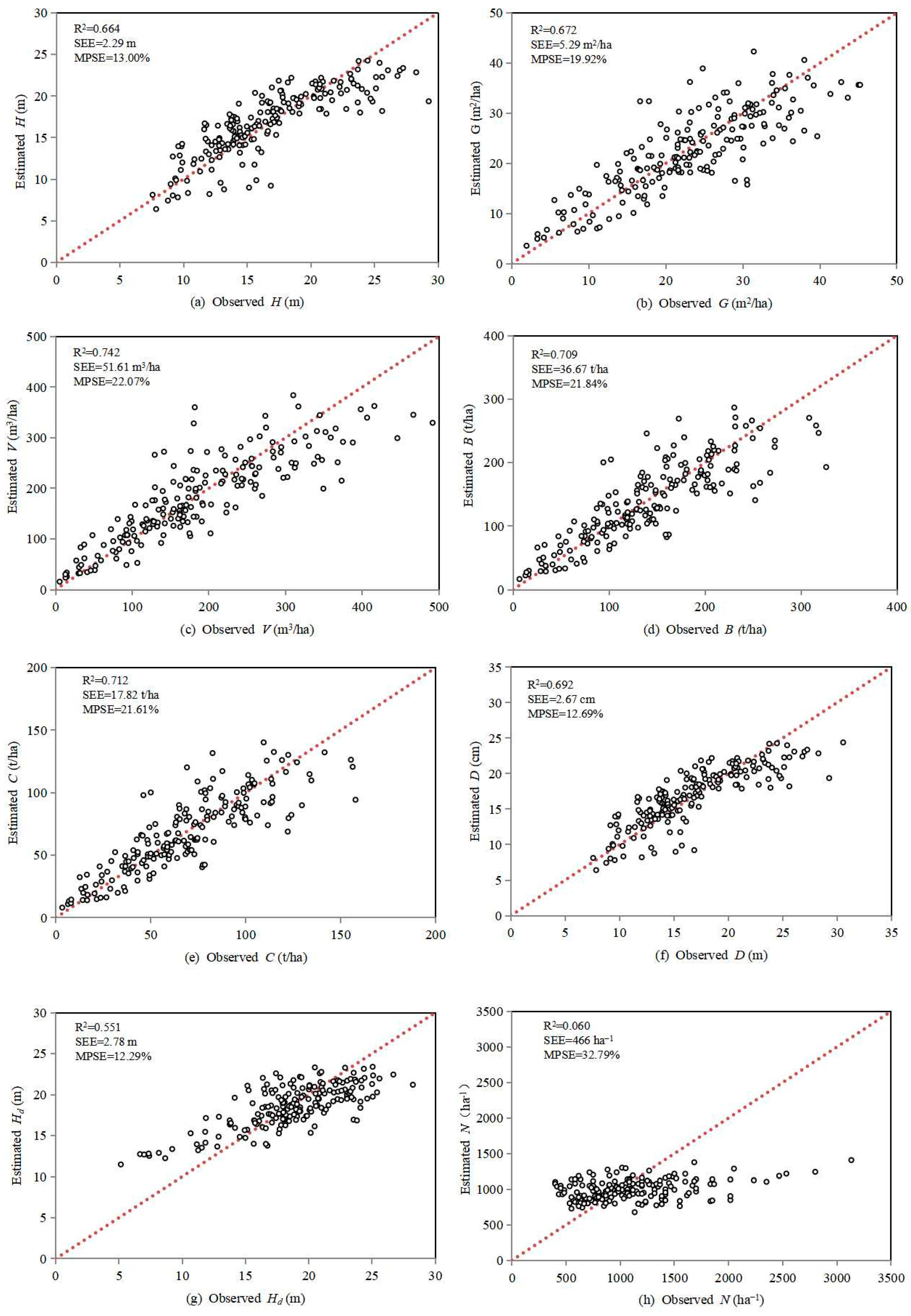
| Simultaneous model | H | 3.46 | 0.6052 | / | 0.664 | 2.29 | −1.37 | −1.97 | 2.32 | 13.00 |
| G | 31.85 | 1.0331 | −0.8960 | 0.672 | 5.29 | 1.84 | 2.93 | 3.29 | 19.92 | |
| V | 71.47 | 1.4719 | −0.8316 | 0.742 | 51.61 | 2.21 | 1.27 | 3.98 | 22.07 | |
| B | 5.085 | 0.7334 | / | 0.709 | 36.67 | 1.24 | 2.67 | 3.75 | 21.84 | |
| C | 0.4890 | / | / | 0.712 | 17.82 | 1.22 | 2.65 | 3.72 | 21.61 | |
| D | 0.7256 | 1.1810 | / | 0.692 | 2.67 | −0.67 | −0.07 | 2.28 | 12.69 | |
| Hd | 5.80 | 0.8968 | / | 0.551 | 2.78 | 0.35 | −0.22 | 2.12 | 12.29 | |
| N | / | / | / | 0.060 | 456 | 10.42 | 10.59 | 5.94 | 32.79 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, W.; Zeng, W.; Sun, X. Simultaneous Models for the Estimation of Main Forest Parameters Based on Airborne LiDAR Data. Forests 2024, 15, 775. https://doi.org/10.3390/f15050775
Zou W, Zeng W, Sun X. Simultaneous Models for the Estimation of Main Forest Parameters Based on Airborne LiDAR Data. Forests. 2024; 15(5):775. https://doi.org/10.3390/f15050775
Chicago/Turabian StyleZou, Wentao, Weisheng Zeng, and Xiangnan Sun. 2024. "Simultaneous Models for the Estimation of Main Forest Parameters Based on Airborne LiDAR Data" Forests 15, no. 5: 775. https://doi.org/10.3390/f15050775
APA StyleZou, W., Zeng, W., & Sun, X. (2024). Simultaneous Models for the Estimation of Main Forest Parameters Based on Airborne LiDAR Data. Forests, 15(5), 775. https://doi.org/10.3390/f15050775






