Changes in the Timing of Autumn Leaf Senescence of Maple and Ginkgo Trees in South Korea over the Past 30 Years: A Comparative Assessment of Process-Based, Linear Regression, and Machine-Learning Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Model Description
2.2.1. Process-Based Model
2.2.2. Linear Regression
2.2.3. Machine-Learning Approach
2.3. Model Development
2.4. Model Evaluation
2.5. Statistical Analysis
3. Results
3.1. Changes in Leaf Senescence Timing
3.2. Model Comparison for Multi-Site Approach
3.3. Model Comparison for Site-Specific Approach
3.4. Importance Analysis
4. Discussion
4.1. Environmental Factors Driving Autumn Leaf Senescence
4.2. Model Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Site ID | Site Name | Latitude [°N] | Longitude [°E] | Elevation [m] | AMT [°C] | Species | LSTA | LSTG |
|---|---|---|---|---|---|---|---|---|
| 90 | Sokcho | 38.2509 | 128.5647 | 17.53 | 14.66 | A, G | ||
| 95 | Cheorwon | 38.1479 | 127.3042 | 155.48 | 11.63 | A, G | ||
| 101 | Chuncheon | 37.9026 | 127.7357 | 75.82 | 12.59 | A, Gr | ||
| 108 | Seoul | 37.5714 | 126.9658 | 85.67 | 14.72 | A, G | 6 | 8 |
| 106 | Donghae | 37.5071 | 129.1243 | 40.46 | 14.72 | A, G | ||
| 202 | Yangpyeong | 37.4886 | 127.4945 | 47.26 | 12.88 | G | ||
| 115 | Ulleungdo | 37.4813 | 130.8986 | 221.14 | 15.15 | A, G | 8 | 7 |
| 112 | Incheon | 37.4777 | 126.6249 | 68.99 | 14.91 | A, G | 6 | 5 |
| 114 | Wonju | 37.3375 | 127.9466 | 150.11 | 13.09 | A, G | ||
| 203 | Icheon | 37.2640 | 127.4842 | 80.09 | 12.87 | G | ||
| 119 | Suwon | 37.2575 | 126.9830 | 39.81 | 14.35 | A, G | 5 | 6 |
| 121 | Yeongwol | 37.1813 | 128.4574 | 240.54 | 12.38 | A | ||
| 216 | Taebaek | 37.1704 | 128.9893 | 714.45 | 10.25 | G | ||
| 221 | Jecheon | 37.1593 | 128.1943 | 264.62 | 11.46 | G | ||
| 130 | Uljin | 36.9918 | 129.4128 | 48.98 | 14.84 | A, G | ||
| 127 | Chungju | 36.9705 | 127.9525 | 114.85 | 12.87 | A, G | ||
| 272 | Yeongju | 36.8718 | 128.5169 | 211.32 | 12.70 | A | ||
| 129 | Seosan | 36.7766 | 126.4939 | 25.25 | 14.03 | A, G | ||
| 232 | Cheonan | 36.7622 | 127.2928 | 84.78 | 13.38 | A, G | ||
| 131 | Cheongju | 36.6392 | 127.4407 | 58.7 | 14.43 | A, G | 4 | 5 |
| 136 | Andong | 36.5729 | 128.7073 | 141.26 | 13.32 | A, G | 5 | 4 |
| 277 | Yeongdeok | 36.5334 | 129.4093 | 40.71 | 14.79 | A, G | ||
| 226 | Boeun | 36.4876 | 127.7342 | 171.31 | 12.26 | A, G | ||
| 133 | Daejeon | 36.3720 | 127.3721 | 67.79 | 14.51 | A, G | 8 | 8 |
| 235 | Boryeong | 36.3272 | 126.5574 | 9.98 | 14.95 | A, G | ||
| 135 | Chupungnyeong | 36.2203 | 127.9946 | 244.98 | 13.02 | A, G | ||
| 279 | Gumi | 36.1306 | 128.3206 | 49.17 | 13.99 | A, G | ||
| 138 | Pohang | 36.0320 | 129.3800 | 3.94 | 16.50 | A, G | 6 | 5 |
| 140 | Gunsan | 36.0053 | 126.7614 | 27.85 | 15.18 | A, G | ||
| 143 | Daegu | 35.8780 | 128.6530 | 54.27 | 15.80 | A, G | 6 | 5 |
| 146 | Jeonju | 35.8409 | 127.1172 | 60.44 | 15.31 | A, G | 5 | 5 |
| 284 | Geochang | 35.6674 | 127.9099 | 228.45 | 12.89 | A, G | ||
| 152 | Ulsan | 35.5824 | 129.3347 | 81.14 | 16.18 | A, G | 5 | 5 |
| 285 | Hapcheon | 35.5651 | 128.1699 | 26.72 | 14.38 | A, G | ||
| 245 | Jeongeup | 35.5634 | 126.8390 | 68.7 | 15.02 | A, G | ||
| 247 | Namwon | 35.4213 | 127.3965 | 133.49 | 13.76 | A, G | ||
| 156 | Gwangju | 35.1729 | 126.8916 | 70.28 | 15.92 | A, G | 6 | 6 |
| 155 | Changwon | 35.1702 | 128.5728 | 34.97 | 16.98 | A, G | 6 | 7 |
| 192 | Jinju | 35.1638 | 128.0400 | 29.35 | 14.83 | A, G | ||
| 159 | Busan | 35.1047 | 129.0320 | 69.56 | 17.46 | A, G | 8 | 7 |
| 256 | Juam | 35.0750 | 127.2391 | 74.63 | 14.04 | A, G | ||
| 162 | Tongyeong | 34.8454 | 128.4356 | 31.24 | 17.10 | A, G | ||
| 165 | Mokpo | 34.8173 | 126.3815 | 44.7 | 16.44 | A, G | 6 | 7 |
| 168 | Yeosu | 34.7393 | 127.7406 | 65.93 | 17.15 | A, G | 7 | 7 |
| 261 | Haenam | 34.5538 | 126.5691 | 16.36 | 15.40 | A, G | ||
| 170 | Wando | 34.3959 | 126.7018 | 35.37 | 16.73 | A, G | ||
| 184 | Jeju | 33.5141 | 126.5297 | 20.79 | 18.38 | G | ||
| 189 | Seogwipo | 33.2462 | 126.5653 | 51.86 | 19.41 | A, G |
References
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Menzel, A.; Sparks, T.H.; Estrella, N.; Koch, E.; Aasa, A.; Ahas, R.; Alm-Kübler, K.; Bissolli, P.; Braslavská, O.; Briede, A.; et al. European phenological response to climate change matches the warming pattern. Glob. Change Biol. 2006, 12, 1969–1976. [Google Scholar] [CrossRef]
- Jeong, S.-J.; Ho, C.-H.; Gim, H.-J.; Brown, M.E. Phenology shifts at start vs. end of growing season in temperate vegetation over the Northern Hemisphere for the period 1982–2008. Glob. Change Biol. 2011, 17, 2385–2399. [Google Scholar] [CrossRef]
- Gill, A.L.; Gallinat, A.S.; Sanders-DeMott, R.; Rigden, A.J.; Short Gianotti, D.J.; Mantooth, J.A.; Templer, P.H. Changes in autumn senescence in northern hemisphere deciduous trees: A meta-analysis of autumn phenology studies. Ann. Bot. 2015, 116, 875–888. [Google Scholar] [CrossRef] [PubMed]
- Vitasse, Y.; Signarbieux, C.; Fu, Y.H. Global warming leads to more uniform spring phenology across elevations. Proc. Natl. Acad. Sci. USA 2018, 115, 1004–1008. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.; Jiang, N.; Peng, D.; Rao, Y.; Huang, Y.; Fu, Y.H.; Yang, W.; Zhu, X.; Cao, R.; Chen, X.; et al. Can changes in autumn phenology facilitate earlier green-up date of northern vegetation? Agric. For. Meteorol. 2020, 291, 108077. [Google Scholar] [CrossRef]
- Piao, S.L.; Friedlingstein, P.; Ciais, P.; Viovy, N.; Demarty, J. Growing season extension and its impact on terrestrial carbon cycle in the Northern Hemisphere over the past 2 decades. Glob. Biogeochem. Cycles 2007, 21. [Google Scholar] [CrossRef]
- Piao, S.; Liu, Q.; Chen, A.; Janssens, I.A.; Fu, Y.; Dai, J.; Liu, L.; Lian, X.; Shen, M.; Zhu, X. Plant phenology and global climate change: Current progresses and challenges. Glob. Change Biol. 2019, 25, 1922–1940. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; McGregor, I.R.; Gray, J.M.; Friedl, M.A.; Moon, M. Observations of Satellite Land Surface Phenology Indicate That Maximum Leaf Greenness Is More Associated With Global Vegetation Productivity Than Growing Season Length. Glob. Biogeochem. Cycles 2023, 37, e2022GB007462. [Google Scholar] [CrossRef]
- Peñuelas, J.; Rutishauser, T.; Filella, I. Phenology Feedbacks on Climate Change. Science 2009, 324, 887–888. [Google Scholar] [CrossRef]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Cook, B.I.; Wolkovich, E.M.; Parmesan, C. Divergent responses to spring and winter warming drive community level flowering trends. Proc. Natl. Acad. Sci. USA 2012, 109, 9000–9005. [Google Scholar] [CrossRef] [PubMed]
- Klosterman, S.; Hufkens, K.; Richardson, A.D. Later springs green-up faster: The relation between onset and completion of green-up in deciduous forests of North America. Int. J. Biometeorol. 2018, 62, 1645–1655. [Google Scholar] [CrossRef] [PubMed]
- Meng, L.; Zhou, Y.Y.; Li, X.; Asrar, G.R.; Mao, J.F.; Wanamaker, A.D.; Wang, Y.Q. Divergent responses of spring phenology to daytime and nighttime warming. Agric. For. Meteorol. 2020, 281, 107832. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, Z.; Guo, L.; He, H.S.; Ling, Y.; Wang, L.; Zong, S.; Na, R.; Du, H.; Li, M.H. Effects of winter chilling vs. spring forcing on the spring phenology of trees in a cold region and a warmer reference region. Sci. Total Environ. 2020, 725, 138323. [Google Scholar] [CrossRef] [PubMed]
- Moon, M.; Seyednasrollah, B.; Richardson, A.D.; Friedl, M.A. Using time series of MODIS land surface phenology to model temperature and photoperiod controls on spring greenup in North American deciduous forests. Remote Sens. Environ. 2021, 260, 112466. [Google Scholar] [CrossRef]
- Zeng, Z.Q.; Wu, W.X.; Ge, Q.S.; Li, Z.L.; Wang, X.Y.; Zhou, Y.; Zhang, Z.T.; Li, Y.M.; Huang, H.; Liu, G.X.; et al. Legacy effects of spring phenology on vegetation growth under preseason meteorological drought in the Northern Hemisphere. Agric. For. Meteorol. 2021, 310, 108630. [Google Scholar] [CrossRef]
- Zhao, H.; Fu, Y.H.; Wang, X.; Zhang, Y.; Liu, Y.; Janssens, I.A. Diverging models introduce large uncertainty in future climate warming impact on spring phenology of temperate deciduous trees. Sci. Total Environ. 2021, 757, 143903. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Kim, T.K.; Yoon, S.; Jang, K.; Chun, J.-H.; Won, M.; Lim, J.-H.; Kim, H.S. Quantifying the importance of day length in process-based models for the prediction of temperate spring flowering phenology. Sci. Total Environ. 2022, 843, 156780. [Google Scholar] [CrossRef]
- Huang, Z.; Zhou, L.; Chi, Y. Spring phenology rather than climate dominates the trends in peak of growing season in the Northern Hemisphere. Glob. Change Biol. 2023, 29, 4543–4555. [Google Scholar] [CrossRef]
- Meier, U.; Bleiholder, H.; Buhr, L.; Feller, C.; Hacks, H.; Hess, M.; Lancashire, P.; Schnock, U.; Stauss, R.; Boom, T.v.d.; et al. The BBCH system to coding the phenological growth stages of plants-history and publications. J. Kult. 2009, 61, 41–52. [Google Scholar]
- Mayer, A. Phenology and Citizen Science: Volunteers have documented seasonal events for more than a century, and scientific studies are benefiting from the data. Bioscience 2010, 60, 172–175. [Google Scholar] [CrossRef]
- Garonna, I.; de Jong, R.; de Wit, A.J.; Mucher, C.A.; Schmid, B.; Schaepman, M.E. Strong contribution of autumn phenology to changes in satellite-derived growing season length estimates across Europe (1982–2011). Glob. Change Biol. 2014, 20, 3457–3470. [Google Scholar] [CrossRef]
- Wu, C.Y.; Chen, J.M.; Black, T.A.; Price, D.T.; Kurz, W.A.; Desai, A.R.; Gonsamo, A.; Jassal, R.S.; Gough, C.M.; Bohrer, G.; et al. Interannual variability of net ecosystem productivity in forests is explained by carbon flux phenology in autumn. Glob. Ecol. Biogeogr. 2013, 22, 994–1006. [Google Scholar] [CrossRef]
- Norby, R.J.; Hartz-Rubin, J.S.; Verbrugge, M.J. Phenological responses in maple to experimental atmospheric warming and CO2 enrichment. Glob. Change Biol. 2003, 9, 1792–1801. [Google Scholar] [CrossRef]
- Xie, Y.Y.; Wang, X.J.; Wilson, A.M.; Silander, J. Predicting autumn phenology: How deciduous tree species respond to weather stressors. Agric. For. Meteorol. 2018, 250, 127–137. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Sanchez-Castillo, M.; Dash, J.; Atkinson, P.M.; Ojeda-Zujar, J. Modelling interannual variation in the spring and autumn land surface phenology of the European forest. Biogeosciences 2016, 13, 3305–3317. [Google Scholar] [CrossRef]
- Wu, C.; Wang, X.; Wang, H.; Ciais, P.; Peñuelas, J.; Myneni, R.B.; Desai, A.R.; Gough, C.M.; Gonsamo, A.; Black, A.T.; et al. Contrasting responses of autumn-leaf senescence to daytime and night-time warming. Nat. Clim. Change 2018, 8, 1092–1096. [Google Scholar] [CrossRef]
- Zhu, G.; Wang, X.; Xiao, J.; Zhang, K.; Wang, Y.; He, H.; Li, W.; Chen, H. Daytime and nighttime warming has no opposite effects on vegetation phenology and productivity in the northern hemisphere. Sci Total Environ 2022, 822, 153386. [Google Scholar] [CrossRef] [PubMed]
- Kloos, S.; Klosterhalfen, A.; Knohl, A.; Menzel, A. Decoding autumn phenology: Unraveling the link between observation methods and detected environmental cues. Glob. Change Biol. 2024, 30, e17231. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.-J.; Medvigy, D. Macroscale prediction of autumn leaf coloration throughout the continental United States. Glob. Ecol. Biogeogr. 2014, 23, 1245–1254. [Google Scholar] [CrossRef]
- Lang, W.; Chen, X.; Qian, S.; Schwartz, M.D. Temperature variations impacting leaf senescence initiation pathways alter leaf fall timing patterns in northern deciduous forests. Sci. Total Environ. 2024, 934, 173280. [Google Scholar] [CrossRef]
- Lang, W.G.; Chen, X.Q.; Qian, S.W.; Liu, G.H.; Piao, S.L. A new process-based model for predicting autumn phenology: How is leaf senescence controlled by photoperiod and temperature coupling? Agric. For. Meteorol. 2019, 268, 124–135. [Google Scholar] [CrossRef]
- Liu, G.H.; Chen, X.Q.; Fu, Y.S.; Delpierre, N. Modelling leaf coloration dates over temperate China by considering effects of leafy season climate. Ecol. Model. 2019, 394, 34–43. [Google Scholar] [CrossRef]
- Luedeling, E.; Schiffers, K.; Fohrmann, T.; Urbach, C. PhenoFlex- an integrated model to predict spring phenology in temperate fruit trees. Agric. For. Meteorol. 2021, 307, 108491. [Google Scholar] [CrossRef]
- Lee, S.; Jeong, S.; Park, C.E.; Kim, J. A Simple Method of Predicting Autumn Leaf Coloring Date Using Machine Learning with Spring Leaf Unfolding Date. Asia-Pac. J. Atmos. Sci. 2022, 58, 219–226. [Google Scholar] [CrossRef]
- Gao, C.; Wang, H.; Ge, Q. Interpretable machine learning algorithms to predict leaf senescence date of deciduous trees. Agric. For. Meteorol. 2023, 340, 109623. [Google Scholar] [CrossRef]
- Basler, D. Evaluating phenological models for the prediction of leaf-out dates in six temperate tree species across central Europe. Agric. For. Meteorol. 2016, 217, 10–21. [Google Scholar] [CrossRef]
- Thessen, A.E. Adoption of Machine Learning Techniques in Ecology and Earth Science. One Ecosyst. 2016, 1, e8621. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Li, X.; Zhou, X.; Geng, X.; Guo, Y.; Zhang, Y. Progress in plant phenology modeling under global climate change. Sci. China Earth Sci. 2020, 63, 1237–1247. [Google Scholar] [CrossRef]
- Bogawski, P.; Grewling, L.; Jackowiak, B. Predicting the onset of Betula pendula flowering in Poznan (Poland) using remote sensing thermal data. Sci. Total Environ. 2019, 658, 1485–1499. [Google Scholar] [CrossRef]
- Dai, W.; Jin, H.; Zhang, Y.; Liu, T.; Zhou, Z. Detecting temporal changes in the temperature sensitivity of spring phenology with global warming: Application of machine learning in phenological model. Agric. For. Meteorol. 2019, 279, 107702. [Google Scholar] [CrossRef]
- Korea Meteorological Administration. Guidelines for Phenological and Seasonal Phenomena Observations. 2016. Available online: https://data.kma.go.kr/data/publication/publicationGlList.do?pgmNo=681 (accessed on 28 December 2024).
- Keskitalo, J.; Bergquist, G.; Gardestrom, P.; Jansson, S. A Cellular Timetable of Autumn Senescence. Plant Physiol. 2005, 139, 1635–1648. [Google Scholar] [CrossRef]
- Hanninen, H.; Tanino, K. Tree seasonality in a warming climate. Trends Plant Sci. 2011, 16, 412–416. [Google Scholar] [CrossRef] [PubMed]
- Way, D.A.; Montgomery, R.A. Photoperiod constraints on tree phenology, performance and migration in a warming world. Plant Cell Environ. 2015, 38, 1725–1736. [Google Scholar] [CrossRef]
- Peano, D.; Hemming, D.; Materia, S.; Delire, C.; Fan, Y.; Joetzjer, E.; Lee, H.; Nabel, J.E.M.S.; Park, T.; Peylin, P.; et al. Plant phenology evaluation of CRESCENDO land surface models– Part 1: Start and end of the growing season. Biogeosciences 2021, 18, 2405–2428. [Google Scholar] [CrossRef]
- Moon, M.; Richardson, A.D.; O’Keefe, J.; Friedl, M.A. Senescence in temperate broadleaf trees exhibits species-specific dependence on photoperiod versus thermal forcing. Agric. For. Meteorol. 2022, 322, 109026. [Google Scholar] [CrossRef]
- Peng, J.; Wu, C.; Zhang, X.; Wang, X.; Gonsamo, A. Satellite detection of cumulative and lagged effects of drought on autumn leaf senescence over the Northern Hemisphere. Glob. Change Biol. 2019, 25, 2174–2188. [Google Scholar] [CrossRef]
- Fu, Y.H.; Piao, S.; Delpierre, N.; Hao, F.; Hänninen, H.; Geng, X.; Peñuelas, J.; Zhang, X.; Janssens, I.A.; Campioli, M. Nutrient availability alters the correlation between spring leaf-out and autumn leaf senescence dates. Tree Physiol. 2019, 39, 1277–1284. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Fu, Y.H.; Zeng, Z.; Huang, M.; Li, X.; Piao, S. Temperature, precipitation, and insolation effects on autumn vegetation phenology in temperate China. Glob. Change Biol. 2016, 22, 644–655. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Keenan, T.F. No evidence for a negative effect of growing season photosynthesis on leaf senescence timing. Glob. Change Biol. 2022, 28, 3083–3093. [Google Scholar] [CrossRef]
- Keenan, T.F.; Richardson, A.D. The timing of autumn senescence is affected by the timing of spring phenology: Implications for predictive models. Glob. Change Biol. 2015, 21, 2634–2641. [Google Scholar] [CrossRef] [PubMed]
- Zani, D.; Crowther, T.W.; Mo, L.; Renner, S.S.; Zohner, C.M. Increased growing-season productivity drives earlier autumn leaf senescence in temperate trees. Science 2020, 370, 1066–1071. [Google Scholar] [CrossRef]
- Forsythe, W.C.; Rykiel, E.J., Jr.; Stahl, R.S.; Wu, H.-I.; Schoolfield, R.M.J.E.M. A model comparison for daylength as a function of latitude and day of year. Ecol. Model. 1995, 80, 87–95. [Google Scholar] [CrossRef]
- Dufrêne, E.; Davi, H.; François, C.; Maire, G.l.; Dantec, V.L.; Granier, A. Modelling carbon and water cycles in a beech forest: Part I: Model description and uncertainty analysis on modelled NEE. Ecol. Model. 2005, 185, 407–436. [Google Scholar] [CrossRef]
- Park, C.-K.; Ho, C.-H.; Jeong, S.-J.; Lee, E.J.; Kim, J.J.P.o. Spatial and temporal changes in leaf coloring date of Acer palmatum and Ginkgo biloba in response to temperature increases in South Korea. PLoS ONE 2017, 12, e0174390. [Google Scholar] [CrossRef] [PubMed]
- Mason, C.H.; Perreault, W.D. Collinearity, Power, and Interpretation of Multiple Regression Analysis. J. Mark. Res. 1991, 28, 268–280. [Google Scholar] [CrossRef]
- Chan, J.Y.-L.; Leow, S.M.H.; Bea, K.T.; Cheng, W.K.; Phoong, S.W.; Hong, Z.-W.; Chen, Y.-L. Mitigating the Multicollinearity Problem and Its Machine Learning Approach: A Review. Mathematics 2022, 10, 1283. [Google Scholar] [CrossRef]
- Chowdhury, S.; Lin, Y.; Liaw, B.; Kerby, L. Evaluation of tree based regression over multiple linear regression for non-normally distributed data in battery performance. In Proceedings of the 2022 International Conference on Intelligent Data Science Technologies and Applications (IDSTA), San Antonio, TX, USA, 5–7 September 2022; pp. 17–25. [Google Scholar]
- Ge, Q.; Wang, H.; Rutishauser, T.; Dai, J. Phenological response to climate change in China: A meta-analysis. Glob. Change Biol. 2015, 21, 265–274. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Fu, Y.H.; Zhu, Z.; Liu, Y.; Liu, Z.; Huang, M.; Janssens, I.A.; Piao, S. Delayed autumn phenology in the Northern Hemisphere is related to change in both climate and spring phenology. Glob. Change Biol. 2016, 22, 3702–3711. [Google Scholar] [CrossRef] [PubMed]
- Laube, J.; Sparks, T.H.; Estrella, N.; Hofler, J.; Ankerst, D.P.; Menzel, A. Chilling outweighs photoperiod in preventing precocious spring development. Glob. Change Biol. 2014, 20, 170–182. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.Y. Reconstruction of a complete global time series of daily vegetation index trajectory from long-term AVHRR data. Remote Sens. Environ. 2015, 156, 457–472. [Google Scholar] [CrossRef]
- Basler, D.; Körner, C. Photoperiod sensitivity of bud burst in 14 temperate forest tree species. Agric. For. Meteorol. 2012, 165, 73–81. [Google Scholar] [CrossRef]
- Korner, C.; Basler, D. Plant science. Phenology under global warming. Science 2010, 327, 1461–1462. [Google Scholar] [CrossRef] [PubMed]
- Caffarra, A.; Donnelly, A. The ecological significance of phenology in four different tree species: Effects of light and temperature on bud burst. Int. J. Biometeorol. 2011, 55, 711–721. [Google Scholar] [CrossRef] [PubMed]
- Tanino, K.K.; Kalcsits, L.; Silim, S.; Kendall, E.; Gray, G.R. Temperature-driven plasticity in growth cessation and dormancy development in deciduous woody plants: A working hypothesis suggesting how molecular and cellular function is affected by temperature during dormancy induction. Plant Mol. Biol. 2010, 73, 49–65. [Google Scholar] [CrossRef]
- Duputié, A.; Rutschmann, A.; Ronce, O.; Chuine, I.J.G.c.b. Phenological plasticity will not help all species adapt to climate change. Glob. Change Biol. 2015, 21, 3062–3073. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.F.; Lin, C.F.; Wang, S.X.; Gong, Y.F.; Zhao, Y.P.; Tang, J.; De Boeck, H.J.; Vitasse, Y.; Fu, Y.S. The sensitivity of ginkgo leaf unfolding to the temperature and photoperiod decreases with increasing elevation. Agric. For. Meteorol. 2022, 315, 108840. [Google Scholar] [CrossRef]
- Caffarra, A.; Eccel, E. Increasing the robustness of phenological models for Vitis vinifera cv. Chardonnay. Int. J. Biometeorol. 2010, 54, 255–267. [Google Scholar] [CrossRef] [PubMed]
- Pereira, M.R.; Ribeiro, H.; Abreu, I.; Eiras-Dias, J.; Mota, T.; Cunha, M. Predicting the flowering date of Portuguese grapevine varieties using temperature-based phenological models: A multi-site approach. J. Agric. Sci. 2018, 156, 865–876. [Google Scholar] [CrossRef]
- Liu, G.; Chen, X.; Zhang, Q.; Lang, W.; Delpierre, N. Antagonistic effects of growing season and autumn temperatures on the timing of leaf coloration in winter deciduous trees. Glob. Change Biol. 2018, 24, 3537–3545. [Google Scholar] [CrossRef] [PubMed]
- Bigler, C.; Vitasse, Y. Premature leaf discoloration of European deciduous trees is caused by drought and heat in late spring and cold spells in early fall. Agric. For. Meteorol. 2021, 307, 108492. [Google Scholar] [CrossRef]
- Hanninen, H.; Kramer, K.; Tanino, K.; Zhang, R.; Wu, J.; Fu, Y.H. Experiments are necessary in process-based tree phenology modelling. Trends Plant Sci. 2019, 24, 199–209. [Google Scholar] [CrossRef] [PubMed]
- Wolkovich, E.M.; Cook, B.I.; Allen, J.M.; Crimmins, T.M.; Betancourt, J.L.; Travers, S.E.; Pau, S.; Regetz, J.; Davies, T.J.; Kraft, N.J.; et al. Warming experiments underpredict plant phenological responses to climate change. Nature 2012, 485, 494–497. [Google Scholar] [CrossRef] [PubMed]
- Olsson, C.; Jönsson, A.M. Process-based models not always better than empirical models for simulating budburst of Norway spruce and birch in Europe. Glob. Change Biol. 2014, 20, 3492–3507. [Google Scholar] [CrossRef]
- Gao, X.; Richardson, A.D.; Friedl, M.A.; Moon, M.; Gray, J.M. Thermal forcing versus chilling? Misspecification of temperature controls in spring phenology models. Glob. Ecol. Biogeogr. 2024, 33, e13932. [Google Scholar] [CrossRef]
- Czernecki, B.; Nowosad, J.; Jabłońska, K. Machine learning modeling of plant phenology based on coupling satellite and gridded meteorological dataset. Int. J. Biometeorol. 2018, 62, 1297–1309. [Google Scholar] [CrossRef]
- Freiesleben, T.; König, G.; Molnar, C.; Tejero-Cantero, Á. Scientific Inference with Interpretable Machine Learning: Analyzing Models to Learn About Real-World Phenomena. Minds Mach. 2024, 34, 32. [Google Scholar] [CrossRef]

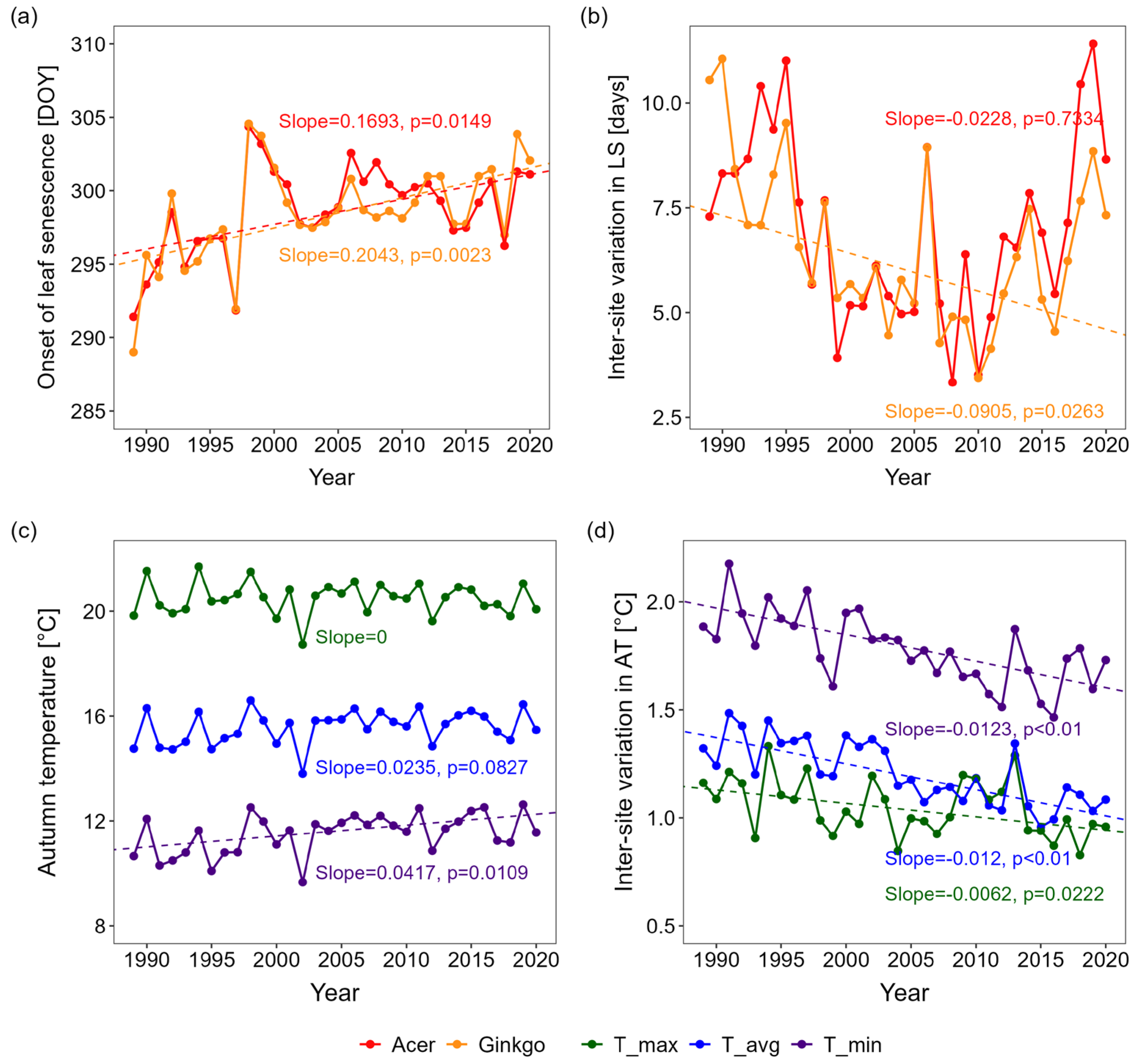


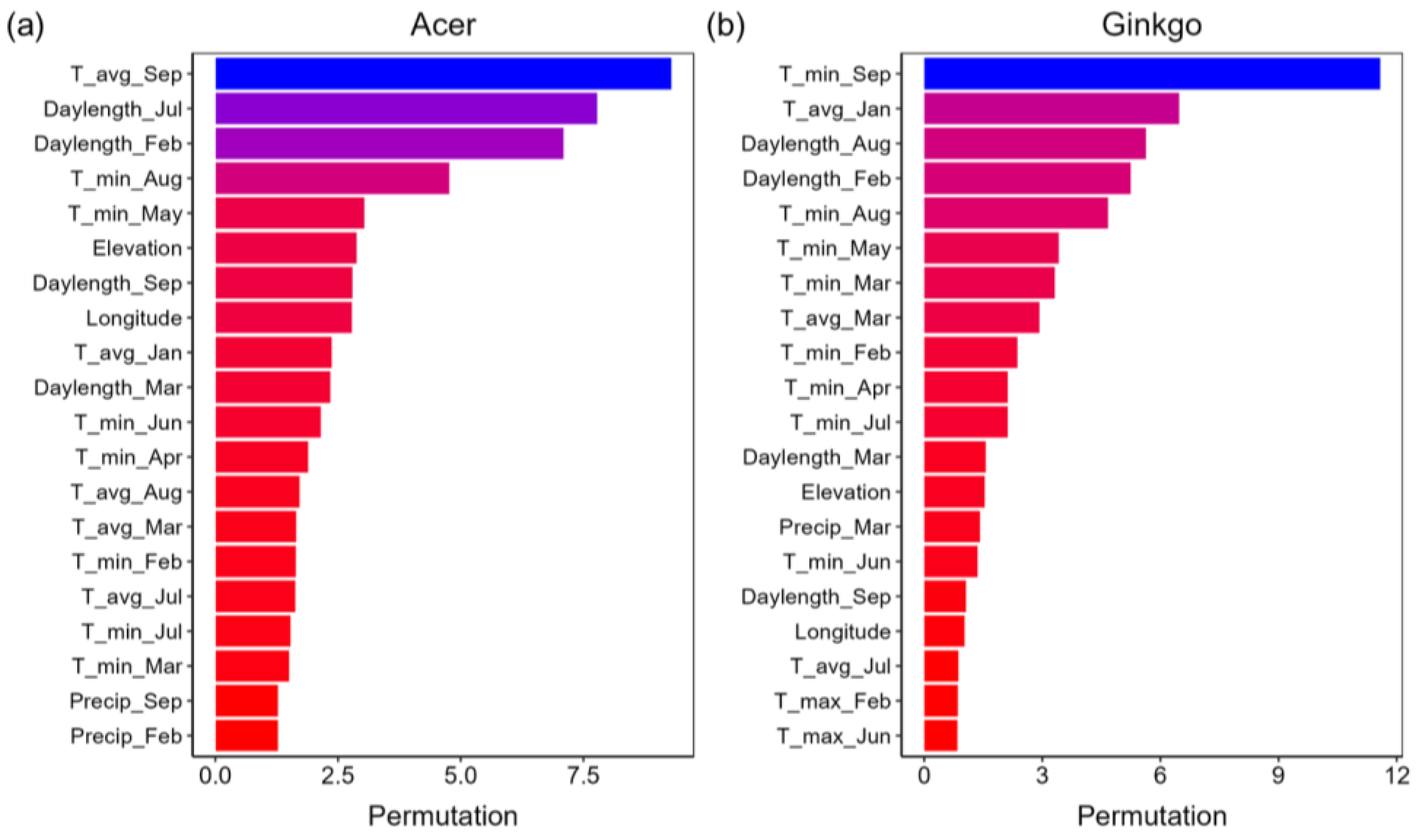
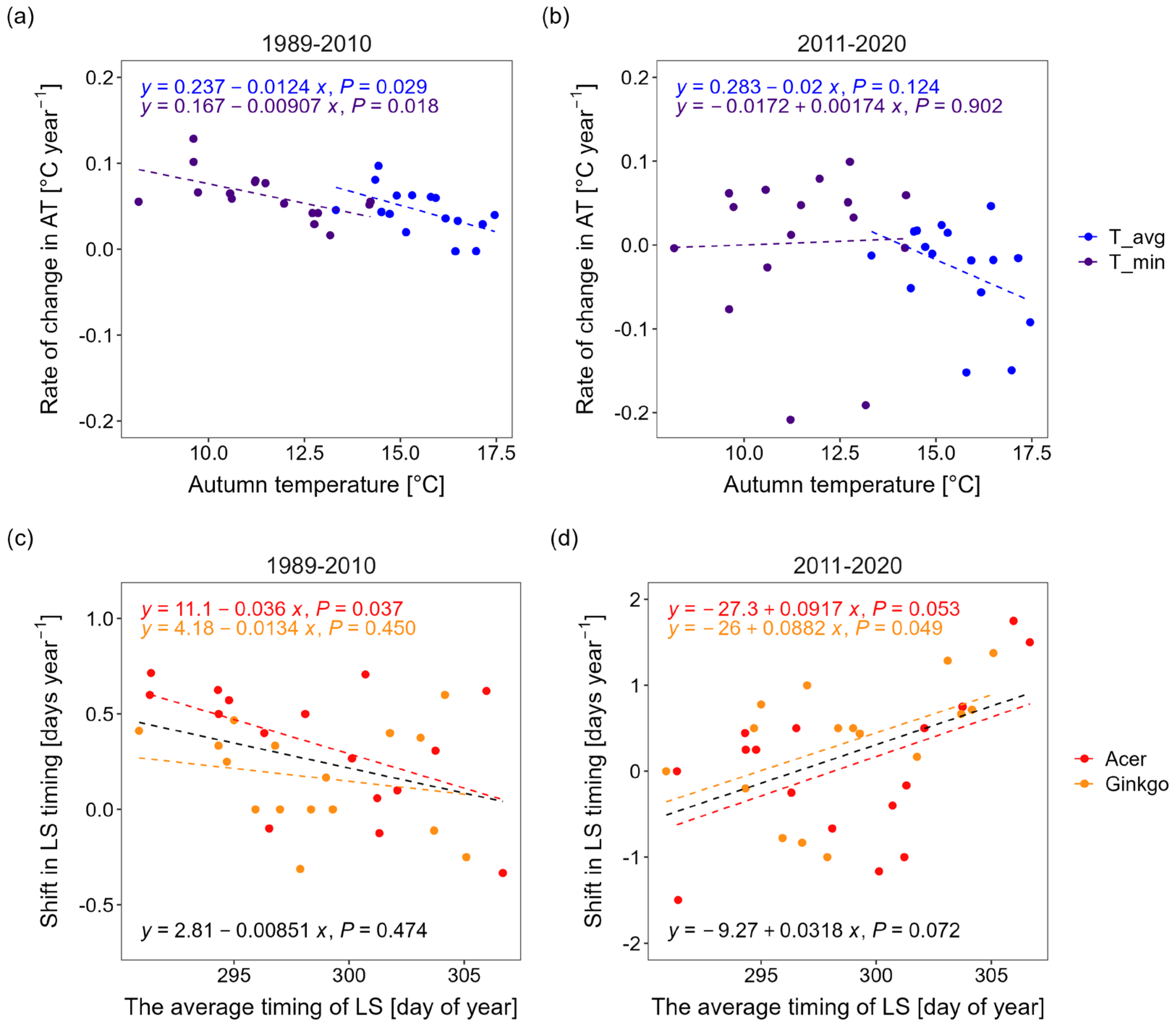
| Model | Parameter | Initiation Condition | Daily Leaf Senescence Rate |
|---|---|---|---|
| CDD_T | |||
| CDD_P | |||
| TP_T | |||
| TP_P |
| (a) | ||||||
| Model | Training Performance | Validation Performance | ||||
| RMSE | NSE | r | RMSE | NSE | r | |
| GBDT | 2.04 | 0.94 | 0.98 | 5.90 | 0.51 | 0.72 |
| RF | 2.67 | 0.90 | 0.96 | 5.90 | 0.50 | 0.71 |
| LR | 5.96 | 0.49 | 0.70 | 6.38 | 0.42 | 0.65 |
| TP_P | 7.30 | 0.23 | 0.55 | 7.21 | 0.26 | 0.58 |
| TP_T | 8.26 | 0.02 | 0.58 | 8.56 | −0.04 | 0.57 |
| CDD_P | 6.75 | 0.34 | 0.61 | 6.86 | 0.33 | 0.60 |
| CDD_T | 7.35 | 0.22 | 0.61 | 7.78 | 0.14 | 0.59 |
| (b) | ||||||
| Model | Training Performance | Validation Performance | ||||
| RMSE | NSE | r | RMSE | NSE | r | |
| GBDT | 2.23 | 0.93 | 0.97 | 5.62 | 0.54 | 0.74 |
| RF | 3.00 | 0.88 | 0.95 | 5.45 | 0.57 | 0.75 |
| LR | 6.07 | 0.51 | 0.71 | 5.80 | 0.51 | 0.72 |
| TP_P | 6.91 | 0.36 | 0.65 | 6.63 | 0.36 | 0.67 |
| TP_T | 7.45 | 0.25 | 0.66 | 7.00 | 0.29 | 0.70 |
| CDD_P | 6.48 | 0.44 | 0.67 | 6.14 | 0.45 | 0.70 |
| CDD_T | 7.34 | 0.28 | 0.68 | 7.27 | 0.23 | 0.69 |
| (a) | ||||||
| Model | Training Performance | Validation Performance | ||||
| RMSE | NSE | r | RMSE | NSE | r | |
| GBDT | 2.43 | 0.92 | 0.96 | 5.90 | 0.50 | 0.72 |
| RF | 3.31 | 0.84 | 0.93 | 5.36 | 0.59 | 0.77 |
| LR | 6.53 | 0.38 | 0.62 | 6.93 | 0.32 | 0.57 |
| TP_P | 5.38 | 0.58 | 0.76 | 5.48 | 0.57 | 0.76 |
| TP_T | 5.72 | 0.53 | 0.74 | 6.18 | 0.46 | 0.70 |
| CDD_P | 5.50 | 0.56 | 0.75 | 5.76 | 0.53 | 0.73 |
| CDD_T | 6.00 | 0.48 | 0.71 | 6.18 | 0.46 | 0.69 |
| (b) | ||||||
| Model | Training Performance | Validation Performance | ||||
| RMSE | NSE | r | RMSE | NSE | r | |
| GBDT | 2.57 | 0.91 | 0.96 | 5.73 | 0.52 | 0.74 |
| RF | 3.33 | 0.85 | 0.94 | 5.37 | 0.58 | 0.76 |
| LR | 6.28 | 0.47 | 0.69 | 6.00 | 0.48 | 0.69 |
| TP_P | 5.40 | 0.61 | 0.78 | 5.27 | 0.60 | 0.77 |
| TP_T | 5.69 | 0.57 | 0.76 | 5.92 | 0.49 | 0.73 |
| CDD_P | 5.57 | 0.58 | 0.76 | 5.50 | 0.56 | 0.75 |
| CDD_T | 6.04 | 0.51 | 0.73 | 6.10 | 0.46 | 0.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Moon, M.; Kim, H.S. Changes in the Timing of Autumn Leaf Senescence of Maple and Ginkgo Trees in South Korea over the Past 30 Years: A Comparative Assessment of Process-Based, Linear Regression, and Machine-Learning Models. Forests 2025, 16, 174. https://doi.org/10.3390/f16010174
Kim S, Moon M, Kim HS. Changes in the Timing of Autumn Leaf Senescence of Maple and Ginkgo Trees in South Korea over the Past 30 Years: A Comparative Assessment of Process-Based, Linear Regression, and Machine-Learning Models. Forests. 2025; 16(1):174. https://doi.org/10.3390/f16010174
Chicago/Turabian StyleKim, Sukyung, Minkyu Moon, and Hyun Seok Kim. 2025. "Changes in the Timing of Autumn Leaf Senescence of Maple and Ginkgo Trees in South Korea over the Past 30 Years: A Comparative Assessment of Process-Based, Linear Regression, and Machine-Learning Models" Forests 16, no. 1: 174. https://doi.org/10.3390/f16010174
APA StyleKim, S., Moon, M., & Kim, H. S. (2025). Changes in the Timing of Autumn Leaf Senescence of Maple and Ginkgo Trees in South Korea over the Past 30 Years: A Comparative Assessment of Process-Based, Linear Regression, and Machine-Learning Models. Forests, 16(1), 174. https://doi.org/10.3390/f16010174






