Next Article in Journal
Global Warming as Revealed Through Thirty Years of Analysis on Breeding of Mediterranean Tits
Previous Article in Journal
Soil Comprehensive Fertility Changes in Response to Stand Age and Initial Planting Density of Long-Term Spacing Trials of Chinese Fir Plantations
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 16
Issue 2
10.3390/f16020225
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Long-Term Growth Trends of 18 Native and Non-Native Tree Species Based on Data from Experimental Plots Since 1878 in Brandenburg, Germany

by
Markus Engel
1,*,
Ulrike Hagemann
1 and
Jens Schröder
1,2
1
State Forestry Research Centre Eberswalde–Landeskompetenzzentrum Forst Eberswalde, Alfred-Möller-Straße 1, 16225 Eberswalde, Germany
2
Department of Forest and Environment, Eberswalde University of Sustainable Development, Alfred-Möller-Straße 1, 16225 Eberswalde, Germany
*
Author to whom correspondence should be addressed.
Forests 2025, 16(2), 225; https://doi.org/10.3390/f16020225
Submission received: 19 December 2024 / Revised: 9 January 2025 / Accepted: 23 January 2025 / Published: 24 January 2025
(This article belongs to the Section Forest Ecology and Management)
Browse Figures
Review Reports Versions Notes

Abstract

:
The rapid environmental changes associated with climate change increase the need for adaptation strategies in forest management based on profound knowledge about tree species, particularly in the context of assisted migration. For research purposes, selected native and non-native tree species were planted in Brandenburg, Germany more than 120 years ago. Today, these sites provide an opportunity to gather insights about their performance and growth-response throughout the past century. We analyzed the height growth increment of 18 tree species on 1765 long-term experimental plots, the earliest of which have been monitored since 1878. We additionally investigated the stand-level volume increments on 60 unmanaged plots for two of these species. Our results show increasing trends in forest stand growth for Scots pine (Pinus sylvestris L.) and Sessile oak (Quercus petraea (Matt.) Liebl.). However, long-term height increment showed positive, negative, and indifferent growth trends in reaction to changing environmental conditions. Remarkably, 16 out of 18 species showed a growth decline between the years 2000 and 2020, likely attributable to increasing frequencies of single and consecutive drought events. We found non-native species to perform comparably to native tree species. Forest management should reconsider the role of native and non-native species in climate-adapted forests. We recommend focusing on provenance and local site adaptability in assisted migration efforts and argue that maintenance of long-term experiments can provide us with valuable insights on species performance in the near future.

1. Introduction

Tree growth dynamics in European forest ecosystems are subject to rapid environmental changes [1], including rising air temperatures [2], disturbance frequencies [3], and varying atmospheric deposition [4]. Recent investigations have shown that resulting growth trends differ between species, European regions, and periods [5,6,7]. We observe growth declines in some species, such as European beech (Fagus sylvatica L.) [8], while other species show growth increases in some areas, such as Norway spruce (Picea abies (L.) H. Karst) in Northern Europe [9]. Some species are expected to increase their potential distribution area if the current warming trend continues, such as Black locust (Robinia pseudoacacia L.) [10]. The pace of the observed environmental changes is fast and might exceed the genetic and phenotypic adaptability of tree species [11], thus threatening our goal to increase forest resilience and ensure forest ecosystem services in the future [12]. Assisted migration, which is the transport of forest reproductive material from regions today featuring expected future climatic conditions in the target area, can support rapid forest management responses to climate change challenges [13]. Assisted migration can have positive effects on species adaption, forest ecosystem stability and productivity, but also comes with risks related to invasive species and maladaptation [14]. The knowledge gap concerning the costs and benefits of assisted migration may be overcome by analyzing data from existing long-term experimental sites with actively “migrated” tree species, some of which have been intensively studied since the end of the 19th century [5,6]. These experiments provide an alternative source of information on the performance of tree species and provenances in a changing environment [15].
In Brandenburg, Germany, the first long-term field experiments were established in 1870 [16]. Since then, they have been dedicated to finding optimal spacing, rotation, and thinning regimes for tree species for the maximum yield, provenance trials, planting experiments, and more [16]. Furthermore, seed sources from various non-native tree species, especially from North America, were transferred to Brandenburg for investigation of their growth, wood quality, and adaptability to local site conditions [17]. Some of these experiments with non-native tree species and provenances are still monitored today and provide insights into the suitability of these species for modern assisted migration efforts.
In contrast, experiments without any treatment are rare, but have been more frequently investigated since 1960. Species-specific, management-independent long-term trends in forest stand growth, such as the change of the self-thinning line, can only be investigated with the help of fully stocked and unmanaged experimental plots [15]. Trends in tree height growth, on the other hand, can be investigated for managed and unmanaged experimental sites if the considered trees are dominant and other factors, such as tree age and site fertility, are accounted for in the analysis [18,19].
This study investigates the height growth trends for 18 tree species on long-term experimental sites and, additionally, the stand growth trend for two major tree species on unmanaged experimental sites in Brandenburg, Germany. Our aim is to reveal the species’ growth reactions to environmental changes, particularly climate warming, on a regional scale and in comparison to changes found in other studies at a European scale. We further investigate if our results are able to classify species to potential “winners” and “losers” under long-term environmental changes and discuss the implications for future assisted migration programs.

2. Materials and Methods

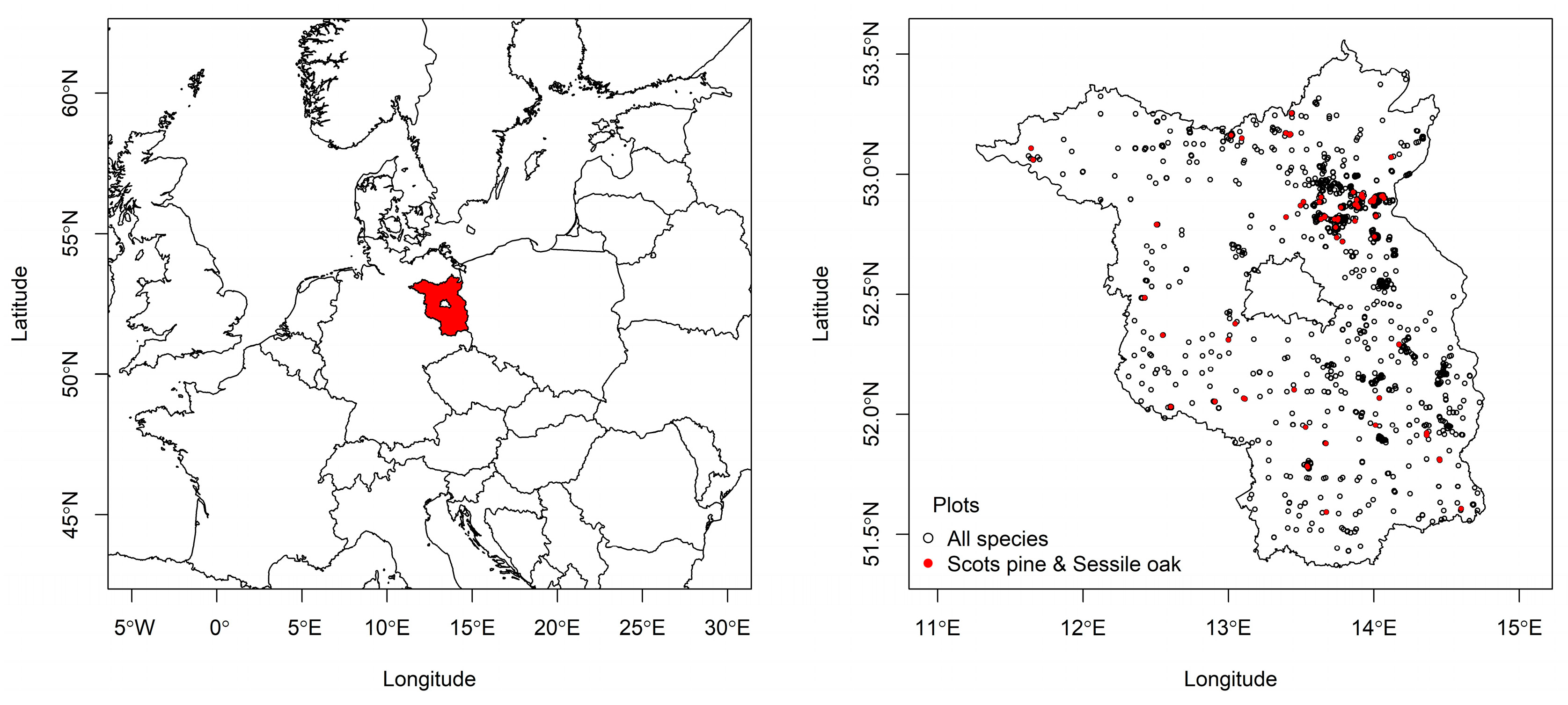
2.1. Tree Data

Overall, we analyzed 18 tree species which have been measured on experimental plots throughout different time periods ranging from 1878–2024 (Table 1). These periods vary among tree species due to the different establishment eras of the studied experimental plots. The data gathered on those experimental sites includes the diameter at breast height (1.3 m), tree height, tree species, and tree age. Other parameters, such as the individual tree position, tree crown radii, or the seed sources, have only rarely been documented. Typical measurement intervals are 5 years, although exceptions occur due to various environmental, societal, or administrative issues. The majority of these long-term experiments focus on a particular management regime.
The tree species were selected based on the available tree height increment measurements, setting the minimum at 700 individual height measurements per species. Nine of the tree species in our analysis are considered non-native, as they were introduced into the study area at the end of the 19th century [17]. Classification of native (N) and non-native (NN) tree species is provided in Table 1.
The technology for measuring tree height changed throughout the study period, but the majority of tree heights were obtained using clinometers and laser dendrometers. Tree height measurements were taken on a representative subsample of the experimental plot trees to reduce the measurement effort on the large number of plots. In contrast, tree diameter was measured for all trees using a caliper at 1.3 m height above ground. Missing tree heights were calculated by first modeling the non-linear relationship between tree height and tree diameter, followed by predicting tree height using tree diameter as input variable. For this purpose, different equations have been developed and applied [20]. Usually, a set of non-linear relationships was compared based on the ordinary least squares method and visual inspection of data fit before using a single best non-linear regression for calculating missing tree heights.
We used tree height data from 1765 experimental plots (Figure 1) with individual plot areas ranging from 0.01 to 10 ha, depending on the scientific purpose. In total, 60 of those plots are unmanaged sites with either Sessile oak (Quercus petraea (Mattuschka) Liebl.) or Scots pine (Pinus sylvestris L.), which we additionally used to analyze stand growth trends. The total experimental plot area in this study amounts to 846 ha.
We only included tree height data from trees that were dominant and without large neighboring competitors, in order to minimize the error from light competition in the subsequent trend analysis. As tree positions were not readily available for most experimental plots, we relied on written documentation to ensure trees were not suppressed by large neighboring individuals and selected dominant trees greater than or equal to the 0.9 quantile height threshold.

2.2. Study Region

The study region is located in Central Europe, featuring a temperate climate with continental influences. The terrain is characterized by small differences in elevation ranging between 0 and 201 m above sea level. The climate has changed drastically between the periods 1880–1910 and 1994–2024: While annual precipitation sums showed very few trend changes, with an annual mean of 560 mm and a standard deviation (sd) of 84.2 mm ([21,22], Figure 2), mean annual air temperatures rose from 8.4 °C (sd 0.56) to 9.8 °C (sd 0.72). A thin-plate regression spline model indicates the observed long-term trend for mean air temperature (Figure 2). Driven by temperature change, the climatic water balance based on the potential evaporation according to Thornthwaite [23] showed a strong negative trend ([21,22], Figure 2). The years 2018–2020 consecutively featured very negative climatic water balances, also classified as severe drought events by other studies [24,25].
Soil conditions in the study region are characterized by prevalent sandy substrates, sometimes with loamy moraine deposits [26]. Most soil types are classified either as cambisols or podzols with low soil pH and nutrient status as well as low water-holding capacity [26]. Soil conditions and tree growth are further influenced by nitrogen deposition, which increased until the 1990s and has decreased ever since [27].

2.3. Tree Height Increment Modeling

We calculated the height increments of dominant trees for the particular measurement period on experimental plots, which was typically 5 years. We then calculated annual tree height increments by dividing the periodic height difference by the number of years of the particular period. This approach technically assumes a constant height growth between two consecutive measurements.
We built height increment models based on the calculated annual height increments for every species (Table 1) using hierarchical generalized additive models [28]. Generalized additive models (GAMs) are a flexible tool using penalized regression splines to model complex real-world phenomena [29]. In general, GAMs can be formulated as:
E ( Y ) = g β 0 + ∑ j = 1 j f x j , p j
where E (Y) is the expected value of the response Y (here specified as height increment), g denotes the link function (here specified as an identity link), β0 is the intercept, and f denotes the jth smooth function of the covariate x and the factor p (experimental plots). The smooth function (f) consists of a number of (k) fixed basis functions (b) multiplied by a set of coefficients (β):
f j x j = ∑ k = 1 K β j , k b j , k x j
GAMs enable us to investigate the non-linear dependence of tree height increment on several variables, such as tree age or site conditions, while analyzing the variables in an additive manner. The use of a hierarchical model approach gives us the opportunity to analyze smoothing functions that vary between different grouping levels [28], which was necessary in our study in order to estimate long-term trends for all 18 tree species. We tested the application of generalized linear models (GLS), but found model fitting to be inferior to GAMs due to clear non-linear relationships between tree height increment and tree age. Furthermore, we expected a possible long-term trend to be non-linear as well, which can be better estimated using smoothing splines.
Tree species-specific height increment was modeled as dependent on tree diameter, tree age, the experimental plot as a factor and a grouping variable, as well as the calendar year. Tree age was modeled as a smooth that varies between experimental plots (grouping variable), as we assume that site conditions affect the relationship between height increment and tree age [30,31]. We tested another modeling set up using mixed models (GAMMs), which showed many similarities in the random effects calculation. However, due to the high number of factor levels (experimental plots), we decided to implement hierarchical models to enhance performance.
Other variables were modeled as single thin-plate-regression spline smooths [29]. We tested 4 different hierarchical model structures, including tensor-product splines, which differed in the smoothing penalties for the hierarchical tree age effect and the interactions between tree age and the experimental plot as well as the interaction with the calendar year [28]. We chose the best-performing model using the Akaike information criterion (AIC, [32]) and minimized the selection bias [33] by taking the Bayesian information criterion (BIC, [34]) and the root mean square error (RMSE) into consideration. Furthermore, we selected models based on the explained deviance by adding penalties for the null space of all smooths allowing them to be shrunk to zero [35], which has been shown to be superior in a GAM variable selection process compared to forward and backward variable selection using p-values. As a result, we did not include tree diameter in the final height increment models, both because it did not improve model performance and because our main focus was not on demonstrating the diameter effect, but on estimating a possible long-term trend.
The final model form estimated the age effect variation between the grouping variable by implementing a factor-smooth interaction between tree age and experimental plot as factor. This approach estimates a smooth for each factor level, allowing the tree age effect to be site-dependent and entirely random [29]. An additional single smooth term for tree age did not improve model performance and was, hence, excluded. The second smooth was estimated for the variable calendar year. We did not log-transform height increments before calculations, but instead used an identity-link function [29]. We finally estimated 18 species-specific height increment models of the form:
E ( H i ) = g β 0 + ∑ i = 1 i f A g e i , P l o t i + f ( Y e a r i )
where E(Hi) is the expected value of the height increment H at an instance i, g denotes the identity link function, β0 denotes the intercept, and f denotes the smooth functions of the interaction between Age and Plot as well as the single smooth term for Year.
We show the long-term trend of the calendar year with the help of partial effect plots [29], in which case the term of the Age-Plot interaction is set to zero and the remaining model effect is plotted over the calendar year centered at the overall mean. Model predictions are additionally provided over the calendar year with Age set to its median in order to investigate the model estimations on the scale of the response. We provide plots on the interaction between tree age and experimental plot in the appendix, Figure A1. The results of the 18 species-specific models are summarized in Table A1 with detailed information on the AIC, BIC, RMSE, and the share of deviance explained by each model. We additionally provide histograms of the model residuals in Figure A2 and plot the model fits against our height increment data in Figure A3.
Data analysis and modeling were accomplished using R Version 4.3.1 [36] and the package mgcv version 1.8–42 [29,37].

2.4. Forest Stand Growth Analysis

We analyzed forest stand growth for unmanaged experimental plots of Sessile oak (6 plots in total) and Scots pine (54 plots in total), both native to the study region. Our analysis focused on the standing volume, which we derived as sum of all single-tree stem volumes on an experimental plot. Single-tree stem volumes were calculated using functions that were specifically developed and calibrated in the study region [38]. These functions provide the estimated volume of all woody components of the tree i with a diameter greater than 7 cm (VD). For Sessile oak:
V D i = 0.000070436 × D 1.8747 × H 1.067808 × 0.98711565 × e − e 3.627465 − 0.51027 × D ,   A < 31 e − 10.7172 + 2.09058 × ln ⁡ D + 0.97769 × ln ⁡ H , A > 30
where D denotes the tree diameter, H denotes the tree height, and A denotes the tree age. For Scots pine:
V D i = e − 9.675966 + 1.999797 × ln ⁡ D + 0.82493 × ln ⁡ H − 0.01
where D denotes the tree diameter and H denotes the tree height. The single-tree volumes VDi were then summed up to the stand total and divided by the experimental plot area, thus yielding the per-hectare standing volume VD [m3/ha]. The standing volume increment VI for a specific period t1 − t0 was then calculated as:
V I = V D t 1 − V D t 0 t 1 − t 0
where VDt1 is the standing volume at the end and VDt0 is the standing volume at the beginning of a specific period, respectively. In order to demonstrate changes in the relationships between VI and tree age, we analyzed three different time periods based on observed mean air temperature and annual precipitation sums in the study region (Figure 2): 1878(1893)–1960, 1961–2000, and 2001–2024. The first period starts in 1878 and 1893 for Sessile oak and Scots pine, respectively. The first and longest period until 1960 is characterized by very small changes in the temperature and precipitation patterns, followed by a period of rapid temperature change, which we separated by the year 2000 for demonstration purposes only.

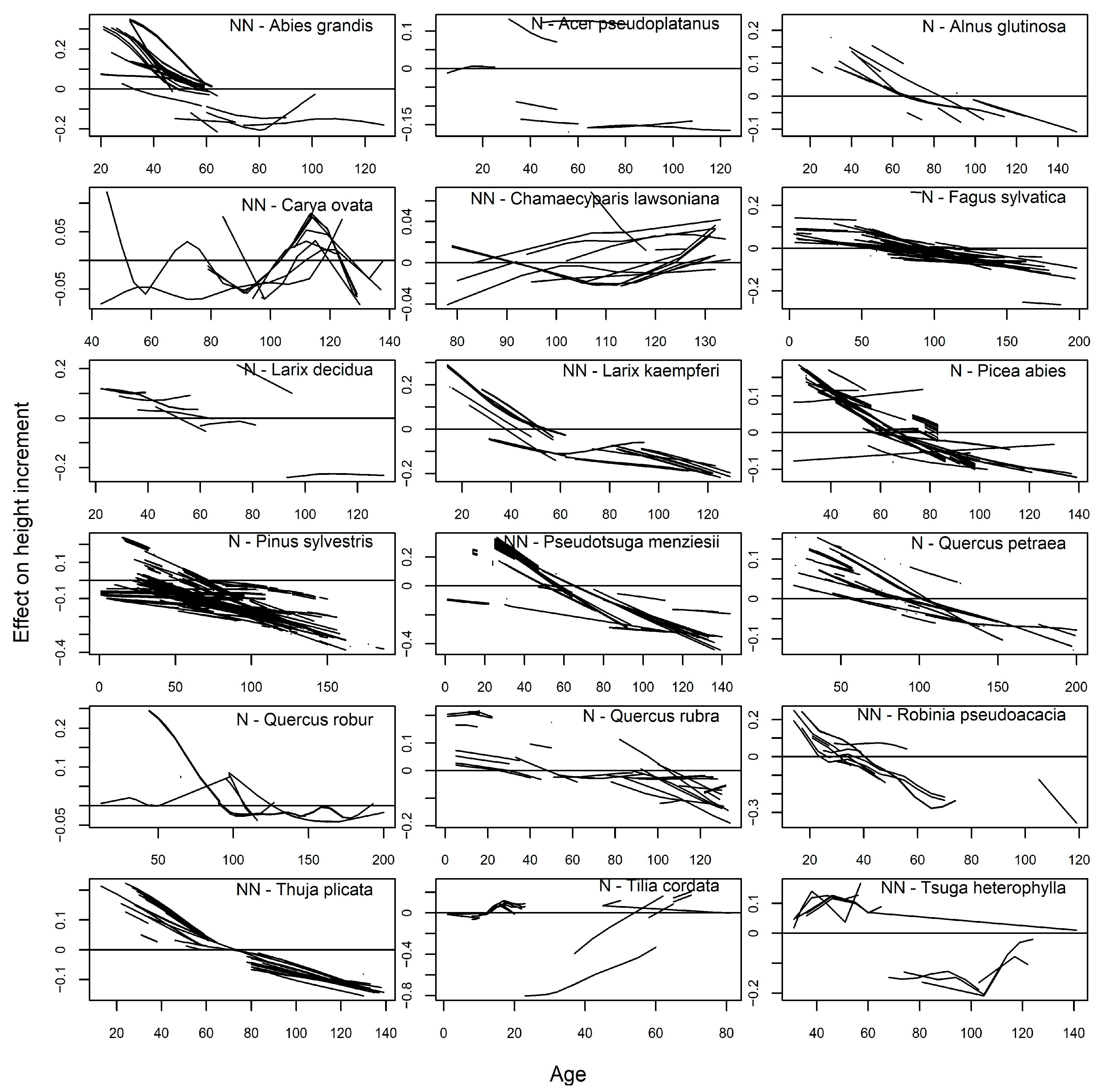
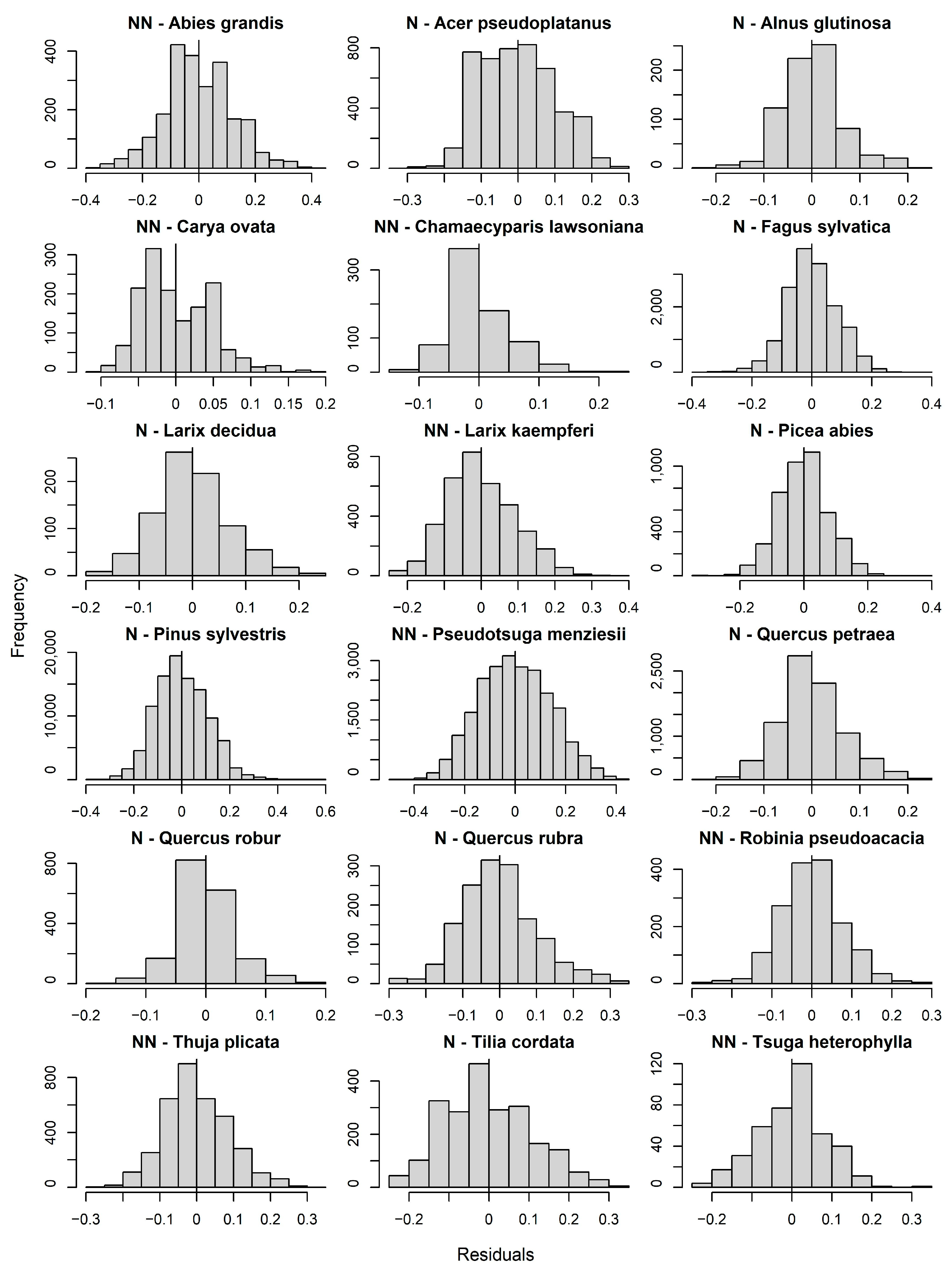
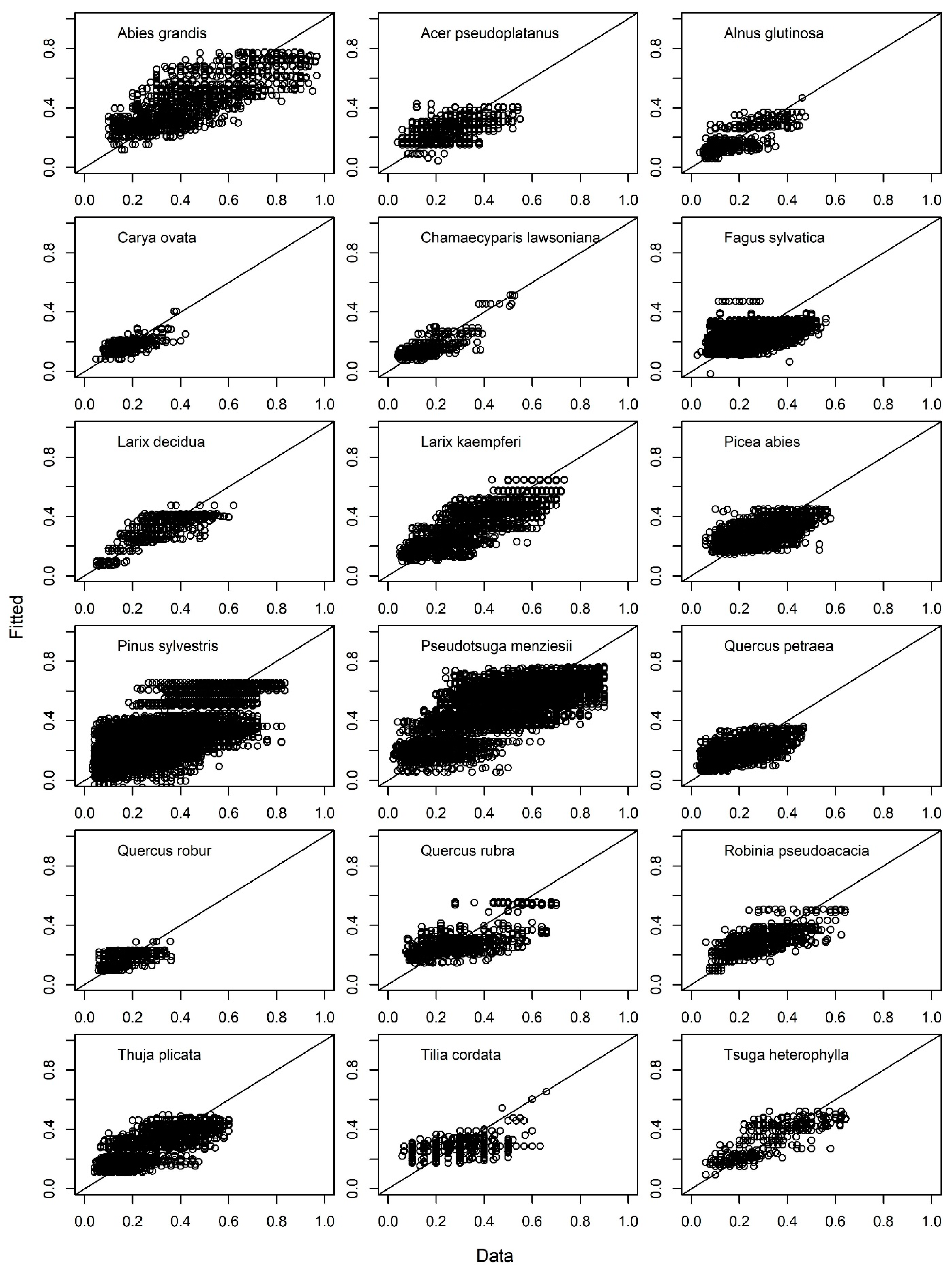
3. Results

In the case of the native species Sessile oak and Scots pine, both standing volumes VD and volume increments VI over tree age increased relative to the first data period of 1878 (1893)–1960 (Figure 3). For Scots pine, the larger number of experimental plots facilitates the distinction between data periods and growth changes, whereas the distinction is less clear for Sessile oak. In contrast to the height growth decline demonstrated in Figure 3 and Figure 4 since the year 2000, neither species shows growth declines in the third period of 2001–2024.
Figure 4 shows plots of the partial effect of the calendar year on tree height increment. Trends were diagnosed for all tree species except for Carya ovata, which shows an almost flat smooth estimate with large standard errors before 1980. Some species show strong fluctuations, but no clear long-term trends, such as Fagus sylvatica or Larix kaempferii. Pinus sylvestris, Pseudotsuga menziesii, Quercus petraea, and Quercus rubra feature long-term increasing trends interrupted by smaller fluctuations. Long-term decreasing trends were observed for Abies grandis, Larix decidua, and Chamaecyparis lawsoniana. Remarkably, a decline between the years 2000 and 2020 was found for almost all species, with only few exceptions, like Alnus glutinosa and Quercus rubra. The onset of this recent growth decline is, however, very different and can be observed before 2010, such as for Pinus sylvestris, or after 2010, such as for Robinia pseudoacacia. Some smooth estimates are accompanied by large standard errors, which leaves partial smooth effects very uncertain, such as for Tilia cordata and Tsuga heterophylla. A clear distinction between the smooth estimates of native and non-native species could not be observed.
Model predictions with tree age set to its median (Figure 5) provide similar observations as the partial effect plots above. However, the additional solid lines for each species indicate the partly substantial experimental plot variation, for instance in the case of Thuja plicata or Pseudotsuga menziesii. The predictions for Acer pseudoplatanus, Alnus glutinosa, and Carya ovata appear erratic, whereas the predictions for Tilia cordata appear to have a clear decreasing trend, which stands in contrast to the partial smooth effect (Figure 3). With few exceptions, most species show a growth decline after the year 2000, although some species, such as Pseudotsuga menziesii, showed a long-term increasing trend for more than 60 years before that period.

4. Discussion

Our analysis of unmanaged experimental plots revealed long-term growth increases for the native species Scots pine and Sessile oak since the end of the 19th century, which is in alignment with previous studies on a European scale in the case of Scots pine [6,39]. Our regional study, therefore, reflects large-scale positive effects of environmental changes like increasing atmospheric CO2-concentrations [40], N-deposition [41], and extended growing seasons [42], but no negative growth trends as reported in the Mediterranean area [6,43,44]. It is noteworthy that atmospheric N-depositions decreased for the last two decades, but are still active in the soil, impacting site conditions [41]. For Sessile oak, we are the first to reveal positive long-term growth trends in our study region based on standing volumes of long-term experimental plots. However, the growth increase found in our study is irrespective of frequent forest disturbances and associated tree mortality [3,45], which overall could cancel out productivity gains due to the above-listed environmental changes [46].
The analyzed height growth trends for dominant trees of 18 species revealed both positive and negative effects of the calendar year. We assume the latter to be associated with multifaceted environmental trends including temperature rise, CO2 increase, and N-deposition. Further investigation on the environmental drivers behind tree growth trends should be focuses to another study and should include accurate data on CO2 concentrations or N-deposition to unravel a mechanistic understanding of the growth processes.
Based on the calendar year effects, we estimated long-term positive growth trends for 6 out of 18 tree species: Pinus sylvestris, Pseudotsuga menziesii, Quercus petraea, Quercus robur, Quercus rubra, and Robinia pseudoacacia. However, 16 of the 18 species showed growth declines after the year 2000 and 2010, respectively, except for Quercus rubra and Alnus glutinosa, which, in the latter case, likely experienced positive effects of hydromorphic soil conditions and flooding even in drought years. The observed recent growth declines might be related to increasing drought frequency observed across Europe, culminating in three severe consecutive drought years 2018–2020 in our study region [47,48,49]. Contrary to the positive long-term trends, Abies grandis, Chamaecyparis lawsoniana, and Larix decidua showed negative growth trends since 1960 and 1970, which could be attributed to the declining climatic water balance in the study region, which possibly exceeded the species adaptive potential [50,51,52]. Instead of a clear long-term trend, some species such as Fagus sylvatica or Larix kaempferii showed strong fluctuating responses. For Fagus sylvatica, the growth decline in recent years was estimated to be the most severe of all species based on the partial effect of the calendar year, which was also reflected in the drought response reported in other studies [53,54]. Our estimates for Carya ovata, Tilia cordata, and Acer pseudoplatanus showed erratic predictions, wide standard errors of the smooth effects, and implausible age effects (Figure A1), indicating biased model data or shortcomings in the model fitting process. We, therefore, cannot draw any conclusions on growth trends of these species.
Recent studies focusing on the site index [55,56,57], which is the stand dominant height at a reference age (usually 100 years), reported positive growth trends for various European tree species [58,59], which support our estimated long-term positive trend for some species. However, studies focusing on ring-width analysis also found growth reductions for some species, such as Picea abies [60,61], Pinus sylvestris [60,62], Fagus sylvatica [8], and Quercus petraea [63], with growth changes largely varying and depending on local site conditions. Environmental changes affect species differently, especially in rear-edge populations [64]. Hence, for instance, Fagus sylvatica might experience negative growth effects through climate change in Northern Germany while Pinus sylvestris experiences positive effects, albeit with a higher climate sensitivity [65]. A similar differentiation between species was observed in our study, where some species benefit from environmental changes in the long term, while others react negatively or show almost no reaction at all. Based on our results, there is no clear distinction between non-native and native tree species, as neither group outperformed the other. Rather, in both groups, some species showed long-term benefits, but also reflected growth declines due to recent drought events.
As negative trends since the year 2000 were observable for 16 out of 18 species in our study region, we assume that recommendations on the future tree species choice [66] based on our results are not feasible if the environmental changes continue with the severity observed in recent years. We believe that assisted migration [67] should focus on specific provenances and assisted gene flow instead of simply targeting tree species, as the intra-specific variability and adaption potential in climate-growth responses might outweigh regional or local environmental changes [68,69,70]. However, local site conditions might exert even more influence on tree growth than provenances [71]. This complexity in tree growth relationships supports our decision to abstain from recommending specific tree species and classifying them as “winners” or “losers”.
Our results question the widespread narrative that non-native tree species can be superior to native species in future climate-adaptive forests. In fact, current forest management programs should be re-evaluated and incorporate current findings on assisted migration and the importance of species provenance and local site conditions on tree growth. However, our regional study focus is not sufficient for altering policy frameworks on a larger scale. Rather, our study supports the need for unraveling a mechanistic understanding of tree growth and environmental factors. This can be improved by forest monitoring networks on a larger scale that enable us to study tree growth reactions over larger environmental gradients.

5. Conclusions

We analyzed regional growth trends for 18 native and non-native tree species based on dominant tree height and forest stand volume of unmanaged experimental plots for two native species. Our results support positive growth trends found on a European scale for Scots pine on a forest stand level. We additionally showed positive regional growth trends for stands of Sessile oak. Long-term positive trends in height growth were found for 6 out of 18 species, which correspond with climate warming and nitrogen deposition. The other species showed either negative long-term trends, highly fluctuating species response, or almost steady growth reactions to environmental change. A vast majority of 16 out of 18 analyzed species showed growth declines between the years 2000 and 2020, probably corresponding to increasing frequencies of single and consecutive drought events. We did not find any eminent differences in the performance of non-native compared to native tree species. We conclude that assisted migration aimed at promoting climate change adaptation should not solely focus on tree species, but rather on species provenances and their adaptability to local site conditions. Despite the enormous effort associated with the maintenance of long-term experimental plots, we argue that incorporating insights gathered from those experiments in the development of future adaptive responses in forest management is still a valuable strategy in the future.

Author Contributions

Conceptualization, M.E., U.H. and J.S.; methodology, M.E.; formal analysis, M.E.; writing—original draft preparation, M.E.; writing—review and editing, U.H. and J.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author due to privacy and legal restrictions.

Acknowledgments

We thank the numerous generations of dedicated people carrying out field measurements on long-term experimental plots, without whom this research would not be possible.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Forests 16 00225 g0a1
Figure A1. Effects of the factor-smooth interaction between tree age and the experimental plot as factor. The factor-smooth interaction calculates one single effect smooth for every factor level. NN denotes non-native tree species, N denotes native tree species.
Figure A1. Effects of the factor-smooth interaction between tree age and the experimental plot as factor. The factor-smooth interaction calculates one single effect smooth for every factor level. NN denotes non-native tree species, N denotes native tree species.
Forests 16 00225 g0a1
Table A1. Model information summary. NBIncr denotes the number of height increments used in the model. Dev.expl. denotes the explained deviance of the model. AIC denotes the Akaike information criterion, BIC denotes the Bayesaian information criterion, and RMSE denotes the root mean square error.
Table A1. Model information summary. NBIncr denotes the number of height increments used in the model. Dev.expl. denotes the explained deviance of the model. AIC denotes the Akaike information criterion, BIC denotes the Bayesaian information criterion, and RMSE denotes the root mean square error.
SpeciesNbIncrDev.Expl.AICBICRMSE
1Abies grandis (Douglas ex D. Don) Lindl.22980.66−3098.89−2901.860.12
2Acer pseudoplatanus L.47390.28−8474.64−8325.570.10
3Alnus glutinosa (L.) Gaertn.7510.63−2030.33−1898.280.06
4Carya ovata (Mill.) K. Koch14800.37−4811.24−4630.230.05
5Chamaecyparis lawsoniana (A. Murr.) Parl.7460.63−2339.16−2210.560.05
6Fagus sylvatica L.15,1920.34−32,418.84−32,119.480.08
7Larix decidua Mill.8520.77−2072.77−1950.820.07
8Larix kaempferi (Lamb.) Carrière36040.64−6859.32−6631.490.09
9Picea abies (L.) H. Karst.43840.42−9854.33−9611.360.08
10Pinus sylvestris L.103,0780.73−167,620.05−167,239.880.11
11Pseudotsuga menziesii (Mirbel) Franco23,5380.43−25,536.73−25,226.380.14
12Quercus petraea (Mattuschka) Liebl.86510.37−22,097.66−21,825.200.07
13Quercus robur L.18810.40−6166.94−5973.880.05
14Quercus rubra L.14960.54−2511.86−2326.670.10
15Robinia pseudoacacia L.16480.53−3722.69−3533.860.08
16Thuja plicata Donn ex D. Don.35450.60−7175.57−6956.550.09
17Tilia cordata Mill.22150.20−3485.10−3314.520.11
18Tsuga heterophylla (Raf.) Sarg.4130.67−789.06−667.540.09
Forests 16 00225 g0a2
Figure A2. Histograms of model residuals for all species-specific models.
Figure A2. Histograms of model residuals for all species-specific models.
Forests 16 00225 g0a2
Forests 16 00225 g0a3
Figure A3. Fitted annual tree height increment [m/year] against the actual height increment [m/year] of the model data.
Figure A3. Fitted annual tree height increment [m/year] against the actual height increment [m/year] of the model data.
Forests 16 00225 g0a3

References

  1. Vacek, Z.; Vacek, S.; Cukor, J. European forests under global climate change: Review of tree growth processes, crises and management strategies. J. Environ. Manag. 2023, 332, 117353. [Google Scholar] [CrossRef]
  2. Charru, M.; Seynave, I.; Hervé, J.-C.; Bertrand, R.; Bontemps, J.-D. Recent growth changes in Western European forests are driven by climate warming and structured across tree species climatic habitats. Ann. For. Sci. 2017, 74, 33. [Google Scholar] [CrossRef]
  3. Patacca, M.; Lindner, M.; Lucas-Borja, M.E.; Cordonnier, T.; Fidej, G.; Gardiner, B.; Hauf, Y.; Jasinevičius, G.; Labonne, S.; Linkevičius, E.; et al. Significant increase in natural disturbance impacts on European forests since 1950. Glob. Change Biol. 2023, 29, 1359–1376. [Google Scholar] [CrossRef]
  4. Schmitz, A.; Sanders, T.G.M.; Bolte, A.; Bussotti, F.; Dirnböck, T.; Peñuelas, J.; Pollastrini, M.; Prescher, A.-K.; Sardans, J.; Verstraeten, A.; et al. Responses of forest ecosystems in Europe to decreasing nitrogen deposition. In Atmospheric Nitrogen Deposition to Global Forests; Spatial Variations, Impacts, and Management Implications; Du, E., de Vries, W., Eds.; Academic Press: Cambridge, MA, USA, 2024; pp. 227–245. [Google Scholar] [CrossRef]
  5. Pretzsch, H.; Biber, P.; Schütze, G.; Uhl, E.; Rötzer, T. Forest stand growth dynamics in Central Europe have accelerated since 1870. Nat. Commun. 2014, 5, 4967. [Google Scholar] [CrossRef] [PubMed]
  6. Pretzsch, H.; Del Rio, M.; Arcangeli, C.; Bielak, K.; Dudzinska, M.; Forrester, D.I.; Klädtke, J.; Kohnle, U.; Ledermann, T.; Matthews, R.; et al. Forest growth in Europe shows diverging large regional trends. Sci. Rep. 2023, 13, 15373. [Google Scholar] [CrossRef]
  7. Kašpar, J.; Tumajer, J.; Altman, J.; Altmanová, N.; Čada, V.; Čihák, T.; Doležal, J.; Fibich, P.; Janda, P.; Kczka, R.; et al. Major tree species in Central European forests differ in their proportion of positive, negative, and nonstationary growth trends. Glob. Change Biol. 2024, 30, e17146. [Google Scholar] [CrossRef]
  8. Del Castillo, E.M.; Zang, C.S.; Buras, A.; Hacket-Pain, A.; Esper, J.; Serrano-Notivoli, R.; Hartl, C.; Weigel, R.; Klesse, S.; de Dios, V.R.; et al. Climate-change-driven growth decline of European beech forests. Commun. Biol. 2022, 5, 163. [Google Scholar] [CrossRef]
  9. Mensah, A.A.; Holmström, E.; Petersson, H.; Nyström, K.; Mason, E.G.; Nilsson, U. The millennium shift: Investigating the relationship between environment and growth trends of Norway spruce and Scots pine in northern Europe. For Ecol. Manag. 2021, 481, 118727. [Google Scholar] [CrossRef]
  10. Puchalka, R.; Dyderski, M.K.; Vitková, M.; Sádlo, J.; Klisz, M.; Netsvetov, M.; Prokopuk, Y.; Matisons, R.; Mionskowski, M.; Wojda, T.; et al. Black locust (Robinia pseudoacacia L.) range contraction and expansion in Europe under changing climate. Glob. Change Biol. 2020, 27, 1587–1600. [Google Scholar] [CrossRef]
  11. Frank, A.; Howe, G.T.; Sperisen, C.; Brang, P.; Clair, J.B.S.; Schmatz, D.R.; Heiri, C. Risk of genetic maladaption due to climate change in three major European species. Glob. Change Biol. 2017, 23, 5358–5371. [Google Scholar] [CrossRef]
  12. Mauri, A.; Girardello, M.; Forzieri, G.; Manca, F.; Beck, P.S.A.; Cescatti, A.; Strona, A. Assisted migration can reduce but not avert the decline of forest ecosystem services in Europe. Glob. Environ. Change 2023, 80, 102676. [Google Scholar] [CrossRef]
  13. Gömöry, D.; Krajmerová, D.; Hrivnák, M.; Longauer, R. Assisted migration vs clos-to-nature forestry: What are the prospects for tree populations under climate change? Cent. Eur. For. J. 2020, 66, 63–70. [Google Scholar] [CrossRef]
  14. Xu, W.; Prescott, C.E. Can assisted migration mitigate climate-change impacts on forests? For Ecol. Manag. 2024, 556, 121738. [Google Scholar] [CrossRef]
  15. Pretzsch, H.; del Rio, M.; Biber, P.; Arcangeli, C.; Bielak, K.; Brang, P.; Dudzinska, M.; Forrester, D.I.; Klädtke, J.; Kohnle, U.; et al. Maintenance of long-term experiments for unique insights into forest growth dynamics and trends: Review and perspectives. Eur. J. For. Res. 2019, 138, 165–185. [Google Scholar] [CrossRef]
  16. Degenhardt, A. Forstliche Versuchsflächen im Spannungsfeld zwischen Tradition, Innovation und Machbarkeit. Eberswalder Forstliche Schriftenreihe 2017, 65, 13–26. [Google Scholar]
  17. Landesforstanstalt Eberswalde. Ausländische Baumarten in Brandenburgs Wäldern. Ministerium für Landwirtschaft, Umweltschutz und Raumordnung; Hendrik Bäßler: Berlin, Germany, 2017; 232p. [Google Scholar]
  18. Sharma, R.P.; Brunner, A.; Eid, T.; Øyen, B.-H. Modeling dominant height growth from national forest inventory individual tree data with short time series and large age errors. For Ecol. Manag. 2011, 262, 2162–2175. [Google Scholar] [CrossRef]
  19. Engel, M.; Mette, T.; Falk, W.; Poschenrieder, W.; Fridman, J.; Skudnik, M. Modeling dominant tree heights of Fagus sylvatica L. using function-on-scalar regression based on forest inventory data. Forests 2023, 14, 304. [Google Scholar] [CrossRef]
  20. Pretzsch, H. Forest Dynamics, Growth and Yield. From Measurement to Model; Springer: Berlin/Heidelberg, Germany, 2009; pp. 187–189. [Google Scholar]
  21. DWD. Climate Data Center (CDC): Annual Regional Averages of Precipitation Height (Annual Sum) in mm, Version v21.3. Available online: https://cdc.dwd.de/portal/ (accessed on 8 October 2024).
  22. DWD. Climate Data Center (CDC): Annual Regional Averages of Air Temperature (Annual Mean) in °C (2 m Above Ground). Version v21.3. Available online: https://cdc.dwd.de/portal/ (accessed on 8 October 2024).
  23. Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
  24. Sachsenmeier, L.; Schnabel, F.; Dietrich, P.; Eisenhauer, N.; Ferlian, O.; Quosh, J.; Richter, R.; Wirth, C. Forest growth resistance and resilience to the 2018–2020 drought depend on tree diversity and mycorrhizal type. J. Ecol. 2024, 112, 1787–1803. [Google Scholar] [CrossRef]
  25. Thom, D.; Buras, A.; Heym, M.; Klemmt, H.-J.; Wauer, A. Varying growth responses of Central European tree species to the extraordinary drought period of 2018–2020. Agric. Forest Meteorol. 2023, 338, 109506. [Google Scholar] [CrossRef]
  26. Holsten, A.; Vetter, T.; Vohland, K.; Krysanova, V. Impact of climate change on soil moisture dynamics in Brandenburg with a focus on nature conservation areas. Ecol. Model. 2009, 220, 2076–2087. [Google Scholar] [CrossRef]
  27. Schmitz, A.; Sanders, T.G.M.; Bolte, A.; Bussotti, F.; Dirnböck, T.; Johnson, J.; Peñuelas, J.; Pollastrini, M.; Prescher, A.-K.; Sardans, J.; et al. Responses of forest ecosystems in Europe to decreasing nitrogen deposition. Environ. Pollut. 2019, 224, 980–994. [Google Scholar] [CrossRef]
  28. Pedersen, E.J.; Miller, D.L.; Simpson, G.L.; Ross, N. Hierarchical generalized additive models in ecology: An introduction with mgcv. PeerJ 2019, 7, e6876. [Google Scholar] [CrossRef]
  29. Wood, S.N. Generalized Additive Models: An Introduction with R, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017; 476p. [Google Scholar]
  30. Calama, R.; Madrigal, G.; del Rio, M.; López-Senespleda, E.; Pardos, M.; Ruiz-Peinado, R.; Menéndez-Miguélez, M. Dynamic height growth equations and site index-based biomass models for young native species afforestations in Spain. Forests 2024, 15, 827. [Google Scholar] [CrossRef]
  31. Yue, C.; Kahle, H.-P.; Klädtke, J.; Kohnle, U. A growth-effective age-based periodic site-index for the estimation of dynamic forest site productivity under environmental changes. Ann. For. Sci. 2024, 81, 33. [Google Scholar] [CrossRef]
  32. Bozdogan, H. model selection and Akaike’s Information Criterion (AIC): The general theory and its analytical extensions. Psychometrika 1987, 52, 345–370. [Google Scholar] [CrossRef]
  33. Sutherland, C.; Hare, D.; Johnson, P.J.; Linden, D.W.; Montgomery, R.A.; Droge, E. Practical advice on variable selection and reporting Akaike information criterion. Proc. R. Soc. B 2023, 290, 2007. [Google Scholar] [CrossRef]
  34. Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar]
  35. Marra, G.; Wood, S.N. Practical variable selection for generalized additive models. Comput. Stat. Data An. 2011, 55, 2372–2387. [Google Scholar] [CrossRef]
  36. R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
  37. Wood, S.N. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Statist. Soc. B 2011, 73, 3–36. [Google Scholar]
  38. Degenhardt, A. Algorithmen und Programme zur Waldwachstumskundlichen Auswertung von Versuchs- und Probeflächen; Landesforstanstalt Eberswalde: Eberswalde, Germany, 2001; 120p. [Google Scholar]
  39. Kauppi, P.E.; Posch, M.; Pirinen, P. Large impacts of climatic warming on growth of Boreal forests since 1960. PLoS ONE 2014, 9, e111340. [Google Scholar] [CrossRef]
  40. Sperlich, D.; Nadal-Sala, D.; Gracia, C.; Kreuzwieser, J.; Hanewinkel, M.; Yousefpour, R. Gains or losses in forest productivity under climate change? The Uncertainty of CO2 fertilization and climate effects. Forests 2020, 8, 141. [Google Scholar] [CrossRef]
  41. Etzold, S.; Ferretti, M.; Reinds, G.J.; Solberg, S.; Gessler, A.; Waldner, P.; Schaub, M.; Sompson, D.; Benham, S.; Hansen, K.; et al. Nitrogen deposition is the most important environmental driver of growth of pure, even-aged and managed European forests. For. Ecol. Manag. 2020, 458, 117762. [Google Scholar] [CrossRef]
  42. Gao, S.; Liang, E.; Liu, R.; Babst, F.; Camarero, J.J.; Fu, Y.H.; Piao, S.; Rossi, S.; Shen, M.; Wang, T.; et al. An earlier start of the thermal growing season enhances tree growth in cold humid areas but not in dry areas. Nat. Ecol. Evol. 2022, 6, 397–404. [Google Scholar] [CrossRef] [PubMed]
  43. Marqués, L.; Madrigal-González, J.; Zavala, M.A.; Camarero, J.J.; Hartig, F. Last-century forest productivity in a managed dry-edge Scots pine population: The two sides of climate warming. Ecol. Appl. 2018, 28, 95–105. [Google Scholar] [CrossRef]
  44. Thabeet, A.; Vennetier, M.; Gadbin-Henry, C.; Denelle, N.; Roux, M.; Caraglio, Y.; Vila, B. Response of Pinus sylvestris L. to recent climatic events in the French Mediterranean region. Trees 2009, 23, 843–853. [Google Scholar] [CrossRef]
  45. Taccoen, A.; Piedallu, C.; Seynave, I.; Perez, I.; Gégout-Petit, A.; Nageleisen, L.-M.; Bontemps, J.-D.; Gégout, J.-C. Background mortality drivers of European tree species: Climate change matters. Proc. R. Soc. B 2019, 286, 1900. [Google Scholar] [CrossRef]
  46. Reyer, C.P.O.; Bathgate, S.; Blennow, K.; Borges, J.G.; Bugmann, H.; Delzon, S.; Faias, S.P.; Garcia-Gonzalo, J.; Gardiner, B.; Gonzalez-Olabarria, J.R.; et al. Are forest disturbances amplifying or canceling out climate change-induced productivity changes in European forests? Environ. Res. Lett. 2017, 12, 034027. [Google Scholar] [CrossRef]
  47. Gazol, A.; Camarero, J.J. Compound climate events increase tree drought mortality across European forests. Sci. Tot. Environ. 2022, 816, 151604. [Google Scholar] [CrossRef]
  48. Senf, C.; Buras, A.; Zang, C.S.; Rammig, A.; Seidl, R. Excess forest mortality is consistently linked to drought across Europe. Nat. Commun. 2020, 11, 6200. [Google Scholar] [CrossRef]
  49. Senf, C.; Seidl, R. Persistent impacts of the 2018 drought on forest disturbance regimes in Europe. Biogeosciences 2021, 18, 5223–5230. [Google Scholar] [CrossRef]
  50. Wilczyński, S.; Kulej, M. The growth of seven Abies grandis provenances in the climatic conditions of the Polish Carpathian mountains. Dendrobiololgy 2019, 81, 1–13. [Google Scholar] [CrossRef]
  51. Cedro, A.; Nowak, G. A comparison of the chronologies of introduced versus native coniferous species growing in Northwestern Poland during periods of global warming. Sustainability 2024, 16, 2215. [Google Scholar] [CrossRef]
  52. Danek, M.; Danek, T. Recent changes in the climate-growth response of European larch (Larix decidua Mill.) in the Polish Sudetes. Trees 2022, 36, 803–817. [Google Scholar] [CrossRef]
  53. Rukh, S.; Sanders, T.G.M.; Krüger, I.; Schad, T.; Bolte, A. Distinct responses of European beech (Fagus sylvatica L.) to drought intensity and length—A review of the impacts of the 2003 and 2018-2019 drought events in Central Europe. Forests 2023, 14, 248. [Google Scholar] [CrossRef]
  54. Chakraborty, T.; Reif, A.; Matzarakis, A.; Saha, S. How does radial growth of water-stressed populations of European beech (Fagus sylvatica L.) trees vary under multiple drought events? Forests 2021, 12, 129. [Google Scholar] [CrossRef]
  55. Skovsgaard, J.P.; Vanclay, J.K. Forest site productivity: A review of the evolution of dendrometric concepts for even-aged stands. Forestry 2008, 81, 13–31. [Google Scholar] [CrossRef]
  56. Skovsgaard, J.P.; Vanclay, J.K. Forest site productivity: A review of spatial and temporal variability in natural site conditions. Forestry 2013, 86, 305–315. [Google Scholar] [CrossRef]
  57. Brandl, S.; Mette, T.; Falk, W.; Vallet, P.; Rötzer, T.; Pretzsch, H. Static site indices from different national forest inventories: Harmonization and prediction from site conditions. Ann. For. Sci. 2018, 758, 56. [Google Scholar] [CrossRef]
  58. Combaud, M.; Cordonnier, T.; Dupire, S.; Vallet, P. Climate change altered the dynamics of stand dominant height in forests during the past century—Analysis of 20 European tree species. For. Ecol. Manag. 2024, 553, 121601. [Google Scholar] [CrossRef]
  59. Socha, J.; Solberg, S.; Tymińska-Czabańska, L.; Tompalski, P.; Vallet, P. Height growth rate of Scots pine in Central Europe increased by 29% between 1900 and 2000 due to changes in site productivity. For. Ecol. Manag. 2021, 491, 119102. [Google Scholar] [CrossRef]
  60. Treml, V.; Mašsek, J.; Tumajer, J.; Rydval, M.; Čada, V.; Ledvinka, O.; Svoboda, M. Trends in climatically driven extreme growth reductions of Picea abies and Pinus sylvestris in Central Europe. Glob. Change Biol. 2021, 28, 557–570. [Google Scholar] [CrossRef] [PubMed]
  61. D’Andrea, G.; Šimůnek, V.; Pericolo, O.; Vacek, Z.; Vacek, S.; Corleto, R.; Olejár, L.; Ripullone, F. Growth response of Norway spruce (Picea abies [L.] Karst.) in Central Bohemia (Czech Republic) to climate change. Forests 2023, 14, 1215. [Google Scholar] [CrossRef]
  62. Brichta, J.; Šimůnek, V.; Bilek, L.; Vacek, Z.; Gallo, J.; Drozdowski, S.; Bravo-Fernández, J.A.; Mason, B.; Gomez, S.R.; Hájek, V.; et al. Effects of climate change on Scots pine (Pinus sylvestris L.) growth across Europe: Decrease of tree-ring fluctuation and amplification of climate stress. Forests 2024, 15, 91. [Google Scholar] [CrossRef]
  63. Mészáros, I.; Adorján, B.; Nyitrai, B.; Kanalas, P.; Oláh, V.; Levanič, T. Long-term radial growth and climate-growth relationships of Quercus petraea (Matt.) Liebel. and Quercus cerris L. in a xeric low elevation site from Hungary. Dendrochronologia 2022, 76, 126014. [Google Scholar] [CrossRef]
  64. Camarero, J.J.; Gazol, A.; Sangüesa-Barreda, G.; Vergarechea, M.; Alfaro-Sánchez, R.; Cattaneo, N.; Vicente-Serrano, S.M. Tree growth is more limited by drought in rear-edge forests most of the times. For. Ecosyst. 2021, 8, 25. [Google Scholar] [CrossRef]
  65. Diers, M.; Weigel, R.; Leuschner, C. Both climate sensitivity and growth trend of European beech decrease in the North German lowlands, while Scots pine still thrives, despite growing sensitivity. Trees 2022, 37, 523–543. [Google Scholar] [CrossRef]
  66. Thurm, E.A.; Hernandez, L.; Baltensweiler, A.; Ayan, S.; Rasztovits, E.; Bielak, K.; Zlatanov, T.M.; Hladnik, D.; Balic, B.; Freudenschuss, A.; et al. Alternative tree species under climate warming in managed European forests. For. Ecol. Manag. 2018, 430, 485–497. [Google Scholar] [CrossRef]
  67. Chakraborty, D.; Ciceu, A.; Ballian, D.; Garzón, M.B.; Bolte, A.; Bozic, G.; Buchacher, R.; Čepl, J.; Cremer, E.; Ducousso, A.; et al. Assisted migration can preserve the European forest carbon sink under climate change. Nat. Clim. Change 2024, 14, 845–852. [Google Scholar] [CrossRef]
  68. Schueler, S.; George, J.-P.; Karanitsch-Ackerl, S.; Mayer, K.; Klumpp, R.T.; Grabner, M. Evolvability of drought response in four native and non-native conifers: Opportunities for forest and genetic resource management in Europe. Front. Plant Sci. 2021, 12, 648312. [Google Scholar] [CrossRef]
  69. Petrik, P.; Grote, R.; Gömöry, D.; Kurjak, D.; Petek-Petrik, A.; Lamarque, L.J.; Konópková, A.S.; Mukarram, M.; Debta, H.; Fleischer, P. The role of provenance for the projected growth of juvenile European beech under climate change. Forests 2023, 14, 26. [Google Scholar] [CrossRef]
  70. Kormann, J.M.; van der Maaten, E.; Liesebach, M.; Liepe, K.J.; van der Maaten-Theunissen, M. High risk, high gain? Trade-offs between growth and resistance to extreme events differ in northern red oak (Quercus rubra L.). Front. Plant Sci. 2024, 15, 1374498. [Google Scholar] [CrossRef]
  71. Unterholzner, L.; Stolz, J.; van der Maaten-Theunissen, M.; Liepe, K.; van der Maaten, E. Site conditions rather than provenance drive tree growth, climate sensitivity and drought responses in European beech in Germany. For. Ecol. Manag. 2024, 572, 122308. [Google Scholar] [CrossRef]
Forests 16 00225 g001
Figure 1. Location of the state of Brandenburg (red) in Central Europe (left). Plot locations in the state of Brandenburg, Germany (right). Hollow circles refer to plots where tree height data was used for analysis; red dots refer to unmanaged plots specifically used for forest stand growth analysis.
Figure 1. Location of the state of Brandenburg (red) in Central Europe (left). Plot locations in the state of Brandenburg, Germany (right). Hollow circles refer to plots where tree height data was used for analysis; red dots refer to unmanaged plots specifically used for forest stand growth analysis.
Forests 16 00225 g001
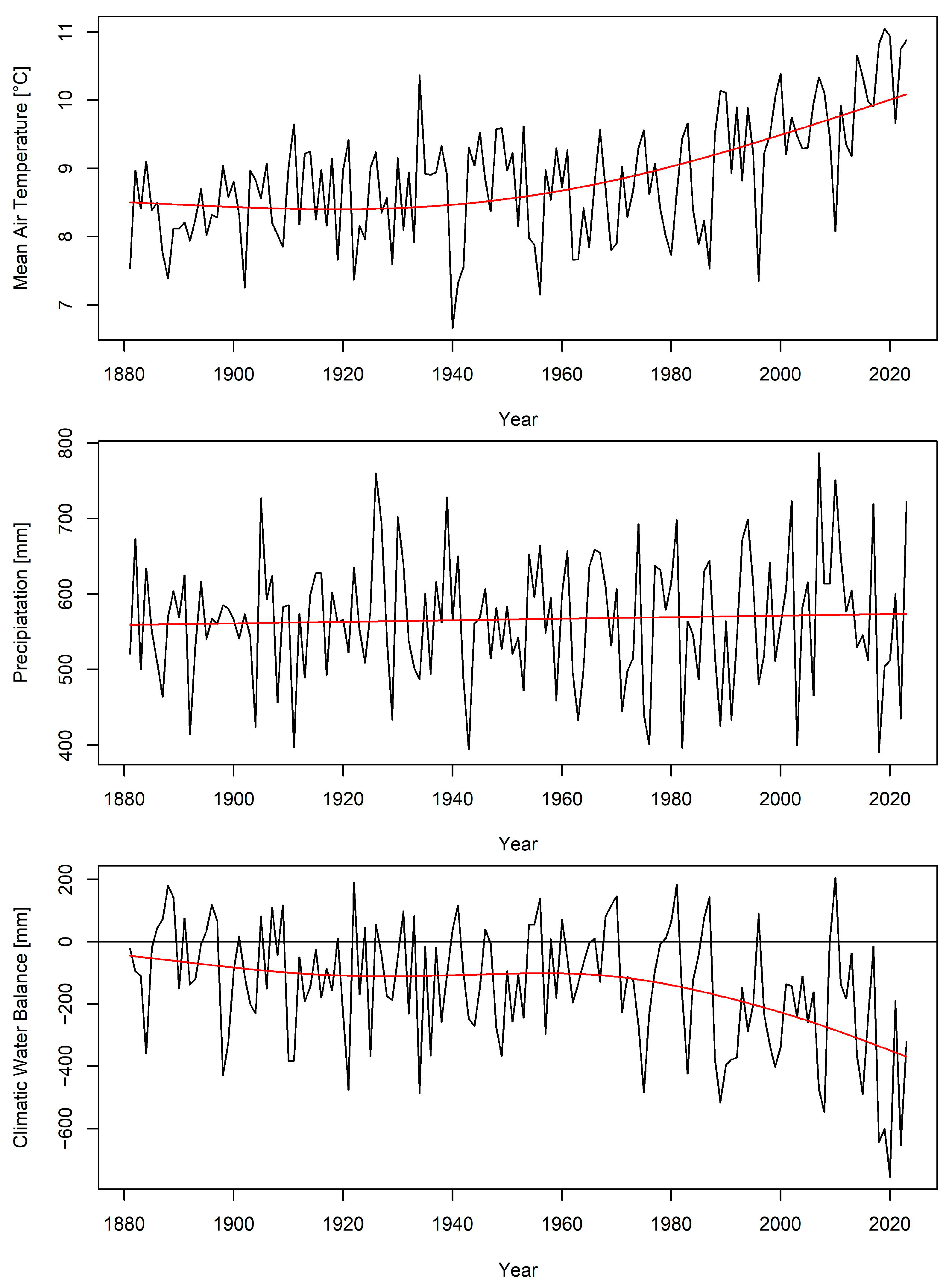
Forests 16 00225 g002
Figure 2. Development of mean annual temperature, total annual precipitation, and annual climatic water balance averaged for the state of Brandenburg, Germany, from 1880 to 2024 (black lines). Red lines show a thin-plate regression spline model.
Figure 2. Development of mean annual temperature, total annual precipitation, and annual climatic water balance averaged for the state of Brandenburg, Germany, from 1880 to 2024 (black lines). Red lines show a thin-plate regression spline model.
Forests 16 00225 g002
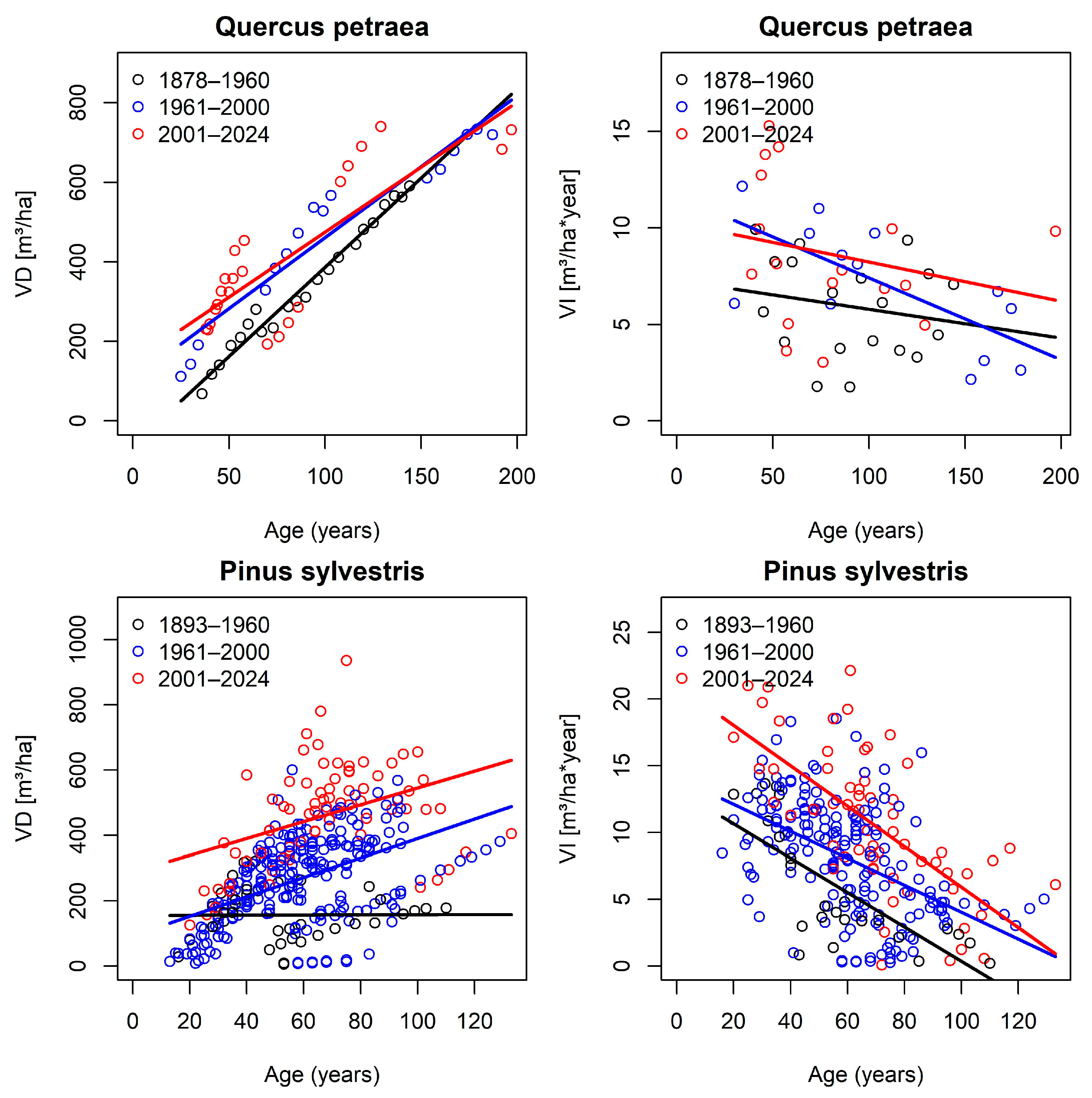
Forests 16 00225 g003
Figure 3. Standing volume VD [m3/ha] (left) and volume increment VI [m3/ha*year] (right) over tree age for Sessile oak (Quercus petraea) (top) and Scots pine (Pinus sylvestris) (bottom). Red, blue, and black refer to different time periods used for circles and lines. Lines indicate linear trend models for each time period and species.
Figure 3. Standing volume VD [m3/ha] (left) and volume increment VI [m3/ha*year] (right) over tree age for Sessile oak (Quercus petraea) (top) and Scots pine (Pinus sylvestris) (bottom). Red, blue, and black refer to different time periods used for circles and lines. Lines indicate linear trend models for each time period and species.
Forests 16 00225 g003
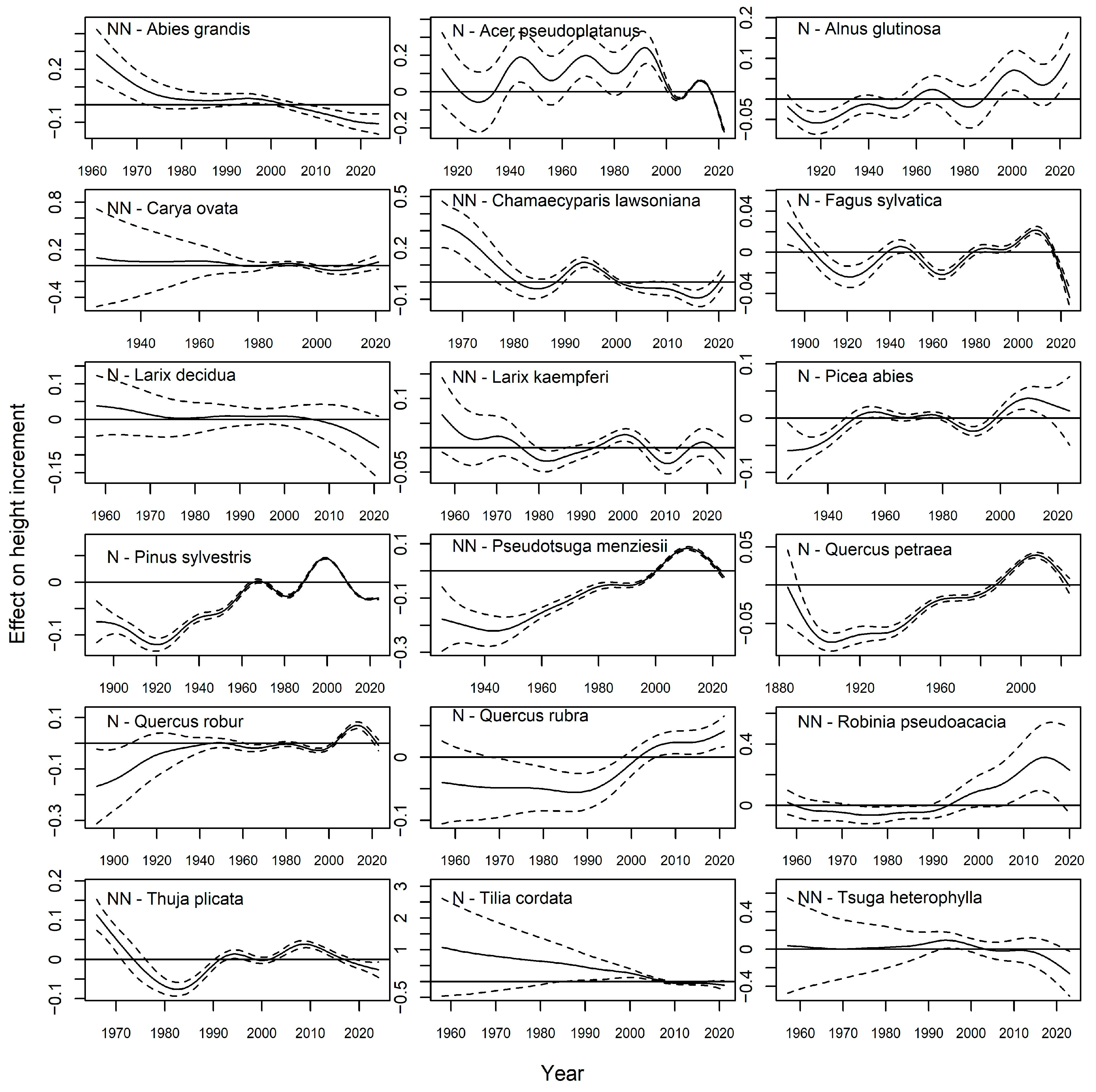
Forests 16 00225 g004
Figure 4. Partial effect plots for the effect of the calendar year on tree height increment. The smooth estimate is shown as a solid line; dashed lines indicate 2 standard errors added to the smooth estimate. Partial effect plots are centered at the overall mean. The term for the interaction between tree age and experimental plot is set to zero. NN and N denote the species classifications as non-native and native, respectively.
Figure 4. Partial effect plots for the effect of the calendar year on tree height increment. The smooth estimate is shown as a solid line; dashed lines indicate 2 standard errors added to the smooth estimate. Partial effect plots are centered at the overall mean. The term for the interaction between tree age and experimental plot is set to zero. NN and N denote the species classifications as non-native and native, respectively.
Forests 16 00225 g004
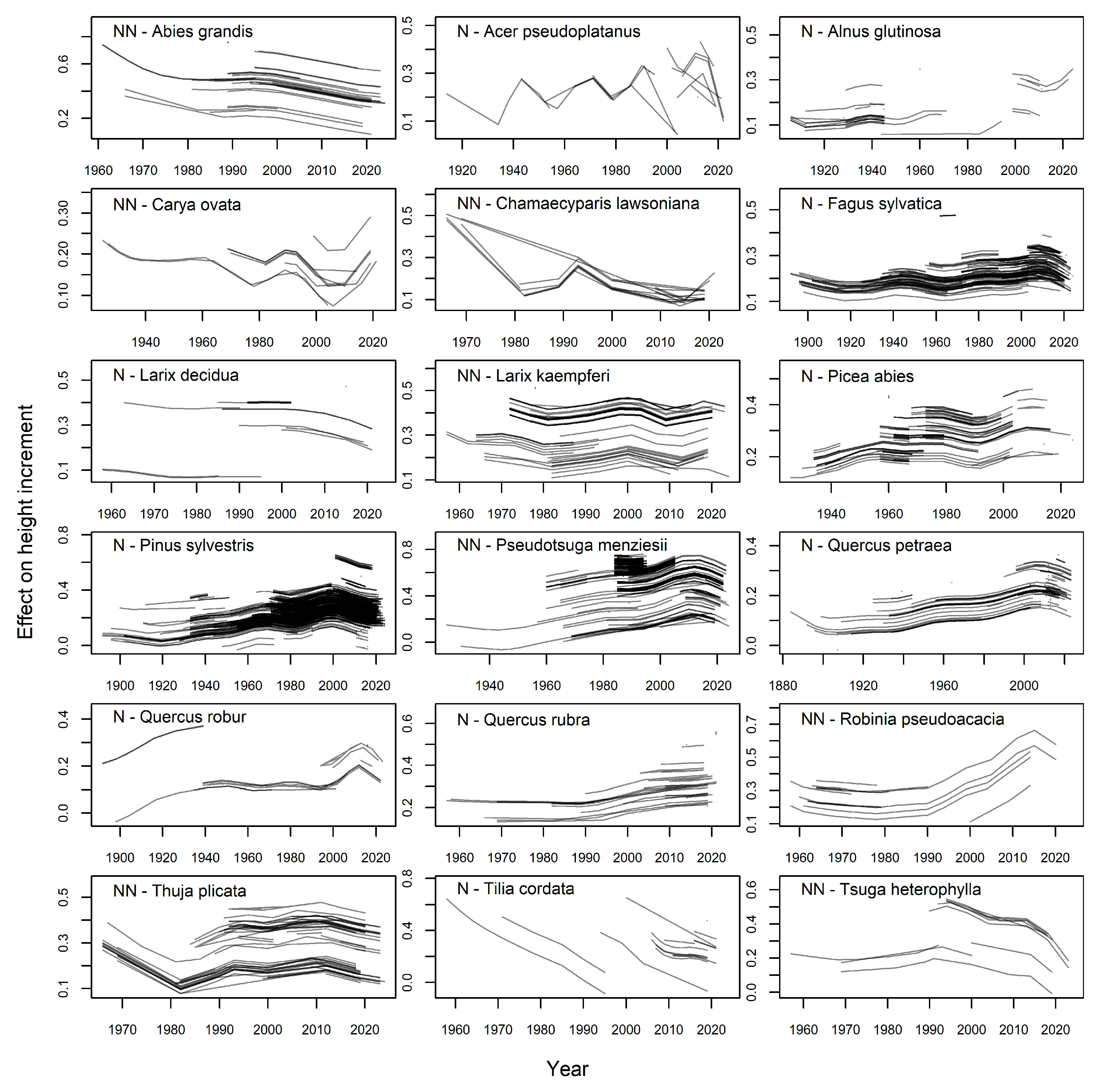
Forests 16 00225 g005
Figure 5. Calendar year effect plots on the model response scale with tree age set to its median. Site-specific variations are depicted with additional lines. NN and N denote the species classifications as non-native and native, respectively.
Figure 5. Calendar year effect plots on the model response scale with tree age set to its median. Site-specific variations are depicted with additional lines. NN and N denote the species classifications as non-native and native, respectively.
Forests 16 00225 g005
Table 1. Tree data summary for 18 tree species used in the analysis and modeling. Orig denotes the species origin: NN in case of non-native, N for native species. Age denotes the age range of trees in the analysis; Years denotes the year range of height measurements in the analysis. Nb Plots denotes the number of plots on which the species occurs, and Nb Incr denotes the number of tree height increments used in the data analysis. Incr denotes the range of annual tree height increments for a particular tree species.
Table 1. Tree data summary for 18 tree species used in the analysis and modeling. Orig denotes the species origin: NN in case of non-native, N for native species. Age denotes the age range of trees in the analysis; Years denotes the year range of height measurements in the analysis. Nb Plots denotes the number of plots on which the species occurs, and Nb Incr denotes the number of tree height increments used in the data analysis. Incr denotes the range of annual tree height increments for a particular tree species.
SpeciesOrigAgeYearsNb PlotsNb IncrIncr [m/Year]
1Abies grandis (Douglas ex D. Don) Lindl.NN20–1271955–20243222980.1–1
2Acer pseudoplatanus L.N5–1241909–20221447390–0.5
3Alnus glutinosa (L.) Gaertn.N12–1491900–2024317510–0.5
4Carya ovata (Mill.) K. KochNN43–1381914–2021814800–0.5
5Chamaecyparis lawsoniana (A. Murr.) Parl.NN78–1351955–2021147460–0.5
6Fagus sylvatica L.N3–1981884–202319415,0030–0.6
7Larix decidua Mill.N22–1301954–2021178520–0.6
8Larix kaempferi (Lamb.) CarrièreNN14–1291953–20244936040.1–0.7
9Picea abies (L.) H.Karst.N25–1391915–202311243760.1–0.6
10Pinus sylvestris L.N1–1871886–2024649103,0700–0.8
11Pseudotsuga menziesii (Mirbel) FrancoNN1–1441914–202441023,5380–0.9
12Quercus petraea (Mattuschka) Liebl.N20–2001878–20239686500–0.5
13Quercus robur L.N12–2001890–20231418810.1–0.4
14Quercus rubra L.NN1–1341953–20213314960.1–0.7
15Robinia pseudoacacia L.NN14–1191954–20201316480.1–0.6
16Thuja plicata Donn ex D. Don.NN13–1391954–20245535450–0.6
17Tilia cordata Mill.N1–811954–20211522150.1–0.6
18Tsuga heterophylla (Raf.) Sarg.NN31–1411953–202394130.1–0.6
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Engel, M.; Hagemann, U.; Schröder, J. Long-Term Growth Trends of 18 Native and Non-Native Tree Species Based on Data from Experimental Plots Since 1878 in Brandenburg, Germany. Forests 2025, 16, 225. https://doi.org/10.3390/f16020225

AMA Style

Engel M, Hagemann U, Schröder J. Long-Term Growth Trends of 18 Native and Non-Native Tree Species Based on Data from Experimental Plots Since 1878 in Brandenburg, Germany. Forests. 2025; 16(2):225. https://doi.org/10.3390/f16020225

Chicago/Turabian Style

Engel, Markus, Ulrike Hagemann, and Jens Schröder. 2025. "Long-Term Growth Trends of 18 Native and Non-Native Tree Species Based on Data from Experimental Plots Since 1878 in Brandenburg, Germany" Forests 16, no. 2: 225. https://doi.org/10.3390/f16020225

APA Style

Engel, M., Hagemann, U., & Schröder, J. (2025). Long-Term Growth Trends of 18 Native and Non-Native Tree Species Based on Data from Experimental Plots Since 1878 in Brandenburg, Germany. Forests, 16(2), 225. https://doi.org/10.3390/f16020225

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop