Characteristics of Biomass and Carbon Stocks Accumulation and Biomass Estimation Model in Kandelia obovata Mangroves at the Northern Edge of Its Distribution in China
Abstract
1. Introduction
2. Materials and Methods
2.1. General Description of the Study Area
2.2. Sample Collection
2.3. Data Analysis
2.3.1. Biomass Model Selection and Evaluation
2.3.2. Carbon Content
3. Results
3.1. The Carbon Content Rate of Each Component
3.2. Biomass and Carbon Storage Distribution Characteristics of Each Component
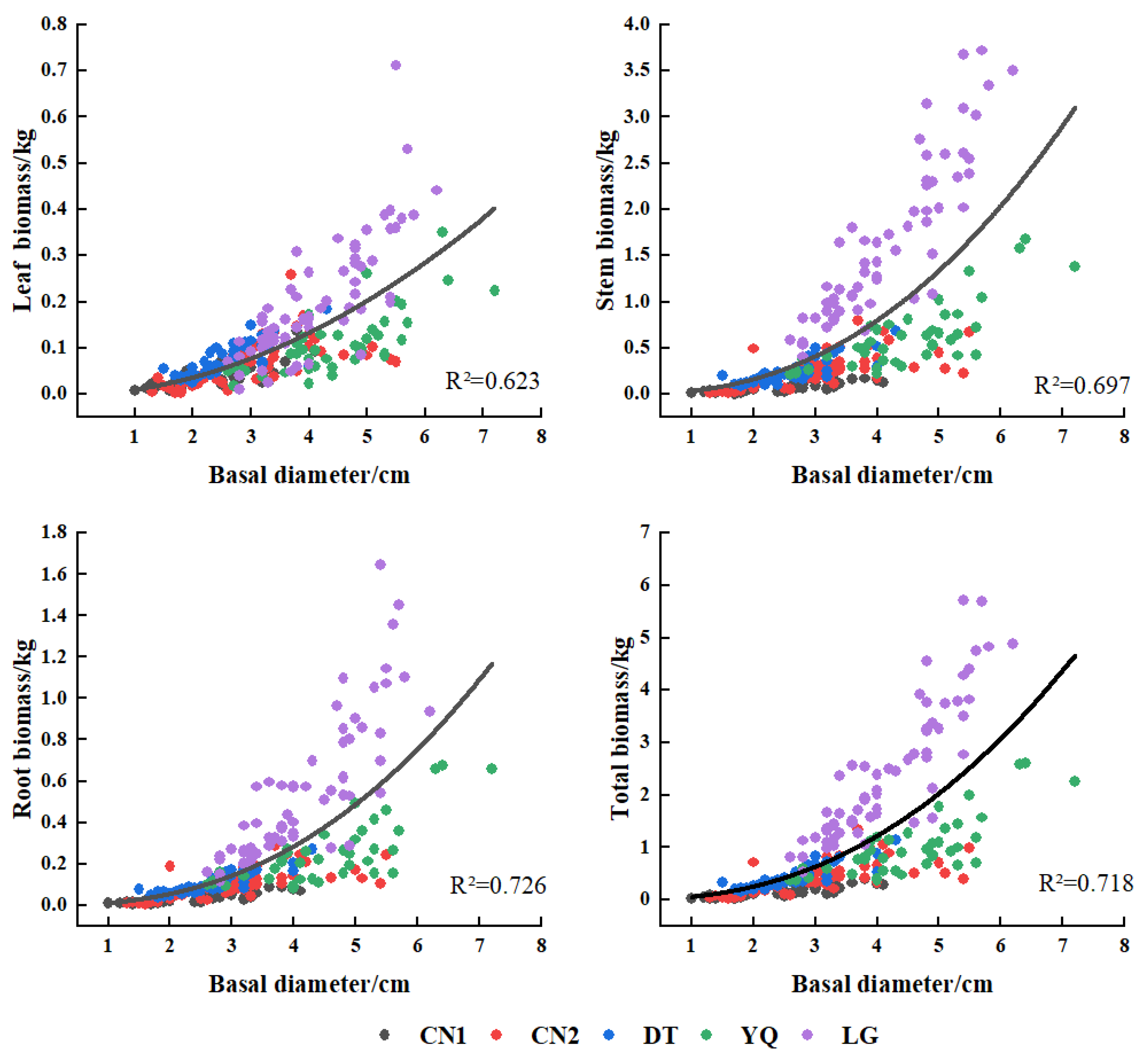
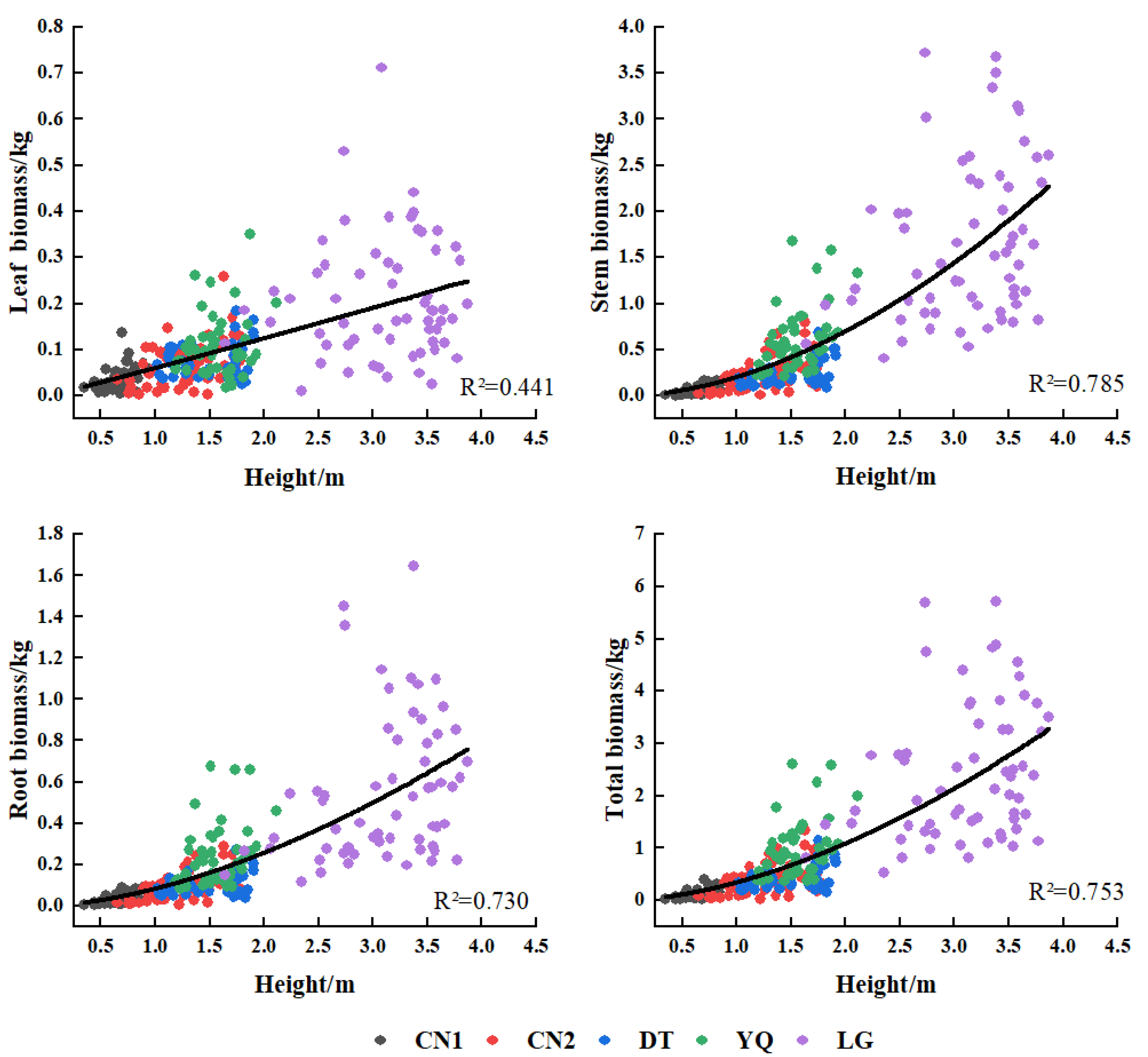
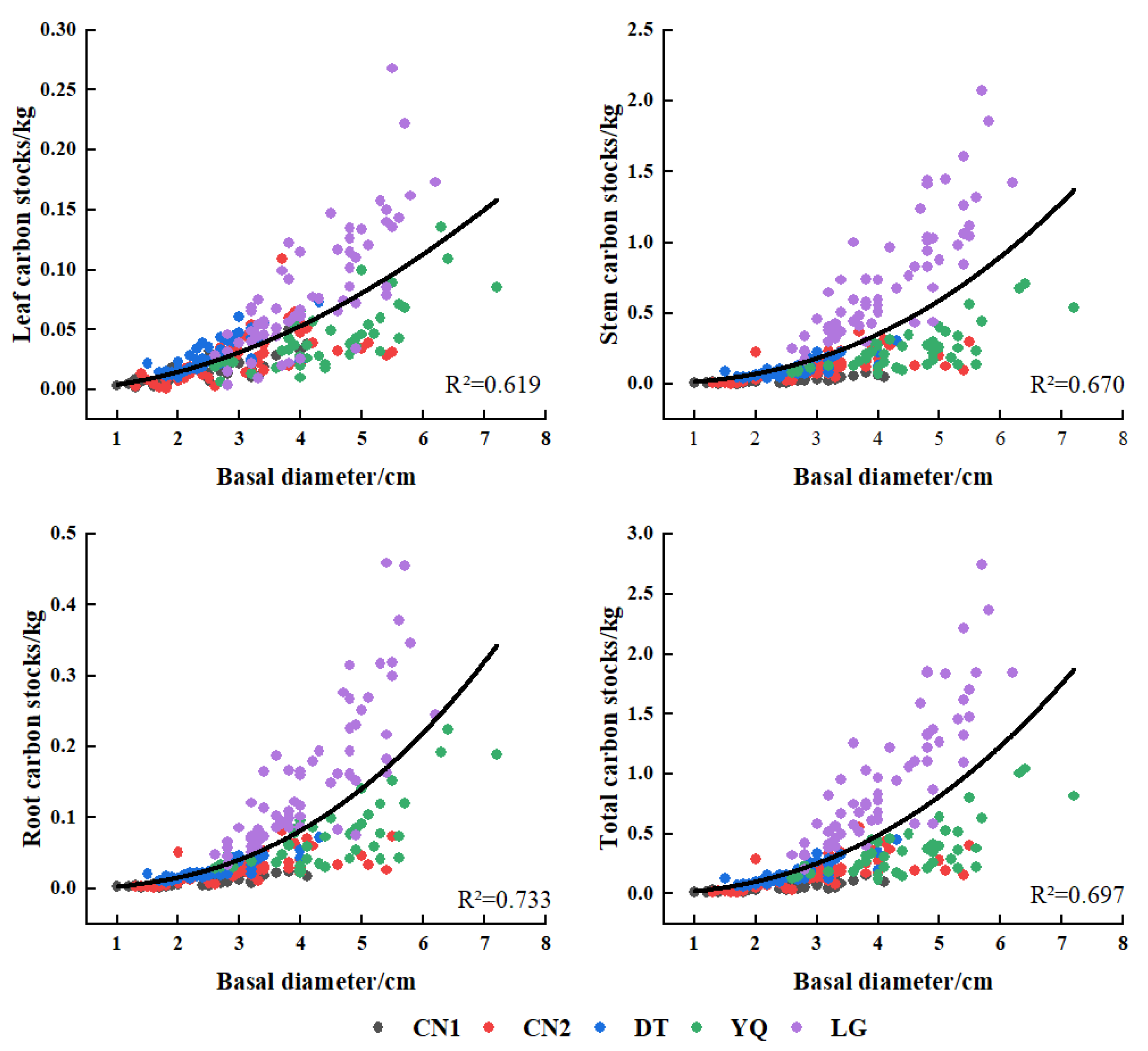
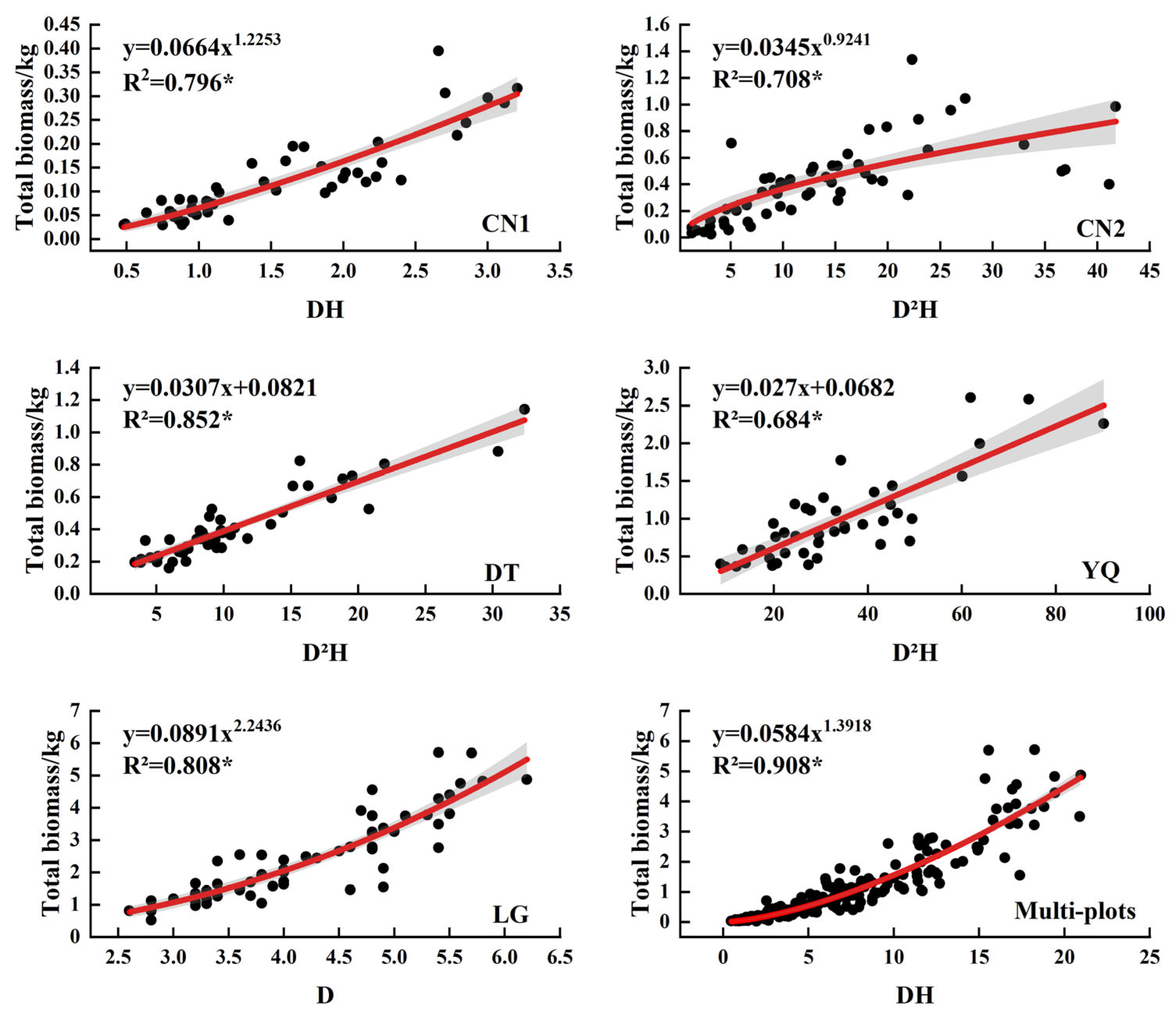
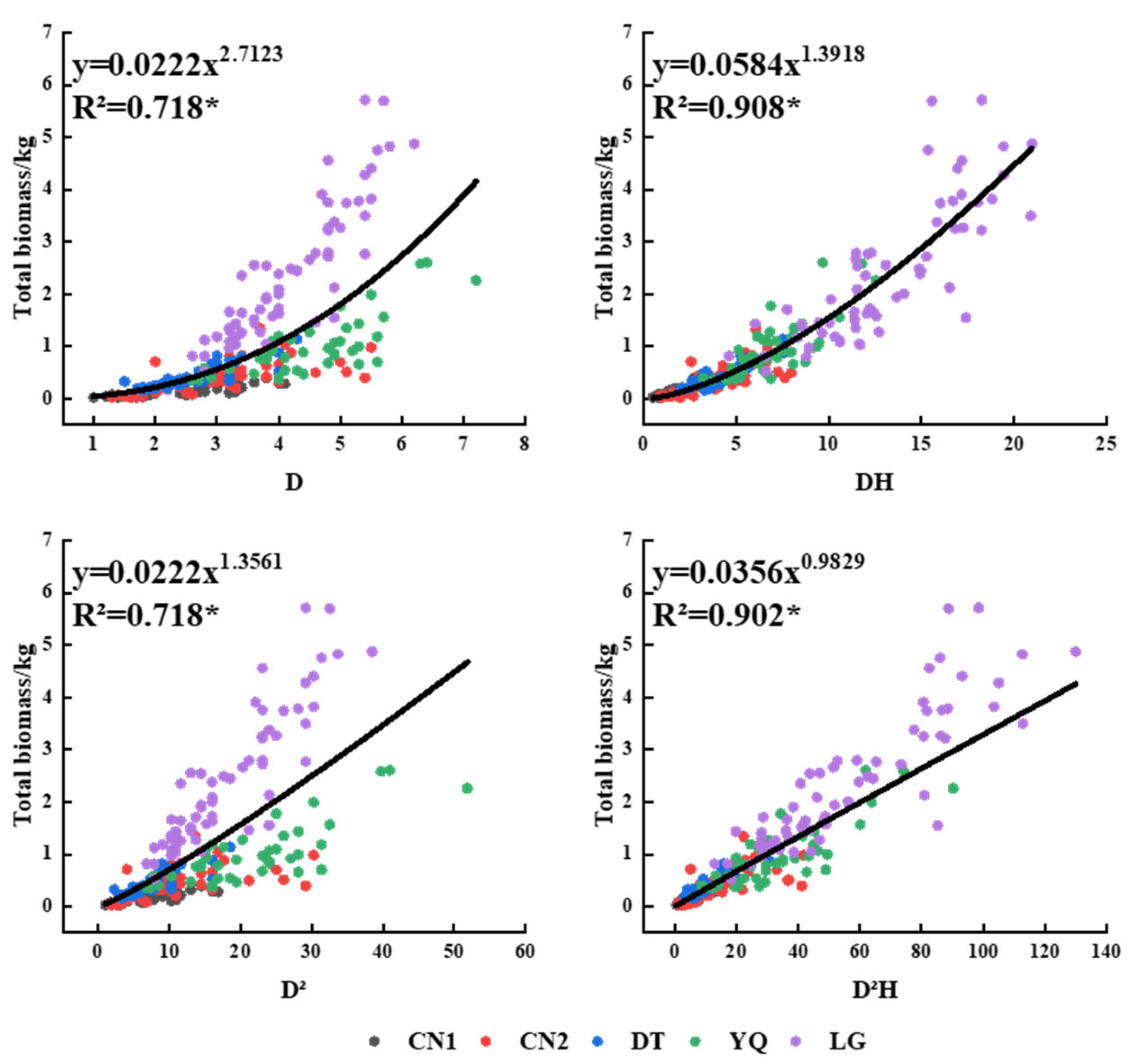
3.3. Biomass Model of Each Component of Kandelia Obovata
3.4. Biomass and Carbon Storage at Each Sample Plot
4. Discussion
4.1. Estimation of Carbon Content Rate in Kandelia obovata Mangroves
4.2. Biomass Distribution and Allocation in Trees at Different Growth Stages
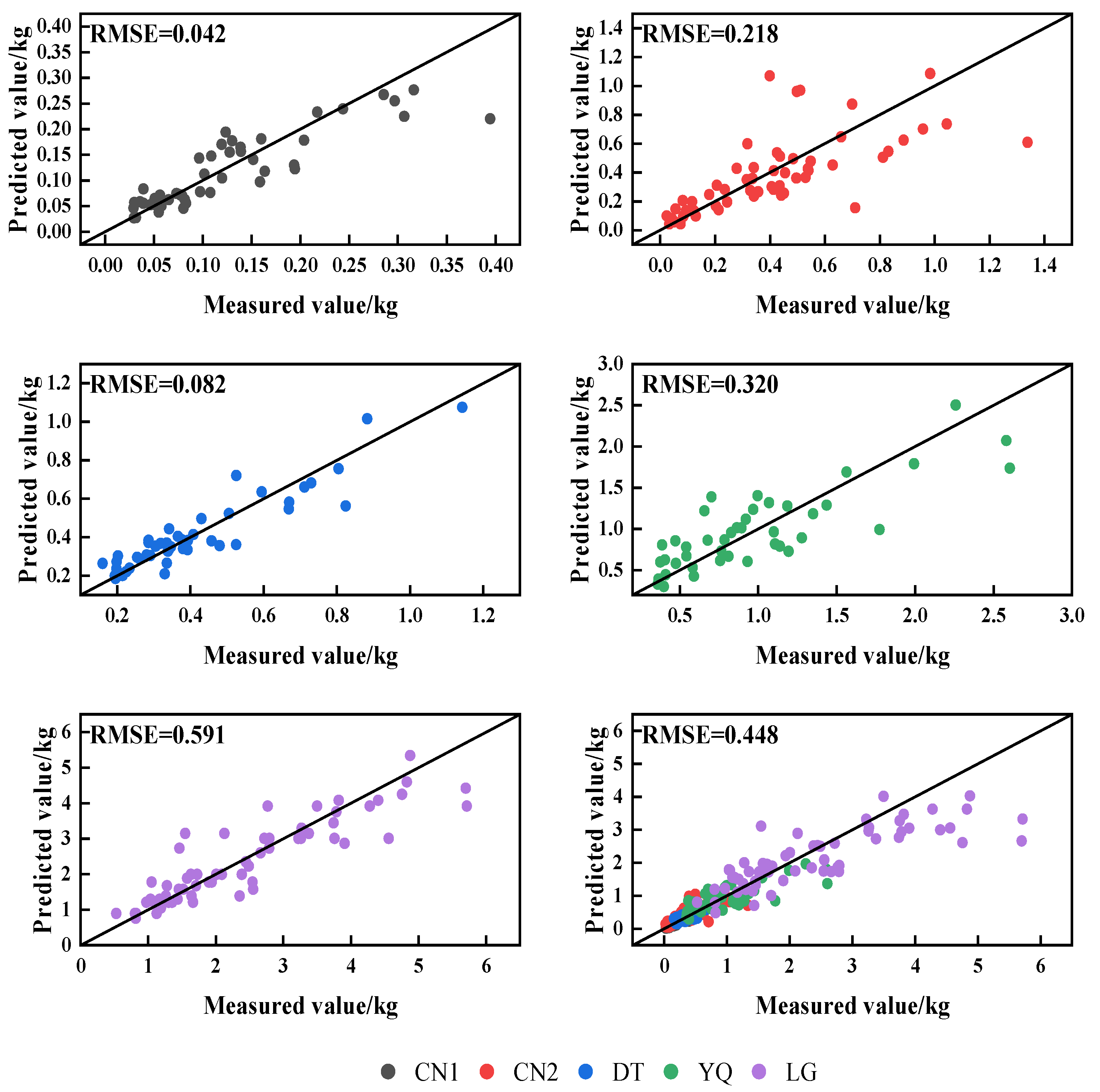
4.3. Analysis of Biomass Estimation Model
4.4. Limitations and Future Research Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Zeng, S.; Gao, M.; Chen, G.; Zhu, H.; Ye, Y.J. Potential effects of sea level rise on the soil-atmosphere greenhouse gas emissions in Kandelia obovata mangrove forests. Acta Oceanol. Sin. 2023, 42, 25–32. [Google Scholar] [CrossRef]
- Nijbroek, R.P. Mangroves, mudbanks and seawalls: Whose environmental knowledge counts when adapting to sea level rise in Suriname? J. Political Ecol. 2014, 21, 533–550. [Google Scholar] [CrossRef][Green Version]
- Bhomia, R.K.; Kauffman, J.B.; McFadden, T.N. Ecosystem carbon stocks of mangrove forests along the Pacific and Caribbean coasts of Honduras. Wetl. Ecol. Manag. 2016, 24, 187–201. [Google Scholar] [CrossRef]
- Yee, S. REDD and BLUE Carbon: Carbon Payments for Mangrove Conservation. 2010. Available online: https://escholarship.org/uc/item/2bc6j8pz (accessed on 15 July 2023).
- Bai, J.; Meng, Y.; Gou, R.; Lyu, J.; Lin, G. Mangrove diversity enhances plant biomass production and carbon storage in Hainan island, China. Funct. Ecol. 2021, 35, 774–786. [Google Scholar] [CrossRef]
- Ellison, A.M.; Felson, A.J.; Friess, D.A. Mangrove Rehabilitation and Restoration as Experimental Adaptive Management. Front. Mar. Sci. 2020, 7, 327. [Google Scholar] [CrossRef]
- Veettil, B.K.; Pereira, S.F.R.; Quang, N.X. Rapidly diminishing mangrove forests in Myanmar (Burma): A review. Hydrobiologia 2018, 822, 19–35. [Google Scholar] [CrossRef]
- Jia, M.; Wang, Z.; Mao, D.; Huang, C.; Lu, C. Spatial-temporal changes of China’s mangrove forests over the past 50 years: An analysis towards the Sustainable Development Goals (SDGs). Chin. Sci. Bull. 2021, 66, 3886–3901. [Google Scholar] [CrossRef]
- Zhao, J.; Xie, H.; Ma, J.; Wang, K. Integrated remote sensing and model approach for impact assessment of future climate change on the carbon budget of global forest ecosystems. Glob. Planet. Change 2021, 203, 103542. [Google Scholar] [CrossRef]
- Richards, D.R.; Friess, D.A. Rates and drivers of mangrove deforestation in Southeast Asia, 2000–2012. Proc. Natl. Acad. Sci. USA 2016, 113, 344–349. [Google Scholar] [CrossRef]
- Jia, M.; Wang, Z.; Zhang, Y.; Mao, D.; Wang, C. Monitoring loss and recovery of mangrove forests during 42 years: The achievements of mangrove conservation in China. Int. J. Appl. Earth Obs. Geoinform. 2018, 73, 535–545. [Google Scholar] [CrossRef]
- Jia, M.; Wang, Z.; Zhang, Y.; Ren, C.; Song, K. Landsat-based estimation of mangrove forest loss and restoration in Guangxi province, China, influenced by human and natural factors. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 311–323. [Google Scholar] [CrossRef]
- Youshao, W. Impacts, challenges and opportunities of global climate change on mangrove ecosystems. J. Trop. Oceanogr. 2021, 40, 1–14. [Google Scholar]
- Wang, Q.X.; Song, L.; Agusti, S.; Duarte, C.; Christakos, G.; Wu, J.P. Changes of the Macrobenthos Community with Non-native Mangrove Rehabilitation (Kandelia obovata) and Salt Marsh Invasion (Spartina alterniflora) in Ximen Island, Zhejiang, China. Ocean Sci. J. 2021, 56, 395–405. [Google Scholar] [CrossRef]
- Hu, T.Y.; Zhang, Y.Y.; Su, Y.J.; Zheng, Y.; Lin, G.H.; Guo, Q.H. Mapping the Global Mangrove Forest Aboveground Biomass Using Multisource Remote Sensing Data. Remote Sens. 2020, 12, 1690. [Google Scholar] [CrossRef]
- Zhu, Z.; Huang, M.M.; Zhou, Z.Y.; Chen, G.X.; Zhu, X.D. Stronger conservation promotes mangrove biomass accumulation: Insights from spatially explicit assessments using UAV and Landsat data. Remote Sens. Ecol. Conserv. 2022, 8, 656–669. [Google Scholar] [CrossRef]
- Dong, L.H.; Li, F.R.; Song, Y.W. Error structure and additivity of individual tree biomass model for four natural conifer species in Northeast China. Yingyong Shengtai Xuebao 2015, 26, 704. [Google Scholar]
- Wang, Z.; Du, H.; Song, T.; Peng, W.; Zeng, F.; Zeng, Z.; Zhang, H. Allometric models of major tree species and forest biomass in Guangxi. Acta Ecol. Sin. 2015, 35, 4462–4472. [Google Scholar]
- Dong, L.H.; Li, F.R.; Jia, W.W. Development of tree biomass model for Pinus koraiensis plantation. J. Beijing For. Univ. 2012, 34, 16–22. [Google Scholar]
- Fu, L.Y.; Tang, S.Z.; Zhang, H.R. Generalized above-ground biomass equations for two main species in northeast China. Acta Ecol Sin. 2015, 35, 150–157. [Google Scholar]
- Zhao, H.; Li, Z.; Zhou, G.; Qiu, Z.; Wu, Z. Site-specific allometric models for prediction of above-and belowground biomass of subtropical forests in Guangzhou, southern China. Forests 2019, 10, 862. [Google Scholar] [CrossRef]
- Kebede, B.; Soromessa, T. Allometric equations for aboveground biomass estimation of Olea europaea L. subsp. cuspidata in Mana Angetu Forest. Ecosyst. Health Sustain. 2018, 4, 1–12. [Google Scholar] [CrossRef]
- Huang, R.X.; Wu, Z.L.; Peng, J.W.; Xue, C.Q.; Luo, Y.; Su, Z.Y. Biomass model of Bruguiera gymnorrhiza in Guangdong. J. Northwest A F Univ.—Nat. Sci. Ed. 2019, 47, 86–94. [Google Scholar]
- Lin, Q.-l.; Gu, X.-x.; Chen, X.-w.; Guo, X.-d.; Cai, L.-z.; Lin, L.; Chen, W.-d.; Dong, Y.; Feng, H.-y.; Cai, H.-c.; et al. Coastal wetland restoration based on mangrove Kandelia obovata substitution controlling Spartina alterniflora invasion: A case study of Aojiang Estuary in Zhejiang Province. Chin. J. Ecol. 2020, 39, 1761. [Google Scholar]
- Wu, W.Z.; Zhao, Z.X.; Yang, S.; Liang, L.C.; Chen, Q.X.; Lu, X.; Liu, X.; Zhang, X.W. The mangrove forest distribution and analysis of afforestation effect in Zhejiang Province. J. Trop. Oceanogr. 2022, 41, 67–74. [Google Scholar]
- Dong, L.; Zhang, L.; Li, F. Allometry and partitioning of individual tree biomass and carbon of Abies nephrolepis Maxim in northeast China. Scand. J. For. Res. 2016, 31, 399–411. [Google Scholar] [CrossRef]
- Ong, J.; Gong, W.; Wong, C. Allometry and partitioning of the mangrove, Rhizophora apiculata. For. Ecol. Manag. 2004, 188, 395–408. [Google Scholar] [CrossRef]
- Vinh, T.V.; Marchand, C.; Linh, T.V.K.; Vinh, D.D.; Allenbachd, M. Allometric models to estimate above-ground biomass and carbon stocks in Rhizophora apiculata tropical managed mangrove forests (Southern Viet Nam). For. Ecol. Manag. 2019, 434, 131–141. [Google Scholar] [CrossRef]
- Yang, S.-C.; Lu, W.-X.; Zhen, Z.; Si, L. Mangrove wetlands: Distribution, species composition and protection in China. Subtrop. Plant Sci. 2017, 46, 301. [Google Scholar]
- Xu, Y.; Du, A.; Wang, Z.; Zhu, W.; Li, C.; Wu, L. Effects of different rotation periods of Eucalyptus plantations on soil physiochemical properties, enzyme activities, microbial biomass and microbial community structure and diversity. For. Ecol. Manag. 2020, 456, 117683. [Google Scholar] [CrossRef]
- Zhu, D.H.; Hui, D.F.; Wang, M.Q.; Yang, Q.; Li, Z.; Huang, Z.J.; Yuan, H.M.; Yu, S.X. Allometric growth and carbon storage in the mangrove Sonneratia apetala. Wetl. Ecol. Manag. 2021, 29, 129–141. [Google Scholar] [CrossRef]
- Rovai, A.S.; Twilley, R.R.; Castañeda-Moya, E.; Riul, P.; Cifuentes-Jara, M.; Manrow-Villalobos, M.; Horta, P.A.; Simonassi, J.C.; Fonseca, A.L.; Pagliosa, P.R. Global controls on carbon storage in mangrove soils. Nat. Clim. Change 2018, 8, 534–538. [Google Scholar] [CrossRef]
- Pandey, P.C.; Anand, A.; Srivastava, P.K. Spatial distribution of mangrove forest species and biomass assessment using field inventory and earth observation hyperspectral data. Biodivers. Conserv. 2019, 28, 2143–2162. [Google Scholar] [CrossRef]
- Rovai, A.S.; Twilley, R.R.; Castañeda-Moya, E.; Midway, S.R.; Friess, D.A.; Trettin, C.C.; Bukoski, J.J.; Stovall, A.E.L.; Pagliosa, P.R.; Fonseca, A.L.; et al. Macroecological patterns of forest structure and allometric scaling in mangrove forests. Glob. Ecol. Biogeogr. 2021, 30, 1000–1013. [Google Scholar] [CrossRef]
- Kauffman, J.B.; Bernardino, A.F.; Ferreira, T.O.; Giovannoni, L.R.; Gomes, L.E.D.; Romero, D.J.; Jimenez, L.C.Z.; Ruiz, F. Carbon stocks of mangroves and salt marshes of the Amazon region, Brazil. Biol. Lett. 2018, 14, 20180208. [Google Scholar] [CrossRef]
- Wang, R.; Li, X.-J.; Cai, J.-B.; Zhang, D.-Q.; He, D.-J.; Liu, C.; Wang, Q.-B.; Zheng, K.-J.; Lin, F. Comparative study on biomass of the natural Kandelia Candel forest and its plantation in the coastal area of east Fujian Province. Xinan Linxueyuan Xuebao/J. Southwest For. Univ. 2010, 30, 16–20. [Google Scholar]
- Wang, X.; Weng, Y.; Liu, G.; Krasowski, M.; Yang, C. Variations in carbon concentration, sequestration and partitioning among Betula platyphylla provenances. For. Ecol. Manag. 2015, 358, 344–352. [Google Scholar] [CrossRef]
- Zanvoa, S.M.G.; Mensah, S.; Salako, K.; Kakaï, R.G. Tree height-diameter, aboveground and belowground biomass allometries for two West African mangrove species. Biomass Bioenerg. 2023, 176, 106917. [Google Scholar] [CrossRef]
- Zhao, H.-b.; Zhou, G.-y.; Li, Z.-j.; Qiu, Z.-j.; Wu, Z.-m.; Wang, X. Biomass allocation and allometric growth models of four common tree species in Southern subtropical evergreen broad-leaved forest. Sci. Silvae Sin. 2022, 58, 23–31. [Google Scholar]
- Njana, M.A.; Bollandsås, O.M.; Eid, T.; Zahabu, E.; Malimbwi, R.E. Above- and belowground tree biomass models for three mangrove species in Tanzania: A nonlinear mixed effects modelling approach. Ann. For. Sci. 2016, 73, 353–369. [Google Scholar] [CrossRef]
- Wang, M.S.; Madden, M.; Hendy, I.; Estradivari; Ahmadia, G.N. Modeling projected changes of mangrove biomass in different climatic scenarios in the Sunda Banda Seascapes. Int. J. Digit. Earth 2017, 10, 457–468. [Google Scholar] [CrossRef]

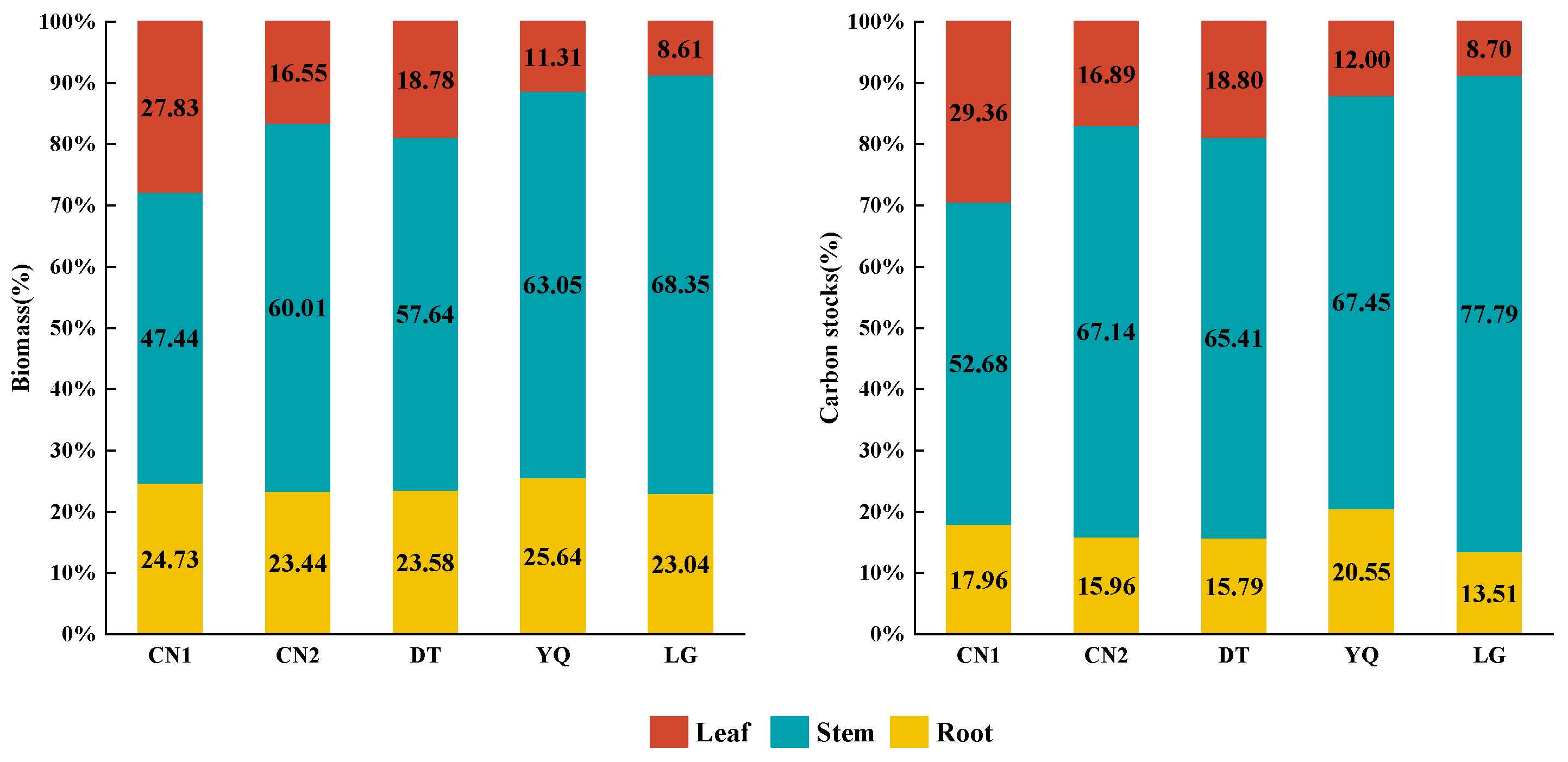
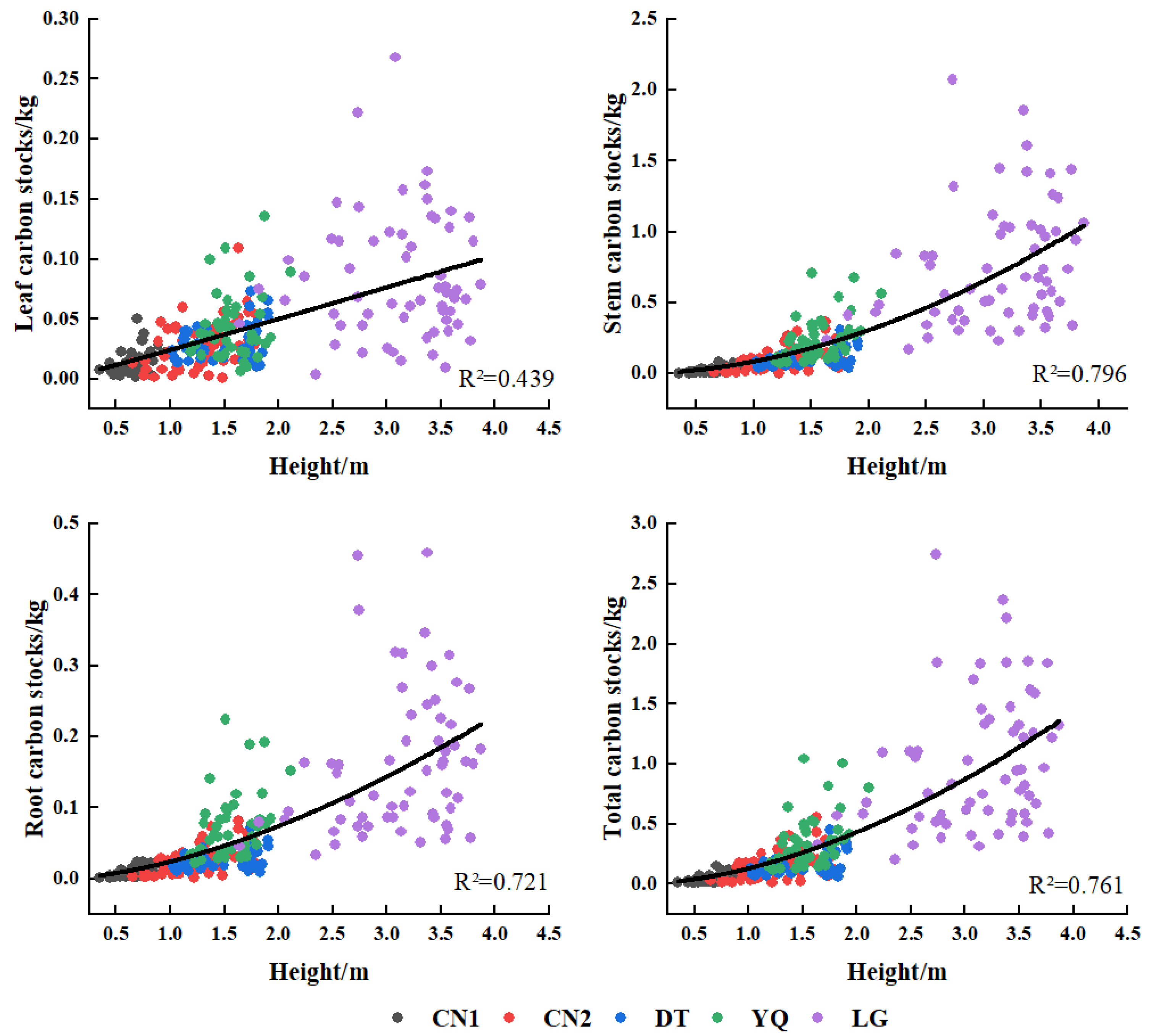

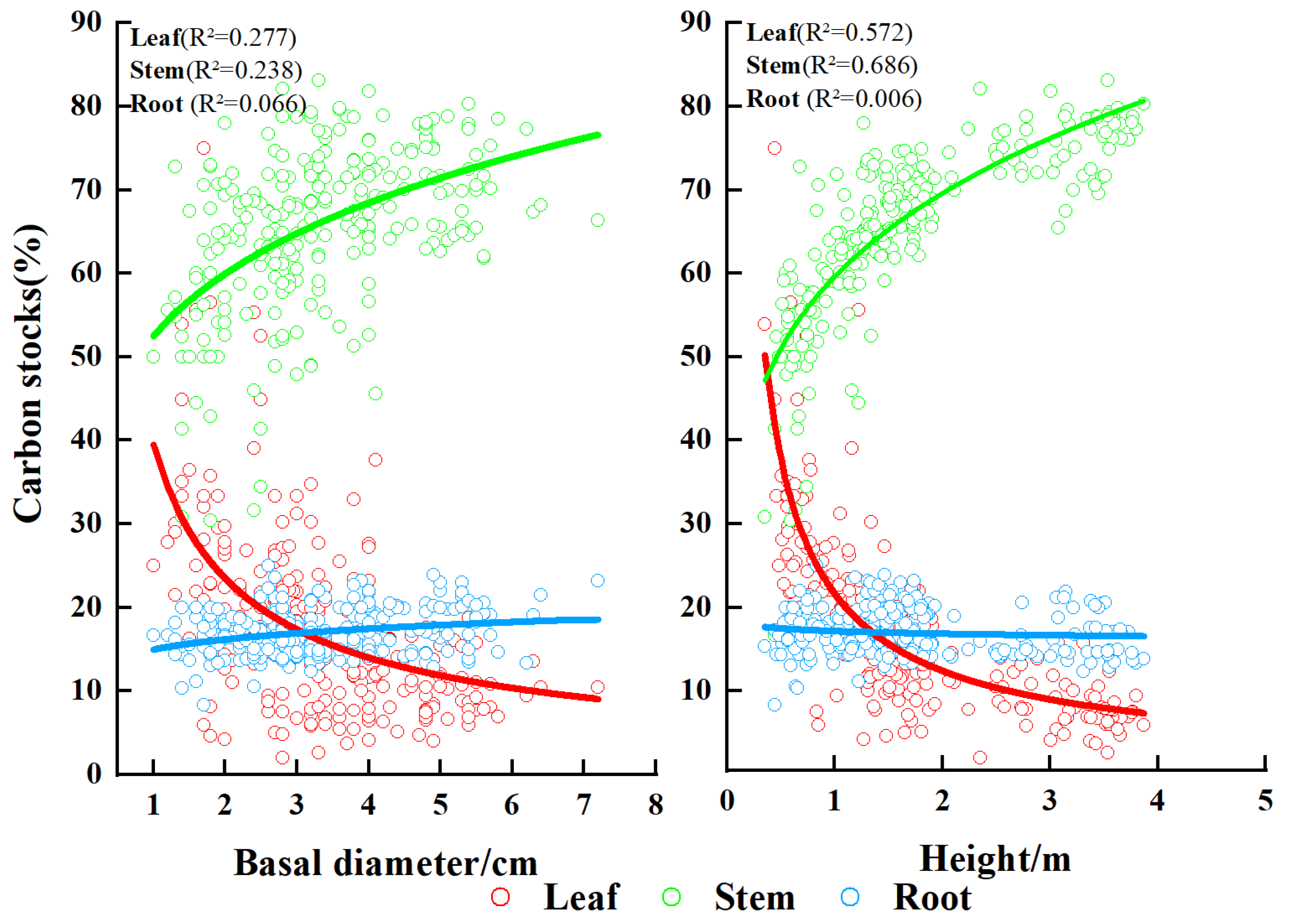
| Plots | Ages | N | D (cm) | H (m) | LB (kg) (Mean ± SD) | SB (kg) (Mean ± SD) | RB (kg) (Mean ± SD) |
|---|---|---|---|---|---|---|---|
| CN1 | 5 | 47 | 1.1~4.1 | 0.35~0.95 | 0.034 ± 0.025 | 0.059 ± 0.043 | 0.031 ± 0.023 |
| CN2 | 7 | 55 | 1.3~5.5 | 0.65~1.78 | 0.069 ± 0.048 | 0.249 ± 0.183 | 0.097 ± 0.067 |
| DT | 9 | 45 | 1.5~4.3 | 1.02~1.91 | 0.078 ± 0.037 | 0.240 ± 0.135 | 0.098 ± 0.049 |
| YQ | 14 | 42 | 2.6~7.2 | 1.19~2.11 | 0.111 ± 0.069 | 0.617 ± 0.361 | 0.251 ± 0.156 |
| LG | 20 | 61 | 2.6~6.2 | 1.64~3.87 | 0.209 ± 0.133 | 1.657 ± 0.868 | 0.559 ± 0.351 |
| average | 3.3 ± 1.2 | 1.70 ± 0.92 | 0.105 ± 0.099 | 0.617 ± 0.769 | 0.223 ± 0.275 |
| plots | LB[C]% (Mean ± SD) | SB[C]% (Mean ± SD) | RB[C]% (Mean ± SD) | TB[C]% (Mean ± SD) |
|---|---|---|---|---|
| CN1 | 39.48 ± 2.61 | 41.85 ± 3.45 | 27.53 ± 2.36 | 37.76 ± 1.90 |
| CN2 | 41.26 ± 2.71 | 45.37 ± 0.53 | 27.58 ± 1.81 | 40.43 ± 1.23 |
| DT | 38.71 ± 1.75 | 44.06 ± 0.73 | 25.88 ± 1.17 | 38.67 ± 1.30 |
| YQ | 39.29 ± 2.80 | 38.92 ± 4.29 | 29.51 ± 2.10 | 36.55 ± 3.27 |
| LG | 40.44 ± 1.88 | 44.73 ± 5.00 | 28.87 ± 1.67 | 40.79 ± 3.71 |
| average | 39.94 ± 2.84 | 43.23 ± 4.15 | 27.90 ± 2.86 | 39.05 ± 3.04 |
| p-value | <0.01 | <0.01 | <0.01 | <0.01 |
| Plots | Variate | Equations | x | a | b | c | R2 | F | rmse | aic | cf |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CN1 | LB | y = a + bx | D2 | 0.0065 | 0.0047 | 0.579 | 61.93 | 0.016 | −383.17 | ||
| SB | y = a + bx + cx2 | DH | 0.0067 | 0.0134 | 0.0104 | 0.822 | 101.93 | 0.018 | −371.40 | ||
| RB | y = a + bx + cx2 | DH | 0.0036 | 0.0068 | 0.0055 | 0.815 | 96.93 | 0.010 | −430.22 | ||
| TB | y = axb | DH | 0.0664 | 1.2253 | 0.796 | 175.46 | 0.042 | −294.94 | 1.05 | ||
| CN2 | LB | y = axb | D2 | 0.0058 | 1.0201 | 0.546 | 63.82 | 0.045 | −337.38 | 1.23 | |
| SB | y = axb | D2H | 0.0172 | 0.9865 | 0.701 | 124.44 | 0.142 | −210.52 | 1.16 | ||
| RB | y = axb | D2H | 0.0076 | 0.9486 | 0.729 | 142.58 | 0.049 | −327.17 | 1.13 | ||
| TB | y = axb | D2H | 0.0345 | 0.9241 | 0.708 | 128.41 | 0.218 | −163.52 | 1.14 | ||
| DT | LB | y = a + bx | D2H | 0.0281 | 0.0046 | 0.635 | 74.68 | 0.022 | −337.88 | ||
| SB | y = a + bx | D2H | 0.0310 | 0.0192 | 0.850 | 244.01 | 0.052 | −262.61 | |||
| RB | y = a + bx | D2H | 0.0229 | 0.0069 | 0.832 | 212.86 | 0.020 | −348.37 | |||
| TB | y = a + bx | D2H | 0.0821 | 0.0307 | 0.852 | 247.54 | 0.082 | −220.97 | |||
| YQ | LB | y = a + bx | D2 | 0.0021 | 0.0053 | 0.563 | 51.50 | 0.045 | −256.45 | ||
| SB | y = a + bx | D2H | 0.0416 | 0.0171 | 0.695 | 91.21 | 0.197 | −132.55 | |||
| RB | y = a + bx | D2H | 0.0120 | 0.0070 | 0.648 | 73.55 | 0.091 | −197.30 | |||
| TB | y = a + bx | D2H | 0.0682 | 0.0270 | 0.684 | 86.43 | 0.320 | −91.75 | |||
| LG | LB | y = a + bx | D2 | 0.0362 | 0.0134 | 0.642 | 105.84 | 0.079 | −1267.05 | ||
| SB | y = axb | D | 0.0689 | 2.1621 | 0.802 | 239.53 | 0.391 | −465.67 | 1.03 | ||
| RB | y = axb | D2H | 0.0073 | 1.0557 | 0.788 | 219.54 | 0.198 | −805.28 | 1.04 | ||
| TB | y = axb | D | 0.0891 | 2.2436 | 0.808 | 247.98 | 0.591 | −258.72 | 1.03 | ||
| Multi-plots | LB | y = a + bx | D2H | 0.0249 | 0.0031 | 0.690 | 552.15 | 0.055 | −1444.09 | ||
| SB | y = axb | DH | 0.0265 | 1.5563 | 0.920 | 2854.15 | 0.273 | −644.80 | 1.08 | ||
| RB | y = axb | DH | 0.0137 | 1.3923 | 0.896 | 2132.50 | 0.128 | −1024.91 | 1.09 | ||
| TB | y = axb | DH | 0.0584 | 1.3918 | 0.908 | 2459.87 | 0.448 | −397.02 | 1.07 |
| Plot | Ages | Number of Branches | Mean ± SD D (m) | Mean ± SD H (m) | Biomass (Mg/ha) | Carbon Stocks (MgC/ha) | Biomass Accumulation Rate (Mgha−1yr−1) | Carbon Stock Accumulation Rate (MgCha−1yr−1) |
|---|---|---|---|---|---|---|---|---|
| CN1-1 | 5 | 382 | 3.0 ± 0.9 | 0.61 ± 0.10 | 0.106 | 0.040 | 0.021 | 0.008 |
| CN1-2 | 5 | 397 | 2.8 ± 1.0 | 0.59 ± 0.11 | 0.100 | 0.038 | 0.020 | 0.008 |
| CN1-3 | 5 | 398 | 2.7 ± 1.0 | 0.61 ± 0.10 | 0.101 | 0.038 | 0.020 | 0.008 |
| CN1-4 | 5 | 400 | 2.8 ± 0.8 | 0.75 ± 0.10 | 0.112 | 0.042 | 0.022 | 0.008 |
| CN2-1 | 7 | 317 | 3.1 ± 0.9 | 1.09 ± 0.17 | 0.256 | 0.104 | 0.037 | 0.015 |
| CN2-2 | 7 | 321 | 2.7 ± 0.9 | 1.04 ± 0.15 | 0.202 | 0.082 | 0.029 | 0.012 |
| CN2-3 | 7 | 309 | 3.6 ± 1.1 | 1.35 ± 0.14 | 0.320 | 0.129 | 0.046 | 0.018 |
| CN2-4 | 7 | 317 | 3.2 ± 1.2 | 1.35 ± 0.17 | 0.274 | 0.111 | 0.039 | 0.016 |
| DT1 | 9 | 360 | 2.7 ± 0.7 | 1.47 ± 0.17 | 0.351 | 0.136 | 0.039 | 0.015 |
| DT2 | 9 | 484 | 2.3 ± 0.6 | 0.90 ± 0.13 | 0.318 | 0.123 | 0.035 | 0.014 |
| DT3 | 9 | 462 | 2.7 ± 0.7 | 1.65 ± 0.24 | 0.432 | 0.167 | 0.048 | 0.019 |
| DT4 | 9 | 408 | 2.5 ± 0.6 | 1.12 ± 0.16 | 0.328 | 0.127 | 0.036 | 0.014 |
| YQ1 | 14 | 364 | 3.9 ± 1.1 | 1.67 ± 0.21 | 0.611 | 0.223 | 0.044 | 0.016 |
| YQ2 | 14 | 403 | 3.3 ± 1.1 | 1.60 ± 0.22 | 0.489 | 0.179 | 0.035 | 0.013 |
| YQ3 | 14 | 288 | 4.0 ± 0.9 | 1.66 ± 0.15 | 0.477 | 0.174 | 0.034 | 0.012 |
| YQ4 | 14 | 317 | 3.2 ± 1.1 | 1.67 ± 0.22 | 0.378 | 0.138 | 0.027 | 0.010 |
| LG1 | 20 | 223 | 3.8 ± 1.1 | 2.97 ± 0.43 | 0.865 | 0.353 | 0.043 | 0.018 |
| LG2 | 20 | 205 | 3.9 ± 1.0 | 3.02 ± 0.40 | 0.809 | 0.330 | 0.040 | 0.016 |
| LG3 | 20 | 213 | 3.9 ± 1.0 | 3.17 ± 0.36 | 0.851 | 0.347 | 0.043 | 0.017 |
| LG4 | 20 | 201 | 4.1 ± 1.1 | 3.05 ± 0.39 | 0.925 | 0.377 | 0.046 | 0.019 |
| LG5 | 20 | 208 | 3.9 ± 1.3 | 2.97 ± 0.46 | 0.865 | 0.353 | 0.043 | 0.018 |
| LG6 | 20 | 181 | 4.3 ± 1.1 | 3.07 ± 0.35 | 0.882 | 0.360 | 0.044 | 0.018 |
| average | 325 ± 87 | 3.2 ± 1.1 | 1.61 ± 0.80 | 0.457 ± 0.282 | 0.180 ± 0.116 | 0.036 ± 0.009 | 0.014 ± 0.004 | |
| p-value | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Dai, W.; Shi, H.; Zhou, Y.; Chen, G.; Yang, S.; Peng, X.; Shi, Y. Characteristics of Biomass and Carbon Stocks Accumulation and Biomass Estimation Model in Kandelia obovata Mangroves at the Northern Edge of Its Distribution in China. Forests 2025, 16, 451. https://doi.org/10.3390/f16030451
Chen J, Dai W, Shi H, Zhou Y, Chen G, Yang S, Peng X, Shi Y. Characteristics of Biomass and Carbon Stocks Accumulation and Biomass Estimation Model in Kandelia obovata Mangroves at the Northern Edge of Its Distribution in China. Forests. 2025; 16(3):451. https://doi.org/10.3390/f16030451
Chicago/Turabian StyleChen, Jiahua, Wenzhe Dai, Haitao Shi, Yufeng Zhou, Guangsheng Chen, Sheng Yang, Xin Peng, and Yongjun Shi. 2025. "Characteristics of Biomass and Carbon Stocks Accumulation and Biomass Estimation Model in Kandelia obovata Mangroves at the Northern Edge of Its Distribution in China" Forests 16, no. 3: 451. https://doi.org/10.3390/f16030451
APA StyleChen, J., Dai, W., Shi, H., Zhou, Y., Chen, G., Yang, S., Peng, X., & Shi, Y. (2025). Characteristics of Biomass and Carbon Stocks Accumulation and Biomass Estimation Model in Kandelia obovata Mangroves at the Northern Edge of Its Distribution in China. Forests, 16(3), 451. https://doi.org/10.3390/f16030451







