Multi-Objective Spatial Optimization of Protective Forests Based on the Non-Dominated Sorting Genetic Algorithm-II Algorithm and Future Land Use Simulation Model: A Case Study of Alaer City, China
Abstract
:1. Introduction
2. Research Area and Data
2.1. Research Area
2.2. Data
- (1)
- Land use data
- (2)
- Driving Factors
- (3)
- Basic Geographic Data
2.3. Field Research
3. Materials and Methods
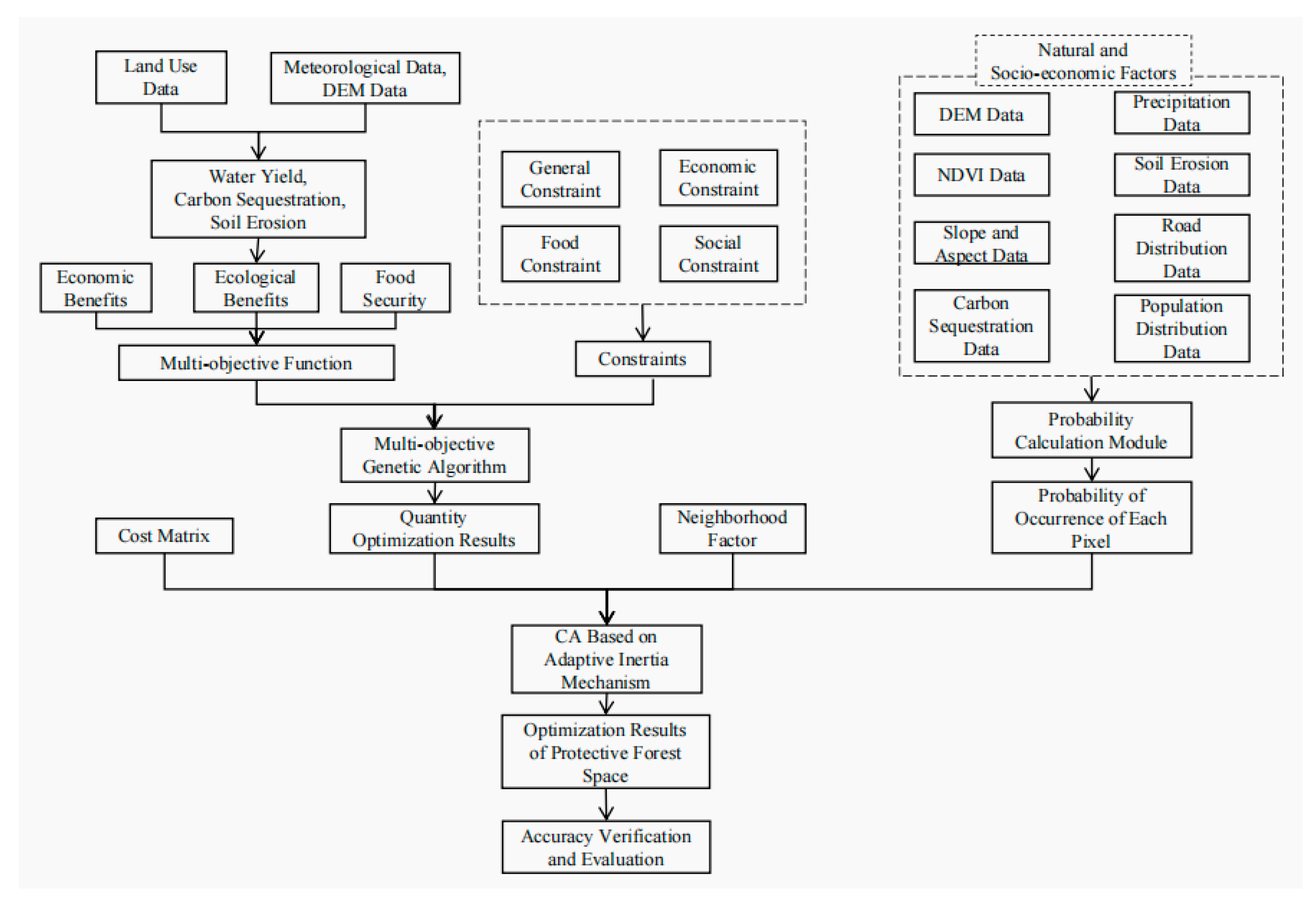
3.1. Technology Roadmap
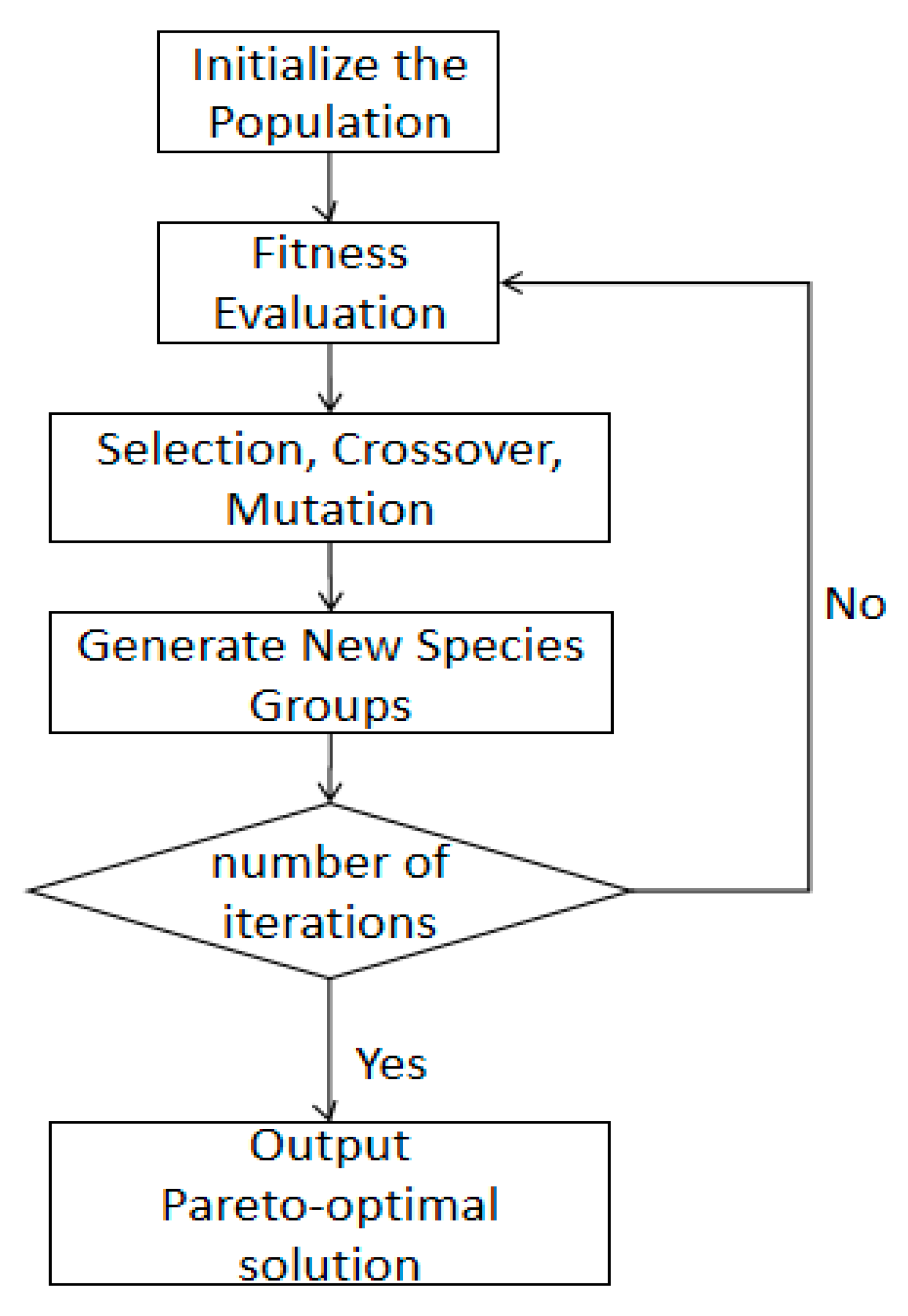
3.2. NSGA-II Algorithm
3.2.1. Algorithm Introduction
3.2.2. Construction of Constraints
- (1)
- Overall constraint: During the planning period, the total area of each land type should be equal to the total area of each land type in the base period, plus the area of reclaimed land. According to the “General Land Use Spatial Planning (Draft) of the First Division of the Corps in Alaer City”, the total area of Alaer City is 6923.29 square kilometers. In 2018, the area of unused land in Alaer City was 1308.50 hectares (hm2). Since the area available for reclamation in Alaer City is limited, the total area of all land types (∑xi) and the area of unused land (x5) in Alaer City must satisfy the following conditions: ∑xi = 6923.29; 0 < x5 ≤ 1308.50.
- (2)
- Ecological constraints: ① Protective forests demand constraint: In 2018, the protective forest area in Alaer City was 339.09 hectares (hm2). Given the significant ecological benefits provided by protective forest, it plays a crucial role in the environment. The area of protective forests (x2) must satisfy the following condition: x2 ≥ 339.09. ② River network water area guarantee: In 2018, the river water surface area in Alaer City was 255.62 hectares (hm2). The area of water bodies x4 must be no less than 90% of the base period’s water: x4 ≥ 230.06.
- (3)
- Food security constraints: ① Food demand constraint: According to projections, by 2028, Alaer City will need to maintain sufficient arable land to meet basic food demands. This means that the area of farmland in the city should be at least 3593.19 hectares (hm2), x1 ≥ 3593.19. ② Farmland potential constraint: The total current area of farmland in Alaer City is 3593.93 hectares (hm2). Based on surveys and analysis, through further development, land reclamation, and rehabilitation measures, the city can theoretically increase its farmland by a maximum of 69.23 hectares (hm2). Therefore, the area of farmland must satisfy the following equation: x1 ≤ 3663.16.
3.2.3. Construction of Objective Function
- (1)
- Economic benefits: In the Xinjiang region, the economic contribution of each land use type is assessed based on the output value of agriculture, forestry, animal husbandry, and fishery. Through normalization, the output values of different land use types are converted into a specific indicator, which is then used to calculate the GDP generated by each land use type. The total economic benefit of land use (Vs) is calculated using the following formula:
- (2)
- Ecological benefits: Ecological benefits include soil erosion, carbon sequestration, and water yield. These are calculated for each land use type using the SDR, carbon, and water yield modules of the InVEST model, which provide estimates of water yield, carbon sequestration, and soil erosion for different land use types. Finally, the total ecological benefit of an optimization scheme is calculated by considering the ecological benefit weights of different land use types (Table 2). The specific calculation methods for each module are outlined as follows:
- (3)
- Food security: The farmland area in Alaer City is 5.20 × 105 hm2, accounting for 15% of the total farmland in Xinjiang. Therefore, ensuring the preservation of farmland in Alaer City is crucial for food security. According to the 2020 grain production statistics from the National Bureau of Statistics, the average yield per hectare in Xinjiang reached 7100 kg, which converts to 7.10 × 105 kg per square kilometer. Considering the land use situation in Alaer City and referencing the “National Land Planning Outline (2016–2030)”, maintaining the current amount of farmland is significant for ensuring food production.
3.2.4. Crossover and Mutation
3.3. Formatting of Mathematical Components
3.4. Quantity Structure Optimization Plan Setting
4. Results
4.1. Optimization Analysis of Protective Forests’ Quantity Structure
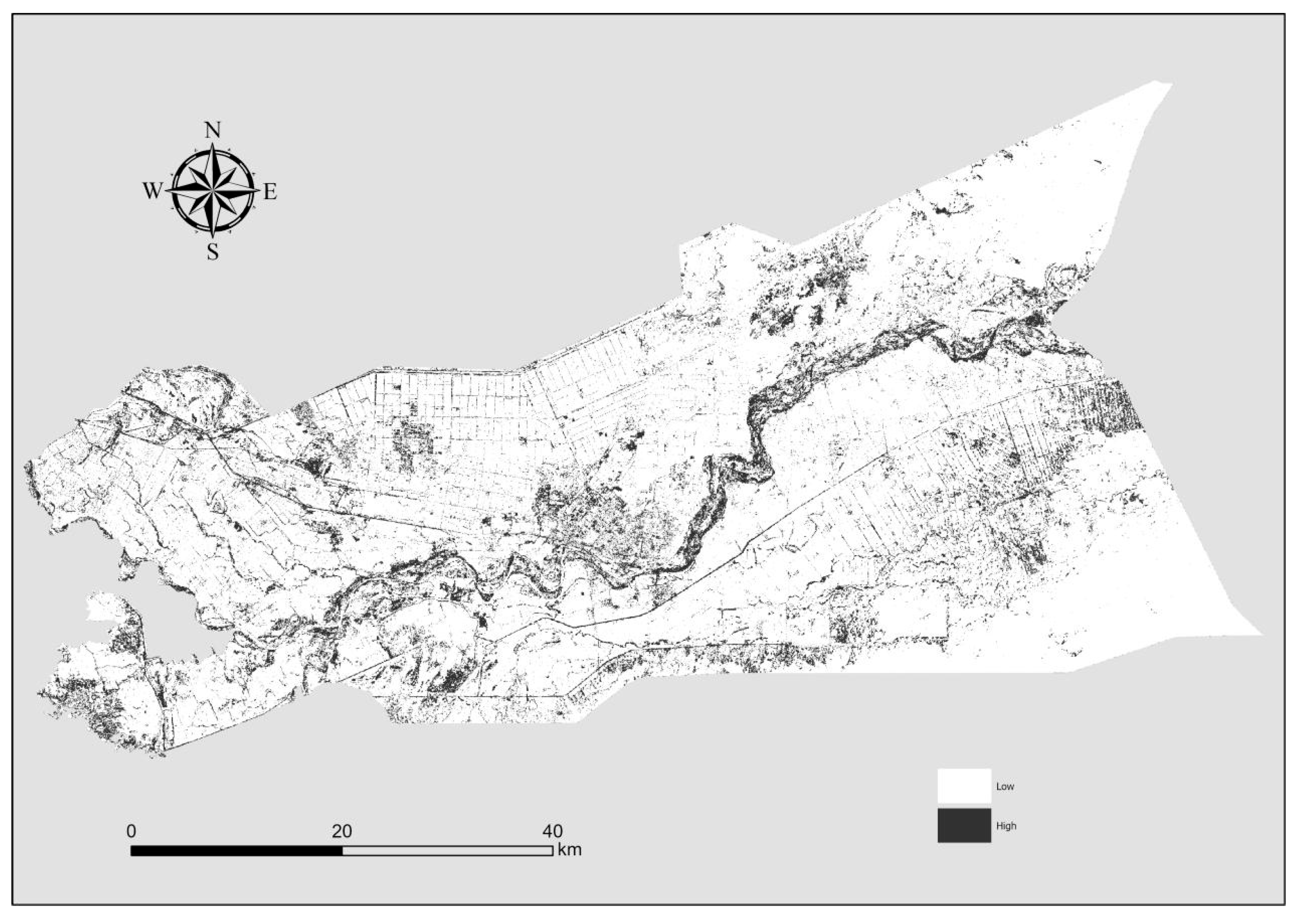
4.2. Suitability Analysis
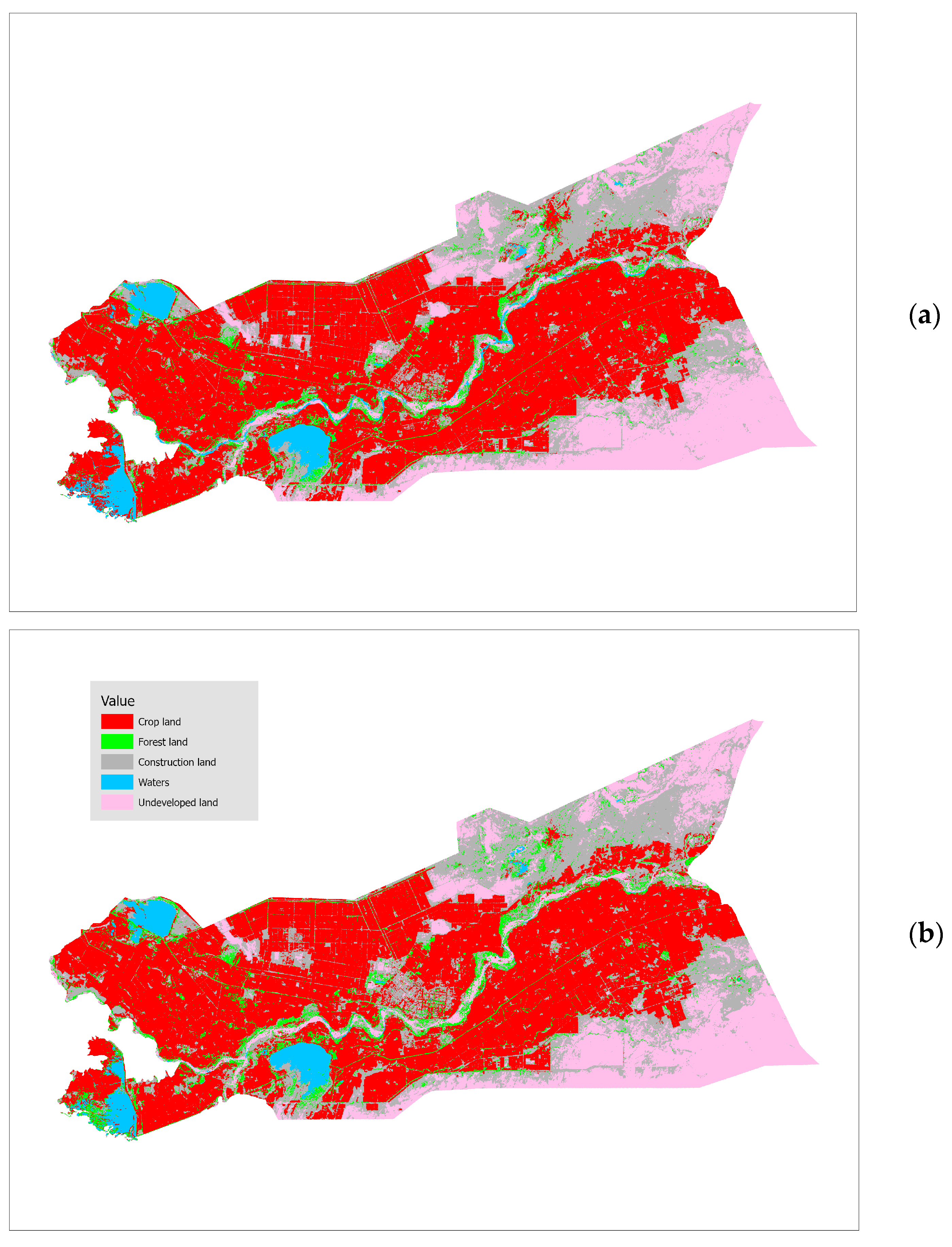
4.3. Optimization Analysis of Protective Forest Space
5. Discussion
6. Conclusions
- (1)
- In terms of quantity structure optimization, the optimized distribution scheme of protective forests has shown improvements in GDP, carbon sequestration, and food production compared to the pre-optimized scenario, while soil erosion has decreased. This indicates that the optimized quantity structure scheme has enhanced both ecological benefits and food security objectives.
- (2)
- According to the land suitability probability distribution map for protective forests, areas with high suitability for protective forests are mainly located along the banks of the Aksu and Tarim Rivers, around farmlands, and on the northern edge of the Taklamakan Desert. In land planning, priority should be given to planting protective forests in areas with high suitability to maximize ecological benefits.
- (3)
- The spatial optimization results show that the FOM index is 0.1339, the Kappa coefficient is 0.8349, and the overall accuracy is 90.73%, confirming the high simulation accuracy of integrating the NSGA-II and FLUS model in predicting the spatial changes of protective forests. After spatial optimization, the distribution of protective forests along the edge of the Taklamakan Desert increased, effectively enhancing their ability to resist wind and sand. Additionally, the construction of the farmland forest network has been improved.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, J.; Song, L. A Review of Ecological Mechanisms for Management Practices of Protective Forests. J. For. Res. 2021, 32, 435–448. [Google Scholar] [CrossRef]
- West, C.; Some, A.; Nebié, E. Famines Are a Thing of the Past: Food Security Trends in Northern Burkina Faso. Hum. Organ. 2014, 73, 340–350. [Google Scholar] [CrossRef]
- Tian, M.; Wang, X.; Liu, F.; Hu, Q.; Qiao, Y.; Wang, Q. Spatial-Temporal Variability and Influence Factors of Cd in Soils of Guangxi, China. PLoS ONE 2023, 18, e0279980. [Google Scholar] [CrossRef]
- Yang, W.; Wang, Y.; Wang, S.; Webb, A.A.; Yu, P.; Liu, X.; Zhang, X. Spatial Distribution of Qinghai Spruce Forests and the Thresholds of Influencing Factors in a Small Catchment, Qilian Mountains, Northwest China. Sci. Rep. 2017, 7, 5561. [Google Scholar] [CrossRef]
- Su, S.; Deng, N.; Ma, F.; Song, Q.; Tian, Y. Crown and Diameter Structure of Pure Pinus massoniana Lamb. Forest in Hunan Province, China. Open Life Sci. 2023, 8, 20220574. [Google Scholar] [CrossRef]
- Kangas, A.; Nurmi, M.; Rasinmäki, J. From a Strategic to a Tactical Forest Management Plan Using a Hierarchic Optimization Approach. Scand. J. For. Res. 2014, 29 (Suppl. S1), 154–165. [Google Scholar]
- Van Herzele, A.; Collins, K.; Tyrväinen, L. Forest Structure Optimization Using Evolutionary Programming and Landscape Ecology Metrics. Eur. J. Oper. Res. 2005, 164, 423–439. [Google Scholar] [CrossRef]
- Liu, Y.; Su, C.; Xu, X. Study on the optimization of land use allocation in the Taiyuan High-tech Zone. China Land Sci. 2013, 10, 9. [Google Scholar] [CrossRef]
- United Nations. Sustainable Development Goal 15: Life on Land. 2015. Available online: https://sdgs.un.org/goals/goal15 (accessed on 1 July 2024).
- Li, L.; Chen, Z.; Wang, S. Optimization of Spatial Land Use Patterns with Low Carbon Target: A Case Study of Sanmenxia, China. Int. J. Environ. Res. Public Health 2022, 19, 14178. [Google Scholar] [CrossRef]
- Cao, K.; Huang, B.; Wang, S.; Lin, H. Sustainable Land Use Optimization Using Boundary-Based Fast Genetic Algorithm. Comput. Environ. Urban Syst. 2012, 36, 257–269. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, M.; He, J.; Liu, Y. Regional Land-Use Allocation with a Spatially Explicit Genetic Algorithm. Landsc. Ecol. Eng. 2015, 11, 209–219. [Google Scholar] [CrossRef]
- Zhong, X. Application of Simulated Annealing Algorithm in the Design of Land Planning and Allocation System. In Proceedings of the International Conference on Multi-Modal Information Analytics, Virtual Event, 15–17 April 2022; Springer: Cham, Switzerland, 2022; pp. 447–454. [Google Scholar]
- Yi, Y.; Zhang, C.; Zhu, J.; Zhang, Y.; Sun, H.; Kang, H. Spatio-Temporal Evolution, Prediction and Optimization of LUCC Based on CA-Markov and InVEST Models: A Case Study of Mentougou District, Beijing. Int. J. Environ. Res. Public Health 2022, 19, 2432. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Lei, X.; Yu, G.; Changchun, Z. Spatio-Temporal Evolution and Trend Prediction of Urban Ecosystem Service Value Based on CLUE-S and GM (1, 1) Compound Model. Environ. Monit. Assess. 2023, 195, 1282. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Huang, X.; Chuai, X.; Yang, H.; Lai, L.; Tan, J. Impact of Land Use Type Conversion on Carbon Storage in Terrestrial Ecosystems of China: A Spatial-Temporal Perspective. Sci. Rep. 2015, 5, 10233. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Liu, D.; Liu, Y.; He, J.; Jiao, L.; Chen, Y.; Hong, X. Rural land use spatial allocation in the semiarid loess hilly area in China: Using a Particle Swarm Optimization model equipped with multi-objective optimization techniques. Sci. China Earth Sci. 2012, 55, 1166–1177. [Google Scholar] [CrossRef]
- López-Fando, C.; Pardo, M.T. Soil Carbon Storage and Stratification Under Different Tillage Systems in a Semi-Arid Region. Soil Tillage Res. 2011, 111, 224–230. [Google Scholar] [CrossRef]
- Mu, Y. Study on Spatial Optimization of Land Use Allocation in Ningqiang County Based on Ant Colony Optimization Algorithm. Master’s Thesis, Chang’an University, Xi’an, China, 2018. (In Chinese). [Google Scholar]
- Gong, X.; Li, Y.; Wang, X.; Zhang, Z.; Lian, J.; Ma, L.; Cao, W. Quantitative Assessment of the Contributions of Climate Change and Human Activities on Vegetation Degradation and Restoration in Typical Ecologically Fragile Areas of China. Ecol. Indic. 2022, 144, 109536. [Google Scholar] [CrossRef]
- He, S.; Wang, D.; Zhao, P.; Li, Y.; Lan, H.; Chen, W.; Chen, X. Quantification of Basin-Scale Multiple Ecosystem Services in Ecologically Fragile Areas. Catena 2021, 202, 105247. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Munro, S.; Barthold, F.; Steffens, M.; Schad, P.; Kögel-Knabner, I. Carbon storage capacity of semi-arid grassland soils and sequestration potentials in northern China. Glob. Change Biol. 2015, 21, 3836–3845. [Google Scholar] [CrossRef]
- Feng, D.; Bao, W.; Fu, M.; Zhang, M.; Sun, Y. Current and future land use characters of a national central city in eco-fragile region—A case study in Xi’an City based on FLUS model. Land 2021, 10, 286. [Google Scholar] [CrossRef]
- Wang, L.; Du, X.; Wang, R.; Yang, Y.; Hu, Y.; Hou, Z. Optimization of the planting structure in the upstream region of Baiyangdian Lake based on the non-dominated sorting genetic algorithm (NSGA-II). Chin. J. Eco Agric. 2021, 29, 1370–1383. [Google Scholar]
- Long, W.; Lu, H.; Qin, Y.; Sun, C.; Jiang, L.; Zhao, J. Multi-objective land use optimization based on low-carbon development using NSGA-II. In Proceedings of the 2013 21st International Conference Geoinformatics, Kaifeng, China, 20–22 June 2013; pp. 1–5. [Google Scholar]
- Hongyu, C.; Yuxiang, D.; Chensong, L. Research on optimization method for low impact development (LID) controls distribution of greenspace in shallow mountain based on D8 and NSGA-II algorithm. J. Beijing For. Univ. 2022, 44, 116–126. [Google Scholar]
- Datta, D.; Deb, K.; Fonseca, C.M.; Lobo, F.; Condado, P. Multi-objective evolutionary algorithm for land-use management problem. Int. J. Comput. Intell. Res. 2007, 3, 371–384. Available online: https://www.researchgate.net/publication/215661096_Multi-Objective_Evolutionary_Algorithm_for_Land-Use_Management_Problem (accessed on 19 February 2025).
- Cao, K.; Batty, M.; Huang, B.; Liu, Y.; Yu, L.; Chen, J. Spatial multi-objective land use optimization: Extensions to the non-dominated sorting genetic algorithm-II. Int. J. Geogr. Inf. Sci. 2011, 25, 1949–1969. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, Y.; Wang, X.; Lin, Q.; Li, L. A new approach to land use optimization and simulation considering urban development sustainability: A case study of Bortala, China. Sustain. Cities Soc. 2022, 87, 104135. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Wang, H.; Liu, Y. PSO-CA model for land use simulation in arid oasis regions. Ecol. Inform. 2022, 68, 101552. [Google Scholar] [CrossRef]
- Wang, W.; Jiao, L.; Jia, Q.; Liu, J.; Mao, W.; Xu, Z.; Li, W. Land use optimization modelling with ecological priority perspective for large-scale spatial planning. Sustain. Cities Soc. 2021, 65, 102575. [Google Scholar] [CrossRef]
- Cong, R.; Qi, J.; Wu, C.; Wang, M.; Guo, J. Multi-UAVs Cooperative Detection Based on Improved NSGA-II Algorithm. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 1524–1529. [Google Scholar]
- Marotz, G.A.; Sorenson, C.J. Depletion of a Great Plains resource: The case of shelter-belts. Environ. Conserv. 1979, 6, 215–224. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]

| Data Usage | Data Name | Data Type | Time | Resolution | Data Sources |
|---|---|---|---|---|---|
| Land classify | Land use data | Raster | 2018, 2023 | 30 m | CLCD Dataset (zenodo.org) |
| Driving Factors | DEM data | Raster | 2023 | 30 m | Geospatial Data Cloud (www.gscloud.cn) |
| Slope data | 2023 | ||||
| Aspect data | 2023 | ||||
| NDVI data | 2023 | China Resource and Environmental Science and Data Platform (www.resdc.cn/) | |||
| Carbon storage data | 2023 | ||||
| Soil erosion data | 2023 | ||||
| Road distribution data | 2022 | ||||
| Population distribution data | 2022 | ||||
| Basic Geographic Data | Administrative boundary | Vector | 2019 | / | Standard Map Service Website of the Ministry of Natural Resources (bzdt.ch.mnr.gov.cn) |
| Land Use Type | Weight of Soil Erosion | Weight of Carbon Sequestration | Weight of Water Production |
|---|---|---|---|
| Crop Land | −0.0446 | 0.1394 | 0.01899 |
| Forest Land | −0.0268 | 0.2307 | 0.00592 |
| Waters | 0.0000 | 0.1639 | 0.8838 |
| Construction Land | 0.0000 | 0.1475 | 0.0000 |
| Undeveloped Land | −0.8929 | 0.1388 | 0.0000 |
| Plan | Crop Land (x1) | Forest Land (x2) | Construction Land (x3) | Waters (x4) | Undeveloped Land (x5) |
|---|---|---|---|---|---|
| Plan A | 3622.96 | 369.7 | 1429.66 | 253.39 | 1247.58 |
| Plan B | 3616.73 | 342.01 | 1430.35 | 254.78 | 1279.42 |
| Plan C | 3628.5 | 371.78 | 1430.34 | 254.77 | 1237.9 |
| Plan D | 3628.49 | 355.16 | 1439.35 | 234.01 | 1266.28 |
| Plan E | 3609.11 | 369.7 | 1439.35 | 254.08 | 1251.05 |
| Plan F | 3593.19 | 362.16 | 1428.28 | 231.93 | 1307.81 |
| Plan G | 3614.65 | 342.7 | 1441.43 | 252.7 | 1271.81 |
| Base Period | 3593.93 | 339.09 | 1428.2 | 255.62 | 1306.45 |
| Plan | GDP/108 Yuan | Carbon Sequestration/t | Water Yield/m3 | Soil Erosion/(t·km−2·a−1) | Grain Yield/104 kg |
|---|---|---|---|---|---|
| Plan A | 750.36 | 559,896,349.17 | 1907.60 | −13,240.20 | 257,230.16 |
| Plan B | 751.64 | 555,041,155.49 | 1911.73 | −13,522.52 | 256,787.83 |
| Plan C | 750.76 | 563,223,081.78 | 1914.25 | −13,154.29 | 257,623.50 |
| Plan D | 753.19 | 558,498,133.61 | 1911.93 | −13,410.71 | 257,622.79 |
| Plan E | 753.09 | 558,966,567.98 | 1907.85 | −13,265.75 | 256,246.81 |
| Plan F | 750.39 | 557,571,286.28 | 1912.99 | −13,726.36 | 255,296.49 |
| Plan G | 754.15 | 555,033,205.26 | 1913.60 | −13,451.77 | 256,640.15 |
| Base Period | 747.36 | 553,153,193.26 | 1906.63 | −13,759.83 | 255,169.03 |
| Type/Conversion Probability | Crop Land | Forest Land | Construction Land | Waters | Undeveloped Land |
|---|---|---|---|---|---|
| Crop Land | 0.938773 | 0.009155 | 0.050317 | 0.000778 | 0.000978 |
| Forest Land | 0.029316 | 0.911907 | 0.041090 | 0.007025 | 0.010662 |
| Construction Land | 0.057326 | 0.028060 | 0.84821 | 0.002664 | 0.063735 |
| Waters | 0.020217 | 0.061114 | 0.029044 | 0.777725 | 0.111900 |
| Undeveloped Land | 0.001977 | 0.009078 | 0.138557 | 0.001615 | 0.848772 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, M.; Yin, X.; Pan, S.; Liu, P. Multi-Objective Spatial Optimization of Protective Forests Based on the Non-Dominated Sorting Genetic Algorithm-II Algorithm and Future Land Use Simulation Model: A Case Study of Alaer City, China. Forests 2025, 16, 452. https://doi.org/10.3390/f16030452
Ding M, Yin X, Pan S, Liu P. Multi-Objective Spatial Optimization of Protective Forests Based on the Non-Dominated Sorting Genetic Algorithm-II Algorithm and Future Land Use Simulation Model: A Case Study of Alaer City, China. Forests. 2025; 16(3):452. https://doi.org/10.3390/f16030452
Chicago/Turabian StyleDing, Mingrui, Xiaojun Yin, Shaoliang Pan, and Pengshuai Liu. 2025. "Multi-Objective Spatial Optimization of Protective Forests Based on the Non-Dominated Sorting Genetic Algorithm-II Algorithm and Future Land Use Simulation Model: A Case Study of Alaer City, China" Forests 16, no. 3: 452. https://doi.org/10.3390/f16030452
APA StyleDing, M., Yin, X., Pan, S., & Liu, P. (2025). Multi-Objective Spatial Optimization of Protective Forests Based on the Non-Dominated Sorting Genetic Algorithm-II Algorithm and Future Land Use Simulation Model: A Case Study of Alaer City, China. Forests, 16(3), 452. https://doi.org/10.3390/f16030452





