Establishing Models for Predicting Above-Ground Carbon Stock Based on Sentinel-2 Imagery for Evergreen Broadleaf Forests in South Central Coastal Ecoregion, Vietnam
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Sample Plots and Estimation of Total Above-Ground Carbon
2.3. Sentinel-2 Image and Identification of Key Indices
2.4. Development of Regression Models
2.5. Cross-Validation
3. Results
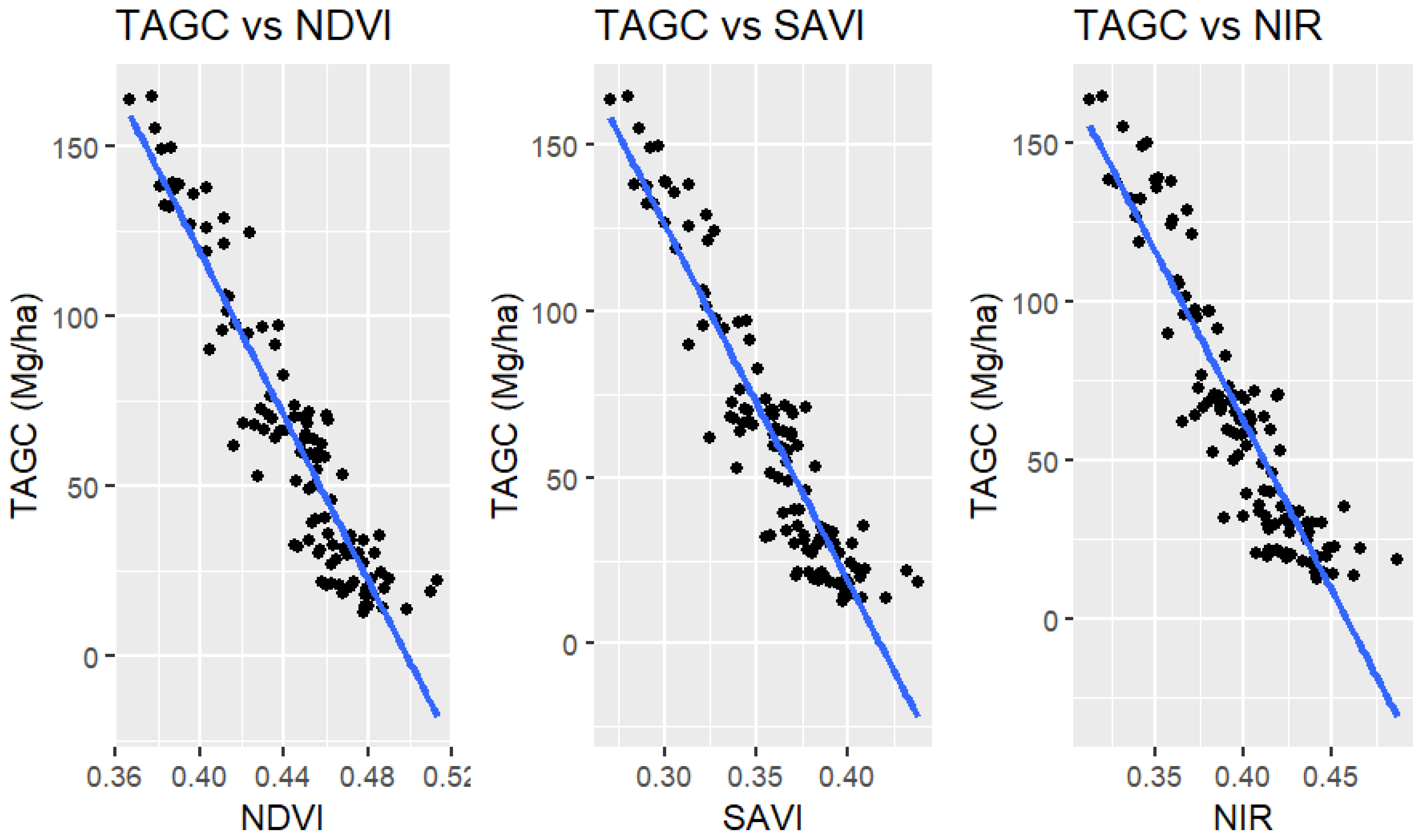
3.1. Vegetation Indices and Multispectral Bands Influencing Above-Ground Carbon
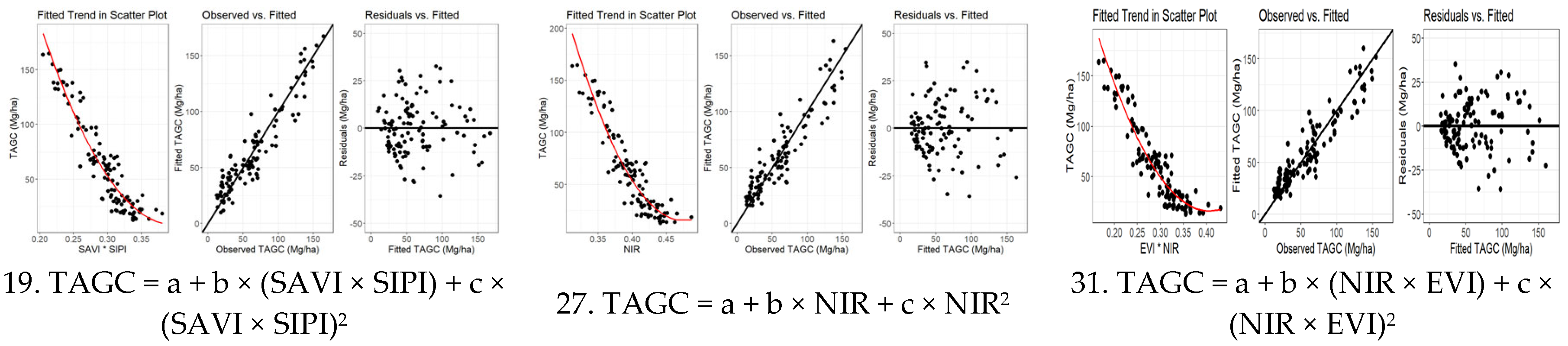
3.2. Establishment of Above-Ground Carbon Estimation Models
3.3. Determination of Above-Ground Carbon Estimation Models
4. Discussion
4.1. Determination of Indices of Sentinel-2 Imagery Influencing TAGC Prediction
4.2. Establishment and Validation of Models for Predicting TAGC
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Wu, J.; Chen, B.; Reynolds, G.; Xie, J.; Liang, S.; O’Brien, M.J.; Hector, A. Monitoring tropical forest degradation and restoration with satellite remote sensing: A test using Sabah Biodiversity Experiment. Adv. Ecol. Res. 2020, 62, 117–146. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Baccini, A.; Friedl, M.A.; Woodcock, C.E.; Warbington, R. Forest biomass estimation over regional scales using multisource data. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef]
- Priatama, A.R.; Setiawan, Y.; Mansur, I.; Masyhuri, M. Regression Models for Estimating Aboveground Biomass and Stand Volume Using Landsat-Based Indices in Post-Mining Area. J. Manaj. Hutan Trop. 2022, 28, 1–14. [Google Scholar] [CrossRef]
- Dang, H.N.; Ba, D.D.; Trung, D.N.; Viet, H.N.H. A Novel Method for Estimating Biomass and Carbon Sequestration in Tropical Rainforest Areas Based on Remote Sensing Imagery: A Case Study in the Kon Ha Nung Plateau, Vietnam. Sustainability 2022, 14, 16857. [Google Scholar] [CrossRef]
- Khan, K.; Iqbal, J.; Ali, A.; Khan, S.N. Assessment of Sentinel-2-Derived Vegetation Indices for the Estimation of Above-Ground Biomass/Carbon Stock, Temporal Deforestation, and Carbon Emissions Estimation in the Moist Temperate Forests of Pakistan. Appl. Ecol. Environ. Res. 2020, 18, 783–815. [Google Scholar] [CrossRef]
- Askar, N.; Nuthammachot, N.; Phairuang, W.; Wicaksono, P.; Sayektiningsih, T. Estimating Aboveground Biomass on Private Forest Using Sentinel-2 Imagery. J. Sens. 2018, 2018, 6745629. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Y.; Ashton, M.S.; Lee, X. Measuring Carbon in Forests. In Managing Forest Carbon in a Changing Climate; Ashton, M., Tyrrell, M., Spalding, D., Gentry, B., Eds.; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Naesset, E.; Gobakken, T.; Solberg, S.; Gregoire, T.G.; Ståhl, G.; Lange, H.; Dick, O.; Gobakken, T.; Astrup, R. Mapping and estimating forest area and aboveground biomass in miombo woodlands in Tanzania using data from airborne laser scanning, TanDEM-X, RapidEye, and global forest maps: A comparison of estimated precision. Remote Sens. Environ. 2016, 175, 282–300. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Estimation for inaccessible and non-sampled forest areas using model-based inference and remotely sensed auxiliary information. Remote Sens. Environ. 2014, 154, 226–233. [Google Scholar] [CrossRef]
- Esteban, J.R.E.; Montealegre, A.L.; Miranda, D.; Segura, A.S.; Ruiz, M.M. A model-based volume estimator that accounts for both land cover misclassification and model prediction uncertainty. Remote Sens. 2020, 12, 3360. [Google Scholar] [CrossRef]
- Jędrych, M.; Zagajewski, B.; Marcinkowska-Ochtyra, A. Application of Sentinel-2 and EnMAP new satellite data to the mapping of environmental changes. Pol. Cartogr. Rev. 2017, 49, 107–119. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Kappas, M. Estimating forest aboveground biomass (AGB) by integrating SPOT-6 data with field-based measurements using the random forest (RF) algorithm. J. Sens. 2020, 4216160. [Google Scholar] [CrossRef]
- Moradi, F.; Darvishsefat, A.A.; Pourrahmati, M.R.; Deljouei, A.; Borz, S.A. Estimating aboveground biomass in dense Hyrcanian forests by the use of Sentinel-2 data. Forests 2022, 13, 104. [Google Scholar] [CrossRef]
- Ma, T.; Hu, Y.; Wang, J.; Beckline, M.; Pang, D.; Chen, L.; Ni, X.; Li, X. A novel vegetation index approach using Sentinel-2 data and Random Forest algorithm for estimating forest stock volume in the Helan Mountains, Ningxia, China. Remote Sens. 2023, 15, 1853. [Google Scholar] [CrossRef]
- Huy, B.; Truong, N.Q.; Poudel, K.P.; Temesgen, H.; Khiem, N.Q. Multi-output deep learning models for enhanced reliability of simultaneous tree above- and below-ground biomass predictions in tropical forests of Vietnam. Comput. Electron. Agric. 2024, 204, 109080. [Google Scholar] [CrossRef]
- Cheng, F.; Ou, G.; Wang, M.; Liu, C. Remote sensing estimation of forest carbon stock based on machine learning algorithms. Forests 2024, 15, 681. [Google Scholar] [CrossRef]
- Phuong, V.T.; Inoguchi, A.; Birigazzi, L.; Henry, M.; Sola, G. Introduction and Background of the Study. In Tree Allometric Equation Development for Estimation of Forest Above-Ground Biomass in Viet Nam (Part A); Inoguchi, A., Henry, M., Birigazzi, L., Sola, G., Eds.; UN-REDD Programme: Hanoi, Vietnam, 2012. [Google Scholar]
- Huy, B. Allometric Model and Remote Sensing-GIS to Estimate Carbon Removal of Evergreen Broadleaf Forests in the Central Highland Region; Publication House of Science and Technique: Hanoi, Vietnam, 2013. [Google Scholar]
- Phuong, V.T.; Linh, N.T.M. Final Report on Forest Ecological Stratification in Vietnam; UN-REDD Programme: Hanoi, Vietnam, 2011. [Google Scholar]
- Sola, G.; Inoguchi, A.; Garcia-Perez, J.; Donegan, E.; Birigazzi, L.; Henry, M. Allometric Equations at National Scale for Tree Biomass Assessment in Viet Nam: Context, Methodology and Summary of the Results; UN-REDD Programme: Hanoi, Vietnam, 2014. [Google Scholar]
- Da Nang Portal. Location and Natural Conditions. Available online: https://danang.gov.vn/web/en/detail?id=26029&_c=16407111 (accessed on 19 March 2025).
- Ministry of Agriculture and Rural Development. Decision 816/QD-BNN-KL on National Forest Status Announcement in 2023; 20 March 2024. Available online: https://thuvienphapluat.vn/van-ban/Tai-nguyen-Moi-truong/Quyet-dinh-816-QD-BNN-KL-2024-cong-bo-hien-trang-rung-toan-quoc-604807.aspx (accessed on 3 April 2025).
- Ministry of Agriculture and Rural Development. Circular No. 33/2018/TT-BNNPTNT on Prescribing Forest Survey, Inventory and Forest Transition Monitoring; 16 November 2018. Available online: https://lawnet.vn/en/vb/Circular-33-2018-TT-BNNPTNT-prescribing-forest-survey-inventory-forest-transition-monitoring-67B66.html (accessed on 19 March 2025).
- Huy, B.; Poudel, K.P.; Temesgen, H. Aboveground biomass equations for evergreen broadleaf forests in South Central Coastal ecoregion of Viet Nam: Selection of eco-regional or pantropical models. For. Ecol. Manag. 2016, 376, 276–283. [Google Scholar] [CrossRef]
- IPCC. Guidelines for National Greenhouse Gas Inventories; Eggleston, H.S., Buendia, L., Miwa, K., Ngara, T., Tanabe, K., Eds.; IGES: Hayama, Japan, 2006. [Google Scholar]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanre, D. Atmospherically Resistant Vegetation Index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I.; Lloret, P.; Muñoz, F.; Vilajeliu, M. Reflectance Assessment of Mite Effects on Apple Trees. Int. J. Remote Sens. 1995, 16, 2727–2733. [Google Scholar] [CrossRef]
- R Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023; Available online: http://www.r-project.org/index.html (accessed on 13 October 2024).
- Greenacre, M.; Groenen, P.J.; Hastie, T.; d’Enza, A.I.; Markos, A.; Tuzhilina, E. Principal Component Analysis. Nat. Rev. Methods Primers 2022, 2, 100. [Google Scholar] [CrossRef]
- Huy, B.; Nam, L.C.; Poudel, K.P.; Temesgen, H. Individual Tree Diameter Growth Modeling System for Dalat Pine (Pinus dalatensis Ferré) of the Upland Mixed Tropical Forests. For. Ecol. Manag. 2021, 480, 118612. [Google Scholar] [CrossRef]
- Huy, B.; Truong, N.Q.; Khiem, N.Q.; Poudel, K.P.; Temesgen, H. Stand Growth Modeling System for Planted Teak (Tectona grandis L.f.) in Tropical Highlands. Trees People 2022, 9, 100308. [Google Scholar] [CrossRef]
- Picard, N.; Saint-André, L.; Henry, M. Manual for Building Tree Volume and Biomass Allometric Equations: From Field Measurement to Prediction; FAO: Italy, Rome; Centre de Coopération Internationale en Recherche Agronomique pour le Développement: Montpellier, France, 2012; 215p.
- Huy, B.; Khiem, N.Q.; Truong, N.Q.; Poudel, K.P.; Temesgen, H. Additive Modeling Systems to Simultaneously Predict Aboveground Biomass and Carbon for Litsea glutinosa of Agroforestry Model in Tropical Highlands. For. Syst. 2023, 32, e006. [Google Scholar] [CrossRef]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Proceedings of the 2nd International Symposium on Information Theory; Akademiai Kiado: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Zeng, W.; Zhang, L.; Chen, X.; Cheng, Z.; Ma, K.; Li, Z. Construction of Compatible and Additive Individual-Tree Biomass Models for Pinus tabulaeformis in China. Can. J. For. Res. 2017, 47, 467–475. [Google Scholar] [CrossRef]
- Pandit, S.; Tsuyuki, S.; Dube, T. Estimating Above-Ground Biomass in Sub-Tropical Buffer Zone Community Forests, Nepal, Using Sentinel-2 Data. Remote Sens. 2018, 10, 601. [Google Scholar] [CrossRef]
- Poudel, A.; Shrestha, H.L.; Mahat, N.; Sharma, G.; Aryal, S.; Kalakheti, R.; Lamsal, B. Modeling and Mapping of Aboveground Biomass and Carbon Stock Using Sentinel-2 Imagery in Chure Region, Nepal. Int. J. For. Res. 2023, 2023, 5553957. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal Component Analysis: A Review and Recent Developments. Philos. Trans. R. Soc. A 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Luong, V.N.; Tateishi, R.; Kondoh, A.; Sharma, R.C.; Hoan, T.N.; Tu, T.T.; Minh, D.H.T. Mapping Tropical Forest Biomass by Combining ALOS-2, Landsat 8, and Field Plots Data. Land 2016, 5, 31. [Google Scholar] [CrossRef]




| VIs | Definition | Sources (References) |
|---|---|---|
| ARVI | (NIR − (2 × RED) + BLUE)/(NIR + (2 × RED) + BLUE) | [31] |
| EVI | 2.5 × (NIR − RED)/(NIR + 6 × RED − 7.5 × BLUE + 1) | [32] |
| NDVI | (NIR − RED)/(NIR + RED) | [2] |
| SAVI | 1.428 × (NIR − RED)/(NIR + RED + 0.428) | [1] |
| SIPI | (NIR − BLUE)/(NIR − RED) | [33] |
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | PC9 | PC10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Standard deviation | 2.8636 | 1.1976 | 0.4521 | 0.3336 | 0.2024 | 0.0923 | 0.0148 | 0.0051 | 0.0026 | 0.0011 |
| Proportion of Variance | 0.8200 | 0.1434 | 0.0204 | 0.0111 | 0.0041 | 0.0009 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Cumulative Proportion | 0.8200 | 0.9635 | 0.9839 | 0.9950 | 0.9991 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Variable | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | PC9 | PC10 |
|---|---|---|---|---|---|---|---|---|---|---|
| TAGC | 0.3243 | −0.1708 | 0.0903 | −0.9174 | 0.0501 | −0.1154 | 0.0032 | −0.0037 | −0.0001 | 0.0007 |
| NDVI | −0.3352 | 0.2288 | −0.0572 | −0.1489 | −0.0633 | −0.1696 | −0.4412 | −0.3152 | −0.6856 | 0.1139 |
| EVI | −0.3443 | 0.0762 | −0.2778 | −0.1636 | −0.1221 | −0.0163 | 0.5489 | −0.6262 | 0.1721 | −0.1829 |
| SAVI | −0.3420 | 0.1606 | −0.0066 | −0.1760 | −0.0599 | 0.1680 | −0.1789 | 0.0147 | 0.4556 | 0.7447 |
| ARVI | −0.3330 | 0.2355 | −0.1884 | −0.1869 | −0.0615 | 0.0034 | −0.4461 | 0.2438 | 0.3780 | −0.5985 |
| SIPI | −0.3270 | 0.1809 | 0.5963 | −0.0173 | −0.0553 | −0.6063 | 0.2808 | 0.2305 | 0.0399 | −0.0172 |
| NIR | −0.3469 | 0.0510 | 0.0809 | −0.2038 | −0.0547 | 0.6048 | 0.3596 | 0.4413 | −0.3643 | −0.0580 |
| RED | −0.2270 | −0.6004 | 0.5318 | 0.0396 | −0.2141 | 0.2608 | −0.2507 | −0.3108 | 0.0926 | −0.1475 |
| GREEN | −0.3204 | −0.2941 | −0.0743 | −0.0082 | 0.8946 | −0.0697 | −0.0022 | 0.0016 | 0.0018 | −0.0003 |
| BLUE | −0.2335 | −0.5909 | −0.4748 | 0.0050 | −0.3449 | −0.3510 | 0.0455 | 0.3231 | −0.0830 | 0.1240 |
| Model | Correlation Equation Form | Weight |
|---|---|---|
| Linear | TAGC = f(NDVI) | 1/NDVI−2 |
| TAGC = f(SAVI) | 1/SAVI−2 | |
| TAGC = f(NIR) | 1/NIR−2 | |
| TAGC = f(NDVI, ARVI) | 1/NDVI−2 | |
| TAGC = f(SAVI, SIPI) | 1/SAVI−2 | |
| TAGC = f(NIR, EVI) | 1/NIR−2 | |
| Non-linear (Power, Exponential, Quadratic) | TAGC = f(NDVI) | 1/NDVIδ |
| TAGC = f(SAVI) | 1/SAVIδ | |
| TAGC = f(NIR) | 1/NIRδ | |
| TAGC = f(NDVI, ARVI) | 1/NDVIδ | |
| TAGC = f(SAVI, SIPI) | 1/SAVIδ | |
| TAGC = f(NIR, EVI) | 1/NIRδ |
| ID | Equation Form | AIC | R2 | ASE (%) | RMSE (Mg ha−1) | MPSE (%) |
|---|---|---|---|---|---|---|
| 1 | TAGC = a + b × NDVI | 762.452 | 0.87215 | 0.75 | 15.08 | 34.47 |
| 2 | TAGC = a × e(b × NDVI) | 769.343 | 0.85502 | −0.96 | 16.15 | 24.67 |
| 3 | TAGC = a + b × NDVI + c × NDVI2 | 754.401 | 0.88567 | 4.76 | 14.34 | 33.30 |
| 4 | TAGC = a × NDVIb | 776.901 | 0.83989 | −2.30 | 16.95 | 25.37 |
| 5 | TAGC = a + b × (NDVI × ARVI) | 773.041 | 0.85401 | −8.30 | 16.32 | 35.60 |
| 6 | TAGC = a × e(b × NDVI × ARVI) | 762.113 | 0.87105 | −3.02 | 15.28 | 23.96 |
| 7 | TAGC = a + b × (NDVI × ARVI) + c × (NDVI × ARVI)2 | 752.085 | 0.88764 | −59.26 | 14.36 | 90.02 |
| 8 | TAGC = a × (NDVI × ARVI)b | 774.778 | 0.84658 | −2.11 | 16.70 | 25.88 |
| 9 | TAGC = a + b × NDVI + c × ARVI | 762.164 | 0.87367 | −3.99 | 14.81 | 33.62 |
| 10 | TAGC = a × e(b × NDVI + c × ARVI) | 769.258 | 0.86312 | −2.83 | 15.89 | 25.34 |
| 11 | TAGC = a + b × NDVI + c × NDVI2 +d × ARVI + e × ARVI2 | 756.739 | 0.88757 | 1.76 | 14.19 | 32.49 |
| 12 | TAGC = a × NDVIb × ARVIc | 775.078 | 0.85231 | −3.17 | 16.40 | 25.57 |
| 13 | TAGC = a + b × SAVI | 765.790 | 0.86697 | −5.12 | 15.38 | 36.42 |
| 14 | TAGC = a × e(b × SAVI) | 762.800 | 0.85757 | −2.84 | 16.35 | 23.62 |
| 15 | TAGC = a + b × SAVI + c × SAVI2 | 748.983 | 0.88897 | 1.27 | 14.14 | 42.69 |
| 16 | TAGC = a × SAVIb | 772.618 | 0.82260 | −1.70 | 17.68 | 24.74 |
| 17 | TAGC = a + b × (SAVI × SIPI) | 771.465 | 0.85792 | −10.79 | 15.83 | 46.47 |
| 18 | TAGC = a × e(b × SAVI × SIPI) | 765.410 | 0.85607 | −2.23 | 15.73 | 23.22 |
| 19 | TAGC = a + b × (SAVI × SIPI) + c × (SAVI × SIPI)2 | 753.226 | 0.88436 | 4.28 | 13.88 | 26.51 |
| 20 | TAGC = a × (SAVI × SIPI)^b | 777.733 | 0.82186 | −1.70 | 17.54 | 25.55 |
| 21 | TAGC = a + b × SAVI + c × SIPI | 766.979 | 0.86804 | 0.03 | 15.44 | 61.61 |
| 22 | TAGC = a × e(b × SAVI + c × SIPI) | 762.561 | 0.86136 | −2.72 | 15.74 | 23.62 |
| 23 | TAGC = a + b × SAVI + c × SAVI2 +d × SIPI + e × SIPI2 | 751.194 | 0.89076 | 3.02 | 14.39 | 29.86 |
| 24 | TAGC = a × SAVIb × SIPIc | 773.127 | 0.82525 | −1.30 | 17.58 | 24.99 |
| 25 | TAGC = a + b × NIR | 785.321 | 0.83064 | 24.52 | 17.03 | 95.31 |
| 26 | TAGC = a × e(b × NIR) | 768.493 | 0.82896 | −0.57 | 16.92 | 23.82 |
| 27 | TAGC = a + b × NIR + c × NIR2 | 756.924 | 0.86649 | 0.70 | 15.50 | 23.17 |
| 28 | TAGC = a × NIRb | 775.476 | 0.78901 | −0.84 | 18.75 | 24.77 |
| 29 | TAGC = a + b × (NIR × EVI) | 785.717 | 0.82968 | −9.43 | 17.54 | 41.36 |
| 30 | TAGC = a × e(b × NIR × EVI) | 761.065 | 0.84910 | −2.65 | 16.20 | 23.33 |
| 31 | TAGC = a + b × (NIR × EVI) + c × (NIR × EVI)2 | 752.493 | 0.87647 | −0.16 | 14.65 | 22.54 |
| 32 | TAGC = a × (NIR × EVI)b | 777.524 | 0.76316 | −0.18 | 20.00 | 24.77 |
| 33 | TAGC = a + b × NIR + c × EVI | 776.007 | 0.85124 | −7.96 | 15.90 | 51.13 |
| 34 | TAGC = a × e(b × NIR + c × EVI) | 768.716 | 0.82342 | −0.27 | 17.77 | 24.71 |
| 35 | TAGC = a + b × NIR + c × NIR2 +d × EVI + e × EVI2 | 756.972 | 0.87294 | 2.35 | 15.23 | 24.13 |
| 36 | TAGC = a × NIRb × EVIc | 775.920 | 0.78908 | −0.02 | 19.85 | 25.11 |
| ID | Equation Form | Parameters | p-Value | Std. Error | R2 | MPSE (%) | |
|---|---|---|---|---|---|---|---|
| 1 | TAGC = a + b × NDVI | a | 590 | <0.001 | 20.8 | 0.87064 | 35.99 |
| b | −1181.4 | <0.001 | 46.1 | ||||
| 3 | TAGC = a + b × NDVI + c × NDVI2 | a | 1523.206 | <0.001 | 217.6896 | 0.88581 | 26.32 |
| b | −5441.707 | <0.001 | 989.7512 | ||||
| c | 4837.304 | <0.001 | 1121.616 | ||||
| 6 | TAGC = a × e(b × NDVI × ARVI) | a | 2617.904 | <0.001 | 356.5325 | 0.87025 | 23.62 |
| b | −26.8626 | <0.001 | 1.0567 | ||||
| 7 | TAGC = a + b × (NDVI × ARVI) + c × (NDVI × ARVI)2 | a | 648.275 | <0.001 | 53.1819 | 0.88712 | 23.03 |
| b | −6450.795 | <0.001 | 743.7517 | ||||
| c | 16,281.53 | <0.001 | 2576.696 | ||||
| 9 | TAGC = a + b × NDVI + c × ARVI | a | 607.43 | <0.001 | 22.71 | 0.87415 | 31.13 |
| b | −2406.51 | <0.001 | 674.97 | ||||
| c * | 1644.34 | 0.071 | 903.84 | ||||
| 11 | TAGC = a + b × NDVI + c × NDVI2 +d × ARVI + e × ARVI2 | a | 1348.19 | <0.001 | 256.874 | 0.88784 | 23.47 |
| b* | 10,401.88 | 0.348 | 11,037.17 | ||||
| c * | −12,747.94 | 0.291 | 12,032.41 | ||||
| d * | −20,840.87 | 0.154 | 14,536.67 | ||||
| e * | 31,994.84 | 0.146 | 21,860.44 | ||||
| 13 | TAGC = a + b × SAVI | a | 432.86 | <0.001 | 15.47 | 0.86581 | 48.71 |
| b | −1031.04 | <0.001 | 42.15 | ||||
| 14 | TAGC = a × e(b × SAVI) | a | 14,563.32 | <0.001 | 3089.371 | 0.85639 | 23.38 |
| b | −15.606 | <0.001 | 0.6266 | ||||
| 15 | TAGC = a + b × SAVI + c × SAVI2 | a | 1070.272 | <0.001 | 109.0798 | 0.88933 | 22.62 |
| b | −4640.056 | <0.001 | 608.0028 | ||||
| c | 5060.527 | <0.001 | 843.6183 | ||||
| 18 | TAGC = a × e(b × SAVI × SIPI) | a | 4288.168 | <0.001 | 701.5295 | 0.85790 | 23.42 |
| b | −14.784 | <0.001 | 0.5977 | ||||
| 19 | TAGC = a + b × (SAVI × SIPI) + c × (SAVI × SIPI)2 | a | 754.192 | <0.001 | 67.7088 | 0.88606 | 22.85 |
| b | −3758.794 | <0.001 | 458.1902 | ||||
| c | 4737.115 | <0.001 | 769.794 | ||||
| 22 | TAGC = a × e(b × SAVI + c × SIPI) | a * | 387.9781 | 0.610 | 759.3648 | 0.86151 | 23.23 |
| b | −20.1558 | <0.001 | 2.5505 | ||||
| c * | 6.3853 | 0.065 | 3.4379 | ||||
| 23 | TAGC = a + b × SAVI + c × SAVI2 +d × SIPI + e × SIPI2 | a * | −762.477 | 0.795 | 2932.537 | 0.88978 | 22.24 |
| b | −5846.867 | <0.001 | 1706.388 | ||||
| c | 6568.468 | 0.004 | 2266.891 | ||||
| d * | 4858.904 | 0.532 | 7756.204 | ||||
| e * | −2845.5 | 0.543 | 4663.326 | ||||
| 27 | TAGC = a + b × NIR + c × NIR2 | a | 1537.576 | <0.001 | 143.5515 | 0.86646 | 22.04 |
| b | −6398.241 | <0.001 | 700.553 | ||||
| c | 6723.375 | <0.001 | 852.3433 | ||||
| 31 | TAGC = a + b × (NIR × EVI) + c × (NIR × EVI)2 | a | 505.7588 | <0.001 | 33.2636 | 0.87646 | 21.63 |
| b | −2411.523 | <0.001 | 214.8227 | ||||
| c | 2967.038 | <0.001 | 343.2117 | ||||
| 35 | TAGC = a + b × NIR + c × NIR2 +d × EVI + e × EVI2 | a | 1513.702 | <0.001 | 205.311 | 0.87259 | 21.76 |
| b | −7727.276 | 0.018 | 3225.838 | ||||
| c | 8721.605 | 0.022 | 3780.838 | ||||
| d * | 790.201 | 0.563 | 1364.302 | ||||
| e | −638.933 | 0.470 | 881.386 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tam, N.H.; Loi, N.V.; Tuan, H.H. Establishing Models for Predicting Above-Ground Carbon Stock Based on Sentinel-2 Imagery for Evergreen Broadleaf Forests in South Central Coastal Ecoregion, Vietnam. Forests 2025, 16, 686. https://doi.org/10.3390/f16040686
Tam NH, Loi NV, Tuan HH. Establishing Models for Predicting Above-Ground Carbon Stock Based on Sentinel-2 Imagery for Evergreen Broadleaf Forests in South Central Coastal Ecoregion, Vietnam. Forests. 2025; 16(4):686. https://doi.org/10.3390/f16040686
Chicago/Turabian StyleTam, Nguyen Huu, Nguyen Van Loi, and Hoang Huy Tuan. 2025. "Establishing Models for Predicting Above-Ground Carbon Stock Based on Sentinel-2 Imagery for Evergreen Broadleaf Forests in South Central Coastal Ecoregion, Vietnam" Forests 16, no. 4: 686. https://doi.org/10.3390/f16040686
APA StyleTam, N. H., Loi, N. V., & Tuan, H. H. (2025). Establishing Models for Predicting Above-Ground Carbon Stock Based on Sentinel-2 Imagery for Evergreen Broadleaf Forests in South Central Coastal Ecoregion, Vietnam. Forests, 16(4), 686. https://doi.org/10.3390/f16040686






