Next Article in Journal
Carbon Emission Prediction Following Pinus koraiensis Plantation Surface Fuel Combustion Based on Carbon Consumption Analysis
Previous Article in Journal
UAV-LiDAR-Based Structural Diversity of Subtropical Forests Under Different Management Practices in Southern China
Previous Article in Special Issue
A Comparison of the Impact of Latitude on the Root-Shoot Ratio of Natural and Planted Forests
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 16
Issue 5
10.3390/f16050724
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Intra-Plant Variation in Leaf Dry Mass per Area (LMA): Effects of Leaf–Shoot Orientation and Vertical Position on Dry Mass and Area Scaling

by
Xuchen Guo
1,
Yiwen Zheng
1,
Yuanmiao Chen
1,
Zhidong Zhou
2 and
Jianhui Xue
1,2,*
1
Co-Innovation Centre for Sustainable Forestry in Southern China, College of Ecology and Environment, Nanjing Forestry University, Nanjing 210037, China
2
Jiangsu Key Laboratory for the Research and Utilization of Plant Resources, Institute of Botany, Jiangsu Province and Chinese Academy of Sciences, Nanjing 210014, China
*
Author to whom correspondence should be addressed.
Forests 2025, 16(5), 724; https://doi.org/10.3390/f16050724
Submission received: 24 March 2025 / Revised: 19 April 2025 / Accepted: 22 April 2025 / Published: 24 April 2025
(This article belongs to the Special Issue Forest Phenology Dynamics and Response to Climate Change)
Browse Figures
Versions Notes

Abstract

:
The intra-plant plasticity of leaves plays a vital role in enabling plants to adapt to changing climatic conditions. However, limited research has investigated the extent of intra-plant leaf trait variation and leaf biomass allocation strategies in herbaceous plants. To address this gap, we collected a total of 1746 leaves from 217 Lamium barbatum Siebold and Zucc. plants and measured their leaf dry mass (M) and leaf area (A). Leaves were categorized by vertical position (upper vs. lower canopy layer) and leaf–shoot orientation (east, south, west, north). ANOVA with Tukey’s HSD test was used to compare differences in M, A, and leaf dry mass per unit area (LMA). Reduced major axis regression was employed to evaluate the scaling relationship between M and A, and the bootstrap percentile method was used to determine differences in scaling exponents. The data indicated that: (i) M, A, LMA, and the scaling exponents of M versus A did not differ significantly among leaf–shoot orientations, and (ii) lower layer leaves exhibited significantly greater M, A, and LMA than upper layer leaves, but their scaling exponents were significantly smaller. These findings highlight that plant vertical growth brings significant intra-plant plasticity in leaf traits and their scaling relationships in herbaceous plants. This plasticity differs from that observed in trees, but is also critical for balancing weight load and optimizing light-use efficiency, potentially enhancing stress resilience in herbaceous plants.

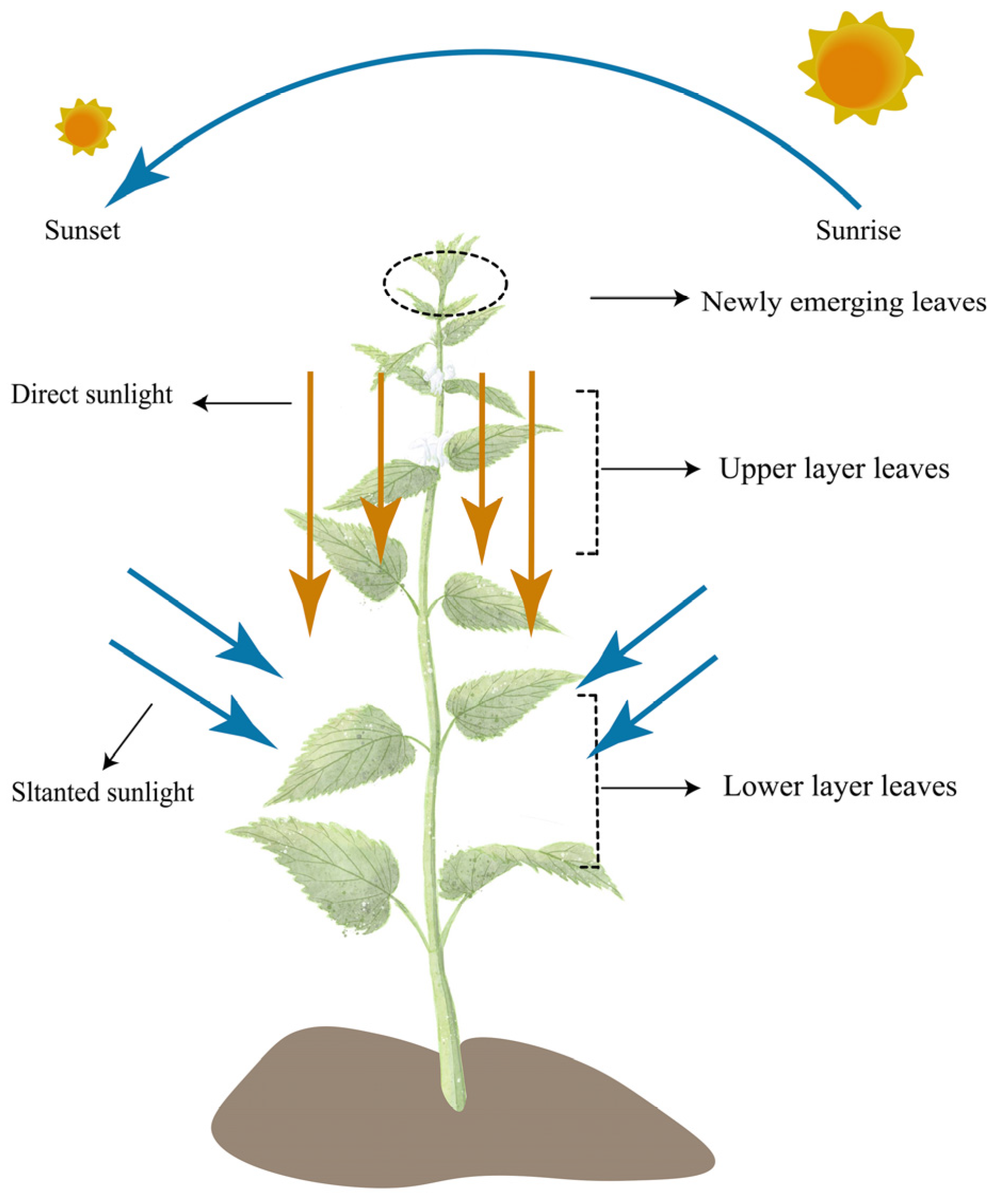
1. Introduction

Foliage leaves, as the primary photosynthetic organ of terrestrial vascular plants, are vital for maintaining plant metabolism, growth, and development [1,2]. Plant adaptability to environmental variations throughout history [3,4], as well as to contemporary environmental stresses such as global warming, drought, and salinity exposure, is reflected in the alterations of their leaf traits [5,6,7,8].
Leaf dry mass (M) and leaf area (A) are key traits of plants, representing the leaf construction cost and the light capture ability, respectively [9,10]. The relationship between these traits reveals fundamental principles of plant economic strategies across diverse taxa [11]. To quantify this relationship, two analytical methods are commonly employed: the ratio approach and the scaling approach [12,13]. The ratio approach calculates the ratios at a given developmental stage (i.e., the leaf dry mass per unit area, LMA) to infer the biomass cost for photosynthesis area construction [14]. However, a high LMA could result from either increased dry mass accumulation or reduced leaf area expansion. This ambiguity limits the ability to interpret the underlying physiological or environmental drivers [13].
To address this limitation, the scaling approach hypothesizes that M and A follow a power-law function, that is, M = β A α , where β is a normalization constant, and α is the scaling exponent [15,16]. In theory, when biomass allocation to leaves is consistent, M increases proportionally with A, resulting in an isometric scaling relationship (i.e., α = 1). However, Niklas et al. compiled data from 1943 plant species and found that A does not keep pace with increases in M (i.e., α < 1.0), a phenomenon called “diminishing return” [17,18,19]. By quantifying the relative growth rates of M to A (i.e., the scaling exponent), the scaling method resolves the interpretational uncertainties inherent in ratio-based metrics and offers a dynamic understanding of how plants allocate biomass for leaf area construction [12,20].
For example, Pan et al. found that the scaling exponent α for 121 species of vascular plants increases with rising altitude, enhancing the leaves’ hydraulic safety and cold resistance [21]. Similarly, Thakur et al. observed that under environmental stresses such as high temperature, drought, and high radiation, the scaling exponent α increased to improve the leaves’ antioxidant capacity [22]. Additionally, Jiao et al. discovered that the mature summer leaves of Photinia × fraseri “Red Robin” have a larger scaling exponent than the young spring leaves [23]. Chen et al. found that the scaling exponent of M versus A for the smaller tree size group of Camptotheca acuminata Decne is significantly lower than that of the larger tree size group [24]. These studies reveal that the leaf’s adaptive strategy is reflected in the variations in the scaling exponent, which may increase or decrease the relative growth rate of M versus A for adaptation to different ontogenetic periods and environmental conditions [25,26,27].
Recently, under changing climatic conditions, intra-plant plasticity in leaf traits has emerged as a critical mechanism enabling plants to adapt to climate-induced environmental stressors [28,29]. In trees, pronounced plasticity is driven by microenvironmental heterogeneity across vertical and horizontal canopy gradients. Leaves at different heights experience varying light conditions, prompting adjustments in LMA, thickness, and thermal resistance [30,31]. Similarly, canopy orientation, such as south-facing leaves exposed to higher solar radiation, can affect antioxidant capacity through altered leaf biomass allocation strategy [32,33,34]. These adaptations are facilitated by the structural complexity of trees, which creates diverse microhabitats, thereby optimizing resource capture and enhancing stress resilience [35]. For instance, trees can adjust their leaf area, leaf angle, and other traits to adapt to changes in light, temperature, and other environmental conditions [36,37,38,39].
However, previous studies have primarily focused on trees and crops, with limited research systematically investigating the extent of intra-plant leaf trait variation and leaf biomass allocation strategies in herbaceous plants [14,40]. Unlike trees, herbaceous plants have smaller statures and simpler architectures. Their leaves and shoots may exhibit distinct growth patterns, such as lateral leaf orientation to optimize light interception in shaded microhabitats [41]. These structural traits, combined with biomechanical requirements for load balance, may drive significant intra-plant plasticity in leaf traits and scaling relationships. However, it remains unclear whether herbaceous plants employ analogous intra-plant plasticity, and this uncertainty may hinder predictions of their adaptive capacity under climate change.
To address this gap, we collected leaves from Lamium barbatum Siebold and Zucc. at different vertical positions (upper vs. lower layer) and leaf–shoot orientations (north, south, east, west). This species was selected due to its decussate phyllotaxis—paired leaves arranged perpendicularly between successive node pairs—which enables the unambiguous determination of leaf–shoot orientations. This growth architecture is typical of many perennial herbs with opposite-leaf arrangements [42]. Our empirical analyses have compared the M, A, LMA, and scaling exponents of M versus A at different intra-plant positions. The goal of study was to evaluate the significance of intra-plant plasticity in herbaceous leaves and its potential implications for climate change adaptation.

2. Materials and Methods

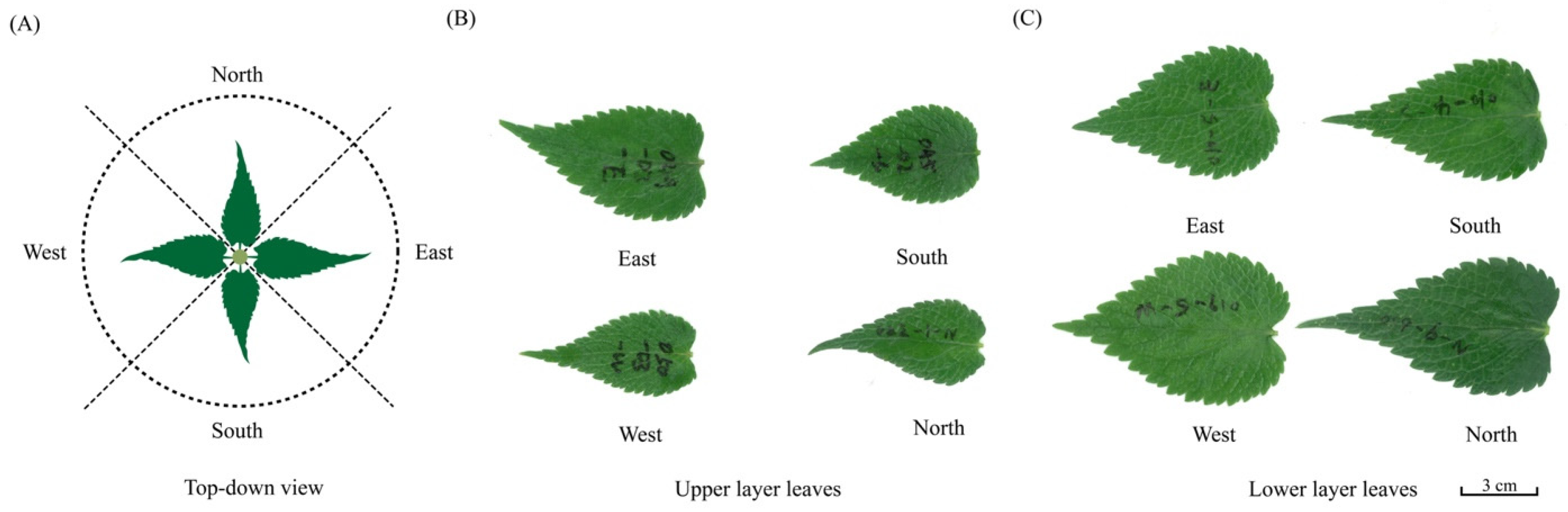
2.1. Leaf Collection

A total of 1746 fully expanded and intact leaves were collected from 217 Lamium barbatum plants. These plants were naturally growing in a secondary forest within the Nanjing Forestry University campus (32°05′53″ N, 118°49′06″ E), and were not influenced by human activities. Leaf sampling was carried out from 10 April to 20 April 2022, between 9:30 and 11:30 A.M. After collection, the leaves were wrapped in wet paper, placed in plastic self-sealing bags (16 cm × 24 cm), and transported to the laboratory for processing within half an hour. The leaf–shoot orientations of the leaf tips in each layer were recorded (Figure 1A). The Lamium barbatum plants typically possess eight to ten layers. The top layer consists of newly emerged leaves. Therefore, the topmost newly emerged leaves were excluded, and the first to third layers (from the top) were classified as upper layer leaves, while the fourth to seventh layers were classified as lower layer leaves. Layers beyond the seventh were not collected, since the bottom layer leaves were generally damaged or unhealthy. Figure 1B illustrates examples of scanned images for upper layer leaves, and Figure 1C shows those for lower layer leaves.

2.2. Leaf Measurements

An Epson photo scanner (V550, Epson Indonesia, Batam, Indonesia) was used to scan each fresh leaf at a resolution of 600-dpi. Adobe Photoshop (version 9.0; Adobe, San Jose, CA, USA) was used to obtain black-and-white images of each leaf. The pixel values of the leaf images were then calculated using an M-file based on MATLAB (version 2009a; MathWorks, Natick, MA, USA) developed by [43] to obtain the leaf planar coordinates. Subsequently, the A was calculated using the “bilat” function in the “biogeom” package (version 1.3.5), [44] based on R software (version 4.2.0) [45]. The M was measured using an electronic balance (type: ML 204; Mettler Toledo Company, Greifensee, Switzerland) after drying the leaves in a ventilated oven (type: XMTD8222; Jinghong Experimental Equipment Co., Ltd., Shanghai, China) at 80 °C for at least 72 h. The raw data of the measured leaf traits can be found in Table S1.

2.3. Statistical Methods

The scaling relationship between M and A across different leaf orientations or vertical positions can be described by a power function:
M = β A α
where β is a normalization constant, and α is the scaling exponent. To stabilize the variance on both sides of the equation, logarithms were taken on both sides of the equation simultaneously. After the logarithmic transformation, the power law function was converted to:
y = γ + α x
where y = ln M , γ = ln β , and x = ln A . The parameters γ and α were estimated using the reduced major axis method [15,46]. The bootstrap percentile method (based on 4000 random resampling) was used to compare the significant differences in the parameters γ and α across different spatial positions [47,48]. The common slope methods were also applied to test the significance of the difference in slope [49]. Log-transformations were applied to both M and A to reduce the skewness of the data from the normal distribution before comparison. Analysis of variance followed by Tukey’s honestly significant difference test is used for comparisons of M, A, and LMA among different spatial positions. The statistical analyses and plotting are all completed using R software (version 4.2.0, R Core Team, 2022).

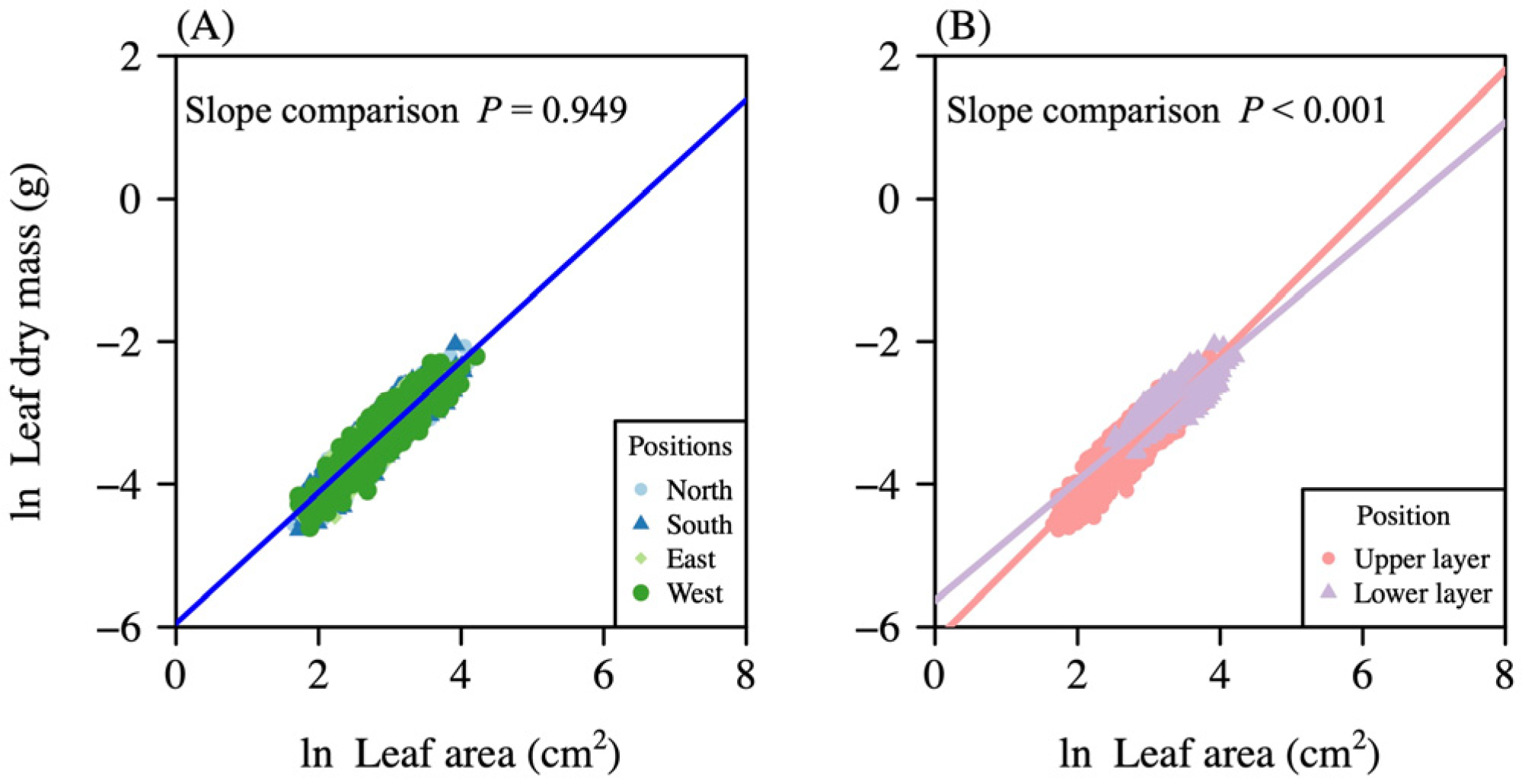
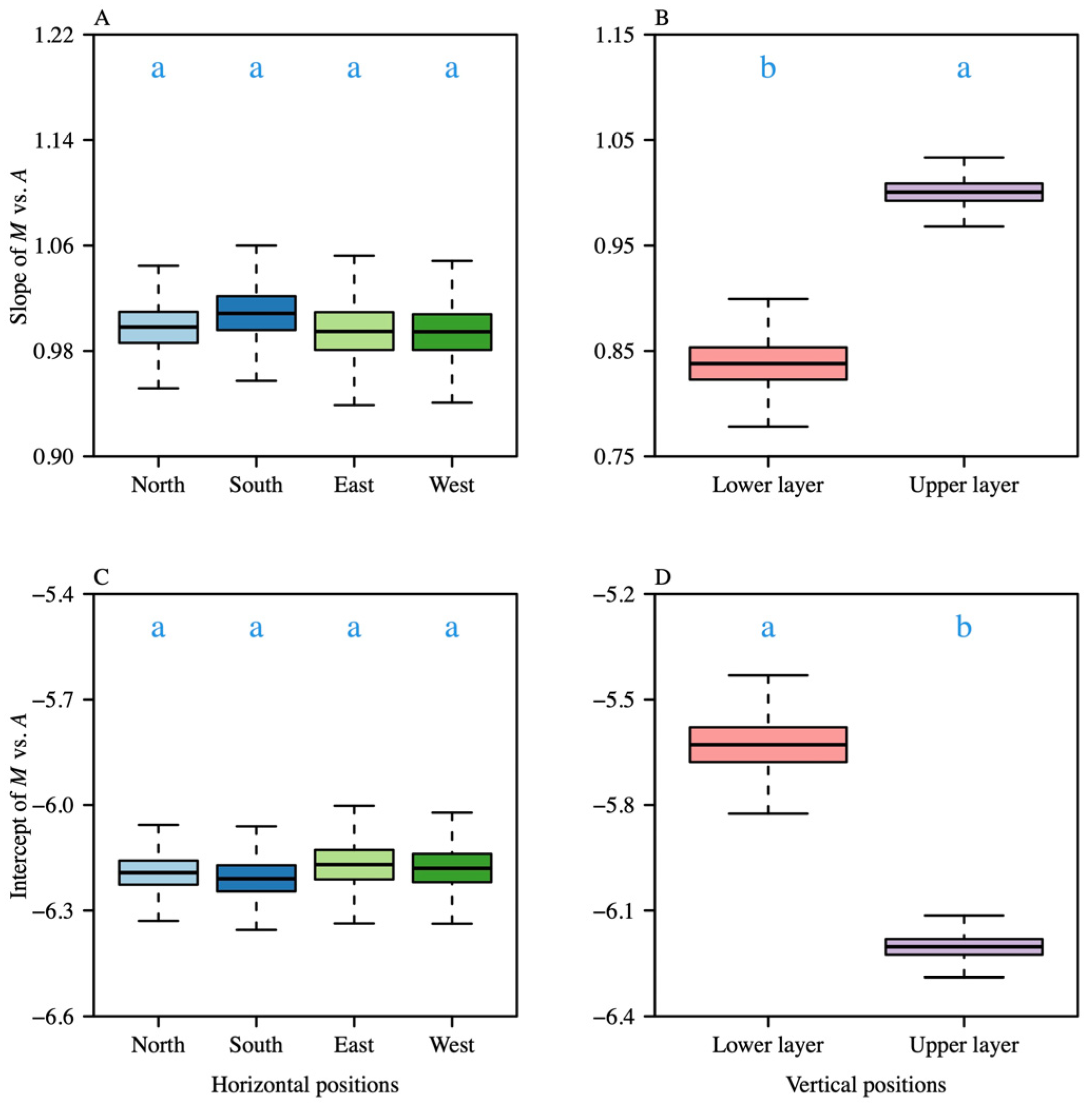
3. Results

The two-way analysis of variance shows that log-transformed M, log-transformed A, and LMA were significantly affected by vertical positions, while the effects of leaf–shoot orientations and the interaction between vertical positions and leaf–shoot orientations were not significant (Table 1). There were no significant differences in log-transformed M, log-transformed A, and LMA across the leaf–shoot orientations (Figure 2A,C,E); however, these leaf traits were significantly larger in the lower layer leaves compared to the upper layer leaves (Figure 2B,D,F).
The pooled data shows an isometric relationship between M and A, as the 95% confidence intervals (CIs) of the scaling exponents of M versus A (0.981, 1.019) includes unity (i.e., α = 1 ). The four leaf–shoot orientations and the upper layer leaves also show an isometric relationship between M and A, as their 95% CIs of the scaling exponent of M versus A include unity (Table 2). However, the lower layer leaves indicate a scaling relationship between M versus A, as the upper bounds of the corresponding 95% CIs (0.793, 0.884) are less than unity (Table 2). The r2 values for the four horizontal positions (north: 0.843; south: 0.826; east: 0.808; west: 0.816) were larger than those for the vertical positions (lower layer: 0.545; upper layer: 0.790, Table 2).
For intra-plant leaf scaling, there was a common slope of the scaling relationships between M and A at the four leaf–shoot orientations (p > 0.05, Figure 3A), while there was no common slope for the upper layer leaves and lower layer leaves (p < 0.05, Figure 3B). The slopes and intercepts of the scaling relationships between M and A for leaves at the four leaf–shoot orientations were not significantly different (Figure 4A,C). In contrast, the slope of the scaling relationship between M and A for the lower layer leaves was significantly smaller than that for the upper layer leaves, while the intercept for the lower layer leaves was significantly larger than that for the upper layer leaves (Figure 4B,D).

4. Discussion

Our research reveals significant intra-plant plasticity in M, A, and LMA, as well as in the scaling relationship between M and A. However, this intra-plant plasticity differs from that observed in trees. Typically, tree leaves on the south-facing canopy and upper layers exhibit larger M, A, and LMA values. This attributed to their exposure to high-light conditions, which tend to result in higher LMA and greater mesophyll cell density [36]. In contrast, our study indicates that leaf traits do not significantly differ between different leaf–shoot orientations. Interestingly, the leaf traits of upper layer leaves are found to be smaller than those of lower layer leaves. This discrepancy may arise because intra-plant plasticity in trees is primarily attributed to their canopy structure, whereas in herbaceous plants, it stems from vertical growth and leaf–shoot orientations. The reason will be discussed in detail in the following section.

4.1. Leaf Biomass Allocation for Photosynthesis Area Across Vertical Positions

Light intensity strongly influences leaf photosynthetic performance and biomass allocation. Higher light levels typically enhance photosynthesis, often leading to increased leaf thickness and shifts in chlorophyll composition. Conversely, low light conditions may reduce photosynthetic rates, driving plants to optimize light capture through biomass reallocation strategies such as larger leaf area or altered nitrogen distribution [50,51,52]. These patterns are further modulated by hydraulic constraints (e.g., root-to-leaf water transport distance) and shading effects from upper canopy layers, both of which influence intra-plant resource partitioning [31]. However, how plants adjust the leaf traits (i.e., M and A) and their leaf scaling relationships vertically to improve leaf adaptive ability remains controversial. For example, Sterck and Bongers indicate that light conditions at different heights affect LMA, but the effects on A are not significant [53]. In contrast, Sack et al. found that both LMA and A are significantly affected by height, while M is only related to whether the leaves are shaded or not, regardless of height [29].
Our study demonstrates that the M, A, and LMA of upper layer leaves were smaller compared to those of lower layer leaves in Lamium barbatum plants. This intra-plant plasticity increases the whole light interception of Lamium barbatum, as the larger upper leaves could shade the lower layer leaves and hinder their ability to harvest slanted sunlight (Figure 5). In addition, LMA is the core trait within the leaf economic spectrum [11]. Leaves with lower LMA may decrease palisade tissue thickness and reduce epidermal cell width to lower the cost of light penetration, making them suitable for the upper canopy layers [40]. Conversely, leaves with larger LMA increase their biomass investment in non-photosynthetic tissue to store more energy and chemical substances [6,54]. As a result, these upper layer leaves of Lamium barbatum may exhibit higher photosynthetic capacity [51,55], while these lower leaves have a higher LMA, which makes them better able to resist environmental stresses such as shading, drought, and mechanical damage caused by pests.
The intra-plant microenvironment difference in Lamium barbatum may also bring a different leaf biomass allocation strategy for photosynthesis area. Upper layer leaves have ample supply of light, making it unnecessary to make a tradeoff for leaf photosynthetic area construction. Therefore, the scaling relationship between M and A in these leaves is isometric [52,56]. The isometric growth also allows upper leaves to increase their biomass investment in support and transport structures, which in turn improves their photosynthetic efficiency under conditions of ample light [13]. Generally, leaves that grow under relatively shadowy conditions, such as those in the lower canopy layers, lack sufficient biomass investment in the photosynthetic area. By altering the allocation of resources and adjusting physiological processes, plants can achieve a balance between carbon gain and resource conservation [34]. Within the framework of the leaf economic spectrum, this adjustment is reflected in both leaf morphology and physiology; lower layer leaves tend to have higher mesophyll porosity, which allows them to expand their leaf area with less mass investment and to harvest more scattered sunlight. Therefore, the scaling exponents of M versus A have less than unity [57,58].

4.2. Leaf Biomass Allocation Photosynthesis Area Across Leaf–Shoot Orientations

Leaf–canopy orientations of trees significantly affect leaf growth and their access to sunlight [32,33]. However, there is a significant different between canopy horizontal directions and leaf–shoot orientations. Our research indicates the leaf traits and the leaf scaling of M versus A are not significantly different across Lamium barbatum leaf–shoot orientations. This is because sun comes from the east to the west during the daytime, which means all orientations are exposed to sunlight relatively equally within a specific level. Therefore, the leaf biomass allocation for the photosynthesis area may not be affected by the different leaf–shoot orientations (Figure 5) [33,54,59], making the leaf traits and the leaf scaling consistent across four leaf–shoot orientations. This leaf–shoot growth pattern of Lamium barbatum facilitates weight load balance between paired leaves, optimizing structural integrity and reducing mechanical stress on petioles and stems during growth, and maintaining photosynthetic efficiency and resource-use optimization under low-light conditions [60,61].
Specifically, given that the resources available to plants over a specific timeframe are relatively finite, the allocation of biomass to one horizontal position can have a cascading effect on the distribution of resources elsewhere. When leaf biomass is allocated to enhance support tissues in one position, it can lead to a simultaneous increase in structural support costs, while potentially resulting in a decrease in biomass in other positions [62,63,64]. Although our study did not directly measure the mass of leaf petioles, existing research has demonstrated a significant allometric scaling relationship between petiole mass and leaf mass [13,65]. This relationship allows for an estimation of petiole mass based on the mass of the leaf itself. Therefore, the consistent horizontal allocation of leaf biomass for the photosynthesis area may enhance the plant’s ability to resist external forces such as wind and to maintain the plant’s structural stability [66,67,68].

5. Conclusions

Our study highlights significant intra-plant plasticity in leaf biomass allocation to photosynthetic areas in herbaceous plants. This plasticity differs from the canopy plasticity of trees, but is critical for balancing weight loads, optimizing light-use efficiency, and potentially enhancing stress resilience in herbaceous plants. Future research should extend to a broader range of plant taxa and investigate how such intra-leaf plasticity functions in response to climate change.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/f16050724/s1, Table S1: The raw data of the measured leaf traits.

Author Contributions

Formal analysis, X.G. and Y.Z.; funding acquisition, X.G. and J.X.; investigation, Y.Z.; writing—original draft, X.G., Y.Z. and Y.C.; writing—review and editing, Z.Z. and J.X. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Postgraduate Research and Practice Innovation Program of Jiangsu Province (KYCX23_1122) and the Evaluation on the Biodiversity and Carbon Sequestration of Typical Wetland Ecosystems in Jiangsu Province (No: LYKJ(2022)02).

Data Availability Statement

The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author(s).

Acknowledgments

The authors thank Weihao Yao, Kexin Yu, and Qingyue Miao for their valuable help in the preparation of this manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Nakamura, Y.; Hashimoto, H. Characteristics of Photosynthate Partitioning during Chloroplast Development in Avena Leaves. Plant Physiol. 1988, 87, 458–462. [Google Scholar] [CrossRef]
  2. Adams, W.W., III; Terashima, I. (Eds.) The Leaf: A Platform for Performing Photosynthesis; Advances in Photosynthesis and Respiration; Springer International Publishing: Cham, Switzerland, 2018; Volume 44, ISBN 978-3-319-93592-8. [Google Scholar]
  3. Niklas, K.J.; Shi, P.; Gielis, J.; Schrader, J.; Niinemets, Ü. Editorial: Leaf Functional Traits: Ecological and Evolutionary Implications. Front. Plant Sci. 2023, 14, 1169558. [Google Scholar] [CrossRef] [PubMed]
  4. Huang, W.; Gielis, J.; Shi, P. Editorial: The Adaptation, Plasticity and Extinction of Forest Plants to Climate Change: Mechanisms behind the Morphological, Physiological, Phenological and Ecological Traits. Front. Ecol. Evol. 2024, 12, 1488465. [Google Scholar] [CrossRef]
  5. Wright, I.J.; Reich, P.B.; Cornelissen, J.H.C.; Falster, D.S.; Groom, P.K.; Hikosaka, K.; Lee, W.; Lusk, C.H.; Niinemets, Ü.; Oleksyn, J.; et al. Modulation of Leaf Economic Traits and Trait Relationships by Climate. Glob. Ecol. Biogeogr. 2005, 14, 411–421. [Google Scholar] [CrossRef]
  6. Shipley, B.; Lechowicz, M.J.; Wright, I.; Reich, P.B. Fundamental Trade-Offs Generating the Worldwide Leaf Economics Epectrum. Ecology 2006, 87, 535–541. [Google Scholar] [CrossRef]
  7. Dolezal, J.; Jandova, V.; Macek, M.; Liancourt, P. Contrasting Biomass Allocation Responses across Ontogeny and Stress Gradients Reveal Plant Adaptations to Drought and Cold. Funct. Ecol. 2021, 35, 32–42. [Google Scholar] [CrossRef]
  8. Bond-Lamberty, B.; Haddock, L.M.; Pennington, S.C.; Sezen, U.U.; Shue, J.; Megonigal, J.P. Salinity Exposure Affects Lower-Canopy Specific Leaf Area of Upland Trees in a Coastal Deciduous Forest. For. Ecol. Manag. 2023, 548, 121404. [Google Scholar] [CrossRef]
  9. Niinemets, Ü.; Portsmuth, A.; Tena, D.; Tobias, M.; Matesanz, S.; Valladares, F. Do We Underestimate the Importance of Leaf Size in Plant Economics? Disproportional Scaling of Support Costs within the Spectrum of Leaf Physiognomy. Ann. Bot. 2007, 100, 283–303. [Google Scholar] [CrossRef] [PubMed]
  10. Mu, Y.; He, K.; Shi, P.; Wang, L.; Deng, L.; Shi, Z.; Liu, M.; Niklas, K.J. Comparison between Computer Recognition and Manual Measurement Methods for the Estimation of Leaf Area. Ann. Bot. 2024, 134, 501–510. [Google Scholar] [CrossRef]
  11. Wright, I.J.; Reich, P.B.; Westoby, M.; Ackerly, D.D.; Baruch, Z.; Bongers, F.; Cavender-Bares, J.; Chapin, T.; Cornelissen, J.H.C.; Diemer, M.; et al. The Worldwide Leaf Economics Spectrum. Nature 2004, 428, 821–827. [Google Scholar] [CrossRef]
  12. Li, G.; Yang, D.; Sun, S. Allometric Relationships between Lamina Area, Lamina Mass and Petiole Mass of 93 Temperate Woody Species Vary with Leaf Habit, Leaf Form and Altitude. Funct. Ecol. 2008, 22, 557–564. [Google Scholar] [CrossRef]
  13. Guo, X.; Schrader, J.; Shi, P.; Jiao, Y.; Miao, Q.; Xue, J.; Niklas, K.J. Leaf-Age and Petiole Biomass Play Significant Roles in Leaf Scaling Theory. Front. Plant Sci. 2023, 14, 1322245. [Google Scholar] [CrossRef] [PubMed]
  14. Poorter, H.; Niinemets, Ü.; Poorter, L.; Wright, I.J.; Villar, R. Causes and Consequences of Variation in Leaf Mass per Area (LMA): A Meta-analysis. New Phytol. 2009, 182, 565–588. [Google Scholar] [CrossRef]
  15. Niklas, K.J. Plant Allometry: The Scaling of Form and Process; The University of Chicago Press: Chicago, IL, USA, 1994. [Google Scholar]
  16. Enquist, B.J. Universal Scaling in Tree and Vascular Plant Allometry: Toward a General Quantitative Theory Linking Plant Form and Function from Cells to Ecosystems. Tree Physiol. 2002, 22, 1045–1064. [Google Scholar] [CrossRef]
  17. Niklas, K.J.; Cobb, E.D.; Niinemets, Ü.; Reich, P.B.; Sellin, A.; Shipley, B.; Wright, I.J. “Diminishing Returns” in the Scaling of Functional Leaf Traits across and within Species Groups. Proc. Natl. Acad. Sci. USA 2007, 104, 8891–8896. [Google Scholar] [CrossRef] [PubMed]
  18. Milla, R.; Reich, P.B. The Scaling of Leaf Area and Mass: The Cost of Light Interception Increases with Leaf Size. Proc. R. Soc. B Biol. Sci. 2007, 274, 2109–2115. [Google Scholar] [CrossRef]
  19. Niklas, K.J.; Cobb, E.D.; Spatz, H.-C. Predicting the Allometry of Leaf Surface Area and Dry Mass. Am. J. Bot. 2009, 96, 531–536. [Google Scholar] [CrossRef]
  20. Ye, Y.; Kitayama, K.; Onoda, Y. A Cost–Benefit Analysis of Leaf Carbon Economy with Consideration of Seasonal Changes in Leaf Traits for Sympatric Deciduous and Evergreen Congeners: Implications for Their Coexistence. New Phytol. 2022, 234, 1047–1058. [Google Scholar] [CrossRef]
  21. Pan, S.; Liu, C.; Zhang, W.; Xu, S.; Wang, N.; Li, Y.; Gao, J.; Wang, Y.; Wang, G. The Scaling Relationships between Leaf Mass and Leaf Area of Vascular Plant Species Change with Altitude. PLoS ONE 2013, 8, e76872. [Google Scholar] [CrossRef]
  22. Thakur, D.; Rathore, N.; Chawla, A. Increase in Light Interception Cost and Metabolic Mass Component of Leaves Are Coupled for Efficient Resource Use in the High Altitude Vegetation. Oikos 2019, 128, 254–263. [Google Scholar] [CrossRef]
  23. Jiao, Y.; Niklas, K.J.; Wang, L.; Yu, K.; Li, Y.; Shi, P. Influence of Leaf Age on the Scaling Relationships of Lamina Mass vs. Area. Front. Plant Sci. 2022, 13, 860206. [Google Scholar] [CrossRef] [PubMed]
  24. Chen, L.; He, K.; Shi, P.; Lian, M.; Yao, W.; Niklas, K.J. Influence of Tree Size on the Scaling Relationships of Lamina and Petiole Traits: A Case Study Using Camptotheca Acuminata Decne. Ecol. Evol. 2024, 14, e70066. [Google Scholar] [CrossRef] [PubMed]
  25. Wright, I.J.; Reich, P.B.; Westoby, M. Strategy Shifts in Leaf Physiology, Structure and Nutrient Content between Species of High- and Low-rainfall and High- and Low-nutrient Habitats. Funct. Ecol. 2001, 15, 423–434. [Google Scholar] [CrossRef]
  26. Atkinson, L.J.; Campbell, C.D.; Zaragoza-Castells, J.; Hurry, V.; Atkin, O.K. Impact of Growth Temperature on Scaling Relationships Linking Photosynthetic Metabolism to Leaf Functional Traits. Funct. Ecol. 2010, 24, 1181–1191. [Google Scholar] [CrossRef]
  27. Chen, R.; Xiao, S.; Dong, C.; Xie, S.; Zhang, L.; Wu, F.; Tu, C.; Liu, Q.-X.; Wang, S.; Niinemets, Ü.; et al. Ontogenetic Shifts in Leaf Biomass Allocation in Crop Plants. Natl. Sci. Rev. 2024, 11, nwae349. [Google Scholar] [CrossRef]
  28. Nicotra, A.B.; Atkin, O.K.; Bonser, S.P.; Davidson, A.M.; Finnegan, E.J.; Mathesius, U.; Poot, P.; Purugganan, M.D.; Richards, C.L.; Valladares, F.; et al. Plant Phenotypic Plasticity in a Changing Climate. Trends Plant Sci. 2010, 15, 684–692. [Google Scholar] [CrossRef] [PubMed]
  29. Sack, L.; Melcher, P.J.; Liu, W.H.; Middleton, E.; Pardee, T. How Strong Is Intracanopy Leaf Plasticity in Temperate Deciduous Trees? Am. J. Bot. 2006, 6, 829–839. [Google Scholar] [CrossRef]
  30. Koike, T.; Kitao, M.; Maruyama, Y.; Mori, S.; Lei, T.T. Leaf Morphology and Photosynthetic Adjustments among Deciduous Broad-Leaved Trees within the Vertical Canopy Profile. Tree Physiol. 2001, 21, 951–958. [Google Scholar] [CrossRef]
  31. Coble, A.P.; Cavaleri, M.A. Vertical Leaf Mass per Area Gradient of Mature Sugar Maple Reflects Both Height-Driven Increases in Vascular Tissue and Light-Driven Increases in Palisade Layer Thickness. Tree Physiol. 2017, 37, 1337–1351. [Google Scholar] [CrossRef]
  32. Valladares, F.; Pearcy, R.W. The Geometry of Light Interception by Shoots of Heteromeles Arbutifolia: Morphological and Physiological Consequences for Individual Leaves. Oecologia 1999, 121, 171–182. [Google Scholar] [CrossRef]
  33. Iio, A.; Fukasawa, H.; Nose, Y.; Kato, S.; Kakubari, Y. Vertical, Horizontal and Azimuthal Variations in Leaf Photosynthetic Characteristics within a Fagus Crenata Crown in Relation to Light Acclimation. Tree Physiol. 2005, 25, 533–544. [Google Scholar] [CrossRef]
  34. Sarlikioti, V.; De Visser, P.H.B.; Marcelis, L.F.M. Exploring the Spatial Distribution of Light Interception and Photosynthesis of Canopies by Means of a Functional–Structural Plant Model. Ann. Bot. 2011, 107, 875–883. [Google Scholar] [CrossRef]
  35. Hikosaka, K.; Niinemets, Ü.; Anten, N.P.R. (Eds.) Canopy Photosynthesis: From Basics to Applications; Advances in Photosynthesis and Respiration; Springer: Dordrecht, The Netherlands, 2016; Volume 42, ISBN 978-94-017-7290-7. [Google Scholar]
  36. Fotis, A.T.; Curtis, P.S. Effects of Structural Complexity on Within-Canopy Light Environments and Leaf Traits in a Northern Mixed Deciduous Forest. Tree Physiol. 2017, 37, 1426–1435. [Google Scholar] [CrossRef] [PubMed]
  37. Asner, G.P.; Martin, R.E.; Carranza-Jiménez, L.; Sinca, F.; Tupayachi, R.; Anderson, C.B.; Martinez, P. Functional and Biological Diversity of Foliar Spectra in Tree Canopies throughout the Andes to Amazon Region. New Phytol. 2014, 204, 127–139. [Google Scholar] [CrossRef] [PubMed]
  38. Challis, A.; Rymer, P.D.; Ahrens, C.W.; Hardy, G.; Byrne, M.; Ruthrof, K.X.; Tissue, D.T. Environmental and Genetic Drivers of Physiological and Functional Traits in a Key Canopy Species. Environ. Exp. Bot. 2024, 226, 105904. [Google Scholar] [CrossRef]
  39. De Freitas, G.V.; Da Cunha, M.; Vitória, A.P. A Systematic Review of Leaf and Wood Traits in the Neotropics: Environmental Gradients and Functionality. Trees 2024, 38, 551–572. [Google Scholar] [CrossRef]
  40. Osnas, J.L.D.; Lichstein, J.W.; Reich, P.B.; Pacala, S.W. Global Leaf Trait Relationships: Mass, Area, and the Leaf Economics Spectrum. Science 2013, 340, 741–744. [Google Scholar] [CrossRef] [PubMed]
  41. Koester, R.P.; Skoneczka, J.A.; Cary, T.R.; Diers, B.W.; Ainsworth, E.A. Historical Gains in Soybean (Glycine Max Merr.) Seed Yield Are Driven by Linear Increases in Light Interception, Energy Conversion, and Partitioning Efficiencies. J. Exp. Bot. 2014, 65, 3311–3321. [Google Scholar] [CrossRef] [PubMed]
  42. Editorial Committee of the Flora of China Lamium Linnaeus. Flora of China; Science Press: Beijing, China, 1994; Volume 17, p. 157. [Google Scholar]
  43. Shi, P.; Ratkowsky, D.; Li, Y.; Zhang, L.; Lin, S.; Gielis, J. A General Leaf Area Geometric Formula Exists for Plants—Evidence from the Simplified Gielis Equation. Forests 2018, 9, 714. [Google Scholar] [CrossRef]
  44. Shi, P.; Gielis, J.; Quinn, B.K.; Niklas, K.J.; Ratkowsky, D.A.; Schrader, J.; Ruan, H.; Wang, L.; Niinemets, Ü. ‘Biogeom’: An R Package for Simulating and Fitting Natural Shapes. Ann. N. Y. Acad. Sci. 2022, 1516, 123–134. [Google Scholar] [CrossRef]
  45. R Core Team R: A Language and Environment for Statistical Computing; The R Foundation for Statistical Computing: Vienna, Austria, 2022.
  46. Smith, R.J. Use and Misuse of the Reduced Major Axis for Line-Fitting. Am. J. Phys. Anthropol. 2009, 140, 476–486. [Google Scholar] [CrossRef] [PubMed]
  47. Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: New York, NY, USA, 1993. [Google Scholar]
  48. Sandhu, H.S.; Shi, P.; Kuang, X.; Xue, F.; Ge, F. Applications of the Bootstrap to Insect Physiology. Fla. Entomol. 2011, 94, 1036–1041. [Google Scholar] [CrossRef]
  49. Warton, D.I.; Weber, N.C. Common Slope Tests for Bivariate Errors-in-Variables Models. Biom. J. 2002, 44, 161–174. [Google Scholar] [CrossRef]
  50. Yamori, W.; Evans, J.R.; Von Caemmerer, S. Effects of Growth and Measurement Light Intensities on Temperature Dependence of CO2 Assimilation Rate in Tobacco Leaves. Plant Cell Environ. 2010, 33, 332–343. [Google Scholar] [CrossRef]
  51. Coble, A.P.; Cavaleri, M.A. Light Drives Vertical Gradients of Leaf Morphology in a Sugar Maple (Acer Saccharum) Forest. Tree Physiol. 2014, 34, 146–158. [Google Scholar] [CrossRef] [PubMed]
  52. Lafont, T.R.; Gallant, M.C.; Julien, F.; Céréghino, R.; Leroy, C. Light Intensity Mediates Phenotypic Plasticity and Leaf Trait Regionalization in a Tank Bromeliad. Ann. Bot. 2023, 132, 443–454. [Google Scholar] [CrossRef]
  53. Sterck, F.J.; Bongers, F. Crown Development in Tropical Rain Forest Trees: Patterns with Tree Height and Light Availability. J. Ecol. 2001, 89, 1–13. [Google Scholar] [CrossRef]
  54. Liu, Z.; Zhao, M.; Zhang, H.; Ren, T.; Liu, C.; He, N. Divergent Response and Adaptation of Specific Leaf Area to Environmental Change at Different Spatio-temporal Scales Jointly Improve Plant Survival. Glob. Change Biol. 2023, 29, 1144–1159. [Google Scholar] [CrossRef]
  55. Zhang, J.; Ge, J.; Dayananda, B.; Li, J. Effect of Light Intensities on the Photosynthesis, Growth and Physiological Performances of Two Maple Species. Front. Plant Sci. 2022, 13, 999026. [Google Scholar] [CrossRef]
  56. West, G.B.; Brown, J.H. The Origin of Allometric Scaling Laws in Biology from Genomes to Ecosystems: Towards a Quantitative Unifying Theory of Biological Structure and Organization. J. Exp. Biol. 2005, 208, 1575–1592. [Google Scholar] [CrossRef]
  57. Oldham, A.R.; Sillett, S.C.; Tomescu, A.M.F.; Koch, G.W. The Hydrostatic Gradient, Not Light Availability, Drives Height-related Variation in Sequoia Sempervirens (Cupressaceae) Leaf Anatomy. Am. J. Bot. 2010, 97, 1087–1097. [Google Scholar] [CrossRef]
  58. Kalve, S.; Fotschki, J.; Beeckman, T.; Vissenberg, K.; Beemster, G.T.S. Three-Dimensional Patterns of Cell Division and Expansion throughout the Development of Arabidopsis Thaliana Leaves. J. Exp. Bot. 2014, 65, 6385–6397. [Google Scholar] [CrossRef]
  59. Butrim, M.J.; Royer, D.L.; Miller, I.M.; Dechesne, M.; Neu-Yagle, N.; Lyson, T.R.; Johnson, K.R.; Barclay, R.S. No Consistent Shift in Leaf Dry Mass per Area Across the Cretaceous—Paleogene Boundary. Front. Plant Sci. 2022, 13, 894690. [Google Scholar] [CrossRef]
  60. López, R.; Cano, F.J.; Martin-StPaul, N.K.; Cochard, H.; Choat, B. Coordination of Stem and Leaf Traits Define Different Strategies to Regulate Water Loss and Tolerance Ranges to Aridity. New Phytol. 2021, 230, 497–509. [Google Scholar] [CrossRef]
  61. Filartiga, A.L.; Klimeš, A.; Altman, J.; Nobis, M.P.; Crivellaro, A.; Schweingruber, F.; Doležal, J. Comparative Anatomy of Leaf Petioles in Temperate Trees and Shrubs: The Role of Plant Size, Environment and Phylogeny. Ann. Bot. 2022, 129, 567–582. [Google Scholar] [CrossRef] [PubMed]
  62. Westoby, M.; Wright, I.J. The Leaf Size—Twig Size Spectrum and Its Relationship to Other Important Spectra of Variation among Species. Oecologia 2003, 135, 621–628. [Google Scholar] [CrossRef] [PubMed]
  63. Funk, J.L.; Vitousek, P.M. Resource-Use Efficiency and Plant Invasion in Low-Resource Systems. Nature 2007, 446, 1079–1081. [Google Scholar] [CrossRef] [PubMed]
  64. Wang, H.; Prentice, I.C.; Wright, I.J.; Warton, D.I.; Qiao, S.; Xu, X.; Zhou, J.; Kikuzawa, K.; Stenseth, N.C. Leaf Economics Fundamentals Explained by Optimality Principles. Sci. Adv. 2023, 9, eadd5667. [Google Scholar] [CrossRef] [PubMed]
  65. Li, Y.; Shi, P.; Niinemets, Ü.; Song, Y.; Yu, K.; Schrader, J.; Niklas, K.J. Diminishing Returns among Lamina Fresh and Dry Mass, Surface Area, and Petiole Fresh Mass among Nine Lauraceae Species. Am. J. Bot. 2022, 109, 377–392. [Google Scholar] [CrossRef]
  66. Niinemets, U.; Kull, O. Biomass Investment in Leaf Lamina versus Lamina Support in Relation to Growth Irradiance and Leaf Size in Temperate Deciduous Trees. Tree Physiol. 1999, 19, 349–358. [Google Scholar] [CrossRef]
  67. Niklas, K.J. A Mechanical Perspective on Foliage Leaf Form and Function. New Phytol. 1999, 143, 19–31. [Google Scholar] [CrossRef]
  68. Niinemets, Ü.; Portsmuth, A.; Tobias, M. Leaf Size Modifies Support Biomass Distribution among Stems, Petioles and Mid-ribs in Temperate Plants. New Phytol. 2006, 171, 91–104. [Google Scholar] [CrossRef] [PubMed]
Forests 16 00724 g001
Figure 1. Top-down view of Lamium barbatum Siebold and Zucc. plant (A) and examples of scans leaves of upper layer leaves (B) and lower layer leaves (C) with different leaf–shoot orientations.
Figure 1. Top-down view of Lamium barbatum Siebold and Zucc. plant (A) and examples of scans leaves of upper layer leaves (B) and lower layer leaves (C) with different leaf–shoot orientations.
Forests 16 00724 g001
Forests 16 00724 g002
Figure 2. Comparison of log-transformed leaf dry mass (M) across leaf–shoot orientations (A) and across vertical positions (B); Comparison of log-transformed leaf area (A) across leaf–shoot orientations (C) and across vertical positions (D); Comparison of leaf dry mass per unit area (LMA) across leaf–shoot orientations (E) and across vertical positions (F). Notation: The lowercase letters a–b on the top of each box denotes the significance of the difference in the means between any two groups based on Tukey’s HSD test at a 0.05 significance level. The numbers above the whiskers represent the coefficients of variation (%). The horizontal solid line indicates the median; the * in each box indicates the means.
Figure 2. Comparison of log-transformed leaf dry mass (M) across leaf–shoot orientations (A) and across vertical positions (B); Comparison of log-transformed leaf area (A) across leaf–shoot orientations (C) and across vertical positions (D); Comparison of leaf dry mass per unit area (LMA) across leaf–shoot orientations (E) and across vertical positions (F). Notation: The lowercase letters a–b on the top of each box denotes the significance of the difference in the means between any two groups based on Tukey’s HSD test at a 0.05 significance level. The numbers above the whiskers represent the coefficients of variation (%). The horizontal solid line indicates the median; the * in each box indicates the means.
Forests 16 00724 g002
Forests 16 00724 g003
Figure 3. Comparison of the slope ( α -values) of the log-transformed leaf mass versus leaf area across leaf–shoot orientations (A) and vertical positions (B) based on the common slope method. Notation: p is the significance test parameter.
Figure 3. Comparison of the slope ( α -values) of the log-transformed leaf mass versus leaf area across leaf–shoot orientations (A) and vertical positions (B) based on the common slope method. Notation: p is the significance test parameter.
Forests 16 00724 g003
Forests 16 00724 g004
Figure 4. Comparison of slope ( α -values) of the scaling relationship between leaf dry mass (M) versus area (A) across leaf–shoot orientations (A) and vertical positions (B); and comparison of intercepts ( β -values) of the scaling relationship between M versus A across leaf–shoot orientations (C) and vertical positions (D). Notation: The lowercase letters a–b on the top of each box denotes the significance of the difference in the means between any two groups based on bootstrap percentile method at a 0.05 significance level.
Figure 4. Comparison of slope ( α -values) of the scaling relationship between leaf dry mass (M) versus area (A) across leaf–shoot orientations (A) and vertical positions (B); and comparison of intercepts ( β -values) of the scaling relationship between M versus A across leaf–shoot orientations (C) and vertical positions (D). Notation: The lowercase letters a–b on the top of each box denotes the significance of the difference in the means between any two groups based on bootstrap percentile method at a 0.05 significance level.
Forests 16 00724 g004
Forests 16 00724 g005
Figure 5. Hand-drawn diagram illustrating the age distribution and sunlight interception pattern of Lamium barbatum leaves. The colored arrows represent different types of sunlight.
Figure 5. Hand-drawn diagram illustrating the age distribution and sunlight interception pattern of Lamium barbatum leaves. The colored arrows represent different types of sunlight.
Forests 16 00724 g005
Table 1. Results of the two-way analysis of variance for leaf traits considering vertical position (VP) and leaf–shoot orientations (LSO) across different leaf–shoot orientations and vertical positions.
Table 1. Results of the two-way analysis of variance for leaf traits considering vertical position (VP) and leaf–shoot orientations (LSO) across different leaf–shoot orientations and vertical positions.
Leaf TraitsSource of VariationSum of SquaresDegrees of FreedomMean SquareF Valuep Value
log (M)LSO0.1330.040.2820.838
VP109.751109.75715.672<0.001
LSO   × VP0.2230.070.4850.693
Residuals266.5217380.15
log (A)LSO0.0730.020.1360.939
VP97.05197.05603.252<0.001
LSO   × VP0.2630.090.5360.658
Residuals279.6017380.16
LMALSO39312.980.8700.456
VP1581158.2810.610<0.01
LSO   × VP2137.140.4780.697
Residuals25926173814.92
Table 2. Fitted results for the scaling relationship between leaf dry mass and area across different leaf–shoot orientations and vertical positions.
Table 2. Fitted results for the scaling relationship between leaf dry mass and area across different leaf–shoot orientations and vertical positions.
Spatial PositionsSample SizeFitted Equation95% Confidence Interval of the Slope95% Confidence Interval of the Interceptr2
Pooled data1746y = −6.189 + 0.999 x(0.981, 1.019)(−6.245, −6.134)0.824
North450y = −6.193 + 0.998 x(0.964, 1.034)(−6.297, −6.093)0.843
South450y = −6.209 + 1.009 x(0.971, 1.047)(−6.321, −6.099)0.826
East423y = −6.171 + 0.995 x(0.955, 1.036)(−6.289, −6.051)0.808
West423y = −6.179 + 0.994 x(0.995, 1.034)(−6.295, −6.064)0.816
Lower layer472y = −5.630 + 0.838 x(0.793, 0.884)(−5.780, −5.485)0.545
Upper layer1274y = −6.202 + 1.001 x(0.977, 1.025)(−6.268, −6.137)0.790
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Guo, X.; Zheng, Y.; Chen, Y.; Zhou, Z.; Xue, J. Intra-Plant Variation in Leaf Dry Mass per Area (LMA): Effects of Leaf–Shoot Orientation and Vertical Position on Dry Mass and Area Scaling. Forests 2025, 16, 724. https://doi.org/10.3390/f16050724

AMA Style

Guo X, Zheng Y, Chen Y, Zhou Z, Xue J. Intra-Plant Variation in Leaf Dry Mass per Area (LMA): Effects of Leaf–Shoot Orientation and Vertical Position on Dry Mass and Area Scaling. Forests. 2025; 16(5):724. https://doi.org/10.3390/f16050724

Chicago/Turabian Style

Guo, Xuchen, Yiwen Zheng, Yuanmiao Chen, Zhidong Zhou, and Jianhui Xue. 2025. "Intra-Plant Variation in Leaf Dry Mass per Area (LMA): Effects of Leaf–Shoot Orientation and Vertical Position on Dry Mass and Area Scaling" Forests 16, no. 5: 724. https://doi.org/10.3390/f16050724

APA Style

Guo, X., Zheng, Y., Chen, Y., Zhou, Z., & Xue, J. (2025). Intra-Plant Variation in Leaf Dry Mass per Area (LMA): Effects of Leaf–Shoot Orientation and Vertical Position on Dry Mass and Area Scaling. Forests, 16(5), 724. https://doi.org/10.3390/f16050724

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop