Acoustic Velocity—Wood Fiber Attribute Relationships for Jack Pine Logs and Their Potential Utility
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Stands, Plot Establishment and Sample Tree Selection
2.2. Sample Tree Measurements, Stem Analysis Procedures, Log-Based Acoustic Measurements and Disk Sampling
2.3. Silviscan-3 Estimation of Fiber Attributes and Preliminary Computations
2.4. Preliminary Data Stratification for Cross-Validation Assessment
2.5. Specifying Functional Forms and Parameterization Methods Utilized
2.6. Goodness-of-fit, Lack-of-fit, and Predictive Ability of Fitted Models
2.7. Predictive Performance when Deploying Acoustic-Derived Wood Density Estimates
3. Results
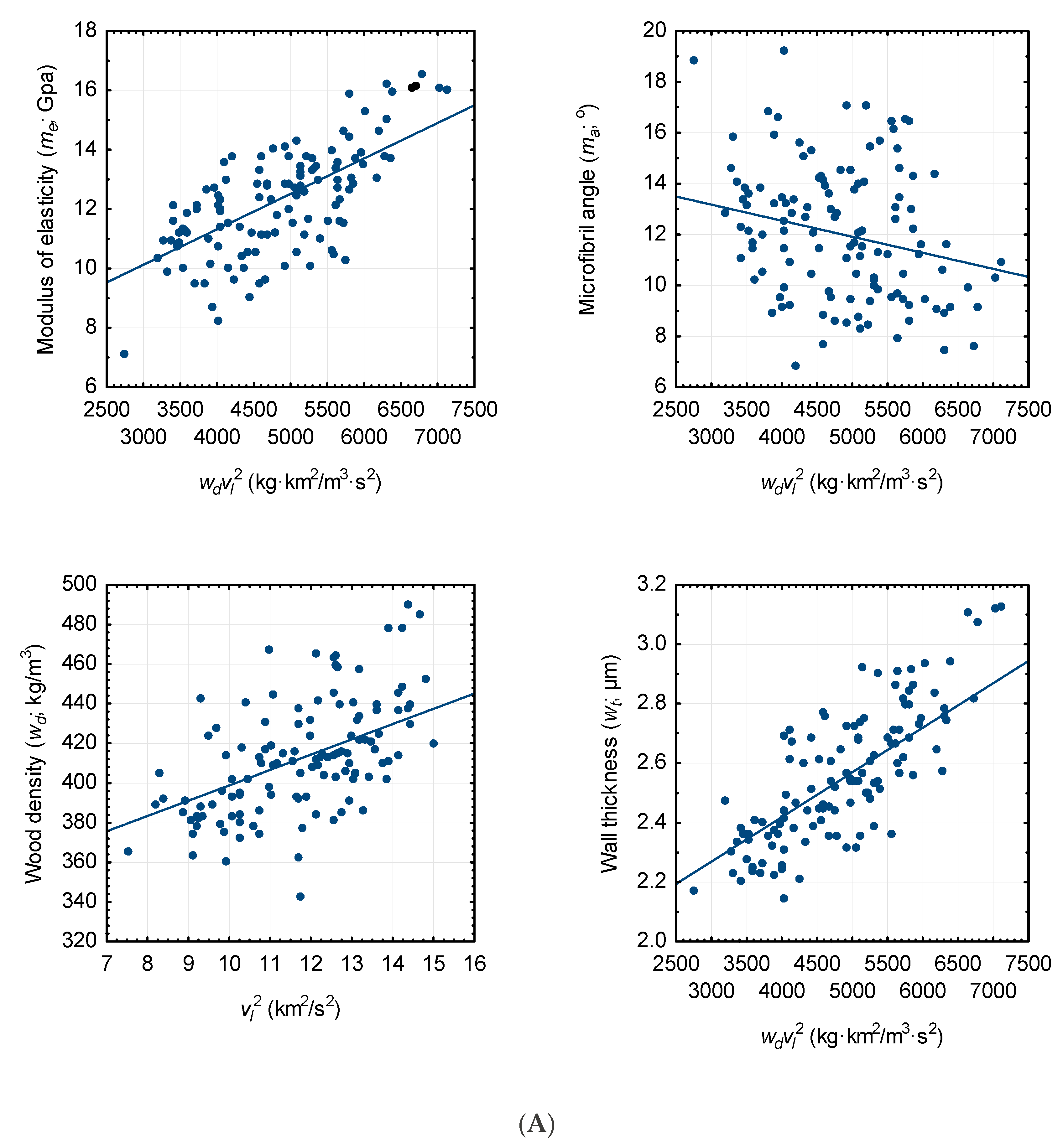
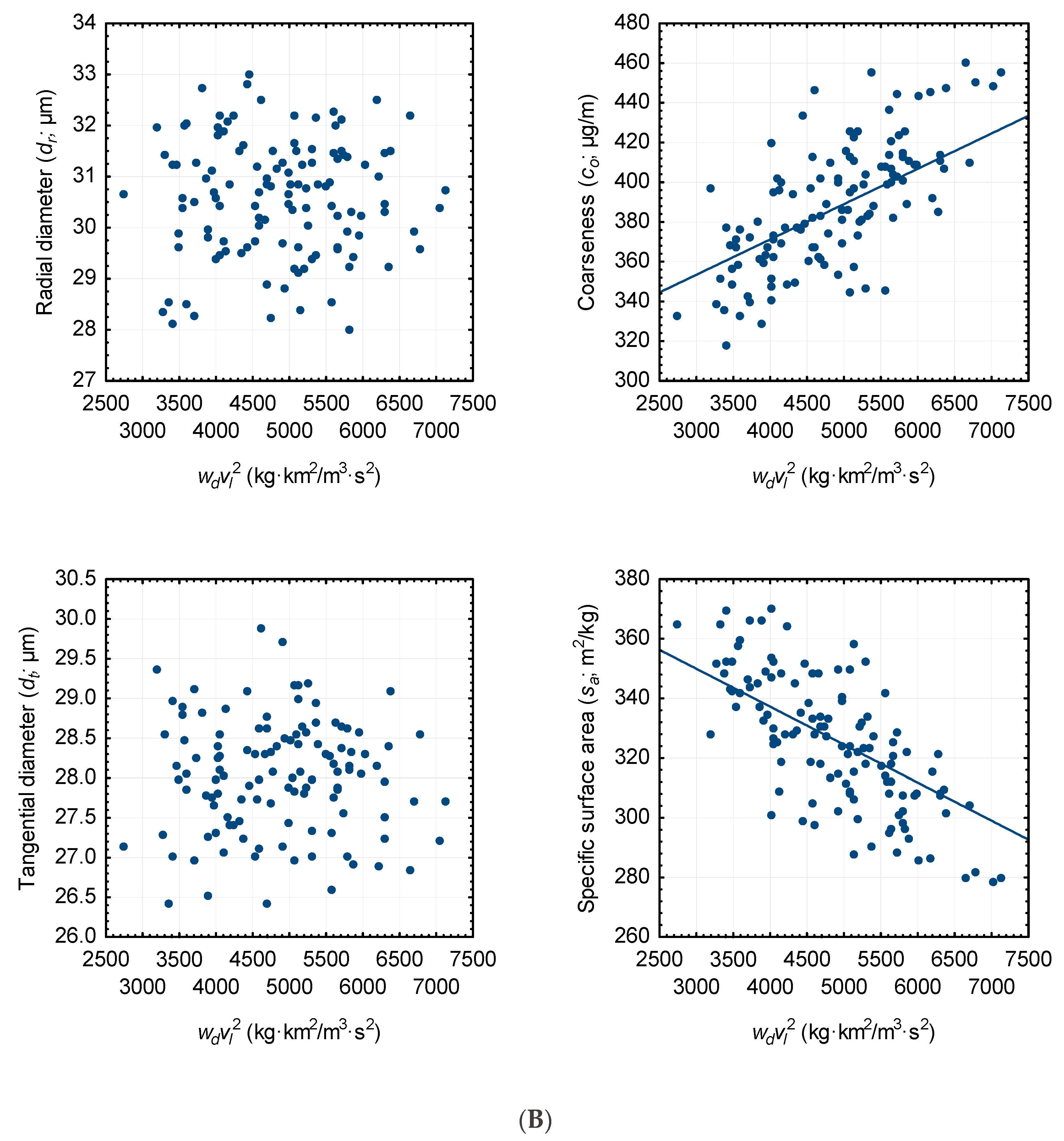
3.1. Attribute—Acoustic Velocity Relationships: Parameter Estimates, Regression Statistics and Tenability of Associated Assumptions
3.2. Goodness-of-fit and Lack-of-fit Assessment
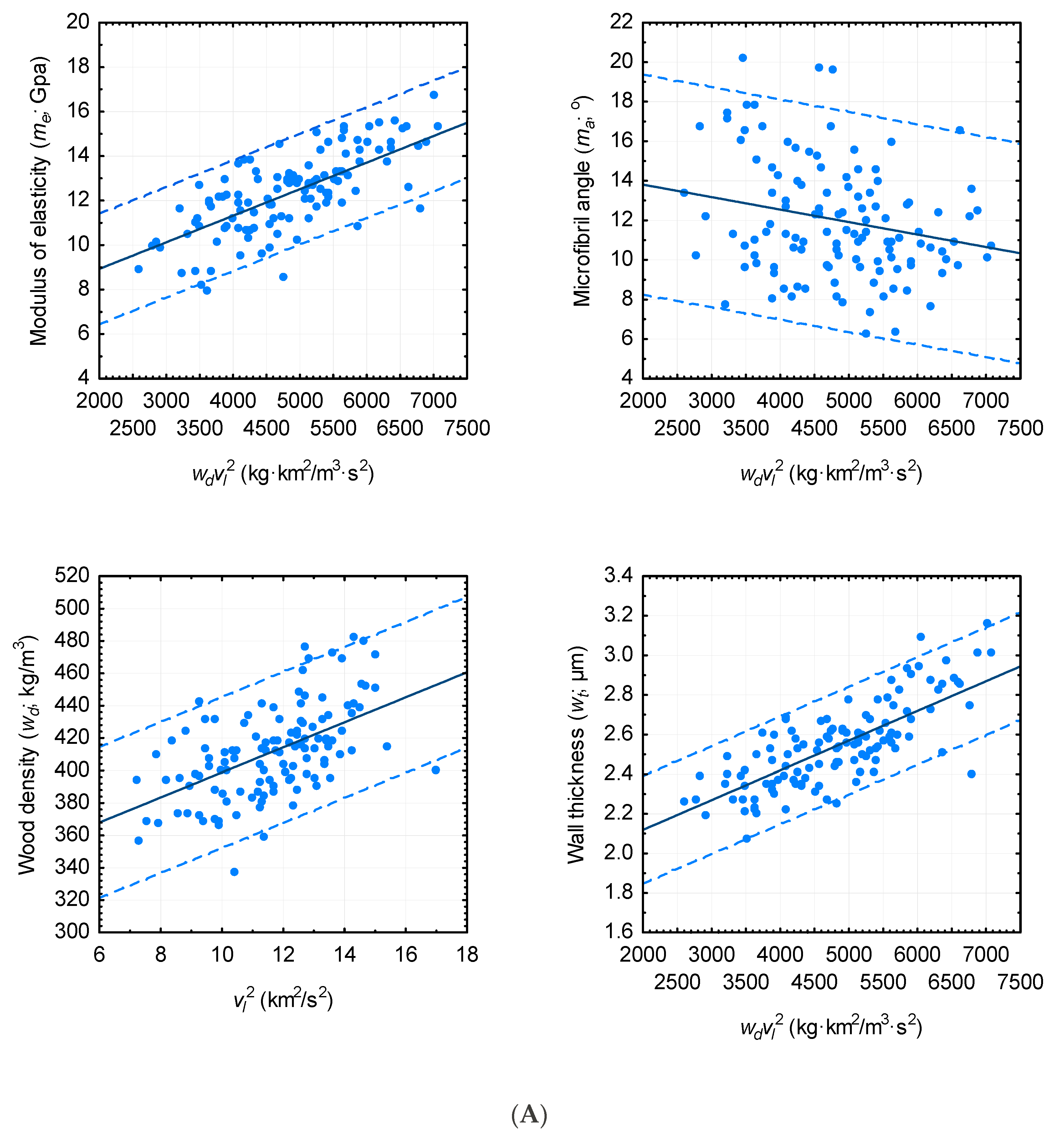
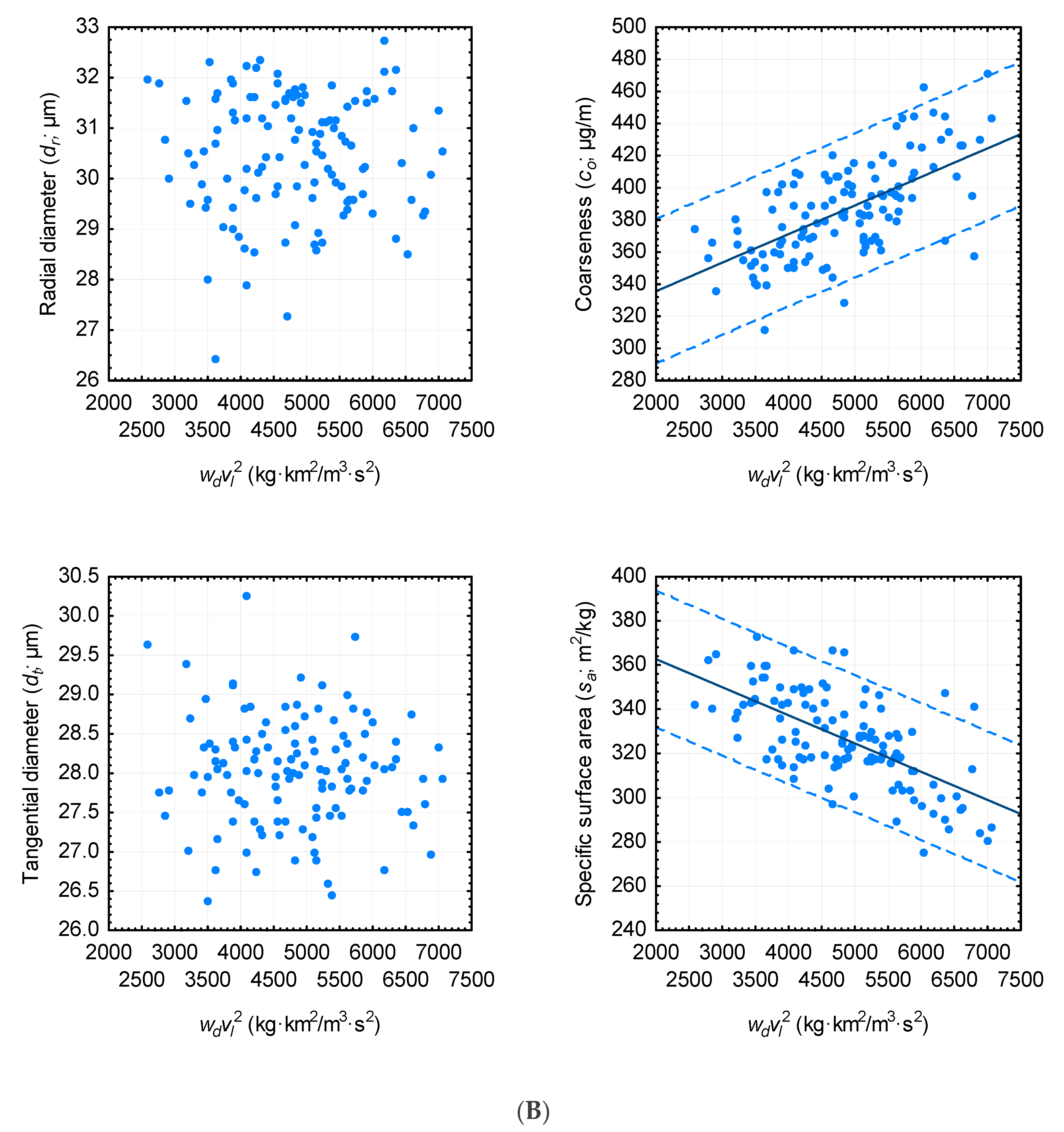
3.3. Predictive Ability
3.4. Predictive Performance of Parameterized Models When Deploying Acoustic Generated Wood Density Estimates
4. Discussion
4.1. Hierarchical Mixed-Effects Acoustic-Based Attribute Prediction Models for Jack Pine
4.2. Potential Utility of the Expanded Acoustic-Based Inferential Framework for Jack Pine
4.3. Similarities and Differences between Tree and Log Acoustic-Based Attribute Relationships
4.4. Advancing Acoustic-Based Attribute Estimation
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Emmett, B. Increasing the value of our forest. For. Chron. 2006, 82, 3–4. [Google Scholar] [CrossRef]
- Emmett, B. Perspectives on sustainable development and sustainability in the Canadian forest sector. For. Chron. 2006, 82, 40–43. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.Y.; Chauret, G.; Ren, H.Q.; Desjardins, R. Impact of plantation black spruce initial spacing on lumber grade yield, bending properties and MSR yield. Wood Fibre Sci. 2002, 34, 460–475. [Google Scholar]
- Tsehaye, A.; Buchanan, A.H.; Walker, J.C.F. Sorting of logs using acoustics. Wood Sci. Technol. 2000, 34, 337–344. [Google Scholar] [CrossRef]
- Carter, P.; Briggs, D.; Ross, R.J.; Wang, X. Acoustic testing to enhance western forest values and meet customer wood quality needs. In Productivity of Western Forests: A Forest Products Focus; Harrington, C.A., Schoenholtz, S.H., Eds.; Gen. Tech. Rep. PNW-GTR-642; USDA, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2005; pp. 121–129. [Google Scholar]
- Wang, X.; Carter, P.; Ross, R.J.; Brashaw, B.K. Acoustic assessment of wood quality of raw materials: A path to increased profitability. For. Prod. J. 2007, 57, 6–14. [Google Scholar]
- National Lumber Grades Authority (NLGA). Standard Grading Rules for Canadian Lumber; NLGA: Surrey, BC, Canada, 2014. [Google Scholar]
- Defo, M. SilviScan-3—A Revolutionary Technology for High-Speed Wood Microstructure and Properties Analysis. Midis de al Foresterie. UQAT. Available online: http://chaireafd.uqat.ca/midiForesterie/pdf/ 20080422PresentationMauriceDefo.pdf (accessed on 1 October 2018).
- Wang, X.; Ross, R.J.; Mattson, J.A.; Erickson, J.R. Nondestructive evaluation techniques for assessing modulus of elasticity and stiffness of small-diameter logs. For. Prod. J. 2002, 52, 79–85. [Google Scholar]
- Dickson, R.L.; Raymond, C.A.; Joe, B.; Wilkinson, C.A. Segregation of Eucalyptus dunnii logs using acoustics. For. Ecol. Manag. 2003, 179, 243–251. [Google Scholar] [CrossRef]
- Ross, R.J. Nondestructive Evaluation of Wood, 2nd ed.; General Technical Report FPL-GTR-238; USDA, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2015; p. 169.
- Legg, M.; Bradley, S. Measurement of stiffness of standing trees and felled logs using acoustics: A review. J. Acoust. Soc. Am. 2016, 139, 588–604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raymond, C.A.; Joe, B.; Evans, R.; Dickson, R.L. Relationship between timber grade, static and dynamic modulus of elasticity, and Silviscan properties for Pinus radiata in New SouthWales. N. Z. J. For. Sci. 2007, 37, 186–196. [Google Scholar]
- Newton, P.F. Development trends of black spruce fibre attributes in maturing plantations. Int. J. For. Res. 2016, 1–12. [Google Scholar] [CrossRef]
- Newton, P.F. Predictive relationships between acoustic velocity and wood quality attributes for red pine logs. For. Sci. 2017, 63, 504–517. [Google Scholar] [CrossRef]
- Newton, P.F. Acoustic-based non-destructive estimation of wood quality attributes within standing red pine trees. Forests 2017, 8, 380. [Google Scholar] [CrossRef]
- Wang, X. Acoustic measurements on trees and logs: A review and analysis. Wood Sci. Technol. 2013, 475, 965–975. [Google Scholar] [CrossRef]
- Brashaw, B.K.; Bucur, V.; Divos, F.; Goncalves, R.; Lu, J.; Meder, R.; Yin, Y. Nondestructive testing and evaluation of wood: A worldwide research update. For. Prod. J. 2009, 59, 7–14. [Google Scholar]
- Wang, X.; Senalik, C.A.; Ross, R.J. (Eds.) 20th International Nondestructive Testing and Evaluation of Wood Symposium; General Technical Report FPL-GTR-249; USDA, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2017; p. 539.
- McKinnon, L.M.; Kayahara, G.J.; White, R.G. Biological Framework for Commercial Thinning Evenaged Single-Species Stands of Jack Pine, White Spruce, and Black Spruce in Ontario; Report TR-046; Ontario Ministry of Natural Resources, Northeast Science and Information Section: Timmins, ON, Canada, 2006; p. 130.
- Carmean, W.H.; Niznowski, G.P.; Hazenberg, G. Polymorphic site index curves for jack pine in Northern Ontario. For. Chron. 2001, 77, 141–150. [Google Scholar] [CrossRef] [Green Version]
- Rowe, J.S. Forest Regions of Canada; Publication No. 1300; Government of Canada, Department of Environment, Canadian Forestry Service: Ottawa, ON, Canada, 1972.
- Evans, R. Rapid measurement of the transverse dimensions of tracheids in radial wood sections from Pinus radiata. Holzforschung 1994, 48, 168–172. [Google Scholar] [CrossRef]
- Siau, J.F. Wood: Influence of Moisture on Physical Properties; Virginia Polytechnic Institute and State University, Department of Wood Science and Forest Products: Blacksburg, VA, USA, 1995.
- Evans, R.; Hughes, M.; Menz, D. Microfibril angle variation by scanning X-ray diffractometry. Appita 1999, 52, 363–367. [Google Scholar]
- Evans, R. Wood stiffness by X-ray diffractometry. In Characterization of the Cellulosic Cell Wall; Stokke, D.D., Groom, L.H., Eds.; Wiley: Hoboken, NJ, USA, 2006; pp. 138–146. [Google Scholar]
- Evans, R.; Downes, G.; Menz, D.; Stringer, S. Rapid measurement of variation in tracheid transverse dimensions in a radiata pine tree. Appita 1995, 48, 134–138. [Google Scholar]
- Raudenbush, S.W.; Bryk, A.S. Hierarchical Linear Models: Applications and Data Analysis Methods, 2nd ed.; Sage: Newbury Park, CA, USA, 2002; p. 485. [Google Scholar]
- Raudenbush, S.W.; Bryk, A.S.; Cheong, Y.F.; Congdon, R.T.; Toit, M., Jr. HLM 7—Hierarchical Linear and Nonlinear Modeling; Scientific Software International Inc.: Lincolnwood, IL, USA, 2011; p. 360. [Google Scholar]
- Gujarati, D.N. Essentials of Econometrics, 3rd ed.; McGraw-Hill/Irwin Inc.: New York, NY, USA, 2006; p. 553. [Google Scholar]
- Ek, A.R.; Monserud, R.A. Performance and comparison of stand growth models based on individual tree and diameter-class growth. Can. J. For. Res. 1979, 9, 231–244. [Google Scholar] [CrossRef]
- Reynolds, M.R., Jr. Estimating the error in model predictions. For. Sci. 1984, 30, 454–469. [Google Scholar]
- Gribko, L.S.; Wiant, H.V., Jr. A SAS template program for the accuracy test. Compiler 1992, 10, 48–51. [Google Scholar]
- National Lumber Grades Authority (NLGA). Special Products Standard for Machine Graded Lumber; NLGA: Surrey, BC, Canada, 2013. [Google Scholar]
- Bérubé-Deschênes, A.; Franceschini, T.; Schneider, R. Factors affecting plantation grown white spruce (Picea glauca) acoustic velocity. J. For. 2016, 114, 629–637. [Google Scholar] [CrossRef]
- Butler, M.A.; Dahlen, J.; Eberhardt, T.L.; Montes, C.; Antony, F.; Daniels, R.F. Acoustic evaluation of loblolly pine tree-and lumber-length logs allows for segregation of lumber modulus of elasticity, not for modulus of rupture. Ann. For. Sci. 2017, 74, 1–15. [Google Scholar] [CrossRef]
- Kang, H.; Booker, R.E. Variation of stress wave velocity with MC and temperature. Wood Sci. Technol. 2002, 36, 41–54. [Google Scholar] [CrossRef]
- Chauhan, S.S.; Walker, J.C.F. Variations in acoustic velocity and density with age, and their interrelationships in radiata pine. For. Ecol. Manag. 2006, 229, 388–394. [Google Scholar] [CrossRef]
- Newton, P.F. Quantifying the effects of wood moisture and temperature variation on time-of-flight acoustic velocity measures within standing red pine and jack pine trees. Forests 2018, 9, 527. [Google Scholar] [CrossRef]
- Wessels, C.B.; Malan, F.S.; Rypstra, T. A review of measurement methods used on standing trees for the prediction of some mechanical properties of timber. Eur. J. For. Res. 2011, 130, 881–893. [Google Scholar] [CrossRef]
- Wang, X.; Carter, P. Acoustic assessment of wood quality in trees and logs. In Nondestructive Evaluation of Wood; Ross, R.J., Ed.; General Technical Report FPL-GTR-238; USDA, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2015; pp. 87–101. [Google Scholar]
- Newton, P.F. In-forest acoustic-based prediction of commercially-relevant wood quality attributes within standing jack pine trees. Forests 2018. in preparation. [Google Scholar]
- Walker, J.C.F.; Nakada, R. Understanding corewood in some softwoods: A selective review on stiffness and acoustics. Int. For. Rev. 1999, 1, 251–259. [Google Scholar]
- Harris, P.; Petherick, R.; Andrews, M. Acoustic resonance tools. In Proceedings of the 13th International Symposium on Nondestructive Testing of Wood; Forest Products Society: Berkeley, CA, USA, 2003; pp. 195–201. [Google Scholar]
- Ross, R.J.; McDonald, K.A.; Green, D.W.; Schad, K.C. Relationship between log and lumber modulus of elasticity. For. Prod. J. 1997, 47, 89–92. [Google Scholar]
- Dickson, R.L.; Matheson, A.C.; Joe, B.; Ilic, J.; Owen, J.V. Acoustic segregation of Pinus radiata logs for sawmilling. N. Z. J. For. Sci. 2004, 34, 175–189. [Google Scholar]
- Vikram, V.; Cherry, M.L.; Briggs, D.; Cress, D.W.; Evans, R.; Howe, G.T. Stiffness of Douglas-fir lumber: Effects of wood properties and genetics. Can. J. For. Res. 2011, 41, 1160–1173. [Google Scholar] [CrossRef]
- Clark, T.A.; Hartmann, J.; Lausberg, M.; Walker, J.C.F. Fibre characterisation of pulp logs using acoustics. In Proceedings of the 56th Appita Annual Conference, Rotorua, New Zealand, 18–20 March 2002; pp. 17–24. [Google Scholar]
- Bradley, A.; Chauhan, S.S.; Walker, J.C.F.; Banham, P. Using acoustics in log segregation to optimise energy use in thermomechanical pulping. Appita 2005, 58, 306–311. [Google Scholar]
- Murphy, G.; Cown, D. Stand, stem and log segregation based on wood properties: A review. Scand. J. For. Res. 2015, 30, 757–770. [Google Scholar] [CrossRef]
- Walsh, D.; Strandgard, M.; Carter, P. Evaluation of the Hitman PH330 acoustic assessment system for harvesters. Scand. J. For. Res. 2014, 29, 593–602. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Koubaa, A. Softwoods of Eastern Canada: Their Silvics, Characteristics, Manufacturing and End-Uses; Special Publication SP-526E; FPInnovations: Quebec City, QC, Canada, 2008. [Google Scholar]
| Product Category | Performance Measure | Relationship with Fiber Attribute a |
|---|---|---|
| Biomass (e.g., pellets) | Calorific value | xylem density |
| Pulp and paper (e.g., paperboards, newsprint, facial tissues, and specialized coated papers) | Tensile strength | (tracheid wall thickness)−1, specific surface area |
| Tear strength | fiber coarseness | |
| Stretch | microfibril angle | |
| Bulk | tracheid wall thickness, (tracheid diameter)−1 | |
| Light scattering | (tracheid wall thickness)−1 | |
| Collapsibility | tracheid wall thickness | |
| Yield | xylem density | |
| Solid wood and composites (e.g., dimensional lumber; glulam-based beams) | Strength | xylem density, (microfibril angle)−1 |
| Stiffness | xylem density, modulus of elasticity, (microfibril angle)−1 | |
| Poles and squared timbers (e.g., utility poles and solid wood beams) | Strength | xylem density, (microfibril angle)−1 |
| Stiffness | xylem density, modulus of elasticity, (microfibril angle)−1 |
| Attribute | Association with Dynamic Modulus of Elasticity as Measured by the Pearson Product Moment Correlation Coefficient a | Statistical Inference | Empirical Linkage to Acoustic Velocity b | ||
|---|---|---|---|---|---|
| Black Spruce | Red Pine | Jack Pine | |||
| Wood density | 0.7765 * | 0.7585 * | 0.6717 * | ||
| Microfibril angle | −0.8981 * | −0.8075 * | −0.7101 * | ||
| Tracheid wall thickness | 0.6765 * | 0.6871 * | 0.6648 * | ||
| Radial tracheid diameter | −0.4477 * | −0.3833 * | −0.3169 * | ||
| Tangential tracheid diameter | −0.3037 * | −0.0886 | −0.0814 | ||
| Fiber coarseness | 0.2044 | 0.4385 * | 0.5412 * | ||
| Specific surface area | −0.5812 * | −0.6355 * | −0.6368 * | ||
| Variable | Site | Mean | Standard Error | Minimum | Maximum | CV a (%) |
|---|---|---|---|---|---|---|
| Diameter at breast-height (cm) | Sewell | 18.8 | 2.11 | 14.7 | 22.6 | 11.2 |
| Tyrol | 24.4 | 2.17 | 19.8 | 29.1 | 8.9 | |
| Breast-height age (year) | Sewell | 50 | 0.96 | 47 | 51 | 1.9 |
| Tyrol | 69 | 1.27 | 66 | 71 | 1.9 | |
| Total height (m) | Sewell | 21.1 | 1.26 | 18.3 | 22.9 | 6.0 |
| Tyrol | 22.2 | 1.57 | 19.5 | 24.6 | 7.1 | |
| Live crown ratio (%) | Sewell | 26.1 | 4.50 | 15.0 | 35.3 | 17.3 |
| Tyrol | 28.2 | 7.20 | 14.1 | 41.5 | 25.5 |
| Variable | Log a | Mean | Median | Standard Error | Minimum | Maximum | CV b (%) |
|---|---|---|---|---|---|---|---|
| Log length (m) | 1st | 4.30 | 4.36 | 0.04 | 3.48 | 5.00 | 7.7 |
| 2nd | 4.28 | 4.35 | 0.04 | 3.47 | 4.91 | 7.8 | |
| 3rd | 4.28 | 4.37 | 0.04 | 3.18 | 4.91 | 7.9 | |
| 4th | 4.25 | 4.37 | 0.06 | 2.27 | 4.89 | 10.8 | |
| Mean log diameter (inside-bark; cm) | 1st | 19.49 | 19.39 | 0.35 | 13.70 | 26.92 | 14.1 |
| 2nd | 16.97 | 17.03 | 0.31 | 10.89 | 21.76 | 14.4 | |
| 3rd | 14.38 | 14.56 | 0.28 | 9.41 | 19.25 | 15.4 | |
| 4th | 11.30 | 10.99 | 0.26 | 7.54 | 15.71 | 17.5 | |
| Longitudinal stress wave velocity (vl; km/s) | 1st | 3.59 | 3.58 | 0.02 | 3.20 | 4.29 | 5.2 |
| 2nd | 3.59 | 3.62 | 0.03 | 3.15 | 4.32 | 5.5 | |
| 3rd | 3.39 | 3.42 | 0.02 | 2.86 | 4.12 | 6.0 | |
| 4th | 3.08 | 3.08 | 0.02 | 2.69 | 3.72 | 6.0 |
| Variable | Log a | Mean | Median | Minimum | Maximum | CV b (%) |
|---|---|---|---|---|---|---|
| Modulus of elasticity (me; GPa) | 1st | 12.72 | 12.68 | 8.59 | 16.73 | 15.0 |
| 2nd | 12.81 | 12.95 | 8.24 | 16.16 | 14.2 | |
| 3rd | 12.38 | 12.82 | 7.93 | 15.89 | 13.7 | |
| 4th | 11.33 | 11.57 | 7.14 | 14.57 | 12.7 | |
| Wood density (wd; kg/m3) | 1st | 430.38 | 421.66 | 372.88 | 489.67 | 6.5 |
| 2nd | 416.48 | 418.68 | 337.88 | 482.02 | 6.6 | |
| 3rd | 407.47 | 405.99 | 359.76 | 467.79 | 6.0 | |
| 4th | 394.23 | 391.66 | 356.95 | 442.25 | 5.1 | |
| Microfibril angle (ma; °) | 1st | 12.98 | 12.79 | 7.49 | 19.71 | 21.1 |
| 2nd | 11.47 | 10.95 | 6.33 | 19.23 | 22.7 | |
| 3rd | 11.25 | 10.92 | 6.24 | 17.84 | 22.6 | |
| 4th | 12.52 | 12.21 | 6.84 | 20.23 | 22.8 | |
| Tracheid wall thickness (wt; µm) | 1st | 2.70 | 2.67 | 2.35 | 3.16 | 7.6 |
| 2nd | 2.60 | 2.60 | 2.08 | 3.01 | 7.8 | |
| 3rd | 2.52 | 2.49 | 2.22 | 2.92 | 7.3 | |
| 4th | 2.39 | 2.37 | 2.17 | 2.77 | 5.9 | |
| Tracheid radial diameter (dr; µm) | 1st | 30.80 | 30.90 | 28.51 | 33.00 | 3.7 |
| 2nd | 30.75 | 30.95 | 28.69 | 32.74 | 3.5 | |
| 3rd | 30.52 | 30.68 | 27.99 | 32.79 | 3.7 | |
| 4th | 30.03 | 30.18 | 26.44 | 31.97 | 4.1 | |
| Tracheid tangential diameter (dt; µm) | 1st | 27.87 | 27.93 | 26.41 | 29.88 | 2.4 |
| 2nd | 28.13 | 28.13 | 26.89 | 30.25 | 2.5 | |
| 3rd | 28.10 | 28.16 | 26.53 | 29.72 | 2.5 | |
| 4th | 27.97 | 27.99 | 26.38 | 29.63 | 2.6 | |
| Fiber coarseness (co; µg/m) | 1st | 406.02 | 406.67 | 360.44 | 471.20 | 6.8 |
| 2nd | 395.23 | 394.97 | 339.39 | 447.85 | 7.1 | |
| 3rd | 383.33 | 383.76 | 328.30 | 455.34 | 7.2 | |
| 4th | 364.51 | 365.10 | 311.38 | 420.68 | 6.3 | |
| Specific surface area (sa; m2/kg) | 1st | 314.32 | 315.76 | 275.59 | 351.46 | 6.4 |
| 2nd | 322.71 | 321.31 | 284.37 | 372.46 | 6.4 | |
| 3rd | 328.16 | 327.71 | 287.81 | 366.30 | 6.4 | |
| 4th | 338.15 | 341.99 | 297.17 | 369.33 | 5.0 |
| Variable | Data Subset | Mean | Minimum | Maximum | CV a (%) |
|---|---|---|---|---|---|
| Longitudinal stress wave velocity (vl; km/s) | Calibration | 3.42 | 2.74 | 4.32 | 7.8 |
| Validation | 3.41 | 2.69 | 4.29 | 8.8 | |
| Modulus of elasticity (me; GPa) | Calibration | 12.28 | 7.14 | 16.57 | 14.8 |
| Validation | 12.34 | 7.93 | 16.73 | 14.7 | |
| Wood density (wd; kg/m3) | Calibration | 412.41 | 343.02 | 489.67 | 6.9 |
| Validation | 412.02 | 337.88 | 482.02 | 6.8 | |
| Microfibril angle (ma; °) | Calibration | 12.10 | 6.84 | 19.23 | 21.7 |
| Validation | 12.01 | 6.24 | 20.23 | 24.3 | |
| Tracheid wall thickness (wt; µm) | Calibration | 2.56 | 2.14 | 3.13 | 8.6 |
| Validation | 2.55 | 2.08 | 3.16 | 8.3 | |
| Tracheid radial diameter (dr; µm) | Calibration | 30.59 | 27.99 | 33.00 | 3.8 |
| Validation | 30.47 | 26.44 | 32.74 | 3.9 | |
| Tracheid tangential diameter (dt; µm) | Calibration | 28.01 | 26.41 | 29.88 | 2.5 |
| Validation | 28.02 | 26.38 | 30.25 | 2.5 | |
| Coarseness (co; µg/m) | Calibration | 388.35 | 318.32 | 459.90 | 8.1 |
| Validation | 386.38 | 311.38 | 471.20 | 7.7 | |
| Specific surface area (sa; m2/kg) | Calibration | 325.22 | 278.70 | 369.90 | 6.8 |
| Validation | 326.36 | 275.59 | 372.46 | 6.4 |
| Relationship | Parameter Estimates a | Regression Statistics and Compliance Indices | |||||
|---|---|---|---|---|---|---|---|
| Degrees of Freedom b (nreg, nres) | I2c | Random Effects d | Homogeneity of Variance e | Spatial Correlation f | |||
| 6.5439 | 0.001194 | 1, 120 | 0.466 | * | H0 | H0 | |
| 321.6483 | 7.7201 | 1, 120 | 0.315 | * | H0 | H0 | |
| 15.0699 | −0.00063 | 1, 120 | 0.079 | * | H0 | H0 | |
| 1.8190 | 0.000150 | 1, 120 | 0.603 | * | H0 | H0 | |
| 30.6445 | −0.000037ns | 1, 120 | - | - | - | - | |
| 28.2502 | −0.000048ns | 1, 120 | - | - | - | - | |
| 300.0200 | 0.017790 | 1, 120 | 0.456 | * | H0 | H0 | |
| 388.1280 | −0.012724 | 1, 120 | 0.497 | * | H0 | H0 | |
| Relationship | Goodness-of-fit Statistic | Lack-of-fit Measures | Predictive Ability: 95% Error Intervals d | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Hypotheses b | Absolute c | Relative c (%) | Prediction | Tolerance | |||||||
| I2a | Mean Bias | 95% CL | Mean Bias | 95% CL | Absolute | Relative (%) | Absolute | Relative (%) | |||
| 95% CL | 95% CL | 95% CL | 95% CL | ||||||||
| 0.526 | H0 | H0 | −0.031 | ±0.226 | 0.986 | ±2.049 | ±2.489 | ±22.543 | ±2.759 | ±24.993 | |
| 0.304 | H0 | H0 | −0.125 | ±4.232 | 0.292 | ±1.028 | ±46.550 | ±11.306 | ±51.610 | ±12.535 | |
| 0.075 | H0 | H0 | 0.050 | ±0.506 | 5.998 * | ±4.553 | ±5.565 | ±50.087 | ±6.170 | ±55.531 | |
| 0.583 | H0 | H0 | 0.004 | ±0.025 | 0.151 | ±0.971 | ±0.272 | ±10.679 | ±0.301 | ±11.840 | |
| 0.426 | H0 | H0 | −0.399 | ±4.082 | 0.250 | ±1.070 | ±44.903 | ±11.764 | ±49.784 | ±13.043 | |
| 0.438 | H0 | H0 | 0.224 | ±2.812 | 0.305 | ±0.861 | ±30.937 | ±9.468 | ±34.299 | ±10.497 | |
| Relationship | Lack-of-fit Measures a | Predictive Ability: 95% Error Intervals b | ||||||
|---|---|---|---|---|---|---|---|---|
| Absolute | Relative (%) | Prediction (Stand-Level) | Tolerance | |||||
| Mean | 95% CL e | Mean | 95% CL | Absolute | Relative (%) | Absolute b | Relative (%) | |
| bias | bias | 95% CL | 95% CL | 95% CL | 95% CL | |||
| −0.033 | ±0.251 | 1.118 | ±2.240 | ±2.756 | ±24.640 | ±3.055 | ±27.318 | |
| (±0.562) | (±5.028) | |||||||
| 0.051 | ±0.505 | 6.000 * | ±4.522 | ±5.554 | ±49.738 | ±6.158 | ±55.144 | |
| (±1.129) | (±10.111) | |||||||
| −0.004 | ±0.025 | 0.151 | ±0.971 | ±0.272 | ±10.679 | ±0.301 | ±11.840 | |
| (±0.055) | (±2.171) | |||||||
| −0.440 | ±4.671 | 0.300 | ±1.219 | ±51.383 | ±13.406 | ±56.968 | ±14.863 | |
| (±10.445) | (±2.725) | |||||||
| 0.253 | ±3.340 | 0.369 | ±1.027 | ±36.734 | ±11.291 | ±40.727 | ±12.519 | |
| (±7.467) | (±2.295) | |||||||
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Newton, P.F. Acoustic Velocity—Wood Fiber Attribute Relationships for Jack Pine Logs and Their Potential Utility. Forests 2018, 9, 749. https://doi.org/10.3390/f9120749
Newton PF. Acoustic Velocity—Wood Fiber Attribute Relationships for Jack Pine Logs and Their Potential Utility. Forests. 2018; 9(12):749. https://doi.org/10.3390/f9120749
Chicago/Turabian StyleNewton, Peter F. 2018. "Acoustic Velocity—Wood Fiber Attribute Relationships for Jack Pine Logs and Their Potential Utility" Forests 9, no. 12: 749. https://doi.org/10.3390/f9120749
APA StyleNewton, P. F. (2018). Acoustic Velocity—Wood Fiber Attribute Relationships for Jack Pine Logs and Their Potential Utility. Forests, 9(12), 749. https://doi.org/10.3390/f9120749




