A Modular Mathematical Model of the Immune Response for Investigating the Pathogenesis of Infectious Diseases
Abstract
Author Summary
1. Introduction
2. Materials and Methods
2.1. Mathematical Model
2.2. Experimental Data
2.2.1. Initial Values
2.2.2. Time-Series Data
2.2.3. Parameter Selection
2.3. Numerical Simulation
2.4. Sensitivity Analysis
2.5. Identifiability Analysis
3. Results
3.1. Local Sensitivity Analysis
3.2. Parameter Identifiability Analysis
3.3. Baseline Model and Optimization
3.4. Modes of the Immune Response During COVID-19
3.5. Validation of the Model
3.5.1. Immune Response
3.5.2. Immunosuppression
3.5.3. SARS-CoV-2 Infectivity
3.5.4. Treatment Strategies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization 2023 Data.who.int, WHO Coronavirus (COVID-19) Dashboard > Cases [Dashboard]. Available online: https://data.who.int/dashboards/covid19/cases (accessed on 1 January 2025).
- Machhi, J.; Herskovitz, J.; Senan, A.M.; Dutta, D.; Nath, B.; Oleynikov, M.D.; Blomberg, W.R.; Meigs, D.D.; Hasan, M.; Patel, M.; et al. The Natural History, Pathobiology, and Clinical Manifestations of SARS-CoV-2 Infections. J. Neuroimmune Pharmacol. 2020, 15, 359–386. [Google Scholar] [CrossRef] [PubMed]
- Hikmet, F.; Méar, L.; Edvinsson, Å.; Micke, P.; Uhlén, M.; Lindskog, C. The protein expression profile of ACE2 in human tissues. Mol. Syst. Biol. 2020, 16, e9610. [Google Scholar] [CrossRef]
- COVID-19 Treatment Guidelines Panel. Coronavirus Disease 2019 (COVID-19) Treatment Guidelines. National Institutes of Health [Internet]. Available online: https://www.ncbi.nlm.nih.gov/books/NBK570371/pdf/Bookshelf_NBK570371.pdf (accessed on 21 April 2024).
- Gallo Marin, B.; Aghagoli, G.; Lavine, K.; Yang, L.; Siff, E.J.; Chiang, S.S.; Salazar-Mather, T.P.; Dumenco, L.; Savaria, M.C.; Aung, S.N.; et al. Predictors of COVID-19 severity: A literature review. Rev. Med. Virol. 2021, 31, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Bates, T.A.; Lu, P.; Kang, Y.J.; Schoen, D.; Thornton, M.; McBride, S.K.; Park, C.; Kim, D.; Messer, W.B.; Curlin, M.E.; et al. BNT162b2-induced neutralizing and non-neutralizing antibody functions against SARS-CoV-2 diminish with age. Cell Rep. 2022, 41, 111544. [Google Scholar] [CrossRef] [PubMed]
- Westmeier, J.; Paniskaki, K.; Karaköse, Z.; Werner, T.; Sutter, K.; Dolff, S.; Overbeck, M.; Limmer, A.; Liu, J.; Zheng, X.; et al. Impaired Cytotoxic CD8 + T Cell Response in Elderly COVID-19 Patients. Palese P, editor. mBio 2020, 11, e02243-20. [Google Scholar]
- De Mol, J.; Kuiper, J.; Tsiantoulas, D.; Foks, A.C. The Dynamics of B Cell Aging in Health and Disease. Front. Immunol. 2021, 12, 733566. [Google Scholar] [CrossRef]
- Frasca, D.; Blomberg, B.B. Aging Affects Human B Cell Responses. J. Clin. Immunol. 2011, 31, 430–435. [Google Scholar] [CrossRef]
- Aguilera, L.U.; Rodríguez-González, J. Studying HIV latency by modeling the interaction between HIV proteins and the innate immune response. J. Theor. Biol. 2014, 360, 67–77. [Google Scholar] [CrossRef]
- Hancioglu, B.; Swigon, D.; Clermont, G. A dynamical model of human immune response to influenza A virus infection. J. Theor. Biol. 2007, 246, 70–86. [Google Scholar] [CrossRef]
- Heldt, F.S.; Frensing, T.; Reichl, U. Modeling the Intracellular Dynamics of Influenza Virus Replication To Understand the Control of Viral RNA Synthesis. J. Virol. 2012, 86, 7806–7817. [Google Scholar] [CrossRef]
- Leander, R.N.; Wu, Y.; Ding, W.; Nelson, D.E.; Sinkala, Z. A model of the innate immune response to SARS-CoV-2 in the alveolar epithelium. R. Soc. Open Sci. 2021, 8, 210090. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.Y.; Topham, D.J.; Park, S.Y.; Hollenbaugh, J.; Treanor, J.; Mosmann, T.R.; Jin, X.; Ward, B.M.; Miao, H.; Holden-Wiltse, J.; et al. Simulation and Prediction of the Adaptive Immune Response to Influenza A Virus Infection. J. Virol. 2009, 83, 7151–7165. [Google Scholar] [CrossRef] [PubMed]
- Nelson, P.W.; Murray, J.D.; Perelson, A.S. A model of HIV-1 pathogenesis that includes an intracellular delay. Math. Biosci. 2000, 163, 201–215. [Google Scholar] [CrossRef]
- Eftimie, R.; Gillard, J.J.; Cantrell, D.A. Mathematical Models for Immunology: Current State of the Art and Future Research Directions. Bull. Math. Biol. 2016, 78, 2091–2134. [Google Scholar] [CrossRef]
- Chowdhury, S.M.E.K.; Chowdhury, J.T.; Ahmed, S.F.; Agarwal, P.; Badruddin, I.A.; Kamangar, S. Mathematical modelling of COVID-19 disease dynamics: Interaction between immune system and SARS-CoV-2 within host. Math 2022, 7, 2618–2633. [Google Scholar] [CrossRef]
- Li, C.; Xu, J.; Liu, J.; Zhou, Y. The within-host viral kinetics of SARS-CoV-2. MBE 2020, 17, 2853–2861. [Google Scholar] [CrossRef]
- Du, S.Q.; Yuan, W. Mathematical modeling of interaction between innate and adaptive immune responses in COVID-19 and implications for viral pathogenesis. J. Med. Virol. 2020, 92, 1615–1628. [Google Scholar] [CrossRef]
- Wang, S.; Hao, M.; Pan, Z.; Lei, J.; Zou, X. Data-driven multi-scale mathematical modeling of SARS-CoV-2 infection reveals heterogeneity among COVID-19 patients. Smith AM, editor. PLoS Comput. Biol. 2021, 17, e1009587. [Google Scholar] [CrossRef]
- Grebennikov, D.; Kholodareva, E.; Sazonov, I.; Karsonova, A.; Meyerhans, A.; Bocharov, G. Intracellular Life Cycle Kinetics of SARS-CoV-2 Predicted Using Mathematical Modelling. Viruses 2021, 13, 1735. [Google Scholar] [CrossRef]
- Grebennikov, D.; Karsonova, A.; Loginova, M.; Casella, V.; Meyerhans, A.; Bocharov, G. Predicting the Cross-Coordinated Immune Response Dynamics in SARS-CoV-2 Infection: Implications for Disease Pathogenesis [Internet]. MATHEMATICS & COMPUTER SCIENCE; 2022. Available online: https://www.preprints.org/manuscript/202207.0426/v1 (accessed on 18 August 2023).
- Zhou, Z.; Li, D.; Zhao, Z.; Shi, S.; Wu, J.; Li, J.; Zhang, J.; Gui, K.; Zhang, Y.; Ouyang, Q.; et al. Dynamical modelling of viral infection and cooperative immune protection in COVID-19 patients. Jenner AL, editor. PLoS Comput. Biol. 2023, 19, e1011383. [Google Scholar] [CrossRef]
- Malik-Sheriff, R.S.; Glont, M.; Nguyen, T.V.N.; Tiwari, K.; Roberts, M.G.; Xavier, A.; Vu, M.T.; Men, J.; Maire, M.; Kananathan, S.; et al. BioModels—15 years of sharing computational models in life science. Nucleic Acids Res. 2019, 48, gkz1055. [Google Scholar] [CrossRef] [PubMed]
- Coronavirus Disease (COVID-19) Epidemiological Updates and Monthly Operational Updates [Internet]. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports (accessed on 24 July 2024).
- Raveendran, A.V.; Jayadevan, R.; Sashidharan, S. Long COVID: An overview. Diabetes Metab. Syndr. Clin. Res. Rev. 2021, 15, 869–875. [Google Scholar] [CrossRef] [PubMed]
- Tao, F.; Xiao, B.; Qi, Q.; Cheng, J.; Ji, P. Digital twin modeling. J. Manuf. Syst. 2022, 64, 372–389. [Google Scholar] [CrossRef]
- Sahal, R.; Alsamhi, S.H.; Brown, K.N. Personal Digital Twin: A Close Look into the Present and a Step towards the Future of Personalised Healthcare Industry. Sensors 2022, 22, 5918. [Google Scholar] [CrossRef]
- Chang, H.C.; Gitau, A.M.; Kothapalli, S.; Welch, D.R.; Sardiu, M.E.; McCoy, M.D. Understanding the need for digital twins’ data in patient advocacy and forecasting oncology. Front. Artif. Intell. 2023, 6, 1260361. [Google Scholar] [CrossRef]
- Heudel, P.E.; Renard, F.; Attye, A. Jumeaux numériques: Futur de la médecine personnalisée en cancérologie. Bull. Du. Cancer 2023, 110, 1085–1087. [Google Scholar] [CrossRef]
- Corral-Acero, J.; Margara, F.; Marciniak, M.; Rodero, C.; Loncaric, F.; Feng, Y.; Gilbert, A.; Fernandes, J.F.; Bukhari, H.A.; Wajdan, A.; et al. The ‘Digital Twin’ to enable the vision of precision cardiology. Eur. Heart J. 2020, 41, 4556–4564. [Google Scholar] [CrossRef]
- Shamanna, P.; Joshi, S.; Shah, L.; Dharmalingam, M.; Saboo, B.; Mohammed, J.; Mohamed, M.; Poon, T.; Kleinman, N.; Thajudeen, M.; et al. Type 2 diabetes reversal with digital twin technology-enabled precision nutrition and staging of reversal: A retrospective cohort study. Clin. Diabetes Endocrinol. 2021, 7, 21. [Google Scholar] [CrossRef]
- Kovatchev, B. The year of transition from research to clinical practice. Nat. Rev. Endocrinol. 2018, 14, 74–76. [Google Scholar] [CrossRef]
- Palsson, S.; Hickling, T.P.; Bradshaw-Pierce, E.L.; Zager, M.; Jooss, K.; O’Brien, P.J.; Spilker, M.E.; Palsson, B.O.; Vicini, P. The development of a fully-integrated immune response model (FIRM) simulator of the immune response through integration of multiple subset models. BMC Syst. Biol. 2013, 7, 95. [Google Scholar] [CrossRef]
- Niarakis, A.; Laubenbacher, R.; An, G.; Ilan, Y.; Fisher, J.; Flobak, Å.; Reiche, K.; Rodríguez Martínez, M.; Geris, L.; Ladeira, L.; et al. Immune digital twins for complex human pathologies: Applications, limitations, and challenges. npj Syst. Biol. Appl. 2024, 10, 141. [Google Scholar] [CrossRef] [PubMed]
- Laubenbacher, R.; Niarakis, A.; Helikar, T.; An, G.; Shapiro, B.; Malik-Sheriff, R.S.; Sego, T.J.; Knapp, A.; Macklin, P.; Glazier, J.A. Building digital twins of the human immune system: Toward a roadmap. npj Digit. Med. 2022, 5, 64. [Google Scholar] [CrossRef] [PubMed]
- Afonyushkin, V.N.; Akberdin, I.R.; Kozlova, Y.N.; Schukin, I.A.; Mironova, T.E.; Bobikova, A.S.; Cherepushkina, V.S.; Donchenko, N.A.; Poletaeva, Y.E.; Kolpakov, F.A. Multicompartmental Mathematical Model of SARS-CoV-2 Distribution in Human Organs and Their Treatment. Mathematics 2022, 10, 1925. [Google Scholar] [CrossRef]
- Akberdin, I.R.; Kiselev, I.N.; Pintus, S.S.; Sharipov, R.N.; Vertyshev, A.Y.; Vinogradova, O.L.; Popov, D.V.; Kolpakov, F.A. A Modular Mathematical Model of Exercise-Induced Changes in Metabolism, Signaling, and Gene Expression in Human Skeletal Muscle. IJMS 2021, 22, 10353. [Google Scholar] [CrossRef]
- Marino, S.; Kirschner, D.E. The human immune response to Mycobacterium tuberculosis in lung and lymph node. J. Theor. Biol. 2004, 227, 463–486. [Google Scholar] [CrossRef]
- Tiwari, K.; Kananathan, S.; Roberts, M.G.; Meyer, J.P.; Sharif Shohan, M.U.; Xavier, A.; Maire, M.; Zyoud, A.; Men, J.; Ng, S.; et al. Reproducibility in systems biology modelling. Mol. Syst. Biol. 2021, 17, e9982. [Google Scholar] [CrossRef]
- Hoffmann, M.; Kleine-Weber, H.; Schroeder, S.; Krüger, N.; Herrler, T.; Erichsen, S.; Schiergens, T.S.; Herrler, G.; Wu, N.-H.; Nitsche, A.; et al. SARS-CoV-2 Cell Entry Depends on ACE2 and TMPRSS2 and Is Blocked by a Clinically Proven Protease Inhibitor. Cell 2020, 181, 271–280.e8. [Google Scholar] [CrossRef]
- Senapati, S.; Banerjee, P.; Bhagavatula, S.; Kushwaha, P.P.; Kumar, S. Contributions of human ACE2 and TMPRSS2 in determining host–pathogen interaction of COVID-19. J. Genet. 2021, 100, 12. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, H.; Liu, Z. Expression of ACE2 in airways: Implication for COVID-19 risk and disease management in patients with chronic inflammatory respiratory diseases. Clin. Exp. Allergy 2020, 50, 1313–1324. [Google Scholar] [CrossRef]
- Wagenmann, M.; Naclerio, R. Anatomic and physiologic considerations in sinusitis. J. Allergy Clin. Immunol. 1992, 90, 419–423. [Google Scholar] [CrossRef]
- Collins, L.M.C.; Dawes, C. The Surface Area of the Adult Human Mouth and Thickness of the Salivary Film Covering the Teeth and Oral Mucosa. J. Dent. Res. 1987, 66, 1300–1302. [Google Scholar] [CrossRef] [PubMed]
- Naumova, E.A.; Dierkes, T.; Sprang, J.; Arnold, W.H. The oral mucosal surface and blood vessels. Head. Face Med. 2013, 9, 8. [Google Scholar] [CrossRef] [PubMed]
- Ceylan, İ.; Oktay, H. A study on the pharyngeal size in different skeletal patterns. Am. J. Orthod. Dentofac. Orthop. 1995, 108, 69–75. [Google Scholar] [CrossRef]
- Daniel, M.M.; Lorenzi, M.C.; Leite, C.D.C.; Lorenzi-Filho, G. Pharyngeal dimensions in healthy men and women. Clinics 2007, 62, 5–10. [Google Scholar] [CrossRef] [PubMed]
- Mukherji, S.K.; Castillo, M. Normal cross-sectional anatomy of the nasopharynx, oropharynx, and oral cavity. Neuroimaging Clin. N. Am. 1998, 8, 211–218. [Google Scholar] [CrossRef]
- Ali, M.Y. Histology of the human nasopharyngeal mucosa. J. Anat. 1965, 99 Pt. 3, 657–672. [Google Scholar]
- Knight, D.A.; Holgate, S.T. The airway epithelium: Structural and functional properties in health and disease. Respirology 2003, 8, 432–446. [Google Scholar] [CrossRef]
- Mogensen, C.; Tos, M. Quantitative histology of the maxillary sinus. Rhinology 1977, 15, 129–140. [Google Scholar]
- Chen, M.; Shen, W.; Rowan, N.R.; Kulaga, H.; Hillel, A.; Ramanathan, M.; Lane, A.P. Elevated ACE-2 expression in the olfactory neuroepithelium: Implications for anosmia and upper respiratory SARS-CoV-2 entry and replication. Eur. Respir. J. 2020, 56, 2001948. [Google Scholar] [CrossRef]
- Hatton, I.A.; Galbraith, E.D.; Merleau, N.S.C.; Miettinen, T.P.; Smith, B.M.; Shander, J.A. The human cell count and size distribution. Proc. Natl. Acad. Sci. USA 2023, 120, e2303077120. [Google Scholar] [CrossRef]
- Hönzke, K.; Obermayer, B.; Mache, C.; Fatykhova, D.; Kessler, M.; Dökel, S.; Wyler, E.; Baumgardt, M.; Löwa, A.; Hoffmann, K.; et al. Human lungs show limited permissiveness for SARS-CoV-2 due to scarce ACE2 levels but virus-induced expansion of inflammatory macrophages. Eur. Respir. J. 2022, 60, 2102725. [Google Scholar] [CrossRef] [PubMed]
- Lamers, M.M.; Haagmans, B.L. SARS-CoV-2 pathogenesis. Nat. Rev. Microbiol. 2022, 20, 270–284. [Google Scholar] [CrossRef] [PubMed]
- Bakhshandeh, B.; Sorboni, S.G.; Javanmard, A.R.; Mottaghi, S.S.; Mehrabi Mreza Sorouri, F.; Abbasi, A.; Jahanafrooz, Z. Variants in ACE2; potential influences on virus infection and COVID-19 severity. Infect. Genet. Evol. 2021, 90, 104773. [Google Scholar] [CrossRef] [PubMed]
- Jia, H.P.; Look, D.C.; Shi, L.; Hickey, M.; Pewe, L.; Netland, J.; Farzan, M.; Wohlford-Lenane, C.; Perlman, S.; McCray, P.B., Jr. ACE2 Receptor Expression and Severe Acute Respiratory Syndrome Coronavirus Infection Depend on Differentiation of Human Airway Epithelia. J. Virol. 2005, 79, 14614–14621. [Google Scholar] [CrossRef]
- Ahlfors, E.E.; Laksson, P.Å.; Bergstresser, P.R. Langerhans cell surface densities in rat oral mucosa and human buccal mucosa. J. Oral. Pathol. Med. 1985, 14, 390–397. [Google Scholar] [CrossRef]
- Jahnsen, F.L.; Gran, E.; Haye, R.; Brandtzaeg, P. Human Nasal Mucosa Contains Antigen-Presenting Cells of Strikingly Different Functional Phenotypes. Am. J. Respir. Cell Mol. Biol. 2004, 30, 31–37. [Google Scholar] [CrossRef]
- Schon-Hegrad, M.A.; Oliver, J.; McMenamin, P.G.; Holt, P.G. Studies on the density, distribution, and surface phenotype of intraepithelial class II major histocompatibility complex antigen (Ia)-bearing dendritic cells (DC) in the conducting airways. J. Exp. Med. 1991, 173, 1345–1356. [Google Scholar] [CrossRef]
- Venet, F.; Huang, X.; Chung, C.S.; Chen, Y.; Ayala, A. Plasmacytoid Dendritic Cells Control Lung Inflammation and Monocyte Recruitment in Indirect Acute Lung Injury in Mice. Am. J. Pathol. 2010, 176, 764–773. [Google Scholar] [CrossRef]
- Villadangos, J.A.; Young, L. Antigen-Presentation Properties of Plasmacytoid Dendritic Cells. Immunity 2008, 29, 352–361. [Google Scholar] [CrossRef]
- Kaiser, M.L.; Rubinstein, M.; Vokes, D.E.; Ridgway, J.M.; Guo, S.; Gu, M.; Crumley, R.L.; Armstrong, W.B.; Chen, Z.; Wong, B.J.F. Laryngeal epithelial thickness: A comparison between optical coherence tomography and histology. Clin. Otolaryngol. 2009, 34, 460–466. [Google Scholar] [CrossRef]
- Prestin, S.; Rothschild, S.I.; Betz, C.S.; Kraft, M. Measurement of epithelial thickness within the oral cavity using optical coherence tomography. Head. Neck 2012, 34, 1777–1781. [Google Scholar] [CrossRef] [PubMed]
- Smith, T.D.; Corbin, H.M.; King, S.E.E.; Bhatnagar, K.P.; DeLeon, V.B. A comparison of diceCT and histology for determination of nasal epithelial type. PeerJ 2021, 9, e12261. [Google Scholar] [CrossRef]
- Thurlbeck, W.M. The internal surface area of nonemphysematous lungs. Am. Rev. Respir. Dis. 1967, 95, 765–773. [Google Scholar] [PubMed]
- Hogan, J.; Smith, P.; Heath Peter Harris, D. The thickness of the alveolar capillary wall in the human lung at high and low altitude. Br. J. Dis. Chest 1986, 80, 13–18. [Google Scholar] [CrossRef]
- Bowden, D.H.B.F. Measurement of the thickness of the Bronchial Epithelium. 1989, 22, p. 75. Available online: https://inis.iaea.org/records/fzh46-78t69 (accessed on 18 April 2024).
- Saetta, M.; Di Stefano, A.; Maestrelli, P.; Ferraresso, A.; Drigo, R.; Potena, A.; Ciaccia, A.; Fabbri, L.M. Activated T-Lymphocytes and Macrophages in Bronchial Mucosa of Subjects with Chronic Bronchitis. Am. Rev. Respir. Dis. 1993, 147, 301–306. [Google Scholar] [CrossRef] [PubMed]
- Weber, M.; Wehrhan, F.; Baran, C.; Agaimy, A.; Büttner-Herold, M.; Öztürk, H.; Neubauer, K.; Wickenhauser, C.; Kesting, M.; Ries, J. Malignant transformation of oral leukoplakia is associated with macrophage polarization. J. Transl. Med. 2020, 18, 11. [Google Scholar] [CrossRef]
- Donners, R.; Yiin, R.S.Z.; Blackledge, M.; Koh, D.M. Whole-body diffusion-weighted MRI of normal lymph nodes: Prospective apparent diffusion coefficient histogram and nodal distribution analysis in a healthy cohort. Cancer Imaging 2021, 21, 64. [Google Scholar] [CrossRef]
- Qatarneh, S.M.; Kiricuta, I.; Brahme, A.; Tiede, U.; Lind, B.K. Three-dimensional atlas of lymph node topography based on the visible human data set. Anat. Rec. Part B 2006, 289, 98–111. [Google Scholar] [CrossRef]
- Varkhede, N.; Forrest, L. Understanding the Monoclonal Antibody Disposition after Subcutaneous Administration using a Minimal Physiologically based Pharmacokinetic Model. J. Pharm. Pharm. Sci. 2018, 21, 130s–148s. [Google Scholar] [CrossRef]
- Ying, M.; Pang, B.S.F. Three-dimensional ultrasound measurement of cervical lymph node volume. BJR 2009, 82, 617–625. [Google Scholar] [CrossRef]
- Kim, H.C.; Han, M.H.; Do, K.H.; Kim, K.H.; Choi, H.J.; Kim, A.Y.; Sung, M.W.; Chang, K.-H. Volume of cervical lymph nodes using 3D ultrasonography. Differentiation of metastatic from reactive lymphadenopathy in primary head and neck malignancy. Acta Radiol. 2002, 43, 571–574. [Google Scholar] [CrossRef] [PubMed]
- Burlew, J.T.; Weber, C.; Banks, K.P. Anatomy, Thorax, Mediastinal Lymph Nodes. In StatPearls [Internet]; StatPearls Publishing: Treasure Island, FL, USA, 2023. Available online: http://www.ncbi.nlm.nih.gov/books/NBK532863/ (accessed on 23 November 2023).
- Kiyono, K.; Sone, S.; Sakai, F.; Imai, Y.; Watanabe, T.; Izuno, I.; Oguchi, M.; Kawai, T.; Shigematsu, H.; Watanabe, M. The number and size of normal mediastinal lymph nodes: A postmortem study. Am. J. Roentgenol. 1988, 150, 771–776. [Google Scholar] [CrossRef] [PubMed]
- Bouget, D.; Pedersen, A.; Vanel, J.; Leira, H.O.; Langø, T. Mediastinal lymph nodes segmentation using 3D convolutional neural network ensembles and anatomical priors guiding. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2023, 11, 44–58. [Google Scholar] [CrossRef]
- Mahendra, A.; Haque, A.; Prabakaran, P.; Mackness, B.C.; Fuller, T.P.; Liu, X.; Kathuria, S.V.; Wang, Y.-H.; Amatya, N.; Yu, X.; et al. Honing-in antigen-specific cells during antibody discovery: A user-friendly process to mine a deeper repertoire. Commun. Biol. 2022, 5, 1157. [Google Scholar] [CrossRef]
- Janeway, C. (Ed.) Immunobiology: The immune System in Health and Disease; [Animated CD-ROM Inside], 5th ed.; Garland Publ.: New York, NY, USA, 2001; 732p. [Google Scholar]
- Punt, J. Adaptive Immunity. In Cancer Immunotherapy [Internet]; Elsevier: Amsterdam, The Netherlands, 2013; pp. 41–53. Available online: https://linkinghub.elsevier.com/retrieve/pii/B978012394296800004X (accessed on 21 July 2024).
- Hu, B.; Guo, H.; Zhou, P.; Shi, Z.L. Characteristics of SARS-CoV-2 and COVID-19. Nat. Rev. Microbiol. 2021, 19, 141–154. [Google Scholar] [CrossRef]
- Basu, S. Computational characterization of inhaled droplet transport to the nasopharynx. Sci. Rep. 2021, 11, 6652. [Google Scholar] [CrossRef]
- Prentiss, M.; Chu, A.; Berggren, K.K. Finding the infectious dose for COVID-19 by applying an airborne-transmission model to superspreader events. PLoS ONE 2022, 17, e0265816. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Bhopal, R.; Nguyen Tien, H. Review of infective dose, routes of transmission and outcome of COVID-19 caused by the SARS-CoV-2: Comparison with other respiratory viruses–CORRIGENDUM. Epidemiol. Infect. 2021, 149, e116. [Google Scholar] [CrossRef]
- Killingley, B.; Mann, A.J.; Kalinova, M.; Boyers, A.; Goonawardane, N.; Zhou, J.; Lindsell, K.; Hare, S.S.; Brown, J.; Frise, R.; et al. Safety, tolerability and viral kinetics during SARS-CoV-2 human challenge in young adults. Nat. Med. 2022, 28, 1031–1041. [Google Scholar] [CrossRef] [PubMed]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef]
- Quesada, J.A.; López-Pineda, A.; Gil-Guillén, V.F.; Arriero-Marín, J.M.; Gutiérrez, F.; Carratala-Munuera, C. Incubation period of COVID-19: A systematic review and meta-analysis. Rev. Clínica Española (Engl. Ed.) 2021, 221, 109–117. [Google Scholar] [CrossRef] [PubMed]
- Lui, G.; Ling, L.; Lai, C.K.; Tso, E.Y.; Fung, K.S.; Chan, V.; Ho, T.H.; Luk, F.; Chen, Z.; Ng, J.K.; et al. Viral dynamics of SARS-CoV-2 across a spectrum of disease severity in COVID-19. J. Infect. 2020, 81, 318–356. [Google Scholar] [CrossRef] [PubMed]
- Wölfel, R.; Corman, V.M.; Guggemos, W.; Seilmaier, M.; Zange, S.; Müller, M.A.; Niemeyer, D.; Jones, T.C.; Vollmar, P.; Rothe, C.; et al. Virological assessment of hospitalized patients with COVID-2019. Nature 2020, 581, 465–469. [Google Scholar] [CrossRef] [PubMed]
- Markov, P.V.; Ghafari, M.; Beer, M.; Lythgoe, K.; Simmonds, P.; Stilianakis, N.I.; Katzourakis, A. The evolution of SARS-CoV-2. Nat. Rev. Microbiol. 2023, 21, 361–379. [Google Scholar] [CrossRef]
- Sender, R.; Bar-On, Y.M.; Gleizer, S.; Bernshtein, B.; Flamholz, A.; Phillips, R.; Milo, R. The total number and mass of SARS-CoV-2 virions. Proc. Natl. Acad. Sci. USA 2021, 118, e2024815118. [Google Scholar] [CrossRef]
- Iyer, A.S.; Jones, F.K.; Nodoushani, A.; Kelly, M.; Becker, M.; Slater, D.; Mills, R.; Teng, E.; Kamruzzaman, M.; Garcia-Beltran, W.F.; et al. Persistence and decay of human antibody responses to the receptor binding domain of SARS-CoV-2 spike protein in COVID-19 patients. Sci. Immunol. 2020, 5, eabe0367. [Google Scholar] [CrossRef]
- Lu, M.; Chamblee, M.; Zhang, Y.; Ye, C.; Dravid, P.; Park, J.G.; KC, M.; Trivedi, S.; Murthy, S.; Sharma, H.; et al. SARS-CoV-2 prefusion spike protein stabilized by six rather than two prolines is more potent for inducing antibodies that neutralize viral variants of concern. Proc. Natl. Acad. Sci. USA 2022, 119, e2110105119. [Google Scholar] [CrossRef]
- Bergamaschi, L.; Mescia, F.; Turner, L.; Hanson, A.L.; Kotagiri, P.; Dunmore, B.J.; Ruffieux, H.; De Sa, A.; Huhn, O.; Morgan, M.D.; et al. Longitudinal analysis reveals that delayed bystander CD8+ T cell activation and early immune pathology distinguish severe COVID-19 from mild disease. Immunity 2021, 54, 1257–1275.e8. [Google Scholar] [CrossRef]
- Sharov, K.S. HIV/SARS-CoV-2 co-infection: T cell profile, cytokine dynamics and role of exhausted lymphocytes. Int. J. Infect. Dis. 2021, 102, 163–169. [Google Scholar] [CrossRef]
- Huang, M.; Wang, Y.; Ye, J.; Da, H.; Fang, S.; Chen, L. Dynamic changes of T-lymphocyte subsets and the correlations with 89 patients with coronavirus disease 2019 (COVID-19). Ann. Transl. Med. 2020, 8, 1145. [Google Scholar] [CrossRef]
- Vadi, S.; Sanwalka, N.; Pednekar, A.; Suthar, D.; Ghodke, K.; Rabade, N. Characteristics and Predictive Value of T-lymphocyte Subset Absolute Counts in Patients with COVID-19-associated Acute Respiratory Failure: A Retrospective Study. Indian J. Crit. Care Med. 2022, 26, 1198–1203. [Google Scholar] [CrossRef] [PubMed]
- Venet, F.; Gossez, M.; Bidar, F.; Bodinier, M.; Coudereau, R.; Lukaszewicz, A.C.; Tardiveau, C.; Brengel-Pesce, K.; Cheynet, V.; Cazalis, M.-A.; et al. T cell response against SARS-CoV-2 persists after one year in patients surviving severe COVID-19. eBioMedicine 2022, 78, 103967. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Yue, D.; Wang, Y.; Wang, F.; Wu, S.; Hou, H. The dynamics of immune response in COVID-19 patients with different illness severity. J. Med. Virol. 2021, 93, 1070–1077. [Google Scholar] [CrossRef] [PubMed]
- Santa Cruz, A.; Mendes-Frias, A.; Oliveira, A.I.; Dias, L.; Matos, A.R.; Carvalho, A.; Capela, C.; Pedrosa, J.; Gil Castro, A.; Silvestre, R. Interleukin-6 Is a Biomarker for the Development of Fatal Severe Acute Respiratory Syndrome Coronavirus 2 Pneumonia. Front. Immunol. 2021, 12, 613422. [Google Scholar] [CrossRef]
- Herold, T.; Jurinovic, V.; Arnreich, C.; Lipworth, B.J.; Hellmuth, J.C.; Von Bergwelt-Baildon, M.; Klein, M.; Weinberger, T. Elevated levels of IL-6 and CRP predict the need for mechanical ventilation in COVID-19. J. Allergy Clin. Immunol. 2020, 146, 128–136.e4. [Google Scholar] [CrossRef]
- Gibaldi, M. Pharmacokinetics in Clinical Practice: I. Concepts. JAMA 1976, 235, 1864. [Google Scholar] [CrossRef]
- Greenblatt, D.J. Elimination Half-Life of Drugs: Value and Limitations. Annu. Rev. Med. 1985, 36, 421–427. [Google Scholar] [CrossRef]
- Rowland, M.; Benet, L.Z.; Graham, G.G. Clearance concepts in pharmacokinetics. J. Pharmacokinet. Biopharm. 1973, 1, 123–136. [Google Scholar] [CrossRef]
- Corti, D.; Voss, J.; Gamblin, S.J.; Codoni, G.; Macagno, A.; Jarrossay, D.; Vachieri, S.G.; Pinna, D.; Minola, A.; Vanzetta, F.; et al. A Neutralizing Antibody Selected from Plasma Cells That Binds to Group 1 and Group 2 Influenza A Hemagglutinins. Science 2011, 333, 850–856. [Google Scholar] [CrossRef]
- Corti, D.; Lanzavecchia, A. Efficient Methods To Isolate Human Monoclonal Antibodies from Memory B Cells and Plasma Cells. Microbiol. Spectr. 2014, 2, AID-0018-2014. [Google Scholar] [CrossRef]
- Eyer, K.; Doineau, R.C.L.; Castrillon, C.E.; Briseño-Roa, L.; Menrath, V.; Mottet, G.; England, P.; Godina, A.; Brient-Litzler, E.; Nizak, C.; et al. Single-cell deep phenotyping of IgG-secreting cells for high-resolution immune monitoring. Nat. Biotechnol. 2017, 35, 977–982. [Google Scholar] [CrossRef] [PubMed]
- Hibi, T.; Dosch, H. Limiting dilution analysis of the B cell compartment in human bone marrow. Eur. J. Immunol. 1986, 16, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Kometani, K.; Nakagawa, R.; Shinnakasu, R.; Kaji, T.; Rybouchkin, A.; Moriyama, S.; Furukawa, K.; Koseki, H.; Takemori, T.; Kurosaki, T. Repression of the Transcription Factor Bach2 Contributes to Predisposition of IgG1 Memory B Cells toward Plasma Cell Differentiation. Immunity 2013, 39, 136–147. [Google Scholar] [CrossRef] [PubMed]
- Lanzavecchia, A. Dissecting human antibody responses: Useful, basic and surprising findings. EMBO Mol. Med. 2018, 10, e8879. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Joyner, C.J.; Sanz, I.; Lee, F.E.H. Factors Affecting Early Antibody Secreting Cell Maturation Into Long-Lived Plasma Cells. Front. Immunol. 2019, 10, 2138. [Google Scholar] [CrossRef]
- Justiz Vaillant, A.A.; Jamal, Z.; Patel, P.; Ramphul, K. Immunoglobulin. In StatPearls [Internet]; StatPearls Publishing: Treasure Island, FL, USA, 2023. Available online: http://www.ncbi.nlm.nih.gov/books/NBK513460/ (accessed on 4 December 2023).
- Ridley, R.G. Antibodies: A Laboratory Manual. Edited by Ed Harlow and David Lane. Cold Spring Harbor: Cold Spring Harbor Laboratory. New York. 1988. 726 pages. Paper $50.00. ISBN 0 87969 314 2. Genet. Res. 1989, 54, 161. [Google Scholar] [CrossRef]
- Chen, H.Y.; Di Mascio, M.; Perelson, A.S.; Ho, D.D.; Zhang, L. Determination of virus burst size in vivo using a single-cycle SIV in rhesus macaques. Proc. Natl. Acad. Sci. USA 2007, 104, 19079–19084. [Google Scholar] [CrossRef]
- Czuppon, P.; Débarre, F.; Gonçalves, A.; Tenaillon, O.; Perelson, A.S.; Guedj, J.; Blanquart, F. Predicted Success of Prophylactic Antiviral Therapy to Block or Delay SARS-CoV-2 Infection Depends on the Drug’s Mechanism of Action [Internet]. 2020. Available online: http://medrxiv.org/lookup/doi/10.1101/2020.05.07.20092965 (accessed on 21 July 2024).
- Einav, T.; Gentles, L.E.; Bloom, J.D. SnapShot: Influenza by the Numbers. Cell 2020, 182, 532–532.e1. [Google Scholar] [CrossRef]
- Heider, S.; Metzner, C. Quantitative real-time single particle analysis of virions. Virology 2014, 462–463, 199–206. [Google Scholar] [CrossRef]
- Sanjuán, R. Collective properties of viral infectivity. Curr. Opin. Virol. 2018, 33, 1–6. [Google Scholar] [CrossRef]
- Cohen, S.D.; Hindmarsh, A.C.; Dubois, P.F. CVODE, A Stiff/Nonstiff ODE Solver in C. Comput. Phys. 1996, 10, 138–143. [Google Scholar] [CrossRef]
- Kolpakov, F.; Akberdin, I.; Kiselev, I.; Kolmykov, S.; Kondrakhin, Y.; Kulyashov, M.; Kutumova, E.; Pintus, S.; Ryabova, A.; Sharipov, R.; et al. BioUML—Towards a universal research platform. Nucleic Acids Res. 2022, 50, W124–W131. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulos, C.E.; Yeung, H. Uncertainty estimation and Monte Carlo simulation method. Flow. Meas. Instrum. 2001, 12, 291–298. [Google Scholar] [CrossRef]
- Runarsson, T.P.; Xin, Y. Stochastic ranking for constrained evolutionary optimization. IEEE Trans. Evol. Comput. 2000, 4, 284–294. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. Available online: http://ieeexplore.ieee.org/document/488968/ (accessed on 26 January 2024).
- Li, M.; Liu, L.; Lin, D. A fast steady-state ε-dominance multi-objective evolutionary algorithm. Comput. Optim. Appl. 2011, 48, 109–138. [Google Scholar] [CrossRef]
- Dorronsoro, B.; Alba, E. Cellular Genetic Algorithms [Internet]; Operations Research/Computer Science Interfaces Series; Springer: Boston, MA, USA, 2008; Volume 42, 248p, Available online: https://link.springer.com/10.1007/978-0-387-77610-1 (accessed on 26 January 2024).
- Nebro, A.J.; Durillo, J.J.; Luna, F.; Dorronsoro, B.; Alba, E. MOCell: A cellular genetic algorithm for multiobjective optimization. Int. J. Intell. Syst. 2009, 24, 726–746. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Contr 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Rabitz, H.; Kramer, M.; Dacol, D. Sensitivity Analysis in Chemical Kinetics. Annu. Rev. Phys. Chem. 1983, 34, 419–461. [Google Scholar] [CrossRef]
- Raue, A.; Becker, V.; Klingmüller, U.; Timmer, J. Identifiability and observability analysis for experimental design in nonlinear dynamical models. Chaos An. Interdiscip. J. Nonlinear Sci. 2010, 20, 045105. [Google Scholar] [CrossRef]
- Lewis, N.M.; Duca, L.M.; Marcenac, P.; Dietrich, E.A.; Gregory, C.J.; Fields, V.L.; Banks, M.M.; Rispens, J.R.; Hall, A.; Harcourt, J.L.; et al. Characteristics and Timing of Initial Virus Shedding in Severe Acute Respiratory Syndrome Coronavirus 2, Utah, USA. Emerg. Infect. Dis. 2021, 27, 352–359. [Google Scholar] [CrossRef]
- Widders, A.; Broom, A.; Broom, J. SARS-CoV-2: The viral shedding vs infectivity dilemma. Infect. Dis. Health 2020, 25, 210–215. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Cao, Z.; Chen, Y.; Cai, M.; Zhang, L.; Xu, H.; Zhang, J.-Y.; Ma, C.-H.; Liu, Y.; Gao, L.-J.; et al. Duration of SARS-CoV-2 RNA shedding and factors associated with prolonged viral shedding in patients with COVID-19. J. Med. Virol. 2021, 93, 506–512. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Ding, M.; Dong, X.; Zhang, J.; Kursat Azkur, A.; Azkur, D.; Gan, H.; Sun, Y.-L.; Fu, W.; Li, W.; et al. Risk factors for severe and critically ill COVID-19 patients: A review. Allergy 2021, 76, 428–455. [Google Scholar] [CrossRef] [PubMed]
- Biswas, M.; Rahaman, S.; Biswas, T.K.; Haque, Z.; Ibrahim, B. Association of Sex, Age, and Comorbidities with Mortality in COVID-19 Patients: A Systematic Review and Meta-Analysis. Intervirology 2021, 64, 36–47. [Google Scholar] [CrossRef] [PubMed]
- Pijls, B.G.; Jolani, S.; Atherley, A.; Derckx, R.T.; Dijkstra, J.I.R.; Franssen, G.H.L.; Hendriks, S.; Richters, A.; Venemans-Jellema, A.; Zalpuri, S.; et al. Demographic risk factors for COVID-19 infection, severity, ICU admission and death: A meta-analysis of 59 studies. BMJ Open 2021, 11, e044640. [Google Scholar] [CrossRef]
- Weyand, C.M.; Goronzy, J.J. Aging of the Immune System. Mechanisms and Therapeutic Targets. Ann. Am. Thorac. Soc. 2016, 13 (Suppl. S5), S422–S428. [Google Scholar] [CrossRef]
- Aydar, Y.; Balogh, P.; Tew, J.G.; Szakal, A.K. Age-related depression of FDC accessory functions and CD21 ligand-mediated repair of co-stimulation. Eur. J. Immunol. 2002, 32, 2817–2826. [Google Scholar] [CrossRef]
- Whisler, R.L.; Williams, J.W.; Newhouse, Y.G. Human B cel proliferative responses during aging. Reduced RNA synthesis and DNA replication after signal transduction by surface immunoglobulins compared to B cell antigenic determinants CD20 and CD40. Mech. Ageing Dev. 1991, 61, 209–222. [Google Scholar] [CrossRef]
- Lee, J.L.; Linterman, M.A. Mechanisms underpinning poor antibody responses to vaccines in ageing. Immunol. Lett. 2022, 241, 1–14. [Google Scholar] [CrossRef]
- Grolleau-Julius, A.; Harning, E.K.; Abernathy, L.M.; Yung, R.L. Impaired Dendritic Cell Function in Aging Leads to Defective Antitumor Immunity. Cancer Res. 2008, 68, 6341–6349. [Google Scholar] [CrossRef]
- Haynes, L.; Eaton, S.M.; Burns, E.M.; Randall, T.D.; Swain, S.L. CD4 T cell memory derived from young naive cells functions well into old age, but memory generated from aged naive cells functions poorly. Proc. Natl. Acad. Sci. USA 2003, 100, 15053–15058. [Google Scholar] [CrossRef] [PubMed]
- Kohler, S.; Wagner, U.; Pierer, M.; Kimmig, S.; Oppmann, B.; Möwes, B.; Jülke, K.; Romagnani, C.; Thiel, A. Post-thymic in vivo proliferation of naive CD4+ T cells constrains the TCR repertoire in healthy human adults. Eur. J. Immunol. 2005, 35, 1987–1994. [Google Scholar] [CrossRef] [PubMed]
- Saenz, R.A.; Quinlivan, M.; Elton, D.; MacRae, S.; Blunden, A.S.; Mumford, J.A.; Daly, J.M.; Digard, P.; Cullinane, A.; Grenfell, B.T.; et al. Dynamics of Influenza Virus Infection and Pathology. J. Virol. 2010, 84, 3974–3983. [Google Scholar] [CrossRef] [PubMed]
- Powers, D.C. Influenza A Virus-Specific Cytotoxic T Lymphocyte Activity Declines with Advancing Age. J. Am. Geriatr. Soc. 1993, 41, 1–5. [Google Scholar] [CrossRef]
- Johnson, S.A.; Cambier, J.C. Ageing, autoimmunity and arthritis: Senescence of the B cell compartment–implications for humoral immunity. Arthritis Res. Ther. 2004, 6, 131. [Google Scholar] [CrossRef]
- Bulati, M.; Caruso, C.; Colonna-Romano, G. From lymphopoiesis to plasma cells differentiation, the age-related modifications of B cell compartment are influenced by “inflamm-ageing”. Ageing Res. Rev. 2017, 36, 125–136. [Google Scholar] [CrossRef]
- Li, M.; Yao, D.; Zeng, X.; Kasakovski, D.; Zhang, Y.; Chen, S.; Zha, X.; Li, Y.; Xu, L. Age related human T cell subset evolution and senescence. Immun. Ageing 2019, 16, 24. [Google Scholar] [CrossRef]
- Lloberas, J.; Celada, A. Effect of aging on macrophage function. Exp. Gerontol. 2002, 37, 1325–1331. [Google Scholar] [CrossRef]
- Konopka, K.E.; Nguyen, T.; Jentzen, J.M.; Rayes, O.; Schmidt, C.J.; Wilson, A.M.; Farver, C.F.; Myers, J.L. Diffuse alveolar damage (DAD) resulting from coronavirus disease 2019 Infection is Morphologically Indistinguishable from Other Causes of DAD. Histopathology 2020, 77, 570–578. [Google Scholar] [CrossRef]
- Cardinal-Fernández, P.; Lorente, J.A.; Ballén-Barragán, A.; Matute-Bello, G. Acute Respiratory Distress Syndrome and Diffuse Alveolar Damage. New Insights on a Complex Relationship. Ann. Am. Thorac. Soc. 2017, 14, 844–850. [Google Scholar] [CrossRef]
- Almasi Nokiani, A.; Shahnazari, R.; Abbasi, M.A.; Divsalar, F.; Bayazidi, M.; Sadatnaseri, A. CT severity score in COVID-19 patients, assessment of performance in triage and outcome prediction: A comparative study of different methods. Egypt. J. Radiol. Nucl. Med. 2022, 53, 116. [Google Scholar] [CrossRef]
- Damiani, S.; Fiorentino, M.; De Palma, A.; Foschini, M.P.; Lazzarotto, T.; Gabrielli, L.; Viale, P.L.; Attard, L.; Riefolo, M.; D’Errico, A. Pathological post-mortem findings in lungs infected with SARS-CoV-2. J. Pathol. 2021, 253, 31–40. [Google Scholar] [CrossRef] [PubMed]
- Soria, M.E.; Cortón, M.; Martínez-González, B.; Lobo-Vega, R.; Vázquez-Sirvent, L.; López-Rodríguez, R.; Almoguera, B.; Mahillo, I.; Mínguez, P.; Herrero, A. High SARS-CoV-2 viral load is associated with a worse clinical outcome of COVID-19 disease. Access Microbiol. 2021, 3, 000259. Available online: https://www.microbiologyresearch.org/content/journal/acmi/10.1099/acmi.0.000259 (accessed on 16 January 2024). [CrossRef] [PubMed]
- Yu, X.; Sun, S.; Shi, Y.; Wang, H.; Zhao, R.; Sheng, J. SARS-CoV-2 viral load in sputum correlates with risk of COVID-19 progression. Crit. Care 2020, 24, 170. [Google Scholar] [CrossRef]
- Silva, J.; Lucas, C.; Sundaram, M.; Israelow, B.; Wong, P.; Klein, J.; Tokuyama, M.; Lu, P.; Venkataraman, A.; Liu, F.; et al. Saliva Viral Load Is a Dynamic Unifying Correlate of COVID-19 Severity and Mortality [Internet]. 2021. Available online: http://medrxiv.org/lookup/doi/10.1101/2021.01.04.21249236 (accessed on 24 July 2024).
- Yang, Y.; Guo, L.; Yuan, J.; Xu, Z.; Gu, Y.; Zhang, J.; Guan, Y.; Liang, J.; Lu, H.; Liu, Y. Viral and antibody dynamics of acute infection with SARS-CoV-2 omicron variant (B.1.1.529): A prospective cohort study from Shenzhen, China. Lancet Microbe 2023, 4, e632–e641. [Google Scholar] [CrossRef]
- Cevik, M.; Tate, M.; Lloyd, O.; Maraolo, A.E.; Schafers, J.; Ho, A. SARS-CoV-2, SARS-CoV, and MERS-CoV viral load dynamics, duration of viral shedding, and infectiousness: A systematic review and meta-analysis. Lancet Microbe 2021, 2, e13–e22. [Google Scholar] [CrossRef]
- Munker, D.; Osterman, A.; Stubbe, H.; Muenchhoff, M.; Veit, T.; Weinberger, T.; Barnikel, M.; Mumm, J.-N.; Milger, K.; Khatamzas, E.; et al. Dynamics of SARS-CoV-2 shedding in the respiratory tract depends on the severity of disease in COVID-19 patients. Eur. Respir. J. 2021, 58, 2002724. [Google Scholar] [CrossRef]
- Mortaz, E.; Tabarsi, P.; Jamaati, H.; Dalil Roofchayee, N.; Dezfuli, N.K.; Hashemian, S.M.; Moniri, A.; Marjani, M.; Malekmohammad, M.; Mansouri, D.; et al. Increased Serum Levels of Soluble TNF-α Receptor Is Associated With ICU Mortality in COVID-19 Patients. Front. Immunol. 2021, 12, 592727. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Sinha, S.; Mohapatra, S.K. Analysis of transcriptomic data sets supports the role of IL-6 in NETosis and immunothrombosis in severe COVID-19. BMC Genom. Data 2021, 22, 49. [Google Scholar] [CrossRef]
- Ruenjaiman, V.; Hirankarn, N.; Palaga, T. Innate immunity in COVID-19: Drivers of pathogenesis and potential therapeutic targets. Asian Pac. J. Allergy Immunol. 2021, 39, 69–77. [Google Scholar]
- Paludan, S.R.; Mogensen, T.H. Innate immunological pathways in COVID-19 pathogenesis. Sci. Immunol. 2022, 7, eabm5505. [Google Scholar] [CrossRef] [PubMed]
- Elahi, R.; Karami, P.; Heidary, A.H.; Esmaeilzadeh, A. An updated overview of recent advances, challenges, and clinical considerations of IL-6 signaling blockade in severe coronavirus disease 2019 (COVID-19). Int. Immunopharmacol. 2022, 105, 108536. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Chen, T.; Mao, X.; Fang, Y.; Sun, H.; Wei, D.Q.; Ji, G. Machine learning of flow cytometry data reveals the delayed innate immune responses correlate with the severity of COVID-19. Front. Immunol. 2023, 14, 974343. [Google Scholar] [CrossRef]
- Allison, T.L. Immunosuppressive Therapy in Transplantation. Nurs. Clin. North. Am. 2016, 51, 107–120. [Google Scholar] [CrossRef]
- G Elfaki, M. Immunosuppression Induced by HIV Infection. Biol. Med. 2014, 6, 1. Available online: https://www.walshmedicalmedia.com/open-access/immunosuppression-induced-by-hiv-infection-0974-8369.1000e111.pdf (accessed on 21 April 2024). [CrossRef]
- Taylor, A.L.; Watson, C.J.E.; Bradley, J.A. Immunosuppressive agents in solid organ transplantation: Mechanisms of action and therapeutic efficacy. Crit. Rev. Oncol. Hematol. 2005, 56, 23–46. [Google Scholar] [CrossRef] [PubMed]
- Holt, C.D. Overview of Immunosuppressive Therapy in Solid Organ Transplantation. Anesthesiol. Clin. 2017, 35, 365–380. [Google Scholar] [CrossRef]
- Kolla, E.; Weill, A.; Zaidan, M.; De Martin, E.; Colin De Verdiere, S.; Semenzato, L.; Zureik, M.; Grimaldi, L. COVID-19 Hospitalization in Solid Organ Transplant Recipients on Immunosuppressive Therapy. JAMA Netw. Open 2023, 6, e2342006. [Google Scholar] [CrossRef]
- Vidya Vijayan, K.K.; Karthigeyan, K.P.; Tripathi, S.P.; Hanna, L.E. Pathophysiology of CD4+ T-Cell Depletion in HIV-1 and HIV-2 Infections. Front. Immunol. 2017, 8, 580. [Google Scholar] [CrossRef]
- Höft, M.A.; Burgers, W.A.; Riou, C. The immune response to SARS-CoV-2 in people with HIV. Cell Mol. Immunol. 2023, 21, 184–196. [Google Scholar] [CrossRef]
- McBrien, J.B.; Kumar, N.A.; Silvestri, G. Mechanisms of CD8+ T cell-mediated suppression of HIV/SIV replication. Eur. J. Immunol. 2018, 48, 898–914. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Zeng, F.; Meng, Y.; Liu, Y.; Liu, H.; Deng, G. Serological response following COVID-19 vaccines in patients living with HIV: A dose–response meta-analysis. Sci. Rep. 2023, 13, 9893. [Google Scholar] [CrossRef] [PubMed]
- Van Laethem, F.; Baus, E.; Smyth, L.A.; Andris, F.; Bex, F.; Urbain, J.; Kioussis, D.; Leo, O. Glucocorticoids Attenuate T Cell Receptor Signaling. J. Exp. Med. 2001, 193, 803–814. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Bai, X.; Cao, W.; Ji, J.; Wang, L.; Yang, Y.; Yang, H. The Influence of Corticosteroids, Immunosuppressants and Biologics on Patients With Inflammatory Bowel Diseases, Psoriasis and Rheumatic Diseases in the Era of COVID-19: A Review of Current Evidence. Front. Immunol. 2021, 12, 677957. [Google Scholar] [CrossRef]
- Olnes, M.J.; Kotliarov, Y.; Biancotto, A.; Cheung, F.; Chen, J.; Shi, R.; Zhou, H.; Wang, E.; Tsang, J.S.; Nussenblatt, R.; et al. Effects of Systemically Administered Hydrocortisone on the Human Immunome. Sci. Rep. 2016, 6, 23002. [Google Scholar] [CrossRef]
- Burki, T. Understanding variants of SARS-CoV-2. Lancet 2021, 397, 462. [Google Scholar] [CrossRef]
- Choi, J.Y.; Smith, D.M. SARS-CoV-2 Variants of Concern. Yonsei Med. J. 2021, 62, 961. [Google Scholar] [CrossRef]
- Cox, M.; Peacock, T.P.; Harvey, W.T.; Hughes, J.; Wright, D.W.; COVID-19 Genomics UK (COG-UK) Consortium; Willett, B.J.; Thomson, E.; Gupta, R.K.; Peacock, S.J.; et al. SARS-CoV-2 variant evasion of monoclonal antibodies based on in vitro studies. Nat. Rev. Microbiol. 2023, 21, 112–124. [Google Scholar] [CrossRef]
- Harvey, W.T.; Carabelli, A.M.; Jackson, B.; Gupta, R.K.; Thomson, E.C.; Harrison, E.M.; Ludden, C.; Reeve, R.; Rambaut, A.; COVID-19 Genomics UK (COG-UK) Consortium; et al. SARS-CoV-2 variants, spike mutations and immune escape. Nat. Rev. Microbiol. 2021, 19, 409–424. [Google Scholar] [CrossRef]
- Hyams, C.; Challen, R.; Marlow, R.; Nguyen, J.; Begier, E.; Southern, J.; King, J.; Morley, A.; Kinney, J.; Clout, M.; et al. Severity of Omicron (B.1.1.529) and Delta (B.1.617.2) SARS-CoV-2 infection among hospitalised adults: A prospective cohort study in Bristol, United Kingdom. Lancet Reg. Health-Eur. 2023, 25, 100556. [Google Scholar] [CrossRef]
- Relan, P.; Motaze, N.V.; Kothari, K.; Askie, L.; Le Polain De Waroux, O.; Van Kerkhove, M.D.; Diaz, J.; Tirupakuzhi Vijayaraghavan, B.K. Severity and outcomes of Omicron variant of SARS-CoV-2 compared to Delta variant and severity of Omicron sublineages: A systematic review and metanalysis. BMJ Glob. Health 2023, 8, e012328. [Google Scholar] [CrossRef] [PubMed]
- Bálint, G.; Vörös-Horváth, B.; Széchenyi, A. Omicron: Increased transmissibility and decreased pathogenicity. Sig. Transduct. Target. Ther. 2022, 7, 151. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.J.; Hanif, M.; Haider, M.A.; Ahmed, M.U.; Sundas, F.; Hirani, A.; Khan, I.A.; Anis, K.; Karim, A.H. Treatment Options for COVID-19: A Review. Front. Med. 2020, 7, 480. [Google Scholar] [CrossRef]
- Liu, H.M. Intracellular innate immunity and mechanism of action of cytosolic nucleic acid receptor-mediated type I IFN against viruses. IUBMB Life 2022, 74, 180–189. [Google Scholar] [CrossRef]
- Van Laarhoven, A.; Kurver, L.; Overheul, G.J.; Kooistra, E.J.; Abdo, W.F.; Van Crevel, R.; Duivenvoorden, R.; Kox, M.; ten Oever, J.; Schouten, J.; et al. Interferon gamma immunotherapy in five critically ill COVID-19 patients with impaired cellular immunity: A case series. Med 2021, 2, 1163–1170.e2. [Google Scholar] [CrossRef]
- Nguyen, L.S.; Ait Hamou, Z.; Gastli, N.; Chapuis, N.; Pène, F. Potential role for interferon gamma in the treatment of recurrent ventilator-acquired pneumonia in patients with COVID-19: A hypothesis. Intensive Care Med. 2021, 47, 619–621. [Google Scholar] [CrossRef]
- Pickard, A.; Calverley, B.C.; Chang, J.; Garva, R.; Gago, S.; Lu, Y.; Kadler, K.E. Discovery of re-purposed drugs that slow SARS-CoV-2 replication in human cells. PLoS Pathog. 2021, 17, e1009840. [Google Scholar] [CrossRef]
- Tanaka, T.; Narazaki, M.; Kishimoto, T. IL-6 in Inflammation, Immunity, and Disease. Cold Spring Harb. Perspect. Biol. 2014, 6, a016295. [Google Scholar] [CrossRef]
- Chang, C.C.; Crane, M.; Zhou, J.L.; Mina, M.; Post, J.J.; Cameron, B.A.; Lloyd, A.R.; Jaworowski, A.; French, M.A.; Lewin, S.R. HIV and co-infections. Immunol. Rev. 2013, 254, 114–142. [Google Scholar] [CrossRef]
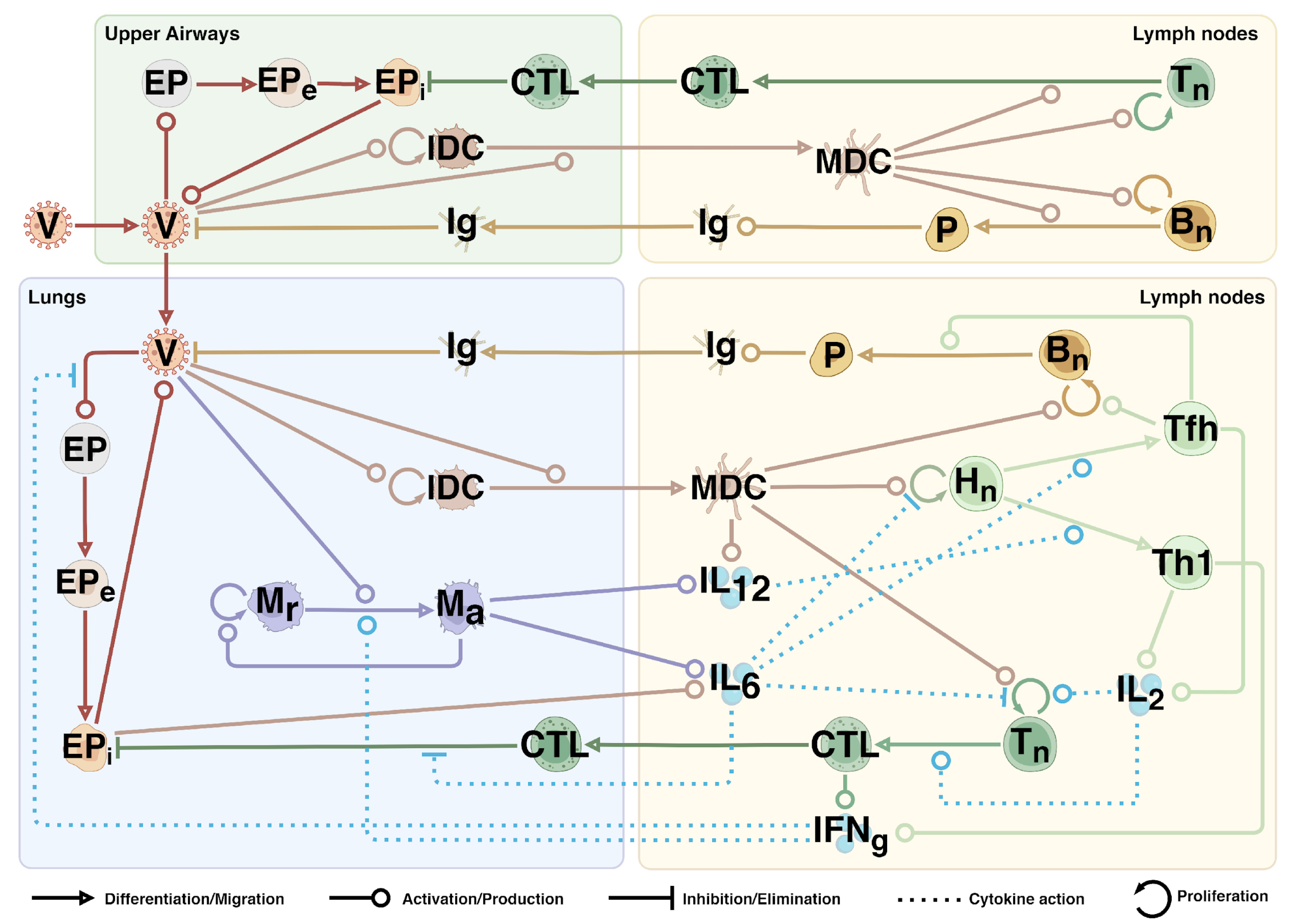
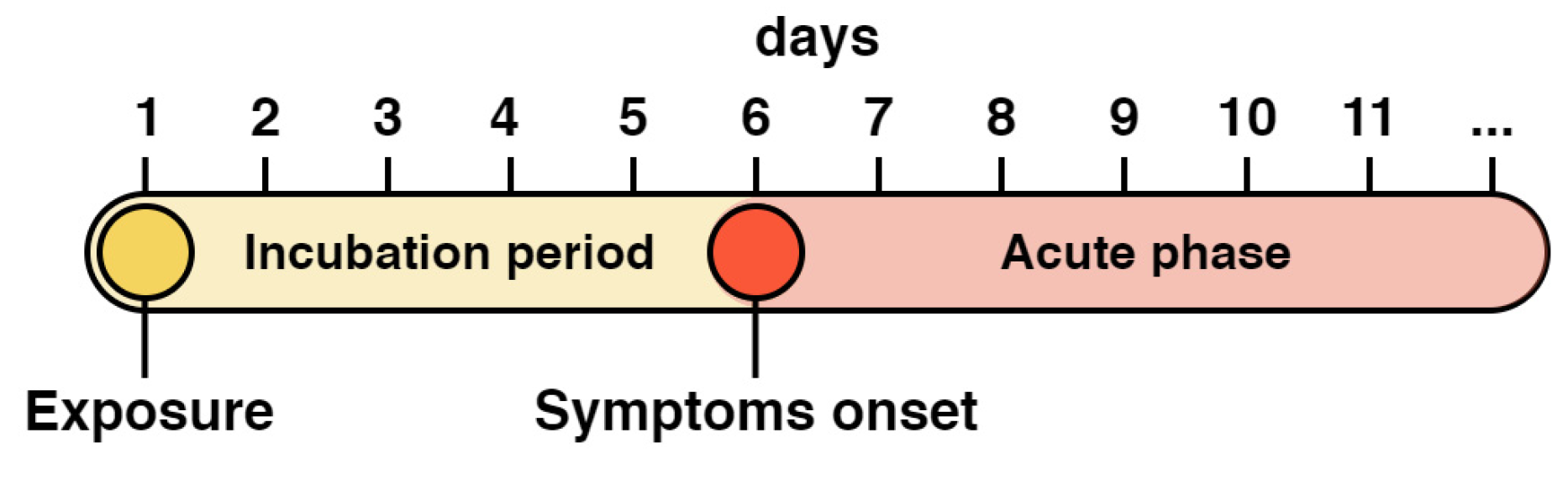


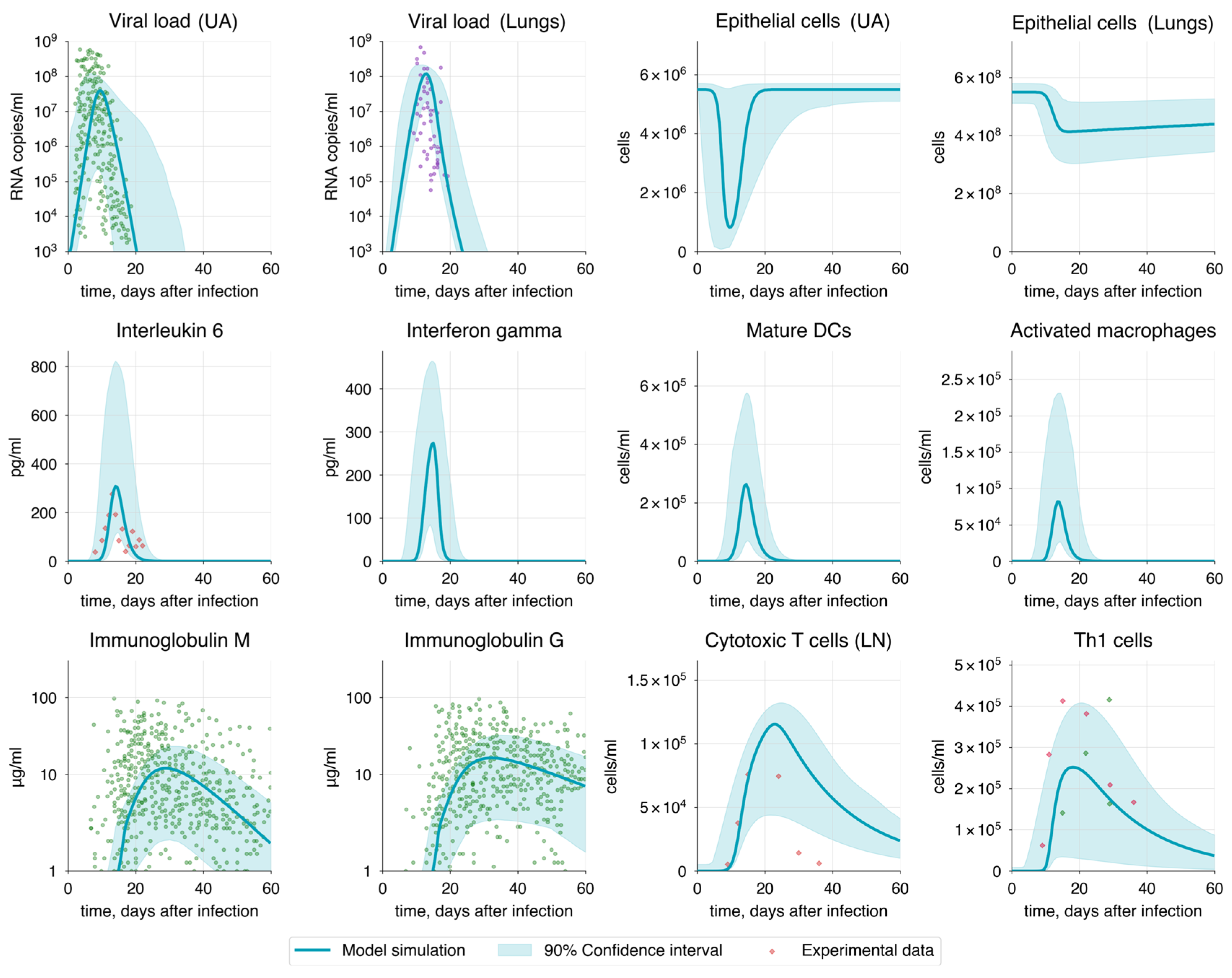
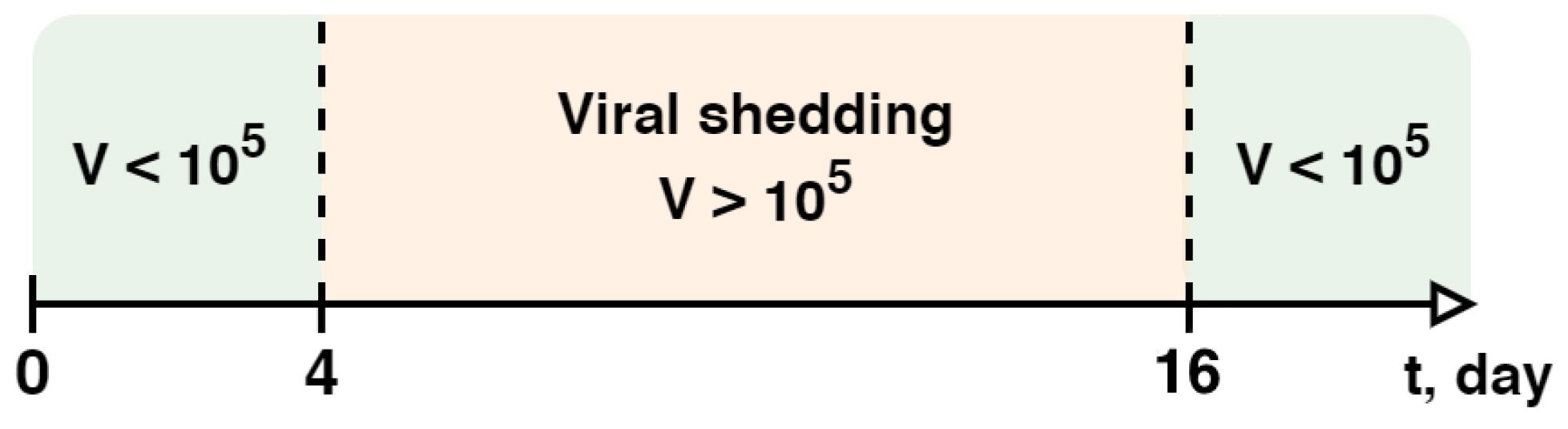
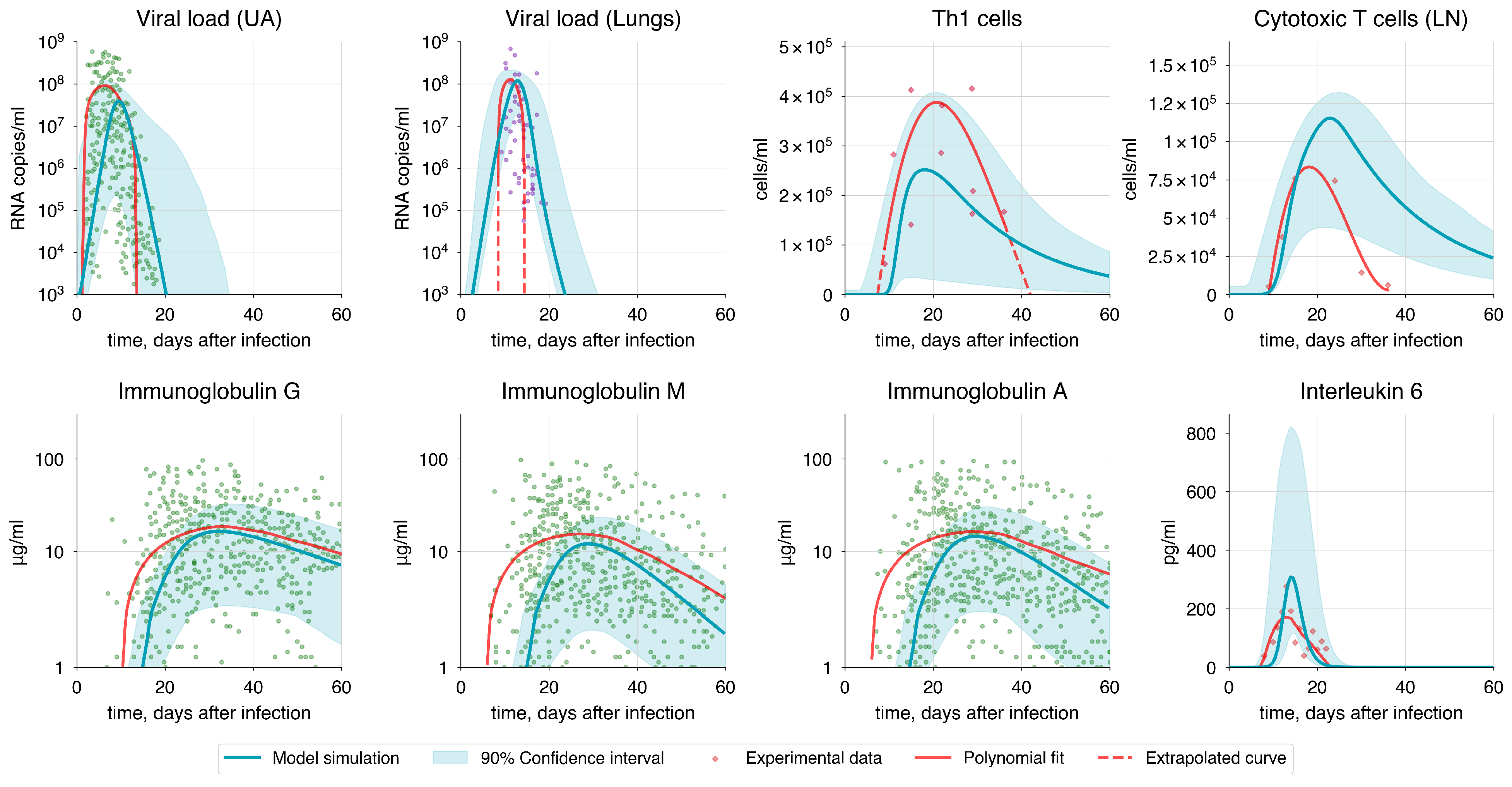

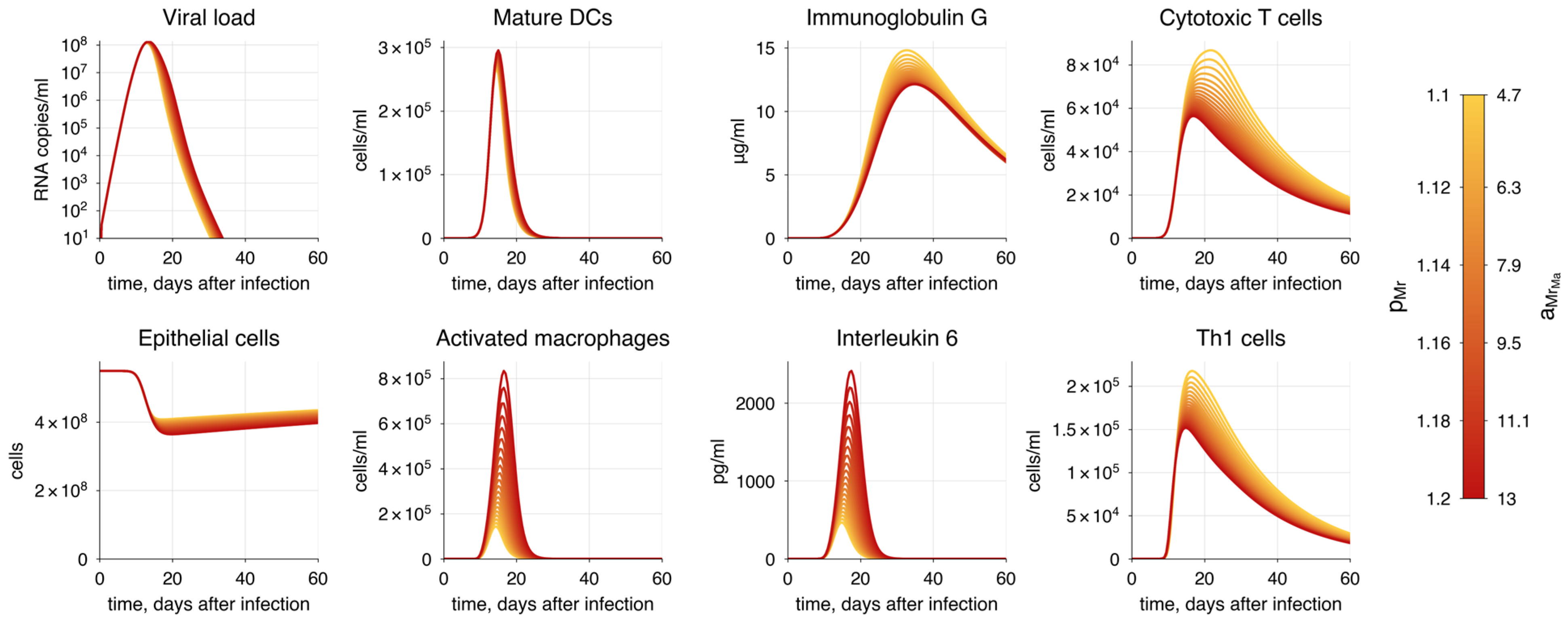
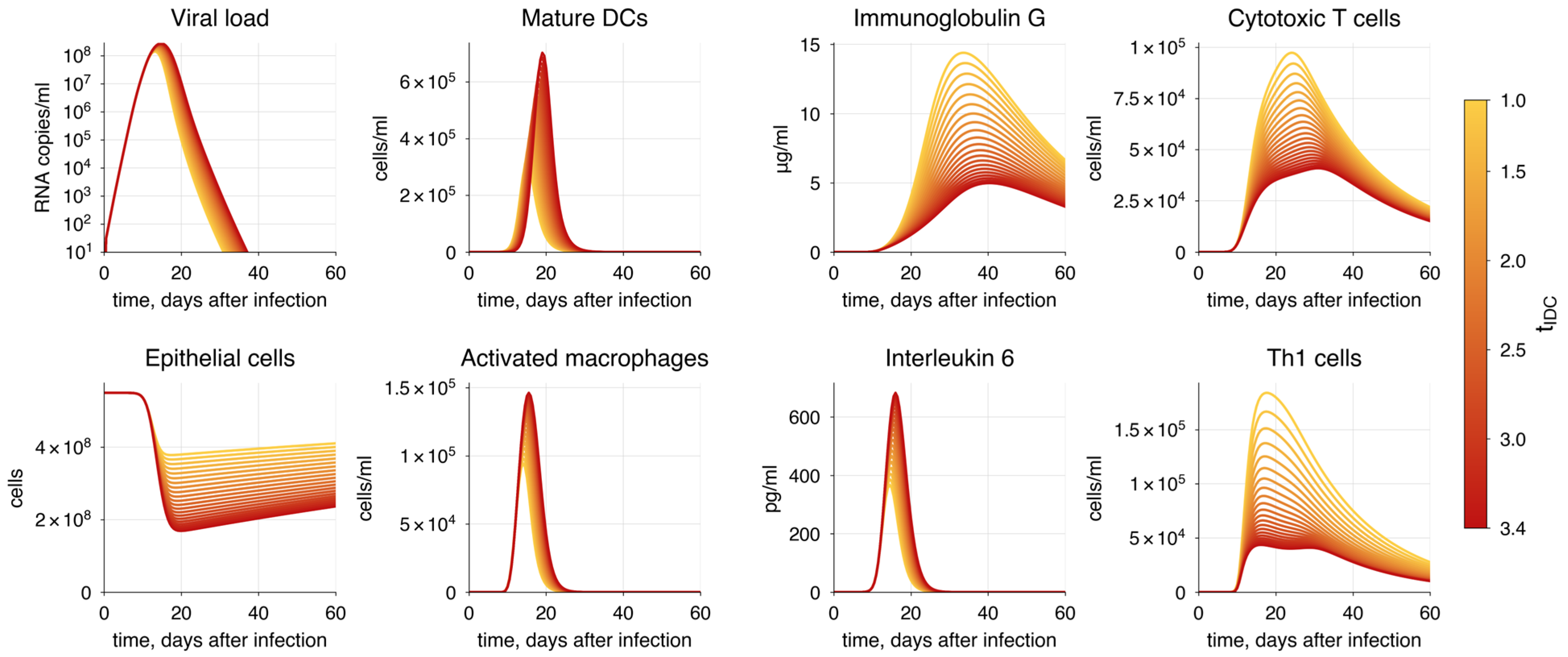
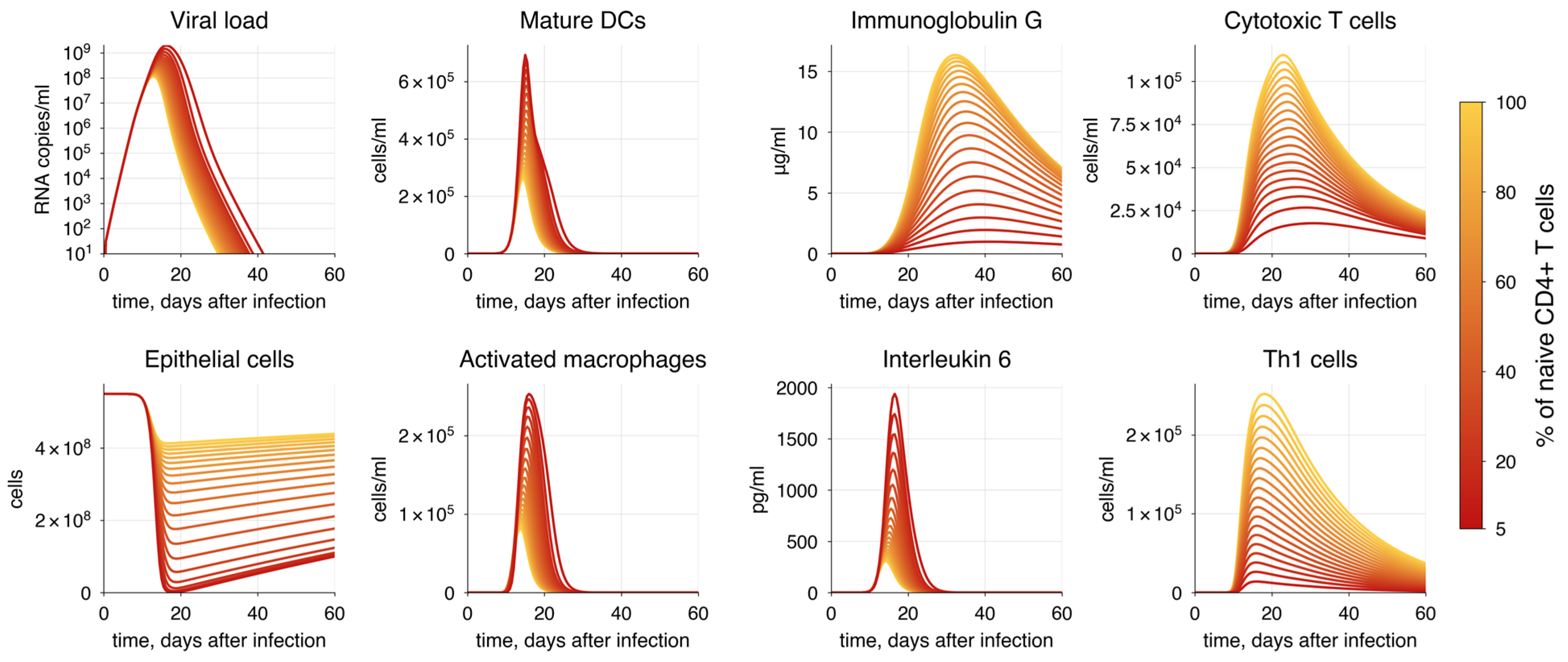

| Method | P | AIC | |
|---|---|---|---|
| MOPSO | 5.7 × 109 | 3 × 103 | 26.4 |
| SRES | 7.3 × 109 | 2 × 109 | 33.4 |
| MOCell | 7.5 × 109 | 1 × 104 | 27.3 |
| Initial model | 2 × 1010 | 8.1 × 1010 | 36.3 |
| Severity Mode | Epithelial Damage (Healthy Cells, ×108) | Epithelial Damage (Healthy Cells, %) | Viral Load (RNA Copies/mL, ×108) | IL-6 (pg/mL) |
|---|---|---|---|---|
| Moderate | >3.85 | >70 | <2.0 | <500 |
| Severe | 2.2–3.85 | 40–70 | 2.0–4.3 | 500–1000 |
| Critical | <2.2 | <40 | >4.3 | >1000 |
| Parameter | Description of the Process | References |
|---|---|---|
| Proliferation of naïve CD4+ T cells | [135,136,137,144] | |
| Proliferation of naïve CD8+ T cells | ||
| Naïve CD8+ T cell differentiation into CTL | ||
| Proliferation of naïve B cells | [132,133] | |
| Immature dendritic cell maturation and migration to the lymph nodes | [135] | |
| Virion neutralization by immunoglobulins (IgA, IgG, IgM) | [140] | |
| Infected epithelial cell elimination by CTLs | [139] | |
| Activation of resting macrophages | [143,150] |
| Parameter | Severity Mode | ||
|---|---|---|---|
| Moderate (100%) | Severe (90–80%) | Critical (80–70%) | |
| 1 | 0.9 | 0.8 | |
| , cell/mL | 60,000 | 48,000 | 42,000 |
| , cell/mL | 33,000 | 26,400 | 23,100 |
| , cell/mL | 100,000 | 80,000 | 70,000 |
| (ua), cell/mL | 16,000 | 12,800 | 11,200 |
| (ua), cell/mL | 33,000 | 26,400 | 23,100 |
| Scenario Name | Model Adjustments | Results | ||||
|---|---|---|---|---|---|---|
| Viral Load | Epithelium Damage | CTLs Response | IgG Response | IL-6 | ||
| Macrophage hyperactivation | (4.7, 14.5) (1.1, 3.1) | - | Increase | Decrease | - | Increase |
| Dendritic cell migration delay | (0.8, 1.8) | Increase | Increase | Decrease | Decrease | Increase |
| CD4+ T cell depletion | (100%, 5%) | Increase | Increase | Decrease | Decrease | Increase |
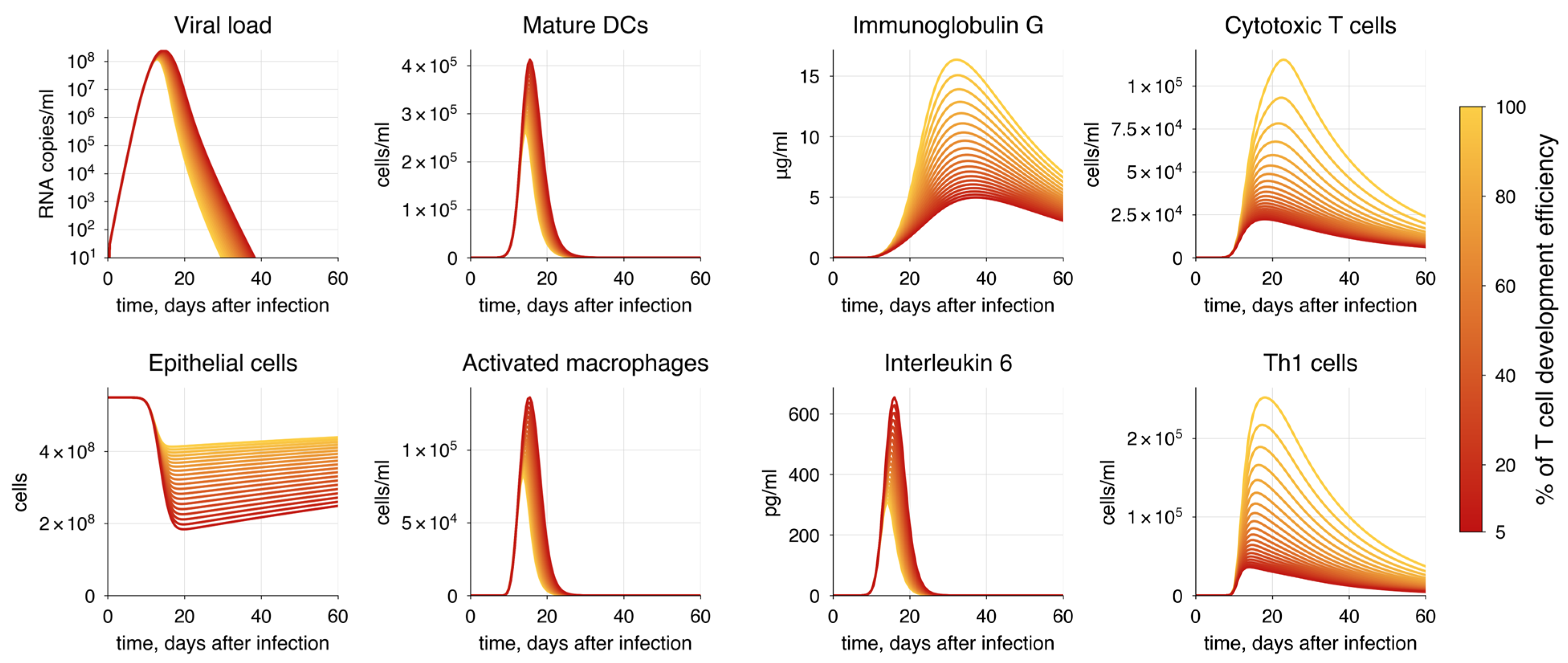
| Impaired T cell development | (100%, 5%) | Increase | Increase | Decrease | Decrease | - |
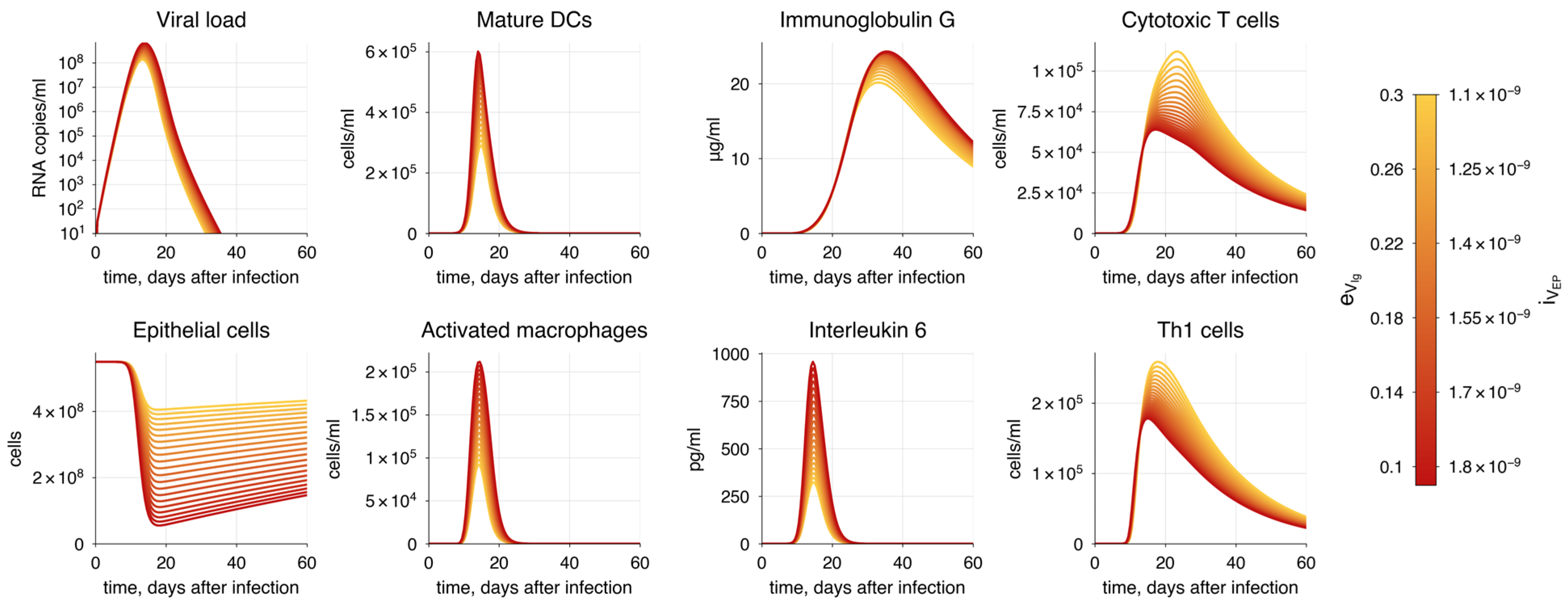
| Enhanced viral infectivity and immune evasion | (1.1 × 10−9, 1.8 × 10−9) (0.3, 0.1) | Increase | Increase | Decrease | - | Increase |
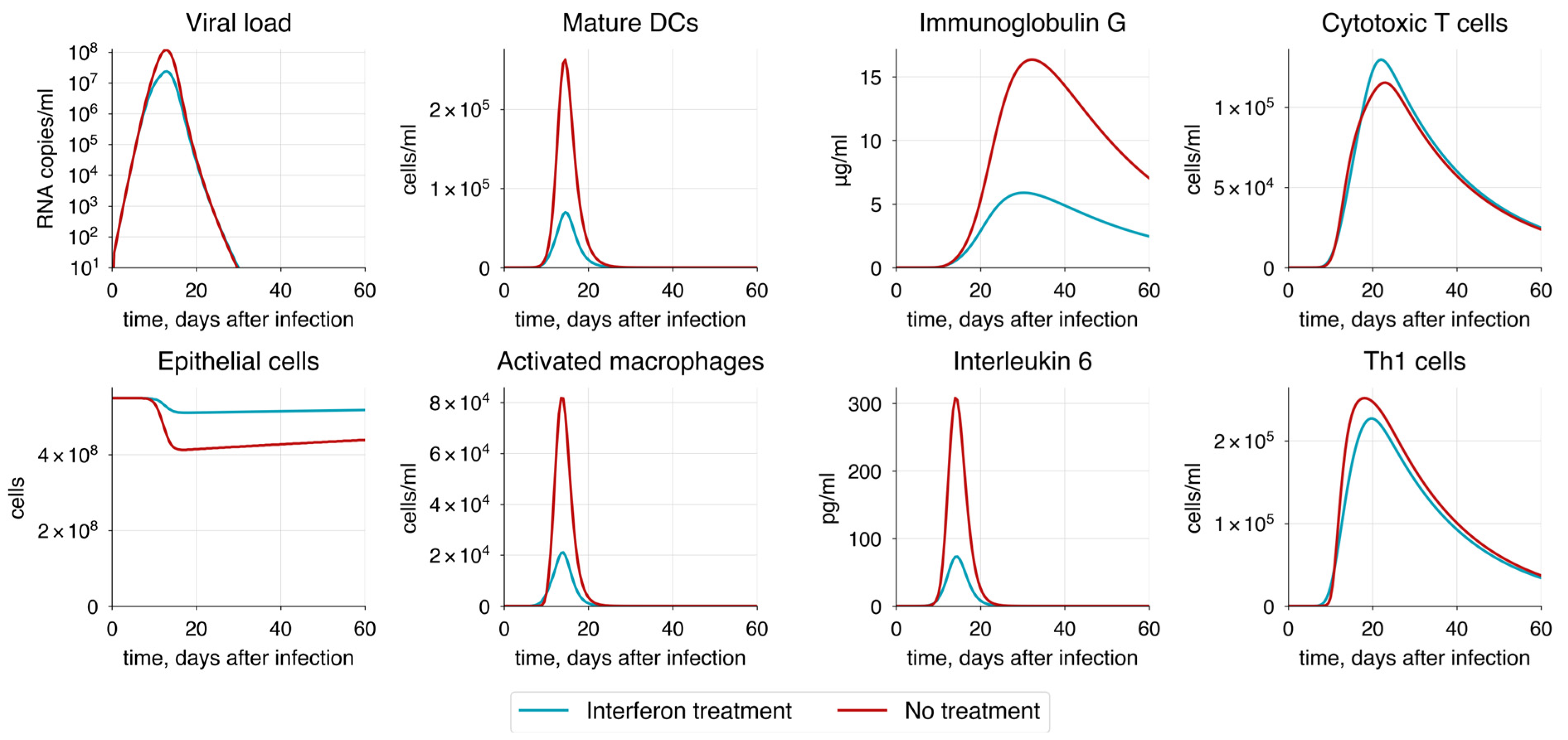
| Interferon administration | 2000 pg/mL of for 5 days after symptom onset | Decrease | Decrease | Increase | Decrease | Decrease |
| Inhibited viral replication | Reduce the efficiency of viral replication by 25% each day for 5 days after the onset of symptoms | Decrease | Decrease | Increase | Decrease | Decrease |
| Model | DE | Parameters | Modules | Adaptive immunity | Innate Immunity | Experimental Data and Dataset Sizes |
|---|---|---|---|---|---|---|
| Current model | 35 | 112 (59) | 4 | + | + | V (UA: 232, L: 56), CD4/8 (12, 6), Ig (A: 677, G: 695, M: 676), IL-6: 14 B* (CD4, CD8, B) |
| Leander et al., 2021 [13] | 14 | 39 (10) | 1 | - | + | V (UA): 11 |
| Du at al., 2020 [19] | 3 | 21 (21) | 1 | + | - | - |
| Wang et al., 2021 [20] | 7 | 40 (31) | 3 | + | + | T: 410 |
| Grebennikov et al., 2021 [22] | 12 | 54 | 1 | + | + | V (UA): 38 B* (IFN, Ig, CD8) |
| Zhou et al., 2023 [23] | 32 | 181 (129) | 1 | + | + | B* (Cytokines) |
| Palsson et al., 2013 [34] | 55 | 171 (103) | 4 | + | + | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miroshnichenko, M.I.; Kolpakov, F.A.; Akberdin, I.R. A Modular Mathematical Model of the Immune Response for Investigating the Pathogenesis of Infectious Diseases. Viruses 2025, 17, 589. https://doi.org/10.3390/v17050589
Miroshnichenko MI, Kolpakov FA, Akberdin IR. A Modular Mathematical Model of the Immune Response for Investigating the Pathogenesis of Infectious Diseases. Viruses. 2025; 17(5):589. https://doi.org/10.3390/v17050589
Chicago/Turabian StyleMiroshnichenko, Maxim I., Fedor A. Kolpakov, and Ilya R. Akberdin. 2025. "A Modular Mathematical Model of the Immune Response for Investigating the Pathogenesis of Infectious Diseases" Viruses 17, no. 5: 589. https://doi.org/10.3390/v17050589
APA StyleMiroshnichenko, M. I., Kolpakov, F. A., & Akberdin, I. R. (2025). A Modular Mathematical Model of the Immune Response for Investigating the Pathogenesis of Infectious Diseases. Viruses, 17(5), 589. https://doi.org/10.3390/v17050589






