Non-Linear Pharmacokinetics of Oral Roscovitine (Seliciclib) in Cystic Fibrosis Patients Chronically Infected with Pseudomonas aeruginosa: A Study on Population Pharmacokinetics with Monte Carlo Simulations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Investigational Drug
2.2. Study Design and Population
2.3. Sample Collection and Analysis
2.4. Genotyping
2.5. Pharmacokinetic Model Development and Evaluation
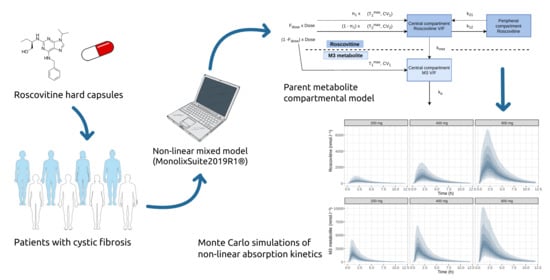
2.6. Monte Carlo Simulations
3. Results
3.1. Population Description
3.2. Population Pharmacokinetic Model
3.3. Monte Carlo Simulations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. MLXTRAN Model File
| [LONGITUDINAL] |
| input = {D50, f1, Tmax_1, dTmax_2, CV_1, CV_2, V, k21, k12, kmet, ke} |
| EQUATION: |
| pi = 3.14159265358979 |
| ;dose-dependent first-pass effect |
| Fr = amtDose/(amtDose + D50) |
| Tmax_3 = Tmax_1 |
| CV_3 = CV_1 |
| ;inverse gaussian distribution absorption |
| MAT_1 = Tmax_1/(sqrt(1+9/4*(CV_1^4))-3/2*(CV_1^2)) |
| MAT_2 = (Tmax_1+dTmax_2)/(sqrt(1+9/4*(CV_2^4))-3/2*(CV_2^2)) |
| MAT_3 = Tmax_3/(sqrt(1+9/4*(CV_3^4))-3/2*(CV_3^2)) |
| inv_gauss_1 = Fr*amtDose*f1*sqrt(MAT_1/(2*pi*(CV_1^2)*(t^3)))*exp(-((t-MAT_1)^2)/(2*(CV_1^2)*MAT_1*t)) |
| inv_gauss_2 = Fr*amtDose*(1-f1)*sqrt(MAT_2/(2*pi*(CV_2^2)*(t^3)))*exp(-((t-MAT_2)^2)/(2*(CV_2^2)*MAT_2*t)) |
| inv_gauss_3 = (1-Fr)*amtDose*sqrt(MAT_3/(2*pi*(CV_3^2)*(t^3)))*exp(-((t-MAT_3)^2)/(2*(CV_3^2)*MAT_3*t)) |
| ;ODE |
| if t < tDose |
| dArosco = 0 |
| else |
| dArosco = inv_gauss_1 + inv_gauss_2 - kmet*Arosco + k21*Aroscop - k12*Arosco |
| dAroscop = k12*Arosco - k21*Aroscop |
| end |
| if t < tDose |
| dAM3 = 0 |
| else |
| dAM3 = kmet*Arosco + inv_gauss_3 − ke*AM3 |
| end |
| ddt_Arosco = dArosco |
| ddt_Aroscop = dAroscop |
| ddt_AM3 = dAM3 |
| ;V/F in litres |
| C_rosco = Arosco/V*1000 |
| C_M3 = AM3/V*1000 |
| ;AUC |
| AUC_rosco_0 = 0 |
| ddt_AUC_rosco = C_rosco |
| AUC_M3_0 = 0 |
| ddt_AUC_M3 = C_M3 |
| OUTPUT: |
| output = {C_rosco, C_M3} |
References
- Tsui, L.C.; Buchwald, M.; Barker, D.; Braman, J.C.; Knowlton, R.; Schumm, J.W.; Eiberg, H.; Mohr, J.; Kennedy, D.; Plavsic, N. Cystic fibrosis locus defined by a genetically linked polymorphic DNA marker. Science 1985, 230, 1054–1057. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rey, M.M.; Bonk, M.P.; Hadjiliadis, D. Cystic Fibrosis: Emerging Understanding and Therapies. Annu. Rev. Med. 2019, 70, 197–210. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, K.D.; McKenzie, K.R.; Zeitlin, P.L. Cystic fibrosis transmembrane regulator protein mutations: ‘class’ opportunity for novel drug innovation. Paediatr. Drugs 2007, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Ramsey, B.W.; Davies, J.; McElvaney, N.G.; Tullis, E.; Bell, S.C.; Dřevínek, P.; Griese, M.; McKone, E.F.; Wainwright, C.E.; Konstan, M.W.; et al. A CFTR potentiator in patients with cystic fibrosis and the G551D mutation. N. Engl. J. Med. 2011, 365, 1663–1672. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keating, D.; Marigowda, G.; Burr, L.; Daines, C.; Mall, M.A.; McKone, E.F.; Ramsey, B.W.; Rowe, S.M.; Sass, L.A.; Tullis, E.; et al. VX-445-Tezacaftor-Ivacaftor in Patients with Cystic Fibrosis and One or Two Phe508del Alleles. N. Engl. J. Med. 2018, 379, 1612–1620. [Google Scholar] [CrossRef]
- Waters, V.; Ratjen, F. Multidrug-resistant organisms in cystic fibrosis: Management and infection-control issues. Expert Rev. Anti-Infect. Ther. 2006, 4, 807–819. [Google Scholar] [CrossRef]
- Meijer, L.; Nelson, D.J.; Riazanski, V.; Gabdoulkhakova, A.G.; Hery-Arnaud, G.; Le Berre, R.; Loaëc, N.; Oumata, N.; Galons, H.; Nowak, E.; et al. Modulating innate and adaptative immunity by (R)-roscovitine: Potential therapeutic opportunity in cystic fibrosis. J. Innate Immun. 2016, 8, 330–349. [Google Scholar] [CrossRef]
- Norez, C.; Vandebrouck, C.; Bertrand, J.; Noel, S.; Durieu, E.; Oumata, N.; Galons, H.; Antigny, F.; Chtelier, A.; Bois, P.; et al. Roscovitine is a proteostasis regulator that corrects the trafficking defect of F508del-CFTR by a CDK-independent mechanism. Br. J. Pharmacol. 2014, 171, 4831–4849. [Google Scholar] [CrossRef]
- Riazanski, V.; Gabdulkhakova, A.G.; Boynton, L.S.; Eguchi, R.R.; Deriy, L.V.; Hogarth, D.K.; Loaëc, N.; Oumata, N.; Galons, H.; Brown, M.E.; et al. TRPC6 channel translocation into phagosomal membrane augments phagosomal function. Proc. Natl. Acad. Sci. USA 2015, 112, 6486–6495. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, E.; Lavielle, M. Coupling a stochastic approximation version of EM with an MCMC procedure. EDP Sci. 2004, 8, 115–131. [Google Scholar] [CrossRef] [Green Version]
- Beal, S.L. Ways to Fit a PK Model with Some Data Below the Quantification Limit. J. Pharm. Pharm. 2001, 28, 481–504. [Google Scholar]
- Savic, R.M.; Jonker, D.M.; Kerbusch, T.; Karlsson, M.O. Implementation of a transit compartment model for describing drug absorption in pharmacokinetic studies. J. Pharm. Pharm. 2007, 34, 711–726. [Google Scholar] [CrossRef] [PubMed]
- Wood, J.H.; Thakker, K.M. Michaelis-menten absorption kinetics in drugs: Examples and implications. Eur. J. Clin. Pharmacol. 1982, 23, 183–188. [Google Scholar] [CrossRef] [PubMed]
- Csajka, C.; Drover, D.; Verotta, D. The Use of a Sum of Inverse Gaussian Functions to Describe the Absorption Profile of Drugs Exhibiting Complex Absorption. Pharm. Res. 2005, 22, 1227–1235. [Google Scholar] [CrossRef] [PubMed]
- Weiss, M. A Novel Extravascular Input Function for the Assessment of Drug Absorption in Bioavailability Studies. Pharm. Res. 1996, 13, 1547–1553. [Google Scholar] [CrossRef] [PubMed]
- Delattre, M.; Lavielle, M.; Poursat, M.-A. A note on BIC in mixed-effects models. Electron. J. Statist. 2014, 8, 456–475. [Google Scholar] [CrossRef]
- Bergstrand, M.; Hooker, A.C.; Wallin, J.E.; Karlsson, M.O. Prediction-Corrected Visual Predictive Checks for Diagnosing Nonlinear Mixed-Effects Models. AAPS J. 2011, 13, 143–151. [Google Scholar] [CrossRef] [Green Version]
- Comets, E.; Brendel, K.; Mentré, F. Computing normalised prediction distribution errors to evaluate nonlinear mixed-effect models: The npde add-on package for R. Comput. Methods Programs Biomed. 2008, 90, 154–166. [Google Scholar] [CrossRef] [Green Version]
- Ollier, E.; Hodin, S.; Lanoiselée, J.; Escal, J.; Accassat, S.; De Magalhaes, E.; Basset, T.; Bertoletti, L.; Mismetti, P.; Delavenne, X.; et al. Effect of Activated Charcoal on Rivaroxaban Complex Absorption. Clin. Pharm. 2017, 56, 793–801. [Google Scholar] [CrossRef]
- Wendling, T.; Ogungbenro, K.; Pigeolet, E.; Dumitras, S.; Woessner, R.; Aarons, L. Model-Based Evaluation of the Impact of Formulation and Food Intake on the Complex Oral Absorption of Mavoglurant in Healthy Subjects. Pharm Res. 2015, 32, 1764–1778. [Google Scholar] [CrossRef]
- Benson, C.; White, J.; Bono, J.D.; O’Donnell, A.; Raynaud, F.; Cruickshank, C.; McGrath, H.; Walton, M.; Workman, P.; Kaye, S.; et al. A phase I trial of the selective oral cyclin-dependent kinase inhibitor seliciclib (CYC202; R-Roscovitine), administered twice daily for 7 days every 21 days. Br. J. Cancer 2007, 96, 29–37. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hsieh, W.-S.; Soo, R.; Peh, B.-K.; Loh, T.; Dong, D.; Soh, D.; Wong, L.-S.; Green, S.; Chiao, J.; Cui, C.-Y.; et al. Pharmacodynamic Effects of Seliciclib, an Orally Administered Cell Cycle Modulator, in Undifferentiated Nasopharyngeal Cancer. Clin. Cacer Res. 2009, 15, 1435–1442. [Google Scholar] [CrossRef] [Green Version]
- De la Motte, S.; Gianella-Borradori, A. Pharmacokinetic model of R-roscovitine and its metabolite in healthy male subjects. Int. J. Clin. Pharmacol. Ther. 2004, 42, 232–239. [Google Scholar] [CrossRef]
- Pohl, O.; Osterloh, I.; Lecomte, V.; Gotteland, J.-P. Changes in gastric pH and in pharmacokinetics of ulipristal acetate—A drug-drug interaction study using the proton pump inhibitor esomeprazole. Int. J. Clin. Pharm. Ther. 2013, 51, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Yin, O.Q.P.; Gallagher, N.; Fischer, D.; Demirhan, E.; Zhou, W.; Golor, G.; Schran, H. Effect of the Proton Pump Inhibitor Esomeprazole on the Oral Absorption and Pharmacokinetics of Nilotinib. J. Clin. Pharmacol. 2010, 50, 960–967. [Google Scholar] [CrossRef] [PubMed]
- McClue, S.J.; Stuart, I. Metabolism of the Trisubstituted Purine Cyclin-Dependent Kinase Inhibitor Seliciclib (R-Roscovitine) in Vitro and in Vivo. Drug Metab. Dispos. 2008, 36, 561–570. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rajnai, Z.; Méhn, D.; Beéry, E.; Okyar, A.; Jani, M.; Tóth, G.K.; Fülöp, F.; Lévi, F.; Krajcsi, P. ATP-Binding Cassette B1 Transports Seliciclib (R -Roscovitine), a Cyclin-Dependent Kinase Inhibitor. Drug Metab. Dispos. 2010, 38, 2000–2006. [Google Scholar] [CrossRef]
- Nyberg, J.; Bazzoli, C.; Ogungbenro, K.; Aliev, A.; Leonov, S.; Duffull, S.; Hooker, A.C.; Mentré, F. Methods and software tools for design evaluation in population pharmacokinetics–pharmacodynamics studies. Br. J. Clin. Pharmacol. 2015, 79, 6–17. [Google Scholar] [CrossRef] [Green Version]










| Number of Data Points | Global | 200 mg Group | 400 mg Group | 800 mg Group |
|---|---|---|---|---|
| Total roscovitine | 138 | 57 | 42 | 49 |
| • Average per subject | 6 | 6.3 | 6 | 5.6 |
| • Minimum per subject | 4 | 4 | 6 | 4 |
| • Maximum per subject | 7 | 7 | 6 | 6 |
| • Total roscovitine BLQ | 19 | 19 | 0 | 0 |
| Total carboxylate metabolite M3 | 138 | 57 | 42 | 49 |
| • Average per subject | 6 | 6.3 | 6 | 5.6 |
| • Minimum per subject | 4 | 4 | 6 | 4 |
| • Maximum per subject | 7 | 7 | 6 | 6 |
| • Total carboxylate metabolite M3 BLQ | 9 | 9 | 0 | 0 |
| Global | 200 mg Group | 400 mg Group | 800 mg Group | |
|---|---|---|---|---|
| Number of subjects | 23 | 9 | 7 | 7 |
| Sex (F) | 10 | 3 | 4 | 3 |
| Age (years) | 33 (22–51) | 32 (22–50) | 33 (22–41) | 37 (28–51) |
| Weight (kg) | 58 (48–90) | 58 (51–90) | 56 (49–78) | 59 (48–80) |
| Height (cm) | 166 (158–182) | 169 (158–182) | 165 (158–182) | 173 (162–182) |
| Glomerular filtration rate (mL·min⁻1) | 113 (61–202) | 125 (92–202) | 113 (72–144) | 107 (61–135) |
| Proton pump inhibitors | 15 | 4 | 4 | 7 |
| Parameters | Population Parameters Estimates | ||
|---|---|---|---|
| Value | %RSE | %Shrinkage | |
| Fixed Effects | |||
| D50 (µmol) | 1190 | 16.5 | |
| π1 | 0.285 | 0.378 | |
| T1max (h) | 0.676 | 14.6 | |
| β (PPI = 1) on T1max | 0.680 | 23.4 | |
| dT2max (h) | 1.04 | 16.3 | |
| CV1 | 0.542 | 10.3 | |
| CV2 | 0.354 | 14.1 | |
| V/F (liters) | 62.2 | 15.4 | |
| β height (cm) on V | 6.47 | 48.3 | |
| k21 (h−1) | 0.768 | 0.206 | |
| k12 (h−1) | 1.82 | 0.636 | |
| kmet (h−1) | 2.07 | 1.13 | |
| ke (h−1) | 2.58 | 9.86 | |
| Inter-patient variability standard deviation | |||
| ω D50 | 0.689 | 18.6 | 7.83 |
| ω T1max | 0.452 | 16.2 | 4.37 |
| ω dT2max | 0.647 | 23.9 | 21.1 |
| ω CV1 | 0.426 | 21.1 | 24.1 |
| ω CV2 | 0.547 | 21.7 | 17.5 |
| ω V/F | 0.678 | 15.7 | −2.28 |
| ω ke | 0.393 | 19.6 | 20.5 |
| Correlations between random effects | |||
| Corr. T1max CV2 | −0.839 | 14 | |
| Corr. dT2max CV1 | 0.624 | 31.8 | |
| Error model parameters | |||
| Roscovitine b1 | 0.297 | 10.3 | |
| M3 a2 (nmol·L−1) | 9.20 | 22.3 | |
| M3 b2 | 0.271 | 10.7 | |
| ε-shrinkage for roscovitine | 20.4% | ||
| ε-shrinkage for metabolite M3 | 22.8% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leven, C.; Schutz, S.; Audrezet, M.-P.; Nowak, E.; Meijer, L.; Montier, T. Non-Linear Pharmacokinetics of Oral Roscovitine (Seliciclib) in Cystic Fibrosis Patients Chronically Infected with Pseudomonas aeruginosa: A Study on Population Pharmacokinetics with Monte Carlo Simulations. Pharmaceutics 2020, 12, 1087. https://doi.org/10.3390/pharmaceutics12111087
Leven C, Schutz S, Audrezet M-P, Nowak E, Meijer L, Montier T. Non-Linear Pharmacokinetics of Oral Roscovitine (Seliciclib) in Cystic Fibrosis Patients Chronically Infected with Pseudomonas aeruginosa: A Study on Population Pharmacokinetics with Monte Carlo Simulations. Pharmaceutics. 2020; 12(11):1087. https://doi.org/10.3390/pharmaceutics12111087
Chicago/Turabian StyleLeven, Cyril, Sacha Schutz, Marie-Pierre Audrezet, Emmanuel Nowak, Laurent Meijer, and Tristan Montier. 2020. "Non-Linear Pharmacokinetics of Oral Roscovitine (Seliciclib) in Cystic Fibrosis Patients Chronically Infected with Pseudomonas aeruginosa: A Study on Population Pharmacokinetics with Monte Carlo Simulations" Pharmaceutics 12, no. 11: 1087. https://doi.org/10.3390/pharmaceutics12111087
APA StyleLeven, C., Schutz, S., Audrezet, M.-P., Nowak, E., Meijer, L., & Montier, T. (2020). Non-Linear Pharmacokinetics of Oral Roscovitine (Seliciclib) in Cystic Fibrosis Patients Chronically Infected with Pseudomonas aeruginosa: A Study on Population Pharmacokinetics with Monte Carlo Simulations. Pharmaceutics, 12(11), 1087. https://doi.org/10.3390/pharmaceutics12111087