Adoption of Machine Learning in Pharmacometrics: An Overview of Recent Implementations and Their Considerations
Abstract
:1. Introduction
1.1. Background
1.2. Structure of This Review
1.3. Literature Search
2. Data Preparation
2.1. Data Imputation
2.1.1. Standard Methods for Data Imputation
2.1.2. Machine Learning Methods for Data Imputation
2.1.3. Considerations
2.2. Dimensionality Reduction
Considerations
3. Hypothesis Generation
3.1. Discovery of Patient Sub-Populations
Considerations
3.2. Covariate Selection
3.2.1. Limitations of Stepwise Covariate Selection Methods
3.2.2. Linear Machine Learning Methods
3.2.3. Tree-Based Methods
3.2.4. Genetic Algorithms
3.3. Considerations
4. Predictive Models
4.1. Machine Learning for Pharmacokinetic Modelling
4.1.1. Evaluation of Different Approaches
4.1.2. Considerations
4.2. Machine Learning for Predicting Treatment Effects
4.2.1. Exposure-Response Modelling
4.2.2. Survival Analysis
4.2.3. Considerations
5. Model Validation
5.1. Choosing a Validation Strategy
5.1.1. Options for Estimating Model Generalizability
5.1.2. Considerations
5.2. Model Interpretation
Considerations
6. Main Points
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AUC | Area under the concentration time curve |
| DeepLIFT | Deep learning important features |
| EM | Expectation maximization |
| GAN | Generative adverserial network |
| GP | Gaussian Process |
| IIV | inter-individual variation |
| k-NN | k-nearest neighbour |
| LASSO | Least absolute shrinkage and selection operator |
| LIME | local interpretable model agnostic explanations |
| LOOCV | Leave-one-out cross validation |
| MAR | Missing at random |
| MARS | Multivariate adaptive regression splines |
| MCAR | Missing completely at random |
| MICE | Multiple imputation by chained equations |
| ML | Machine learning |
| MNAR | Missing not at random |
| NLME | Non-linear mixed effect |
| ODE | Ordinary differential equation |
| PCA | Principal component analysis |
| PD | Pharmacodynamic |
| PK | Pharmacokinetic |
| SCM | Stepwise covariate modelling |
| SHAP | Shapley additive explanations |
| t-SNE | t-distributed stochastic neighbour embedding |
| UMAP | Uniform manifold approximation and projection |
| VAE | Variational autoencoder |
Appendix A. Machine Learning for Covariate Selection
Appendix A.1. Data
Appendix A.2. Models
Appendix B. Neural Network for Drug Concentration Prediction
Appendix B.3. Data
Appendix B.4. Prediction of Warfarin Concentrations
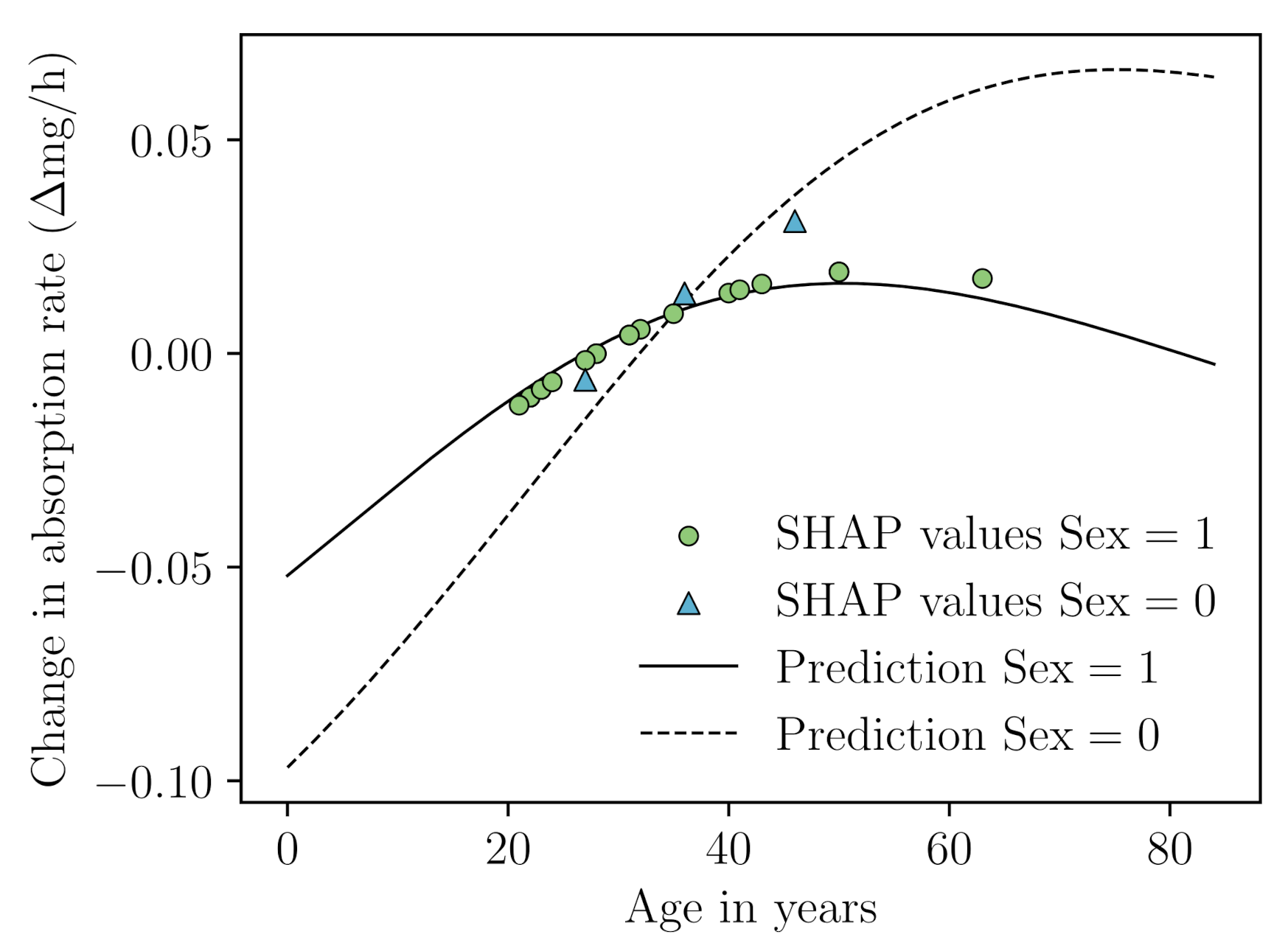
Appendix B.5. SHAP Analysis
References
- Beal, S.L.; Sheiner, L.B. Estimating population kinetics. Crit. Rev. Biomed. Eng. 1982, 8, 195–222. [Google Scholar] [PubMed]
- Lindstrom, M.J.; Bates, D.M. Nonlinear mixed effects models for repeated measures data. Biometrics 1990, 46, 673–687. [Google Scholar] [CrossRef] [PubMed]
- Racine-Poon, A.; Smith, A.F. Population models. Stat. Methodol. Pharm. Sci. 1990, 1, 139–162. [Google Scholar]
- Chaturvedula, A.; Calad-Thomson, S.; Liu, C.; Sale, M.; Gattu, N.; Goyal, N. Artificial intelligence and pharmacometrics: Time to embrace, capitalize, and advance? CPT: Pharmacometrics Syst. Pharmacol. 2019, 8, 440. [Google Scholar] [CrossRef]
- McComb, M.; Bies, R.; Ramanathan, M. Machine learning in pharmacometrics: Opportunities and challenges. Br. J. Clin. Pharmacol. 2021, 88, 1482–1499. [Google Scholar] [CrossRef]
- Osareh, A.; Shadgar, B. Machine learning techniques to diagnose breast cancer. In Proceedings of the IEEE 2010 5th International Symposium on Health Informatics and Bioinformatics, Antalya, Turkey, 20–22 April 2010; pp. 114–120. [Google Scholar]
- van IJzendoorn, D.G.; Szuhai, K.; Briaire-de Bruijn, I.H.; Kostine, M.; Kuijjer, M.L.; Bovée, J.V. Machine learning analysis of gene expression data reveals novel diagnostic and prognostic biomarkers and identifies therapeutic targets for soft tissue sarcomas. PLoS Comput. Biol. 2019, 15, e1006826. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.B.; Blackstone, E.H.; Lauer, M.S. Random survival forests. Ann. Appl. Stat. 2008, 2, 841–860. [Google Scholar] [CrossRef]
- Badillo, S.; Banfai, B.; Birzele, F.; Davydov, I.I.; Hutchinson, L.; Kam-Thong, T.; Siebourg-Polster, J.; Steiert, B.; Zhang, J.D. An introduction to machine learning. Clin. Pharmacol. Ther. 2020, 107, 871–885. [Google Scholar] [CrossRef]
- Wu, H.; Wu, L. A multiple imputation method for missing covariates in non-linear mixed-effects models with application to HIV dynamics. Stat. Med. 2001, 20, 1755–1769. [Google Scholar] [CrossRef]
- Johansson, Å.M.; Karlsson, M.O. Comparison of methods for handling missing covariate data. AAPS J. 2013, 15, 1232–1241. [Google Scholar] [CrossRef]
- Bräm, D.S.; Nahum, U.; Atkinson, A.; Koch, G.; Pfister, M. Opportunities of Covariate Data Imputation with Machine Learning for Pharmacometricians in R. In Proceedings of the 30th Annual Meeting of the Population Approach Group in Europe. Abstract 9982. 2022. Available online: www.page-meeting.org/?abstract=9982 (accessed on 15 July 2022).
- Batista, G.E.; Monard, M.C. An analysis of four missing data treatment methods for supervised learning. Appl. Artif. Intell. 2003, 17, 519–533. [Google Scholar] [CrossRef]
- Stekhoven, D.J.; Bühlmann, P. MissForest—Non-parametric missing value imputation for mixed-type data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef] [PubMed]
- Shah, A.D.; Bartlett, J.W.; Carpenter, J.; Nicholas, O.; Hemingway, H. Comparison of random forest and parametric imputation models for imputing missing data using MICE: A CALIBER study. Am. J. Epidemiol. 2014, 179, 764–774. [Google Scholar] [CrossRef]
- Jin, L.; Bi, Y.; Hu, C.; Qu, J.; Shen, S.; Wang, X.; Tian, Y. A comparative study of evaluating missing value imputation methods in label-free proteomics. Sci. Rep. 2021, 11, 1–11. [Google Scholar] [CrossRef] [PubMed]
- van Buuren, S.; Oudshoorn, K. Flexible Multivariate Imputation by MICE; TNO Public Health Institution: Leiden, The Netherlands, 1999. [Google Scholar]
- Yoon, J.; Jordon, J.; Schaar, M. Gain: Missing data imputation using generative adversarial nets. In Proceedings of the International Conference on Machine Learning (PMLR), Stockholm, Sweden, 10–15 July 2018; pp. 5689–5698. [Google Scholar]
- Mattei, P.A.; Frellsen, J. MIWAE: Deep generative modelling and imputation of incomplete datasets. In Proceedings of the International Conference on Machine Learning (PMLR), Long Beach, CA, USA, 9–15 June 2019; pp. 4413–4423. [Google Scholar]
- Jafrasteh, B.; Hernández-Lobato, D.; Lubián-López, S.P.; Benavente-Fernández, I. Gaussian Processes for Missing Value Imputation. arXiv 2022, arXiv:2204.04648. [Google Scholar] [CrossRef]
- Lopes, T.J.; Rios, R.; Nogueira, T.; Mello, R.F. Prediction of hemophilia A severity using a small-input machine-learning framework. NPJ Syst. Biol. Appl. 2021, 7, 1–8. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2565–2579. [Google Scholar]
- Xiang, R.; Wang, W.; Yang, L.; Wang, S.; Xu, C.; Chen, X. A comparison for dimensionality reduction methods of single-cell RNA-seq data. Front. Genet. 2021, 12, 6936. [Google Scholar] [CrossRef]
- Becht, E.; McInnes, L.; Healy, J.; Dutertre, C.A.; Kwok, I.W.; Ng, L.G.; Ginhoux, F.; Newell, E.W. Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol. 2019, 37, 38–44. [Google Scholar] [CrossRef]
- Ciuculete, D.M.; Bandstein, M.; Benedict, C.; Waeber, G.; Vollenweider, P.; Lind, L.; Schiöth, H.B.; Mwinyi, J. A genetic risk score is significantly associated with statin therapy response in the elderly population. Clin. Genet. 2017, 91, 379–385. [Google Scholar] [CrossRef] [PubMed]
- Kanders, S.H.; Pisanu, C.; Bandstein, M.; Jonsson, J.; Castelao, E.; Pistis, G.; Gholam-Rezaee, M.; Eap, C.B.; Preisig, M.; Schiöth, H.B.; et al. A pharmacogenetic risk score for the evaluation of major depression severity under treatment with antidepressants. Drug Dev. Res. 2020, 81, 102–113. [Google Scholar] [CrossRef] [PubMed]
- Zwep, L.B.; Duisters, K.L.; Jansen, M.; Guo, T.; Meulman, J.J.; Upadhyay, P.J.; van Hasselt, J.C. Identification of high-dimensional omics-derived predictors for tumor growth dynamics using machine learning and pharmacometric modeling. CPT Pharmacometrics Syst. Pharmacol. 2021, 10, 350–361. [Google Scholar] [CrossRef] [PubMed]
- Kapralos, I.; Dokoumetzidis, A. Population Pharmacokinetic Modelling of the Complex Release Kinetics of Octreotide LAR: Defining Sub-Populations by Cluster Analysis. Pharmaceutics 2021, 13, 1578. [Google Scholar] [CrossRef] [PubMed]
- Paul, R.; Andlauer, T.F.; Czamara, D.; Hoehn, D.; Lucae, S.; Pütz, B.; Lewis, C.M.; Uher, R.; Müller-Myhsok, B.; Ising, M.; et al. Treatment response classes in major depressive disorder identified by model-based clustering and validated by clinical prediction models. Transl. Psychiatry 2019, 9, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Tomás, E.; Vinga, S.; Carvalho, A.M. Unsupervised learning of pharmacokinetic responses. Comput. Stat. 2017, 32, 409–428. [Google Scholar] [CrossRef]
- Bunte, K.; Smith, D.J.; Chappell, M.J.; Hassan-Smith, Z.K.; Tomlinson, J.W.; Arlt, W.; Tiňo, P. Learning pharmacokinetic models for in vivo glucocorticoid activation. J. Theor. Biol. 2018, 455, 222–231. [Google Scholar] [CrossRef]
- Chapfuwa, P.; Li, C.; Mehta, N.; Carin, L.; Henao, R. Survival cluster analysis. In Proceedings of the ACM Conference on Health, Inference, and Learning, Toronto, ON, Canada, 2–4 April 2020; pp. 60–68. [Google Scholar]
- Guerra, R.P.; Carvalho, A.M.; Mateus, P. Model selection for clustering of pharmacokinetic responses. Comput. Methods Programs Biomed. 2018, 162, 11–18. [Google Scholar] [CrossRef]
- Blömer, J.; Bujna, K. Adaptive seeding for Gaussian mixture models. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Auckland, New Zealand, 19–22 April 2016; pp. 296–308. [Google Scholar]
- Harrell, F.E. Regression modeling strategies. Bios 2017, 330, 14. [Google Scholar]
- Ribbing, J.; Jonsson, E.N. Power, selection bias and predictive performance of the Population Pharmacokinetic Covariate Model. J. Pharmacokinet. Pharmacodyn. 2004, 31, 109–134. [Google Scholar] [CrossRef]
- Ribbing, J.; Nyberg, J.; Caster, O.; Jonsson, E.N. The lasso—A novel method for predictive covariate model building in nonlinear mixed effects models. J. Pharmacokinet. Pharmacodyn. 2007, 34, 485–517. [Google Scholar] [CrossRef]
- Ahamadi, M.; Largajolli, A.; Diderichsen, P.M.; de Greef, R.; Kerbusch, T.; Witjes, H.; Chawla, A.; Davis, C.B.; Gheyas, F. Operating characteristics of stepwise covariate selection in pharmacometric modeling. J. Pharmacokinet. Pharmacodyn. 2019, 46, 273–285. [Google Scholar] [CrossRef]
- Tibshirani, R. The lasso method for variable selection in the Cox model. Stat. Med. 1997, 16, 385–395. [Google Scholar] [CrossRef]
- Chan, P.; Zhou, X.; Wang, N.; Liu, Q.; Bruno, R.; Jin, J.Y. Application of Machine Learning for Tumor Growth Inhibition–Overall Survival Modeling Platform. CPT Pharmacometr. Syst. Pharmacol. 2021, 10, 59–66. [Google Scholar] [CrossRef]
- Sibieude, E.; Khandelwal, A.; Hesthaven, J.S.; Girard, P.; Terranova, N. Fast screening of covariates in population models empowered by machine learning. J. Pharmacokinet. Pharmacodyn. 2021, 48, 597–609. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Ki, D.; Fang, B.; Guntuboyina, A. MARS via LASSO. arXiv 2021, arXiv:2111.11694. [Google Scholar]
- Mitov, V.; Kuemmel, A.; Gobeau, N.; Cherkaoui, M.; Bouillon, T. Dose selection by covariate assessment on the optimal dose for efficacy—Application of machine learning in the context of PKPD. In Proceedings of the 30th Annual Meeting of the Population Approach Group in Europe. Abstract 10066. 2022. Available online: www.page-meeting.org/?abstract=10066 (accessed on 15 July 2022).
- Wang, R.; Shao, X.; Zheng, J.; Saci, A.; Qian, X.; Pak, I.; Roy, A.; Bello, A.; Rizzo, J.I.; Hosein, F.; et al. A machine-learning approach to identify a prognostic cytokine signature that is associated with nivolumab clearance in patients with advanced melanoma. Clin. Pharmacol. Ther. 2020, 107, 978–987. [Google Scholar] [CrossRef] [PubMed]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Gong, X.; Hu, M.; Zhao, L. Big data toolsets to pharmacometrics: Application of machine learning for time-to-event analysis. Clin. Transl. Sci. 2018, 11, 305–311. [Google Scholar] [CrossRef] [PubMed]
- Lou, Y.; Caruana, R.; Gehrke, J.; Hooker, G. Accurate intelligible models with pairwise interactions. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 623–631. [Google Scholar]
- Nori, H.; Jenkins, S.; Koch, P.; Caruana, R. InterpretML: A Unified Framework for Machine Learning Interpretability. arXiv 2019, arXiv:1909.09223. [Google Scholar]
- Bies, R.R.; Muldoon, M.F.; Pollock, B.G.; Manuck, S.; Smith, G.; Sale, M.E. A genetic algorithm-based, hybrid machine learning approach to model selection. J. Pharmacokinet. Pharmacodyn. 2006, 33, 195–221. [Google Scholar] [CrossRef] [PubMed]
- Ismail, M.; Sale, M.; Yu, Y.; Pillai, N.; Liu, S.; Pflug, B.; Bies, R. Development of a genetic algorithm and NONMEM workbench for automating and improving population pharmacokinetic/pharmacodynamic model selection. J. Pharmacokinet. Pharmacodyn. 2021, 49, 243–256. [Google Scholar] [CrossRef]
- Sibieude, E.; Khandelwal, A.; Girard, P.; Hesthaven, J.S.; Terranova, N. Population pharmacokinetic model selection assisted by machine learning. J. Pharmacokinet. Pharmacodyn. 2021, 49, 257–270. [Google Scholar] [CrossRef] [PubMed]
- Janssen, A.; Hoogendoorn, M.; Cnossen, M.H.; Mathôt, R.A.; Group, O.C.S.; Consortium, S.; Cnossen, M.; Reitsma, S.; Leebeek, F.; Mathôt, R.; et al. Application of SHAP values for inferring the optimal functional form of covariates in pharmacokinetic modeling. CPT Pharmacometr. Syst. Pharmacol. 2022, 11, 1100–1110. [Google Scholar] [CrossRef]
- Xu, Y.; Lou, H.; Chen, J.; Jiang, B.; Yang, D.; Hu, Y.; Ruan, Z. Application of a backpropagation artificial neural network in predicting plasma concentration and pharmacokinetic parameters of oral single-dose rosuvastatin in healthy subjects. Clin. Pharmacol. Drug Dev. 2020, 9, 867–875. [Google Scholar] [CrossRef]
- Pellicer-Valero, O.J.; Cattinelli, I.; Neri, L.; Mari, F.; Martín-Guerrero, J.D.; Barbieri, C. Enhanced prediction of hemoglobin concentration in a very large cohort of hemodialysis patients by means of deep recurrent neural networks. Artif. Intell. Med. 2020, 107, 101898. [Google Scholar] [CrossRef]
- Huang, X.; Yu, Z.; Bu, S.; Lin, Z.; Hao, X.; He, W.; Yu, P.; Wang, Z.; Gao, F.; Zhang, J.; et al. An Ensemble Model for Prediction of Vancomycin Trough Concentrations in Pediatric Patients. Drug Des. Dev. Ther. 2021, 15, 1549. [Google Scholar] [CrossRef]
- Lu, J.; Deng, K.; Zhang, X.; Liu, G.; Guan, Y. Neural-ODE for pharmacokinetics modeling and its advantage to alternative machine learning models in predicting new dosing regimens. Iscience 2021, 24, 102804. [Google Scholar] [CrossRef]
- Ulas, C.; Das, D.; Thrippleton, M.J.; Valdes Hernandez, M.d.C.; Armitage, P.A.; Makin, S.D.; Wardlaw, J.M.; Menze, B.H. Convolutional neural networks for direct inference of pharmacokinetic parameters: Application to stroke dynamic contrast-enhanced MRI. Front. Neurol. 2019, 9, 1147. [Google Scholar] [CrossRef]
- Gim, J.A.; Kwon, Y.; Lee, H.A.; Lee, K.R.; Kim, S.; Choi, Y.; Kim, Y.K.; Lee, H. A Machine Learning-Based Identification of Genes Affecting the Pharmacokinetics of Tacrolimus Using the DMETTM Plus Platform. Int. J. Mol. Sci. 2020, 21, 2517. [Google Scholar] [CrossRef]
- Tao, Y.; Chen, Y.J.; Xue, L.; Xie, C.; Jiang, B.; Zhang, Y. An ensemble model with clustering assumption for warfarin dose prediction in Chinese patients. IEEE J. Biomed. Health Inform. 2019, 23, 2642–2654. [Google Scholar] [CrossRef]
- Woillard, J.B.; Labriffe, M.; Debord, J.; Marquet, P. Tacrolimus exposure prediction using machine learning. Clin. Pharmacol. Ther. 2021, 110, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Yu, Z.; Wei, X.; Shi, J.; Wang, Y.; Wang, Z.; Chen, J.; Bu, S.; Li, L.; Gao, F.; et al. Prediction of vancomycin dose on high-dimensional data using machine learning techniques. Expert Rev. Clin. Pharmacol. 2021, 14, 761–771. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Liu, C.; Huang, R.; Zhu, H.; Liu, Q.; Mitra, S.; Wang, Y. Long short-term memory recurrent neural network for pharmacokinetic-pharmacodynamic modeling. Int. J. Clin. Pharmacol. Ther. 2020, 59, 138. [Google Scholar] [CrossRef] [PubMed]
- Bräm, D.S.; Parrott, N.; Hutchinson, L.; Steiert, B. Introduction of an artificial neural network–based method for concentration-time predictions. CPT Pharmacometr. Syst. Pharmacol. 2022, 11, 745–754. [Google Scholar] [CrossRef]
- Chen, R.T.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D. Neural ordinary differential equations. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 2–8 December 2018; p. 31. [Google Scholar]
- Janssen, A.; Leebeek, F.W.; Cnossen, M.H.; Mathôt, R.A.A. For the OPTI- CLOT study group and SYMPHONY consortium. Deep compartment models: A deep learning approach for the reliable prediction of time-series data in pharmacokinetic modeling. CPT Pharmacometr. Syst. Pharmacol. 2022, 11, 934–945. [Google Scholar] [CrossRef]
- Janssen, A.; Leebeek, F.W.G.; Cnossen, M.H.; Mathôt, R.A.A. The Neural Mixed Effects algorithm: Leveraging machine learning for pharmacokinetic modelling. In Proceedings of the 29th Annual Meeting of the Population Approach Group in Europe. Abstract 9826. 2021. Available online: www.page-meeting.org/?abstract=9826 (accessed on 19 July 2022).
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and scalable predictive uncertainty estimation using deep ensembles. Adv. Neural Inf. Process. Syst. 2017, 30, 1–12. [Google Scholar]
- Fort, S.; Hu, H.; Lakshminarayanan, B. Deep ensembles: A loss landscape perspective. arXiv 2019, arXiv:1912.02757. [Google Scholar]
- Zou, H.; Banerjee, P.; Leung, S.S.Y.; Yan, X. Application of pharmacokinetic-pharmacodynamic modeling in drug delivery: Development and challenges. Front. Pharmacol. 2020, 11, 997. [Google Scholar] [CrossRef]
- Danhof, M.; de Lange, E.C.; Della Pasqua, O.E.; Ploeger, B.A.; Voskuyl, R.A. Mechanism-based pharmacokinetic-pharmacodynamic (PK-PD) modeling in translational drug research. Trends Pharmacol. Sci. 2008, 29, 186–191. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Bender, B.; Jin, J.Y.; Guan, Y. Deep learning prediction of patient response time course from early data via neural-pharmacokinetic/pharmacodynamic modelling. Nat. Mach. Intell. 2021, 3, 696–704. [Google Scholar] [CrossRef]
- Kurz, D.; Sánchez, C.S.; Axenie, C. Data-driven Discovery of Mathematical and Physical Relations in Oncology Data using Human-understandable Machine Learning. Front. Artif. Intell. 2021, 4, 713690. [Google Scholar] [CrossRef] [PubMed]
- Qian, Z.; Zame, W.R.; van der Schaar, M.; Fleuren, L.M.; Elbers, P. Integrating Expert ODEs into Neural ODEs: Pharmacology and Disease Progression. arXiv 2021, arXiv:2106.02875. [Google Scholar]
- Wong, H.; Alicke, B.; West, K.A.; Pacheco, P.; La, H.; Januario, T.; Yauch, R.L.; de Sauvage, F.J.; Gould, S.E. Pharmacokinetic–pharmacodynamic analysis of vismodegib in preclinical models of mutational and ligand-dependent Hedgehog pathway activation. Clin. Cancer Res. 2011, 17, 4682–4692. [Google Scholar] [CrossRef]
- Randall, E.C.; Emdal, K.B.; Laramy, J.K.; Kim, M.; Roos, A.; Calligaris, D.; Regan, M.S.; Gupta, S.K.; Mladek, A.C.; Carlson, B.L.; et al. Integrated mapping of pharmacokinetics and pharmacodynamics in a patient-derived xenograft model of glioblastoma. Nat. Commun. 2018, 9, 1–13. [Google Scholar] [CrossRef]
- Kong, J.; Lee, H.; Kim, D.; Han, S.K.; Ha, D.; Shin, K.; Kim, S. Network-based machine learning in colorectal and bladder organoid models predicts anti-cancer drug efficacy in patients. Nat. Commun. 2020, 11, 1–13. [Google Scholar] [CrossRef]
- Chiu, Y.C.; Chen, H.I.H.; Zhang, T.; Zhang, S.; Gorthi, A.; Wang, L.J.; Huang, Y.; Chen, Y. Predicting drug response of tumors from integrated genomic profiles by deep neural networks. BMC Med. Genom. 2019, 12, 143–155. [Google Scholar]
- Wang, D.; Hensman, J.; Kutkaite, G.; Toh, T.S.; Galhoz, A.; Dry, J.R.; Saez-Rodriguez, J.; Garnett, M.J.; Menden, M.P.; Dondelinger, F.; et al. A statistical framework for assessing pharmacological responses and biomarkers using uncertainty estimates. Elife 2020, 9, e60352. [Google Scholar] [CrossRef]
- Keyvanpour, M.R.; Shirzad, M.B. An analysis of QSAR research based on machine learning concepts. Curr. Drug Discov. Technol. 2021, 18, 17–30. [Google Scholar] [CrossRef]
- Katzman, J.L.; Shaham, U.; Cloninger, A.; Bates, J.; Jiang, T.; Kluger, Y. DeepSurv: Personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med. Res. Methodol. 2018, 18, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Zame, W.R.; Yoon, J.; van der Schaar, M. Deephit: A deep learning approach to survival analysis with competing risks. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Ren, K.; Qin, J.; Zheng, L.; Yang, Z.; Zhang, W.; Qiu, L.; Yu, Y. Deep recurrent survival analysis. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4798–4805. [Google Scholar]
- Giunchiglia, E.; Nemchenko, A.; van der Schaar, M. RNN-SURV: A deep recurrent model for survival analysis. In Proceedings of the International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; pp. 23–32. [Google Scholar]
- Meira-Machado, L.; de Uña-Álvarez, J.; Cadarso-Suárez, C.; Andersen, P.K. Multi-state models for the analysis of time-to-event data. Stat. Methods Med. Res. 2009, 18, 195–222. [Google Scholar] [CrossRef] [PubMed]
- Gerstung, M.; Papaemmanuil, E.; Martincorena, I.; Bullinger, L.; Gaidzik, V.I.; Paschka, P.; Heuser, M.; Thol, F.; Bolli, N.; Ganly, P.; et al. Precision oncology for acute myeloid leukemia using a knowledge bank approach. Nat. Genet. 2017, 49, 332–340. [Google Scholar] [CrossRef] [PubMed]
- Groha, S.; Schmon, S.M.; Gusev, A. A General Framework for Survival Analysis and Multi-State Modelling. arXiv 2020, arXiv:2006.04893. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning requires rethinking generalization (2016). arXiv 2017, arXiv:1611.03530. [Google Scholar]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the IJCAI, Montreal, ON, Canada, 20–25 August 1995; Volume 14, pp. 1137–1145. [Google Scholar]
- Molinaro, A.M.; Simon, R.; Pfeiffer, R.M. Prediction error estimation: A comparison of resampling methods. Bioinformatics 2005, 21, 3301–3307. [Google Scholar] [CrossRef]
- Gronau, Q.F.; Wagenmakers, E.J. Limitations of Bayesian leave-one-out cross-validation for model selection. Comput. Brain Behav. 2019, 2, 1–11. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, Y.; Xing, F.; McGough, M.; Yang, L. Mdnet: A semantically and visually interpretable medical image diagnosis network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6428–6436. [Google Scholar]
- Singh, A.; Mohammed, A.R.; Zelek, J.; Lakshminarayanan, V. Interpretation of deep learning using attributions: Application to ophthalmic diagnosis. In Proceedings of the Applications of Machine Learning 2020; SPIE: London, UK, 2020; Volume 11511, pp. 39–49. [Google Scholar]
- Shrikumar, A.; Greenside, P.; Kundaje, A. Learning important features through propagating activation differences. In Proceedings of the International Conference on Machine Learning (PMLR), Sydney, Australia, 6–11 August 2017; pp. 3145–3153. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 31, 4768–4777. [Google Scholar]
- Holzinger, A.; Saranti, A.; Molnar, C.; Biecek, P.; Samek, W. Explainable AI methods-a brief overview. In Proceedings of the International Workshop on Extending Explainable AI Beyond Deep Models and Classifiers, Vienna, Austria, 17 July 2020; pp. 13–38. [Google Scholar]
- Ogami, C.; Tsuji, Y.; Seki, H.; Kawano, H.; To, H.; Matsumoto, Y.; Hosono, H. An artificial neural network- pharmacokinetic model and its interpretation using Shapley additive explanations. CPT Pharmacometr. Syst. Pharmacol. 2021, 10, 760–768. [Google Scholar] [CrossRef] [PubMed]
- Hafner, D.; Tran, D.; Lillicrap, T.; Irpan, A.; Davidson, J. Noise contrastive priors for functional uncertainty. In Proceedings of the Uncertainty in Artificial Intelligence (PMLR), Online, 3–6 August 2020; pp. 905–914. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Molnar, C.; König, G.; Herbinger, J.; Freiesleben, T.; Dandl, S.; Scholbeck, C.A.; Casalicchio, G.; Grosse-Wentrup, M.; Bischl, B. General pitfalls of model-agnostic interpretation methods for machine learning models. In Proceedings of the International Workshop on Extending Explainable AI Beyond Deep Models and Classifiers, Vienna, Austria, 17 July 2020; pp. 39–68. [Google Scholar]
- Yang, G.; Ye, Q.; Xia, J. Unbox the black-box for the medical explainable ai via multi-modal and multi-centre data fusion: A mini-review, two showcases and beyond. Inform. Fus. 2022, 77, 29–52. [Google Scholar] [CrossRef] [PubMed]
- Björkman, S.; Oh, M.; Spotts, G.; Schroth, P.; Fritsch, S.; Ewenstein, B.M.; Casey, K.; Fischer, K.; Blanchette, V.S.; Collins, P.W. Population pharmacokinetics of recombinant factor VIII: The relationships of pharmacokinetics to age and body weight. Blood, J. Am. Soc. Hematol. 2012, 119, 612–618. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janssen, A.; Bennis, F.C.; Mathôt, R.A.A. Adoption of Machine Learning in Pharmacometrics: An Overview of Recent Implementations and Their Considerations. Pharmaceutics 2022, 14, 1814. https://doi.org/10.3390/pharmaceutics14091814
Janssen A, Bennis FC, Mathôt RAA. Adoption of Machine Learning in Pharmacometrics: An Overview of Recent Implementations and Their Considerations. Pharmaceutics. 2022; 14(9):1814. https://doi.org/10.3390/pharmaceutics14091814
Chicago/Turabian StyleJanssen, Alexander, Frank C. Bennis, and Ron A. A. Mathôt. 2022. "Adoption of Machine Learning in Pharmacometrics: An Overview of Recent Implementations and Their Considerations" Pharmaceutics 14, no. 9: 1814. https://doi.org/10.3390/pharmaceutics14091814
APA StyleJanssen, A., Bennis, F. C., & Mathôt, R. A. A. (2022). Adoption of Machine Learning in Pharmacometrics: An Overview of Recent Implementations and Their Considerations. Pharmaceutics, 14(9), 1814. https://doi.org/10.3390/pharmaceutics14091814





