Anomalous Water-Sorption Kinetics in ASDs
Abstract
:1. Introduction
2. Modeling
2.1. Diffusion–Relaxation Model
2.2. Viscosity Modeling
2.3. Model Parameters
2.4. Water-Sorption Measurements
3. Results
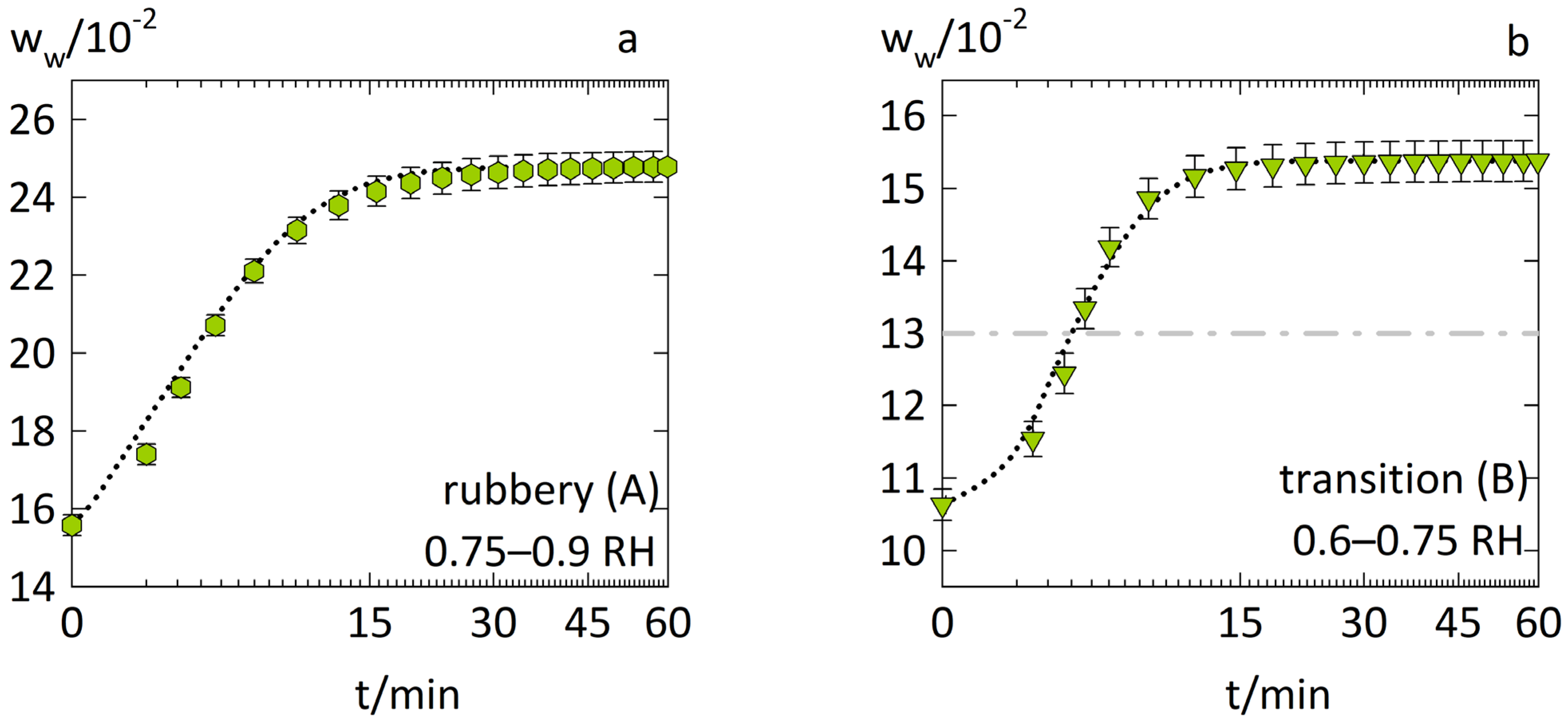
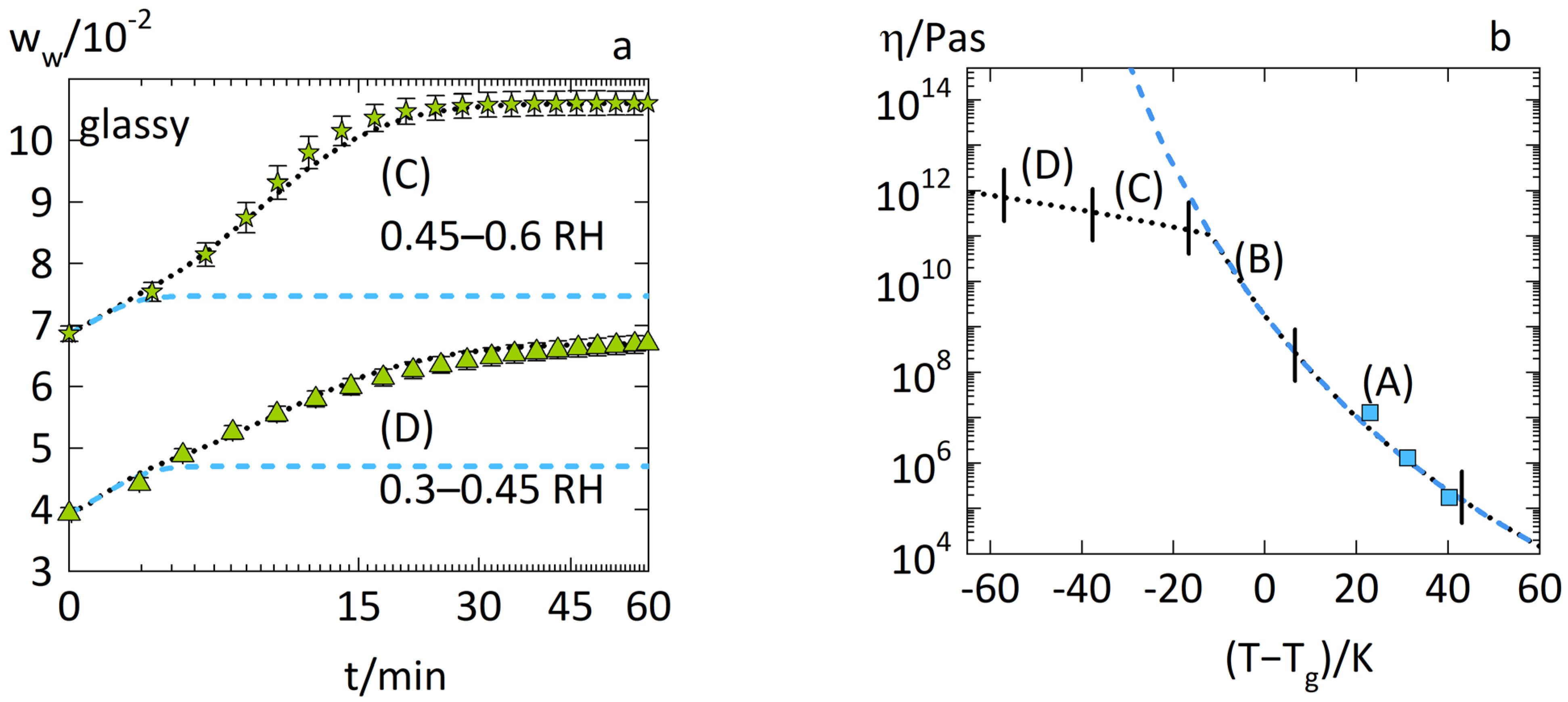
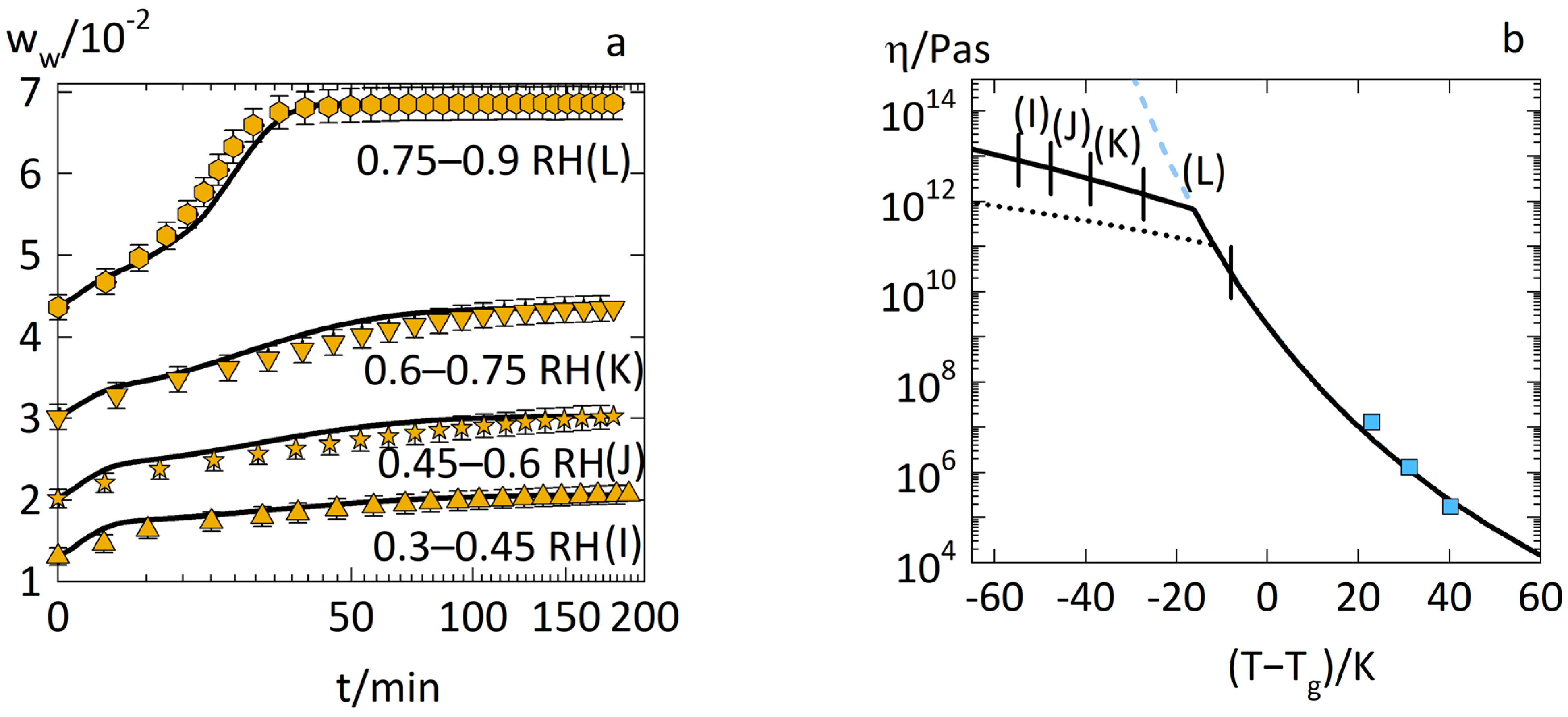
3.1. Anomalous Water-Sorption Kinetics in PVPVA
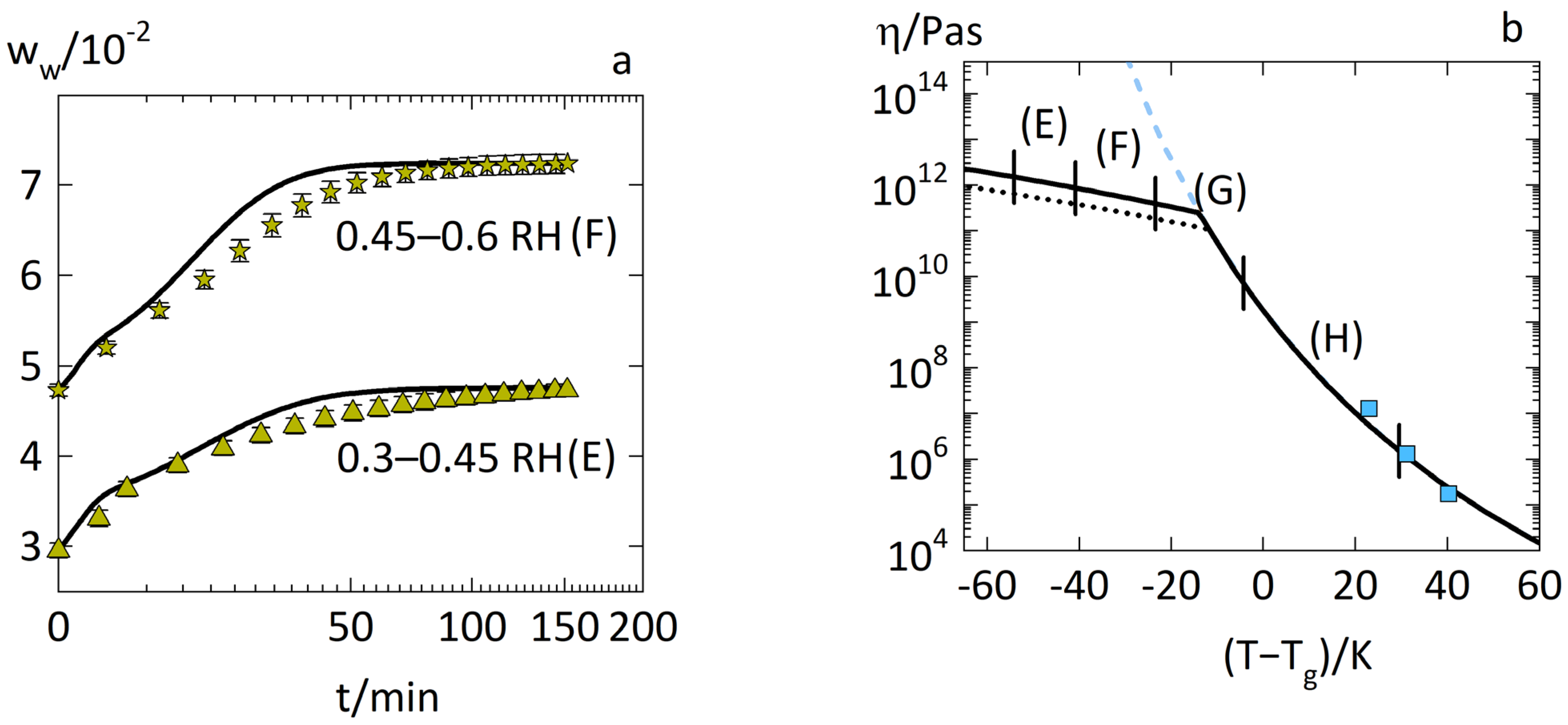
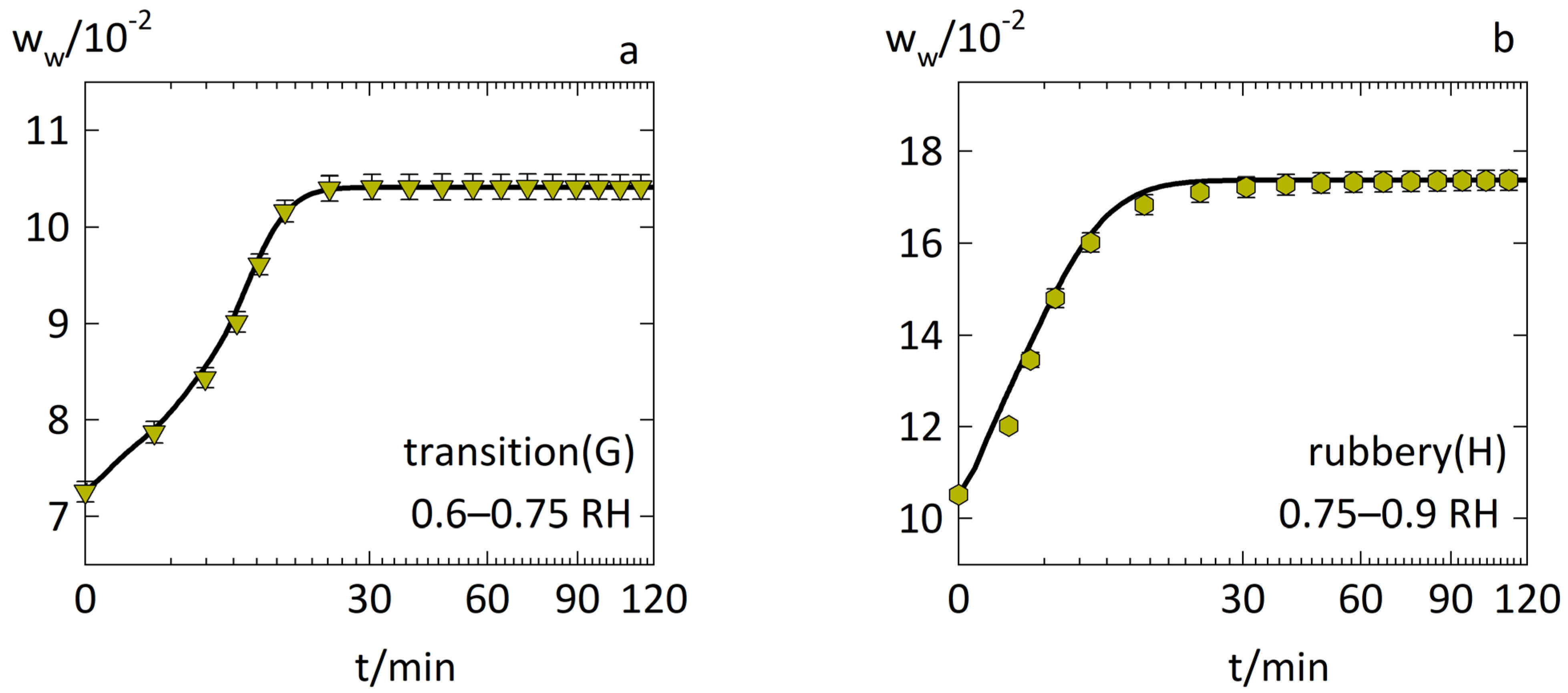
3.2. Anomalous Water-Sorption Kinetics in Low-Drug-Load PVPVA–IND ASDs
3.3. Anomalous Water-Sorption Kinetics in High-Drug-Load PVPVA–IND ASDs
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peppas, N.A.; Narasimhan, B. Mathematical Models in Drug Delivery: How Modeling Has Shaped the Way We Design New Drug Delivery Systems. J. Control. Release 2014, 190, 75–81. [Google Scholar] [CrossRef]
- Korsmeyer, R.W.; Lustig, S.R.; Peppas, N.A. Solute and Penetrant Diffusion in Swellable Polymers. I. Mathematical Modeling. J. Polym. Sci. Part B Polym. Phys. 1986, 24, 395–408. [Google Scholar] [CrossRef]
- Ritger, P.L.; Peppas, N.A. A Simple Equation for Description of Solute Release II. Fickian and Anomalous Release from Swellable Devices. J. Control. Release 1987, 5, 37–42. [Google Scholar] [CrossRef]
- Korsmeyer, R.W.; Peppas, N.A. Solute and Penetrant Diffusion in Swellable Polymers. III. Drug Release from Glassy Poly(HEMA-Co-NVP) Copolymers. J. Control. Release 1984, 1, 89–98. [Google Scholar] [CrossRef]
- Kalam, M.; Humayun, M.; Parvez, N.; Yadav, S. Release Kinetics of Modified Pharmaceutical Dosage Forms: A Review. Cont. J. Pharm. Sci. 2007, 1, 30–35. [Google Scholar]
- Punčochová, K.; Ewing, A.V.; Gajdošová, M.; Sarvašová, N.; Kazarian, S.G.; Beránek, J.; Štěpánek, F. Identifying the Mechanisms of Drug Release from Amorphous Solid Dispersions Using MRI and ATR-FTIR Spectroscopic Imaging. Int. J. Pharm. 2015, 483, 256–267. [Google Scholar] [CrossRef]
- Miller-Chou, B.A.; Koenig, J.L. A Review of Polymer Dissolution. Prog. Polym. Sci. 2003, 28, 1223–1270. [Google Scholar] [CrossRef]
- Van Drooge, D.J.; Hinrichs, W.L.J.; Frijlink, H.W. Anomalous Dissolution Behaviour of Tablets Prepared from Sugar Glass-Based Solid Dispersions. J. Control. Release 2004, 97, 441–452. [Google Scholar] [CrossRef]
- Colombo, P.; Bettini, R.; Peppas, N.A. Observation of Swelling Process and Diffusion Front Position during Swelling in Hydroxypropyl Methyl Cellulose (HPMC) Matrices Containing a Soluble Drug. J. Control. Release 1999, 61, 83–91. [Google Scholar] [CrossRef]
- Brazel, C.S.; Peppas, N.A. Mechanisms of Solute and Drug Transport in Relaxing, Swellable, Hydrophilic Glassy Polymers. Polymer 1999, 40, 3383–3398. [Google Scholar] [CrossRef]
- Borrmann, D.; Danzer, A.; Sadowski, G. Generalized Diffusion–Relaxation Model for Solvent Sorption in Polymers. Ind. Eng. Chem. Res. 2021, 60, 15766–15781. [Google Scholar] [CrossRef]
- Rodríguez, O.; Fornasiero, F.; Arce, A.; Radke, C.J.; Prausnitz, J.M. Solubilities and Diffusivities of Water Vapor in Poly(Methylmethacrylate), Poly(2-Hydroxyethylmethacrylate), Poly(N-Vinyl-2-Pyrrolidone) and Poly(Acrylonitrile). Polymer 2003, 44, 6323–6333. [Google Scholar] [CrossRef]
- Borrmann, D.; Danzer, A.; Sadowski, G. Water Sorption in Glassy Polyvinylpyrrolidone-Based Polymers. Membranes 2022, 12, 434. [Google Scholar] [CrossRef] [PubMed]
- Borrmann, D.; Danzer, A.; Sadowski, G. Predicting the Water Sorption in ASDs. Pharmaceutics 2022, 14, 1181. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zordan, C.; Ponce, S.; Lu, X. Impact of Swelling of Spray Dried Dispersions in Dissolution Media on Their Dissolution: An Investigation Based on UV Imaging. J. Pharm. Sci. 2021, 111, 1761–1769. [Google Scholar] [CrossRef]
- Wolbert, F.; Stecker, J.; Luebbert, C.; Sadowski, G. Viscosity of ASDs at Humid Conditions. Eur. J. Pharm. Biopharm. 2020, 154, 387–396. [Google Scholar] [CrossRef]
- Brinson, H.F.; Brinson, L.C. Polymer Engineering Science and Viscoelasticity, 2nd ed.; Springer: New York, NY, USA, 2008; ISBN 978-1-4899-7484-6. [Google Scholar]
- Hiki, Y. Mechanical Relaxation in Glasses. Mater. Sci. Eng. A 2004, 370, 253–259. [Google Scholar] [CrossRef]
- Hiki, Y.; Kobayashi, H.; Takahashi, H. Shear Viscosity of Inorganic Glasses and Polymers. J. Alloys Compd. 2000, 310, 378–381. [Google Scholar] [CrossRef]
- Baird, J.A.; Taylor, L.S. Evaluation of Amorphous Solid Dispersion Properties Using Thermal Analysis Techniques. Adv. Drug Deliv. Rev. 2012, 64, 396–421. [Google Scholar] [CrossRef]
- Cameretti, L.F.; Sadowski, G. Modeling of Aqueous Amino Acid and Polypeptide Solutions with PC-SAFT. Chem. Eng. Process. Process Intensif. 2008, 47, 1018–1025. [Google Scholar] [CrossRef]
- Lehmkemper, K.; Kyeremateng, S.O.; Heinzerling, O.; Degenhardt, M.; Sadowski, G. Long-Term Physical Stability of PVP- and PVPVA-Amorphous Solid Dispersions. Mol. Pharm. 2017, 14, 157–171. [Google Scholar] [CrossRef] [PubMed]
- Tong, P.; Zografi, G. Solid-State Characteristics of Amorphous Sodium Indomethacin Relative to Its Free Acid. Pharm. Res. 1999, 16, 1186–1192. [Google Scholar] [CrossRef]
- Andronis, V.; Yoshioka, M.; Zografi, G. Effects of Sorbed Water on the Crystallization of Indomethacin from the Amorphous State. J. Pharm. Sci. 1997, 86, 346–351. [Google Scholar] [CrossRef] [PubMed]
- Saito, S.; Bagchi, B.; Ohmine, I. Crucial Role of Fragmented and Isolated Defects in Persistent Relaxation of Deeply Supercooled Water. J. Chem. Phys. 2018, 149, 124504. [Google Scholar] [CrossRef] [PubMed]
- Prudic, A.; Ji, Y.; Sadowski, G. Thermodynamic Phase Behavior of API/Polymer Solid Dispersions. Mol. Pharm. 2014, 11, 2294–2304. [Google Scholar] [CrossRef]
- Correia, N.T.; Moura Ramos, J.J.; Descamps, M.; Collins, G. Molecular Mobility and Fragility in Indomethacin: A Thermally Stimulated Depolarization Current Study. Pharm. Res. 2001, 18, 1767–1774. [Google Scholar] [CrossRef]
- Andronis, V.; Zografi, G. The Molecular Mobility of Supercooled Amorphous Indomethacin as a Function of Temperature and Relative Humidity. Pharm. Res. 1998, 15, 835–842. [Google Scholar] [CrossRef]
- Cassu, S.N.; Felisberti, M.I. Poly(Vinyl Alcohol) and Poly(Vinylpyrrolidone) Blends: 2. Study of Relaxations by Dynamic Mechanical Analysis. Polymer 1999, 40, 4845–4851. [Google Scholar] [CrossRef]
- Mezger, T.G. Das Rheologie Handbuch; Farbe Und Lack: Hannover, Germany, 2019; ISBN 9783748600121. [Google Scholar]
- Taylor, L.S.; Langkilde, F.W.; Zografi, G. Fourier Transform Raman Spectroscopic Study of the Interaction of Water Vapor with Amorphous Polymers. J. Pharm. Sci. 2001, 90, 888–901. [Google Scholar] [CrossRef]
- Ramesh, N.; Davis, P.K.; Zielinski, J.M.; Danner, R.P.; Duda, J.L. Application of Free-Volume Theory to Self Diffusion of Solvents in Polymers below the Glass Transition Temperature: A Review. J. Polym. Sci. Part B Polym. Phys. 2011, 49, 1629–1644. [Google Scholar] [CrossRef]
- Xiang, T.X.; Anderson, B.D. Molecular Dynamics Simulation of Amorphous Indomethacin. Mol. Pharm. 2013, 10, 102–114. [Google Scholar] [CrossRef] [PubMed]

| /Pa·s | /- | /K | /kJ·mol−1 | /kJ·mol−1 | /K | /K | /GPa | m2·s−1 |
|---|---|---|---|---|---|---|---|---|
| 1.83 × 105 | 10.04 | 147.4 | 41.29 | 79 | −12.31 | −20 | 4 | 3.93 × 10−13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borrmann, D.; Danzer, A.; Sadowski, G. Anomalous Water-Sorption Kinetics in ASDs. Pharmaceutics 2022, 14, 1897. https://doi.org/10.3390/pharmaceutics14091897
Borrmann D, Danzer A, Sadowski G. Anomalous Water-Sorption Kinetics in ASDs. Pharmaceutics. 2022; 14(9):1897. https://doi.org/10.3390/pharmaceutics14091897
Chicago/Turabian StyleBorrmann, Dominik, Andreas Danzer, and Gabriele Sadowski. 2022. "Anomalous Water-Sorption Kinetics in ASDs" Pharmaceutics 14, no. 9: 1897. https://doi.org/10.3390/pharmaceutics14091897
APA StyleBorrmann, D., Danzer, A., & Sadowski, G. (2022). Anomalous Water-Sorption Kinetics in ASDs. Pharmaceutics, 14(9), 1897. https://doi.org/10.3390/pharmaceutics14091897







