Comprehensive Physiologically Based Pharmacokinetic Model to Assess Drug–Drug Interactions of Phenytoin
Abstract
:1. Introduction
2. Materials and Methods
2.1. Software
2.2. Clinical PK Data
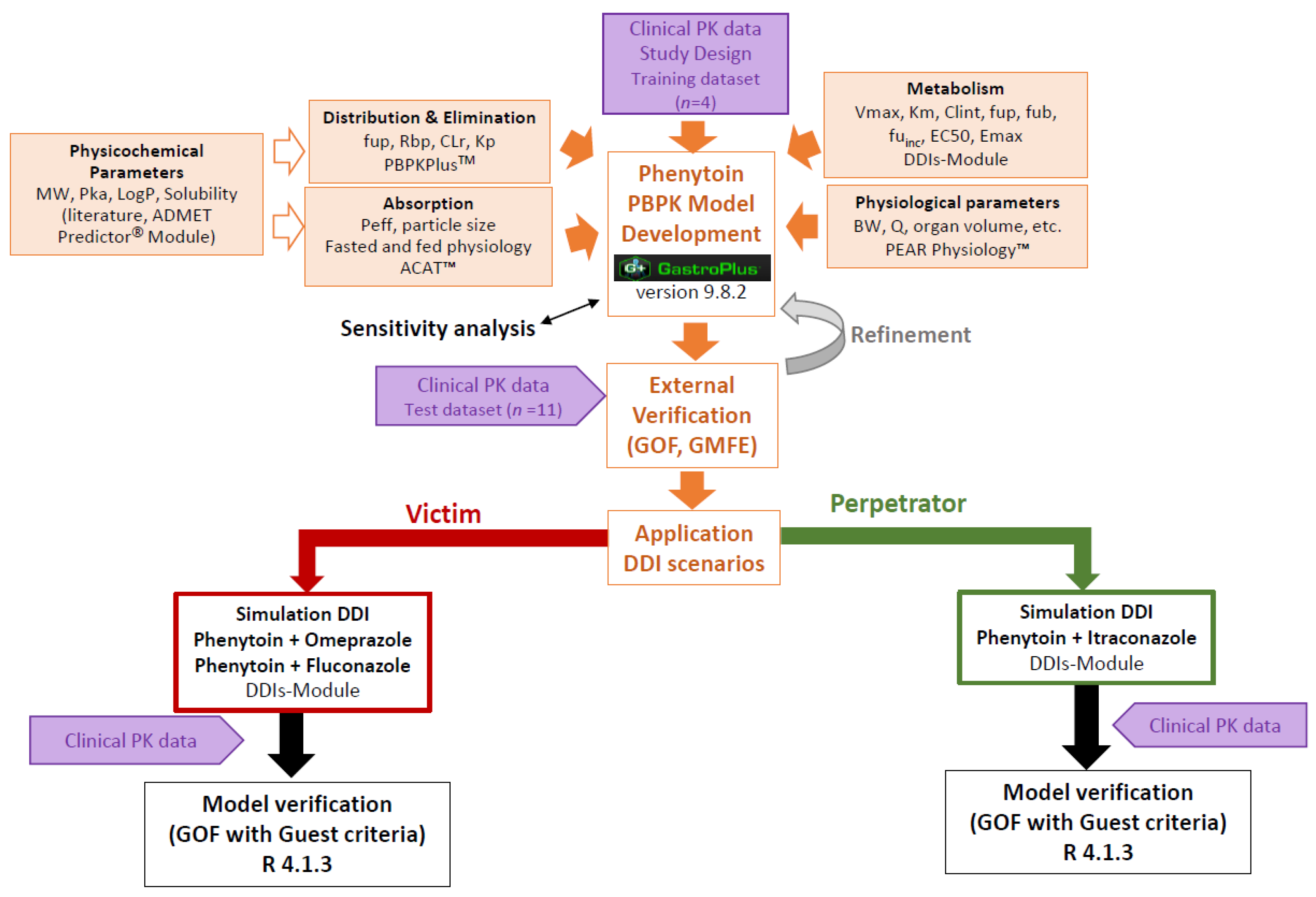
2.3. PBPK Model Development of Phenytoin
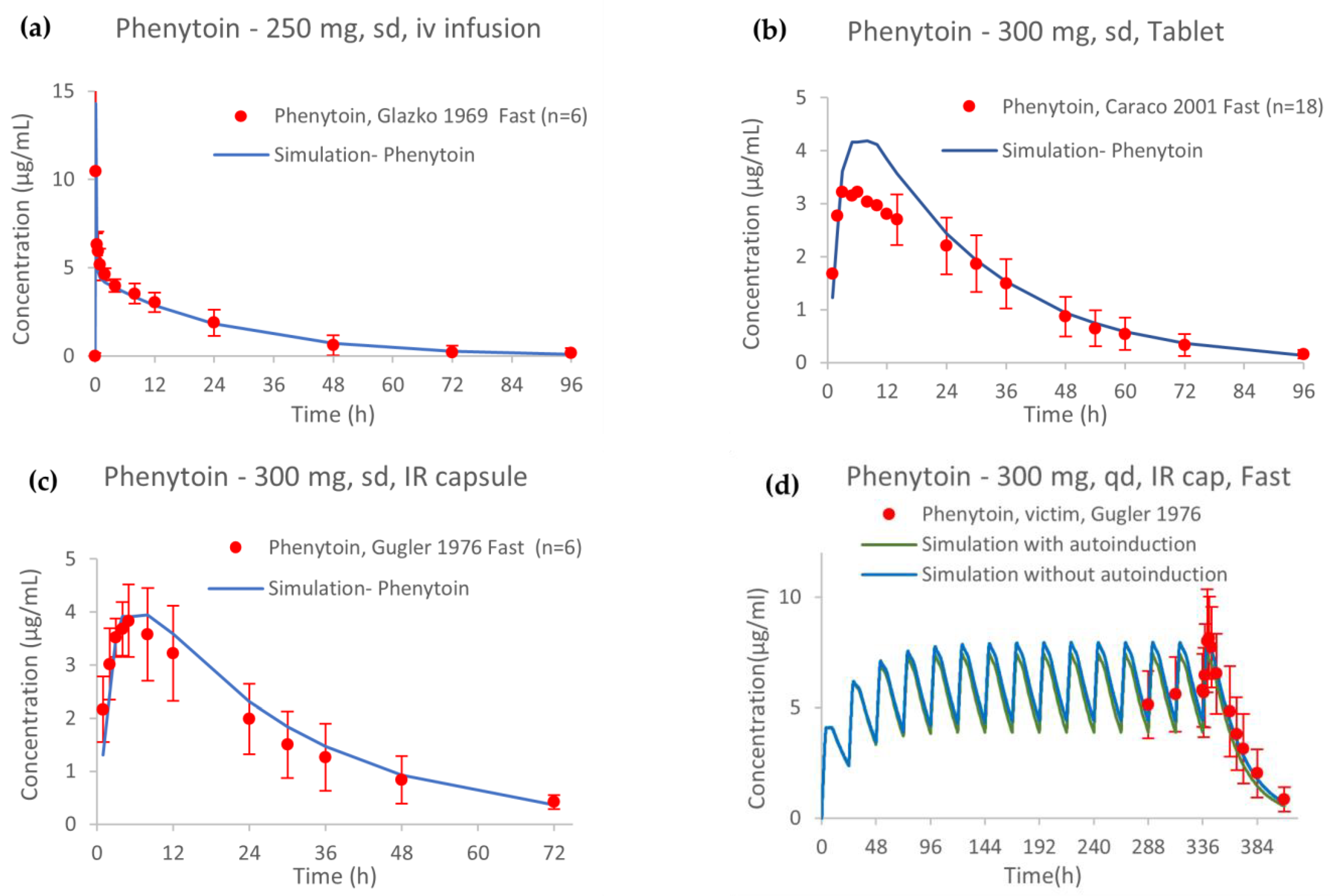
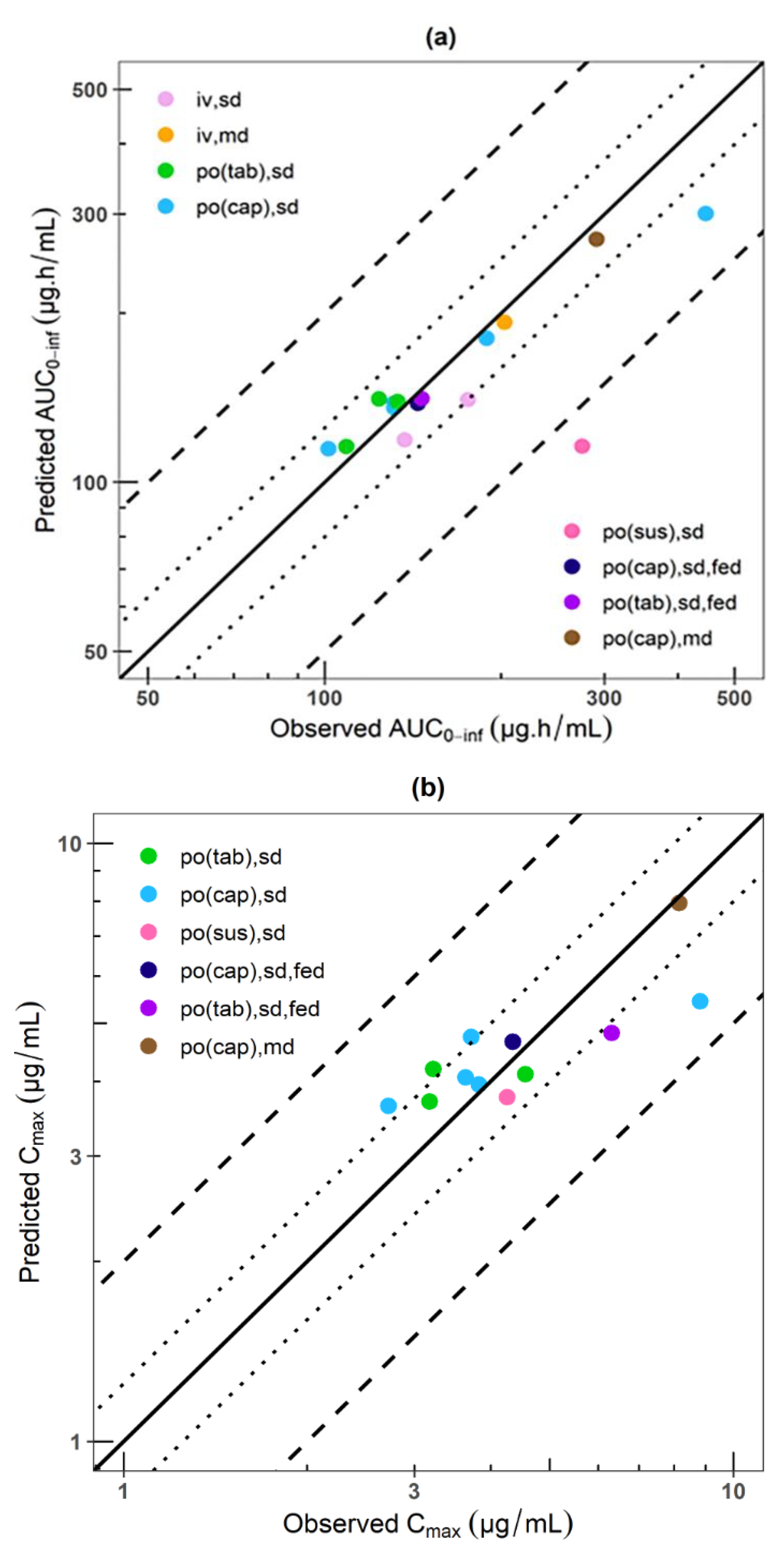
2.4. PBPK Model External Verification
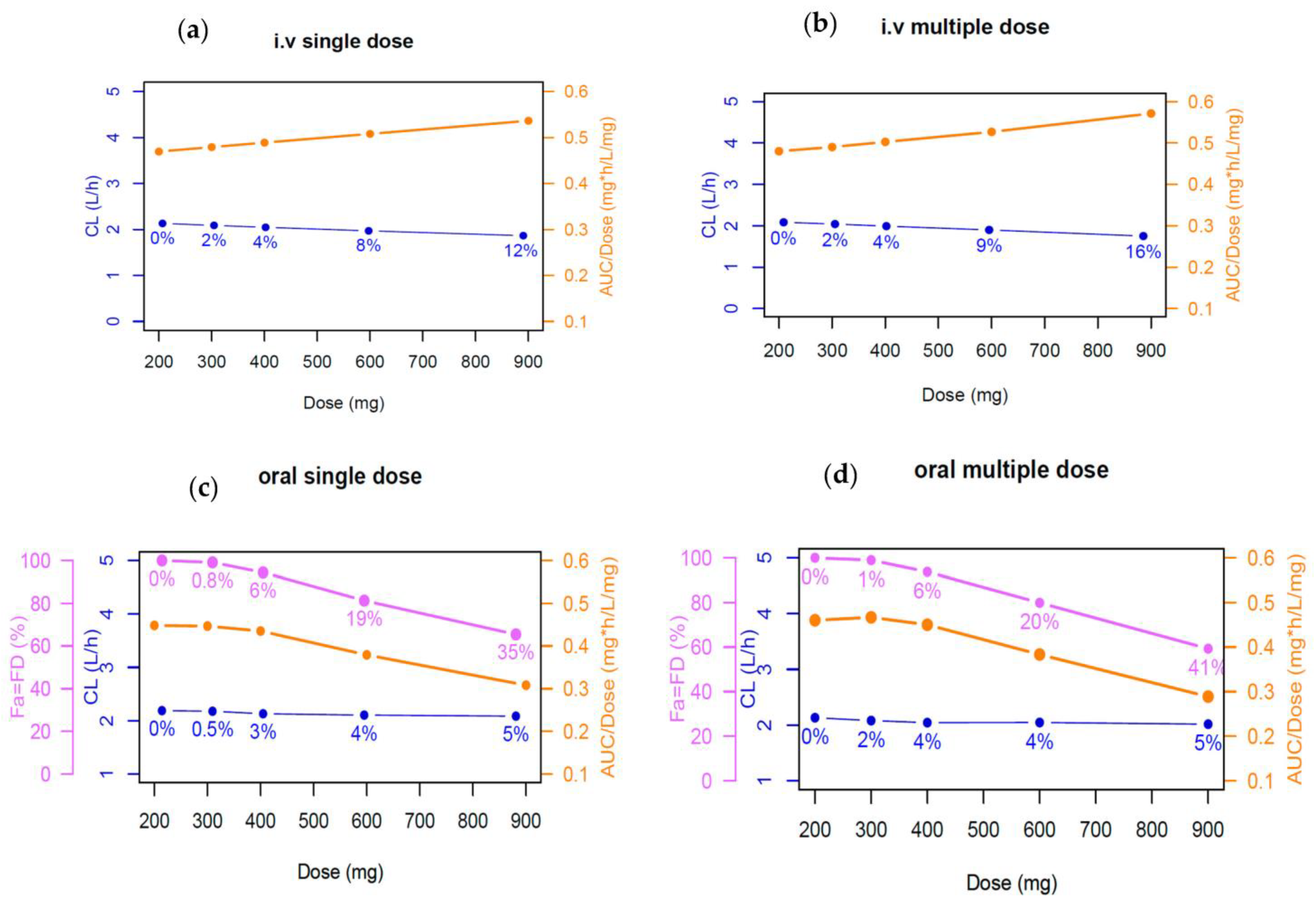
2.5. Impact of Plasma Protein Binding on Phenytoin Exposure
2.6. DDI Simulations
2.7. DDIs Model Verification
3. Results
3.1. PBPK Model of Phenytoin
3.2. Impact of Plasma Protein Binding of Phenytoin Exposure
3.3. DDI Simulations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Juurlink, D.N.; Mamdani, M.; Kopp, A.; Laupacis, A.; Redelmeier, D.A. Drug-Drug Interactions among Elderly Patients Hospitalized for Drug Toxicity. JAMA 2003, 289, 1652–1658. [Google Scholar] [CrossRef]
- Doucet, J.; Chassagne, P.; Trivalle, C.; Landrin, I.; Pauty, M.D.; Kadri, N.; Ménard, J.F.; Bercoff, E. Drug-Drug Interactions Related to Hospital Admissions in Older Adults: A Prospective Study of 1000 Patients. J. Am. Geriatr. Soc. 1996, 44, 944–948. [Google Scholar] [CrossRef] [PubMed]
- Prueksaritanont, T.; Chu, X.; Gibson, C.; Cui, D.; Yee, K.L.; Ballard, J.; Cabalu, T.; Hochman, J. Drug-Drug Interaction Studies: Regulatory Guidance and an Industry Perspective. AAPS J. 2013, 15, 629–645. [Google Scholar] [CrossRef] [PubMed]
- Shebley, M.; Sandhu, P.; Emami Riedmaier, A.; Jamei, M.; Narayanan, R.; Patel, A.; Peters, S.A.; Reddy, V.P.; Zheng, M.; de Zwart, L.; et al. Physiologically Based Pharmacokinetic Model Qualification and Reporting Procedures for Regulatory Submissions: A Consortium Perspective. Clin. Pharmacol. Ther. 2018, 104, 88–110. [Google Scholar] [CrossRef] [PubMed]
- Talati, R.; Scholle, J.M.; Phung, O.J.; Baker, W.L.; Baker, E.L.; Ashaye, A.; Kluger, J.; Quercia, R.; Mather, J.; Giovenale, S.; et al. Effectiveness and Safety of Antiepileptic Medications in Patients with Epilepsy, 40th ed.; Agency for Healthcare Research and Quality (US): Rockville, MD, USA, 2011. [Google Scholar]
- Thorn, C.F.; Whirl-Carrillo, M.; Leeder, J.S.; Klein, T.E.; Altman, R.B. PharmGKB Summary: Phenytoin Pathway. Pharmacogenet. Genom. 2012, 22, 466–470. [Google Scholar] [CrossRef] [PubMed]
- Giancarlo, G.M.; Venkatakrishnan, K.; Granda, B.W.; Von Moltke, L.L.; Greenblatt, D.J. Relative Contributions of CYP2C9 and 2C19 to Phenytoin 4-Hydroxylation in Vitro: Inhibition by Sulfaphenazole, Omeprazole, and Ticlopidine. Eur. J. Clin. Pharmacol. 2001, 57, 31–36. [Google Scholar] [CrossRef]
- Caraco, Y.; Muszkat, M.; Wood, A.J.J. Phenytoin Metabolic Ratio: A Putative Marker of CYP2C9 Activity in Vivo. Pharmacogenetics 2001, 11, 587–596. [Google Scholar] [CrossRef]
- Silvado, C.E.; Terra, V.C.; Twardowschy, C.A. CYP2C9 Polymorphisms in Epilepsy: Influence on Phenytoin Treatment. Pharmgenom. Pers. Med. 2018, 11, 51–58. [Google Scholar] [CrossRef]
- Miners, J.O.; Birkett, D.J. Cytochrome P4502C9: An Enzyme of Major Importance in Human Drug Metabolism. Br. J. Clin. Pharmacol. 1998, 45, 525–538. [Google Scholar] [CrossRef]
- U.S. Food and Drug Administration. Drug Development and Drug Interactions: Table of Substrates, Inhibitors and Inducers. 2006. Available online: https://Www.Fda.Gov/Drugs/Drug-Interactions-Labeling/Drug-Development-and-Drug-Interactions-Table-Substrates-Inhibitors-and-Inducers (accessed on 29 November 2022).
- Bolleddula, J.; Gopalakrishnan, S.; Hu, P.; Dong, J.; Venkatakrishnan, K. Alternatives to Rifampicin: A Review and Perspectives on the Choice of Strong CYP3A Inducers for Clinical Drug-Drug Interaction Studies. Clin. Transl. Sci. 2022, 15, 2075–2095. [Google Scholar] [CrossRef]
- Reddy, D.S. Clinical Pharmacokinetic Interactions between Antiepileptic Drugs and Hormonal Contraceptives. Expert Rev. Clin. Pharmacol. 2010, 3, 183–192. [Google Scholar] [CrossRef]
- Zaccara, G.; Lattanzi, S. A Review of Pharmacokinetic Drug Interactions between Antimicrobial and Antiseizure Medications in Children. Epileptic Disord. 2021, 23, 229–256. [Google Scholar] [CrossRef]
- Murray, P.; Ducharme, R.; Slaughter, L.; Warbasse, P.; Chandrasekar, V.; Edwards, D. Itraconazole and Hydroxyitraconazole Serum Concentrations Are Reduced More than Tenfold by Phenytoin. Clin. Pharmacol. Ther. 1995, 58, 617–624. [Google Scholar]
- Li, A.; Li, M.K.; Crowther, M.; Vazquez, S.R. Drug-Drug Interactions with Direct Oral Anticoagulants Associated with Adverse Events in the Real World: A Systematic Review. Thromb. Res. 2020, 194, 240–245. [Google Scholar] [CrossRef] [PubMed]
- Lim, M.L.; Min, S.S.; Eron, J.J.; Bertz, R.J.; Robinson, M.; Gaedigk, A.; Kashuba, A.D.M. Coadministration of Lopinavir/Ritonavir and Phenytoin Results in Two-Way Drug Interaction through Cytochrome P-450 Induction. J. Acquir. Immune Defic. Syndr. 2004, 36, 1034–1040. [Google Scholar] [CrossRef]
- Vlase, L.; Popa, A.; Neag, M.; Muntean, D.; Leucuta, S.E. Pharmacokinetic Interaction between Ivabradine and Phenytoin in Healthy Subjects. Clin. Drug Investig. 2012, 32, 533–538. [Google Scholar] [CrossRef]
- Bullman, J.; Nicholls, A.; Van Landingham, K.; Fleck, R.; Vuong, A.; Miller, J.; Alexander, S.; Messenheimer, J. Effects of Lamotrigine and Phenytoin on the Pharmacokinetics of Atorvastatin in Healthy Volunteers. Epilepsia 2011, 52, 1351–1358. [Google Scholar] [CrossRef]
- Michelucci, R.; Cipolla, G.; Passarelli, D.; Gatti, G.; Ochan, M.; Heinig, R.; Tassinari, C.A.; Perucca, E. Reduced Plasma Nisoldipine Concentrations Phenytoin-Treated Patients with Epilepsy. Epilepsia 1996, 37, 1107–1110. [Google Scholar] [CrossRef]
- Backman, J.T.; Olkkola, K.T.; Ojala, M.; Laaksovirta, H.; Neuvonen, P.J. Concentrations and Effects of Oral Midazolam Are Greatly Reduced in Patients Treated with Carbamazepine or Phenytoin. Epilepsia 1996, 37, 253–257. [Google Scholar] [CrossRef]
- Wong, Y.W.J.; Yeh, C.; Thyrum, P.T. The Effects of Concomitant Phenytoin Administration on the Steady-State Pharmacokinetics of Quetiapine. J. Clin. Psychopharmacol. 2001, 21, 89–93. [Google Scholar] [CrossRef]
- Rameis, H. On the Interaction between Phenytoin and Digoxin. Eur. J. Clin. Pharmacol. 1985, 29, 49–53. [Google Scholar] [CrossRef]
- Guastaldi, R.B.F.; Reis, A.M.M.; Figueras, A.; Secoli, S.R. Prevalence of Potential Drug-Drug Interactions in Bone Marrow Transplant Patients. Int. J. Clin. Pharm. 2011, 33, 1002–1009. [Google Scholar] [CrossRef]
- Blum, R.A.; Wilton, J.H.; Hilligoss, D.M.; Gardner, M.J.; Henry, E.B.; Harrison, N.J.; Schentag, J.J. Effect of Fluconazole on the Disposition of Phenytoin. Clin. Pharmacol. Ther. 1991, 49, 420–425. [Google Scholar] [CrossRef]
- Touchette, M.; Chandrasekar, P.; Milad, M.; Edwards, D. Contrasting Effects of Fluconazole and Ketoconazole on Phenytoin and Testosterone Disposition in Man. Br. J. Clin. Pharmacol. 1992, 34, 75–78. [Google Scholar] [CrossRef]
- Iwamoto, T.; Kagawa, Y.; Naito, Y.; Kuzuhara, S.; Okuda, M. Clinical Evaluation of Plasma Free Phenytoin Measurement and Factors Influencing Its Protein Binding. Biopharm. Drug Dispos. 2006, 27, 77–84. [Google Scholar] [CrossRef]
- Banh, H.L.; Burton, M.E.; Sperling, M.R. Interpatient and Intrapatient Variability in Phenytoin Protein Binding. Ther. Drug Monit. 2002, 24, 379–385. [Google Scholar] [CrossRef]
- Musteata, F.M. Calculation of Normalized Drug Concentrations in the Presence of Altered Plasma Protein Binding. Clin. Pharmacokinet. 2012, 51, 55–68. [Google Scholar] [CrossRef]
- Peterson, G.; McLean, S.; Aldous, S.; Von Witt, R.; Millingen, K. Plasma Protein Binding of Phenytoin in 100 Epileptic Patients. Br. J. Clin. Pharmacol. 1982, 14, 298–300. [Google Scholar] [CrossRef]
- Burt, M.; Anderson, D.C.; Kloss, J.; Apple, F.S. Evidence-Based Implementation of Free Phenytoin Therapeutic Drug Monitoring. Clin. Chem. 2000, 46, 1132–1135. [Google Scholar] [CrossRef]
- Tassaneeyakul, W.; Veronese, M.E.; Birkett, D.J.; Doecke, C.J.; McManus, M.E.; Sansom, L.N.; Miners, J.O. Co-Regulation of Phenytoin and Tolbutamide Metabolism in Humans. Br. J. Clin. Pharmacol. 1992, 34, 494–498. [Google Scholar]
- Ter Heine, R.; Kane, S.P.; Huitema, A.D.R.; Krasowski, M.D.; van Maarseveen, E.M. Nonlinear Protein Binding of Phenytoin in Clinical Practice: Development and Validation of a Mechanistic Prediction Model. Br. J. Clin. Pharmacol. 2019, 85, 2360–2368. [Google Scholar] [CrossRef]
- Ludden, T.M. Nonlinear Pharmacokinetics. Clin. Pharmacokinet. 1991, 20, 429–446. [Google Scholar] [CrossRef] [PubMed]
- Pfizer. Dilantin [Package Insert]; Pfizer: New York, NY, USA, 1953. Available online: https://www.accessdata.fda.gov/drugsatfda_docs/label/2021/084349s087lbl.pdf (accessed on 15 May 2023).
- Glazko, A.J.; Chang, T.; Baukema, J.; Dill, W.A.; Goulet, J.R.; Buchanan, R.A. Metabolic Disposition of Diphenylhydantoin in Normal Human Subjects Following Intravenous Administration. Clin. Pharmacol. Ther. 1969, 10, 498–504. [Google Scholar] [CrossRef]
- Gugler, R.; Manion, C.V.; Azarnoff, D.L. Phenytoin: Pharmacokinetics and Bioavailability. Clin. Pharmacol. Ther. 1976, 19, 135–142. [Google Scholar] [CrossRef] [PubMed]
- Prichard, P.J.; Walt, R.P.; Kitchingman, G.K.; Somervilee, K.W.; Langman, M.J.; Williams, J.; Richens, A. Oral Phenytoin Pharmacokinetics during Omeprazole Therapy. Br. J. Clin. Pharmac. 1987, 24, 543–545. [Google Scholar] [CrossRef]
- Dill, W.A.; Glazko, A.J.; Kazenko, A.; Wolf, L.M. Studies on 5,5′-Diphenylhydantoin (Dilantin) in Animals and Man. J. Pharmacol. Exp. Ther. 1956, 118, 270–279. [Google Scholar]
- Fraser, D.G.; Ludden, T.M.; Evens, R.P.; Sutherland, E.W. Displacement of Phenytoin from Plasma Binding Sites by Salicylate. Clin. Pharmacol. Ther. 1980, 27, 165–169. [Google Scholar] [CrossRef]
- Melander, A.; Brante, G.; Johansson, O.; Lindberg, T.; Wåhlin-Boll, E. Influence of Food on the Absorption of Phenytoin in Man. Eur. J. Clin. Pharmacol. 1979, 15, 269–274. [Google Scholar] [CrossRef] [PubMed]
- Smith, T.C.; Kinkel, A. Absorption and Metabolism of Phenytoin from Tablets and Capsules. Clin. Pharmacol. Ther. 1976, 20, 738–742. [Google Scholar] [CrossRef]
- Stella, V.J.; Martodihardjo, S.; Terada, K.; Rao, V.M. Some Relationships between the Physical Properties of Various 3-Acyloxymethyl Prodrugs of Phenytoin to Structure: Potential in Vivo Performance Implications. J. Pharm. Sci. 1998, 87, 1235–1241. [Google Scholar] [CrossRef]
- Poulin, P.; Schoenlein, K.; Theil, F.P. Prediction of Adipose Tissue: Plasma Partition Coefficients for Structurally Unrelated Drugs. J. Pharm. Sci. 2001, 90, 436–447. [Google Scholar] [CrossRef]
- Serajuddin, A.T.M.; Jarowski, C.I. Influence of PH on Release of Phenytoin Sodium from Slow-release Dosage Forms. J. Pharm. Sci. 1993, 82, 306–310. [Google Scholar] [CrossRef]
- Chiang, P.C.; Wong, H. Incorporation of Physiologically Based Pharmacokinetic Modeling in the Evaluation of Solubility Requirements for the Salt Selection Process: A Case Study Using Phenytoin. AAPS J. 2013, 15, 1109–1118. [Google Scholar] [CrossRef]
- Yasuji, T.; Haslam, J.; Kajiyama, A.; McIntosh, M.P.; Rajewski, R.A. Preliminary Evaluation of Polymer-Based Drug Composite Microparticle Production by Coacervate Desolvation with Supercritical Carbon Dioxide. J. Pharm. Sci. 2006, 95, 581–588. [Google Scholar] [CrossRef]
- Pade, V. Link between Drug Absorption Solubility and Permeability Measurements in Caco-2 Cells. J. Pharm. Sci. 1998, 87, 1604–1607. [Google Scholar] [CrossRef] [PubMed]
- Kong, S.T.; Lim, S.-H.; Lee, W.B.; Kumar, P.K.; Wang, H.Y.S.; Ng, Y.L.S.; Wong, P.S.; Ho, P.C. Clinical Validation and Implications of Dried Blood Spot Sampling of Carbamazepine, Valproic Acid and Phenytoin in Patients with Epilepsy. PLoS ONE 2014, 9, e108190. [Google Scholar] [CrossRef] [PubMed]
- Almond, L.M.; Mukadam, S.; Gardner, I.; Okialda, K.; Wong, S.; Hatley, O.; Tay, S.; Rowland-Yeo, K.; Jamei, M.; Rostami-Hodjegan, A.; et al. Prediction of Drug-Drug Interactions Arising from CYP3A Induction Using a Physiologically Based Dynamic Model. Drug Metab. Dispos. 2016, 44, 821–832. [Google Scholar] [CrossRef]
- Fahmi, O.A.; Hurst, S.; Plowchalk, D.; Cook, J.; Guo, F.; Youdim, K.; Dickins, M.; Phipps, A.; Darekar, A.; Hyland, R.; et al. Comparison of Different Algorithms for Predicting Clinical Drug-Drug Interactions, Based on the Use of CYP3A4 in Vitro Data: Predictions of Compounds as Precipitants of Interaction. Drug Metab. Dispos. 2009, 37, 1658–1666. [Google Scholar] [CrossRef] [PubMed]
- Lukacova, V.; Parrott, N.J.; Lave, T.; Fraczkiewicz, G.; Bolger, M.B.; Woltosz, W.S. General Approach to Calculation of Tissue:Plasma Partition Coefficients for Physiologically Based Pharmacokinetic (PBPK) Modeling. In Proceedings of the 2008 AAPS National Annual Meeting and Exposition, Atlanta, GA, USA, 16–30 November 2008. [Google Scholar]
- Nolan, P.E.; Marcus, F.I.; Hoyer, G.L.; Bliss, M.; Gear, K. Pharmacokinetic Interaction between Intravenous Phenytoin and Amiodarone in Healthy Volunteers. Clin. Pharmacol. Ther. 1989, 46, 43–49. [Google Scholar] [CrossRef]
- Tsamandouras, N.; Rostami-Hodjegan, A.; Aarons, L. Combining the “bottom up” and “Top down” Approaches in Pharmacokinetic Modelling: Fitting PBPK Models to Observed Clinical Data. Br. J. Clin. Pharmacol. 2015, 79, 48–55. [Google Scholar] [CrossRef]
- Nishimura, M.; Ejiri, Y.; Kishimoto, S.; Suzuki, S.; Satoh, T.; Horie, T.; Narimatsu, S.; Naito, S. Expression Levels of Drug-Metabolizing Enzyme, Transporter, and Nuclear Receptor MRNAs in a Novel Three-Dimensional Culture System for Human Hepatocytes Using Micro-Space Plates. Drug Metab. Pharmacokinet. 2011, 26, 137–144. [Google Scholar] [CrossRef] [PubMed]
- Brill, M.J.E.; Diepstraten, J.; Van Rongen, A.; Van Kralingen, S.; Van Den Anker, J.N.; Knibbe, C.A.J. Impact of Obesity on Drug Metabolism and Elimination in Adults and Children. Clin. Pharmacokinet. 2012, 51, 277–304. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, S.; Schaefer, O.; Kawakami, H.; Inoue, T.; Liehner, S.; Saito, A.; Ishiguro, N.; Kishimoto, W.; Ludwig-Schwellinger, E.; Ebner, T.; et al. Simultaneous Absolute Protein Quantification of Transporters, Cytochromes P450, and UDP-Glucuronosyltransferases as a Novel Approach for the Characterization of Individual Human Liver: Comparison with MRNA Levels and Activities. Drug Metab. Dispos. 2012, 40, 83–92. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhang, H.; Li, J.; Wei, J.; Zhai, R.; Peng, B.; Qiao, H.; Zhang, Y.; Qian, X. A New Calibration Curve Calculation Method for Absolute Quantification of Drug Metabolizing Enzymes in Human Liver Microsomes by Stable Isotope Dilution Mass Spectrometry. Anal. Methods 2015, 7, 5934–5941. [Google Scholar] [CrossRef]
- Wood, J.H.; Syarto, J.E.; Letterman, H. Improved Holder for Intrinsic Dissolution Rate Studies. J. Pharm. Sci. 1965, 54, 1068. [Google Scholar] [CrossRef]
- Smith, B.P.; Vandenhende, F.R.; DeSante, K.A.; Farid, N.A.; Welch, P.A.; Callaghan, J.T.; Forgue, S.T. Confidence Interval Criteria for Assessment of Dose Proportionality. Pharm. Res. 2000, 17, 1278–1283. [Google Scholar] [CrossRef]
- Kunze, K.L.; Wienkers, L.C.; Thummel, K.E.; Trager, W.F. Warfarin-Fluconazole I. Inhibition of the Human Cytochrome P450-Dependent Metabolism of Warfarin by Fluconazole: In Vitro Stduies. Drug Metab. Dispos. 1996, 24, 414–421. [Google Scholar]
- Zvyaga, T.; Chang, S.Y.; Chen, C.; Yang, Z.; Vuppugalla, R.; Hurley, J.; Thorndike, D.; Wagner, A.; Chimalakonda, A.; Rodrigues, A.D. Evaluation of Six Proton Pump Inhibitors as Inhibitors of Various Human Cytochromes P450: Focus on Cytochrome P450 2C19. Drug Metab. Dispos. 2012, 40, 1698–1711. [Google Scholar] [CrossRef]
- Shirasaka, Y.; Sager, J.E.; Lutz, J.D.; Davis, C.; Isoherranen, N. Inhibition of CYP2C19 and CYP3A4 by Omeprazole Metabolites and Their Contribution to Drug-Drug Interactionss. Drug Metab. Dispos. 2013, 41, 1414–1424. [Google Scholar] [CrossRef]
- Guest, E.J.; Aarons, L.; Houston, J.B.; Rostami-Hodjegan, A.; Galetin, A. Critique of the Two-Fold Measure of Prediction Success for Ratios: Application for the Assessment of Drug-Drug Interactions. Drug Metab. Dispos. 2011, 39, 170–173. [Google Scholar] [CrossRef]
- Ibarra, M.; Pietro, F. Concentration-Dependent Nonlinear Pharmacokinetics. In The ADME Encyclopedia; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Zhang, C.; Kwan, P.; Zuo, Z.; Baum, L. The Transport of Antiepileptic Drugs by P-Glycoprotein. Adv. Drug Deliv. Rev. 2012, 64, 930–942. [Google Scholar] [CrossRef]
- Baltes, S.; Gastens, A.M.; Fedrowitz, M.; Potschka, H.; Kaever, V.; Löscher, W. Differences in the Transport of the Antiepileptic Drugs Phenytoin, Levetiracetam and Carbamazepine by Human and Mouse P-Glycoprotein. Neuropharmacology 2007, 52, 333–346. [Google Scholar] [CrossRef]
- Luna-Tortós, C.; Fedrowitz, M.; Löscher, W. Several Major Antiepileptic Drugs Are Substrates for Human P-Glycoprotein. Neuropharmacology 2008, 55, 1364–1375. [Google Scholar] [CrossRef]
- Zhang, C.; Kwan, P.; Zuo, Z.; Baum, L. In Vitro Concentration Dependent Transport of Phenytoin and Phenobarbital, but Not Ethosuximide, by Human P-Glycoprotein. Life Sci. 2010, 86, 899–905. [Google Scholar] [CrossRef] [PubMed]
- Soryal, I.; Richens, A. Bioavailability and Dissolution of Proprietary and Generic Formulations of Phenytoin. J. Neurol. Neurosurg. Psychiatry 1992, 55, 688–691. [Google Scholar] [CrossRef]
- Mauro, L.S.; Mauro, V.F.; Brown, D.L.; Somani, P.; Ohio, T. Enhancement of Phenytoin Elimination by Multiple-Dose Activated Charcoal. Ann. Emerg. Med. 1987, 16, 1132–1135. [Google Scholar] [CrossRef] [PubMed]
- van Haarst, A.; Smith, S.; Garvin, C.; Benrimoh, N.; Paglialunga, S. Rifampin Drug–Drug–Interaction Studies: Reflections on the Nitrosamine Impurities Issue. Clin. Pharmacol. Ther. 2023, 113, 816–821. [Google Scholar] [CrossRef]
- Boucher, B.A.; Jaresko, G.S.; Rasmussen, S.N.; Watridge, C.B.; Fabian, T.C. Phenytoin pharmacokinetics in critically ill trauma patients. Clin Pharmacol. Ther. 1988, 44, 675–683. [Google Scholar] [CrossRef]
- De Leon, J. Efectos de Los Inductores Antiepilépticos En La Neuropsicofarmacología: Una Cuestión Ignorada. Parte II: Cuestiones Farmacológicas y Comprensión Adicional. Rev. Psiquiatr. Salud Ment. 2015, 8, 167–188. [Google Scholar] [CrossRef] [PubMed]
- Fagiolino, P.; Ibarra, M. Time-Dependent Nonlinear Pharmacokinetics. In The ADME Encyclopedia: A Comprehensive Guide on Biopharmacy and Pharmacokinetics; Springer International Publishing: Cham, Switzerland, 2021; pp. 1–8. ISBN 978-3-030-51519-5. [Google Scholar]
- Kunze, K.L.; Trager, W.F. Warfarin-Fluconazole III—A Rational Approach to Management of a Metabolically Based Drug Interaction. Drug Metab. Dispos. 1996, 24, 429–435. [Google Scholar] [PubMed]
- Zhang, J.G.; Ho, T.; Callendrello, A.L.; Clark, R.J.; Santone, E.A.; Kinsman, S.; Xiao, D.; Fox, L.G.; Einolf, H.J.; Stresser, D.M.; et al. Evaluation of Calibration Curve—Based Approaches to Predict Clinical Inducers and Noninducers of CYP3A4 with Plated Human Hepatocytes. Drug Metab. Dispos. 2014, 42, 1379–1391. [Google Scholar] [CrossRef] [PubMed]
- Hariparsad, N.; Ramsden, D.; Palamanda, J.; Dekeyser, J.G.; Fahmi, A.; Kenny, J.R.; Einolf, H.; Mohutsky, M.; Pardon, M.; Siu, A.Y.; et al. Considerations from the IQ Induction Working Group in Response to Drug-Drug Interaction Guidances from Regulatory Agencies: Focus on Down-Regulation, CYP2C Induction and CYP2B6 Positive Control. Drug Metab. Dispos. 2017, 45, 1049–1059. [Google Scholar] [CrossRef] [PubMed]
- Moore, A.; Chothe, P.P.; Tsao, H.; Hariparsad, N. Evaluation of the Interplay between Uptake Transport and CYP3A4 Induction in Micropatterned Cocultured Hepatocytes. Drug Metab. Dispos. 2016, 44, 1910–1919. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.H.; Choi, K.Y.; Kim, Y.C.; Lee, M.G. Dose-Dependent Pharmacokinetics of Itraconazole after Intravenous or Oral Administration to Rats: Intestinal First-Pass Effect. Antimicrob. Agents Chemother. 2004, 48, 1756–1762. [Google Scholar] [CrossRef]



| Parameter | Value | Reference |
|---|---|---|
| Molecular weight (g/mol) logP | 252.27 2.21 | Stella VJ et al., 1998 [43] Poulin et al., 2000 [44] |
| Diffusion coefficient (cm2/s) | 0.86 × 10−5 | ADMET Predictor v.10.0 |
| pKa | 8.249 | Estimated from Solubility vs. pH profile a |
| Reference solubility (mg/mL) at pH 3.29 | 0.04 | Serajuddin et al., 1993 [45] and Chiang et al., 2013 b [46] |
| Particle radius (μm) | 2.5 (SD = 0.75, Bins = 4) | Dill et al., 1956 [39] and Yasuji et al., 2006 [47] |
| Drug particle density (g/mL) | 1.2 | GastroPlus default value |
| Mean precipitation time (s) | 900 | GastroPlus default value |
| CaCo2 apparent permeability (Papp), cm/s | 34.3 × 10−6 | Pade et al., 1998 [48] |
| Solubility (mg/mL, SGF at pH 4 at 0 mM) Solubility (mg/mL, FaSSIF at pH 6.4 at 10 mM) Solubility (mg/mL, FeSSIF at pH 6.4 at 20 mM) Solubility (mg/mL, FeSSIF at pH 6.4 at 30 mM) Solubility (mg/mL, FeSSIF at pH 6.4 at 40 mM) | 0.04 0.0546 0.0764 0.1183 0.1392 | Stella VJ et al., 1998 [43] |
| Distribution | ||
| Kp calculation method | Lukacova (Rodgers-single) | |
| fut calculation method | fut = S + 9.5v. (default) | |
| Tissues | Perfusion limited | |
| Blood: plasma concentration ratio (Rbp) | 1.33 | Kong et al., 2014 [49] |
| Plasma protein binding (fup), % | 9.7 | Fitted from Peterson et al., 1982 [30] |
| Renal Clearance (CLfilt), L/h | 0.015 | Almond et al., 2016 [50] |
| Metabolism (in vitro values converted to in vivo—Enzyme table) | ||
| CYP 2C19 Km, mg/L | 5.474 | Giancarlo et al., 2001 [7] |
| CYP 2C19 Vmax, ×10−4 mg/s/mg-enzyme | 2.0042 | Fitted to in vivo data from Caraco et al., 2001 [8] |
| CYP 2C9 Km, mg/L | 3.316 | Giancarlo et al., 2001 [7] |
| CYP 2C9 Vmax, ×10−5 mg/s/mg-enzyme | 6.4531 | Fitted to in vivo data from Caraco et al., 2001 [8] |
| Induction | ||
| Emax (CYP3A4) | 12.6 | Almond et al., 2016 [50] |
| EC50invitro,T (CYP3A4), µM | 3.7 | Fahmi et al., 2008 [51] |
| Emax (CYP2C9) | 0.9 | Almond et al., 2016 [50] |
| EC50invitro,T (CYP2C9), µM | 15.3 | Almond et al., 2016 [50] |
| fuinvitro, % | 89.9 | Calculated with Hallifax–HLM method |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez-Vera, L.; Yin, X.; Almoslem, M.; Romahn, K.; Cicali, B.; Lukacova, V.; Cristofoletti, R.; Schmidt, S. Comprehensive Physiologically Based Pharmacokinetic Model to Assess Drug–Drug Interactions of Phenytoin. Pharmaceutics 2023, 15, 2486. https://doi.org/10.3390/pharmaceutics15102486
Rodriguez-Vera L, Yin X, Almoslem M, Romahn K, Cicali B, Lukacova V, Cristofoletti R, Schmidt S. Comprehensive Physiologically Based Pharmacokinetic Model to Assess Drug–Drug Interactions of Phenytoin. Pharmaceutics. 2023; 15(10):2486. https://doi.org/10.3390/pharmaceutics15102486
Chicago/Turabian StyleRodriguez-Vera, Leyanis, Xuefen Yin, Mohammed Almoslem, Karolin Romahn, Brian Cicali, Viera Lukacova, Rodrigo Cristofoletti, and Stephan Schmidt. 2023. "Comprehensive Physiologically Based Pharmacokinetic Model to Assess Drug–Drug Interactions of Phenytoin" Pharmaceutics 15, no. 10: 2486. https://doi.org/10.3390/pharmaceutics15102486
APA StyleRodriguez-Vera, L., Yin, X., Almoslem, M., Romahn, K., Cicali, B., Lukacova, V., Cristofoletti, R., & Schmidt, S. (2023). Comprehensive Physiologically Based Pharmacokinetic Model to Assess Drug–Drug Interactions of Phenytoin. Pharmaceutics, 15(10), 2486. https://doi.org/10.3390/pharmaceutics15102486








