Reviewing the Impact of Powder Cohesion on Continuous Direct Compression (CDC) Performance
Abstract
1. Introduction
- 1.
- Formulation modification, through the introduction of glidants or lubricants [37].
- 2.
- Operational process changes which are documented in many different studies for each unit operation [38].
- 3.
- Granulation, which also manages cohesion as poor flowing powder fines are made into coarser more uniform agglomerates. (This is beyond the scope of this literature review as this unit operation is not a part of CDC processes [39]).
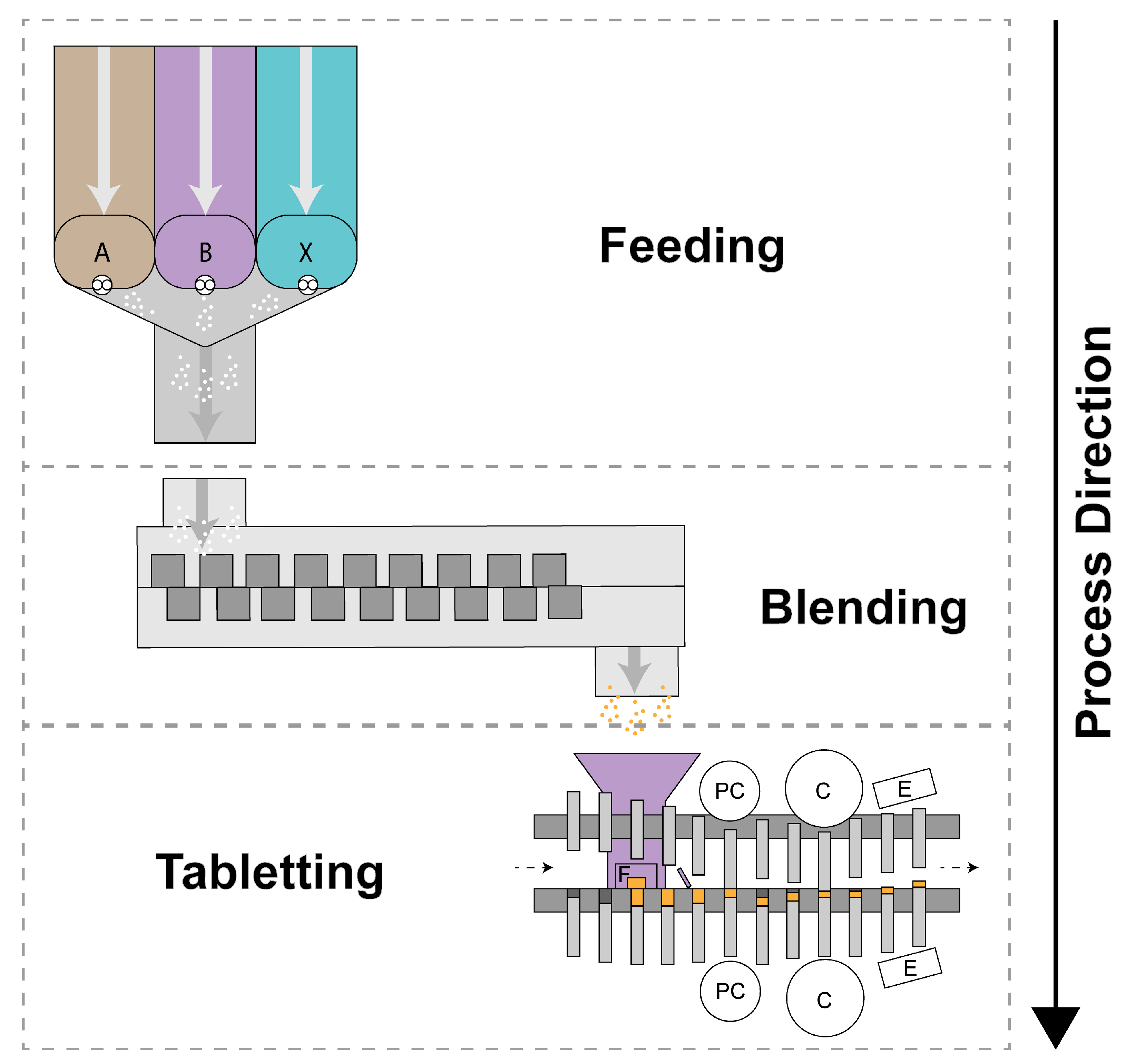
2. Powder Feeding
2.1. Feeding Introduction
2.2. Feeding Discussion
2.3. Feeding Summary
3. Blending
3.1. Blending Introduction
3.2. Blending Discussion
3.3. Blending Summary
A Perspective on Continuously Blending Cohesive Species
4. Tabletting
4.1. Tabletting Introduction
- Die filling;
- Compaction;
- Tablet ejection.
4.2. Tabletting Discussion
4.2.1. Die Filling Introduction
4.2.2. Die Filling Discussion
4.2.3. Compression Introduction
4.2.4. Compression Discussion
4.3. Tabletting Summary
5. Summary Table
| Unit Operation | Cohesion Effects Results in … | Cohesion Control or Compromise | Future Work /Considerations Δ | |
|---|---|---|---|---|
| Feeding | Inconsistent screw filling | Modifying bulk density and cohesive particle-particle contact through additives, such as Silica [5,47,57] | Understand and be able to modify thixotropic powder behaviour | |
| Increase/Decrease conveying screw speeds [57] | ||||
| Bridging/Arching | Refill Strategy [41,65] | DEM simulations exploring optimum hopper agitator design | ||
| Agitator Design | ||||
| Blending | Reduced micro-mixing | Increase in rpm (Fr) balanced by changes to system geometry to maintain macro [75,78,90] | ||
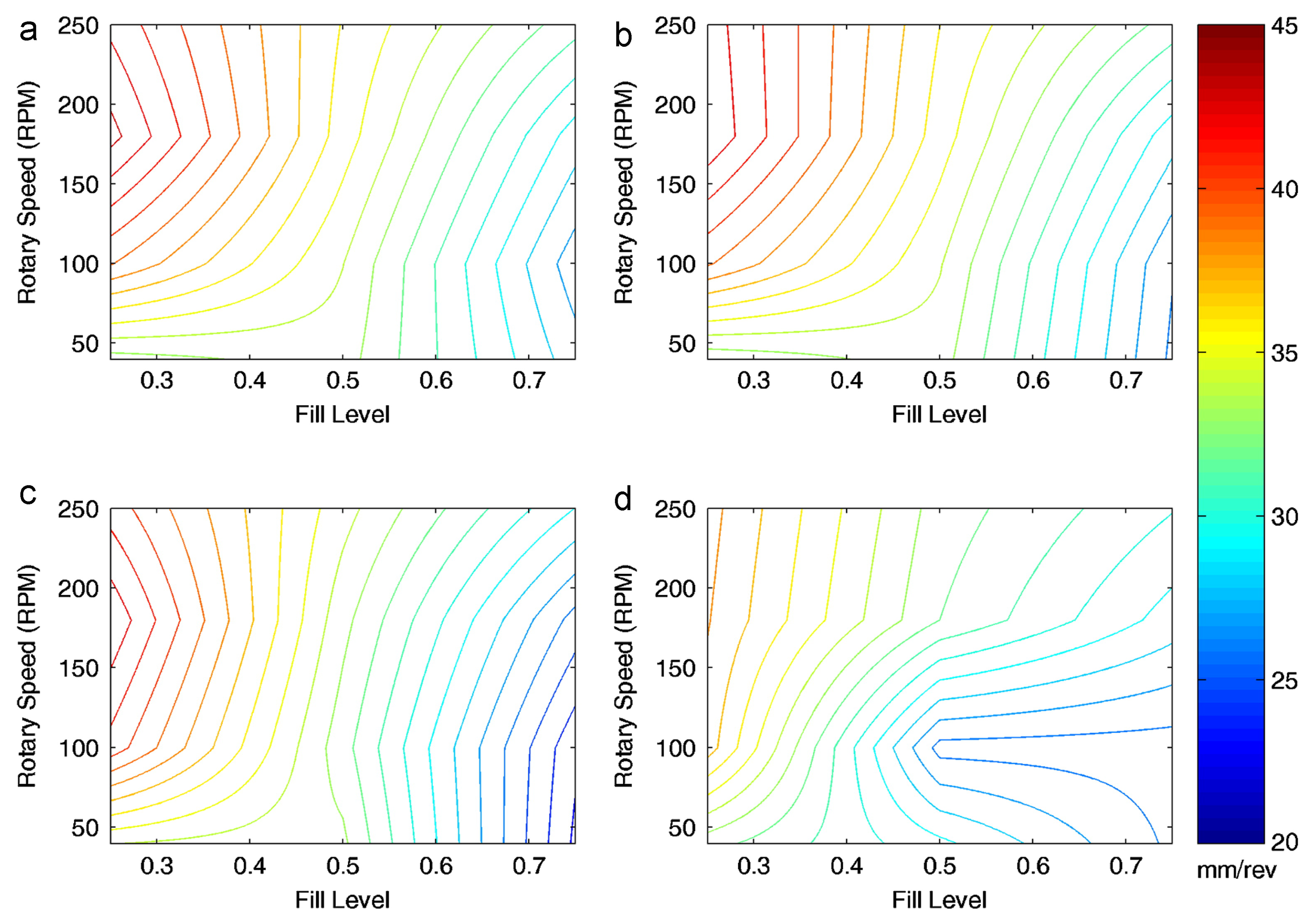
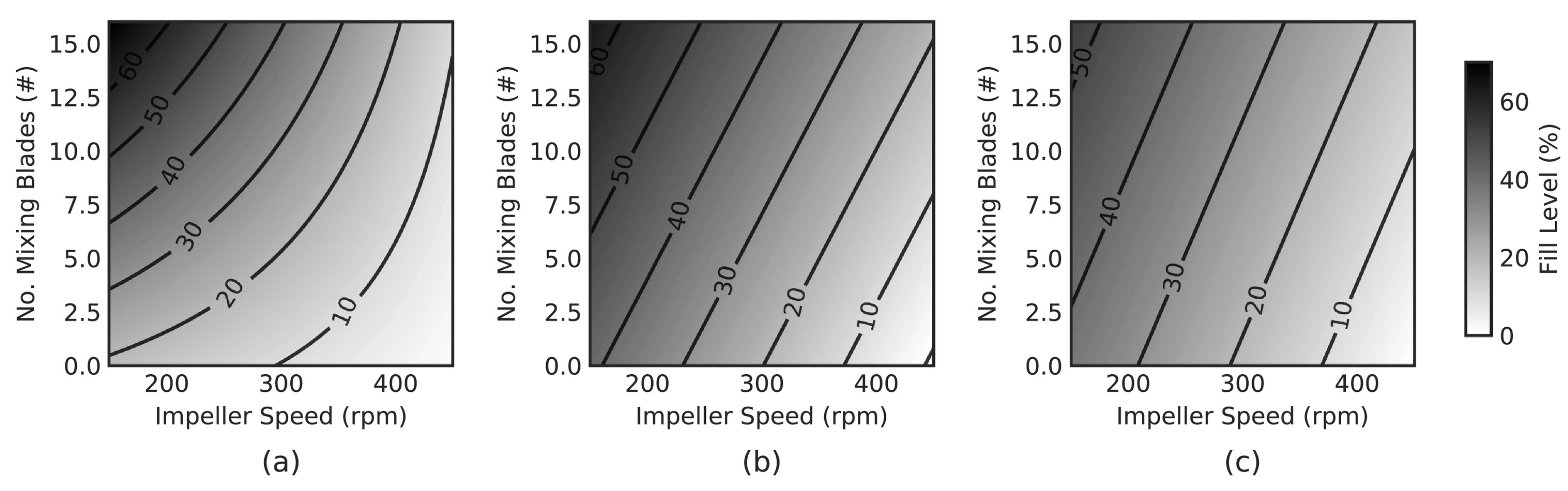
| Complex bulk behaviour, which results in poor mixing | Modify the three contributing factors: Fill level, Magnitude of Cohesion, and Froude Number [43,75,88,90] | |||
| Mechanistic understanding of how these factors interact [90] | ||||
| Tabletting | Find a more efficient way to find the right solvents | |||
| Die filling | Incomplete die fill and weight [102,110] | Spherical agglomeration [3] | Understand how spherical agglomeration will affect other CDC unit operations (feeding and blending) | |
| Investigate the possibility of a scale-up method as the will be hard as the process is difficult and time consuming on small scale | ||||
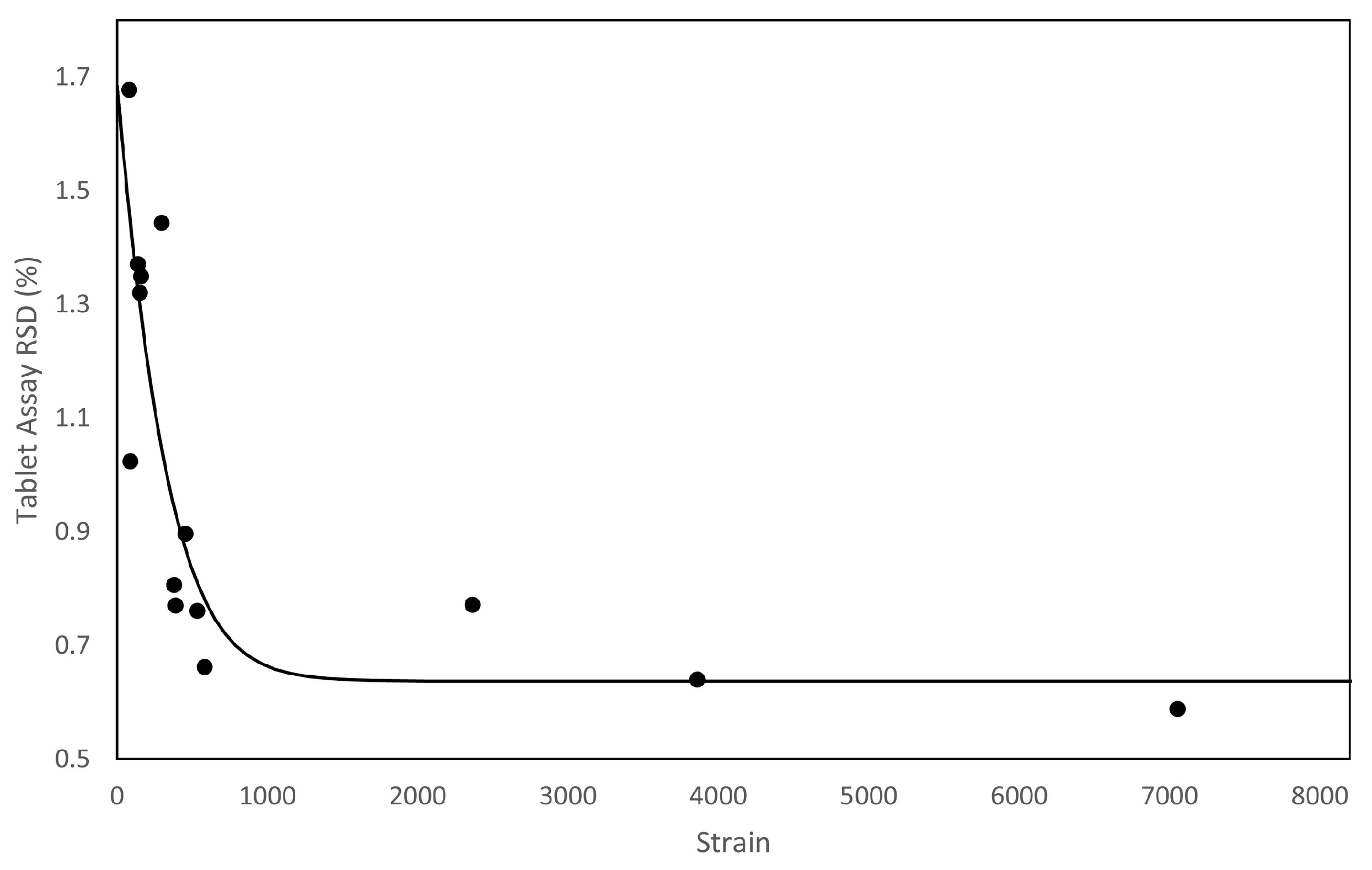
| Paddle speed [107] | Overlubrication can occur if the paddle speed is too high [115]. A compromise will need to be taken to ensure an increase of paddle speed will not effect tablet strength Δ | |||
| Introduction of air in the system acting like a lubricant [27] | As this can create an adverse pressure gradient which will then resist the motion of particles. Find the ranges when air introduction is beneficial by Quality by Design experiments Δ | |||
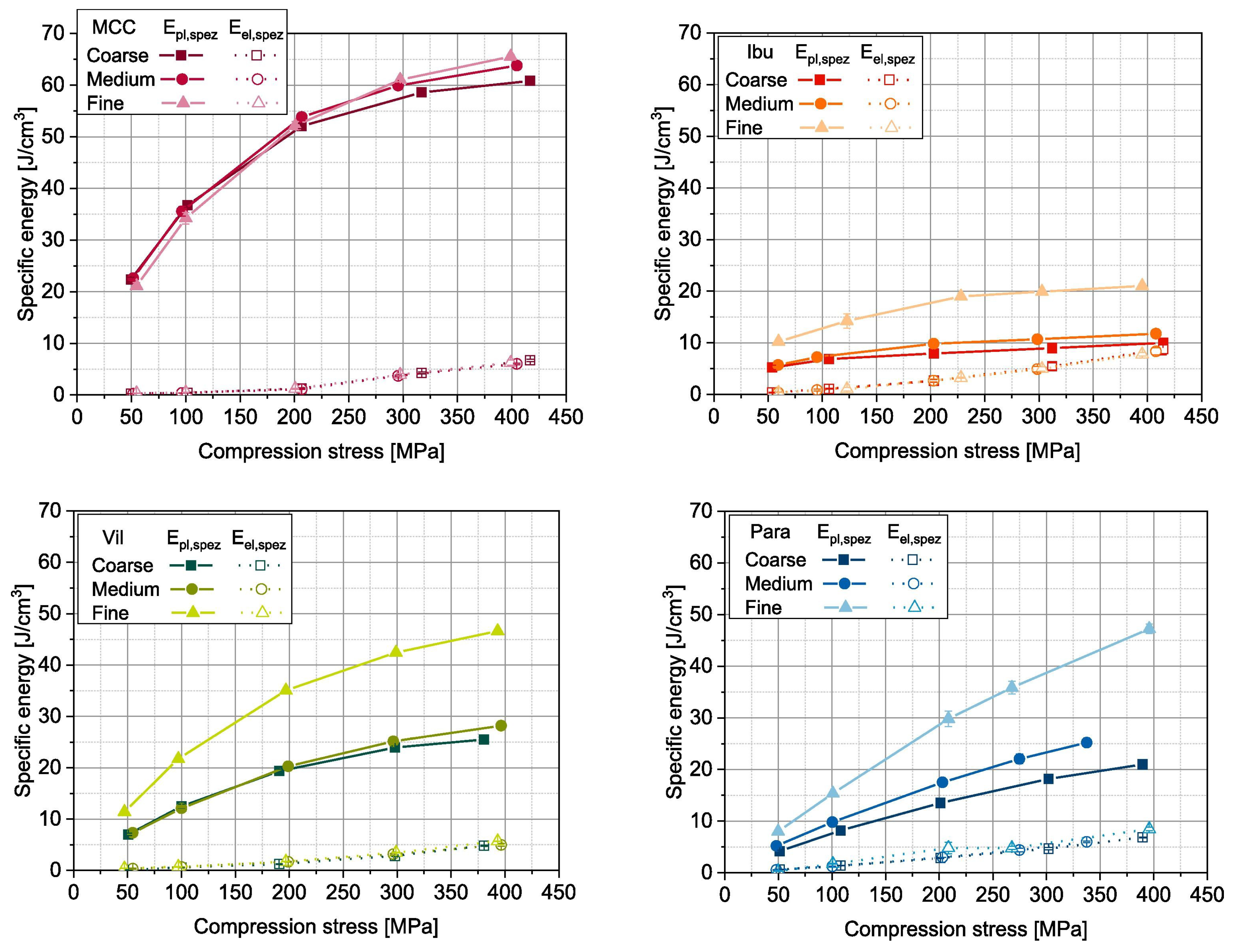
| Compaction | Better tabletability; generally lower particle size and higher surface energy results in stronger tablets but can have bad effects on dissolution if the tablet strength is too high [157] | Nano-silica and other novel glidants (magnesium aluminosilicate) can help promote better flowability and has little to no effect on tablet strength [151] | Understand the impacts of different types of nano-silica. Magnesium aluminosilicate will need to be tabletted with other common excipients and dissolution testing will to be conducted to assess the limitations | |
| Number of bonds is more important than the strength of the bond could be able to compromise lower surface energy/cohesivity if there is sufficient contact area gained during compaction | Understanding crystal structure fundamentally and how that changes material properties. This may be what is causing discrepancies regarding particle size and the tablet strength outcome [130] | |||
6. Conclusions
- Silication has benefits similar to glidants and lubricants as it can lower the cohesive behaviour of the powder and therefore increase flowability [6]. However, there are contradictions on whether silication negatively affects tabletability; this will need to be further investigate [67,145]. Alternative glidants, e.g., magnesium aluminosilicates, are a promising option however, more work needs to be carried out to understand the impact on tablet performance.
- Discrete Element Method (DEM) modelling, allowing researchers to create a digital twin(s) of an existing experiment and conduct statistical analysis on the simulated powder behaviour would allow researchers to gather metrics to quantify mixing/feeding performance (as discussed in Escotet-Espinoza et al. [80]) that were not accessible experimentally.
- Utilising triboelectric charging for the blending stage: static surface charge is developed on the surface of particles due to the strain given to the powder during mixing/transport [47], potentially allowing a formulation to be altered to promote attraction/repulsion between constituent species in order to gain a more-ordered well-mixed system.
- Spherical agglomeration/crystallisation can improve the flowability and tabletability of APIs, which is normally the most cohesive component of the tablet formulation [3,18]. However, further work needs to be performed to improve the solvent selection and process parameters to allow for scale-up [123].
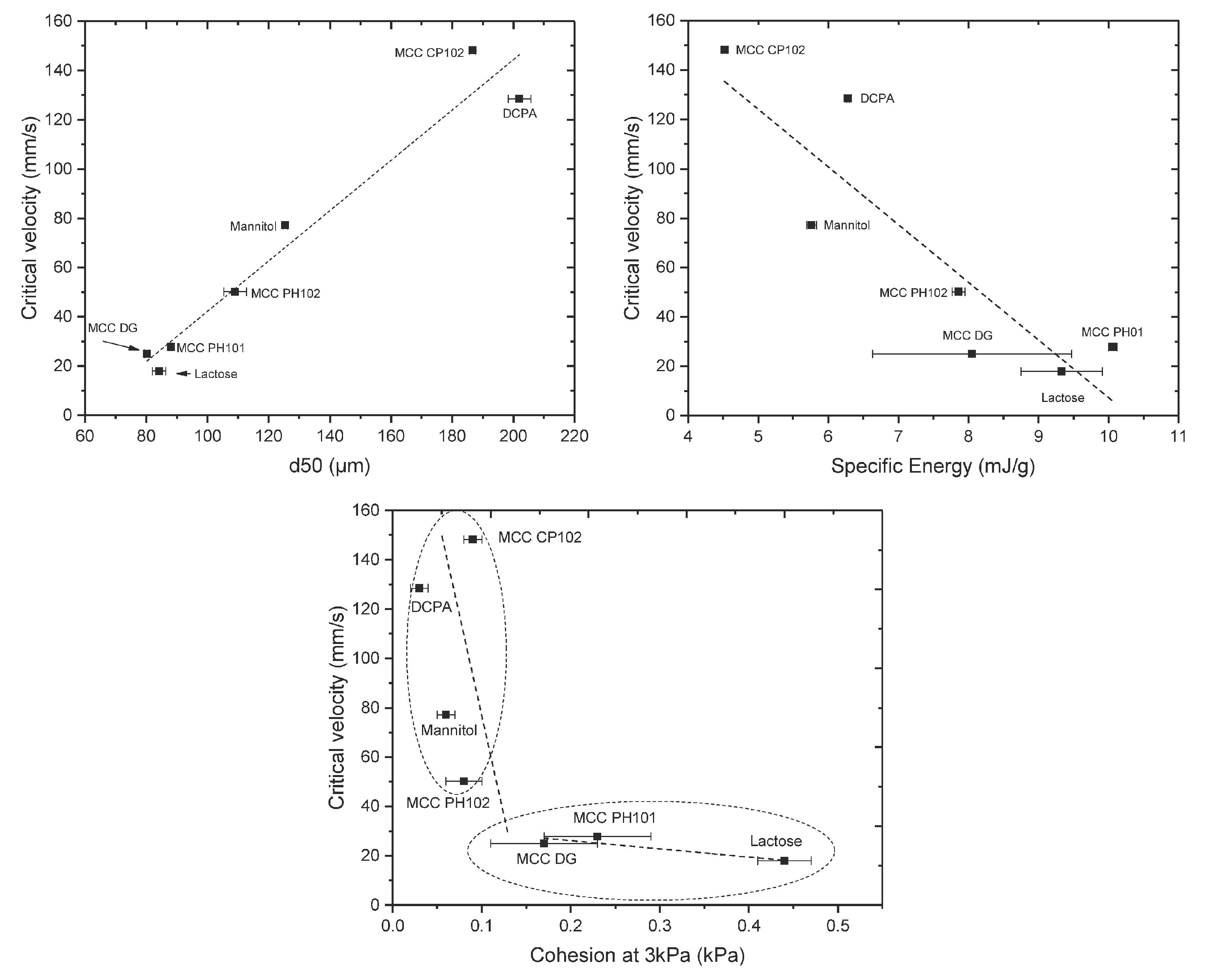
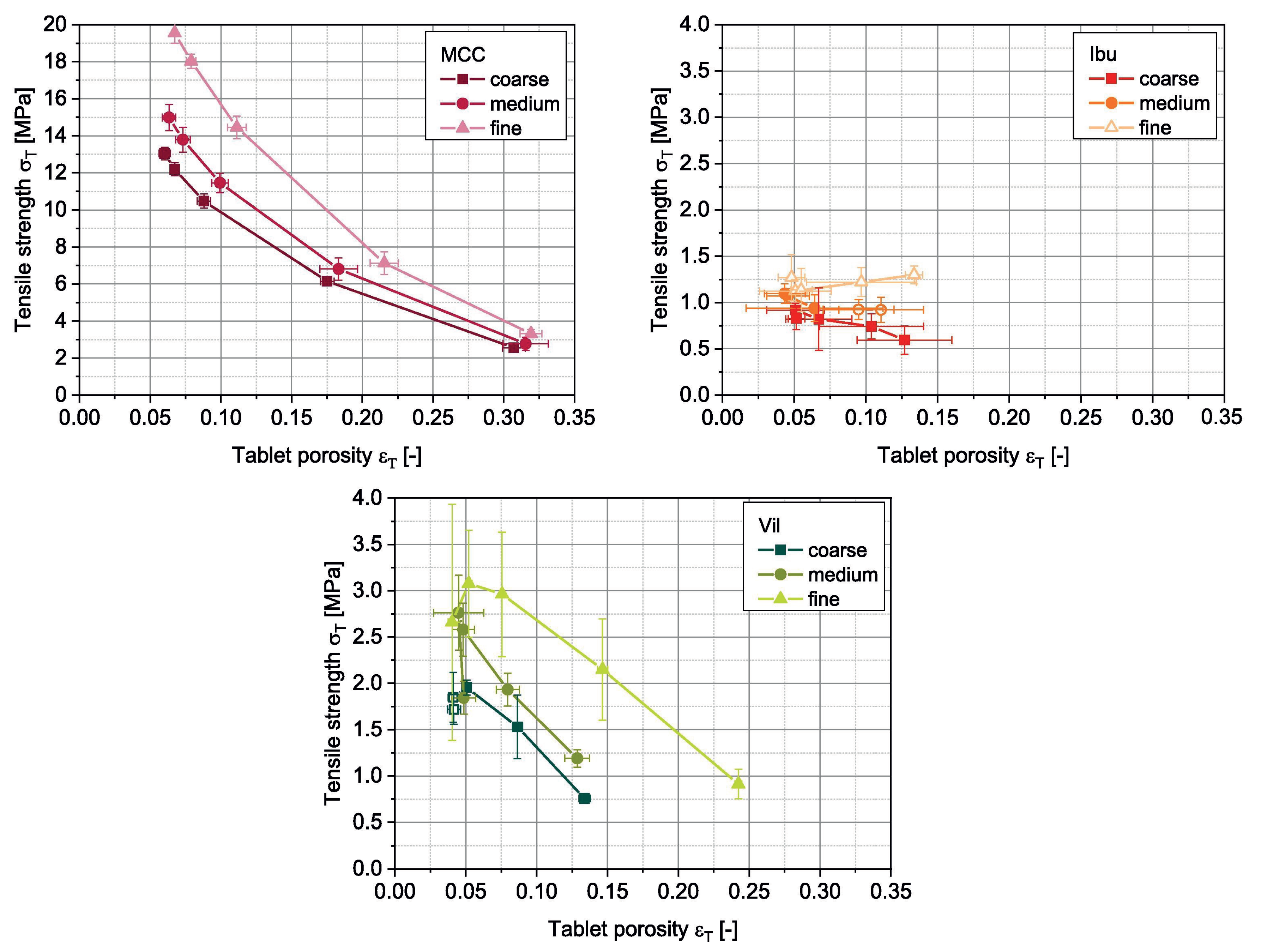
- The many discrepancies in the literature regarding the manner in which particle size affects the tabletability of the powder should be comprehensively addressed, as this represents an important gap in the fundamental understanding of powder compression [39,128]. Understanding which types of powders are affected by particle size and which are not could lead to compromises to have larger particle sizes to lower cohesivity and therefore improve flow while not affecting the tabletability.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CDC | Continuous Direct Compression |
| CQAs | Critical Quality Attributes |
| CMAs | Critical Material Attributes |
| API | Active Pharmaceutical Ingredient |
| FFC | Flow Function Coefficient |
| SEM | Scanning Electron Microscope |
| DEM | Discrete Element Method |
| MPS | Mesoporous Sillica |
| rpm | Revolutions Per Minuite |
| cBD | Conditioned Bulk Density |
| LIW | Loss in Weight |
| APAP | Acetaminophen |
| RSD | Relative Standard Deviation |
| PCA | Principle Component Analysis |
| RTD | Residence Time Distribution |
| MCC | Microcrystalline Cellulose |
| MgSt | Magnesium Stearate |
| MAS | Magnesium Aluminosilicate |
| TCP | Tricalcium Phosphate |
| mAPAP | Micronised Acetaminophen |
| pAPAP | Powdered Acetaminophen |
| sgAPAP | Special Granular Acetaminophen |
| RH | Relative Humidity |
| GMP | Good Manufacturing Practice |
| HVAC | Heating Ventilation & Air Conditioning |
| FT4 | Freeman Powder Rheometer |
| QESD | Quasi-emulsion solvent diffusion |
| DCP | Calcium hydrogen phosphate dehydrate |
References
- Vercruysse, J.; Delaet, U.; Van Assche, I.; Cappuyns, P.; Arata, F.; Caporicci, G.; De Beer, T.; Remon, J.P.; Vervaet, C. Stability and repeatability of a continuous twin screw granulation and drying system. Eur. J. Pharm. Biopharm. 2013, 85, 1031–1038. [Google Scholar] [CrossRef] [PubMed]
- Engisch, W.E.; Muzzio, F.J. Loss-in-Weight Feeding Trials Case Study: Pharmaceutical Formulation. J. Pharm. Innov. 2015, 10, 56–75. [Google Scholar] [CrossRef]
- Chattoraj, S.; Sun, C.C. Crystal and Particle Engineering Strategies for Improving Powder Compression and Flow Properties to Enable Continuous Tablet Manufacturing by Direct Compression. J. Pharm. Sci. 2018, 107, 968–974. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.X.; Marziano, I.; Bentham, A.C.; Litster, J.D.; White, E.T.; Howes, T. Influence of particle size on the direct compression of ibuprofen and its binary mixtures. Powder Technol. 2013, 240, 66–73. [Google Scholar] [CrossRef]
- Leung, L.Y.; Mao, C.; Srivastava, I.; Du, P.; Yang, C.Y. Flow Function of Pharmaceutical Powders Is Predominantly Governed by Cohesion, Not by Friction Coefficients. J. Pharm. Sci. 2017, 106, 1865–1873. [Google Scholar] [CrossRef] [PubMed]
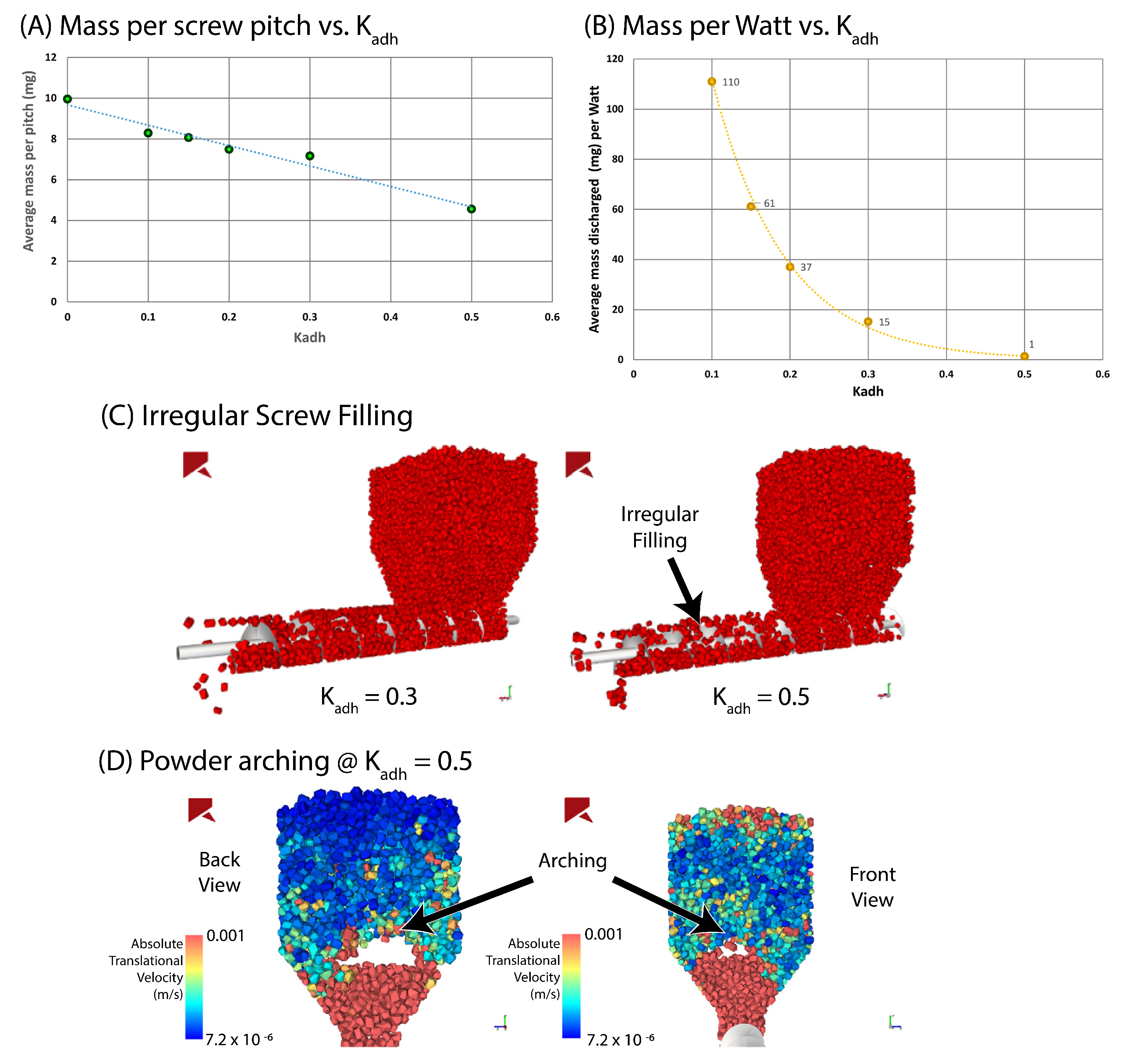
- Escotet-Espinoza, M.S.; Scicolone, J.V.; Moghtadernejad, S.; Sanchez, E.; Cappuyns, P.; Van Assche, I.; Di Pretoro, G.; Ierapetritou, M.; Muzzio, F.J. Improving Feedability of Highly Adhesive Active Pharmaceutical Ingredients by Silication. J. Pharm. Innov. 2021, 16, 279–292. [Google Scholar] [CrossRef]
- Visser, J. Van der Waals and other cohesive forces affecting powder fluidization. Powder Technol. 1989, 58, 1–10. [Google Scholar] [CrossRef]
- Juarez-Enriquez, E.; Olivas, G.I.; Zamudio-Flores, P.B.; Perez-Vega, S.; Salmeron, I.; Ortega-Rivas, E.; Sepulveda, D.R. A review on the influence of water on food powder flowability. J. Food Process Eng. 2022, 45, e14031. [Google Scholar] [CrossRef]
- Zafar, U.; Vivacqua, V.; Calvert, G.; Ghadiri, M.; Cleaver, J.S. A review of bulk powder caking. Powder Technol. 2017, 313, 389–401. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, Y.P. Growth of liquid bridge in AFM. J. Phys. D Appl. Phys. 2007, 40, 4368. [Google Scholar] [CrossRef]
- Hou, Q.; Dong, K.; Yu, A. DEM study of the flow of cohesive particles in a screw feeder. Powder Technol. 2014, 256, 529–539. [Google Scholar] [CrossRef]
- Allenspach, C.; Timmins, P.; Lumay, G.; Holman, J.; Minko, T. Loss-in-weight feeding, powder flow and electrostatic evaluation for direct compression hydroxypropyl methylcellulose (HPMC) to support continuous manufacturing. Int. J. Pharm. 2021, 596, 120259. [Google Scholar] [CrossRef] [PubMed]
- Karner, S.; Urbanetz, N.A. Arising of electrostatic charge in the mixing process and its influencing factors. Powder Technol. 2012, 226, 261–268. [Google Scholar] [CrossRef]
- Abouzeid, A.Z.M.; Fuerstenau, D.W. Effect of Humidity on Mixing of Particulate Solids. Ind. Eng. Chem. Process Des. Dev. 1972, 11, 296–301. [Google Scholar] [CrossRef]
- Beretta, M.; Hörmann, T.R.; Hainz, P.; Hsiao, W.K.; Paudel, A. Investigation into powder tribo–charging of pharmaceuticals. Part II: Sensitivity to relative humidity. Int. J. Pharm. 2020, 591, 120015. [Google Scholar] [CrossRef] [PubMed]
- Haycocks, N.; Goldschmidt, N.A.; Thomsen, U. Temperature & Humidity Requirements in Pharmaceutical Facilities. 2023. Available online: https://ispe.org/pharmaceutical-engineering/september-october-2021/temperature-humidity-requirements-pharmaceutical (accessed on 31 March 2023).
- Sun, C.C. Mechanism of moisture induced variations in true density and compaction properties of microcrystalline cellulose. Int. J. Pharm. 2008, 346, 93–101. [Google Scholar] [CrossRef]
- Chen, H.; Aburub, A.; Sun, C.C. Direct Compression Tablet Containing 99% Active Ingredient—A Tale of Spherical Crystallization. J. Pharm. Sci. 2019, 108, 1396–1400. [Google Scholar] [CrossRef]
- Sun, C.C. Decoding powder tabletability: Roles of particle adhesion and plasticity. J. Adhes. Sci. Technol. 2011, 25, 483–499. [Google Scholar] [CrossRef]
- Haywood, A.; Glass, B.D. Pharmaceutical excipients—Where do we begin? Aust. Prescr. 2011, 34, 112–114. [Google Scholar] [CrossRef]
- Jivraj, M.; Martini, L.G.; Thomson, C.M. An overview of the different excipients useful for the direct compression of tablets. Pharm. Sci. Technol. Today 2000, 3, 59–63. [Google Scholar] [CrossRef]
- Escotet-Espinoza, M.S. Phenomenological and Residence Time Distribution Models for Unit Operations in a Continuous Pharmaceutical Manufacturing Process. Ph.D. Thesis, Rutgers University-School of Graduate Studies, New Brunswick, NJ, USA, 2018; p. 312. [Google Scholar]
- Shah, U.V.; Olusanmi, D.; Narang, A.S.; Hussain, M.A.; Tobyn, M.J.; Hinder, S.J.; Heng, J.Y. Decoupling the contribution of surface energy and surface area on the cohesion of pharmaceutical powders. Pharm. Res. 2015, 32, 248–259. [Google Scholar] [CrossRef]
- Shah, R.B.; Tawakkul, M.A.; Khan, M.A. Comparative evaluation of flow for pharmaceutical powders and granules. AAPS PharmSciTech 2008, 9, 250–258. [Google Scholar] [CrossRef] [PubMed]
- Engisch, W.E.; Muzzio, F.J. Method for characterization of loss-in-weight feeder equipment. Powder Technol. 2012, 228, 395–403. [Google Scholar] [CrossRef]
- Mazumder, M.K.; Sims, R.A.; Biris, A.S.; Srirama, P.K.; Saini, D.; Yurteri, C.U.; Trigwell, S.; De, S.; Sharma, R. Twenty-first century research needs in electrostatic processes applied to industry and medicine. Chem. Eng. Sci. 2006, 61, 2192–2211. [Google Scholar] [CrossRef]
- Wu, C.Y.; Dihoru, L.; Cocks, A.C. The flow of powder into simple and stepped dies. Powder Technol. 2003, 134, 24–39. [Google Scholar] [CrossRef]
- Freeman, R.; Fu, X. Characterisation of power bulk, dynamic flow and shear properties in relation to die filling. Powder Metall. 2008, 51, 196–201. [Google Scholar] [CrossRef]
- De Boer, A.H.; Vromans, H.; Leur, C.F.; Bolhuis, G.K.; Kussendrager, K.D.; Bosch, H. Studies on tableting properties of lactose—Part III. The consolidation behaviour of sieve fractions of crystalline α-lactose monohydrate. Pharm. Weekbl. Sci. Ed. 1986, 8, 145–150. [Google Scholar] [CrossRef]
- Johansson, B.; Alderborn, G. The effect of shape and porosity on the compression behaviour and tablet forming ability of granular materials formed from microcrystalline cellulose. Eur. J. Pharm. Biopharm. 2001, 52, 347–357. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.Y.; Sun, C.C. Insights into the effect of compaction pressure and material properties on interfacial bonding strength of bilayer tablets. Powder Technol. 2019, 354, 867–876. [Google Scholar] [CrossRef]
- Cabiscol, R.; Shi, H.; Wünsch, I.; Magnanimo, V.; Finke, J.H.; Luding, S.; Kwade, A. Effect of particle size on powder compaction and tablet strength using limestone. Adv. Powder Technol. 2020, 31, 1280–1289. [Google Scholar] [CrossRef]
- El Gindy, N.A.; Samaha, M.W. Tensile strength of some pharmaceutical compacts and their relation to surface free energy. Int. J. Pharm. 1982, 13, 35–46. [Google Scholar] [CrossRef]
- Fichtner, F.; Mahlin, D.; Welch, K.; Gaisford, S.; Alderborn, G. Effect of surface energy on powder compactibility. Pharm. Res. 2008, 25, 2750–2759. [Google Scholar] [CrossRef] [PubMed]
- Luangtana-Anan, M.; Fell, J.T. Bonding mechanisms in tabletting. Int. J. Pharm. 1990, 60, 197–202. [Google Scholar] [CrossRef]
- Etzler, F.M.; Pisano, S. Tablet tensile strength: Role of surface free energy. Adv. Contact Angle Wettability Adhes. 2015, 2, 397–418. [Google Scholar]
- Pingali, K.; Mendez, R.; Lewis, D.; Michniak-Kohn, B.; Cuitino, A.; Muzzio, F. Mixing order of glidant and lubricant—Influence on powder and tablet properties. Int. J. Pharm. 2011, 409, 269–277. [Google Scholar] [CrossRef]
- Mills, L.A.; Sinka, I.C. Effect of particle size and density on the die fill of powders. Eur. J. Pharm. Biopharm. 2013, 84, 642–652. [Google Scholar] [CrossRef]
- Herting, M.G.; Kleinebudde, P. Roll compaction/dry granulation: Effect of raw material particle size on granule and tablet properties. Int. J. Pharm. 2007, 338, 110–118. [Google Scholar] [CrossRef]
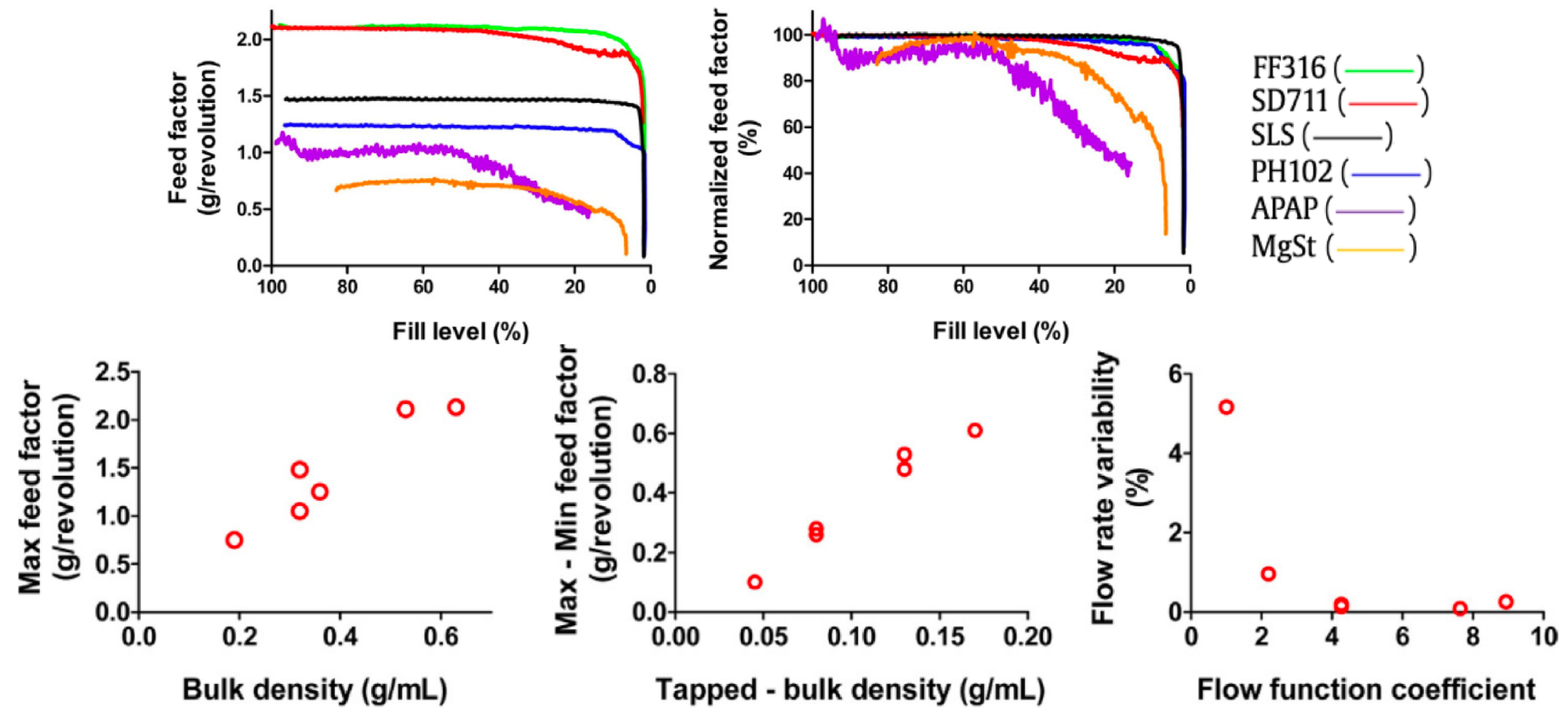
- Kehlenbeck, V.; Sommer, K. Possibilities to improve the short-term dosing constancy of volumetric feeders. Powder Technol. 2003, 138, 51–56. [Google Scholar] [CrossRef]
- Engisch, W.E.; Muzzio, F.J. Feedrate deviations caused by hopper refill of loss-in-weight feeders. Powder Technol. 2015, 283, 389–400. [Google Scholar] [CrossRef]
- Bekaert, B.; Van Snick, B.; Pandelaere, K.; Dhondt, J.; Di Pretoro, G.; De Beer, T.; Vervaet, C.; Vanhoorne, V. In-depth analysis of the long-term processability of materials during continuous feeding. Int. J. Pharm. 2022, 614, 121454. [Google Scholar] [CrossRef]
- Van Snick, B.; Holman, J.; Vanhoorne, V.; Kumar, A.; De Beer, T.; Remon, J.P.; Vervaet, C. Development of a continuous direct compression platform for low-dose drug products. Int. J. Pharm. 2017, 529, 329–346. [Google Scholar] [CrossRef]
- Simonaho, S.P.; Ketolainen, J.; Ervasti, T.; Toiviainen, M.; Korhonen, O. Continuous manufacturing of tablets with PROMIS-line—Introduction and case studies from continuous feeding, blending and tableting. Eur. J. Pharm. Sci. 2016, 90, 38–46. [Google Scholar] [CrossRef]
- García-Muñoz, S.; Butterbaugh, A.; Leavesley, I.; Manley, L.F.; Slade, D.; Bermingham, S. A flowsheet model for the development of a continuous process for pharmaceutical tablets: An industrial perspective. AIChE J. 2018, 64, 511–525. [Google Scholar] [CrossRef]
- Gyürkés, M.; Madarász, L.; Köte, Á.; Domokos, A.; Mészáros, D.; Beke, K.; Nagy, B.; Marosi, G.; Pataki, H.; Nagy, Z.K.; et al. Process design of continuous powder blending using residence time distribution and feeding models. Pharmaceutics 2020, 12, 1119. [Google Scholar] [CrossRef] [PubMed]
- Beretta, M.; Hörmann, T.R.; Hainz, P.; Hsiao, W.K.; Paudel, A. Investigation into powder tribo-charging of pharmaceuticals. Part I: Process-induced charge via twin-screw feeding. Int. J. Pharm. 2020, 591, 120014. [Google Scholar] [CrossRef]
- Windows-Yule, C.R.; Neveu, A. Calibration of DEM simulations for dynamic particulate systems. Pap. Phys. 2022, 14, 140010. [Google Scholar] [CrossRef]
- Rhodes, M.J. Introduction to Particle Technology; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Windows-Yule, K.; Nicuşan, L.; Herald, M.T.; Manger, S.; Parker, D. Comparison with other techniques. In Positron Emission Particle Tracking: A Comprehensive Guide; IOP Publishing: Bristol, UK, 2022. [Google Scholar]
- Thornton, C. Granular Dynamics, Contact Mechanics and Particle System Simulations: A DEM Study; Springer’s International Publishing: Berlin/Heidelberg, Germany, 2015; Volume 24, pp. 1–195. [Google Scholar] [CrossRef]
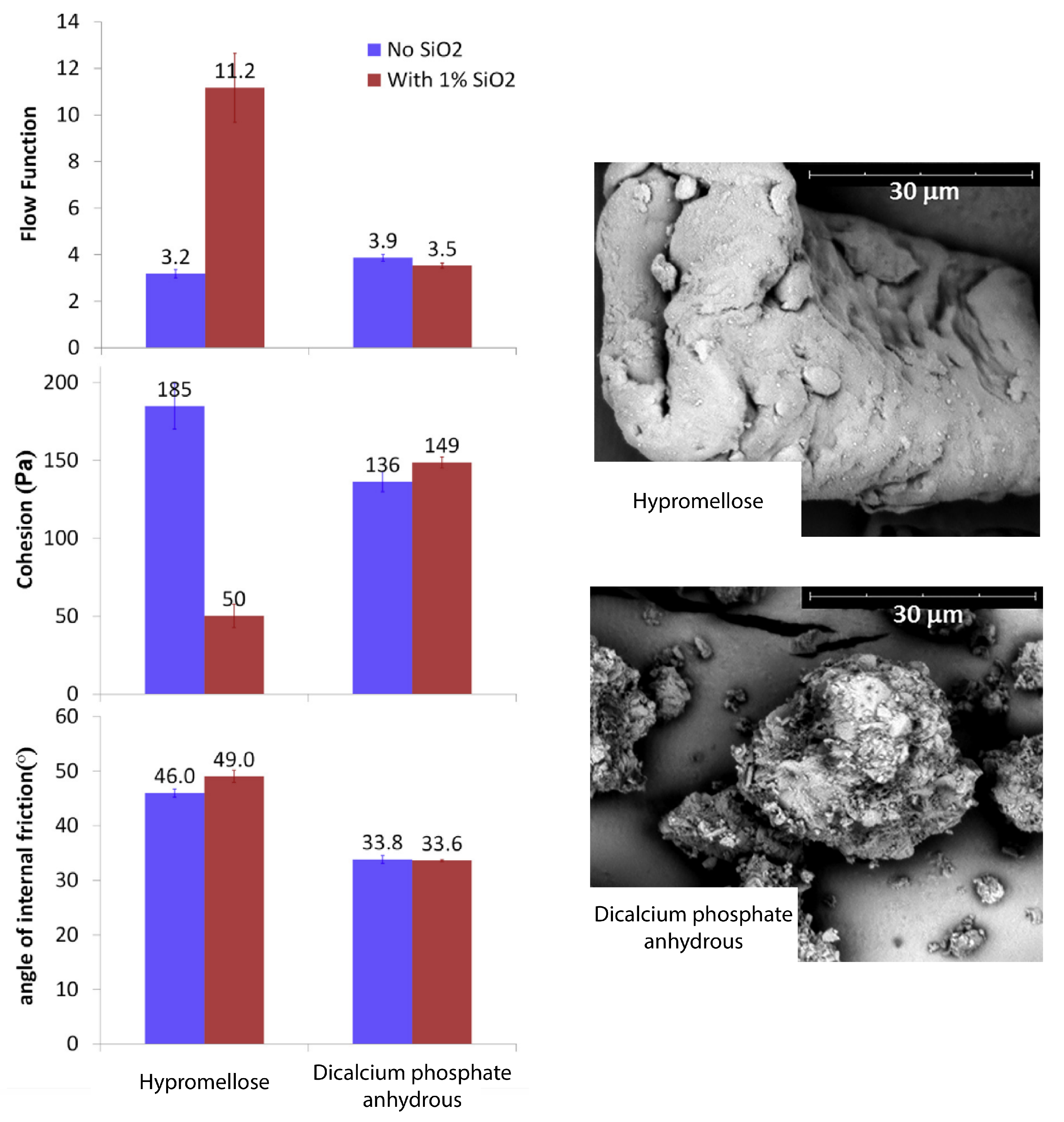
- Kojima, T.; Elliott, J.A. Effect of silica nanoparticles on the bulk flow properties of fine cohesive powders. Chem. Eng. Sci. 2013, 101, 315–328. [Google Scholar] [CrossRef]
- Meyer, K.; Zimmermann, I. Effect of glidants in binary powder mixtures. Powder Technol. 2004, 139, 40–54. [Google Scholar] [CrossRef]
- Tran, D.T.; Majerová, D.; Veselý, M.; Kulaviak, L.; Ruzicka, M.C.; Zámostný, P. On the mechanism of colloidal silica action to improve flow properties of pharmaceutical excipients. Int. J. Pharm. 2019, 556, 383–394. [Google Scholar] [CrossRef]
- López, A.; Vivacqua, V.; Hammond, R.; Ghadiri, M. Analysis of screw feeding of faceted particles by discrete element method. Powder Technol. 2020, 367, 474–486. [Google Scholar] [CrossRef]
- Krantz, M.; Zhang, H.; Zhu, J. Characterization of powder flow: Static and dynamic testing. Powder Technol. 2009, 194, 239–245. [Google Scholar] [CrossRef]
- Lumay, G.; Pillitteri, S.; Marck, M.; Monsuur, F.; Pauly, T.; Ribeyre, Q.; Francqui, F.; Vandewalle, N. Influence of mesoporous silica on powder flow and electrostatic properties on short and long term. J. Drug Deliv. Sci. Technol. 2019, 53, 101192. [Google Scholar] [CrossRef]
- Neveu, A.; Francqui, F.; Lumay, G. Measuring powder flow properties in a rotating drum. Measurement 2022, 200, 111548. [Google Scholar] [CrossRef]
- Patel, D.; Francqui, F.; Defrêne, R.J.L.; Neveu, A. Influence of additives on the electrostatic charge build-up of excipients. Powder Technol. 2003, 132, 192–198. [Google Scholar]
- Ramirez-Dorronsoro, J.C.; Jacko, R.B.; Kildsig, D.O. Chargeability measurements of selected pharmaceutical dry powders to assess their electrostatic charge control capabilities. AAPS PharmSciTech 2006, 7, 103. [Google Scholar] [CrossRef] [PubMed]
- Escotet-Espinoza, M.S.; Moghtadernejad, S.; Oka, S.; Wang, Z.; Wang, Y.; Roman-Ospino, A.; Schäfer, E.; Cappuyns, P.; Van Assche, I.; Futran, M.; et al. Effect of material properties on the residence time distribution (RTD) characterization of powder blending unit operations. Part II of II: Application of models. Powder Technol. 2019, 344, 525–544. [Google Scholar] [CrossRef]
- Escotet-Espinoza, M.S.; Moghtadernejad, S.; Scicolone, J.; Wang, Y.; Pereira, G.; Schäfer, E.; Vigh, T.; Klingeleers, D.; Ierapetritou, M.; Muzzio, F.J. Using a material property library to find surrogate materials for pharmaceutical process development. Powder Technol. 2018, 339, 659–676. [Google Scholar] [CrossRef]
- Shier, A.P.; Kumar, A.; Mercer, A.; Majeed, N.; Doshi, P.; Blackwood, D.O.; Verrier, H.M. Development of a predictive model for gravimetric powder feeding from an API-rich materials properties library. Int. J. Pharm. 2022, 625, 122071. [Google Scholar] [CrossRef]
- Yadav, I.K.; Holman, J.; Meehan, E.; Tahir, F.; Khoo, J.; Taylor, J.; Benedetti, A.; Aderinto, O.; Bajwa, G. Influence of material properties and equipment configuration on loss-in- weight feeder performance for drug product continuous manufacture. Powder Technol. 2019, 348, 126–137. [Google Scholar] [CrossRef]
- De Souter, L.; Waeytens, R.; Van Hauwermeiren, D.; Grymonpré, W.; Bekaert, B.; Nopens, I.; De Beer, T. Elucidation of the powder flow pattern in a twin-screw LIW-feeder for various refill regimes. Int. J. Pharm. 2023, 631, 122534. [Google Scholar] [CrossRef]
- Mužíková, J.; Louženská, M.; Pekárek, T. A study of compression process and properties of tablets with microcrystalline cellulose and colloidal silicon dioxide. Acta Pol. Pharm.—Drug Res. 2016, 73, 1259–1265. [Google Scholar]
- Apeji, Y.E.; Olowosulu, A.K. Quantifying the effect of glidant on the compaction and tableting properties of paracetamol granules. J. Res. Pharm. 2020, 24, 44–55. [Google Scholar] [CrossRef]
- Uzunović, A.; Vranić, E. Effect of magnesium stearate concentration on dissolution properties of ranitidine hydrochloride coated tablets. Biomol. Biomed. 2007, 7, 279–283. [Google Scholar] [CrossRef] [PubMed]
- Bolhuis, G.K.; Anthony Armstrong, N. Excipients for Direct Compaction—An Update. Pharm. Dev. Technol. 2006, 11, 111–124. [Google Scholar] [CrossRef]
- Huang, Z.; Scicolone, J.V.; Gurumuthy, L.; Davé, R.N. Flow and bulk density enhancements of pharmaceutical powders using a conical screen mill: A continuous dry coating device. Chem. Eng. Sci. 2015, 125, 209–224. [Google Scholar] [CrossRef]
- Bridgwater, J. Fundamental powder mixing mechanisms. Powder Technol. 1976, 15, 215–236. [Google Scholar] [CrossRef]
- Cooke, M.H.; Stephens, D.J.; Bridgwater, J. Powder mixing—A literature survey. Powder Technol. 1976, 15, 1–20. [Google Scholar] [CrossRef]
- Laurent, B.; Bridgwater, J. Influence of agitator design on powder flow. Chem. Eng. Sci. 2002, 57, 3781–3793. [Google Scholar] [CrossRef]
- Van Snick, B.; Grymonpré, W.; Dhondt, J.; Pandelaere, K.; Di Pretoro, G.; Remon, J.P.; De Beer, T.; Vervaet, C.; Vanhoorne, V. Impact of blend properties on die filling during tableting. Int. J. Pharm. 2018, 549, 476–488. [Google Scholar] [CrossRef]
- Palmer, J.; Reynolds, G.K.; Tahir, F.; Yadav, I.K.; Meehan, E.; Holman, J.; Bajwa, G. Mapping key process parameters to the performance of a continuous dry powder blender in a continuous direct compression system. Powder Technol. 2020, 362, 659–670. [Google Scholar] [CrossRef]
- Venables, H.J.; Wells, J.I. Powder mixing. Drug Dev. Ind. Pharm. 2001, 27, 599–612. [Google Scholar] [CrossRef]
- Asachi, M.; Nourafkan, E.; Hassanpour, A. A review of current techniques for the evaluation of powder mixing. Adv. Powder Technol. 2018, 29, 1525–1549. [Google Scholar] [CrossRef]
- Portillo, P.M.; Vanarase, A.U.; Ingram, A.; Seville, J.K.; Ierapetritou, M.G.; Muzzio, F.J. Investigation of the effect of impeller rotation rate, powder flow rate, and cohesion on powder flow behavior in a continuous blender using PEPT. Chem. Eng. Sci. 2010, 65, 5658–5668. [Google Scholar] [CrossRef]
- Poux, M.; Fayolle, P.; Bertrand, J.; Bridoux, D.; Bousquet, J. Powder mixing: Some practical rules applied to agitated systems. Powder Technol. 1991, 68, 213–234. [Google Scholar] [CrossRef]
- Sebastian Escotet-Espinoza, M.; Moghtadernejad, S.; Oka, S.; Wang, Y.; Roman-Ospino, A.; Schäfer, E.; Cappuyns, P.; Van Assche, I.; Futran, M.; Ierapetritou, M.; et al. Effect of tracer material properties on the residence time distribution (RTD) of continuous powder blending operations. Part I of II: Experimental evaluation. Powder Technol. 2019, 342, 744–763. [Google Scholar] [CrossRef]
- Gao, Y.; Vanarase, A.; Muzzio, F.; Ierapetritou, M. Characterizing continuous powder mixing using residence time distribution. Chem. Eng. Sci. 2011, 66, 417–425. [Google Scholar] [CrossRef]
- Vanarase, A.U.; Muzzio, F.J. Effect of operating conditions and design parameters in a continuous powder mixer. Powder Technol. 2011, 208, 26–36. [Google Scholar] [CrossRef]
- Fan, L.; Chen, Y.m.; Lai, F. Recent developments in solids mixing. Powder Technol. 1990, 61, 255–287. [Google Scholar] [CrossRef]
- Rosato, A.D.; Windows-Yule, C. Segregation in Vibrated Granular Systems; Academic Press: Cambridge, MA, USA, 2020; pp. 197–218. [Google Scholar]
- Rennie, P.R.; Chen, X.D.; Hargreaves, C.; MacKereth, A.R. Study of the cohesion of dairy powders. J. Food Eng. 1999, 39, 277–284. [Google Scholar] [CrossRef]
- De Villiers, M.M. Description of the kinetics of the deagglomeration of drug particle agglomerates during powder mixing. Int. J. Pharm. 1997, 151, 1–6. [Google Scholar] [CrossRef]
- Mehrotra, A.; Muzzio, F.J.; Shinbrot, T. Spontaneous separation of charged grains. Phys. Rev. Lett. 2007, 99, 058001. [Google Scholar] [CrossRef] [PubMed]
- Bekaert, B.; Grymonpré, W.; Novikova, A.; Vervaet, C.; Vanhoorne, V. Impact of blend properties and process variables on the blending performance. Int. J. Pharm. 2022, 613, 121421. [Google Scholar] [CrossRef] [PubMed]
- Vanarase, A.U.; Osorio, J.G.; Muzzio, F.J. Effects of powder flow properties and shear environment on the performance of continuous mixing of pharmaceutical powders. Powder Technol. 2013, 246, 63–72. [Google Scholar] [CrossRef]
- Gao, Y.; Ierapetritou, M.; Muzzio, F. Periodic section modeling of convective continuous powder mixing processes. AIChE J. 2012, 58, 69–78. [Google Scholar] [CrossRef]
- Portillo, P.M.; Ierapetritou, M.G.; Muzzio, F.J. Characterization of continuous convective powder mixing processes. Powder Technol. 2007, 182, 368–378. [Google Scholar] [CrossRef]
- Werner, D.; Davison, H.; Robinson, E.; Sykes, J.; Seville, J.; Wellings, A.; Bhattacharya, S.; Monsalve, D.S.; Wheldon, T.K.; Windows-Yule, C. Effect of system composition on mixing in binary fluidised beds. Chem. Eng. Sci. 2023, 271, 118562. [Google Scholar] [CrossRef]
- Goldhirsch, I. Introduction to granular temperature. Powder Technol. 2008, 182, 130–136. [Google Scholar] [CrossRef]
- Ogawa, S. Multitemperature theory of granular materials. In Proceedings of the US-Japan Seminar on Continuum Mechanical and Statistical Approaches in the Mechanics of Granular Materials, Sendai, Japan, 5–9 June 1978; pp. 208–217. [Google Scholar]
- Gao, Y.; Muzzio, F.J.; Ierapetritou, M.G. Optimizing continuous powder mixing processes using periodic section modeling. Chem. Eng. Sci. 2012, 80, 70–80. [Google Scholar] [CrossRef]
- Sarkar, A.; Wassgren, C.R. Simulation of a continuous granular mixer: Effect of operating conditions on flow and mixing. Chem. Eng. Sci. 2009, 64, 2672–2682. [Google Scholar] [CrossRef]
- Tomita, Y.; Nagato, T.; Takeuchi, Y.; Takeuchi, H. Control of residence time of pharmaceutical powder in a continuous mixer with impeller and scraper. Int. J. Pharm. 2020, 586, 119520. [Google Scholar] [CrossRef]
- Tran, D.; Komínová, P.; Kulaviak, L.; Zámostnỳ, P. Evaluation of multifunctional magnesium aluminosilicate materials as novel family of glidants in solid dosage products. Int. J. Pharm. 2021, 592, 120054. [Google Scholar] [CrossRef] [PubMed]
- Toson, P.; Siegmann, E.; Trogrlic, M.; Kureck, H.; Khinast, J.; Jajcevic, D.; Doshi, P.; Blackwood, D.; Bonnassieux, A.; Daugherity, P.D.; et al. Detailed modeling and process design of an advanced continuous powder mixer. Int. J. Pharm. 2018, 552, 288–300. [Google Scholar] [CrossRef] [PubMed]
- Kale, D.P.; Zode, S.S.; Bansal, A.K. Challenges in translational development of pharmaceutical cocrystals. J. Pharm. Sci. 2017, 106, 457–470. [Google Scholar] [CrossRef] [PubMed]
- Zakhvatayeva, A.; Zhong, W.; Makroo, H.A.; Hare, C.; Wu, C.Y. An experimental study of die filling of pharmaceutical powders using a rotary die filling system. Int. J. Pharm. 2018, 553, 84–96. [Google Scholar] [CrossRef] [PubMed]
- Schomberg, A.K.; Kwade, A.; Finke, J.H. The challenge of die filling in rotary presses—A systematic study of material properties and process parameters. Pharmaceutics 2020, 12, 248. [Google Scholar] [CrossRef] [PubMed]
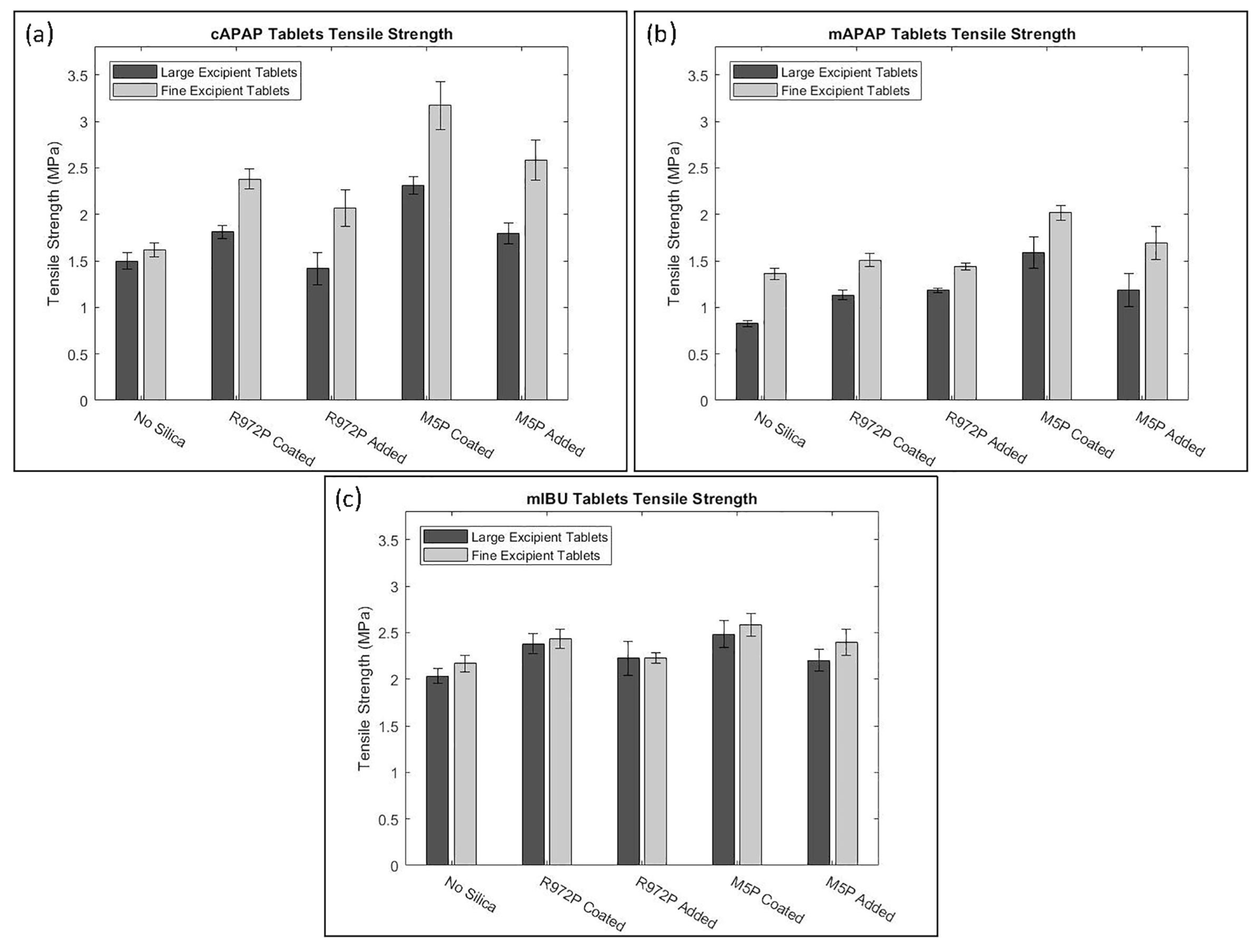
- Qu, L.; Stewart, P.J.; Hapgood, K.P.; Lakio, S.; Morton, D.A.; Zhou, Q.T. Single-step coprocessing of cohesive powder via mechanical dry coating for direct tablet compression. J. Pharm. Sci. 2017, 106, 159–167. [Google Scholar] [CrossRef] [PubMed]
- Baserinia, R.; Sinka, I.C. Powder die filling under gravity and suction fill mechanisms. Int. J. Pharm. 2019, 563, 135–155. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Zakhvatayeva, A.; Zhang, L.; Wu, Z.F.; Sun, P.; Wu, C.Y. Flow behaviour of pharmaceutical powders during rotary die filling with a paddle feeder. Int. J. Pharm. 2020, 585, 119547. [Google Scholar] [CrossRef]
- Jackson, S.; Sinka, I.C.; Cocks, A.C. The effect of suction during die fill on a rotary tablet press. Eur. J. Pharm. Biopharm. 2007, 65, 253–256. [Google Scholar] [CrossRef]
- Goh, H.P.; Heng, P.W.S.; Liew, C.V. Understanding effects of process parameters and forced feeding on die filling. Eur. J. Pharm. Sci. 2018, 122, 105–115. [Google Scholar] [CrossRef]
- Han, X.; Jallo, L.; To, D.; Ghoroi, C.; Davé, R. Passivation of high-surface-energy sites of milled ibuprofen crystals via dry coating for reduced cohesion and improved flowability. J. Pharm. Sci. 2013, 102, 2282–2296. [Google Scholar] [CrossRef]
- Zakhvatayeva, A.; Hare, C.; Wu, C.Y. Size-induced segregation during die filling. Int. J. Pharm. X 2019, 1, 100032. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.Y. DEM simulations of die filling during pharmaceutical tabletting. Particuology 2008, 6, 412–418. [Google Scholar] [CrossRef]
- Mittal, B. How to Develop Robust Solid Oral Dosage Forms: From Conception to Post-Approval; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Bansal, A.K.; Balwani, G.; Sheokand, S. Critical Material Attributes in Wet Granulation; Academic Press: Cambridge, MA, USA, 2019; pp. 421–453. [Google Scholar]
- Eidevåg, T.; Abrahamsson, P.; Eng, M.; Rasmuson, A. Modeling of dry snow adhesion during normal impact with surfaces. Powder Technol. 2020, 361, 1081–1092. [Google Scholar] [CrossRef]
- Peeters, E.; Beer, T.D.; Vervaet, C.; Remon, J.p.; Peeters, E.; Beer, T.D.; Vervaet, C.; Remon, J.p. Reduction of tablet weight variability by optimizing paddle speed in the forced feeder of a high-speed rotary tablet press forced feeder of a high-speed rotary tablet press. Drug Dev. Ind. Pharm. 2015, 41, 530–539. [Google Scholar] [CrossRef] [PubMed]
- Kushner, J.; Moore, F. Scale-up model describing the impact of lubrication on tablet tensile strength. Int. J. Pharm. 2010, 399, 19–30. [Google Scholar] [CrossRef]
- Mosig, J.; Kleinebudde, P. Critical evaluation of root causes of the reduced compactability after roll compaction/dry granulation. J. Pharm. Sci. 2015, 104, 1108–1118. [Google Scholar] [CrossRef] [PubMed]
- Almaya, A.; Aburub, A. Effect of Particle Size on Compaction of Materials with Different Deformation Mechanisms with and without Lubricants. Aaps Pharmscitech 2008, 9, 414–418. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Wu, C.Y.; Thornton, C. The effects of air and particle density difference on segregation of powder mixtures during die filling. Chem. Eng. Sci. 2011, 66, 661–673. [Google Scholar] [CrossRef]
- Schneider, L.C.; Sinka, I.C.; Cocks, A.C. Characterisation of the flow behaviour of pharmaceutical powders using a model die-shoe filling system. Powder Technol. 2007, 173, 59–71. [Google Scholar] [CrossRef]
- Kukkar, V.; Anand, V.; Kataria, M.; Gera, M.; Choudhury, P.K. Mixing and formulation of low dose drugs: Underlying problems and solutions. Thai J. Pharm. Sci 2008, 32, 43–58. [Google Scholar]
- Byrne, F.P.; Jin, S.; Paggiola, G.; Petchey, T.H.M.; Clark, J.H.; Farmer, T.J.; Hunt, A.J.; Robert McElroy, C.; Sherwood, J. Tools and techniques for solvent selection: Green solvent selection guides. Sustain. Chem. Process. 2016, 4, 7. [Google Scholar] [CrossRef]
- Javadzadeh, Y.; Vazifehasl, Z.; Maleki Dizahj, S.; Mokhtarpor, M. Spherical crystallization of drugs. Acta Pharm. 2012, 62, 1–14. [Google Scholar] [CrossRef]
- Pitt, K.; Peña, R.; Tew, J.D.; Pal, K.; Smith, R.; Nagy, Z.K.; Litster, J.D. Particle design via spherical agglomeration: A critical review of controlling parameters, rate processes and modelling. Powder Technol. 2018, 326, 327–343. [Google Scholar] [CrossRef]
- Quodbach, J.; Kleinebudde, P. A critical review on tablet disintegration. Pharm. Dev. Technol. 2016, 21, 763–774. [Google Scholar] [CrossRef]
- Nicolas, V.; Chambin, O.; Andrès, C.; Rochat-Gonthier, M.H.; Pourcelot, Y. Preformulation: Effect of moisture content on microcrystalline cellulose (Avicel PH-302) and its consequences on packing performances. Drug Dev. Ind. Pharm. 1999, 25, 1137–1142. [Google Scholar] [CrossRef]
- Tye, C.K.; Sun, C.; Amidon, G.E. Evaluation of the effects of tableting speed on the relationships between compaction pressure, tablet tensile strength, and tablet solid fraction. J. Pharm. Sci. 2005, 94, 465–472. [Google Scholar] [CrossRef] [PubMed]
- Osei-Yeboah, F.; Zhang, M.; Feng, Y.; Sun, C.C. A formulation strategy for solving the overgranulation problem in high shear wet granulation. J. Pharm. Sci. 2014, 103, 2434–2440. [Google Scholar] [CrossRef]
- McKenna, A.; McCafferty, D.F. Effect of particle size on the compaction mechanism and tensile strength of tablets. J. Pharm. Pharmacol. 1982, 34, 347–351. [Google Scholar] [CrossRef] [PubMed]
- Hallam, C.N.; Gabbott, I.P. Increasing tensile strength by reducing particle size for extrudate-based tablet formulations. J. Drug Deliv. Sci. Technol. 2019, 52, 825–830. [Google Scholar] [CrossRef]
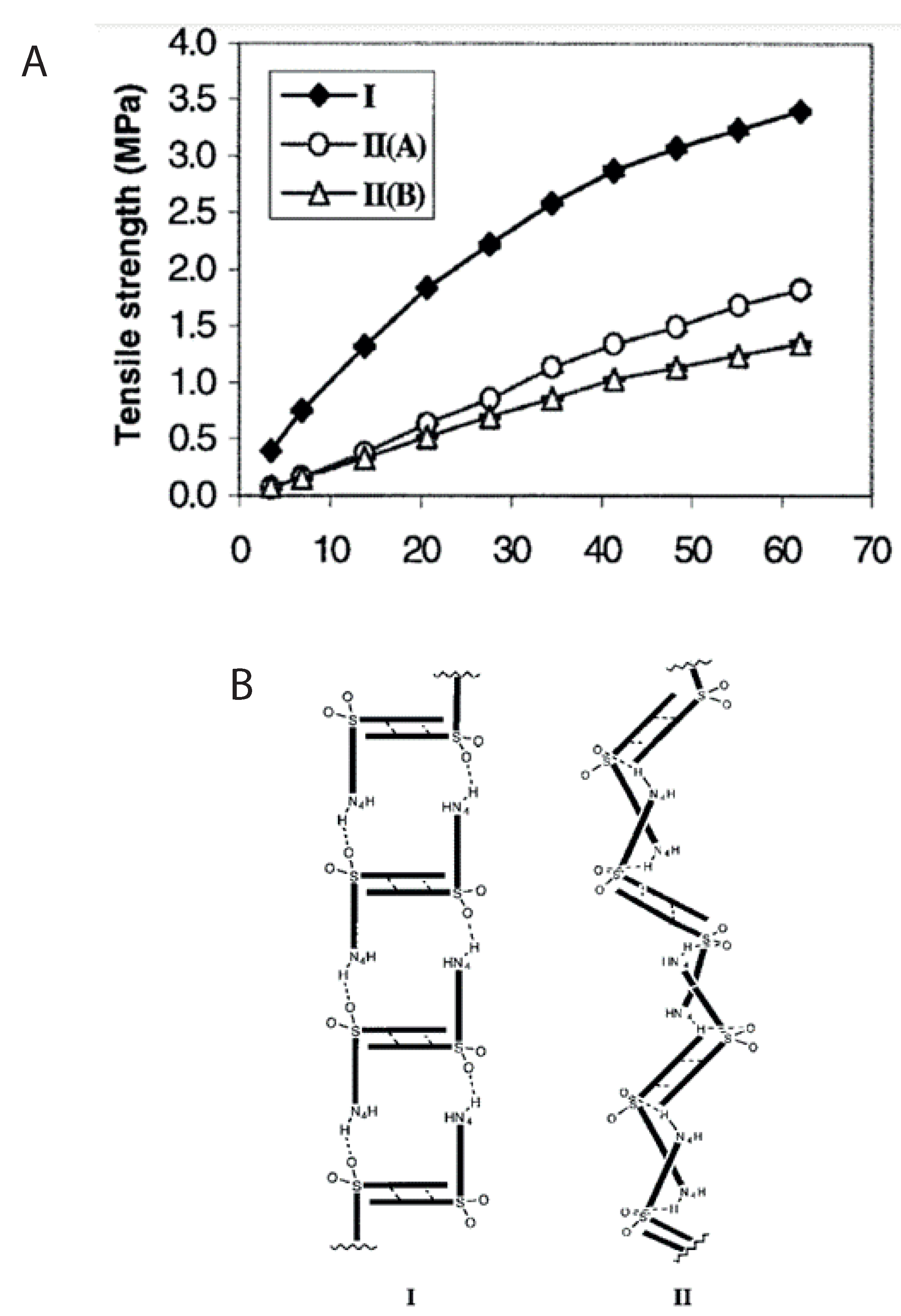
- Sun, C.; Grant, D.J. Influence of crystal structure on the tableting properties of sulfamerazine polymorphs. Pharm. Res. 2001, 18, 274–280. [Google Scholar] [CrossRef] [PubMed]
- Eriksson, M.; Alderborn, G. The effect of particle fragmentation and deformation on the interparticulate bond formation process during powder compaction. Pharm. Res. 1995, 12, 1031–1039. [Google Scholar] [CrossRef] [PubMed]
- Wünsch, I.; Finke, J.H.; John, E.; Juhnke, M.; Kwade, A. The influence of particle size on the application of compression and compaction models for tableting. Int. J. Pharm. 2021, 599, 120424. [Google Scholar] [CrossRef]
- Šimek, M.; Grünwaldová, V.; Kratochvíl, B. Comparison of compression and material properties of differently shaped and sized paracetamols. KONA Powder Part J. 2017, 2017, 197–206. [Google Scholar] [CrossRef]
- Choi, D.H.; Kim, N.A.; Chu, K.R.; Jung, Y.J.; Yoon, J.h.; Jeong, S.H. Material Properties and Compressibility Using Heckel and Kawakita Equation with Commonly Used Pharmaceutical Excipients. J. Pharm. Investig. 2010, 40, 237–244. [Google Scholar] [CrossRef]
- Prasad, K.V.; Sheen, D.B.; Sherwood, J.N. Fracture property studies of paracetamol single crystals using microindentation techniques. Pharm. Res. 2001, 18, 867–872. [Google Scholar] [CrossRef]
- Roberts, R.; Rowe, R.C. The compaction of pharmaceutical and other model materials—A pragmatic approach. Chem. Eng. Sci. 1987, 42, 903–911. [Google Scholar] [CrossRef]
- Skelbæk-pedersen, A.L.; Vilhelmsen, T.K.; Wallaert, V. Investigation of the e ff ects of particle size on fragmentation during tableting. Int. J. Pharm. 2020, 576, 118985. [Google Scholar] [CrossRef]
- Wong, L.W.; Pilpel, N. The effect of particle shape on the mechanical properties of powders. Int. J. Pharm. 1990, 59, 145–154. [Google Scholar] [CrossRef]
- Upadhyay, P.; Khomane, K.S.; Kumar, L.; Bansal, A.K. Relationship between crystal structure and mechanical properties of ranitidine hydrochloride polymorphs. CrystEngComm 2013, 15, 3959–3964. [Google Scholar] [CrossRef]
- Khomane, K.S.; Bansal, A.K. Effect of particle size on in-die and out-of-die compaction behavior of ranitidine hydrochloride polymorphs. AAPS PharmSciTech 2013, 14, 1169–1177. [Google Scholar] [CrossRef] [PubMed]
- Packham, D.E. Surface energy, surface topography and adhesion. Int. J. Adhes. Adhes. 2003, 23, 437–448. [Google Scholar] [CrossRef]
- Annamalai, M.; Gopinadhan, K.; Han, S.A.; Saha, S.; Park, H.J.; Cho, E.B.; Kumar, B.; Patra, A.; Kim, S.W.; Venkatesan, T. Surface energy and wettability of van der Waals structures. Nanoscale 2016, 8, 5764–5770. [Google Scholar] [CrossRef]
- Li, Q.; Rudolph, V.; Weigl, B.; Earl, A. Interparticle van der Waals force in powder flowability and compactibility. Int. J. Pharm. 2004, 280, 77–93. [Google Scholar] [CrossRef]
- Fichtner, F.; Rasmuson, A.; Alderborn, G. Particle size distribution and evolution in tablet structure during and after compaction. Int. J. Pharm. 2005, 292, 211–225. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Ding, X.; He, Z.; Huang, Z.; Kunnath, K.T.; Zheng, K.; Davé, R.N. Surface engineered excipients: I. improved functional properties of fine grade microcrystalline cellulose. Int. J. Pharm. 2018, 536, 127–137. [Google Scholar] [CrossRef] [PubMed]
- Ho, R.; Hinder, S.J.; Watts, J.F.; Dilworth, S.E.; Williams, D.R.; Heng, J.Y. Determination of surface heterogeneity of d-mannitol by sessile drop contact angle and finite concentration inverse gas chromatography. Int. J. Pharm. 2010, 387, 79–86. [Google Scholar] [CrossRef] [PubMed]
- Shinebaum, R. Investigating the Mechanical Properties of Pharmaceutical Excipients in Granule and Tablet Production. Ph.D. Thesis, Univerisity of Birmingham, Edgbaston, UK, 2021. [Google Scholar]
- Morin, G.; Briens, L. The effect of lubricants on powder flowability for pharmaceutical application. AAPS PharmSciTech 2013, 14, 1158–1168. [Google Scholar] [CrossRef] [PubMed]
- Lakio, S.; Vajna, B.; Farkas, I.; Salokangas, H.; Marosi, G.; Yliruusi, J. Challenges in detecting magnesium stearate distribution in tablets. AAPS PharmSciTech 2013, 14, 435–444. [Google Scholar] [CrossRef] [PubMed]
- Abe, H.; Otsuka, M. Effects of lubricant-mixing time on prolongation of dissolution time and its prediction by measuring near infrared spectra from tablets. Drug Dev. Ind. Pharm. 2012, 38, 412–419. [Google Scholar] [CrossRef]
- Kunnath, K.; Huang, Z.; Chen, L.; Zheng, K.; Davé, R. Improved properties of fine active pharmaceutical ingredient powder blends and tablets at high drug loading via dry particle coating. Int. J. Pharm. 2018, 543, 288–299. [Google Scholar] [CrossRef]
- Hentzschel, C.M.; Alnaief, M.; Smirnova, I.; Sakmann, A.; Leopold, C.S. Tableting properties of silica aerogel and other silicates. Drug Dev. Ind. Pharm. 2012, 38, 462–467. [Google Scholar] [CrossRef]
- Khunawattanakul, W.; Puttipipatkhachorn, S.; Rades, T.; Pongjanyakul, T. Novel chitosan-magnesium aluminum silicate nanocomposite film coatings for modified-release tablets. Int. J. Pharm. 2011, 407, 132–141. [Google Scholar] [CrossRef] [PubMed]
- Holman, J.; Tantuccio, A.; Palmer, J.; van Doninck, T.; Meyer, R. A very boring 120 h:15 million tablets under a continuous state of control. Powder Technol. 2021, 382, 208–231. [Google Scholar] [CrossRef]
- Tahara, K.; Kono, Y.; Myerson, A.S.; Takeuchi, H. Development of Continuous Spherical Crystallization to Prepare Fenofibrate Agglomerates with Impurity Complexation Using Mixed-Suspension, Mixed-Product Removal Crystallizer. Cryst. Growth Des. 2018, 18, 6448–6454. [Google Scholar] [CrossRef]
- Chen, Y.; Yao, Z.; Tang, S.; Tong, H.; Yanagishima, T.; Tanaka, H.; Tan, P. Morphology selection kinetics of crystallization in a sphere. Nat. Phys. 2021, 17, 121–127. [Google Scholar] [CrossRef]
- Van Snick, B.; Holman, J.; Cunningham, C.; Kumar, A.; Vercruysse, J.; De Beer, T.; Remon, J.P.; Vervaet, C. Continuous direct compression as manufacturing platform for sustained release tablets. Int. J. Pharm. 2017, 519, 390–407. [Google Scholar] [CrossRef]
- Ierapetritou, M.; Muzzio, F.; Reklaitis, G. Perspectives on the continuous manufacturing of powder-based pharmaceutical processes. AIChE J. 2016, 62, 1846–1862. [Google Scholar] [CrossRef]

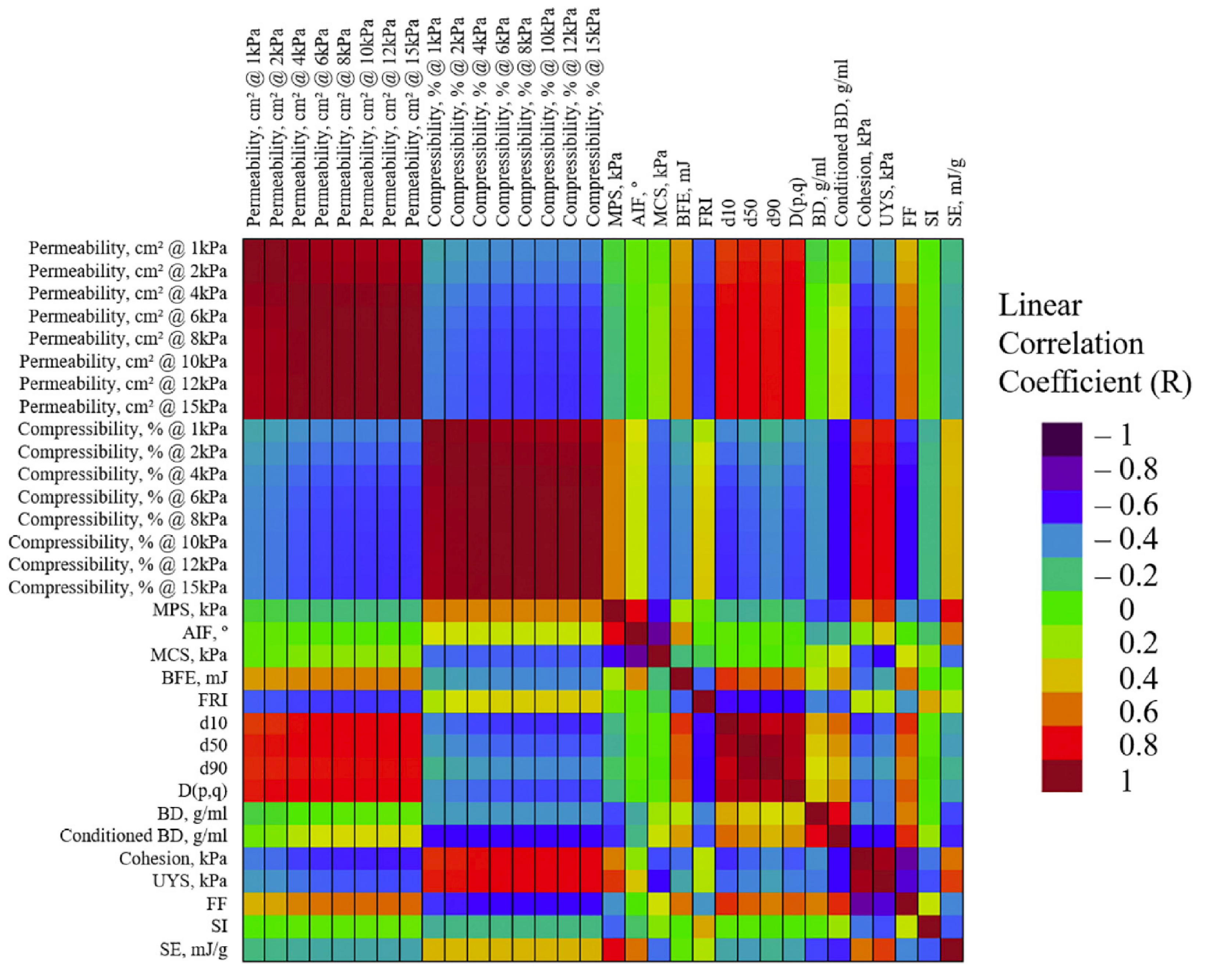

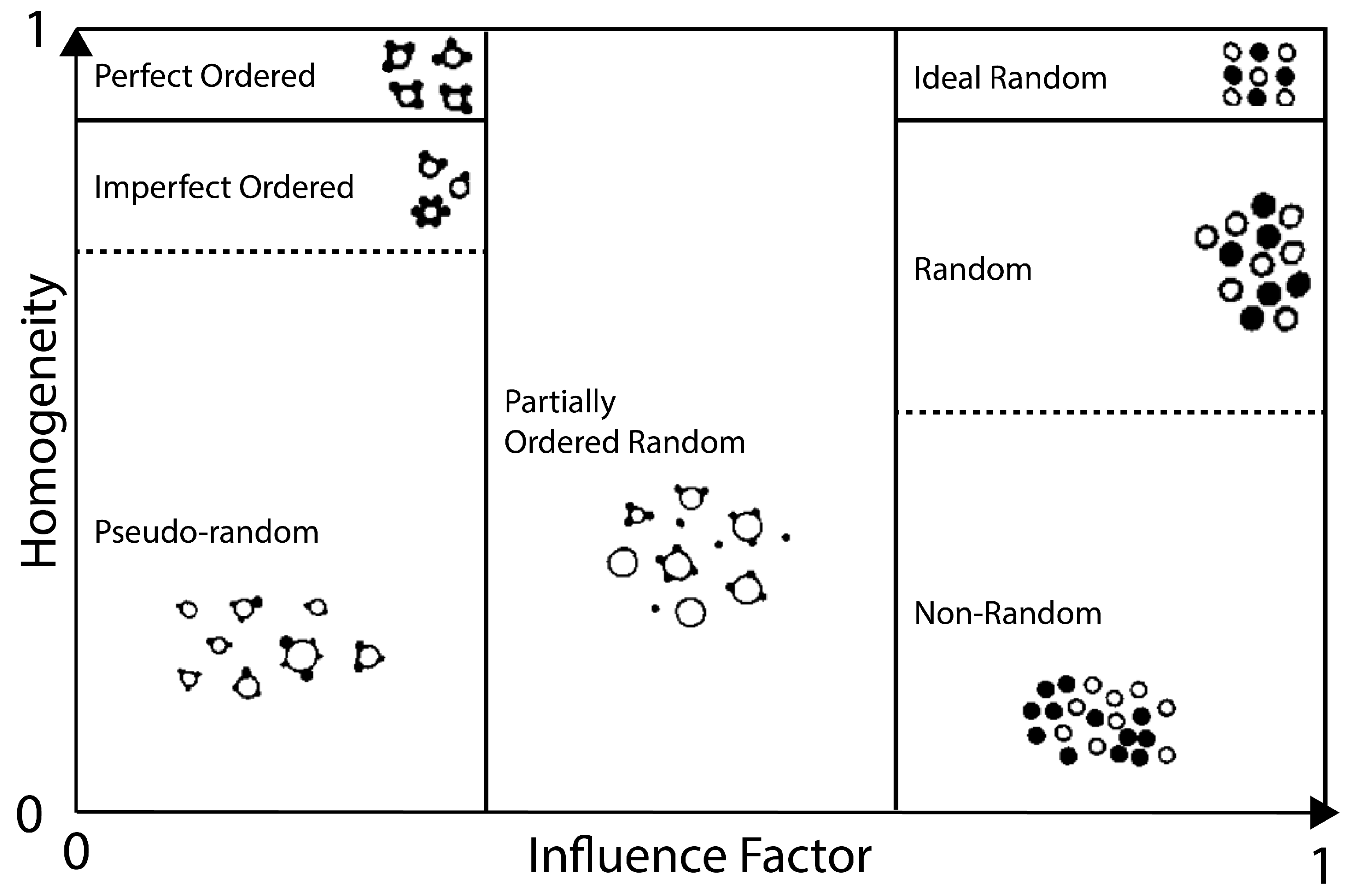

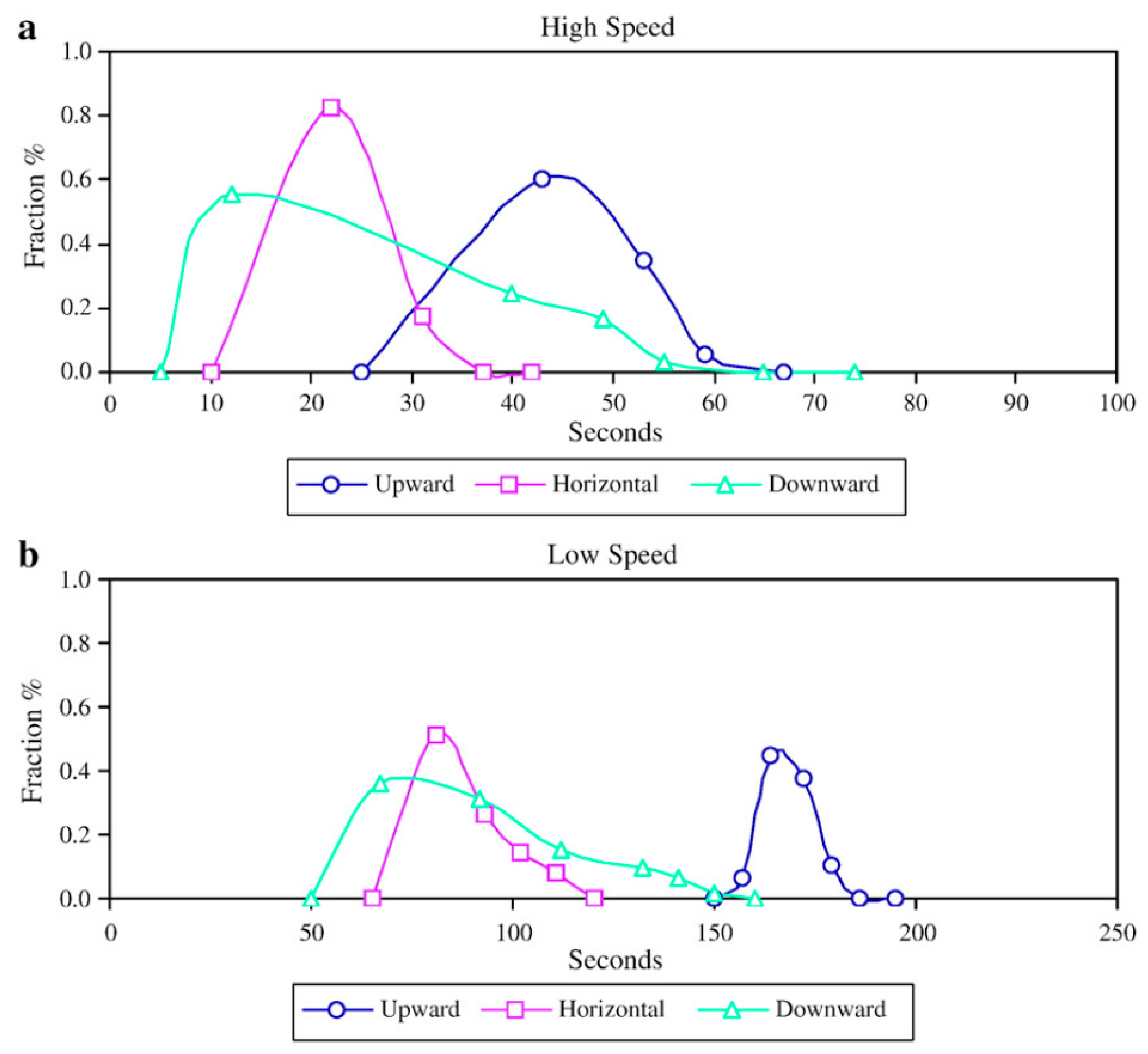

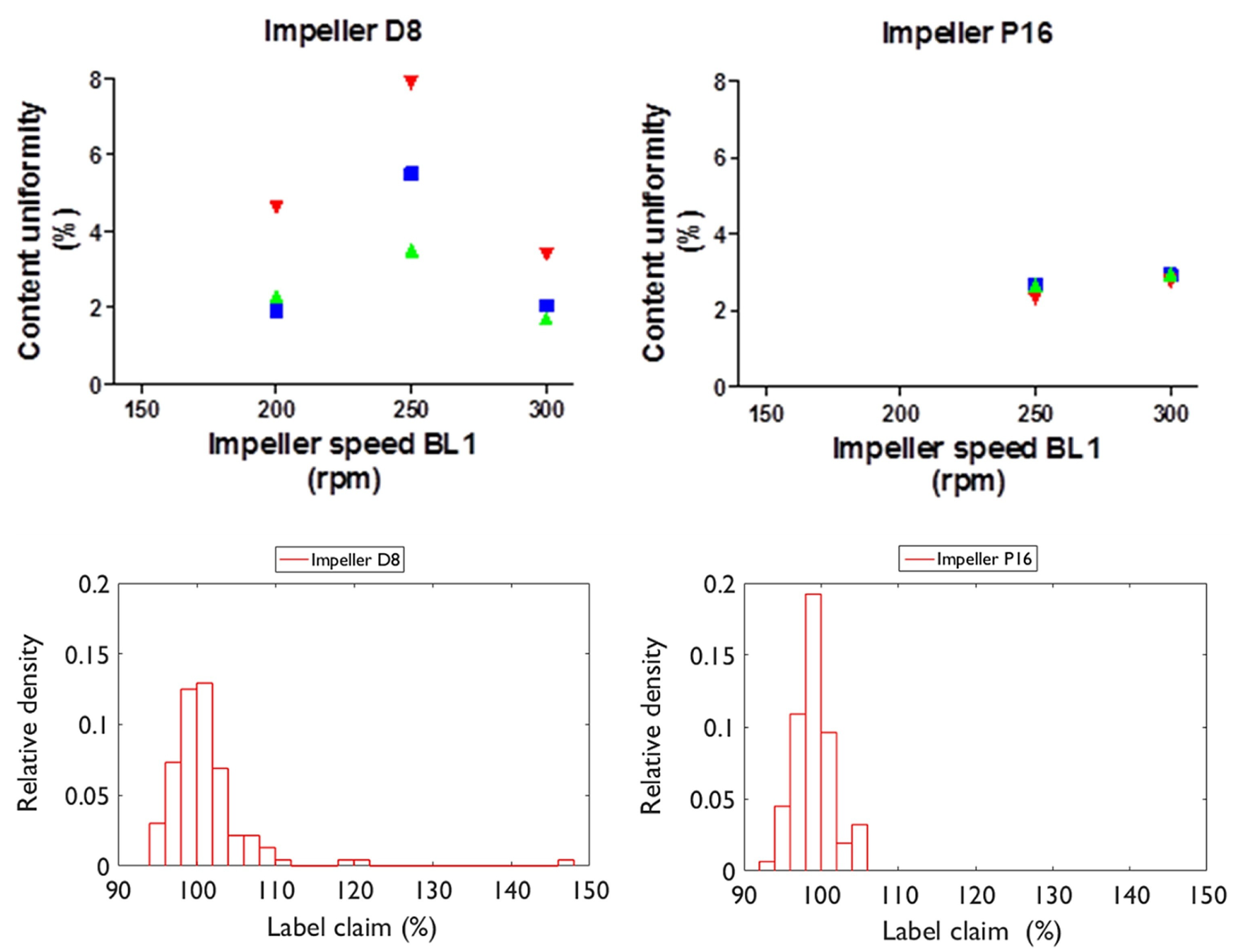





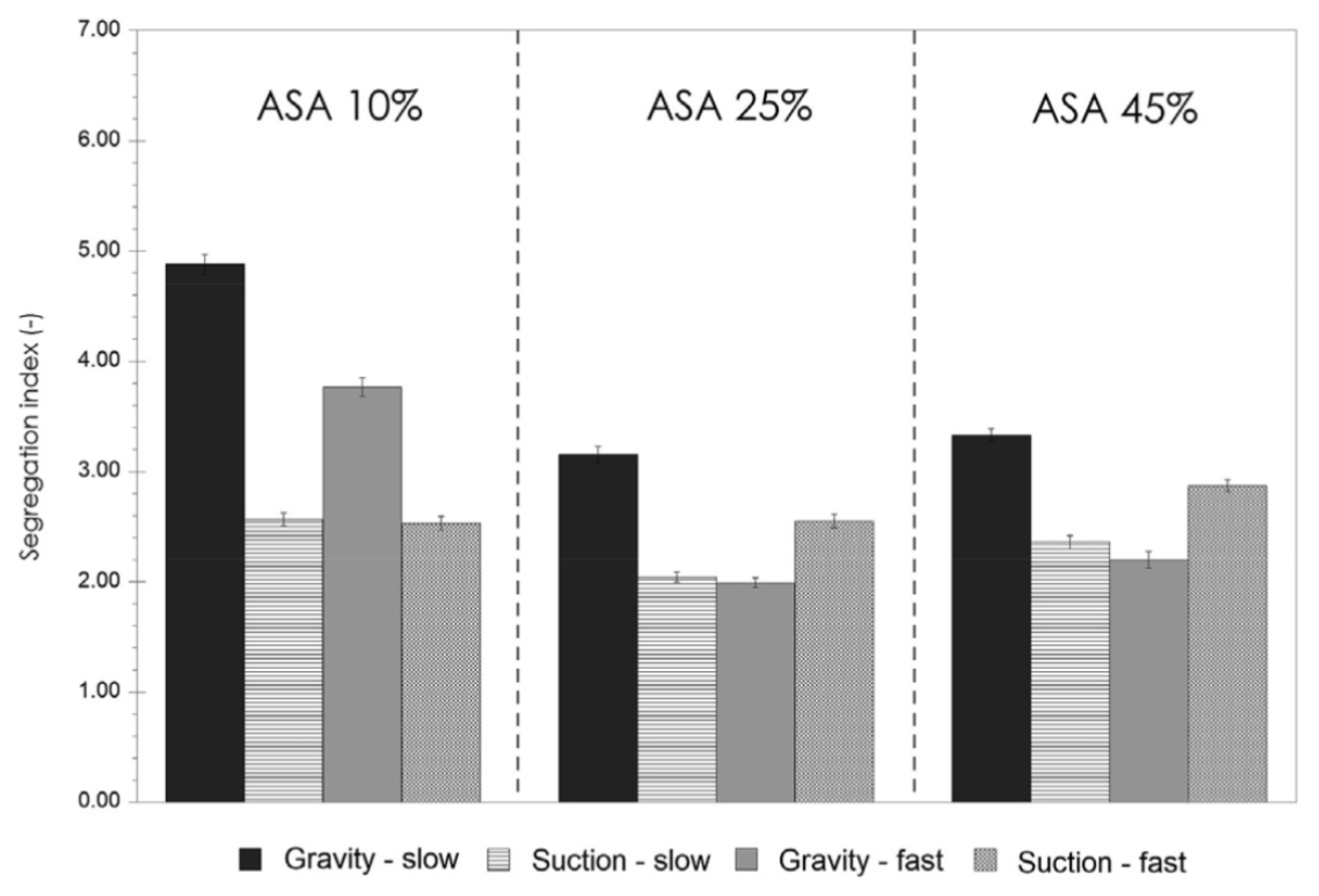

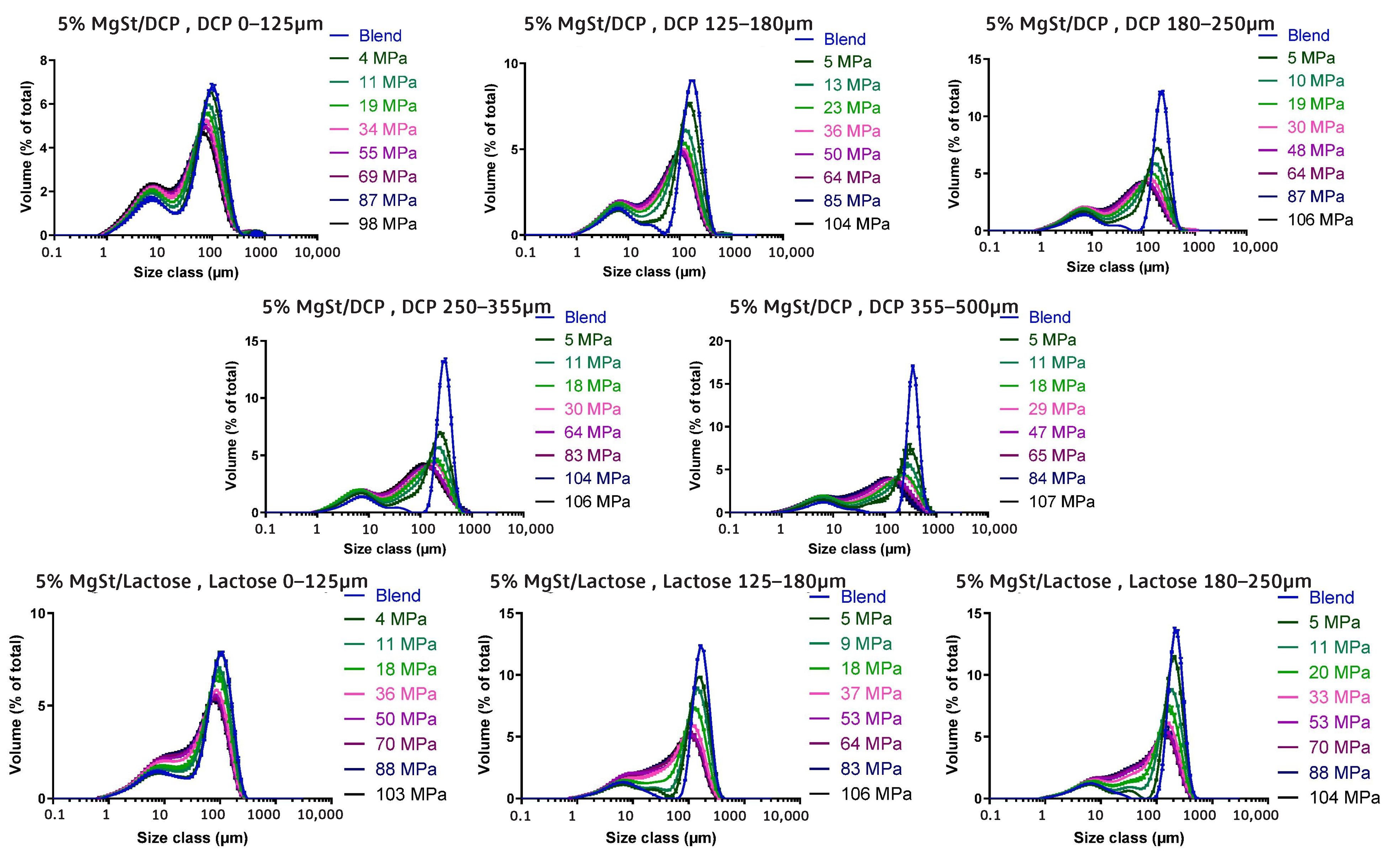
| Material | FFC | Bulk Density (g cm) | Tapped Density (g cm) | Hausner Ratio | Carr’s Index |
|---|---|---|---|---|---|
| Micronized APAP | 1.4 | 0.19 | 0.30 | 1.58 | 36.67 |
| Powdered APAP | 1.9 | 0.31 | 0.53 | 1.71 | 41.51 |
| Special Granular APAP | 19.4 | 0.73 | 0.83 | 1.14 | 12.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jones-Salkey, O.; Chu, Z.; Ingram, A.; Windows-Yule, C.R.K. Reviewing the Impact of Powder Cohesion on Continuous Direct Compression (CDC) Performance. Pharmaceutics 2023, 15, 1587. https://doi.org/10.3390/pharmaceutics15061587
Jones-Salkey O, Chu Z, Ingram A, Windows-Yule CRK. Reviewing the Impact of Powder Cohesion on Continuous Direct Compression (CDC) Performance. Pharmaceutics. 2023; 15(6):1587. https://doi.org/10.3390/pharmaceutics15061587
Chicago/Turabian StyleJones-Salkey, Owen, Zoe Chu, Andrew Ingram, and Christopher R. K. Windows-Yule. 2023. "Reviewing the Impact of Powder Cohesion on Continuous Direct Compression (CDC) Performance" Pharmaceutics 15, no. 6: 1587. https://doi.org/10.3390/pharmaceutics15061587
APA StyleJones-Salkey, O., Chu, Z., Ingram, A., & Windows-Yule, C. R. K. (2023). Reviewing the Impact of Powder Cohesion on Continuous Direct Compression (CDC) Performance. Pharmaceutics, 15(6), 1587. https://doi.org/10.3390/pharmaceutics15061587






