Dynamic Ex Vivo Porcine Eye Model to Measure Ophthalmic Drug Penetration under Simulated Lacrimal Flow
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Drug Assay
2.3. Formulations
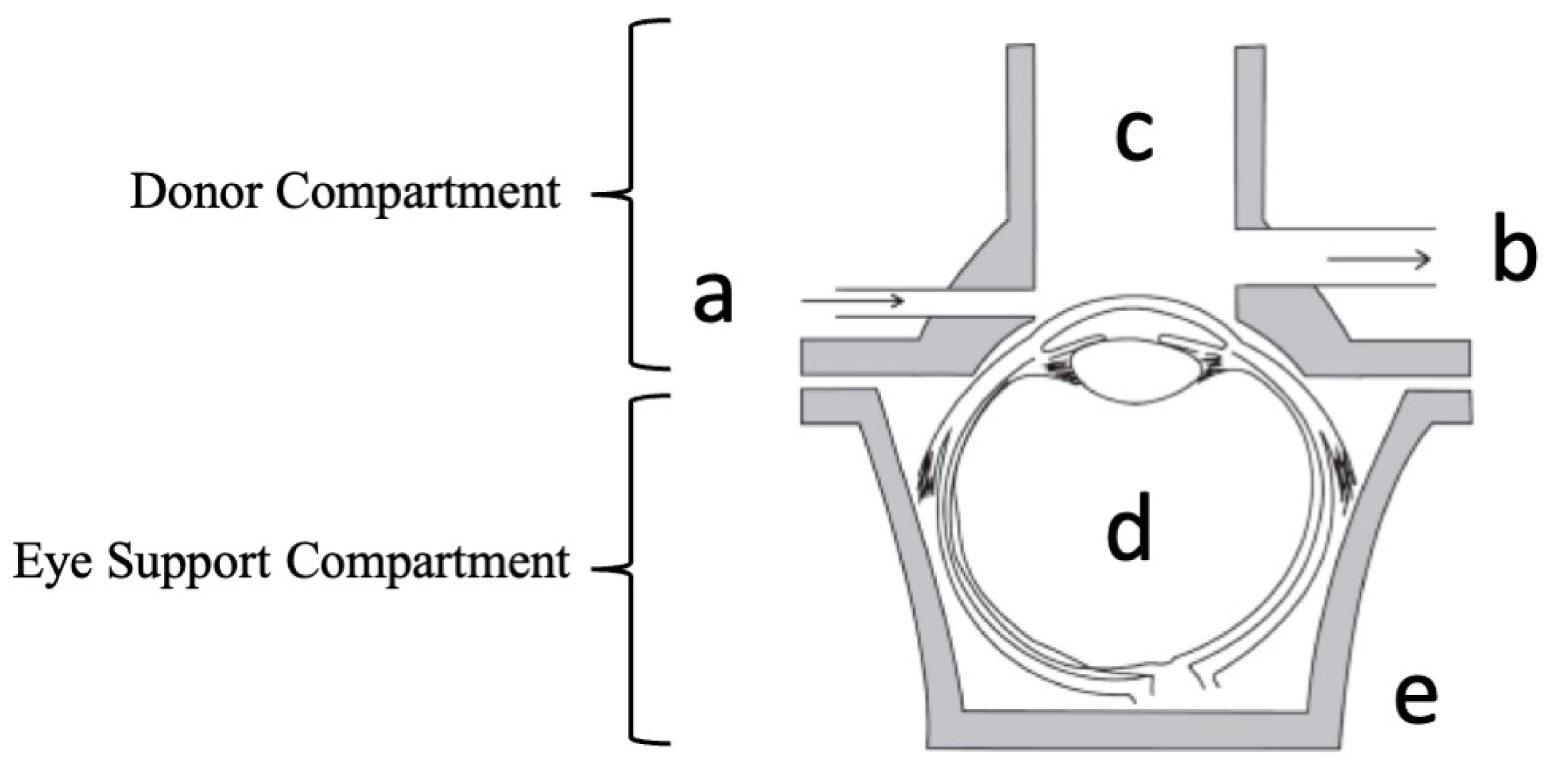
2.4. Design of Dynamic Model System
2.5. Static Penetration Model
2.6. Statistical Analyses
3. Results
3.1. Design of Dynamic Model System
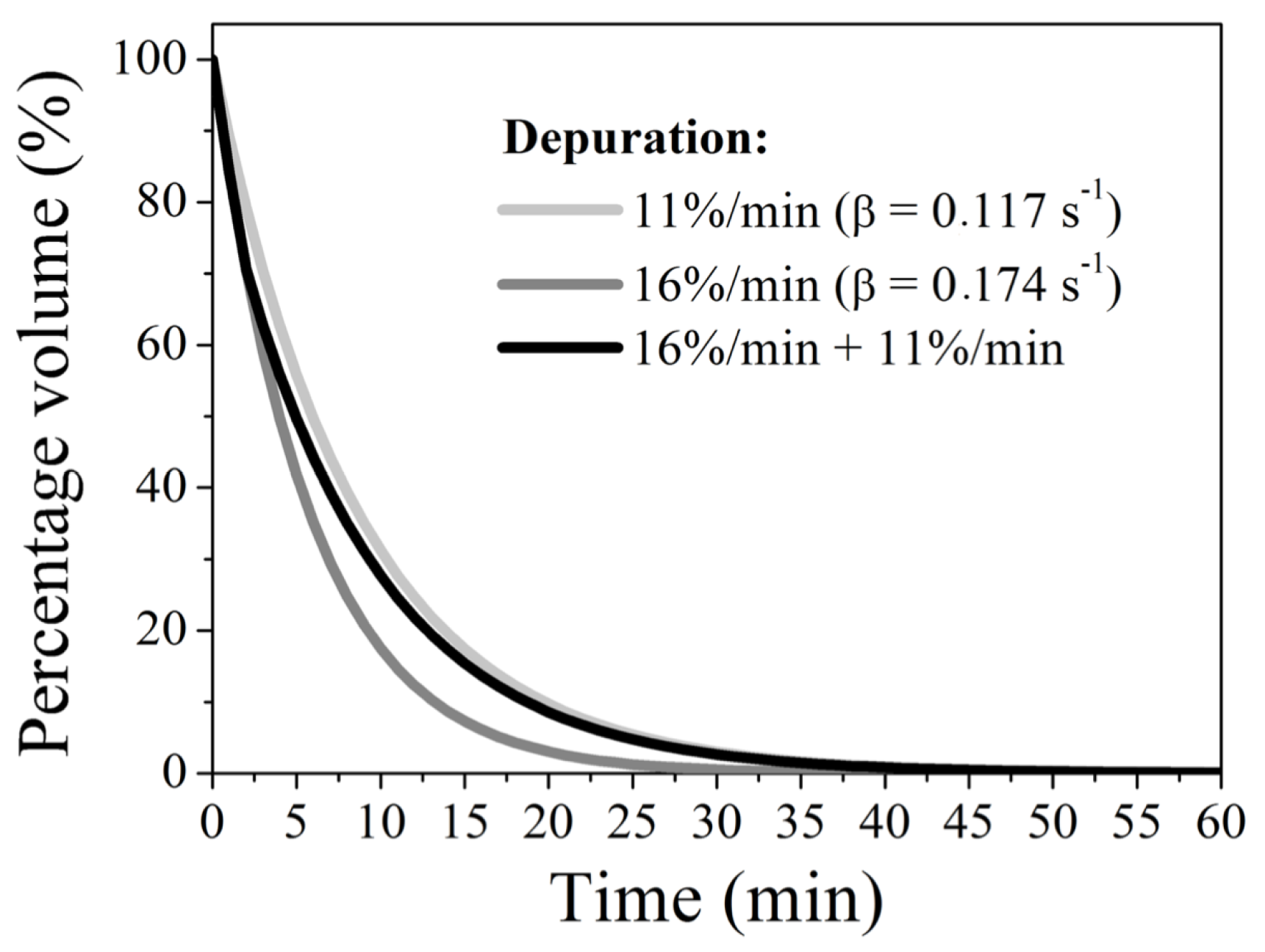
3.2. Mathematical Description of System Clearance Effects
3.3. Operating Conditions of the Dynamic Model
3.4. Ex Vivo Ocular Drug Penetration with the Simulated Lacrimal Flow and Static Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akkermans, A.; Chapsal, J.-M.; Coccia, E.M.; Depraetere, H.; Dierick, J.-F.; Duangkhae, P.; Goel, S.; Halder, M.; Hendriksen, C.; Levis, R.; et al. Animal Testing for Vaccines. Implementing Replacement, Reduction and Refinement: Challenges and Priorities. Biologicals 2020, 68, 92–107. [Google Scholar] [CrossRef]
- Díez-Solinska, A.; Vegas, O.; Azkona, G. Refinement in the European Union: A Systematic Review. Animals 2022, 12, 3263. [Google Scholar] [CrossRef]
- Krombholz, R.; Fressle, S.; Nikolić, I.; Pantelić, I.; Savić, S.; Sakač, M.C.; Lunter, D. Ex Vivo–in Vivo Comparison of Drug Penetration Analysis by Confocal Raman Microspectroscopy and Tape Stripping. Exp. Dermatol. 2022, 31, 1908–1919. [Google Scholar] [CrossRef]
- Bao, Q.; Newman, B.; Wang, Y.; Choi, S.; Burgess, D.J. In Vitro and Ex Vivo Correlation of Drug Release from Ophthalmic Ointments. J. Control. Release 2018, 276, 93–101. [Google Scholar] [CrossRef]
- Pistollato, F.; Madia, F.; Corvi, R.; Munn, S.; Grignard, E.; Paini, A.; Worth, A.; Bal-Price, A.; Prieto, P.; Casati, S.; et al. Current EU Regulatory Requirements for the Assessment of Chemicals and Cosmetic Products: Challenges and Opportunities for Introducing New Approach Methodologies. Arch. Toxicol. 2021, 95, 1867–1897. [Google Scholar] [CrossRef]
- Loftsson, T. Topical Drug Delivery to the Retina: Obstacles and Routes to Success. Expert Opin. Drug Deliv. 2021, 19, 9–21. [Google Scholar] [CrossRef]
- Durgun, M.E.; Kahraman, E.; Hacıoğlu, M.; Güngör, S.; Özsoy, Y. Posaconazole Micelles for Ocular Delivery: In Vitro Permeation, Ocular Irritation and Antifungal Activity Studies. Drug Deliv. Transl. Res. 2022, 12, 662–675. [Google Scholar] [CrossRef]
- Juretić, M.; Cetina-Čižmek, B.; Filipović-Grčić, J.; Hafner, A.; Lovrić, J.; Pepić, I. Biopharmaceutical Evaluation of Surface Active Ophthalmic Excipients Using In Vitro and Ex Vivo Corneal Models. Eur. J. Pharm. Sci. 2018, 120, 133–141. [Google Scholar] [CrossRef]
- Doane, M.G. Blinking and the Mechanics of the Lacrimal Drainage System. Ophthalmology 1981, 88, 844–851. [Google Scholar] [CrossRef]
- Mcclellan, K.A. Mucosal Defense of the Outer Eye. Surv. Ophthalmol. 1997, 42, 233–246. [Google Scholar] [CrossRef]
- Tsubota, K. Tear Dynamics and Dry Eye. Prog. Retin. Eye Res. 1998, 17, 565–596. [Google Scholar] [CrossRef]
- Cardoso, C.O.; Ferreira-Nunes, R.; Cunha-Filho, M.; Gratieri, T.; Gelfuso, G.M. In Situ Gelling Microemulsion for Topical Ocular Delivery of Moxifloxacin and Betamethasone. J. Mol. Liq. 2022, 360, 119559. [Google Scholar] [CrossRef]
- Almeida, G.; Santos, D.; Ferreira-Nunes, R.; Facco Dalmolin, L.; Carolina, A.; Ré, S.; Luiz, J.; Anjos, V.; Mendanha, S.A.; Aires, C.P.; et al. Besifloxacin Liposomes with Positively Charged Additives for an Improved Topical Ocular Delivery. Sci. Rep. 2020, 10, 19285. [Google Scholar] [CrossRef]
- Alhakamy, N.A.; Hosny, K.M.; Rizg, W.Y.; Eshmawi, B.A.; Badr, M.Y.; Safhi, A.Y.; Murshid, S.S. Development and Optimization of Hyaluronic Acid-Poloxamer In-Situ Gel Loaded with Voriconazole Cubosomes for Enhancement of Activity against Ocular Fungal Infection. Gels 2022, 8, 241. [Google Scholar] [CrossRef]
- Gratieri, T.; Gelfuso, G.M.; Rocha, E.M.; Sarmento, V.H.; de Freitas, O.; Lopez, R.F.V. A Poloxamer/Chitosan in Situ Forming Gel with Prolonged Retention Time for Ocular Delivery. Eur. J. Pharm. Biopharm. 2010, 75, 186–193. [Google Scholar] [CrossRef]
- Gratieri, T.; Gelfuso, G.M.; De Freitas, O.; Rocha, E.M.; Lopez, R.F.V. Enhancing and Sustaining the Topical Ocular Delivery of Fluconazole Using Chitosan Solution and Poloxamer/Chitosan in Situ Forming Gel. Eur. J. Pharm. Biopharm. 2011, 79, 320–327. [Google Scholar] [CrossRef]
- Popova, E.V.; Tikhomirova, V.E.; Beznos, O.V.; Chesnokova, N.B.; Grigoriev, Y.V.; Klyachko, N.L.; Kost, O.A. Chitosan-Covered Calcium Phosphate Particles as a Drug Vehicle for Delivery to the Eye. Nanomedicine 2022, 40, 102493. [Google Scholar] [CrossRef]
- Kollross, B.; Gelfuso, G.M.; Cunha-Filho, M.; Gratieri, T. Topical Ophthalmic Antimicrobials: Unfulfilled Demands and Possibility of New Investments in Brazil and in the United States. Braz. J. Pharm. Sci. 2019, 55, e18481. [Google Scholar] [CrossRef]
- Andrade, L.M.; Rocha, K.A.D.; De Sá, F.A.P.; Marreto, R.N.; Lima, E.M.; Gratieri, T.; Taveira, S.F. Voriconazole-Loaded Nanostructured Lipid Carriers for Ocular Drug Delivery. Cornea 2016, 35, 866–871. [Google Scholar] [CrossRef]
- Diebold, Y.; Calonge, M. Applications of Nanoparticles in Ophthalmology. Prog. Retin. Eye Res. 2010, 29, 596–609. [Google Scholar] [CrossRef]
- Kaur, I.P.; Kanwar, M. Ocular Preparations: The Formulation Approach. Drug Deliv. Ind. Pharm. 2002, 28, 473–493. [Google Scholar] [CrossRef] [PubMed]
- Sebastián-Morelló, M.; Alambiaga-Caravaca, A.M.; Calatayud-Pascual, M.A.; Rodilla, V.; Balaguer-Fernández, C.; Miranda, M.; López-Castellano, A. Ex-Vivo Trans-Corneal and Trans-Scleral Diffusion Studies with Ocular Formulations of Glutathione as an Antioxidant Treatment for Ocular Diseases. Pharmaceutics 2020, 12, 861. [Google Scholar] [CrossRef] [PubMed]
- Almeida, H.; Amaral, M.; Lobao, P.; Frigerio, C.; Sousa Lobo, J. Nanoparticles in Ocular Drug Delivery Systems for Topical Administration: Promises and Challenges. Curr. Pharm. Des. 2015, 21, 5212–5224. [Google Scholar] [CrossRef] [PubMed]
- Gratieri, T.; Thomazini, J.A.; Gelfuso, G.M.; Lopez, R.F.V. Excised Porcine Cornea Integrity Evaluation in an in Vitro Model of Iontophoretic Ocular Research. Ophthalmic Res. 2010, 43, 208–216. [Google Scholar] [CrossRef]
- Kompella, U.B.; Sundaram, S.; Raghava, S.; Escobar, E.R. Luteinizing Hormone-Releasing Hormone Agonist and Transferrin Functionalizations Enhance Nanoparticle Delivery in a Novel Bovine Ex Vivo Eye Model. Mol. Vis. 2006, 12, 1185–1198. [Google Scholar]
- Morrison, P.W.J.; Khutoryanskiy, V.V. Enhancement in Corneal Permeability of Riboflavin Using Calcium Sequestering Compounds. Int. J. Pharm. 2014, 472, 56–64. [Google Scholar] [CrossRef]
- Morrison, P.W.J.; Connon, C.J.; Khutoryanskiy, V.V. Cyclodextrin-Mediated Enhancement of Riboflavin Solubility and Corneal Permeability. Mol. Pharm. 2013, 10, 756–762. [Google Scholar] [CrossRef]
- Thiel, M.A.; Coster, D.J.; Standfield, S.D.; Brereton, H.M.; Mavrangelos, C.; Zola, H.; Taylor, S.; Yusim, A.; Williams, K.A. Penetration of Engineered Antibody Fragments into the Eye. Clin. Exp. Immunol. 2002, 128, 67. [Google Scholar] [CrossRef]
- Cañadas-Enrich, C.; Abrego, G.; Alvarado, H.L.; Calpena-Campmany, A.C.; Boix-Montañes, A. Pranoprofen quantification in ex vivo corneal and scleral permeation samples: Analytical validation. J. Pharm. Biomed. Anal. 2018, 160, 109–118. [Google Scholar] [CrossRef]
- Pepić, I.; Lovrić, J.; Cetina-Čižmek, B.; Reichl, S.; Filipović-Grčić, J. Toward the Practical Implementation of Eye-Related Bioavailability Prediction Models. Drug Discov. Today 2014, 19, 31–44. [Google Scholar] [CrossRef]
- Rossi, S.; Ferrari, F.; Bonferoni, M.C.; Caramella, C. Characterization of Chitosan Hydrochloride–Mucin Rheological Interaction: Influence of Polymer Concentration and Polymer:Mucin Weight Ratio. Eur. J. Pharm. Sci. 2001, 12, 479–485. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Ferreiro, A.; Fernández Bargiela, N.; Santiago Varela, M.; Gil Martínez, M.; Pardo, M.; Ces, A.P.; Blanco Méndez, J.; González Barcia, M.; Lamas, M.J.; Otero-Espinar, F.J. Cyclodextrin-Polysaccharide-Based, in Situ-Gelled System for Ocular Antifungal Delivery. Beilstein J. Org. Chem. 2014, 10, 2903–2911. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.Y.; Gao, Z.G.; Park, J.S.; Li, H.; Han, K. RhEGF/HP-β-CD Complex in Poloxamer Gel for Ophthalmic Delivery. Int. J. Pharm. 2002, 233, 159–167. [Google Scholar] [CrossRef]
- Hassan, E.E.; Gallo, J.M. A Simple Rheological Method for the in Vitro Assessment of Mucin-Polymer Bioadhesive Bond Strength. Pharm. Res. 1990, 7, 491–495. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Wang, Y.; Ping, Q.; Xiao, Y.; Huang, X. Mucoadhesive Effect of Thiolated PEG Stearate and Its Modified NLC for Ocular Drug Delivery. J. Control. Release 2009, 137, 217–223. [Google Scholar] [CrossRef]
- Xu, K.P.; Tsubota, K. Correlation of Tear Clearance Rate and Fluorophotometric Assessment of Tear Turnover. Br. J. Ophthalmol. 1995, 79, 1042. [Google Scholar] [CrossRef]
- Cerretani, C.F.; Radke, C.J. Tear Dynamics in Healthy and Dry Eyes. Curr. Eye Res. 2014, 39, 580–595. [Google Scholar] [CrossRef]
- Klouda, L. Thermoresponsive Hydrogels in Biomedical Applications: A Seven-Year Update. Eur. J. Pharm. Biopharm. 2015, 97, 338–349. [Google Scholar] [CrossRef]




| N° | Donor Compartment Parameters (mm) | Geometric Parameters (mm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| din | dout | dout/din | Hin | Hout | Hin/Hout | θ | Dt | Db | Hb | H | |
| 1 | 2.05 | 3.61 | 1.76 | 7.44 | 8.70 | 0.85 | 90° | 12.18 | - | - | 43.96 |
| 2 | 2.61 | 5.34 | 2.04 | 4.30 | 3.00 | 1.43 | <90° | 14.27 | - | - | 30.17 |
| 3 | 1.29 | 2.9 | 2.24 | 13.0 | 13.0 | 1.00 | <90° | 14.37 | 20 | 9.30 | 28.08 |
| 4 | 1.26 | 2.95 | 2.34 | 10.8 | 11.5 | 0.93 | 90° | 14.37 | 20 | 7.15 | 20.14 |
| 5 | 2.43 | 5.00 | 2.05 | 10.1 | 5.60 | 1.80 | <90° | 13.38 | 20 | 12.72 | 18.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbalho, G.N.; Falcão, M.A.; Lopes, J.M.S.; Lopes, J.M.; Contarato, J.L.A.; Gelfuso, G.M.; Cunha-Filho, M.; Gratieri, T. Dynamic Ex Vivo Porcine Eye Model to Measure Ophthalmic Drug Penetration under Simulated Lacrimal Flow. Pharmaceutics 2023, 15, 2325. https://doi.org/10.3390/pharmaceutics15092325
Barbalho GN, Falcão MA, Lopes JMS, Lopes JM, Contarato JLA, Gelfuso GM, Cunha-Filho M, Gratieri T. Dynamic Ex Vivo Porcine Eye Model to Measure Ophthalmic Drug Penetration under Simulated Lacrimal Flow. Pharmaceutics. 2023; 15(9):2325. https://doi.org/10.3390/pharmaceutics15092325
Chicago/Turabian StyleBarbalho, Geisa N., Manuel A. Falcão, Jefferson M. S. Lopes, Júlia M. Lopes, Jonad L. A. Contarato, Guilherme M. Gelfuso, Marcilio Cunha-Filho, and Tais Gratieri. 2023. "Dynamic Ex Vivo Porcine Eye Model to Measure Ophthalmic Drug Penetration under Simulated Lacrimal Flow" Pharmaceutics 15, no. 9: 2325. https://doi.org/10.3390/pharmaceutics15092325
APA StyleBarbalho, G. N., Falcão, M. A., Lopes, J. M. S., Lopes, J. M., Contarato, J. L. A., Gelfuso, G. M., Cunha-Filho, M., & Gratieri, T. (2023). Dynamic Ex Vivo Porcine Eye Model to Measure Ophthalmic Drug Penetration under Simulated Lacrimal Flow. Pharmaceutics, 15(9), 2325. https://doi.org/10.3390/pharmaceutics15092325





