Forecasting E-Commerce Products Prices by Combining an Autoregressive Integrated Moving Average (ARIMA) Model and Google Trends Data
Abstract
:1. Introduction
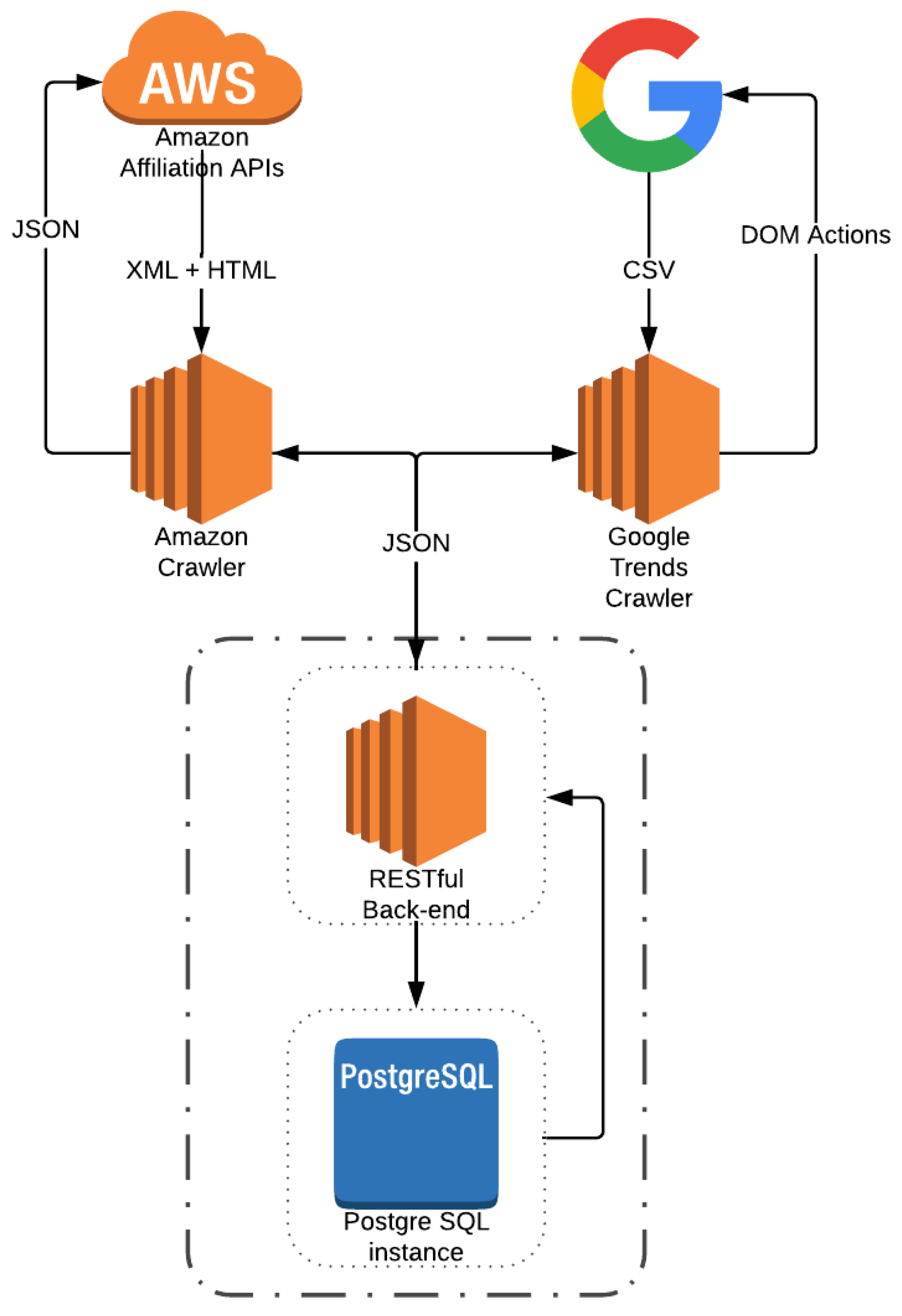
- First, this is the first work analyzing the correlation of Google Trends and products reviews information with Amazon products’ prices, using huge amount of real world data. We have developed crawlers that extracted about 9 millions of products and 96 millions of tuples with information related to their prices, their manufacturers, categories they belong, Google Trends, and reviews.
- Second, a deep analysis of how Google Trends information improved the forecast task when used as exogenous variable within our ARIMA model is performed;
- Finally, we developed and made available an open source framework which allows downloading and crawling of Amazon products information and the tuning and employment of the ARIMA model.
- Last but not least, we built a database of a huge collection of Amazon products, their reviews, their price over time and the related Google Trends information.
2. Related Work
3. Data Description
- Products—which contains main information on the Amazon products;
- Manufacturers—which contains information about the manufacturers;
- Categories—which contains information about the categories of the products;
- Categories products—which contains the associations between products and categories;
- Prices—which contains information about the prices of the Amazon products;
- reviews—which contains information about the reviews of the products.
- trends—which contains information about Google Trends on the manufacturers of the Amazon products;
3.1. Products
3.2. Manufacturers
3.3. Categories
3.4. Categories Products
3.5. Prices
3.6. Reviews
3.7. Trends
4. Price Probe
4.1. Amazon
4.2. Google Trends
5. Our Approach
5.1. ARIMA
- AutoRegressive model (AR):An autoregressive model AR(p) specifies that the output variable depends linearly on its own previous values and on a stochastic term. The order of an autoregressive model is the number of immediately preceding values in the series that are used to predict the value at the present time. The notation AR(p) indicates an autoregressive model of order p. The AR(p) model is defined as:where are the parameters of the model, c is a constant and is white noise.
- Integrated (I):It indicates the degree of differencing of order d of the series. Differencing in statistics is a transformation applied to time series data in order to make it stationary. As formalized in [16], a process is stationary if the probability distributions of the random vectors and are the same arbitrary times , all n, and all lags or leads . A stationary time series does not depend on the time at which the series is observed. To differentiate the data, the difference between consecutive observations is computed. Mathematically, this is shown as:where are the values of the series, respectively, at time t, t-1, and is the differenced value of the series at time t.More formally, denoting as y the difference of Y, the forecasting equation can be defined as follows:It should be noted that the second difference of Y (i.e., case) does not represent the difference from 2 periods ago but the first-difference-of-the-first difference, since it is the discrete analog of a second derivative [43].The ARIMA approach requires that the data are stationary. When the times series is already stationary, then an ARMA model is estimated. On the contrary, if the time series is not stationary, then the series must be transformed to become stationary (order of integration “I” meaning the number of times that the series must be differentiated to get stationarity), and we work with an ARIMA model. If a time series is stationary, then taking first-differences is not needed. The series is integrated of order zero (), and we specify an ARMA model since differencing does not eliminate the seasonal structure existing in the data. For time series forecasting, in ARIMA models it is common to use the following transformation of the data:This transformation allows reducing the variability of the series, and the transformed variable can be interpreted as an approximation of the growth rate. Further details can be found in [16] where authors indicate the adoption of preprocessing approaches, such as the Seasonal Decomposition one [44], in order to reduce seasonality.
- Moving Average model (MA):In time series analysis, the moving-average MA(q) model is a common approach for modeling univariate time series. The moving-average model specifies that the output variable depends linearly on the current and various past values of a stochastic term. The notation MA(q) refers to the moving average model of order q. The MA(q) model is defined as:where is the mean of the series, are the parameters of the model and is white noise.
5.2. Tuning ARIMA
5.2.1. Preprocessing
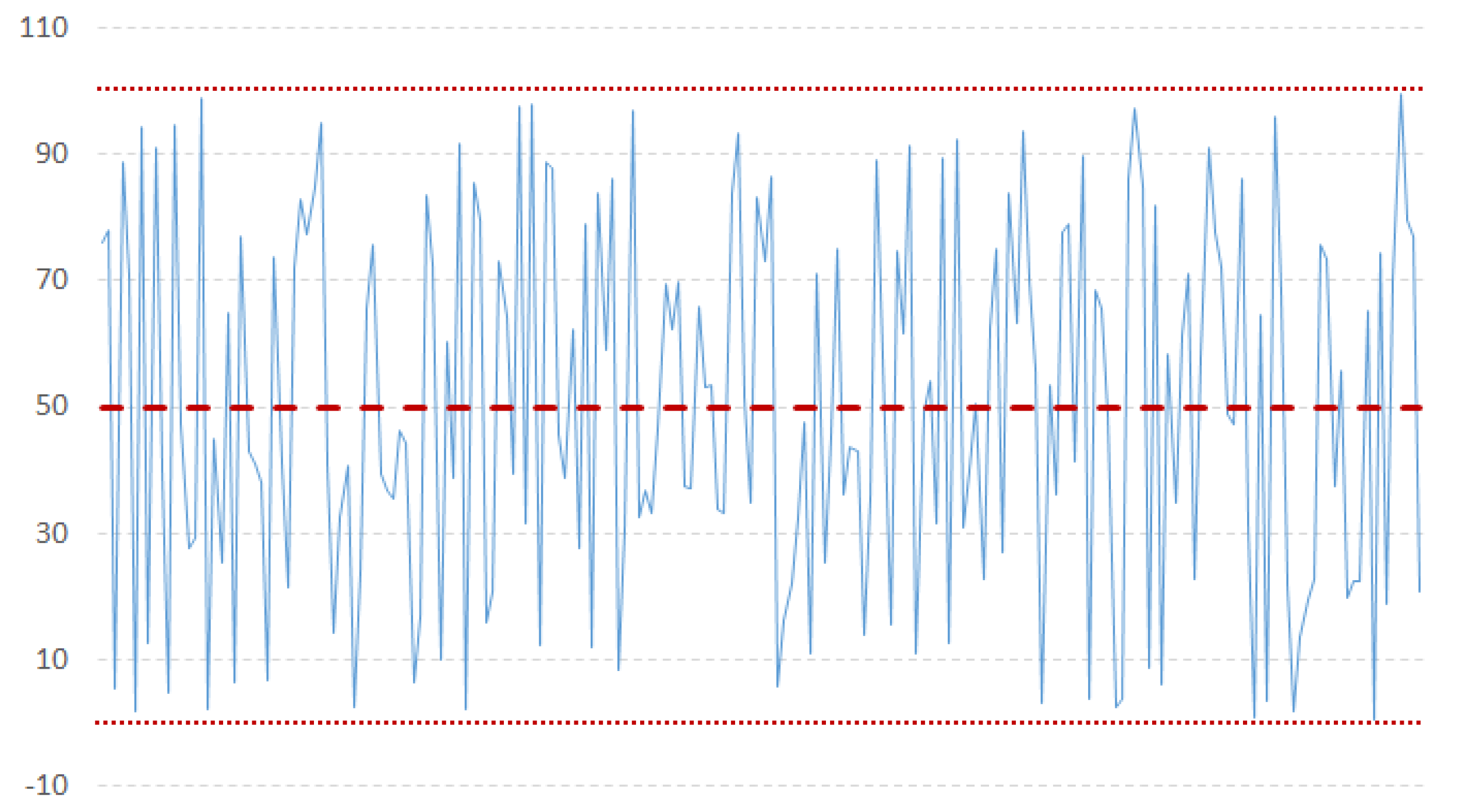
- Model identification: The first step is to check the stationarity of the series, needed by the ARIMA model. Based on some work in literature [31], we used the NG and Perron modified unit root test as it has been proved to be more efficient than the ADF test. A time series has stationarity if a shift in time does not cause a change in the shape of the distribution; unit roots are one cause for non-stationarity.According to the literature about probability theory and statistics, a unit root represents a feature that in a stochastic process can lead toward problems in statistical inference when time series models are involved. In our context, if a time series has a unit root, it is characterized by a systematic pattern that is unpredictable [48], as it happens in the non-invertible processes [16,49].The augmented Dickey-Fuller test is built with a null hypothesis that there is a unit root. The null hypothesis could be rejected if the p-value of the test result is less than 5%. Furthermore, we checked also that the Dickey-Fuller statistical value is more negative than the associated t-distribution critical value; the more negative the statistical value, the more we can reject the hypothesis that there is a unit root. If the test result shows that we cannot reject the hypothesis, we have to differentiate the series and repeat the test again. Usually, differencing more than twice a series means that the series is not good to fit into ARIMA. Figure 3 and Figure 4 show examples of stationary and non-stationary time series of our data (Examples taken from http://ciaranmonahan.com/supply-chain-models-arima-models-non-stationary-data/).
- Parameters estimation: Within the domain of time series, two important functions deal with lags. The first, the Partial AutoCorrelation Function (PACF), is the correlation between a time series and its own lagged values. The other, the AutoCorrelation Function (ACF), defines how points are correlated with each other, based on how many time steps they are separated by. These two functions are necessary for time series analysis as they are able to identify the extent of the lag in an autoregressive model (PACF) and in a moving average model (ACF) [50].Figure 5 and Figure 6 show an example of an ACF and PACF. The use of these functions was introduced as part of the Box–Jenkins approach to time series modeling, where computing the partial autocorrelation function could be determined by the appropriate lags p in an ARIMA (p, d, q) model, and computing the autocorrelation function could be determined by the appropriate lag q in an ARIMA (p, d, q) model. Because the (partial) autocorrelation of a MA(q) (AR(p)) process is zero at lag q + 1 (p + 1) and higher, we take into account the sample (partial) autocorrelation function to check where it becomes zero (any departure from zero). This is achieved by considering a 95% confidence interval for the sample (partial) autocorrelation plot. The confidence band is approximately , where N corresponds to the sample size.
- Model evaluation: To determine the best ARIMA model for the Amazon products, we always perform the following steps:
- -
- check stationarity, with the Ng and Perron modified unit root test [31], useful also to find an appropriate d value.
- -
- find p and q based on PACF and ACF. The result on ACF and PACF gives us an upper bound for iterating the fitting of the model, keeping the best combination, based on the least MSE value, described as:where is a vector of n predictions, and Y is the vector of the observed values of the variable being predicted.
5.2.2. Algorithm
- perform data retrieving - Retrieve products’ external data. For instance, if a product has Google Trends entries for itsManufacturerwe retrieve that and add it to the current external features.
- Model Fit - Fit a model for each combination of products’ available basic and external features.
6. Performance Evaluation
Methodology
7. Conclusions and Future Directions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zimmermann, S.; Herrmann, P.; Kundisch, D.; Nault, B. Decomposing the Variance of Consumer Ratings and the Impact on Price and Demand. Inf. Syst. Res. 2018. [Google Scholar] [CrossRef]
- Cavalcante, R.C.; Brasileiro, R.C.; Souza, V.L.; Nobrega, J.P.; Oliveira, A.L. Computational Intelligence and Financial Markets: A Survey and Future Directions. Expert Syst. Appl. 2016, 55, 194–211. [Google Scholar] [CrossRef]
- Atsalakis, G.S.; Valavanis, K.P. Surveying stock market forecasting techniques—Part II: Soft computing methods. Expert Syst. Appl. 2009, 36, 5932–5941. [Google Scholar] [CrossRef]
- Pai, P.F.; Lin, C.S. A hybrid ARIMA and support vector machines model in stock price forecasting. Omega 2005, 33, 497–505. [Google Scholar] [CrossRef]
- Conejo, A.J.; Plazas, M.A.; Espinola, R.; Molina, A.B. Day-ahead electricity price forecasting using the wavelet transform and ARIMA models. IEEE Trans. Power Syst. 2005, 20, 1035–1042. [Google Scholar] [CrossRef]
- Jadhav, V.; Chinnappa Reddy, B.; Gaddi, G. Application of ARIMA model for forecasting agricultural prices. J. Agric. Sci. Technol. 2017, 19, 981–992. [Google Scholar]
- Wang, Y.; Wang, C.; Shi, C.; Xiao, B. Short-term cloud coverage prediction using the ARIMA time series model. Remote Sens. Lett. 2018, 9, 274–283. [Google Scholar] [CrossRef]
- Rangel-González, J.A.; Frausto-Solis, J.; Javier González-Barbosa, J.; Pazos-Rangel, R.A.; Fraire-Huacuja, H.J. Comparative Study of ARIMA Methods for Forecasting Time Series of the Mexican Stock Exchange. In Fuzzy Logic Augmentation of Neural and Optimization Algorithms: Theoretical Aspects and Real Applications; Castillo, O., Melin, P., Kacprzyk, J., Eds.; Springer: Cham, Germany, 2018; pp. 475–485. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, C.; Guo, J.; Ding, Z. ARIMA forecasting of China’s coal consumption, price and investment by 2030. Energy Sources Part B Econ. Plan. Policy 2018, 13, 190–195. [Google Scholar] [CrossRef]
- Ozturk, S.; Ozturk, F. Forecasting Energy Consumption of Turkey by Arima Model. J. Asian Sci. Res. 2018, 8, 52–60. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.; Stewart, R.A.; Lu, J. Autoregressive with exogenous variables and neural network short-term load forecast models for residential low voltage distribution networks. Energies 2014, 7, 2938–2960. [Google Scholar] [CrossRef]
- Bakir, H.; Chniti, G.; Zaher, H. E-Commerce Price Forecasting Using LSTM Neural Networks. Int. J. Mach. Learn. Comput. 2018, 8, 169–174. [Google Scholar] [CrossRef]
- Liu, W.W.; Liu, Y.; Chan, N.H. Modeling eBay Price Using Stochastic Differential Equations. J. Forecast. 2018. [Google Scholar] [CrossRef]
- Hand, C.; Judge, G. Searching for the picture: forecasting UK cinema admissions using Google Trends data. Appl. Econ. Lett. 2012, 19, 1051–1055. [Google Scholar] [CrossRef] [Green Version]
- Bangwayo-Skeete, P.F.; Skeete, R.W. Can Google data improve the forecasting performance of tourist arrivals? Mixed-data sampling approach. Tour. Manag. 2015, 46, 454–464. [Google Scholar] [CrossRef]
- Wei, W.W.S. Time Series Analysis: Univariate and Multivariate Methods; Pearson Addison Wesley: Boston, MA, USA, 2006. [Google Scholar]
- Tyralis, H.; Papacharalampous, G. Variable selection in time series forecasting using random forests. Algorithms 2017, 10, 114. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. One-step ahead forecasting of geophysical processes within a purely statistical framework. Geosci. Lett. 2018, 5, 12. [Google Scholar] [CrossRef] [Green Version]
- Meyler, A.; Kenny, G.; Quinn, T. Forecasting Irish Inflation Using ARIMA Models; Central Bank of Ireland: Dublin, Ireland, 1998. [Google Scholar]
- Geetha, A.; Nasira, G. Time-series modelling and forecasting: Modelling of rainfall prediction using ARIMA model. Int. J. Soc. Syst. Sci. 2016, 8, 361–372. [Google Scholar] [CrossRef]
- Pincheira, P.; Hardy, N. Forecasting Base Metal Prices with Commodity Currencies; MPRA Paper 83564; University Library of Munich: Munich, Germany, 2018. [Google Scholar]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Yu, L.; Zhao, Y.; Tang, L.; Yang, Z. Online big data-driven oil consumption forecasting with Google trends. Int. J. Forecast. 2018. [Google Scholar] [CrossRef]
- Szczech, M.; Turetken, O. The Competitive Landscape of Mobile Communications Industry in Canada: Predictive Analytic Modeling with Google Trends and Twitter. In Analytics and Data Science: Advances in Research and Pedagogy; Deokar, A.V., Gupta, A., Iyer, L.S., Jones, M.C., Eds.; Springer: Cham, Germany, 2018; pp. 143–162. [Google Scholar] [CrossRef]
- Tuladhar, J.G.; Gupta, A.; Shrestha, S.; Bania, U.M.; Bhargavi, K. Predictive Analysis of E-Commerce Products. In Intelligent Computing and Information and Communication; Bhalla, S., Bhateja, V., Chandavale, A.A., Hiwale, A.S., Satapathy, S.C., Eds.; Springer: Singapore, 2018; pp. 279–289. [Google Scholar]
- Tseng, K.K.; Lin, R.F.Y.; Zhou, H.; Kurniajaya, K.J.; Li, Q. Price prediction of e-commerce products through Internet sentiment analysis. Electron. Commer. Res. 2018, 18, 65–88. [Google Scholar] [CrossRef]
- Guo, K.; Sun, Y.; Qian, X. Can investor sentiment be used to predict the stock price? Dynamic analysis based on China stock market. Phys. A Stat. Mech. Appl. 2017, 469, 390–396. [Google Scholar] [CrossRef]
- Brockwell, P.J.; Davis, R.A. Introduction. In Introduction to Time Series and Forecasting; Springer: Cham, Germany, 2016; pp. 1–37. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Ng, S.; Perron, P. Lag Length Selection and the Construction of Unit Root Tests with Good Size and Power. Econometrica 2001, 69, 1519–1554. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G. Time Series Analysis, Forecasting and Control; Holden-Day, Incorporated: San Francisco, CA, USA, 1990. [Google Scholar]
- Ke, Z.; Zhang, Z.J. Testing autocorrelation and partial autocorrelation: Asymptotic methods versus resampling techniques. Br. J. Math. Stat. Psychol. 2018, 71, 96–116. [Google Scholar] [CrossRef] [PubMed]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, L.; Xue, Y. Model and forecast stock market behavior integrating investor sentiment analysis and transaction data. Clust. Comput. 2017, 20, 789–803. [Google Scholar] [CrossRef]
- Ho-Dac, N.N.; Carson, S.J.; Moore, W.L. The effects of positive and negative online customer reviews: Do brand strength and category maturity matter? J. Mark. 2013, 77, 37–53. [Google Scholar] [CrossRef]
- Goh, K.Y.; Heng, C.S.; Lin, Z. Social media brand community and consumer behavior: Quantifying the relative impact of user-and marketer-generated content. Inf. Syst. Res. 2013, 24, 88–107. [Google Scholar] [CrossRef]
- Goes, P.B.; Lin, M.; Au Yeung, C.M. “Popularity effect” in user-generated content: Evidence from online product reviews. Inf. Syst. Res. 2014, 25, 222–238. [Google Scholar] [CrossRef]
- Kim, Y.; Srivastava, J. Impact of social influence in e-commerce decision making. In Proceedings of the Ninth International Conference on Electronic Commerce, Minneapolis, MN, USA, 19–22 August 2007; pp. 293–302. [Google Scholar]
- Gilbert, C.H.E. Vader: A parsimonious rule-based model for sentiment analysis of social media text. In Proceedings of the Eighth International Conference on Weblogs and Social Media (ICWSM-14), Ann Arbor, MI, USA, 1–4 June 2014; Available online: http://comp. social. gatech.edu/papers/icwsm14.vader.hutto.pdf (accessed on 21 December 2018).
- Velicer, W.F.; Colby, S.M. A Comparison of Missing-Data Procedures for Arima Time-Series Analysis. Educ. Psychol. Meas. 2005, 65, 596–615. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. Predictability of monthly temperature and precipitation using automatic time series forecasting methods. Acta Geophys. 2018, 66, 807–831. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The forecast Package for R. J. Stat. Softw. 2008, 27. [Google Scholar] [CrossRef] [Green Version]
- Box, G.E.; Jenkins, G.M. Some recent advances in forecasting and control. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1968, 17, 91–109. [Google Scholar] [CrossRef]
- Taieb, S.B.; Bontempi, G.; Atiya, A.F.; Sorjamaa, A. A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition. Expert Syst. Appl. 2012, 39, 7067–7083. [Google Scholar] [CrossRef] [Green Version]
- Khobai, H.; Chitauro, M. The Impact of Trade Liberalisation on Economic Growth in Switzerland. 2018. Available online: https://mpra.ub.uni-muenchen.de/89884/ (accessed on 21 December 2018).
- Lopes, S.R.C.; Olbermann, B.P.; Reisen, V.A. Non-stationary Gaussian ARFIMA processes: Estimation and application. Braz. Rev. Econom. 2002, 22, 103–126. [Google Scholar] [CrossRef]
- Flores, J.H.F.; Engel, P.M.; Pinto, R.C. Autocorrelation and partial autocorrelation functions to improve neural networks models on univariate time series forecasting. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Armstrong, J.S.; Collopy, F. Error measures for generalizing about forecasting methods: Empirical comparisons. Int. J. Forecast. 1992, 8, 69–80. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Wang, J.; Niu, T.; Du, P. A hybrid forecasting system based on a dual decomposition strategy and multi-objective optimization for electricity price forecasting. Appl. Energy 2019, 235, 1205–1225. [Google Scholar] [CrossRef]
- Mehmanpazir, F.; Asadi, S. Development of an evolutionary fuzzy expert system for estimating future behavior of stock price. J. Ind. Eng. Int. 2017, 13, 29–46. [Google Scholar] [CrossRef]
- de Myttenaere, A.; Golden, B.; Grand, B.L.; Rossi, F. Mean Absolute Percentage Error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Afendras, G.; Markatou, M. Optimality of training/test size and resampling effectiveness in cross-validation. J. Stat. Plan. Inference 2019, 199, 286–301. [Google Scholar] [CrossRef]
- Diebold, F.X. Comparing Predictive Accuracy, Twenty Years Later: A Personal Perspective on the Use and Abuse of Diebold–Mariano Tests. J. Bus. Econ. Stat. 2015, 33, 1. [Google Scholar] [CrossRef]




| Extracted Features | Occurrences | Percentage |
|---|---|---|
| Manufacturer | 36k | 36% |
| Sentiment | 55k | 55.2% |
| Manufacturer, Google Trends | 23k | 23% |
| Manufacturer, Sentiment | 33k | 33.1% |
| Manufacturer, Google Trends, Sentiment | 21k | 21.1% |
| MAPE | ||||
|---|---|---|---|---|
| Exogenous Variables | Test 10% | Test 20% | Test 30% | Average |
| None | 2.31% | 9.56% | 9.25% | 7.04% |
| Google Trends | 1.98% | 5.69% | 6.64% | 4.77% |
| Sentiment | 1.83% | 7.69% | 7.9% | 5.81% |
| Google Trends, Sentiment | 3.59% | 11.37% | 10.65% | 8.54% |
| Test Size | N. of Products Having a Manufacturer | N. of Products Having Manufacturer and Google Trends Entries | Percentage of How Often (Price, Date, Trend) Has Been the Best Combination in ARIMA |
|---|---|---|---|
| 10% | 36k | 23k | 61% |
| 20% | 56% | ||
| 30% | 43% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carta, S.; Medda, A.; Pili, A.; Reforgiato Recupero, D.; Saia, R. Forecasting E-Commerce Products Prices by Combining an Autoregressive Integrated Moving Average (ARIMA) Model and Google Trends Data. Future Internet 2019, 11, 5. https://doi.org/10.3390/fi11010005
Carta S, Medda A, Pili A, Reforgiato Recupero D, Saia R. Forecasting E-Commerce Products Prices by Combining an Autoregressive Integrated Moving Average (ARIMA) Model and Google Trends Data. Future Internet. 2019; 11(1):5. https://doi.org/10.3390/fi11010005
Chicago/Turabian StyleCarta, Salvatore, Andrea Medda, Alessio Pili, Diego Reforgiato Recupero, and Roberto Saia. 2019. "Forecasting E-Commerce Products Prices by Combining an Autoregressive Integrated Moving Average (ARIMA) Model and Google Trends Data" Future Internet 11, no. 1: 5. https://doi.org/10.3390/fi11010005
APA StyleCarta, S., Medda, A., Pili, A., Reforgiato Recupero, D., & Saia, R. (2019). Forecasting E-Commerce Products Prices by Combining an Autoregressive Integrated Moving Average (ARIMA) Model and Google Trends Data. Future Internet, 11(1), 5. https://doi.org/10.3390/fi11010005








