What Makes a UI Simple? Difficulty and Complexity in Tasks Engaging Visual-Spatial Working Memory
Abstract
:1. Introduction
- visual complexity and its metrics are rather weakly related to the accuracy in VSWM-related tasks,
- the strongest regularity used for grouping is best described with von Neumann range 1 neighborhood rule,
- the index of difficulty and throughput measure for the tasks engaging VSWM can be formulated as inspired by Fitts’ law,
- the throughput of 3.75 bit/s that we obtained in the experiment is consistent with the estimated range of 2–4 bit/s for memory-engaging tasks known from the literature.
2. Methods and Related Work
2.1. Information Theory-Based Measures
2.2. Human Information Processing
2.3. Gestalt Principles of Perception and Algorithmic Complexity-Based Measures
- “proximity”: objects that are placed nearby or in the same area (e.g., inside a frame) are perceived as a group;
- “similarity”: objects that are matching in color, size, behavior (e.g., movement direction or speed), etc. are perceived as a group;
- “good form” and “closure”: groups are perceived in such a way that the objects form more simple and familiar figures (e.g., cross as two intersecting lines, not as two adjoined angles; or separate dots and strokes as discontinuous drawing of a letter);
- the principles that relate to interaction between foreground and background.
2.4. Von Neumann and Moore Neighbourhoods in Cellular Automata
- (1)
- Von Neumann neighborhood of range R is defined as:
- (2)
- Moore neighborhood of range R is defined as:
3. Experiment Description
3.1. Goals and Hypotheses
- Performance in VSWM tasks is best predicted with the same compression-based factors as visual complexity.
- Performance in VSWM tasks is best predicted with the simpler proximity-based factors.
- Performance in VSWM tasks is best predicted with our proposed index of difficulty.
- The values calculated for the corresponding quantitative task setup-independent measure of performance that also encompasses time are consistent with the ones found in the literature.
3.2. Material and Procedure
3.3. Design
- Number of filled cells in the grid, which were set to range from 4 to 13: Sp;
- Number of all cells in the square grid, for which we used two levels, 25 (5 × 5 grid) and 36 (6 × 6 grid): S0;
- Configuration—i.e., allocation of filled cells in the grid, coded as a matrix of 1s (corresponding to the cells filled with blue) and 0s (corresponding to the blank cells)—see example in Figure 5.
- Length of the shortest string compressed with the RLE algorithm (from the row-based or the column-based conversion): LRLE;
- Length of the shortest string compressed with the RLE algorithm (from the row-based or the column-based conversion): LDEF;
- Number of figures composed from adjacent cells based on the range 1 von Neumann neighborhood rule (elements that touch diagonally do not constitute a figure): FN;
- Number of figures composed from adjacent cells based on the range 1 Moore neighborhood rule (elements that touch diagonally do constitute a figure): FM.
- the number of correctly designated cells in a trial (SC);
- the performance time in the trial (TM)—excluding the 2 s of the initial blue cells demonstration;
- the subjective evaluation of the configuration’s visual complexity, for which we used 5-point Likert scale (1 being “low complexity” and 5 being “high complexity”): Complexity.
3.4. Subjects
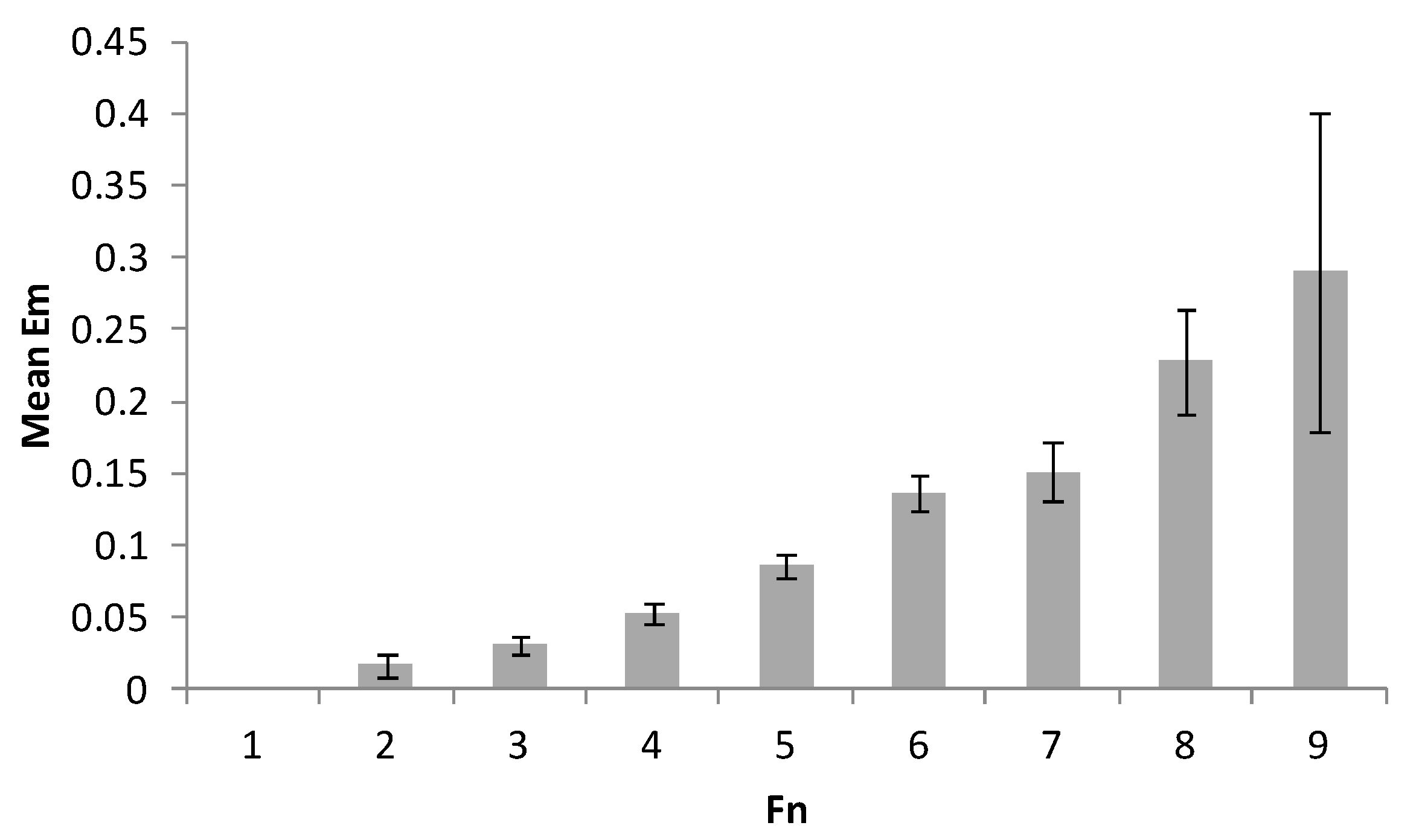
4. Results
4.1. Descriptive Statistics
4.2. Correlation Analysis
4.3. Regression Analysis
4.4. Index of Difficulty
4.5. Effective Index of Difficulty and VSWM Throughput
5. Discussion
6. Conclusions
- We demonstrated that the information-theoretic and compression algorithms-based metrics that are known to be representative of visual complexity do not adequately predict performance in tasks that engage visual-spatial working memory.
- We found that the memorized information chunks in 2D area containing uniform cells are not individual elements, but figures composed per the range 1 von Neumann neighborhood rule.
- We proposed the corresponding formulation for the index of difficulty for the tasks engaging visual-spatial working memory (16), quantitatively expressing it in “spatial bits”.
- We outlined the approach for calculating throughput (24), which can be used to predict users’ memorization performance with different designs of a GUI screen. We also believe that the approach can be generalized to other tasks that emerge in HCI.
7. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Oulasvirta, A. Can computers design interaction? In Proceedings of the 8th ACM SIGCHI Symposium on Engineering Interactive Computing Systems, Brussels, Belgium, 21–24 June 2016; pp. 1–2. [Google Scholar]
- Bailly, G.; Oulasvirta, A.; Brumby, D.P.; Howes, A. Model of visual search and selection time in linear menus. Proc. SIGCHI Conf. Hum. Factors Comput. Syst. 2014, 3865–3874. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Starke, S.D.; Baber, C.; Howes, A. A cognitive model of how people make decisions through interaction with visual displays. In Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems, Denver, CO, USA, 6–11 May 2017; pp. 1205–1216. [Google Scholar]
- Chen, X.; Bailly, G.; Brumby, D.P.; Oulasvirta, A.; Howes, A. The emergence of interactive behavior: A model of rational menu search. In Proceedings of the 33rd Annual ACM Conference on Human Factors in Computing Systems, Seoul, Korea, 18–23 April 2015; pp. 4217–4226. [Google Scholar]
- Tseng, Y.-C.; Howes, A. The adaptation of visual search to utility, ecology and design. Int. J. Hum. Comput. Stud. 2015, 80, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Gray, W.D.; Sims, C.R.; Fu, W.-T.; Schoelles, M.J. The soft constraints hypothesis: A rational analysis approach to resource allocation for interactive behavior. Psychol. Rev. 2006, 113, 461–482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miniukovich, A.; Marchese, M. Relationship between Visual Complexity and Aesthetics of Webpages. In Proceedings of the 2020 CHI Conference on Human Factors in Computing Systems, Honolulu, HI, USA, 25–30 April 2020; pp. 1–13. [Google Scholar]
- Rosenholtz, R.; Li, Y.; Nakano, L. Measuring visual clutter. J. Vis. 2007, 7, 17–22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carballal, A.; Santos, A.; Romero, J.; Machado, J.T.A.P.; Correia, J.; Castro, L. Distinguishing paintings from photographs by complexity estimates. Neural Comput. Appl. 2018, 30, 1957–1969. [Google Scholar] [CrossRef]
- Chang, L.-Y.; Chen, Y.-C.; Perfetti, C.A. GraphCom: A multidimensional measure of graphic complexity applied to 131 written languages. Behav. Res. Methods 2017, 50, 427–449. [Google Scholar] [CrossRef] [Green Version]
- Reinecke, K.; Yeh, T.; Miratrix, L.; Mardiko, R.; Zhao, Y.; Liu, J.; Gajos, K.Z. Predicting users’ first impressions of website aesthetics with a quantification of perceived visual complexity and colorfulness. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Paris, France, 27 April–2 May 2013; pp. 2049–2058. [Google Scholar]
- Bakaev, M.; Goltsova, E.; Khvorostov, V.; Razumnikova, O. Data Compression Algorithms in Analysis of UI Layouts Visual Complexity. In International Andrei Ershov Memorial Conference on Perspectives of System Informatics; Springer: Cham, Switzerland, 2019; pp. 167–184. [Google Scholar]
- Harper, S.; Michailidou, E.; Stevens, R. Toward a definition of visual complexity as an implicit measure of cognitive load. ACM Trans. Appl. Percept. TAP 2009, 6, 1–18. [Google Scholar] [CrossRef]
- Schnur, S.; Bektaş, K.; Çöltekin, A. Measured and perceived visual complexity: A comparative study among three online map providers. Cartogr. Geogr. Inf. Sci. 2018, 45, 238–254. [Google Scholar] [CrossRef]
- Kondyli, V.; Bhatt, M.; Suchan, J. Towards a Human-Centred Cognitive Model of Visuospatial Complexity in Everyday Driving. arXiv 2020, arXiv:2006.00059. [Google Scholar]
- Conway, A.R.; Cowan, N.; Bunting, M.F.; Therriault, D.J.; Minkoff, S.R. A latent variable analysis of working memory capacity, short-term memory capacity, processing speed, and general fluid intelligence. Intelligence 2002, 30, 163–183. [Google Scholar] [CrossRef]
- Unsworth, N.; Fukuda, K.; Awh, E.; Vogel, E.K. Working Memory Delay Activity Predicts Individual Differences in Cognitive Abilities. J. Cogn. Neurosci. 2015, 27, 853–865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cowan, N. Chapter 20 What are the differences between long-term, short-term, and working memory? Prog. Brain Res. 2008, 169, 323–338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aben, B.; Stapert, S.Z.; Blokland, A. About the Distinction between Working Memory and Short-Term Memory. Front. Psychol. 2012, 3, 301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cowan, N. The magical mystery four: How is working memory capacity limited, and why? Curr. Dir. Psychol. Sci. 2010, 19, 51–57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cowan, N. Working memory maturation: Can we get at the essence of cognitive growth? Perspect. Psychol. Sci. 2016, 11, 239–264. [Google Scholar] [CrossRef] [PubMed]
- Emacken, B.; Etaylor, J.; Ejones, D. Limitless capacity: A dynamic object-oriented approach to short-term memory. Front. Psychol. 2015, 6, 293. [Google Scholar] [CrossRef] [Green Version]
- Proctor, R.W.; Schneider, D.W. Hick’s Law for Choice Reaction Time: A Review. Q. J. Exp. Psychol. 2017, 24, 1–56. [Google Scholar] [CrossRef]
- Baddeley, A.D.; Logie, R.H. Working memory: The multiple-component model. In Models of Working Memory: Mechanisms of Active Maintenance and Executive Control; Miyake, A., Shah, P., Eds.; Cambridge University Press: Cambridge, UK, 1999; pp. 28–61. [Google Scholar]
- Filipe, S.; Alexandre, L.A. From the human visual system to the computational models of visual attention: A survey. Artif. Intell. Rev. 2013, 39, 1–47. [Google Scholar]
- Peterson, D.J.P.; Berryhill, M.E. The Gestalt principle of similarity benefits visual working memory. Psychon. Bull. Rev. 2013, 20, 1282–1289. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Gao, Q.; Tang, N.; Shui, R.; Shen, M. Organization principles in visual working memory: Evidence from sequential stimulus display. Cognition 2016, 146, 277–288. [Google Scholar] [CrossRef]
- Kałamała, P.; Sadowska, A.; Ordziniak, W.; Chuderski, A. Gestalt Effects in Visual Working Memory. Exp. Psychol. 2017, 64, 5–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schneider, D.W.; Anderson, J.R. A memory-based model of Hick’s law. Cogn. Psychol. 2011, 62, 193–222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soukoreff, R.W.; MacKenzie, I.S. Towards a standard for pointing device evaluation, perspectives on 27 years of Fitts’ law research in HCI. Int. J. Hum. Comput. Stud. 2004, 61, 751–789. [Google Scholar] [CrossRef]
- Seow, S. Information Theoretic Models of HCI: A Comparison of the Hick-Hyman Law and Fitts’ Law. Hum. Comput. Interact. 2005, 20, 315–352. [Google Scholar] [CrossRef]
- Landauer, T.K.; Nachbar, D.W. Selection from alphabetic and numeric menu trees using a touch screen: Breadth, depth, and width. In Proceedings of the CHI ‘85 Conference: Human Factors in Computer Systems, San Francisco, CA, USA, 14–18 April 1985; pp. 73–78. [Google Scholar]
- Bakaev, M.; Avdeenko, T.; Cheng, H.-I. Modelling selection tasks and assessing performance in web interaction. IADIS Int. J. Comput. Sci. Inf. Syst. 2012, 7, 94–105. [Google Scholar]
- Cockburn, A.; Gutwin, C.; Greenberg, S. A predictive model of menu performance. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, San Jose, CA, USA, 27 April–2 May 2007; pp. 627–636. [Google Scholar]
- Longstreth, L.E.; El-Zahhar, N.; Alcorn, M.B. Exceptions to Hick’s law: Explorations with a response duration measure. J. Exp. Psychol. Gen. 1985, 114, 417–434. [Google Scholar] [CrossRef]
- Huesmann, L.R.; Card, S.K.; Moran, T.P.; Newell, A. The Psychology of Human-Computer Interaction. Am. J. Psychol. 1984, 97, 625. [Google Scholar] [CrossRef]
- Prisnyakov, V.F.; Prisnyakova, L.M. Mathematic Modeling of Information Processing by Human-Machine Systems’ Operator; Mashinostroenie: Moscow, Russia, 1990. (In Russian) [Google Scholar]
- Bakaev, M.; Avdeenko, T. A quantitative measure for information transfer in human-machine control systems. In Proceedings of the 2015 International Siberian Conference on Control and Communications (SIBCON), Omsk, Russia, 21–23 May 2015; pp. 1–4. [Google Scholar]
- Pierce, B.F.; Woodson, W.E.; Conover, D.W. Human Engineering Guide for Equipment Designers. Technol. Cult. 1966, 7, 124. [Google Scholar] [CrossRef]
- Sperling, G. A Model for Visual Memory Tasks. Hum. Factors J. Hum. Factors Ergon. Soc. 1963, 5, 19–31. [Google Scholar] [CrossRef]
- Solomonoff, R. The application of algorithmic probability to problems in artificial intelligence. Mach. Intell. Pattern Recognit. 1986, 4, 473–491. [Google Scholar]
- Wagemans, J.; Elder, J.H.; Kubovy, M.; Palmer, S.E.; Peterson, M.A.; Singh, M.; von der Heydt, R. A century of Gestalt psychology in visual perception: I. Perceptual grouping and figure–ground organization. Psychol. Bull. 2012, 138, 1172–1217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donderi, D.C. Visual complexity: A review. Psychol. Bull. 2006, 132, 73. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robinson, A.; Cherry, C. Results of a prototype television bandwidth compression scheme. Proc. IEEE 1967, 55, 356–364. [Google Scholar] [CrossRef]
- Deutsch, P. DEFLATE Compressed Data Format Specification Version 1.3. 1996. Available online: https://dl.acm.org/doi/pdf/10.17487/RFC1951 (accessed on 18 January 2021).
- Bakaev, M.A.; Razumnikova, O. Defining complexity for visual-spatial memory tasks and human operator s throughput. Upr. Bol’shimi Sist. 2017, 70, 25–57. (In Russian) [Google Scholar]
- Wolfe, J.M. Saved by a log: How do humans perform hybrid visual and memory search? Psychol. Sci. 2012, 23, 698–703. [Google Scholar] [CrossRef]
- Xing, J. Measures of Information Complexity and the Implications for Automation Design; No. DOT/FAA/AM-04/17; Federal Aviation Administration: Washington, DC, USA; Oklahoma City Ok Civil Aeromedical Inst.: Oklahoma City, OK, USA, 2004. [Google Scholar]
- Miniukovich, A.; Sulpizio, S.; De Angeli, A. Visual complexity of graphical user interfaces. In Proceedings of the 2018 International Conference on Big Data and Education, Honolulu, HI, USA, 9–11 March 2018; p. 20. [Google Scholar]
- Blough, P.M.; Slavin, L.K. Reaction time assessments of gender differences in visual-spatial performance. Percept. Psychophys. 1987, 41, 276–281. [Google Scholar] [CrossRef] [Green Version]
- Halpern, D.F. Sex Differences in Cognitive Abilities, 3rd ed.; Psychology Press: New York, NY, USA, 2013. [Google Scholar]
- Loring-Meier, S.; Halpern, D.F. Sex differences in visuospatial working memory: Components of cognitive processing. Psychon. Bull. Rev. 1999, 6, 464–471. [Google Scholar] [CrossRef]
- Razumnikova, O.M.; Volf, N.V. Re-organization of relation of intelligence with attention and memory in aging. Zhurnal Vyss. Nervn. Deyatelnosti Im. I.P. Pavlov. 2017, 67, 55–67. (In Russian) [Google Scholar]








| Variable | Range | Mean (SD) |
|---|---|---|
| S0 | 25, 36 | - |
| SP | 4–13 | 7.42 (1.99) |
| FN | 1–10 | 4.58 (1.42) |
| FM | 1–8 | 3.21 (1.19) |
| LRLE | 8–30 | 17.07 (3.52) |
| LDEF | 8–20 | 13.91 (1.98) |
| SC | 1–13 | 6.76 (1.96) |
| EM | 0–0.75 | 0.08 (0.14) |
| TM | 1–14 s | 6.03 (2.21) |
| Complexity | 1.0–5.0 | 2.57 (0.96) |
| Variable | r (EM) | τ (Complexity) |
|---|---|---|
| S0 | 0.176 | 0.13 |
| SP | 0.231 | 0.424 |
| FN | 0.332 | 0.329 |
| FM | 0.239 | 0.115 |
| LRLE | 0.302 | 0.410 |
| LDEF | 0.215 | 0.342 |
| Index of Difficulty | Range | Mean (SD) | r (EM) | r (TM) | τ (Complexity) |
|---|---|---|---|---|---|
| IDMSP | 18.6–67.2 | 36.5 (10.2) | 0.259 | 0.390 | 0.421 |
| IDMFN | 4.6–51.7 | 22.6 (7.5) | 0.340 | 0.211 | 0.314 |
| IDMFM | 4.6–41.4 | 15.9 (6.3) | 0.251 | 0.068 | 0.124 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakaev, M.; Razumnikova, O. What Makes a UI Simple? Difficulty and Complexity in Tasks Engaging Visual-Spatial Working Memory. Future Internet 2021, 13, 21. https://doi.org/10.3390/fi13010021
Bakaev M, Razumnikova O. What Makes a UI Simple? Difficulty and Complexity in Tasks Engaging Visual-Spatial Working Memory. Future Internet. 2021; 13(1):21. https://doi.org/10.3390/fi13010021
Chicago/Turabian StyleBakaev, Maxim, and Olga Razumnikova. 2021. "What Makes a UI Simple? Difficulty and Complexity in Tasks Engaging Visual-Spatial Working Memory" Future Internet 13, no. 1: 21. https://doi.org/10.3390/fi13010021
APA StyleBakaev, M., & Razumnikova, O. (2021). What Makes a UI Simple? Difficulty and Complexity in Tasks Engaging Visual-Spatial Working Memory. Future Internet, 13(1), 21. https://doi.org/10.3390/fi13010021






