Abstract
The Social Internet of Things (SIoT) means that every node can use a set of nodes that are considered as friends to search for a specific service. However, this is a slow process because each node is required to manage a high number of friends. Thus, the SIoT issue consists of how to select the right friends that improve the network navigability. The enhancement of the network navigability boosts the search for a service to be rapid but not guaranteed. Furthermore, sending requests from the shortest paths involves the rapid search, but the network lifetime can be reduced due to the number of requests that can be transmitted and processed by the nodes that have low power energy. This paper proposes a new approach that improves the network navigability, speeds up the search process, and increases the network lifetime. This approach aims at creating groups dynamically by nodes where each group has a master node, second, using a consensus algorithm between master nodes to agree with a specific capability, finally adopting a friendship selection method to create a social network. Thus, the friends will be sorted periodically for the objective of creating simultaneously a balance between the energy consumption and the rapid search process. Simulation results on the Brightkite location-based online social network dataset demonstrate that our proposal outperforms baseline methods in terms of some parameters of network navigability, path length to reach the providers, and network lifetime.
1. Introduction
The term Internet of Things (IoT) has been known for the last few years. IoT describes a vision where every object becomes a part of the Internet, and has been recognized as one of the major technological revolutions of this century [1,2].
IoT allows things and people to be connected anytime, from anyplace, with anything and anyone, preferably using any network/path and any service [3]. The fundamental goal is to create a more desirable world for human beings, where objects and things around them know what they want, what they like, and what they need and act accordingly without any explicit instructions [4]. The outspread use of IoT in various domains, such as transportation [5,6,7], health [8,9,10], manufacturing [11,12,13], and other fields aims to create a new environment of applications which will influence our lives [14,15].
The search for a specific service is a crucial challenge such as battery energy, interoperability, reliability, scalability, availability, etc. Moreover, network lifetime is the total amount of time to maintain its full functionality [16], it is constrained by the battery of nodes [17]. These constraints that are related to the nature of a node and are named as the “Capability” of the node. A capability indicates the capacity to perform a particular service, task, activity, or function [18,19,20].
Due to the rapid technology and development that are happening in our social lives, a new concept named Social Internet of Things (SIoT) has been proposed [21,22]. It is an integration of social network and Internet of Things, introducing a new vision of social relationships among different devices/things, independently from the fact that they belong to the same or to different platforms owned and managed by different organizations. This vision makes all the IoT devices ready to cooperate with others and create relationships among them as human beings do. According to the growth of intelligent devices especially in smart cities, the social Internet of Things offers a new mechanism of communication among nodes, in a distributed manner, with only local information. This mechanism allows the nodes to search for services and resources by themselves instead of the central systems such as servers, cloud computing, etc.
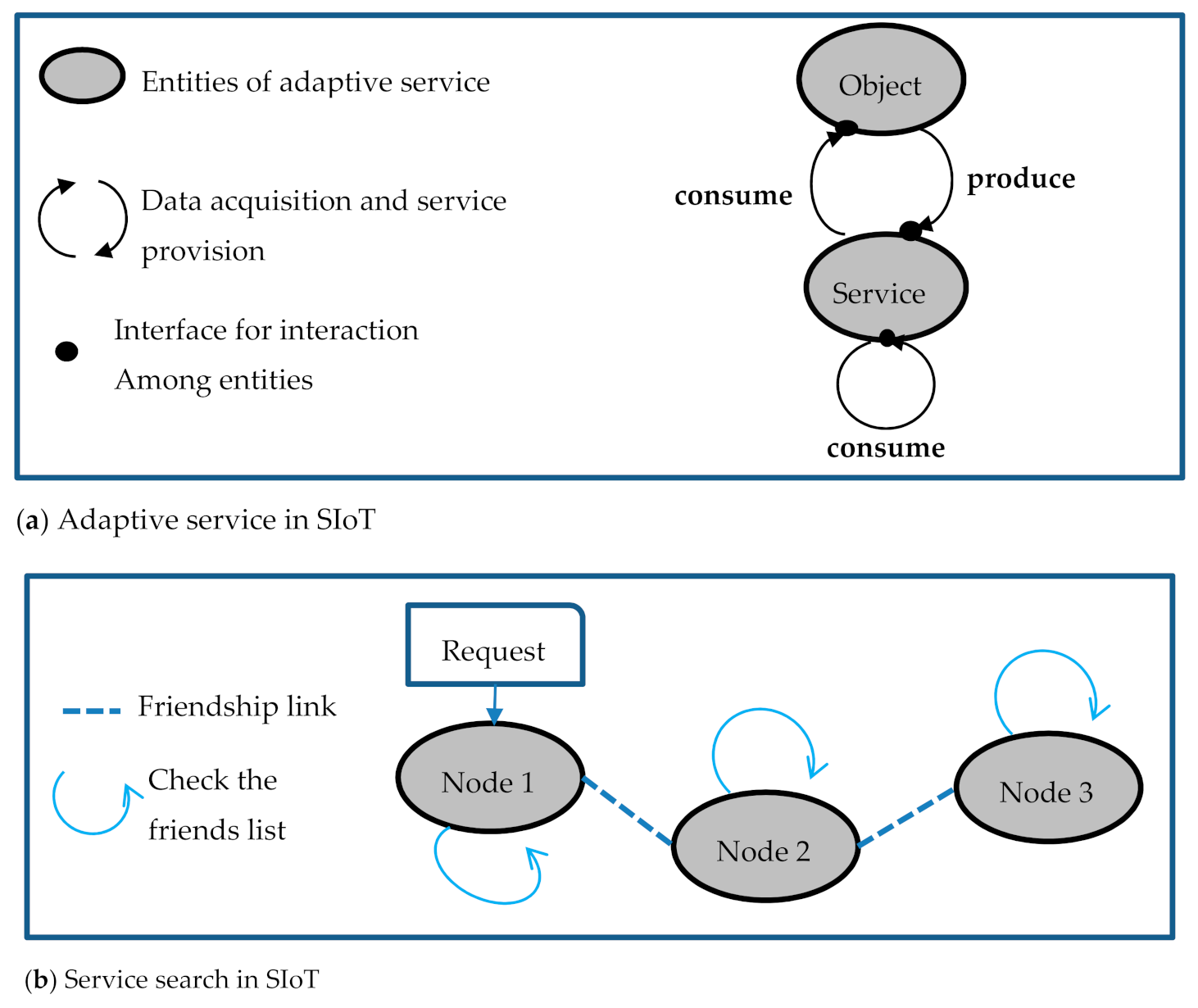
Figure 1a illustrates the concept of SIoT, there are two entities: object and service. These entities can provide and consume services and/or data. In this sense, services themselves can consume data produced by other services to form a composite service or to be used for other objectives. Figure 1b shows a mechanism of service search in SIoT, where the communication is in a decentralized manner. When a node receives a request that includes the requirements of a customer node, it verifies if it can respond to this request by itself or by its friends, elsewhere it will be transmitted to a given node until the provider node is found. The similarity between the request requirements and service is divided into two types that are proximity and point. The point type is the provider node should respond strictly to the declared requirements such as monitoring the temperature at a fixed location, while in the proximity type is the provider node could respond flexibly to the declared requirements such as monitoring the temperature at a specific area.
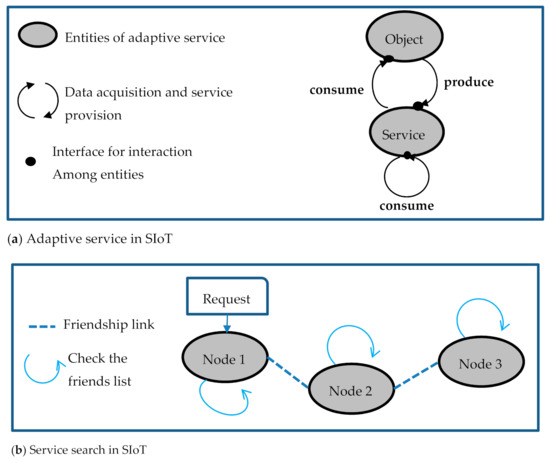
Figure 1.
Concept of the social internet of things (SIoT).
According to [23], there are five types of friendship in the SIoT, namely:
- Parental Object Relationship (POR): It is established among similar objects. They have the same producer, model, and production batch.
- Co-location Object Relationship (C-LOR): It is established among heterogeneous or homogenous objects that share the same location.
- Ownership Object Relationship (OOR): It is established if the objects are owned by the same user.
- Co-work Object Relationship (CWOR): It is established when two or more devices collaborate to accomplish a common goal.
- Social Object Relationship (SOR): It is established if there is a liaison between the objects.
In SIoT every node will be able to search for the desired service using its friends. As a node can be surrounded by many nodes, selecting a set of friends from the neighboring nodes is an essential phase, which affects the service search task. The efficiency of Friendship selection strategies is often measured in terms of the parameters of network navigability: giant component, average path length, average local clustering coefficient, average degree, and diameter of the network. The enhancement of these parameters boosts rapid search for the service but does not guarantee it.
Furthermore, each node must manage the selected friends, such that the selection of many friends affects negatively the capacity of storage, battery power, etc. So, it is desirable to limit the number of friendships for each node. On another side, during the service search, the nodes lose their energy which leads to reduce network lifetime; therefore, the customer nodes can be unable to obtain the requested services. The research question is how to create efficient strategies that improve the parameters of network navigability and increase the network lifetime, also to propose a new mechanism to speed up more the service search process.
The objective is to create a new approach for the fastest, dynamic, and autonomous service search among nodes in SIoT by considering the capacities of different devices in SIoT. Furthermore, the current work can provide many benefits for practitioners and researchers who want to develop or integrate IoT applications that can exploit the services provided by the systems of smart healthcare, smart agriculture, smart city, etc. Moreover, it is designed to support the 5th generation (5G) that is required to quickly and efficiently respond to complex IoT requests.
To overcome the limitations associated with SIoT, we propose a new approach with features described as follows.
- Firstly, we create the node groups, where each group has only one master node, and these groups run a consensus algorithm to agree on a specific value.
- Secondly, we create a new friendship selection strategy using groups of nodes based on an agreed value and other properties. The social network is built to achieve a better navigability and to be a suitable network for minimizing the number of hops and balancing the resources.
- Thirdly, a node sorts and resorts all the friendships based on the capabilities of nodes, groups, their centrality, and popularity, in order to speed up the search task and increase the network lifetime.
The performance of our contribution has been analyzed in terms of giant component, average degree, average local clustering coefficient, average path length, network diameter, number of hops to achieve the providers, and network lifetime.
The remainder of this paper is organized as follows: Section 2 introduces the related works, Section 3 includes the problem definition and parameters of a network, Section 4 presents our proposed contribution, Section 5 gives simulation results and discussion, and the final section concludes the paper.
2. Related Works
The social networks’ navigability improvement is equivalent to the achievement of the following criteria, stated simultaneously: maximizing the giant component and local clustering coefficient, and minimizing the average degree, the average path length and the diameter.
In [24], the authors presented five strategies to select the friendships in a network. At first, a node accepts all the friendship requests until it reaches the maximum number of allowed connections. Then, to manage any further requests, one of the following strategies is proposed to select the new friendships:
- Strategy 1: A node accepts any new request of friendship.
- Strategy 2: A node accepts requests of nodes that have a greater number of connections (decreasing order).
- Strategy 3: A node accepts requests of nodes that have a fewer number of connections (increasing order).
- Strategy 4: A node accepts requests of nodes that have a greater number of common connections.
- Strategy 5: A node accepts requests of nodes that have a fewer number of common connections.
These five strategies are applied separately to create the social network. The results show that strategies 3 and 5 achieve the total giant component of nodes, strategies 2 and 5 have a low average path length, strategies 2 and 4 have the lowest average degrees, and strategies 1 and 4 have a high value of local clustering coefficient.
The algorithm in [25] based on the strategies presented in [24] applies the genetic algorithm for friendship selection in IoT. The algorithm is used to maximize the number of friends (strategy 2) and friends of friends (common friends) (strategy 4) simultaneously, for selecting the optimal near node i.e., reaching the destinations rapidly. The results achieve an enhancement in the shortest path length, and also an acceptable average degree and average local clustering coefficient values in comparison with the work presented in [24].
A heuristic method is proposed in [26] to select friends in the SIoT, based on reachability and type of relationship properties. When a node achieves the maximal number of friends and there is another node that sends a friend request, it checks the ability of its friends and the candidate friend to achieve their destinations, by calculating the reachability factor and verifying the relationship type. Based on these two factors, the node decides to add or to reject the candidate friend. This heuristic method improves the average degree and average path length, but the giant component is modest (52%).
Authors in [27] proposed an algorithm to resolve the link selection (friends selection) issue in SIoT, by restricting the number of connections for each node using a threshold value in order to improve the properties of navigability: path length, average clustering coefficient, and giant component. The threshold value is adjusted dynamically based on the number of hubs in network, which allows to add new friends and to remove old mutual friends. The experimental results show higher average clustering coefficient, shorten path length, and higher giant component. The enhancement of the properties of navigability makes service discovery task faster.
To decrease the path length from a requestor node to a provider node, authors in [28] proposed two mechanisms:
- A caching system: The nodes store pieces of information such as a document, web page or video. The storage location is based on the requestors of these services: the more these services are requested, the closer they are to the node’s storage location.
- Friendship selection: Established when a node creates new paths of friendship to decrease the path length to the provider node and removes friends that do not belong to the shortest path.
The results show that the caching system strategy has a less than average hop length than the friendship selection strategy but it is expensive in terms of memory consumption.
To overcome the issues of the search/discovery phase in SIoT, the authors in [29] proposed an algorithm to select a friend that can receive/execute the requested services using a combination of two properties. The first property is the centrality (the degree) of a friend; a friend (intermediate node) with a high centrality is selected to receive the requested service, which can achieve the provider quickly. The second property is node similarity; it determines the similarity between request requirements and nodes using distance similarity. The intermediate node that has the higher probability is chosen to receive the request.
A service discovery and selection model [30] is proposed based on artificial potential fields (APFs) which is initially introduced by [31] to resolve the reboot navigation problems in dynamic environments. In this model, for each node a service agent is responsible for the provision of a service and the requester agent is responsible for the management of the incoming requests. When a node receives a request, the service agent gets the requested service and verifies if it can be executed by this node, elsewhere the requested service is sent to the most promising node by the requester agent using the resultant force of APFs. The resultant force is a combination of service satisfaction and availability; it can be either attractive or repulsive toward the neighboring nodes. The service satisfaction assures that the next node can execute the desired service for a request, and the service availability assures that the time of waiting for the desired service is fewer for the next node. The service availability makes nodes to choose different intermediate nodes for each request. The number of hops required is reduced and the queue length (the number of services waiting to execute) among nodes is balanced in comparison with the flooding-based approach [32].
Authors in [33] proposed an approach to discover and search for a specific service in SIoT among communities, where a community is defined as a cohesive group of nodes that are densely connected to each other and sparsely connected to the other nodes in a SIoT. The communities are constructed based on preference and social similarities, and subcommunity within a community is constructed based on services similarity. The coordinator node (considered as the master node of a community) is responsible for holding the services of the community. When a node receives a request for a service that is not within the subcommunity of the node, it forwards it to the coordinator node of a neighboring community until the provider node is found. The experimental results show that the proposed approach has a promise results in terms success rate, average delay, and modularity.
As the search for a specific service in SIoT is performed in a distributed manner with only local information, it is important to apply a method that makes the task efficient, subject to the energy consumption of nodes. As illustrated in Table 1, there are studies focused on the enhancement of the network navigability (giant component, average path length, average degree, local clustering coefficient, diameter) during the friendship selection to obtain an efficient search task, but this strategy is not enough to speed up the search for a desired service. While the other ones focus on service search itself in which the friendship selection has been assumed already performed by nodes (assuming that the social network has already been created). However, in both cases the energy consumption of nodes and the network lifetime are not considered. Our approach deals with the problem of service search in SIoT considering network navigability, service discovery/search itself, energy consumption of nodes, and network lifetime.

Table 1.
Functional comparison of our proposal work with the previous studies.
3. Preliminaries
This section presents the necessary background for understanding the remainder of this paper, including the problem definition and the parameters of a network.
3.1. Problem Definition
In a constraint network, each node has a set of neighbors, where the communication is one hop (from a node to another), in both directions (undirected network), and is unicast (a request is sent to just one node).
In a social network, each node has a set of friends which are considered useful neighbors to reach the requested services. So, the problem consists of how to select these friends in a way that can improve network navigability. Furthermore, the search process must be rapid with an increased network lifetime.
In more details, when any network does not achieve the total giant component (100%), the possibility to respond to the users’ or nodes’ requirements will be decreased. The average degree should be minimized considering that the total giant component should be maximized, where a high number of friends affect the nodes’ capabilities such as power energy and memory capacity. Moreover, the minimization of average path length and diameter, and the maximization of the average local coefficient boost the service search to find a short path from a requestor to a provider. Besides, until the provider node is not achieved, the request/queries should move through the nodes that have high capabilities, especially the ones with sufficient energy. This is because intermediate nodes with insufficient resources could break down after several tasks.
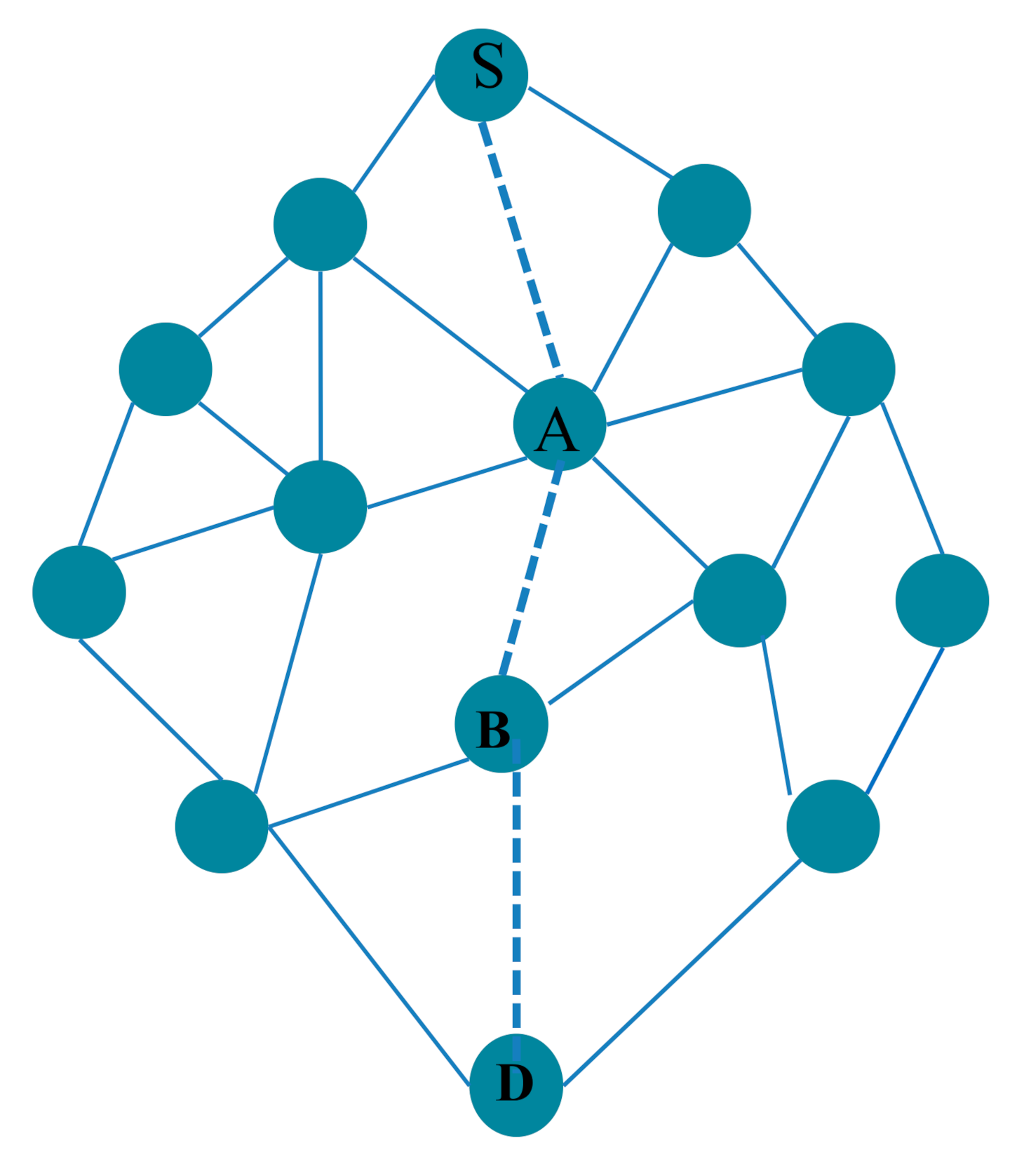
Figure 2 shows a simple example of a social network (it is considered as a mesh-like network), where links represent friendships’ connection ties, while the dashed lines are the path followed by node S to reach the provider node D. When a node S receives a request, it can retransmit or execute it; in case of retransmission, the node S can choose the friend A, and by the same manner, the request will reach to the provider (executor) node D. The path achieved by the request in this example is the shortest path length; it makes the service search rapid, but that does not mean that it is the best path. Node A can transmit the requests more frequently than others; therefore, it will consume more energy. For this, during the search phase, the best path to achieve a provider is a short path (for the rapid search phase), where the associated/constructed nodes have sufficient energies (to extend the network lifetime [34]).
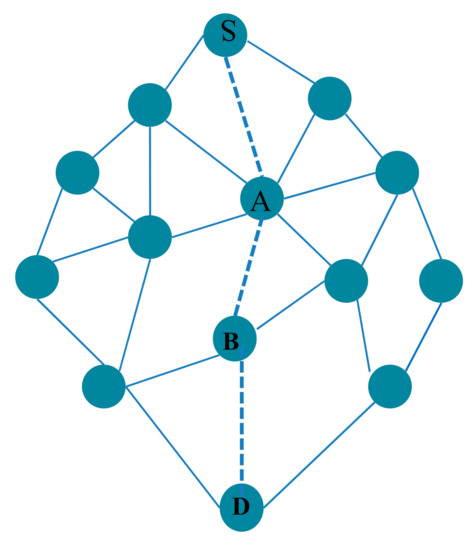
Figure 2.
A simple example of a social network.
Table 2 summarizes the main notations used in the rest of this paper.

Table 2.
Notations used in the rest of this paper.
3.2. Parameters of a Network
There are a set of parameters that are computed to measure the efficiency of a network. In the following, we explain the most important parameters for the undirected network as discussed below.
- The giant component: it is a connected component of a network that contains a significant proportion of the entire nodes in the network.
- The average path length: it measures the efficiency of information or mass transport on a network and it is calculated as follows:where N is the number of nodes and is the shortest path length between two nodes i and j. The shortest average path length boosts the rapid transmission of data and reduces costs.
- The average degree: The degree of the node i is the number of its neighbors/connections. The average degree of a network is calculated as follows:The average degree increases with the increase of the number of connections among nodes.
- The local clustering coefficient: It measures how close the neighbors of a node are to make a complete graph, and it is calculated as follows:where is the number of edges among the neighbors of the node i, and is the number of neighbors of the node i. The average local clustering coefficient of a network is computed as follows:
- Diameter of a network: It is the shortest path length between the two most distant nodes in a network.
The giant component, the average degree, and the local clustering coefficient values of a social network are always fewer than or equal to those of its initial network. Whereas, average path length and diameter values in social network are always greater than or equal to those of its initial network.
4. Our Proposal
In this section, we present a new approach to create a social network and manage the service search by taking into account the nodes’ capabilities. As stated above, several factors may impact these tasks, such as network navigability, the number of hops to achieve the providers, and the network lifetime. The main novelty of our contribution is to address all these criteria at once, and it is designed to maintain the 5th generation wireless technology.
4.1. Main Steps
The objective of this contribution is to create a social network that can improve network navigability, boost rapid service discovery, and prolong the network lifetime, knowing that the enhancement of network navigability alone is not sufficient to quickly search for a service.
Algorithm 1 shows the main steps to achieve our objective. At first, the nodes create groups dynamically, where each group possesses only one master. Then, the master groups agree on a specific value using a consensus algorithm. After that, the friendship selection begins using the agreed value and other properties. The three steps above are applied once.
| Algorithm 1: The general steps of our contribution |
| 1. /* Initial phase */ |
| 2. Creation of groups |
| 3. A consensus algorithm on a common value |
| 4. Friendship selection |
| 5. /* Second phase*/ |
| 6. Sorting the friends |
| 7. For each request |
| 8. Service search process |
| 9. / / Resorting the friends if needed |
| 10. End |
The scenario of the proposed algorithm can be given in case of a smart city where a large number of devices are connected peer-to-peer and each device is surrounded by connected devices, such as, monitoring of temperature, monitoring of temperature, control electricity consumption, human detection movement, human detection, human identification, etc. The devices can request each other (one-hop communication) for a given service until the target device is found. The devices that exist in the same communication range could create a group dynamically according to some criteria (Section 4.2). Then the devices will create a social network by selecting a set of devices as friends (Section 4.5) that will be capable to achieve efficiency at the destinations of a device, for example, a detection movement device can use monitoring of temperature and monitoring of temperature devices as friends. For efficient service search, the devices sort their friends periodically (Section 4.6) considering the capability to process the incoming requests and rapid search process (Section 4.3).
The social network is created to improve network navigability, to be a suitable network that can be used to prolong the network lifetime, and to support the optimal paths during the service search task. The service search can be launched after the creation of the social network. Each node sorts its friends in a decreasing manner in order to balance between the rapid search and the available resources. When a node does not find any friend that can provide or execute a given service, it chooses the friend on the top of the list to receive this request.
4.2. Construction of Node Groups
The construction of groups is used principally to support a social network that improves the network navigability and initialize the balanced resources between friends. However, its role is secondary during the search phase.
In IoT networks, there are nodes with a low number of connections and others with a high number of connections, and with different capabilities. Therefore, a semi-uniform distribution of density and resources is needed. Furthermore, the search process in lossy networks is often not exploited due to several reasons, such as the longest path length from the requestor to the provider, a high number of services, limited capabilities of the nodes, etc. To deal with these issues, the mechanism of groups is adopted as a key concept to achieve the given goals.
A mechanism for automatic and self-organizing groups has been proposed, the groups are created according to two rules as stated below:
- Rule (1): In an area with N neighbors, the node with a high number of connections has a priority to be the master group.
- Rule (2): The group with a low number of members has a priority to add a new node.
Each node has information about its neighbor nodes (nodes that are in communication range) such as the number of connections, information groups (if they were constructed), etc. A node i sends a request to join as a member node to the node j (candidate master group) that has a high number of connections, if the node j has a high number of connections for all neighboring nodes such that it possesses a high capacity (for example residual energy is more than 50%), in this case, the node j responses positively for the node i. In the second scenario, when a node j sends a request to join as a member node and receives a request to be considered as the master node, node j will choose to be as member node and respond negatively to the request (Rule 1). In the third scenario, when a new node has been deployed in an area, firstly, it gathers information from its neighbors, secondly, it sends a request to join the group that has a low number of members (Rule 2).
Rule (1) makes the network assemble a set of nodes that have low degrees within the node that has a high degree; its goal is to expand the proportion of connections when the social network is created. The objective of Rule (2) is to decrease the difference that exists between groups in terms of cardinality.
During the discovery/search phase, the importance of groups is decreased, where each node has its own capability to realize tasks independently from its master group. The nature of groups is flexible in order to avoid some problems related to the creation of groups, such as nodes’ mobility.
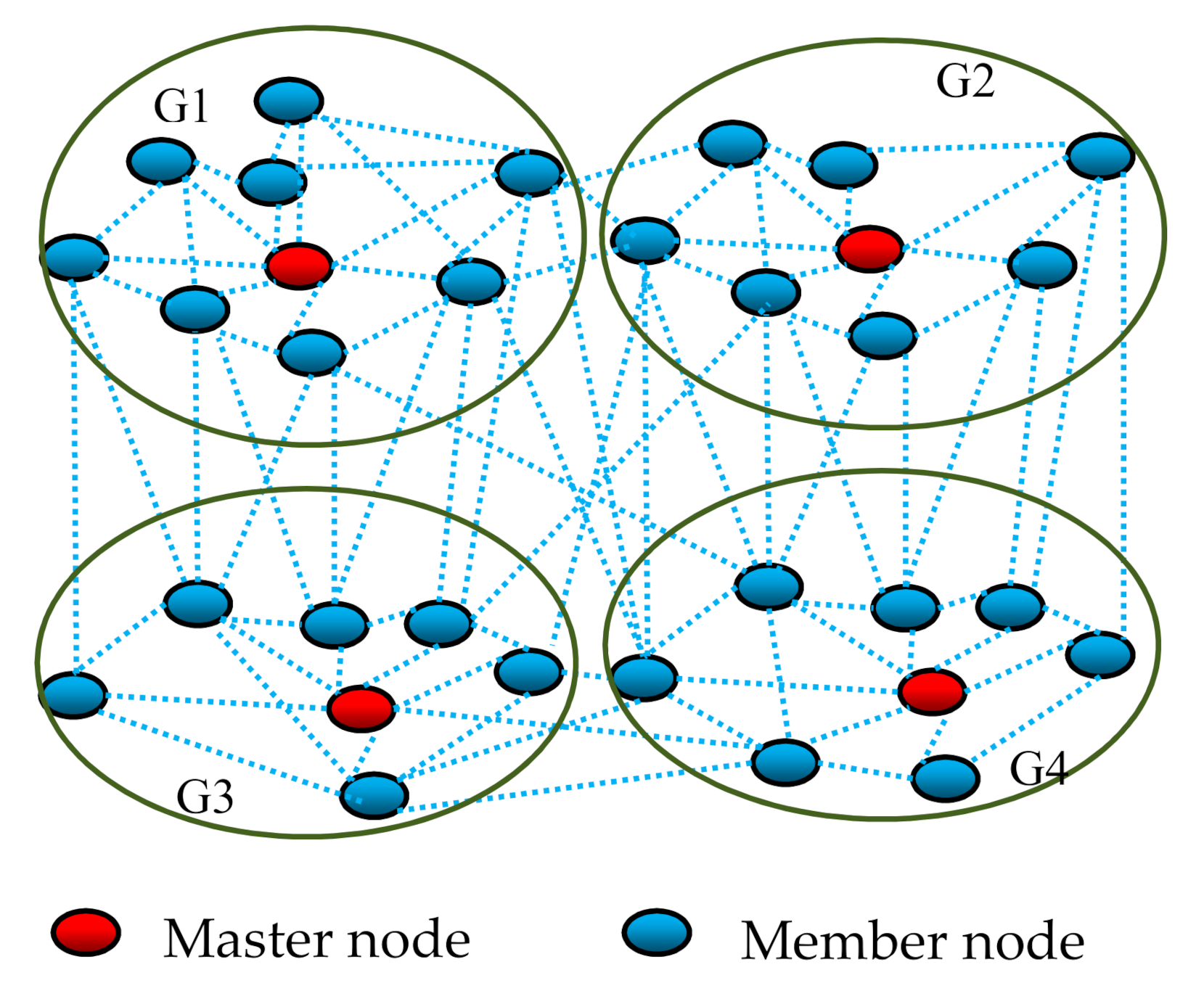
Figure 3 provides an example of the groups’ creation in a simple lossy network; there are four groups G1, G2, G3, and G4 with 9, 8, 7, and 8 nodes, respectively. The number of nodes in the groups does not exceed 9 (Gmax = 9).
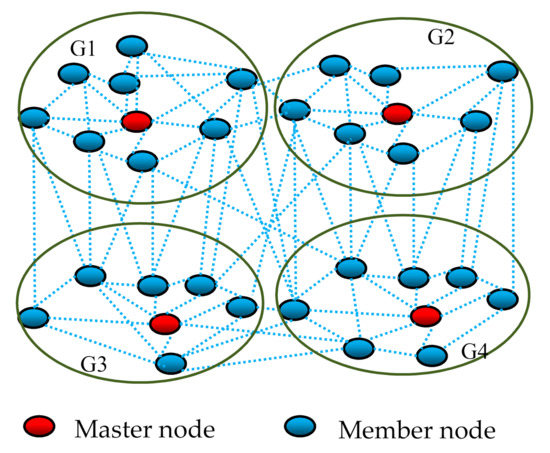
Figure 3.
An example of the node groups.
4.3. Available Resources and Search Factors
To determine the nature of the available resources of a network, node and group capabilities are proposed. Furthermore, the group centrality and popularity predict the search path of a request to achieve the provider rapidly.
Node capability:
Node capability is a set of properties of a node such as quality of service, capacity of storage, power energy, etc. It combines all these properties and takes into account the weight of each property. We categorize the properties into two types:
Maximized Property: when we want to select the best node, we search for a high value of certain properties such as power energy, memory capacity, etc.
Minimized Property: when we want to select the best node, we search for a low value of certain properties such as execution time, etc.
We normalize the property of node i by calculating the value of property which is given below:
where and
The Equation (5) allows to limit the values of properties in range 0 and 1, and to determine their influence for each node.
After that we define the node capability as follows:
where is the weight of property , , is the number of properties, and .
Equation (6) combines all properties of a node with the weight of each property to determine the capability of the node using the normalized values obtained from Equation (5). The node with a high value of capability denotes a high efficiency. The most capable nodes are preferred to be master nodes or intermediate nodes.
Group capability:
We define another factor related to the capability of a group, which is the capability of all nodes in the group (master node and member nodes). Group capability of the group k is defined as follows:
where , and is the cardinal of group k.
Equation (7) combines all capabilities of nodes in a group to determine the group capability using the capabilities values obtained from Equation (6). The group with a high value of capability denotes a high efficiency. The most capable groups are preferred to be intermediate groups for requests.
Group centrality:
In a social network, we define the centrality of group , which depends on the number of nodes and the sum of friends of each member h in the group k as given below:
where is the number of friends of the node h. The highest value of the group centrality refers to the high values of and , and indicates the probability to find rapidly a provider through this group. Equation (8) uses the cardinal of the group and the number of friends of friends in this group, where the group with a high number of nodes that have a high number of friends is preferred. For that, the group that has a centrality degree is preferred to find quickly the provider nodes.
Group popularity:
In a social network, when a node does not find a friend that can provide/execute the requested service, it chooses the receiver of the request using the group popularity. More precisely, the node knows the neighbor group that is declared in such path execution or path discovery, when this group is declared multiple times; that means it has a high probability to be selected to transmit the given request to the provider. For that, we define the group popularity of the node i as below:
where (resp. ) is the number of times that the group k (resp. z) is declared in the path discoveries or executions, is the groups of friends of the node i, and is the cardinality of .
The high value of group popularity of a node denotes that the group is more used for the requested services.
Equation (9) is used to calculate the degree of popularity of a group based on the previous paths found by friends for the executed requests. The group with a high popularity value indicates that there is a high probability to find provider nodes via this group.
4.4. Agreement on the Common Group Capability Using a Consensus Algorithm
The master groups agree on a common capability value, which is named AC, and they calculate it based on the capabilities of all groups using a consensus algorithm. We cannot initialize AC because it must be between the minimum and maximum capabilities of the groups, and these capabilities are determined by the nodes themselves.
Algorithm 2 is used to find AC, and was proposed to agree on the same clock for synchronizing a wireless sensor using local information [35], with a decentralized manner. It is a simple and lightweight algorithm.
| Algorithm 2: An agreement on common value AC |
| 1. : Capability group value |
| 2. : Deviation factor |
| 3. : The neighbor masters of the master node j |
| 4. Main Loop |
| 5. t = 1 |
| 6. While (non-converge) |
| 7. Each master j sends to |
| 8. For each master i from |
| 9. |
| 10. End |
| 11. End |
At first, each master group j sends its group capability to its surrounding master groups i. Thus, each master i adjusts its value of , using the following formula:
where , t is the iteration number (it is also considered as an instant), and is the deviation factor .
In each iteration master node i calculates the sequence , if for k iterations, the Algorithm 2 will be converged for node i, where is a threshold value, and k is the number of surrounding master nodes.
The value of is initialized by the capability of a group, in this case AC value is always between the minimum and the maximum capability of groups as declared in the next proposition.
Proposition.
Letbe a positive integer, anda set of sequences such thatif,,andfor all i in , with m and M two real numbers. Then:
Proof.
We proceed by induction on t. For t = 0, we have so, the proposition is true at t = 0 for all i in . □
Let , assume that , we will prove that for all i in .
So, we have that means
by the same method, we find:
The addition of two inequalities (*) and (**) will be:
So, the proposition is true for t + 2, in the finally the proposition is true for t + 1.
4.5. Social Network Creation
The objective of the proposed social network is to improve the network navigability, support the rapid service search, and initialize a semi-balance of the available resources. The friendship selection strategy uses the obtained groups, AC value, and other criteria to create a social network that can achieve the goals stated above.
Firstly, each node selects its neighbors that belong to its group as friends. Then, while the maximum number of allowed friends does not exceed Fmax (the maximal number of allowed friends), the process of friendship selection is performed using Algorithm 3.
| Algorithm 3: Friendship selection |
| 1. Notations |
| 2. : The master group of the node i |
| 3. : The capability of node x |
| 4. : The list of the friends of the node x |
| 5. : The list of neighbors of the node i |
| 6. : The list of groups of the friends of node i |
| 7. : The sum of capabilities of nodes in |
| 8. : The correspondent criteria are verified by j |
| 9. Output: Social network |
| 10. For each node i |
| 11. Send , , , , and to |
| 12. End |
| 13. For each node j from do |
| 14. If == true |
| 15. Send confirmation to the node j |
| 16. |
| 17. |
| 18. |
| 19. |
| 20. Else |
| 21. Decline the friend request |
| 22. End |
Secondly, each node i sends friend requests to its neighbors that are accompanied by the group id, the capability, the list of friends, the sum of friends’ capabilities, and the list of groups in which its friends belong to. Thus, when a node j receives a friend request, it checks the corresponding criteria with node i, they are verified if each criterion below is true:
- Criterion 1: Nodes i and j belong to different groups.
- Criterion 2: Non-common friends between groups of i and j.
- Criterion 3: The friends’ sum of capabilities of i and j should be less or equal to the AC value, respectively.
- Criterion 4: The number of friends of i and j must not exceed Fmax.
The following set of criteria is taken into consideration when creating a social network:
- The nodes will have the same role, no master node is needed.
- The diversification of friendships in an area, where each node has friends that belong to different groups.
- The enhancement of network navigability.
- The initialization of a balanced resource between groups (same group capability AC).
- The support of the rapid service search mechanism.
- The degree of friends will be in the shortest range.
4.6. Friends Sorting for Service Search
To reach the providers rapidly and balance the available resources during the service search process in a social network, the ordering and reordering of friends is performed by the nodes.
To choose the efficient friends, we calculate the sorting factor based on four factors which are: capability of node c, capability of group , centrality of group , and popularity of group .
is the factor value of node j at node i, and it is given by:
where , , and are the weights of , , and , respectively, , , and j belongs to group k.
Using the sorting factor, the nodes list their friends; the node with the highest value of will receive the future request. Furthermore, the sorting factor is recalculated after a period of time.
Below some explanations and limitations of the proposed solution.
- Our proposed approach considers several issues that can happen during the communication among nodes in SIoT by supporting self-organization and self-healing. Each node has different friends and the communication is decentralized using local information. For that, the failure that can happen at the level of a node is local. Thus, the failed nodes are avoided in the incoming requests according to the sorting factor proposed in subsection.
- The friendship selection in our proposed work is based on four factors: node capability, group capability, popularity, and centrality. Each node has different friends that are sorted periodically based on their capabilities (Section 4.6), such that the most capable nodes will receive the incoming request, they have higher residual energy than other nodes in a community. Using the proposed mechanism, the residual energies of all nodes will be semi-balanced, which increases the lifespan of nodes. In our work, we try to increase the lifespan of nodes to avoid their failure. In the case of the failure of the non-master node, it will be removed from the friends’ list of all nodes.
- The master node is the most competent node in a group, which is selected based on its capability, it has more energy than others in the group. Moreover, the role of the master node is flexible, its importance is to make an agreement on a group capability between surrounding master nodes, where this task is realized once. After that, it is considered as a normal friend. Then, if the master node fails, it will be removed from the list of friends without affecting the communication in the group.
5. Simulation and Evaluation
5.1. Simulation Setup
In this simulation, we used Python language to implement our algorithms on a Dell Inspiron 155567 computer with an Intel i7 CPU running at 2.4 GHz, Windows 7 (64-bit), and 8 GB of RAM.
To implement our contribution, we extracted data from the dataset of the location-based online social network Brightkite, which was obtained from the Stanford Large Network Dataset Collection [36]. The extracted dataset includes 3000 nodes with their neighbors.
As discussed before, we take into account the properties of nodes where each node has specific ones different from the other nodes. Then from these properties, we calculate the capability of each node using Equations (5) and (6) above. To facilitate the implementation, we assume that each node has a capability. For that, we assign to our dataset a capability for each node; these capabilities are generated randomly in the range from 0.1 to 0.9. The final dataset includes for each node a capability and a set of neighbors, as shown in Table 3.

Table 3.
A sample dataset of nodes’ information and capabilities used in the simulations.
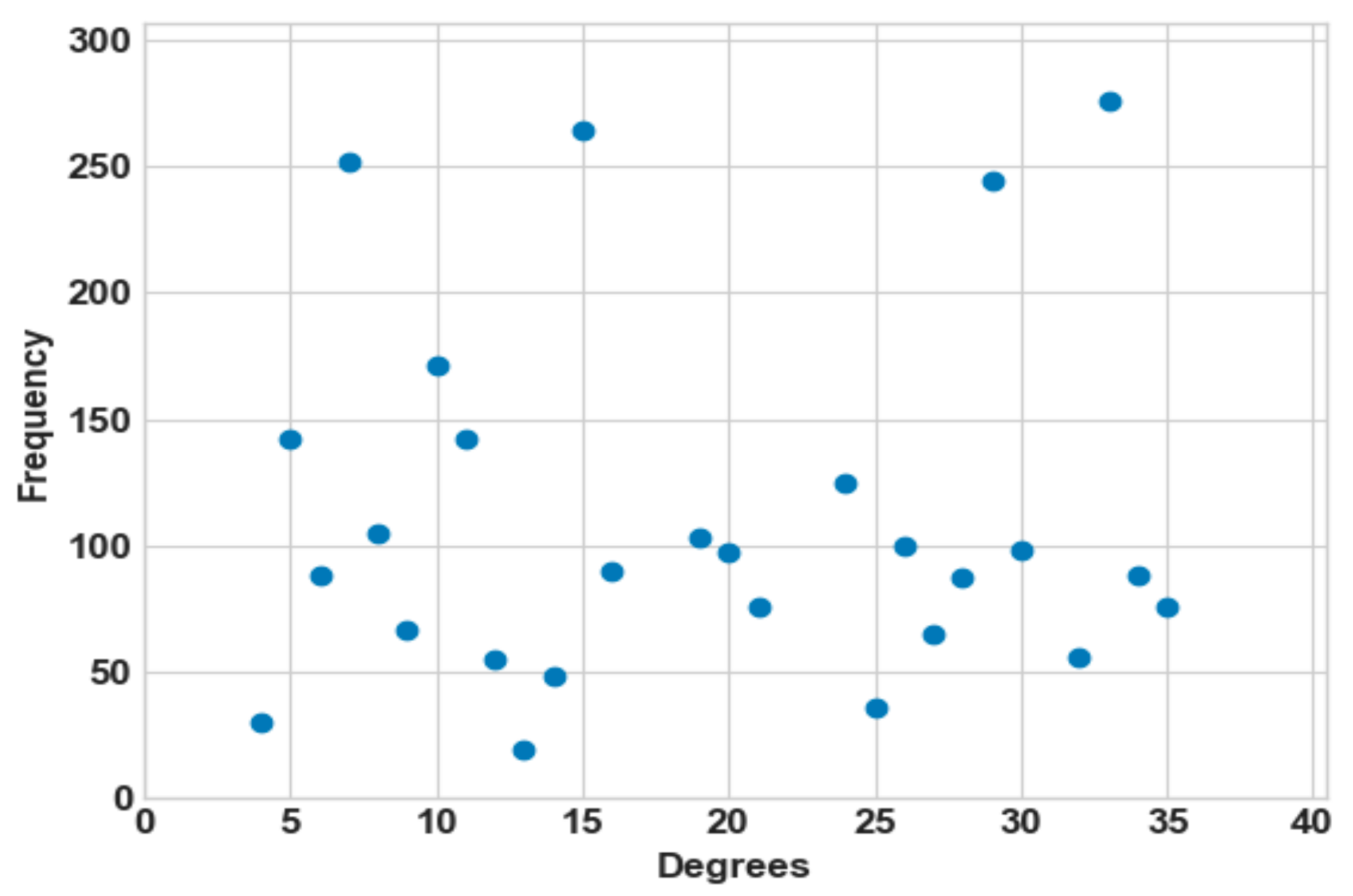
The network is a single-hop, bi-directional communication, and unicast. To study the initial network, i.e., before the creation of the social network, we measure a set of its parameters as shown in Table 4 and Figure 4 in order to better analyze and compare both types of networks. The parameters of the networks are calculated using the simulator Gephi [37].

Table 4.
Parameters of the initial network.
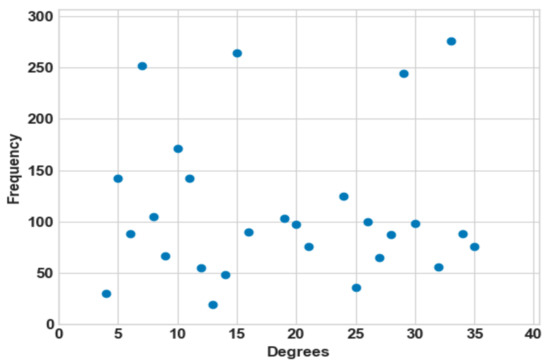
Figure 4.
Degree distribution of the initial network.
5.2. Simulation Results and Discussion
As denoted above, our contribution includes two phases: the construction of a social network and service search. So, the results of each phase are discussed in the next following subsections.
5.2.1. Social Network Parameters
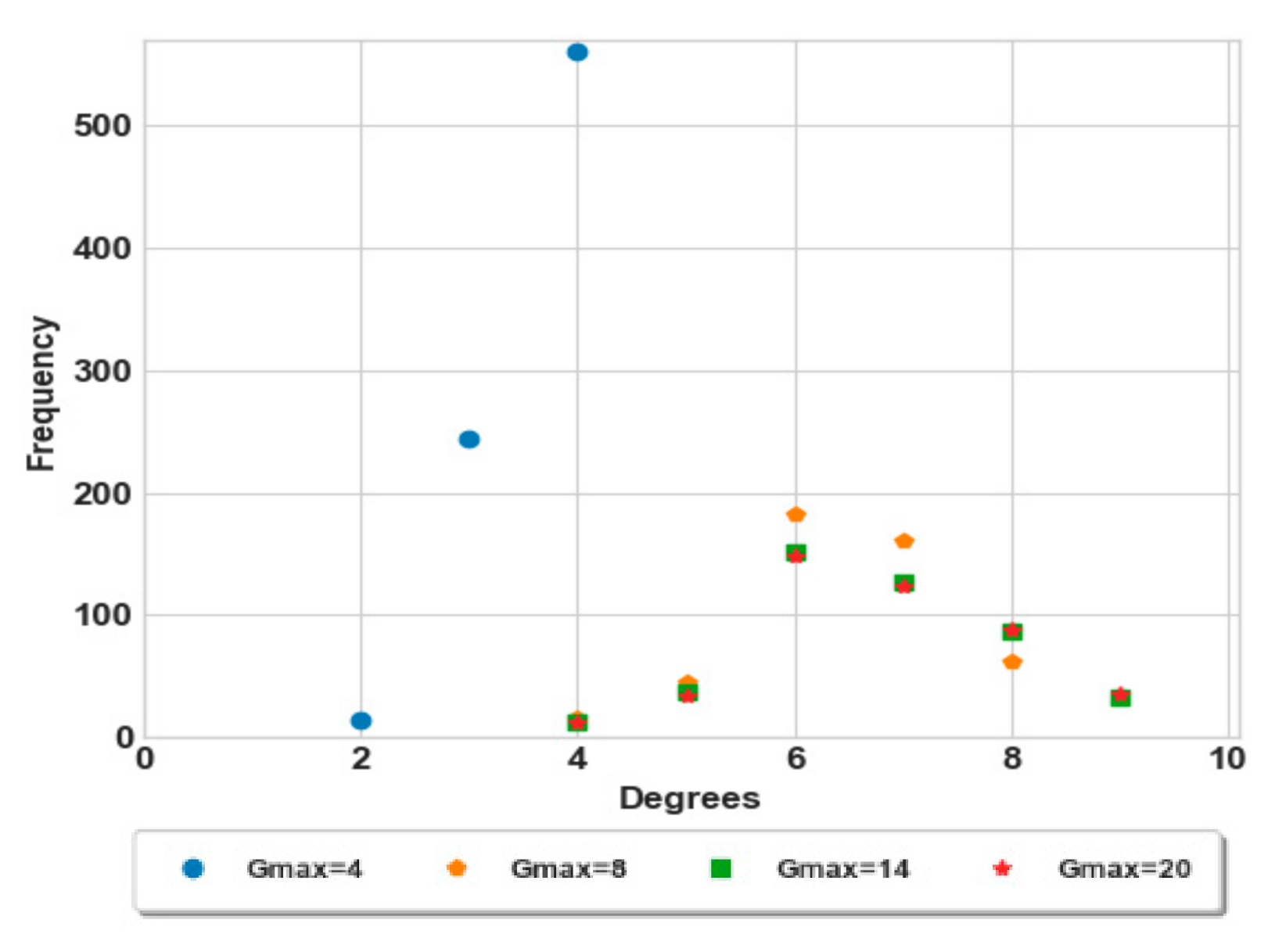
Before the creation of the social network, we made four trials to construct groups of nodes, and the maximum number of nodes in the groups did not exceed and 20. As illustrated in Figure 5, the difference between the obtained degrees of groups is in the range 4 and 9, which means that this difference is not exceed 6 members between any two groups in the worst cases. Furthermore, most of the degrees range between 4 and 8, so that, the groups’ cardinalities are approximately semi-equal.
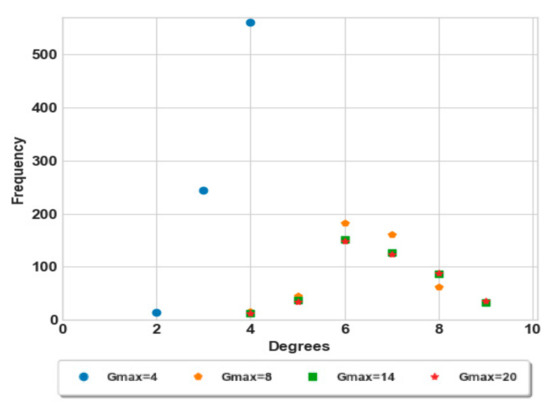
Figure 5.
Degree distribution of groups.
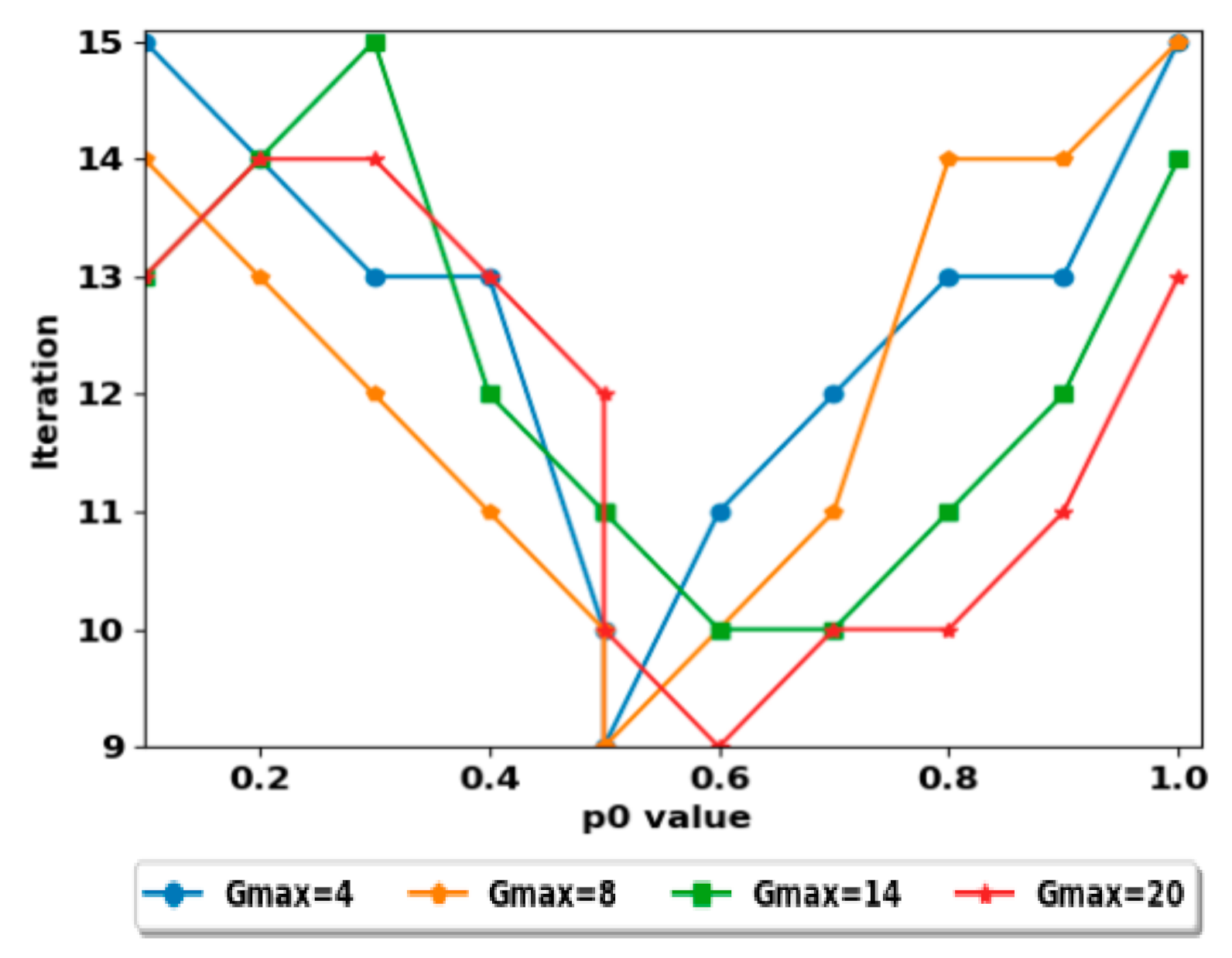
After the creation of groups, the consensus algorithm begins to find the agree capability AC. The average AC obtained is 1.4 with an error of 0.01 (the threshold value). The AC is computed by calculating the sum of ACs obtained from and 20, divided by four. The number of iterations to obtain the AC is changed according to the initial value of the deviation factor . As shown in Figure 6, the minimal and the maximal number of iterations obtained is 9 and 15, respectively. The best-chosen value of minimizes the number of iterations. So, initializing the best value of is difficult, because it depends on the groups’ cardinals. Anyway, the maximal number of iterations is fewer because the AC has been calculated strictly by the master groups, and the range of the groups’ cardinality is short, where they are semi-equal. However, in case where group construction is undefined, the number of iterations will be higher, and the algorithm will converge to the AC after a high number of iterations.
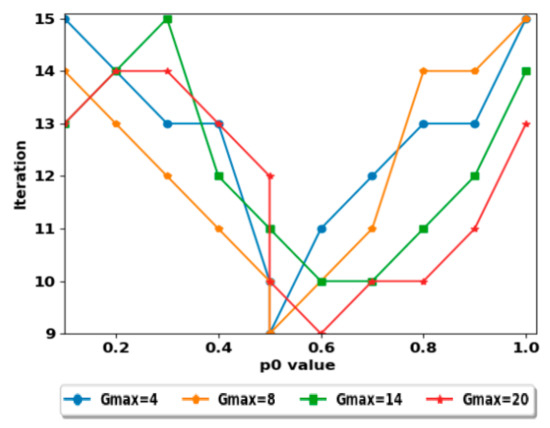
Figure 6.
The number of iterations to obtain AC according to p0 value.
In order to validate our approach results for friendship selection, we implement also the five strategies proposed in 24. The number of friends in the trials should not exceed and 20.
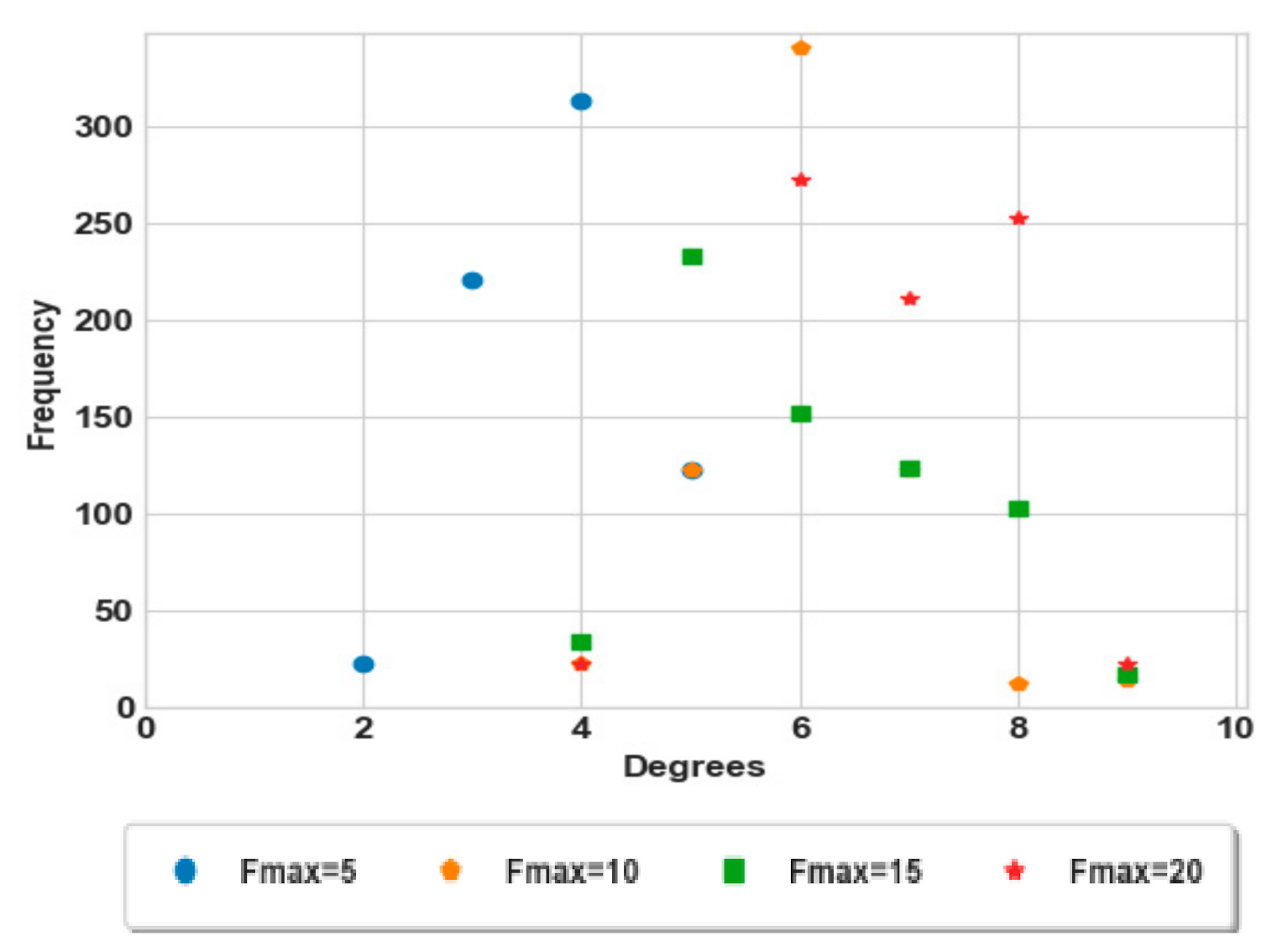
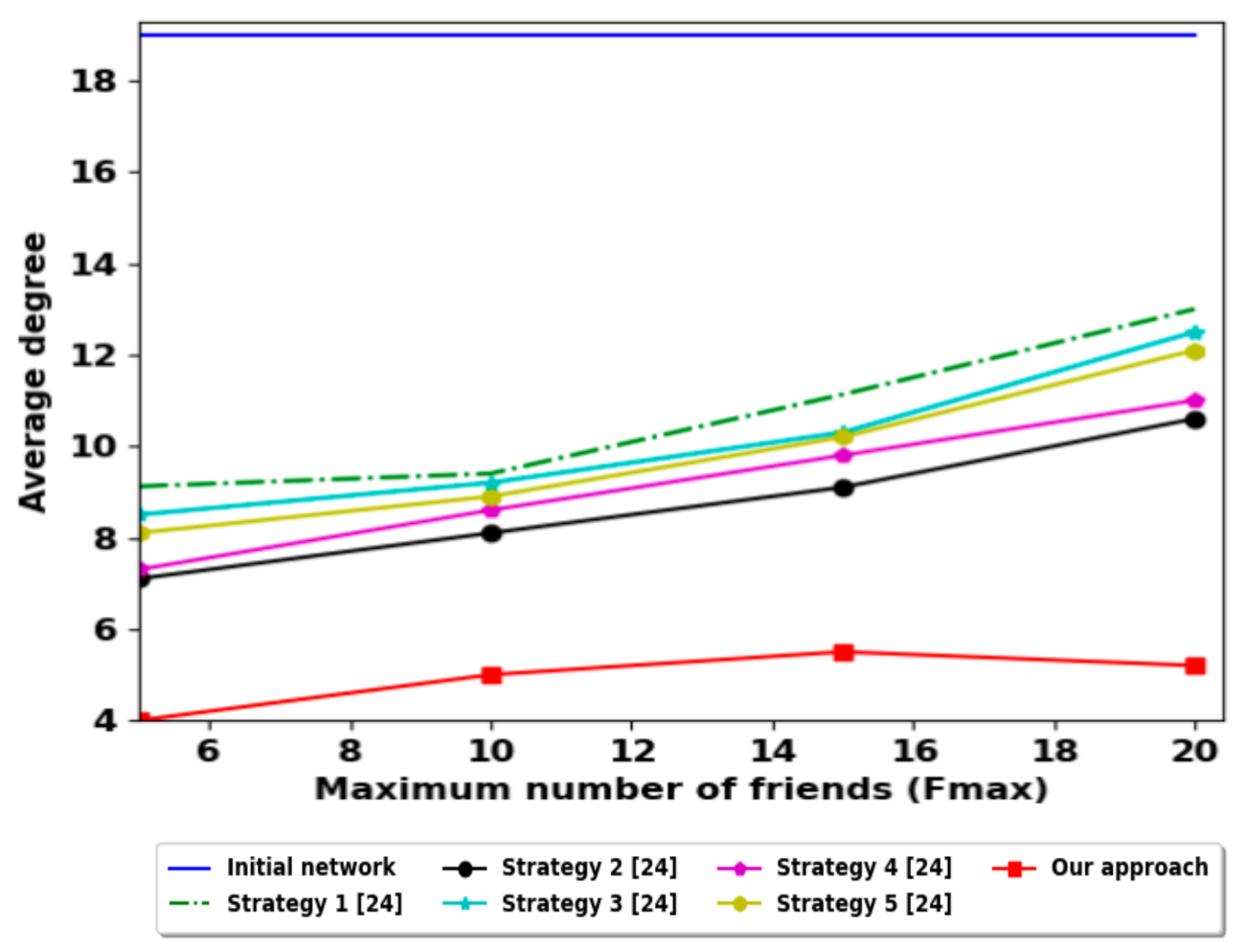
Figure 7 shows the degree distribution after execution of the friendship selection strategy; the degrees are converged to the same range which is between 4 and 9 for and 20. The range degrees are reduced because the friendship selection depends on the number of groups around the group, where a high number of friends belong to different groups. This result is reinforced by Figure 8, such that the average degree for our approach gives better results than all the strategies presented before.
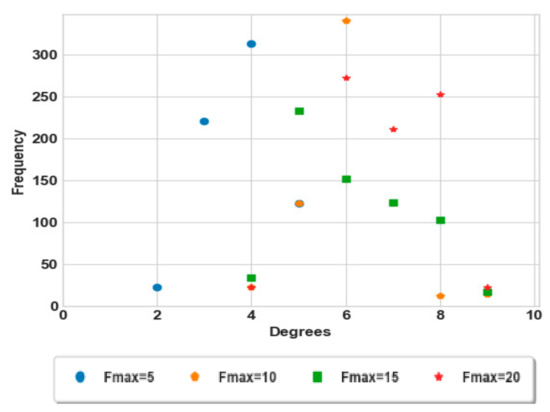
Figure 7.
Degree distribution of the social network.
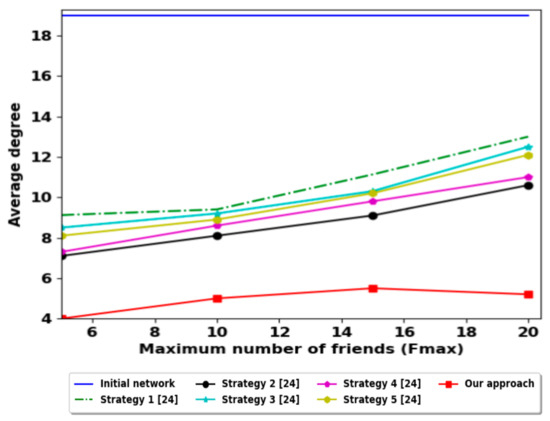
Figure 8.
The average degree comparison with other strategies.
Table 5 shows the giant component and diameter of the network for our strategy compared with the other ones; the obtained value of each parameter is the average of four values obtained from and 20. Our approach and strategies 3 and 5 give the total giant component; as a result, there is a connection between any two pairs in the social network for our approach. Therefore, the greatest distance between any pairs of nodes should not exceed , where N is the number of nodes in the network, this parameter is minimized for our approach and for strategies 2 and 5, respectively.

Table 5.
Giant component and diameter comparison with the other strategies.
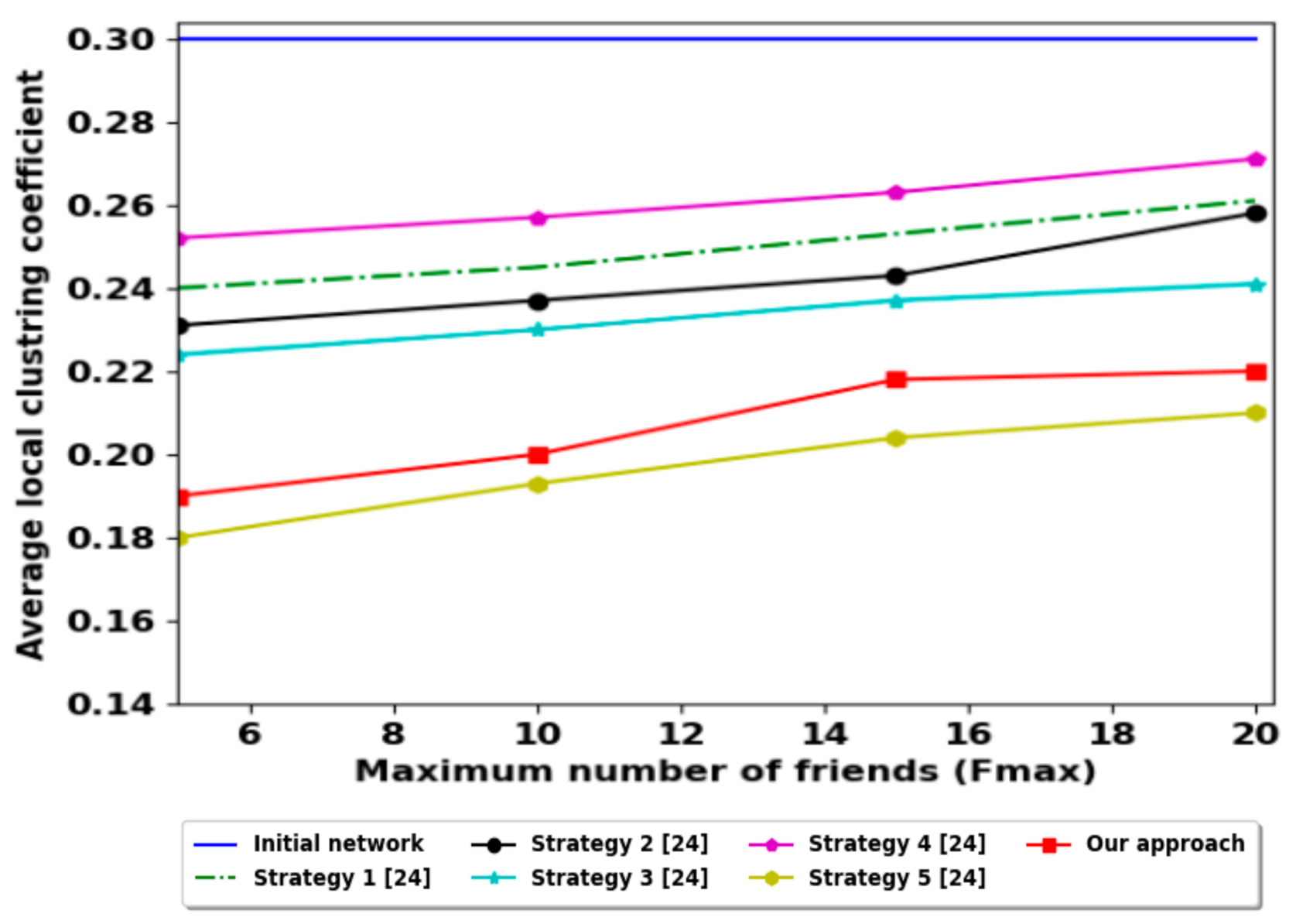
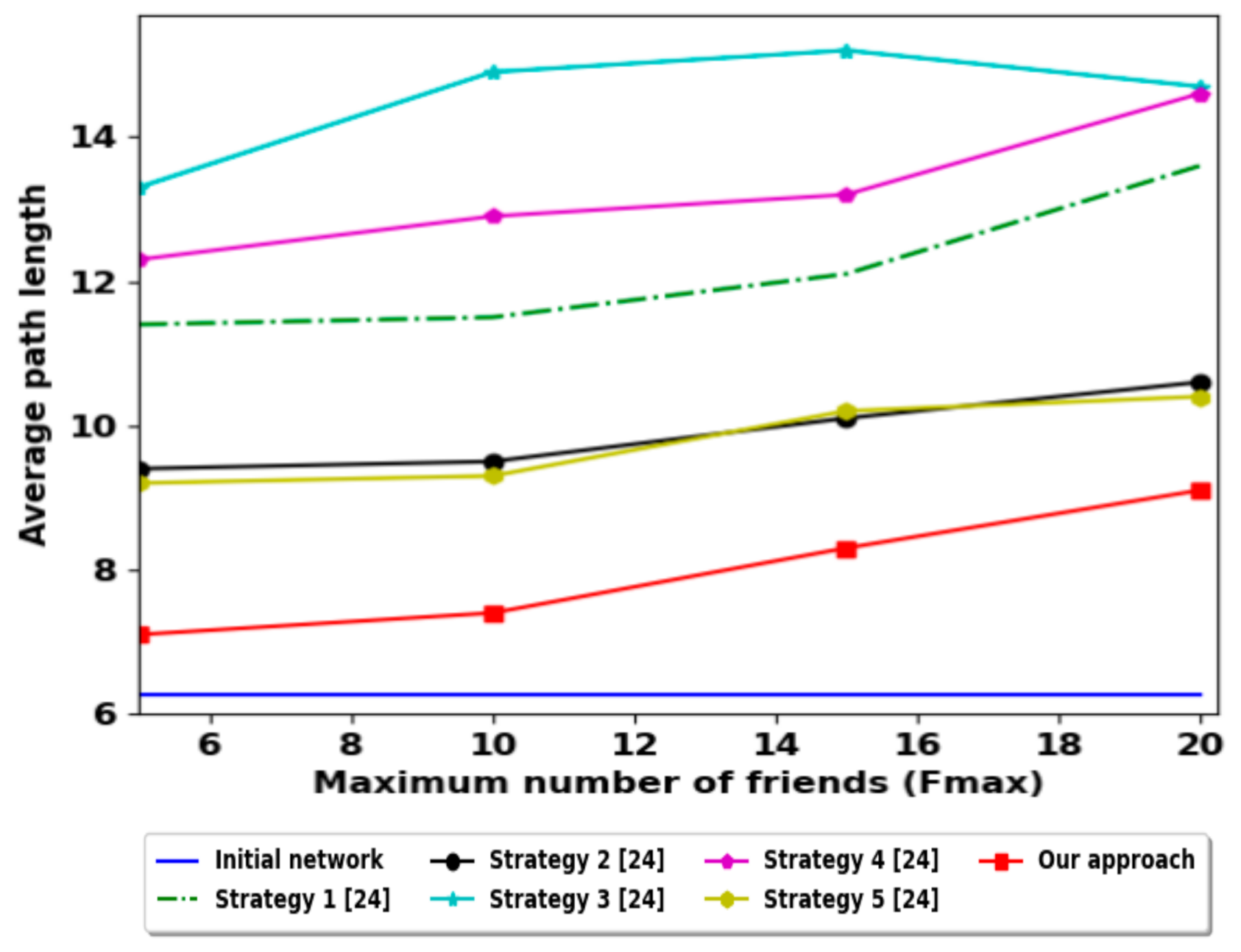
The high value of the local clustering coefficient indicates that the nodes are highly connected i.e., we can achieve the provider node quickly [38]. Figure 9 shows that our contribution is not more efficient for this parameter. However, the average path length value as shown in Figure 10 is the best in comparison with all these strategies. This result denotes that we can achieve the provider node quickly. The results of these two parameters are not contradictory, due to the friendship selection in our contribution is focused on the diversification of friends; i.e., it ignores an important number of candidate friends (reduces local clustering coefficient) but encourages the social network nodes to make friends from different surrounding areas (decreases the average path length).
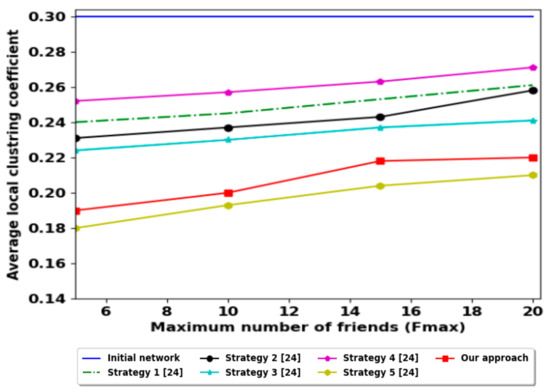
Figure 9.
Average local clustering coefficient comparison with other strategies.
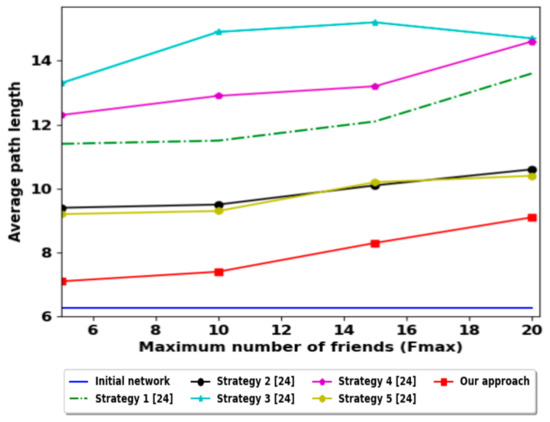
Figure 10.
Average path length comparison with other strategies.
5.2.2. Service Search Efficiency
The service search process can be started by incoming requests. When a node generates or receives a request that cannot be executed, it searches among its friends. In the case where the desired service is not available within its friends, then the search proceeds to the next level.
In our contribution, the service search process uses the sorting factor, which is calculated using the four factors (Section 4.3). We set the weights , , and for node capability, group capability, group centrality, and group popularity, respectively, all the factors have the same importance, i.e., we do balance between the rapid search process and an increase of the network lifetime simultaneously. Furthermore, the updating values of the four factors are fixed previously with a specific period.
The service search process is performed by sending 10,000 requests in our social network (the case where Fmax = 15), we then compared our search process with two approaches Nitti et al. [29] and Rapti et al. [30], which are discussed in the related works section of this paper, where the service satisfaction and node similarity are not considered. To facilitate the simulation, we choose randomly a requestor node and a provider node for each request; therefore, the matching similarity is not considered between the query and nodes. Additionally, we consider the capability as the residual energy.
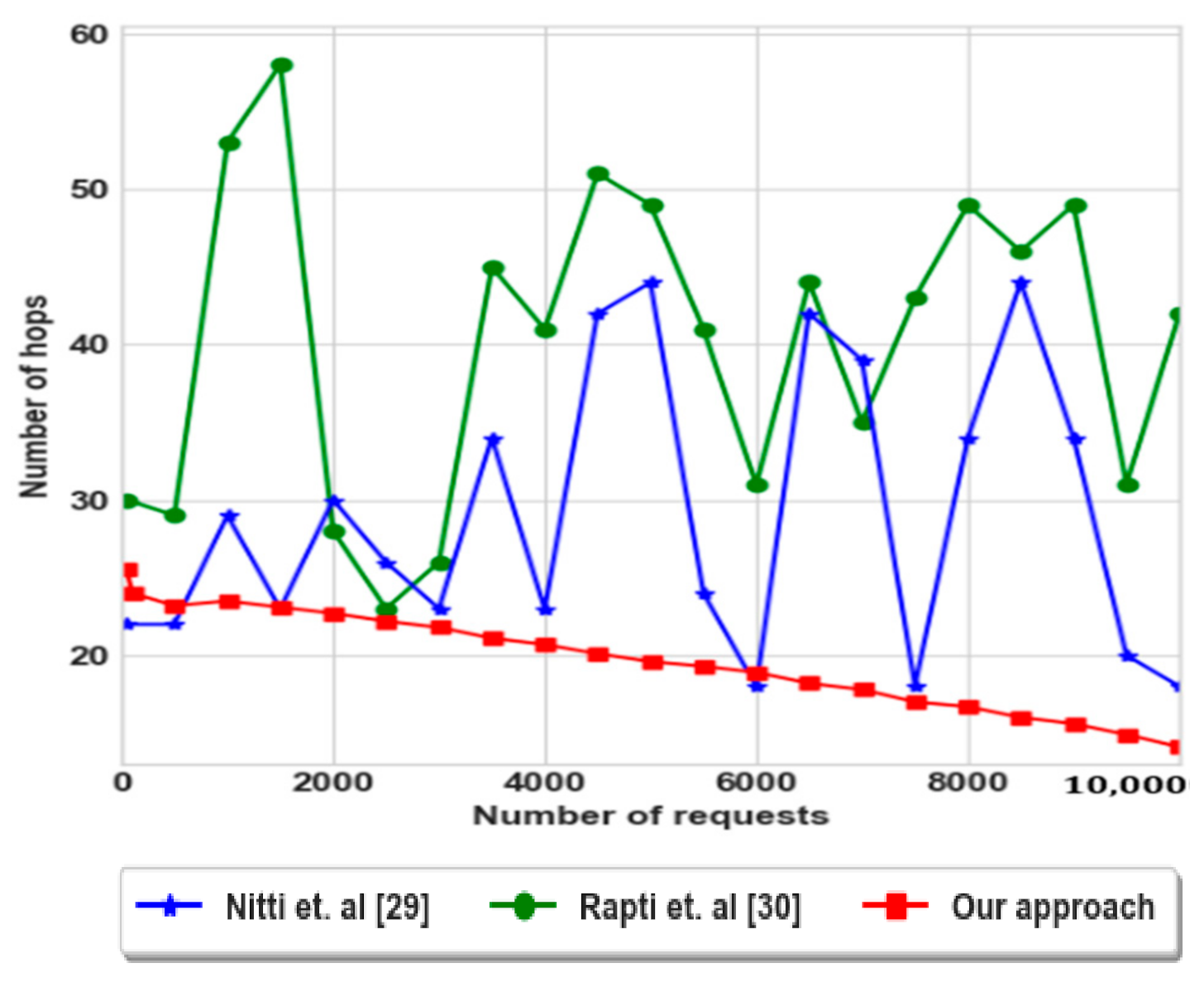
Figure 11 shows the number of hops to achieve the providers according to the number of requests. As illustrated, Nitti et al. [29] gives minimal hops than Rapti et al. [30] approach, but by a wobbling manner due to the requests that are retransmitted to the friends that have more centrality. However, the number of hops during the first requests is not minimal, but after a number of requests, our approach exploits its previous solutions, so that it converges to minimal hops. Therefore, our approach speeds up the search process by exploiting the obtained solutions.
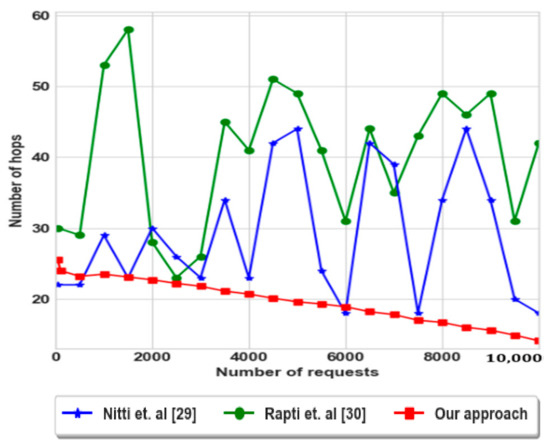
Figure 11.
Number of hops to find the provider node according to the number of requests.
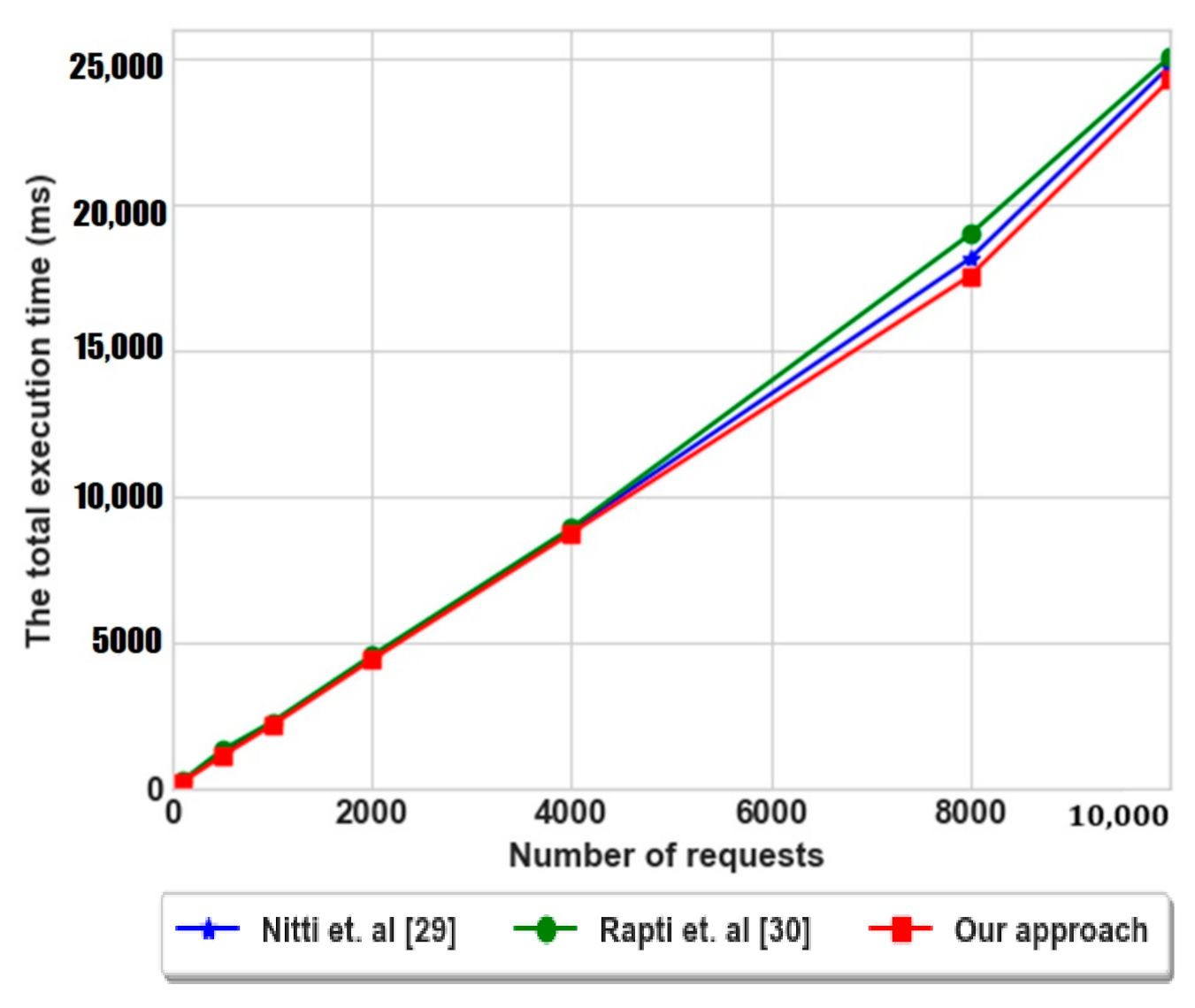
To determine the behavior of the execution time consumed during the service search phase, we have measured the total execution time after each executed request as shown in Figure 12 with a comparison of Nitti et al. [29] and Rapti et al. [30]. As illustrated, the execution time for our approach is reduced in comparison to the other ones, this indicates that the requests are executed with a short period of time. This result is a consequence of sending requests via the shortest paths (Figure 11) based on factors of centrality and popularity, which make the nodes to exploit the previous solutions locally.
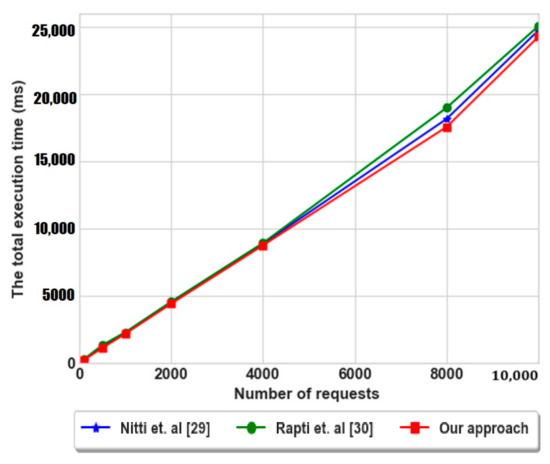
Figure 12.
The total execution time during service search.
To study the behavior of energy consumption during the search process, according to [39,40] we consider that the energy for reception, transmission, and execution is 0.001 J, 0.004 J, and 0.001 J, respectively. Moreover, the processing information (by an intermediate node) is 0.0015 J. To simplify the simulation, we calculate the deviation of residual energies between nodes, and it is computed as follows:
where is the average of all residual energies, is the residual energy of node i.
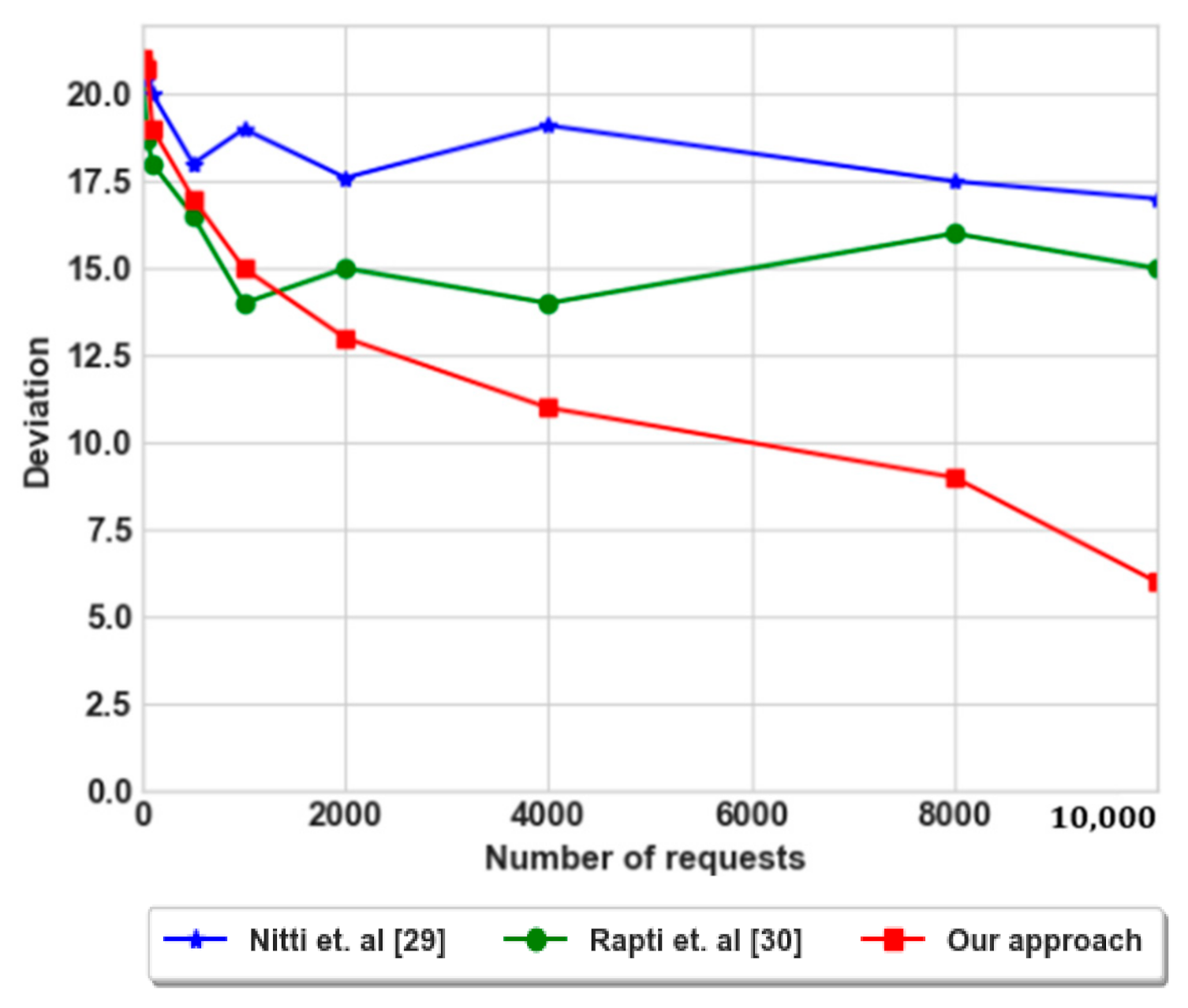
At first, as shown in Figure 13, the deviation of our approach was high and it is decreased after several numbers of requests. As a result, our mechanism balances between energies during the search process, and therefore leads to an increase in the network lifetime where high number of nodes converge to same residual energies. In contrast, the deviation of consumed energies for Rapti et al. [30] is less than Nitti et al. [29], where for each iteration the requests are sent to different intermediate nodes that makes nodes to share the costs especially for the consumed energy.
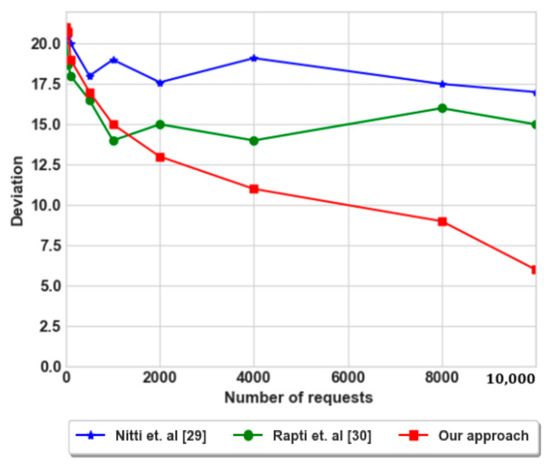
Figure 13.
The deviation of residual energies in the social network.
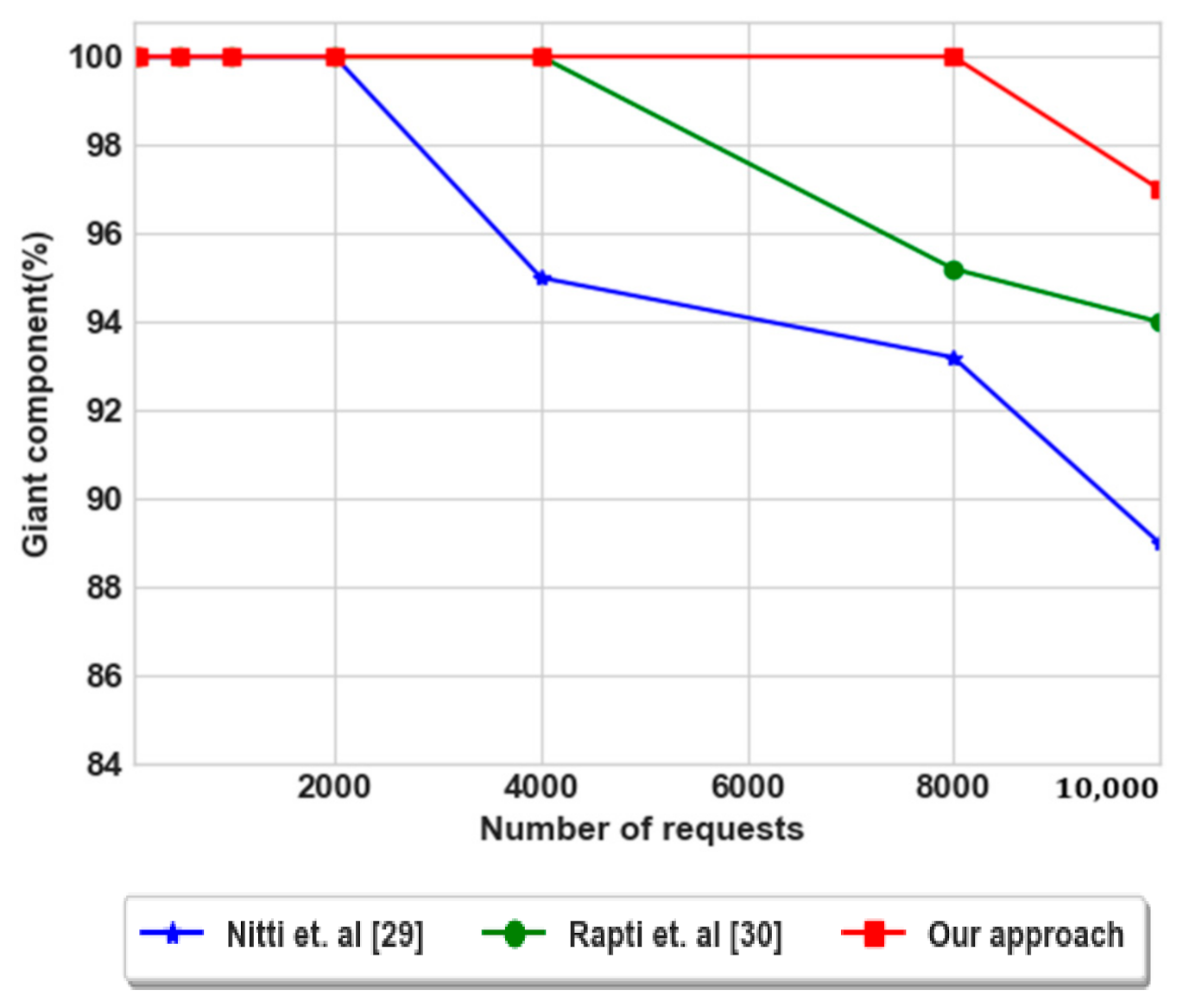
The obtained result in terms of consumed energies is reinforced by computing the giant component of the three approaches during this process, as shown in Figure 14. We have achieved 100% of giant component until the 8000 requests, which means that the energies are balanced and the connection between any pair nodes is achieved. In contrast, for Rapti et al. [30] the giant component is 100% until the number of requests is 4000. We conclude that the network lifetime of our approach is twice than Rapti approach. The increase of network lifetime allows nodes to be connected as long as possible.
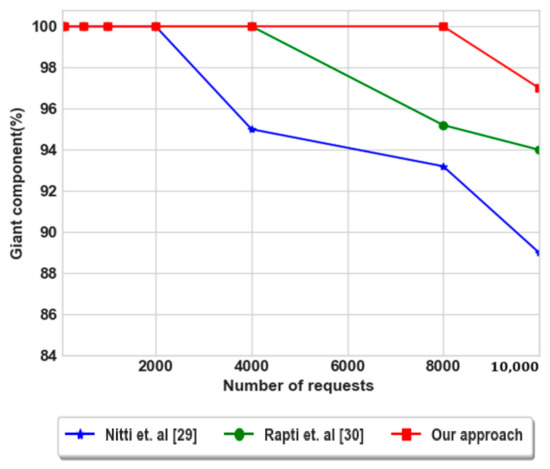
Figure 14.
Giant component of social network during service search.
6. Conclusions
In this paper, to resolve the search process for a service provided by a node in a social network, we proposed an approach to allow the search to be more rapid and to take into consideration the capabilities of nodes especially the residual energies. This approach enables nodes in a constraint network to create a social network dynamically using a new strategy that initializes a balance of the capabilities in the friendships selection and supports the rapid search. Then during the search phase, the nodes decide to choose the optimal path, which is the shortest path length with high capabilities. As a result, the obtained social network is completely navigable and achieves better enhancements in terms of other parameters such as average degree, average path length, and diameter. Furthermore, during the search process, the providers are reached rapidly and the network lifetime is increased in comparison with baseline works.
In future work, we will propose a mechanism to secure the communication in the SIoT, where each node must be able to make its own decision about whether to accept a command or execute it.
Author Contributions
Writing—original draft, A.Z.; Writing—review and editing, A.B. and E.H.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guillemin, P.; Friess, P. Internet of things strategic research roadmap. Clust Eur. Res. Proj. Tech. Rep. 2011, 1, 9–52. [Google Scholar]
- Links, C. The Internet of Things will change our world. ERCIM News 2015, 101, 76. [Google Scholar]
- Zannou, A.; Boulaalam, A.; Nfaoui, E.H. A Node Capability Classification in Internet of Things. In Proceedings of the 2020 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 9–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Dohr, A.; Modre-Opsrian, R.; Drobics, M.; Hayn, D.; Schreier, G. The internet of things for ambient assisted living. In Proceedings of the 2010 Seventh International Conference on Information Technology: New Generations, Las Vegas, NV, USA, 12–14 April 2010; pp. 804–809. [Google Scholar]
- Hackl, J.; Dubernet, T. Epidemic spreading in urban areas using agent-based transportation models. Futur. Internet 2019, 11, 92. [Google Scholar] [CrossRef]
- Autili, M.; Di Salle, A.; Gallo, F.; Pompilio, C.; Tivoli, M. A choreography-based and collaborative road mobility system for l’aquila city. Futur. Internet 2019, 11, 132. [Google Scholar] [CrossRef]
- Mtonga, K.; Kumaran, S.; Mikeka, C.; Jayavel, K.; Nsenga, J. Machine Learning-Based Patient Load Prediction and IoT Integrated Intelligent Patient Transfer Systems. Futur. Internet 2019, 11, 236. [Google Scholar] [CrossRef]
- Hyla, T.; Pejaś, J. eHealth integrity model based on permissioned blockchain. Futur. Internet 2019, 11, 76. [Google Scholar] [CrossRef]
- Hammood, D.A.; Rahim, H.A.; Alkhayyat, A.; Ahmad, R.B. Body-to-Body Cooperation in Internet of Medical Things: Toward Energy Efficiency Improvement. Futur. Internet 2019, 11, 239. [Google Scholar] [CrossRef]
- Ramakrishnan, A.M.; Ramakrishnan, A.N.; Lagan, S.; Torous, J. From Symptom Tracking to Contact Tracing: A Framework to Explore and Assess COVID-19 Apps. Futur. Internet 2020, 12, 153. [Google Scholar] [CrossRef]
- Trakadas, P.; Simoens, P.; Gkonis, P.; Sarakis, L.; Angelopoulos, A.; Ramallo-González, A.P.; Skarmeta, A.; Trochoutsos, C.; Calvo, D.; Pariente, T.; et al. An Artificial Intelligence-Based Collaboration Approach in Industrial IoT Manufacturing: Key Concepts, Architectural Extensions and Potential Applications. Sensors 2020, 20, 5480. [Google Scholar] [CrossRef] [PubMed]
- Zannou, A.; Boulaalam, A.; Nfaoui, E.H. System Service Provider–Customer for IoT (SSPC-IoT). In Embedded Systems and Artificial Intelligence. Advances in Intelligent Systems and Computing; Bhateja, V., Satapathy, S., Satori, H., Eds.; Springer: Singapore, 2020; Volume 1076. [Google Scholar] [CrossRef]
- Bader, S.R.; Maleshkova, M.; Lohmann, S. Structuring reference architectures for the industrial internet of things. Futur. Internet 2019, 11, 151. [Google Scholar] [CrossRef]
- Yao, F.; Alkan, B.; Ahmad, B.; Harrison, R. Improving Just-in-Time Delivery Performance of IoT-Enabled Flexible Manufacturing Systems with AGV Based Material Transportation. Sensors 2020, 20, 6333. [Google Scholar] [CrossRef] [PubMed]
- Zannou, A.; Boulaalam, A.; Nfaoui, E.H. A Multi-layer Architecture for Services Management in IoT. In Innovations in Smart Cities and Applications. SCAMS 2017. Lecture Notes in Networks and Systems; Ben, A.M., Boudhir, A., Eds.; Springer: Cham, Germany, 2018; Volume 37. [Google Scholar] [CrossRef]
- Dietrich, I.; Dressler, F. On the lifetime of wireless sensor networks. ACM Trans. Sens. Netw. 2009, 5, 1–39. [Google Scholar] [CrossRef]
- Sung, Y.; Lee, S.; Lee, M. A Multi-Hop Clustering Mechanism for Scalable IoT Networks. Sensors 2018, 18, 961. [Google Scholar] [CrossRef] [PubMed]
- Zannou, A.; Boulaalam, A.; Nfaoui, E.H. Relevant node discovery and selection approach for the Internet of Things based on neural networks and ant colony optimization. Pervasive Mobile Comput. 2020, 70, 101311. [Google Scholar] [CrossRef]
- Boussada, R.; Hamdane, B.; Elhdhili, M.E.; Saidane, L.A. Privacy-preserving aware data transmission for IoT-based e-health. Comput. Netw. 2019, 162, 106866. [Google Scholar] [CrossRef]
- Zannou, A.; Boulaaam, A.; Nfaoui, E.H. A Task Allocation In IoT Using Ant Colony Optimization. In Proceedings of the 2019 International Conference on Intelligent Systems and Advanced Computing Sciences (ISACS), Taza, Morocco, 26–27 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Atzori, L.; Iera, A.; Morabito, G. Siot: Giving a social structure to the internet of things. IEEE Commun. Lett. 2011, 15, 1193–1195. [Google Scholar] [CrossRef]
- Atzori, L.; Iera, A.; Morabito, G.; Nitti, M. The social internet of things (siot)—When social networks meet the internet of things: Concept, architecture and network characterization. Comput. Netw. 2012, 56, 3594–3608. [Google Scholar] [CrossRef]
- Fiske, A.P. The four elementary forms of sociality: Framework for a unified theory of social relations. Psychol. Rev. 1992, 99, 689. [Google Scholar] [CrossRef]
- Nitti, M.; Atzori, L.; Cvijikj, I.P. Friendship selection in the social internet of things: Challenges and possible strategies. IEEE Internet Things J. 2014, 2, 240–247. [Google Scholar] [CrossRef]
- Mardini, W.; Khamayseh, Y.; Yassein, M.B.; Khatatbeh, M.H. Mining Internet of Things for intelligent objects using genetic algorithm. Comput. Electr. Eng. 2018, 66, 423–434. [Google Scholar] [CrossRef]
- Arjunasamy, A.; Rathi, S. Relationship Based Heuristic for Selecting Friends in Social Internet of Things. Wirel Pers. Commun. 2019, 107, 1537–1547. [Google Scholar] [CrossRef]
- Amin, F.; Abbasi, R.; Rehman, A.; Choi, G.S. An advanced algorithm for higher network navigation in social Internet of Things using small-world networks. Sensors 2019, 19, 2007. [Google Scholar] [CrossRef] [PubMed]
- Nitti, M.; Atzori, L. What the SIoT needs: A new caching system or new friendship selection mechanism? In Proceedings of the 2015 IEEE 2nd World Forum on Internet of Things (WF-IoT), Milan, Italy, 14–16 December 2015; pp. 424–429. [Google Scholar]
- Nitti, M.; Pilloni, V.; Giusto, D.D. Searching the social Internet of Things by exploiting object similarity. In Proceedings of the 2016 IEEE 3rd World Forum on Internet of Things (WF-IoT), Reston, VA, USA, 12–14 December 2016; pp. 371–376. [Google Scholar]
- Rapti, E.; Karageorgos, A.; Houstis, C.; Houstis, E. Decentralized service discovery and selection in Internet of Things applications based on artificial potential fields. Serv. Oriented Comput. Appl. 2017, 11, 75–86. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Autonomous Robot Vehicles; Springer: New York, NY, USA, 1986; pp. 396–404. [Google Scholar]
- Ho, C.; Obraczka, K.; Tsudik, G.; Viswanath, K. Flooding for reliable multicast in multi-hop ad hoc networks. In Proceedings of the 3rd International Workshop on Discrete Algorithms and Methods for Mobile Computing and Communications, Seattle, WA, USA, 1 August 1999; pp. 64–71. [Google Scholar]
- Kowshalya, A.M.; Gao, X.-Z.; Ml, V. Efficient service search among Social Internet of Things through construction of communities. Cyber Phys. Syst. 2020, 6, 33–48. [Google Scholar] [CrossRef]
- Yetgin, H.; Cheung, K.T.K.; El-Hajjar, M.; Hanzo, L.H. A survey of network lifetime maximization techniques in wireless sensor networks. IEEE Commun. Surv. Tutor. 2017, 19, 828–854. [Google Scholar] [CrossRef]
- Schenato, L.; Gamba, G. A distributed consensus protocol for clock synchronization in wireless sensor network. Proc. IEEE Conf. Decis. Control. 2007, 2007, 2289–2294. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. Node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An open source software for exploring and manipulating networks. In Proceedings of the Third International AAAI Conference on Weblogs and Social Media, San Jose, CA, USA, 17–20 May 2009. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef] [PubMed]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Hawaii, HI, USA, 4–7 January 2000. [Google Scholar]
- Rappaport, T.S. Wireless Communications: Principles and Practice; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1996; Volume 2. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).