Fast Library Recommendation in Software Dependency Graphs with Symmetric Partially Absorbing Random Walks

Abstract

To help developers discover libraries suited to their software projects, automated approaches often start from already employed libraries and recommend more based on co-occurrence patterns in other projects. The most accurate project–library recommendation systems employ Graph Neural Networks (GNNs) that learn latent node representations for link prediction. However, GNNs need to be retrained when dependency graphs are updated, for example, to recommend libraries for new projects, and are thus unwieldy for scalable deployment. To avoid retraining, we propose that recommendations can instead be performed with graph filters; by analyzing dependency graph dynamics emulating human-driven library discovery, we identify low-pass filtering with memory as a promising direction and introduce a novel filter, called symmetric partially absorbing random walks, which infers rather than trains the parameters of filters with node-specific memory to guarantee low-pass filtering. Experiments on a dependency graph between Android projects and third-party libraries show that our approach makes recommendations with a quality and diversification loosely comparable to those state-of-the-art GNNs without computationally intensive retraining for new predictions.

1. Introduction

The pervasive integration of mobile phones in everyday life and the digitization of practically all aspects of human activities have led to a constant need for new software services, applications and platforms. This need drives a highly motivated software development industry, whose aim is to cater quickly to user needs with new or repurposed software. In this regime, agile and component-based engineering practices are predominantly adopted [1] that reuse previously developed software and quickly share it between developers, mostly in the form of well-documented and tested libraries. These are distributed by online services such as the Maven repository of Java libraries [2], the PyPI repository of Python libraries [3], and the npm registry of Javascript libraries [4].

However, the sheer size of coding ecosystems/repositories [5] makes it a daunting prospect to find which libraries would best support new projects. For example, as of writing, Maven hosts more than three million software artifacts. In this setting, programmers, especially those working in unfamiliar domains, need to conduct time-consuming research through many libraries to select those suited to their needs, or else they risk incurring technical debt to their projects in the long run [6]. To reduce search effort, automated tools have been proposed to recommend which libraries to use (Section 2.1). This is often achieved by analyzing the dependencies between projects and libraries and adopting a collaborative filtering outlook [7] that recommends additional libraries based on those already used. For example, the inclusion of server-related libraries could imply potential interest in database management libraries frequently used together in other projects. Collaborative filtering approaches organize projects and libraries in graphs, whose edges correspond to project–library dependencies. These then mine structural patterns to recommend new dependencies, for example, with Graph Neural Networks (GNNs—Section 2.3).

As far as predictive accuracy is concerned, collaborative filtering approaches yield high-quality recommendations. To achieve this, they typically learn latent representations (e.g., embeddings) for all software projects and libraries and let pairwise project and library representation comparisons (e.g., the cosine similarity of their embeddings) rank libraries based on their similarity to projects under examination. The most similar libraries are considered to implement the functionality needed by projects and are thus recommended for adoption. However, when dependency graphs evolve with more libraries and—importantly—projects for which to make recommendations, these approaches need to be retrained to create representations accounting for new nodes and dependencies. In practice, this translates to usability costs by locking recommendation pipelines until training is over (Section 3).

To create deployment-friendly library recommendation services, in this work, we argue that collaborative filtering can be conducted with no-learning alternatives that make informed ad hoc assumptions about which co-usage patterns to mine. These alternatives sacrifice some predictive quality for the benefit of avoiding training and its associated costs. In particular, we look at graph filters (Section 2.2) to recommend libraries based on how structurally proximate they are within dependency graphs to libraries already being used. Graph filters are computationally efficient (their running times scale near-linearly with the number of dependencies and their outcomes can be quickly computed, even without high-end GPU hardware) and only rely on their chosen understanding of structural proximity. We specifically choose absorbing random walks’ filters that emulate human-driven library discovery combining co-usage exploration and memory of previous discoveries (Section 4.3); we employ such filters with the goal of quickly finding libraries similar to those that humans use in their projects and hence reduce the effort of searching for these.

Our contribution lies in (a) proposing graph filters as a viable alternative to more sophisticated but ultimately unwieldy library recommendation tools; (b) analyzing which types of filters to employ for high-quality library recommendations; and (c) introducing a new variation of absorbing random walk filters, called symmetric partially absorbing random walks for link prediction that has no learnable parameters—not even hyperparameters. The usefulness of our approach is experimentally demonstrated on a large real-world dependency graph of third-party library dependencies, where it outperforms representation learning based on matrix factorization in terms of the predictive quality and diversification of results and lags only a little behind state-of-the-art GNNs that require computationally intensive retraining for every new recommendation task.

The rest of this paper is organized as follows. In Section 2, we overview the related literature and present theoretical concepts needed to position our analysis, namely from the domains of graph signal processing and GNNs. In Section 3, we showcase practical issues with deploying representation learning for library recommendation and explain how these can be resolved when switching to graph filters. Based on this explanation, in Section 4, we analyze real-world library discovery practices and selected the appropriate filters that are automated yet emulate human-driven discovery. To show the effectiveness of these filters, in Section 5, we organize experiments to compare our approach with existing alternatives. In Section 6, we discuss the experimental results in terms of real-world usefulness, address threats to validity, and point out promising future work. Finally, in Section 7, we summarize our work and conclude the paper.

2. Background and Related Work

2.1. Library Recommendation

Many recommendation system approaches are applied in the field of assisted software engineering [8,9]. Among other tasks, these have also been used to recommend relevant libraries to developers to commence their work. Originally, library recommendation tools were similar to other search engines in that they used query terms pertaining to project keywords (e.g., extracted from source code). However, state-of-the-art systems employ co-usage patterns of libraries to recommend new ones based on those already included in projects [10,11,12]. This is effectively a type of collaborative filtering [13] which eventually coalesced to the matrix factorization of the LibSeek tool [14].

In practice, library recommendation is conducted on project–library dependency graphs, where software projects and libraries are nodes that are linked based on usage. That is, projects are linked to libraries they import. In terms of collaborative filtering, which aims to produce item recommendations for users based on item co-usage patterns (e.g., being bought by the same users in e-commerce platforms), libraries would correspond to items and software projects to users. Assuming that only links between projects and libraries are captured and not dependencies between libraries, dependency graphs are bipartite and described by matrices $A_{bip}:P\times I$ of P rows and I columns, where P is the number of projects and I the number of libraries. Their elements obtain values $A_{bip}[u,v]=\{1\mathrm{if}\mathrm{project}u\mathrm{depends}\mathrm{on}\mathrm{library}v,0\mathrm{otherwise}\}$. For this formulation, matrix factorization approaches aim to generate representation matrices $H_{proj}:P\times h$ and $H_{lib}:I\times h$ whose rows correspond to underlying h-dimensional representations (embeddings) of projects and libraries, respectively. These representations are trained so that the dot product (the dot product between representations also models cosine similarity if L2 normalization is applied on representations) is higher between projects and their used libraries than between projects and unrelated libraries. In matrix form, the representation matching would ideally be able to reconstruct the bipartite graph per:

$$A_{bip}\approx H_{proj}{H}_{lib}^T$$

(1)

For example, LibSeek learns to approximate this factorization through stochastic gradient descent [15] on a loss function that heuristically weighs the differences between matrix elements, introduces L2 regularization on the representation matrices, and penalizes dissimilar representations of libraries and projects of similar graph neighborhoods.

A natural evolution of matrix factorization is to detect more complex library co-usage patterns with Graph Neural Networks (GNNs—Section 2.3). This direction has only recently been explored with the introduction of GRec [16] and similar works that also account for metadata other than dependencies [17]. Approaches consider adjacency matrices $A:(P+I)\times (P+I)$ describing the bipartite dependency graphs per $A=[{\mathbf{0}}_P{A}_{bip};A_{bip}^T{\mathbf{0}}_I]$, where ${\mathbf{0}}_X:X\times X$ are square matrices of zeros. Adjacency matrices are then input in the GNN link recommendation pipelines, such as the ones described in Section 2.3.

2.2. Graph Signal Processing

Graph signal processing [18] is a way to systematize information propagation in graphs through their edges. In particular, it starts from a similar definition of adjacency matrices as above $A=\{1\mathrm{if}\mathrm{edge}u,v\mathrm{exists},0\mathrm{otherwise}\}$, which is modified to be applicable to any type of graphs, not only bipartite ones. It then considers normalizations $\widehat{A}$ that reduce the importance of profligately connected nodes’ edges. One popular type of normalization is the symmetric expression

$$\widehat{A}=D^{-1/2}A{D}^{-1/2}$$

(2)

where D are diagonal matrices of node degrees with elements $D[u,v]=\{{\sum }_{v^{\prime }}A[u,v^{\prime }]\mathrm{if}u=v,0\mathrm{otherwise}\}$. This regards edges $(u,v)$ as bidirectional and re-weighs them by considering both endpoint degrees per $\widehat{A}[u,v]=A[u,v]/\sqrt{D[u,u]D[v,v]}$.

Given adjacency matrix normalizations $\widehat{A}$, graph signal processing explores information propagation through graphs by considering graph signals $h_0$ whose elements $h_0\left[u\right]$ hold values corresponding to nodes u. These values can be propagated to one-hop neighbors through the matrix-vector multiplication operation $\widehat{A}{h}_0$. This is equivalent to the discrete signal processing shift operator (graph signal processing can model discrete signal processing if points in time are expressed as a line graph whose edges connect points with the next points) and is a type of additive aggregation across graph neighbor values, where neighbors v of nodes u are weighted by $\widehat{A}[u,v]$. Iterating the shift operator k times per ${\widehat{A}}^k{h}_0$ yields graph signal propagations k hops away from original values. Under this formalization, graph filters are defined as a weighted averaging of multi-hop propagation to obtain filtered signals h per:

$$\begin{array}{c}\hfill h=F(\widehat{A})h_0\\ \hfill F(\widehat{A})=\sum _{k=0}^{\infty }{f}_k{\widehat{A}}^k\end{array}$$

(3)

where $F(·)$ is the graph filter and $f_k$ are the weights placed on node values k hops away. Notably, symmetrically normalized adjacency matrices $\widehat{A}$ can be decomposed into $\widehat{A}=U\Lambda U^{-1}$, where $\Lambda$ are diagonal matrices of eigenvalues $\lambda \in [-1,1]$ and U is the orthonormal base of eigenvectors. Applying graph filters on this decomposition yields:

$$\begin{array}{c}\hfill F\left(\widehat{A}\right)=\sum _{k=0}^{\infty }{f}_k{(U\Lambda U^{-1})}^k=\sum _{k=0}^{\infty }{f}_{k}U{\Lambda }^k{U}^{-1}=UF(\Lambda )U^{-1}\end{array}$$

Hence, graph filters transform normalized adjacency matrix eigenvalues from $\lambda$ to:

$$F\left(\lambda \right)=\sum _{k=0}^{\infty }{f}_k{\lambda }^k$$

(4)

Based on the above properties, spectral graph theory generalizes the concept of Fourier transformations to node-domain graph signals $h_0$ as $\mathcal{F}\left\{h_0\right\}=U^{-1}{h}_0$ and the inverse transform as ${\mathcal{F}}^{-1}\left\{h_0^{\prime }\right\}=U{h}_0^{\prime }$. Analogously to traditional signal processing, graph (convolutional) filtering is defined as element-by-element multiplication ⊙ in the Fourier domain. The node-domain equivalent of filtering can be written as convolution with a Fourier-domain filter $F\left(\overline{\lambda }\right)$ as:

$${\mathcal{F}}^{-1}\{F\left(\overline{\lambda }\right)\odot \mathcal{F}\left\{h_0\right\}\}={\mathcal{F}}^{-1}\left\{F(\Lambda )\mathcal{F}\left\{h_0\right\}\right\}=UF(\Lambda )U^{-1}{h}_0=F(\widehat{A})h_0$$

where $\overline{\lambda }$ is the vector of the adjacency matrix eigenvalues and is considered its spectrum, whilst $F\left(\overline{\lambda }\right)$ is applied on all spectrum dimensions.

Since Fourier-domain operations can be translated into node-domain filtering computations, graph filters are easy to implement [19] and require only an informed assumption of how the normalized adjacency matrix’s spectrum needs to be transformed. For instance, two popular graph filters are (a) personalized PageRank [20,21,22], which arises from Markovian-like equivalents to random walks with restart within graphs and have parameters $f_k=(1-a)a^k$ controlled by one hyperparameter $a\in [0,1]$; and (b) HeatKernel [23,24] which emulates heat diffusion dynamics in graphs with parameters $f_k=e^{-t}{t}^k/k!$, where $k\in \{1,2,3,\dots \}$ is the number of hops away in which maximal importance is placed.

These filters are low-pass in the sense that parameters $f_k$ are generally larger for smaller k, which in turn translates into a lesser impact on eigenvalues with absolute values closer to 0 than high-frequency eigenvalues with larger absolute values. In practical terms of node domain operations, low-pass filters place more emphasis onto diffusing node values of fewer hops away and thus introduce a type of graph signal smoothing that removes non-local implicit node relations, which can be thought of as high-frequency noise.

The above spectral analysis is tailored to the symmetric normalization of graph adjacency matrices and undirected graphs, i.e., for which $\widehat{A}[u,v]=\widehat{A}[v,u]$. However, some filters, such as personalized PageRank, are better known for non-symmetric normalizations arising from Markov chain modeling, such as $\widehat{A}=A{D}^{-1}$, where graphs are defined by directed edges. Spectral theories are also available for these filters, but lay outside the scope of our work. Instead, when analyzing bipartite project–library graphs, we work with undirected edges that allow the transfer of graph signal values from both projects to libraries and libraries to projects (otherwise, filtering with graph signals would be stuck at recommending only immediate neighbors). Therefore, we adopt the adjacency matrix normalization of (2).

2.3. Graph Neural Networks for Link Prediction

Graph Neural Networks (GNNs) [25,26] are a popular machine learning paradigm that lets traditional feature-based neural network learning account for the relational information of data samples organized into graphs. This is achieved through message-passing protocols that gather and aggregate latent representations of graph neighbors, which are then transformed with neural network layers shared between all nodes before being passed on. Many industry-level applications focus exclusively on GNNs that employ the shift operation of graph signal processing as the aggregation operation, since the latter performs a (weighted) averaging of graph neighbor representations that can be efficiently implemented with sparse matrix multiplication within GPUs.

All GNNs start from initial matrices of node representations $H^{\left(0\right)}$, whose rows $H^{\left(0\right)}\left[u\right]$ correspond to features of nodes u. These could be unsupervised embeddings obtained by multilayer architectures and trained end-to-end [27] or other pre-processed machine learning features, such as weighted bag-of-word vectors. Then, given normalized adjacency matrices $\widehat{A}$, convolutional GNNs average graph neighbor representations where these are weighted by corresponding edge weights. This kind of smoothing is understood as a natural extension of graph signal processing to vector-valued graph signals can be expressed in matrix form with the operation $\widehat{A}{H}^{(\ell )}$, where $H^{(\ell )}$ are matrices of (latent) node representations.

Most GNNs add computational stability to the graph shift operation with a practice dubbed the renormalization trick. This adds self-loops to all nodes before computing the normalized adjacency matrix and will also be used throughout this work. Compared to the original matrix, the renormalization trick computes $\widehat{A}={(I+D)}^{-1/2}(I+A){(I+D)}^{-1/2}$, where I the unit matrix. Since matrix multiplication can be efficiently computed by modern GPUs, especially if graphs are not fully connected and sparse representations can be leveraged to make computation time scales with the number of edges, convolutional GNNs have become a widely popular variety for analyzing the graphs of many nodes and edges [25,26].

Original GNN approaches (e.g., the architecture of Kipf and Welling [28] that helped popularize the domain) defined graph convolutional layers per:

$$H^{(\ell )}=\sigma \left(\widehat{A}{H}^{(\ell -1)}{W}^{(\ell )}\right)$$

(5)

where $\sigma (·)$ are nonlinear activation functions applied on matrices element-by-element, such as rectified linear unit activations $ReLU\left(x\right)=max\{x,0\}$ [29] and $W^{(\ell )}$ are learnable weights that help determine the output of GNN layers $\ell =1,\dots ,L$. The output of the final layer is used for predictions, which for node classification have dimensions equal to the number of classes and arise from a softmax activation on the top layer to obtain an estimation of a binary one-hot encoding of class labels. On the other hand, for link prediction tasks, any number of latent representation dimensions can be outputted and compared pairwise to select the most similar pairs of nodes to recommend links for, for example, through a sigmoid activation of their dot product [30].

To avoid the oversmoothing of representations along multiple graph convolutions, state-of-the-art GNNs often include recurrent terms in the predictions. This is achieved either by adding feedback loops that trade-off between layer outputs (before being passed through the activation function) and $H^{(\ell )}$ with linear or feature-specific terms [31,32], or by aggregating the outcomes of all convolutional layers [27]. Recursive loops effectively inject the graph signal transformations of trained features in all layers.

One popular link prediction framework using GNNs is NGCF [27] which is also employed by the aforementioned GRec library recommendation system. This calculates the similarity between combined node representations found in the rows of the matrix:

$$H_{final}=H^{\left(0\right)}\left|\right|H^{\left(1\right)}\left|\right|\dots \left|\right|H^{\left(L\right)}$$

(6)

where $\left|\right|$ represents the horizontal matrix concatenation and L the number of graph convolutional layers. That is, the elements of $(H_{final}{H}_{final}^T)[u,v]$ are considered the scores of linking nodes u and v (in the case of library recommendation, only project–library scores are kept from these to find the most related libraries to projects). The same framework also refines the convolutional layers of (5) with a self-attention mechanism to node layers per:

$$H^{(\ell )}=\sigma \left(\widehat{A}{H}^{(\ell -1)}{W}^{(\ell )}+\widehat{A}{H}^{(\ell -1)}\odot H^{(\ell -1)}{W}_{att}^{(\ell )}\right)$$

(7)

where ⊙ represents the element-by-element matrix product with lesser priority than matrix multiplication and $W^{(\ell )},W_{att}^{(\ell )}$ learnable parameters at layers ℓ.

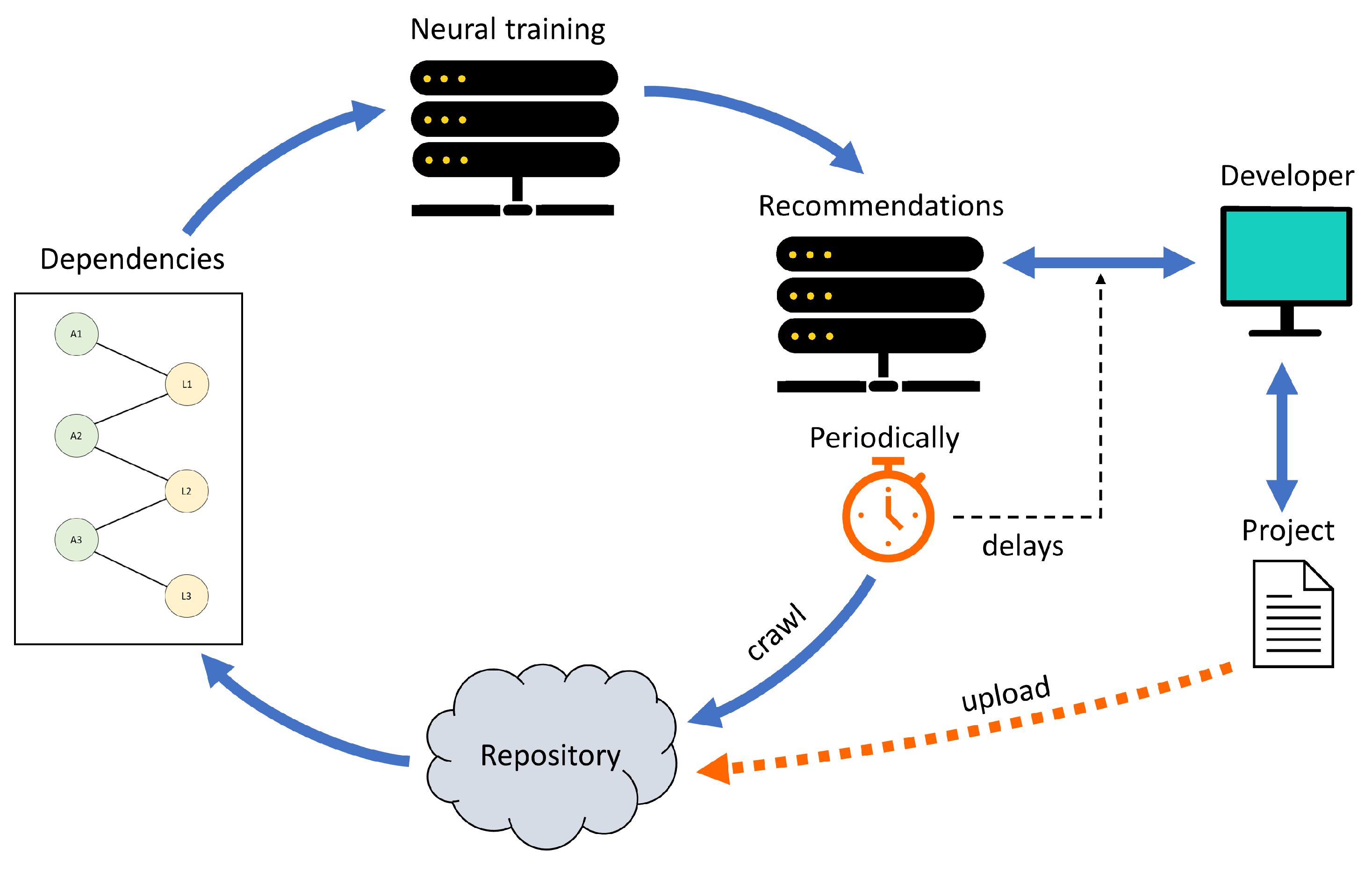
3. Deploying Library Recommendation Services

As per all software services, it is important to look at the deployment and usage flows of library recommendation from a software engineering perspective. In this section, we analyze how well real-world systems can adopt the flows of (a) existing representation-based library recommendation algorithms overviewed in Section 2.1; and (b) no-learning algorithms that perform inference based on informed ad hoc assumptions. We introduced an algorithm of the second type in the next section. In both cases, we envisioned the deployment of algorithms as online (e.g., RESTful [33]) services that developers query to obtain recommendations for their software projects.

3.1. Deploying Representation Learning for Library Recommendations

Representation-based recommendation algorithms need to be retrained when new nodes are added to dependency graphs, so as to arrive at representations that implicitly capture both old and new node relational information. This does not scale well when many recommendation requests are made for services for new projects or project prototypes, for example, by many independent agile development teams. Accommodating requests for yet-unseen graph nodes (projects) is more important in software engineering compared to other domains where representation learning has been applied, because a primary use case is to aid the development of new software rather than altering existing projects. In fact, changing or integrating new dependencies mid-development requires rewriting software project components and is a form of technical debt.

Keeping the above in mind, let us consider the recommendation system flow of notifying users about interesting items, which is popular among previous library recommendation works, such as those overviewed in Section 2.1. These usually perform real-world evaluation by first creating recommendations on the whole corpus of software projects after one training run and then recommending those to developers. In practice, developer notifications about potentially useful libraries translate to service subscription models where developers sign up their projects and obtain periodic recommendations.

However, when deploying library recommendation systems “in the wild”, subscription services neglect the practical needs of the software industry that require system interfaces to be queried at will and immediately produce results for new projects. This is particularly important for agile development, where delays to software project design, especially at the first exploratory or rapid prototyping stages, can undermine the whole development process [34]. At the same time, retraining accrues significant upkeep costs to keep being deployed, as representations need to be extracted periodically using computationally savvy hardware, such as GPUs or clusters of GPUs able to fit large dependency graphs in-memory. For example, if representation-based library recommendations were integrated in query-able online code repositories (e.g., GitHub), the latter would need to periodically retrain library and project representations on snapshots of dependency graph databases. Thus, to obtain recommendations for new projects, developers would need to first upload their implementations to be integrated in the databases and wait for the next training round to complete, as shown in Figure 1.

To make matters worse, the above flow runs the risk of mining library usage from projects for which recommendation is the goal and existing dependencies are hastily selected. In particular, mining too many non-expert designs promotes co-usage pattern recommendations that replicate the perfunctory knowledge of early designs rather than well-maintained projects. To address this issue when designing real-world systems, there is an uncomfortable balance to be found between allowing any project as system input and letting hastily assembled projects (e.g., experimental versions during rapid prototyping) potentially ruin recommendation quality. Even in the best of cases, it is difficult to create tools that do not exclude the vast majority of experimental prototype queries. One realistic solution is for training to be conducted by integrating only a few low-quality projects in copies of dependency graphs, mining those for recommendations, and then discarding the integrated changes. However, this practice is unsustainable if library recommendation services are to become sufficiently popular for many hastily assembled recommendation requests to be made back-to-back; these would require a proportional number of training instances to run simultaneously.

Finally, beyond tangible workflow costs arising from long recommendation delays that are not able to immediately access recommendations could also discourage developers from adopting automated library recommendation. For instance, they could instead try to accelerate development cycles by ignoring automation and investing manual effort into library discovery instead. If so, the high usefulness of library recommendation systems—even high-quality ones— becomes obsolete once they fail to achieve high enough throughput.

3.2. Deploying No-Learning Library Recommendations

In this work, we propose moving away from representation learning and instead employing no-learning graph inference that only requires forward passes. Given that such algorithms exist and exhibit high enough predictive quality to be comparable to existing representation learning approaches, their recommendations can be computed on-demand for new libraries. For example, project and dependency metadata can be uploaded to no-learning recommendation systems to add them to dependency graphs just before inference takes place.

The advantage of no-learning algorithms is that, even if we consider the periodical mining of code repositories to extract new versions of dependency graphs, the latter do not make recommendation pipelines wait for their completion. In particular, for new project predictions, dependencies can be directly injected in the graphs before inference and removed afterwards—two operations with the minimal cost of, respectively, adding and removing one graph node and its edges. This is demonstrated in Figure 2, where the recommendation flow (the data flow cycle between the developer, the project, and the recommendation system) does not depend on the conclusion of periodical updates to recommend libraries.

Furthermore, the above-described recommendation flow can run in parallel to the mechanism extracting dependency graphs, such as by crawling repositories; if dependency graph snapshots already comprise enough usage patterns, mining the last known instead of the next graph would minimally affect recommendation outcomes given that the two differ only by a few nodes and edges. As a result, there would be a negligible impact on inference quality. By comparison, representation learning discussed in the previous subsection cannot make predictions with representations extracted by the last-known dependency graphs, because these do not have entries for new query projects.

Finally, given that repository crawling takes care to not extract dependencies from low-quality code (e.g., from recent projects with too few commits), the above flow sidesteps the issue of mining many confounding dependency patterns by undoing changes after inference. Since no training is required, and given that graph inference can be quickly computed, we envision that queue-based sequential pipelines can support high query loads before infrastructure parallelization (e.g., many servers providing access to the same recommendation service) is to be considered.

4. Graph Filters for Library Recommendations

In this section, we introduce graph filters as a collaborative filtering approach applicable to library recommendation. Although vanilla filters are often outperformed by state-of-the-art representation learning, we recognize that they also follow the no-learning paradigm described in the previous section. Thus, they fit well into the real-world sensibilities of deploying library recommendation services. Having identified this point, we look at the promising filters that were previously neglected by the recommendation system literature, but match high-level assumptions of how humans could go about mining project–library dependency graphs.

We start by describing the usage of graph filters for collaborative filtering and how these translate into our setting (Section 4.1). We then theorize which types of library co-usage patterns filters should model to emulate one potential human-driven library discovery process in hyperlink-like dependency graph exploration. In this regard, we identify the memory of past discoveries as a promising component often overlooked by previous approaches (Section 4.2). Finally, we translate our analysis to existing absorbing random walk filters, which model memory components for community detection tasks but have not been used in collaborative filtering, and infer node-wise memory strength to adhere to symmetric normalization principles instead of applying heuristics or training to determine it (Section 4.3). Experimental probing to demonstrate practical usefulness and to compare our approach to representation learning follows in the next section.

4.1. Revisiting Graph Filters for Collaborative Library Recommendations

We base our approach on collaborative filtering paradigms that run graph filters in bipartite graphs to find nodes relevant to ones of interest. Graph filters, especially personalized PageRank, were at some point a popular collaborative filtering tool [22], but this direction has in large part been abandoned in favor of the added accuracy offered by representation learning approaches such as GNNs. Other graph-mining tasks, however, have recently seen a resurgence of graph filters as equivalence to those is now understood as a primary contributor towards the efficacy of many GNN architectures [31,32,35,36]. Therefore, given that GNNs already boast a high predictive quality for library recommendations, we search for filters that are not lagging significantly behind with respect to predictive performance, while also satisfying our no-learning requirement.

To reconcile the opposite trends of collaborative filtering having abandoned graph filters and the latter being revisited by state-of-the-art research from other domains, we theorize that widely adopted graph filters are missing crucial assumptions that more sophisticated collaborative filtering mechanisms do not; these assumptions may not be as important in other predictive tasks, but are crucial for recommendation systems. In the next subsection, we identify lack of memory as one such assumption when emulating human-driven library recommendation.

We consider a general formulation of graph filters $F(\widehat{A})$ that can take any functional form dependent on adjacency matrix normalizations $\widehat{A}$ such as those described in Section 2. To recommend libraries for query projects with these, they need to parse project inputs. However, singleton data samples can lead to non-informed graph mining due to a lack of pairwise structural relations to mine. Thus, we employ the neighborhood inflation heuristic of Gleich et al. [37] to expand the search terms by including the immediate neighborhood of projects, i.e., their known dependent libraries, as query-able information to be included within graph signals. This kind of information was already sent to graph inference systems following the deployment of Figure 1 so that dependencies between the query project and at least one library are added to the dependency graph. Hence, there are no additional communication or computational costs associated with following this practice.

We hereby consider query graph signal $h_0$ with elements

$$h_0\left[v\right]=\{1\mathrm{if}u=v\mathrm{or}v\mathrm{is}\mathrm{a}\mathrm{dependency}\mathrm{of}u,0\mathrm{otherwise}\}$$

(8)

where u are the projects for which we provide library recommendations. Given these query signals, we pass them through filters of choice to obtain their structural proximity of all graph nodes $h=F(\widehat{A})$. Finally, our methodology focuses on the proximity scores $h\left[v\right]$ of libraries v, where higher scores are structurally “closer” to target projects and thus indicate preferred recommendations.

4.2. Low-Pass Filters with Memory to Emulate Human-Driven Library Search

To design graph filters well-suited to library recommendation, we explore a search procedure within dependency graphs that emulates human exploration if no external sources of recommendation (e.g., expert guidance) was provided. In this, developers searching for the libraries best-fitting their projects look at projects using the same libraries and investigate which other dependencies are found there. This process is iterated to find projects and libraries that are more hops away, although presumably with lesser zeal, since after some time, irrelevant projects and libraries would start being found. To avoid getting “lost” in the dependency graph, the search would at some point restart. Up to this point, this process applies the popular random walk with restart search, whose probability of visiting nodes for stationary transition probabilities between pairs of nodes is proportional to the elements of graph signal outcomes of personalized PageRank [38].

We already discussed that recommendation systems based on personalized PageRank fail to reach a similar recommendation quality as more recent collaborative filtering approaches. For this reason, we argue that a missing assumption in the above exploration is the lack of memory during random walks. In particular, we propose that developers would not only backtrack during link-based exploration, but would also keep track of projects and libraries highly related to their query to also restart from there in future walks. Overall, we recognize four types of actions that can occur during human-driven random walks with restart and memory, given that developers would have arrived on a particular node: (a) visit a neighbor; (b) stay on the node; (c) remember the node; and (d) restart the random walk. These are visually illustrated in Figure 3.

Due to the chance of restarting random walks at all steps, it becomes progressively more likely to have restarted the more hops away developers move from query projects. In other words, recommendations will be more concentrated on libraries laying fewer hops away. In graph signal processing terms, the proposed filters would be low-pass and hence would not excessively smoothen the query across dependency graph edges and instead retain its original position within dependencies.

We stress that the theorization presented throughout this section is in large part derived by graph mining literature. Our contribution lies in identifying the key points best fitting the problem of automated library recommendation, and ultimately motivate the usage of appropriate graph filters in this setting.

4.3. Symmetric Absorbing Random Walks

In this subsection, we transcribe the above human-driven library discovery process to graph filters with minimal (ideally no) parameters. To do this, we make the assumption that all choices during random walks follow static distributions that only depend the nodes that developers are currently looking at. We also ignore real-world semantics, such as project names or descriptions, whose exploration is left for future work. Instead, we only use the structural characteristics of dependency graphs.

Given these assumptions, one possible tool to model random walks with memory are partially absorbing random walks [39]. Instead of only defining one type of filter, these introduce a framework for accounting for memory by letting a portion of random walks passing through nodes stay there. In terms of our theorization, this corresponds to developers remembering the nodes they visit and their relatedness to original queries. Various graph filters arise for different assumptions of how memory works, such as the probability of staying on nodes being proportional to node degrees, which is theoretically equivalent to personalized PageRank (more details below), or the alternative of assigning the same absorption rate to all nodes to retrieve tightly knit structural communities [39], where the absorption rate effectively describes the memorability of nodes.

Partially absorbing random walks account for the four types of random walk with memory actions described in the previous section and are recursively computable through the following formula:

$$h=S{(S+\widehat{D})}^{-1}{h}_0+S{(S+\widehat{D})}^{-1}\widehat{A}{S}^{-1}h$$

(9)

where $\widehat{A}$ are symmetric normalizations of adjacency matrices presented in (2), S is a diagonal matrix whose diagonal elements $S[u,u]$ correspond to the absorption rates of nodes u, and $\widehat{D}$ are diagonal matrices with elements $\widehat{D}[u,v]=\{{\sum }_{v^{\prime }}\widehat{A}[u,v^{\prime }]\mathrm{if}u=v,0\mathrm{otherwise}\}$. We stress that $\widehat{D}$ are the node degrees of the normalized (not the original) graph adjacency matrix. Correspondence between quantities appearing in (9) and the random walk procedure with memory in dependency graphs is demonstrated in Figure 3.

Partially absorbing random walks can implement different graph filters, depending on chosen absorption rates S. For example, selecting $S=\frac{1-a}{a}\widehat{D}$ for a parameter $a\in (0,1)$ reduces this scheme to the power method iteration of computing personalized PageRank, whereas $S=\frac{1-a}{a}I$ discovers tightly connected structural communities around query nodes with high probability [39]. In both cases, absorption rates only depend on one (hyper)parameter.

We now provide a novel way of selecting absorption rates. This starts by solving (9) with respect to h and expressing the graph signal outcome h of partially absorbing random walks per:

$$\begin{array}{cc}\hfill & h=F(\widehat{A}){\widehat{h}}_0\hfill \\ \hfill & F(\widehat{A})={\left(\mathcal{I}-S{(S+\widehat{D})}^{-1}\widehat{A}{S}^{-1}\right)}^{-1}\hfill \\ \hfill & {\widehat{h}}_0=S{(S+\widehat{D})}^{-1}{h}_0\hfill \end{array}$$

In this context, ${\widehat{h}}_0$ is an adjusted version of the query graph signal that weighs the query project and its dependencies based on their absorption rates. $F(\widehat{A})$ is the graph filter responsible for diffusing the adjusted query graph signal. Effectively, this can be expressed as a spectral filter $F(\widehat{A})=\widehat{F}(\widehat{\widehat{A}})={(\mathcal{I}-\widehat{\widehat{A}})}^{-1}$, where $\widehat{\widehat{A}}=S{(S+\widehat{D})}^{-1}\widehat{A}{S}^{-1}$ is a new normalization applied on the normalized adjacency matrix $\widehat{A}$ ($F(\widehat{A})$ is not a spectral filter of $\widehat{A}$ because it arise from a non-polynomial graph operations of the latter, but $\widehat{F}(\widehat{\widehat{A}})$ is a spectral filter of $\widehat{\widehat{A}}$).

In the previous section, we formulated that graph signal filtering should be low-pass around query graph signals. To achieve this effect for $\widehat{F}(\widehat{\widehat{A}})$, one simple solution would be to make $\widehat{\widehat{A}}$ symmetric. This way, and given that this matrix effectively has a non-negative shrunken version of $\widehat{A}$’s elements, it would obtain eigenvalues $\lambda$ in the range $\lambda \in [-1,1]$, which in turn would be transformed into $\widehat{F}(\lambda )={\sum }_{k=0}^{\infty }{\lambda }^k$. Therefore, given that only positive absorption rates are accepted, i.e., visiting nodes lets developers retain at least some memory of them, a satisfactory condition to achieve a symmetric normalization $\widehat{\widehat{A}}$ of the normalized adjacency matrix and hence a low-pass effect on the non-principal (i.e., those less than 1) eigenvalues of $\widehat{A}$ can be computed per:

$$S{(S+\widehat{D})}^{-1}=S^{-1}\iff S^2-S-\widehat{D}=0\iff S=\frac{1}{2}\left(\mathcal{I}+\sqrt{\mathcal{I}+4\widehat{D}}\right)$$

(10)

5. Experiments

In this section, we conduct the experiments to evaluate the efficacy of no-learning library recommendation compared to existing representation learning alternatives. We start by describing the evaluation dataset and measures used in experiments (Section 5.1), outline competing approaches (Section 5.2), and present experimental results (Section 5.3). Results and insights are discussed in the next section.

5.1. Experiment Setting

As a proof-of-concept for our proposed system, we experiment on the publicly available MALib dataset. This comprises 704,128 dependencies between a collection of 56,091 Android GitHub projects to 763 Android third-party libraries. To evaluate recommendation quality, we follow a methodology common in library recommendation research [11,14,16]. In particular, we select all projects with at least 10 dependencies as test ones (these are 31,438 in total), by merit of them comprising enough dependencies to be considered high-quality known ground truth. For these projects, we remove $rm\in \{1,3,5\}$ dependencies to emulate the real-world scenario where not all relevant libraries are used and conduct experiments where we use the remaining dependencies to rediscovering the removed ones.

For each approach, the following measures assess the quality of the top $T\in \{5,10\}$ library recommendations. All measures output values in the range $[0,1]$, with higher values indicating recommendations closer to ideal ones.

MAP. The mean average precision of the top T recommendations. In detail, given the notation $L_{proj}\left[i\right]=\{1$ if the i-th top library recommendation for project $proj$ is a true positive, 0 otherwise}, we compute the average precision for each project’s top T library recommendations per

$$A{P}_{proj}=\frac{{\sum }_{i=1}^T{L}_{proj}\left[i\right]{\sum }_{j=1}^T{L}_{proj}\left[j\right]/i}{{\sum }_{i=1}^T{L}_{proj}\left[i\right]}$$

and report its mean across all projects. Average precision provides a more granular understanding than precision by accounting for recommendation order and is thus able to differentiate between recommendation algorithm quality even for large T.

MP. The mean precision of the top T recommendations across all projects. Higher values indicate that there are fewer erroneous library recommendations in the list of top ones. Perfect library recommendations yield MP equal to $min\{rm/T,1\}$.

MR. The mean recall of the top T recommendations across all projects. Higher values indicate that there are fewer desired library recommendations (i.e., from those of each project’s test set) left out. Perfect library recommendations yield an MR equal to 1.

MF1. The mean F1 score of the top T recommendation across all projects. The F1 score for a project is the harmonic mean between its precision and recall. Then, the mean of all these scores is obtained.

Cov. The coverage of recommendations is the percentage of libraries that reside in the top T recommendation of at least one software project. A coverage value of 1 means that all libraries can be recommended, whereas low percentages indicate approaches that prioritize a few well-known libraries—an undesirable outcome when the goal of recommendation is also to discover fitting non-popular libraries.

5.2. Compared Approaches

In addition to our approach (LibFilter), our experiments assess the following representation learning architectures and graph filters. These are summarized in

Table 1. Overview of compared library recommendation approaches, including training and inference (for one project) times. Recommendation times are bottlenecked by both training and inference.

Approach	Citation	Type	Training Time	Inference Time
LibSeek	[14]	Repr. learning	$O(E·dims·layers·epochs)$	$O(I·dims)$
GRec	[16]	Repr. learning	$O(E·dims·epochs)$	$O(I·dims)$
LibPPR	[22], this work	Graph filter	—	$O(-E·logϵ)$
LibARW	[39], this work	Graph filter	—	$O(-E·logϵ)$
LibFilter	[this work]	Graph filter	—	$O(-E·logϵ)$

alongside amortized training and inference (making recommendations for one project) times. Time analysis holds for connected dependency graphs and explores terms pertaining to scalability with regards to the numbers of dependencies E and of libraries $I<E$, as well as architectural characteristics, namely the latent representation dimensions $dims$, the number of training $epochs$, and the constant numerical tolerance $ϵ$ of iterative methods computing graph filters. In practice, the number of layers, dimensions and training epochs introduce huge multiplicative terms to running times (in the tens or hundreds order of magnitude each). They could also grow with the number of dependencies, as more effort is required to learn from larger datasets. Thus, even when dimension terms can be removed with parallelized GPU computing, representation training times could scale worse than linearly with the number of mined dependencies.

GRec. A library recommendation approach based on state-of-the-art GNNs for link prediction [16]. It implements convolutional self-attention layers of (7), whose outcomes are concatenated and used as representations. Layers are trained with 10% dropout and comprise 128 latent dimensions and representation matrices inputted to the first layer $H^{\left(0\right)}$ are trained end-to-end. We refer to the architecture of the respective paper for more details. This architecture’s latent representations need to be retrained to make predictions for new software projects.

LibSeek. A matrix factorization approach [14] that aims to find project and library representations able reconstruct dependency graph adjacency matrices per (1). It was the previous and widely recognized state-of-the-art approaches before GRec and was one of the first to explicitly recognize the diversification of recommendations (i.e., high coverage) as an important goal of library recommendation. Notably, we do not compare against previous works because these have been found to yield a similar or lower recommendation quality across all measures on the dataset we experiment on [14].

LibPPR. Collaborative filtering that employs the personalized PageRank graph filter for recommendation. As described by Bahmani et al. [22], this was once a popular approach. Although it has since been abandoned in favor of GNNs, it is the approach that is closest to ours since it also employs graph filters. Notably, personalized PageRank depends on a diffusion parameter $a\in [0,1)$, which for smaller values creates lower-pass versions of the graph filter. We follow a random walk with restart formulation that has an equal chance to restart the walks as moving to neighbors and set this parameter to $a=0.5$. Given that $\frac{1}{1-a}=2$ is the average length of the random walk processes modeled by personalized PageRank [40], this creates a receptive field that places emphasis on projects and libraries co-used with the query ones, as these lie two hops away from the query ones. We empirically corroborated that this is better-performing than the most widely adopted alternative $a=0.85$ or even shorter average random walk lengths arising from $a=0.25$.

LibARW. Collaborative filtering that employs the partially absorbing random walks of (9) for absorption rates $S=\frac{1-a}{a}\mathcal{I}$. This graph filter was proposed [39]. Given that the parameter $a\in (0,1)$ is equivalent to the one of personalized PageRank, we select $a=0.5$ for this approach, the same value as LibPPR. We also empirically corroborate that this is performs better than alternatives, such as $a=0.25$ and $a=0.85$. Importantly, since LibARW is not our proposed approach, empirical investigation does not introduce overtraining bias to experiment results.

LibFilter. Collaborative filtering that employs our proposed symmetric partially absorbing random walks that apply on (9) the absorption rates determined by (10). This approach is a true no-learning one in that it requires no parameter training and no hyperparameter tuning.

5.3. Results

Table 2. Comparison of library recommendation approaches.

	Top 5 Recommendations					Top 10 Recommendations
Approach	MP	MR	MF1	MAP	Cov	MP	MR	MF1	MAP	Cov	No-Learn
	Leave out 1 test library per project
GRec	0.152	0.761	0.254	0.623	0.695	0.083	0.828	0.151	0.636	0.792	✕
LibSeek	0.135	0.674	0.225	0.524	0.335	0.076	0.755	0.137	0.535	0.396	✕
LibPPR	0.119	0.596	0.199	0.461	0.211	0.072	0.715	0.130	0.477	0.283	✔
LibARW	0.135	0.676	0.226	0.528	0.520	0.077	0.772	0.140	0.541	0.602	✔
LibFilter	0.140	0.700	0.234	0.552	0.544	0.079	0.789	0.143	0.564	0.620	✔
	Leave out 3 test libraries per project
GRec	0.410	0.692	0.514	0.797	0.685	0.234	0.788	0.360	0.761	0.782	✕
LibSeek	0.371	0.618	0.464	0.728	0.325	0.216	0.719	0.332	0.697	0.391	✕
LibPPR	0.330	0.550	0.413	0.575	0.241	0.207	0.691	0.319	0.509	0.324	✔
LibARW	0.377	0.628	0.471	0.595	0.557	0.224	0.746	0.344	0.535	0.640	✔
LibFilter	0.391	0.652	0.489	0.597	0.579	0.228	0.760	0.351	0.542	0.655	✔
	Leave out 5 test libraries per project
GRec	0.587	0.594	0.590	0.840	0.657	0.361	0.731	0.483	0.786	0.754	✕
LibSeek	0.529	0.529	0.529	0.790	0.314	0.329	0.658	0.439	0.740	0.380	✕
LibPPR	0.495	0.495	0.495	0.572	0.282	0.329	0.658	0.438	0.470	0.369	✔
LibARW	0.570	0.570	0.570	0.562	0.599	0.357	0.714	0.476	0.474	0.689	✔
LibFilter	0.588	0.588	0.588	0.558	0.602	0.363	0.725	0.484	0.476	0.688	✔

presents the outcome of experimentally evaluating competing approaches. Since GRec and LibSeek follow the same evaluation methodology as we do, we pull evaluation results for these approaches from respective publications. We do not run the publicly available code of GRec and LibSeek to avoid biasing our comparison with lower-quality results arising from post-publication experimental probing by development teams. For instance, we failed to set up GRec’s latest published code version to reach the same high evaluation scores as those reported by their paper and found architectural inconsistencies (including different types of layers and activations) between the paper and the code while investigating the issue. Thus, we decided to err on the side of caution and present the better reported values. Graph filters were implemented by building on the filter definition framework provided by the pygrank Python package [19] and were run on its numpy backend to ${10}^{-12}$ mean absolute error numerical tolerance. (pygrank’s numpy backend implements the graph shift operator by wrapping the C++ code for sparse matrix multiplication and runs faster than the respective operation provided by existing GPU computing frameworks. We ran experiments five times and reported measure averages across runs. Standard deviations are less than $0.007$ for coverage and less than $0.002$ for other recommendation quality measures and thus facilitate robust pairwise approach comparisons. An implementation of the symmetric absorbing random walk filter and the experiment methodology are publicly available online (https://github.com/maniospas/libFilter, accessed on 2 March 2022).

For all recommendation quality measures aside from MAP, there is a clear evaluation order where GRec is the best approach and is followed by LibFiter (our approach), where the latter lags behind by an at most 5–23% relative decrease that shrinks as more dependencies are omitted from the training graph. Although the two approaches do not always enjoy similar levels of recommendation quality, they can be considered roughly comparable when factoring in the much lower predictive quality of LibSeek and LibPPR. In fact, these last two approaches lag significantly behind, especially in terms of coverage, for which they exhibit near-half or less of GRec. Characteristically, LibFilter lies approximately mid-way between GRec and LibSeek in terms of evaluation measures. Furthermore, it outperforms the other two filter-based alternatives LibPPR and LibARW by a large and small margin, respectively, across all experiments.

With regard to practical deployment, we ran graph filters (LibPPR, LibARW, LibFilter) in a machine with 2.6 GHz CPU base clock and 16 GB DDR3 RAM. This extracts library recommendation scores for each project approximately within a fifth of a second—and well within $0.1$ second when LibFilter is deployed. By comparison, the out-of-the-box running of the publicly available implementation of GRec on the same machine’s GPU with 1680 MHz base clock and 6GB DDR6 graphics memory requires over 5.5 h for training alone (approximately 25 s per training epoch for 800 epochs); this would be the minimum recommendation delay in case of deployment as a query-able service.

6. Discussion

In this section, we discuss the experiment results and how these can be interpreted within the scope of library recommendation. We also point out promising research directions motivated by our findings, both in automated software engineering and in broader collaborative filtering research. We start by comparing our approach to representation learning techniques (Section 6.1) and assess whether we meet the goal of performing fast library recommendation without lagging excessively far behind in terms of recommendation quality. We also explore the role of filtering memory in improving recommendation algorithms and propose that this direction needs to be explored more thoroughly in the future. Furthermore, based on comparison between graph filter alternatives with different memory mechanisms in their ability to predict relevant libraries to software projects, we propose that searching for new libraries among popular ones is less important than looking at the libraries employed by similar software projects (Section 6.2). Finally, we outline the threats to evaluation validity and describe how these can be addressed when creating real-world systems (Section 6.3).

6.1. Qualitative Approach Comparison

Looking at the experimental results of Table 2 in greater detail, our proposed LibFilter system outperforms the matrix factorization of LibSeek in terms of recommendation quality, which we attribute to the wider receptive field of graph filters that explicitly accounts for co-usage patterns more than one hop away in dependency graphs. On the other hand, LibFilter lags behind the GNN architecture of GRec, which both learns representations and accounts for a wide receptive field. Nonetheless, evaluation in all experiments lies significantly closer to GRec and we consider deviations from the latter small enough for practical deployment sensibilities to play a greater role when choosing which approach to employ. In fact, when dependency graphs have many missing links, as happens for $rm=5$, our approach catches up in terms of the MP, MR and MF1 measures. Therefore, we argue that the usage of LibFilter should be preferred as an out-of-the-box solution in place of more sophisticated representation-learning alternatives, as the latter need hours instead of fractions of a second to recommend libraries for a new project and would require additional software engineering investigation to determine their viability for the services being developed.

We then point out that the well-established practice of deploying personalized PageRank filters, which we modeled with LibPPR, fails to achieve a similar recommendation quality across all experiments and thus cannot be considered for real-world usage. In fact, it is outperformed by LibSeek to say nothing of the more sophisticated GRec. This result corroborates why collaborative filtering has moved away from graph filters and towards representation learning. However, at least for library recommendation tasks, our experiments suggest that the issue lies less with the inherent power of filters and more with naive structural assumptions (e.g., memory-less random walks) firmly embedded in popular literature, which tend to promote the blind usage of personalized PageRank filters.

Our research escapes from this line of thinking by theorizing that the explicit memory-aware components of partially absorbing random walks can capture dynamics similar to a human-driven library search. Although personalized PageRank is also a type of partially absorbing random walk, it exhibits a memory strongly biased towards node popularity rather than relevance to search outcomes, i.e., an equivalent human search would prioritize remembering and looking at popular libraries (more on this in the next subsection). The importance of search memory for library recommendation is further accentuated if we consider that GRec introduces memory-like constructs in the form of node self-attention terms that multiply incoming representations with those already found in nodes. On the other hand, matrix factorization approaches, such as LibSeek, do not model similar phenomena.

Together, these two findings indicate that, contrary to the popularity-based biasing of results, node-specific memory could be the critical research direction for qualitative collaborative filtering algorithms. Given the success of GNN attention in other link prediction tasks, these findings could also translate to domains beyond library recommendation. Furthermore, our research indicates that the usage of graph filters in link prediction systems should be reconsidered as a viable alternative that can compete at, if not the same, at least comparable levels to GNNs while accommodating practical considerations. In particular, our approach is deployed in the form of a graph filter that can be applied to any structure-based link prediction task, even in other domains where it can potentially remove the need for GNN training. Nonetheless, its efficacy in new tasks should be investigated first.

6.2. Library Popularity and Memorability

Leaving aside representation learning for a moment, the three graph filters we experimented with were derived from partially absorbing random walks and differ only with respect to what type of memory they employ. In particular, LibPPR places higher emphasis on remembering higher-degree nodes, LibARW places the same emphasis on remembering all nodes, and LibFilter performs a type of trade-off between the two. The results indicate that the trade-off yields better recommendations than the other two, thus validating our symmetric principle. Nonetheless, LibARW follows closely behind, which indicates that it is more important for mechanisms remembering relevant libraries to be near-unbiased with respect to popularity, i.e., the number of projects using them.

Looking at this finding from a practical perspective, real-world popularity is only a small indicator of library quality. That is, it is not always worth using popular libraries marginally matching the project at hand. To the contrary, our findings indicate that using highly specialized libraries should be preferred as long as they better fit target tasks—though when suitability is a tie, then selecting the more popular ones to remember is still a valid practice. By extension, we propose that popularity-based metrics (e.g., stars, forks) often used as indicators of potential impact to development communities could be misleading by themselves and new qualitative-based metrics should be introduced.

6.3. Threats to Validity

Before concluding this work, we outline potential threats to our research’s validity.

First, we used popular measures to assess the quality of library recommendations. Previous related works have often performed developer surveys to corroborate the efficacy of experiments, for example, by emailing developers with libraries recommended for their projects with multiple systems and obtaining feedback on whether these could be of actual interest. In this work, we did not do this. However, we point out that developer feedback for the assessment of previous systems (including those we compare our approach against) has shown strong correlation between practical usefulness and the evaluation measures we employ [14,16]. Therefore, recreating the same small-scale studies could be considered redundant, especially since evaluation measure values lay in interpolate-able points between existing approaches. That is, our approach does not further improve recommendation quality but changes computational costs to be scalable. Thus, there exist no reasonable concerns over employed metrics failing to capture a practical impact.

When interpreting training and inference time measures, we caution that different approaches integrate different computing frameworks and exact numbers could be subject to change depending on the hardware or algorithmic optimizations available. For example, we run pygrank on its numpy backend because at the time of writing, it is faster than GPU computing for sparse matrix multiplication, but this could change in the future. Nonetheless, we expect that the amortized running times presented in Table 1 will yield the similar scalability of approaches. In this case, the driving criteria of algorithmic comparisons are still the training vs. no-training paradigm.

In a related vein, this work considers representation learning to be so time-consuming that architectures cannot be quickly and repeatedly retrained. This is not likely to change in the foreseeable future, especially since data tend to grow at faster rates than computational resources. However, one promising alternative would be to perform the warm-start training of GNNs to answer queries, for example, with streaming training principles [41]. Whether this would be useful for a library recommendation is yet unknown, for instance, due to the often degraded predictive quality of stream learning, or due to the local optimal regions drifting substantially so that minor representation tweaks are not sufficient.

Another threat to validity comes from experimenting on only one dataset. Although evaluation on this dataset is the gold standard in collaborative library recommendation literature, we stress that competing approaches could exhibit different efficacies if applied to different types of dependency graphs, such as the library-to-library dependency graphs, which are not bipartite. Thus, we point out that future research could also move towards benchmarking approaches on multiple datasets. We stress that this concern is shared across the whole collaborative library recommendation literature and not only our approach. For the time being, we propose that developers of real-world library recommendation services perform experimental probings to verify that selected recommendation algorithms replicate promised quality benefits on their own data, for example, with the evaluation methodology described in this work.

Finally, in line with previous research, we follow a collaborative recommendation approach. This makes use of known project–library dependencies to recommend more links but ignores real-world semantics such as project names or descriptions. Enriching library recommendations with semantics is a promising direction for future work as it could potentially procure recommendations with no known dependencies, for example to bootstrap development in unfamiliar domains. However, additional exploration is needed to (a) formulate how to extend graph inference on content features without resorting to the end-to-end training of latent representations; and (b) verify whether semantics are useful for library recommendation.

7. Conclusions

In this work, we discussed the problem of recommending library dependencies for new software projects based on co-usage patterns in other projects. For this task, we recognized that existing representation learning approaches exhibit the practical limitation of needing to retrain to make recommendations for new projects, hindering widespread adoption, and explained that no-learning project–library dependency graph inference circumvents this shortcoming. We proposed that graph filters match this paradigm and introduced a novel variation of partially absorbing random walk filters, which we theorized to emulate human-driven library discovery by modeling the memorization of libraries and projects similar to query ones. To show our approach’s efficacy, we experimented in a real-world dependency graph of Android project third-party library dependencies, where we found that it did not lag significantly behind state-of-the-art representation learning, where the latter introduces long recommendation delays when deployed to factual systems.