2. Formulation of the Problem
A dominating set (DS) [
22] of a graph (i.e., the set of
dominators) is defined as a subset of the nodes with the property that the rest of the nodes are adjacent (i.e., 1-hop neighbors) from some dominator(s). If the network induced by the DS is additionally connected, then the DS is called connected DS (CDS). In the IoBT setting, we seek for minimum CDS (MCDS), i.e., CDS with minimum cardinality. We treat an IoBT network as a multilayer network, i.e., as a multilayer graph [
5,
7]. We assume that there exist only bidirectional links (In principle, the paper ideas can be applied to networks with unidirectional links as well). A multilayer network comprised of
n layers is a pair
, where
is a set of networks
(i.e., with
nodes and
links), and a set of interlayer links
.
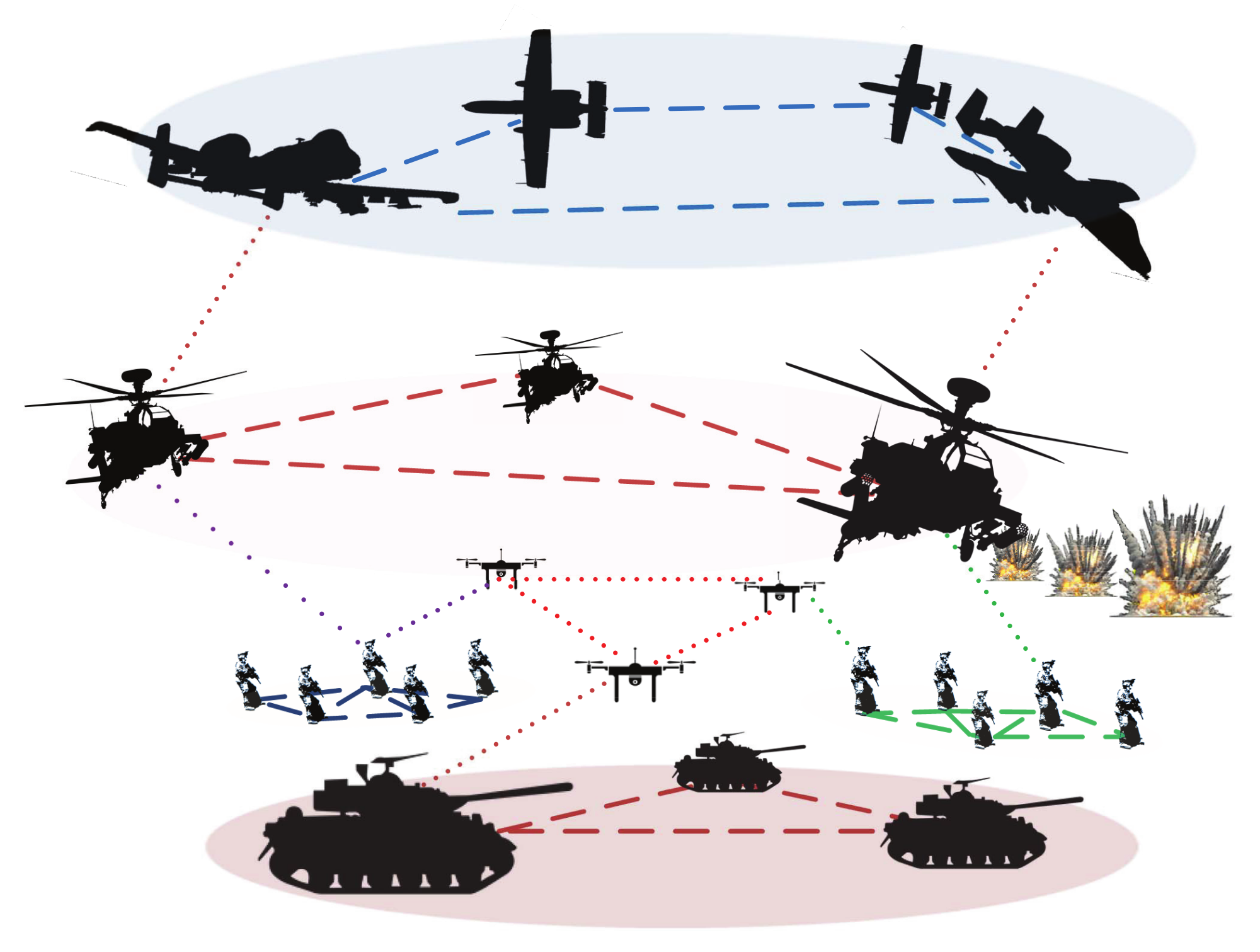
Figure 1 illustrates such a network, where we can see a
layer of soldiers, a layer comprised by helicopters, the
intralayer links connecting “nodes” of the same layer, and
interlayer links connecting “nodes” belonging to different layers.
Apparently, the requirement of calculating a CDS with minimum cardinality stems from scalability issues [
3]. Additionally, from the discussion in
Section 1 and in ([
3] Section III.B), where “…resilience and latency requirements for synthesizing a near-optimal network” [
3] are emphasized, we conclude that the more nodes with many interlayer links are included in our IoBT backbone the better it is. The inclusion of many nodes with “a lot” of interlayer links supports low-latency communication among layers; we can consider them as the hubs encountered in the literature on complex networks that reduce the “degrees of separation”. Moreover, the existence within the backbone of many nodes with “a lot” of interlayer links, reduces the danger of partitioning among layers. Therefore, we provide Definition 1 for the problem of calculating a MCDS for IoBT networks, and establish its computational complexity (Proposition 1) in the centralized setting, closing a gap in the literature which is open since [
5] and it was not dealt with in [
23].
Definition 1 (Multilayer MCDS problem for IoBT).
Solve the for a multilayer graph in a distributed manner, i.e., calculate the set comprised by the minimum number of nodes with the following properties: (a) their induced subgraph is connected (with intra and/or inter-layer links) and the rest of the nodes are adjacent to one node (or more) belonging to , (b) maximize the number of dominators with many interlayer links, (c) knowing only the k-hop neighborhood of each node; we work with here. (Working with broader neighborhoods (i.e., ) would cause a severe broadcast storm problem [24] in order to acquire the topology deploying successive rounds of “beacon” messages). In the rest of this section, we will investigate and establish the computational complexity of the centralized version of our problem for connected dominating sets. In particular, we will define the decision and optimization version of the examined problem, and then establish their complexities. The validity of these results for the case of connected dominating sets calculated in a distributed fashion is straightforward.
MULTILAYER CONNECTED DOMINATING SET PROBLEM
INSTANCE: A positive integer K, and a multilayer network consisting of n layers, i.e., a set of n pairs , where is the node set of a usual network and is a set of edges, for , and a set of interlayer links .
QUESTION: Is there a dominating set of size K for , i.e., a subset with such that for all there is some for which , and moreover the induced subgraph defined by is connected?
MULTILAYER MINIMUM CONNECTED DOMINATING SET PROBLEM
INSTANCE: A multilayer network consisting of n layers, i.e., a set of n pairs , where is the node set of a usual network and is a set of edges, for , and a set of interlayer links .
QUESTION: What is the minimum cardinality dominating set for , i.e., what is the minimum cardinality subset such that for all there is some for which , and moreover the induced subgraph defined by is connected?
We can now proceed to establish the computational complexity of the second problem. Our proof method will also establish the complexity of the first problem as well. The result is described in Proposition 1, but firstly we remind some background on proving the computational complexity of problems. So, a problem is NP-complete if the following two conditions hold:
- (a)
we can prove that the problem belongs to the class of NP problems, and
- (b)
we can
- (b1)
either transform in polynomial-time a known NP-complete problem to the problem at hand ([
25] p. 45),
or - (b2)
prove that the problem at hand contains a known NP-complete problem as a special case ([
25] p. 63, Section 3.2.1); this is called the “restriction” approach to proving NP-completeness.
We will now construct the proof that the problem of finding a minimum connected dominating set for is NP-complete. Recall that our problem is an optimization problem, i.e., “…finding the minimum dominating set”.
Proposition 1. The Multilayer MDS problem is NP-complete.
Proof. Our proof consists of three steps: (a) Transform the problem into a decision version, (b) Prove that it belongs to the class of NP problems. (c) Establish its NP-completeness complexity by following the “restriction” approach, i.e., by showing that our problem contains a known NP-complete problem as a special case.
[STEP 1. Transform our optimization problem into the decision version of the same problem.]
Without violating the validity of the proof, we will work with the decision version of the problem:
Given an integer , does our multilayer network contain a connected dominating set of cardinality equal to k?
Apparently, the smallest k for which the answer to the above problem is ‘yes’ is the size of the minimum connected dominating set of our multilayer network.
From the perspective of computational complexity, the two problems are equivalent (see item (b1) above): With the use of binary search, we need to solve the decision version for different values of k, i.e., which is a polynomial time of searches.
[STEP 2. Proving that the decision problem belongs to the NP class.]
The MULTILAYER CONNECTED DOMINATING SET PROBLEM is clearly in NP, as given a graph , a set of nodes, and a number k, we can test if S is a connected dominating set of of size k or less by first checking if its cardinality is less than or equal to k and then checking if every node in is either in S or adjacent to a node in S. This process clearly takes polynomial time, i.e., . Should we wish to check whether S is actually connected, we can resort to any polynomial-time algorithm, e.g., breadth/depth first search. Therefore, the MULTILAYER CONNECTED DOMINATING SET PROBLEM is indeed in NP.
[STEP 3. Proving that the decision problem contains a known NP-complete problem as a special case.]
The third step of our proof involves proving that the MULTILAYER CONNECTED DOMINATING SET PROBLEM contains as a special case the problem of finding a connected dominating set for a single layer graph
—a known NP-complete problem ([
25] p. 190, Problem GT2).
We state the following corollary:
Corollary 1. From ([5] Theorem 1), it follows immediately that if we wish to connect with each other two connected dominating sets of two separate graphs by adding a single edge among the two graphs, then we will need at most 2 more nodes (one from each separate graph) to be included in the single “united” connected dominating set. We assume the existence of a single layer graph , and we construct a multilayer graph with two layers, where and is any non-empty set of interlayer edges between and . Then, we erase all but one interlayer edges from . We assume that this edge is the with and .
Then, the problem of finding whether the graph contains a connected dominating set of size is in an obvious one-to-one correspondence with the problem of finding whether the graph contains a connected dominating set of size . Note here, that there is no need—from the computational complexity perspective—for the size- connected dominating set of to be a double-size clone of the size- connected dominating set of , and thus the two problems do not need to be an exact duplicate of each other.
Thus, the MULTILAYER CONNECTED DOMINATING SET problem is NP-complete. □
4. Performance Evaluation
Competing Algorithms. We compare the proposed algorithms, namely
and
, but in order to explain the usefulness of their pruning procedures, we develop and include in our comparison their annotated with an asterisk version of them, namely
and
; these versions are simply the same algorithms but without activating the pruning procedure. Solely for illustrative purposes we include the experimentation, and
algorithm which constructs minimum but
unconnected ; we proved in [
5] that any (unconnected)
of size
can be turned into a
by adding
additional nodes in the
in the worst case.
Table 1 summarizes the competing algorithms.
Simulation testbed. Due to the lack of available, real military networks, and the inability (The requirement of modern battlefields is to able to operate ad hoc networks consisting of an order of magnitude more nodes; for instance a battalion would need a thousand nodes. e.g.,
https://www.darpa.mil/news-events/2013-04-30 (accessed on 15 May 2022)) of wireless testbeds and emulation environments for ad hoc networks to deal with several hundreds of nodes, we developed a generator for multilayer networks in MATLAB. The details of our generator can be found in [
6,
23], and here we present its basic features. The construction of a multilayer network is driven by the average node degree, by the nodes’ number per layer (i.e., the so-called layer size), and the number of layers. The interconnection of the layers is driven by: (a) the number of a node’s links towards nodes in different layers, and (b) the distribution of the interconnections to the nodes within a particular layer. We apply the
Zipfian distribution to our connectivity generator. Skewness is managed by parameter
. We make use of four distinct
Zipfian distributions, one per parameter of interest:
: to generate the frequency of appearance of highly interconnected nodes,
: to choose how frequently a specific layer is selected,
: to choose how frequently a specific node is selected in a specific layer.
: to choose how uniformly the energy is distributed in the nodes.
We call these parameters as the topology skewness, and represent it as a sequence of four floats, meaning that , , and (which are the default settings we used to create the datasets).
Performance measures. The competitors are compared in terms of the cardinality of the
; apparently an algorithm is more efficient than another, if it generates a
having smaller cardinality [
16]. Moreover, an algorithm that establishes a (per node) relay set with larger residual energy is naturally considered to be more efficient in terms of energy than another algorithm whose per node relay set has less residual energy.
Datasets. We created networks which vary with respect to the topology density, the network diameter, the number of network layers and their size. The topology density’s impact on the performance is evaluated with 4-layer networks. Each layer consists of 50 nodes, and the mean node degree is 3, or 6, or 10, or 16, or 20. The network diameter’s impact on the performance is evaluated with 4-layer networks as well. Each layer consists of 50 nodes, and the mean node degree is 6. The diameter of each layer is 3, or 5, or 8, or 12, or 17. The number of layers’ impact is examined in networks with 2, or, 3, or 4, or 5, or 7 layers. Each layer consists of 50 nodes, and the mean node degree is 6. The increase in the layer size’s impact is evaluated with 4-layer networks. The “base” layer consists of 50 nodes, and each next layer is larger than the previous by 10%, or 20%, or 30%, or 50%, or 70%. The mean node degree in each layer is 6.
Table 2 records all the independent parameters.
4.1. Experimental Evaluation
Each experiment was repeated 5 times. The variation around the mean was so negligible that the error bars are hardly recognizable in the plots. We conduct experiments with , , , parameters into (Medium skewness), and (Low skewness), and (High skewness) setting, respectively.
4.1.1. Impact of Topology Density
Firstly, we consider the impact of topology density on the performance of each competitor. In
Figure 2 we evaluate, for medium skewness, the
per layer size of the
. The main conclusion is that the size of the CDS is practically a decreasing function of the node density. This happens because the higher the network density is, the greater the coverage capability of the network nodes becomes, and therefore the size of the
gets smaller. In the case we succeed medium skewness, there is no clear winner between
and
as the topology becomes denser (degree ≥ 6) and both competitors present similar performance (<10% variance). The explanation is that in such topologies, there exist multiple redundant paths towards nodes, and thus both pruning mechanisms work equally well. On the contrary, in sparse topologies (degree
)
is up to 15% more efficient. This is due to the fact that during the pruning process, the redundant paths are less in sparse topologies, and their discovery requires knowledge of the topology further away than 2-hops, which is beyond the capabilities of localized algorithms deployed in wireless ad hoc networks. Apparently, the centralized nature of
provides a clear advantage, since its pruning task has a broader overview of the topology. If we exclude the pruning task, then
and
present similar performance (less than 10% variance) when degree ≤10, and the performance of the latter is up to 15% better to the former when degree >10. However, these results are not good news, because both algorithms do not perform well in terms of the—
per layer—CDS size; i.e., the—
per layer—
size is up to 98% of that of the total number of nodes in that layer. This is considered natural in multilayer networks when the traditional methods are used (2-hop neighborhood coverage).
redundancy justifies the use of the pruning mechanism (up to
and
size reduction for
and
, respectively, in this particular case).
We expanded our experiments in case of low skewness. The results, depicted in
Figure 3 show that there are no important differences regarding the efficiency, between
and
, when topology becomes denser (degree ≥ 6). As mentioned above, this happens because pruning mechanisms work well, when nodes have multiple ways to connect with one another. When degree = 3 (sparse topologies),
is about 10% less efficient than
, something which is justified due to the centralized control of the
. In this case, the reduction size of
is about 90% for
algorithm and up to 88%.
In case of high skewness (see
Figure 4), when degree ≥ 10, both the proposed algorithms behaves in a quite similar way (less than 10% variance), too, regarding the size of
. Here,
outperforms
, due to the centralized control of the first one which makes the procedure of finding surplus paths easier inside the Multilayer network. Examining the case when topology is sparse (degree = 3), we see that
is less efficient than the other pruning proposed algorithm, bearing in mind that due to the lack of enough connections, it is more difficult for a distributed algorithm to find minimum
. Also, when degree = 6,
continues to outperform
, but both algorithms create
with smaller size than the above implementations do. So, in this case the efficiency of the proposed algorithms are up to 86% and up to 82% for both
and
, respectively.
So, as it is also shown in
Figure 5 which shows CDS sizes aggregated over all layers, for all the parameters tested, the results are quite similar regarding both
and
algorithm, with the corresponding results with parameters
to be a little more efficient, probably due to the more uniform distribution this case implements.
4.1.2. Impact of Network Diameter
In
Figure 6,
Figure 7 and
Figure 8, we evaluate the effect of the network diameter in the size of the
. The main conclusion is that as the network diameter increases the size of the resulting
increases, and this observations is valid for all competitors. In case of medium skewness (
Figure 6), the diameter increases and also the topology gets sparser. So, we have fewer, longer (in hops), and less redundant paths. In that way, the selection of 1-hop neighbor nodes that cover the
neighborhood of a particular node requires more 1-hop neighbors. Now, in terms of the competitors’ performance, we see that in bushy topologies (diameter ≤ 5)
presents up to
smaller
compared to
. This gain is attributed to the employment of the
by
and which helps in getting a better pruning. On the other hand, in bushy topologies an unfortunate erase from the
of a strategically located
node will probably result in keeping a lot of (practically “useless”)
nodes just to ensure connectivity. When diameter
or diameter
the competitors have similar performance (less than 10% variance). As expected, in long and skinny topologies (diameter
)
outperforms
by
, due to its centralized nature. Examining the pruning-free versions of the competitors, we see that both of them practically exhibit the worst-case behaviour, i.e., almost all nodes are selected as
nodes; the performance of the pruning mechanism for
and
regarding the
size reduction is up to
and
, respectively.
In case of low skewness as it is illustrated in
Figure 7, we can also say that when diameter ≤ 5,
algorithm outperforms FAST-CMDSM and when diameter
or diameter
, both proposed algorithms have similar performance (less than 10% variance). Finally, we see that for diameter = 17,
has a better performance than
, due to the benefits of its centralized form, in long paths. So, in this case,
reduction is up to 85% for
and 81% for
.
Finally, when the interconnectivity generator parameters are
(high skewness), as it is depicted in
Figure 8, we observe a general increase in
size, due to the fact that the degrees of the nodes have a great variance in this case and as a result, more nodes needed to join the
. When diameter
,
has better performance than the other proposed algorithm, due to the fact that we have smaller paths to check and as a result the distributed algorithm can discover easier the redundant paths (2-hop coverage). When diameter
, or diameter
,
starts to have a better performance, as it creates
with smaller size. This is expected, since the centralized control of this algorithm contributes efficiently in finding the redundant paths. The longer the diameter is, the better performance
has as it is shown in
Figure 8. To sum up, in this case,
can achieve up to 81% reduction in the size of total
, while
can achieve 79%. As a summary, we provide
Figure 9 to show average performance of the competitors.
4.1.3. Impact of the Number of Layers
We investigated the impact of the network layers’ number on the competitors. In
Figure 10 we show the
per layer CDS cardinality for the competing algorithms (for medium skewness). The first observation we make is somewhat counter-intuitive: we see that the
per layer CDS cardinality is independent on the number of layers(!) even though we would expect to be a decreasing function of the number of layers, because when a multilayer network has more layers, then it will (most probably) have more connections among layers (i.e., interlayer links), and thus the network will become more dense. So, even though we expected an increase in the coverage capability of the nodes, this does not happen, and it is attributed to the generic topology of the network. Turning now our focus on the competitors, we observe that with 5 or less layers both
and
FAST-CMDSM perform very good (10% or less variance). However,
is the best of the two presenting a
better performance. Overall, the obtained results are consistent with our earlier which state that both competitors perform very good in dense networks. In general, the main reason for
CCDS’ superior performance with respect to
FAST-CMDSM’ s performance is the very effective pruning mechanism. When looking at the version of these algorithms without the pruning mechanism, we see that as expected they perform poor; in particular the performance of the pruning mechanism for
CCDS and
FAST-CMDSM regarding the
size reduction is up to
and
, respectively.
Next, we present the case where the parameters of the interconnectivity generator are:
(low skewness). We see in
Figure 11, that both the proposed algorithms achieve similar performance, with the
algorithm to be a little bit more efficient (less than 10% variance). The total reduction in
size is up to 80% for
and up to 78% for
. The last experiment in this section is conducted by setting the respective interconnectivity generator variables to:
(high skewness). In this case, when number of layers is less than 4,
outperforms
, while when the number of layers is greater than 4, then the two proposed algorithms are barely equally efficient, as it is shown in
Figure 12. Specifically, the total reduction provided by this experiment is up to 74% for CCDS and up to 73% for
(1% variance). In
Figure 13 we show the competitors average performance.
4.1.4. Impact of Layer’s Size Increase
Here we consider the impact of layer’s size increase on the competitors’ performance; we evaluate the
per layer size of the
for medium skewness, and depict the results in
Figure 14. A first, generic observation is that the cardinality of CDS increases with increasing layer size. This is easily explained by the fact that the as the size of each layer increases, so does the need for more nodes to act as connectors, and consequently we get a larger CDS. Looking at the performance of the competitors, we note that an increase in the size of each subsequent layer by
or less results in having
to outperform
with a margin from 11% up to
. The basic reason behind that is the dense topology, with the consequence that many redundant paths remain within the vicinity of
(i.e., 2-hop), and therefore the pruning process eliminates many redundant dominators. On the contrary, an increase in the size of each subsequent layer by
or more results in having the centralized
outperform
from
up to
. This is expected, since the large difference in the cardinality of the layers implies a large number of interlayer links, and therefore the calculation of the redundant paths by the pruning process requires a broader/global view of the topology, which is only available to the centralized
FAST-CMDSM algorithm and not the distributed
algorithm. As a last comment to this experiment, we see that the versions without pruning of the algorithms select almost all nodes as dominators; in particular the performance of the pruning mechanism for
and
regarding the
size reduction is up to
and
, respectively.
Conducting the experiment by changing the set of variables in the interconnectivity generator to
(almost uniform distribution), we observe that
is the champion algorithm, because of the dense topologies formed, as it is shown in
Figure 15. In this case,
achieves 82% reduction in the total
size, while
achieves 80%. The last experiment in this section is conducted by setting the respective interconnectivity generator parameters to:
and the results are presented in
Figure 16. In this case, we have a barely arbitrarily-formed distribution (high skewness). We see that while increasing the number of nodes, set in every layer, the
algorithm remains our best option, as it is justified above. In this case,
achieves 76% reduction in the total
size, while
achieves 75%.
Comparing the experiments, done, by changing the values in variables of skewness, we conclude that having a more uniform distribution (Low Skewness) is the best scenario, in which, our algorithms achieves their highest efficiency. This happens because this type of distribution, normalizes well the degree of every node in every layer, which means less nodes are important for the coverage of the network and this results in smaller size. On the other hand, when we have high skewness, nodes are arbitrarily connected which means, more nodes in total are needed in order to cover the whole network properly. Furthermore, in every case, is the more efficient algorithm to use, bearing in mind that in every section, it provides better reduction from , except for the one in which we examine low skewness and our variables are set to 0.5 in which outperforms (3% variance).
4.1.5. Energy Awareness of the Competing Algorithms
We repeated all experiments taking now into account the residual energy of each node, and we show here the obtained results which concern the aggregated over all network layers performance of the competitors. In
Figure 17, we report the results for medium skewness and we see that
selects the most energy efficient
in, almost, any case, followed by
. We end up in the same conclusion about
algorithm’s energy consumption regarding both the experiments of low and high skewness, as it is depicted in both
Figure 18 and
Figure 19, respectively.
4.1.6. Results’ Summary
In
Table 3 we provide a summary of
average performance gain (percentage-wise) over the second best performing distributed algorithm across the independent parameter space.