The Energy Efficiency of Heterogeneous Cellular Networks Based on the Poisson Hole Process
Abstract
1. Introduction
1.1. Related Works
1.2. Paper Organization
2. System Model
3. Energy Efficiency Analysis
3.1. Coverage Probability
3.2. Average Achievable Rate
3.3. Energy Efficiency
4. Energy Efficiency Optimization
| Algorithm 1: Quadratic interpolation method specific algorithm steps |
| Input: Output: the minimum point 1: is defined, where x represents the optimization variable, and the optimization interval [a, b] is given, where , , and the calculation accuracy is . 2: Given three points , , , where , , , the corresponding functions , , and are reckoned. 3: The minimum point of the quadratic interpolation function and its corresponding function values and are calculated, where and . 4: If , the sizes of and are compared, if , go to step 5; otherwise, go to step 6; otherwise go to step 7. 5: If , then , , , and , and go to step 3; otherwise, and , and go to step 3 and the minimum point of the quadratic interpolation function can be calculated in the new search interval. 6: If , then , , , , and go to step 3; otherwise, , , and go to step 3 and the minimum point of the quadratic interpolation function can be calculated in the new search interval. 7: The iteration is stopped and the minimum value is outputted; If , ; otherwise, . |
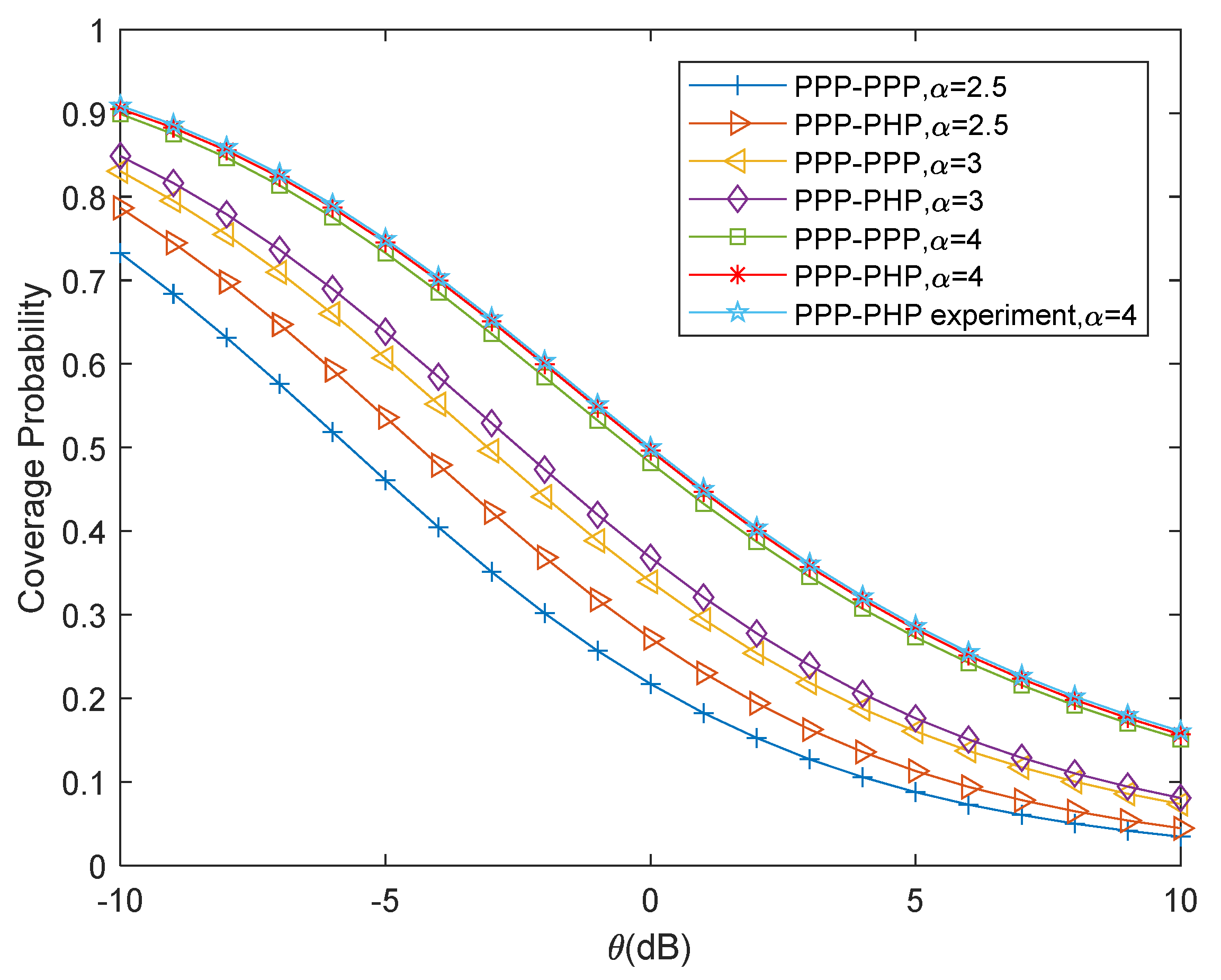
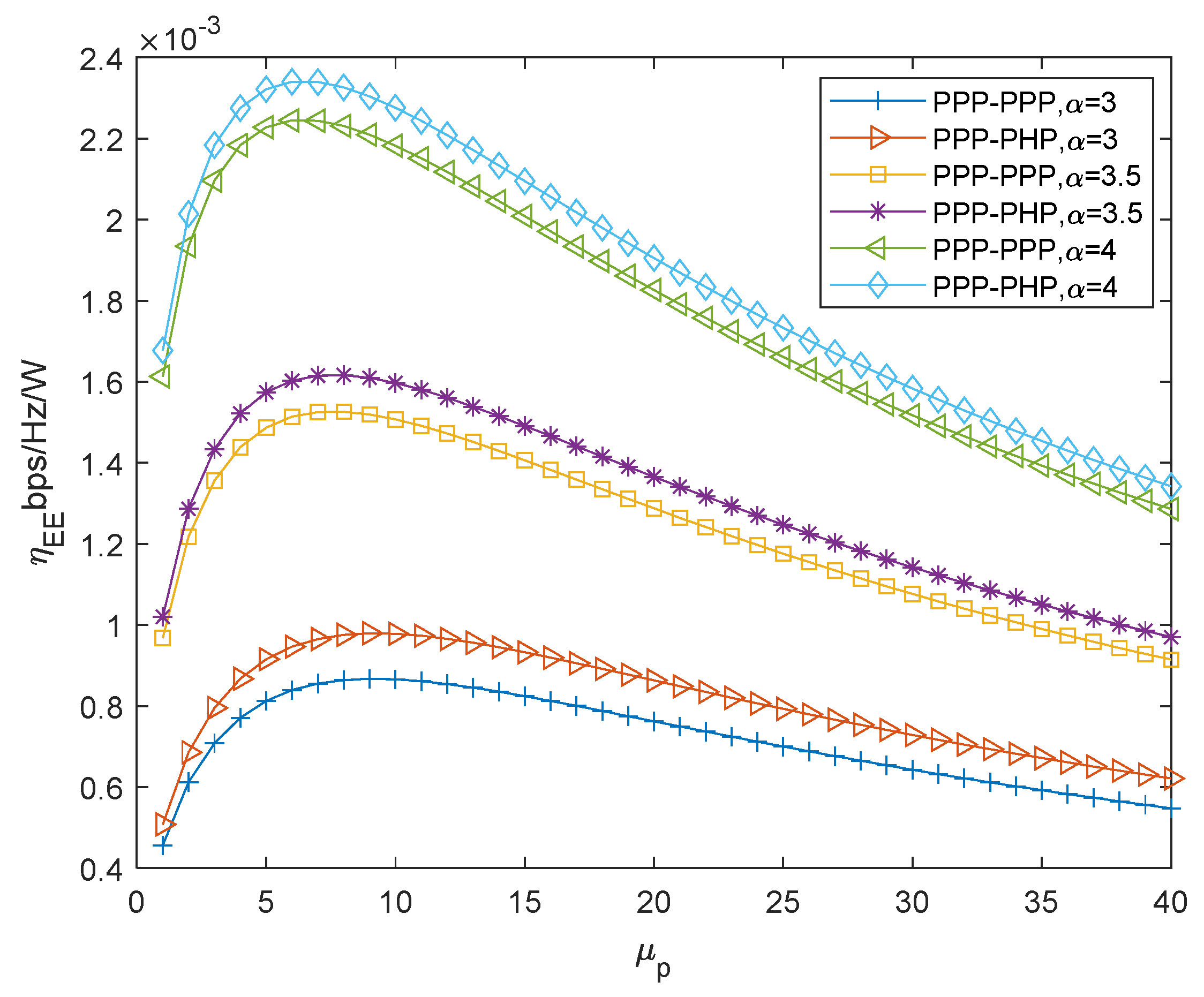
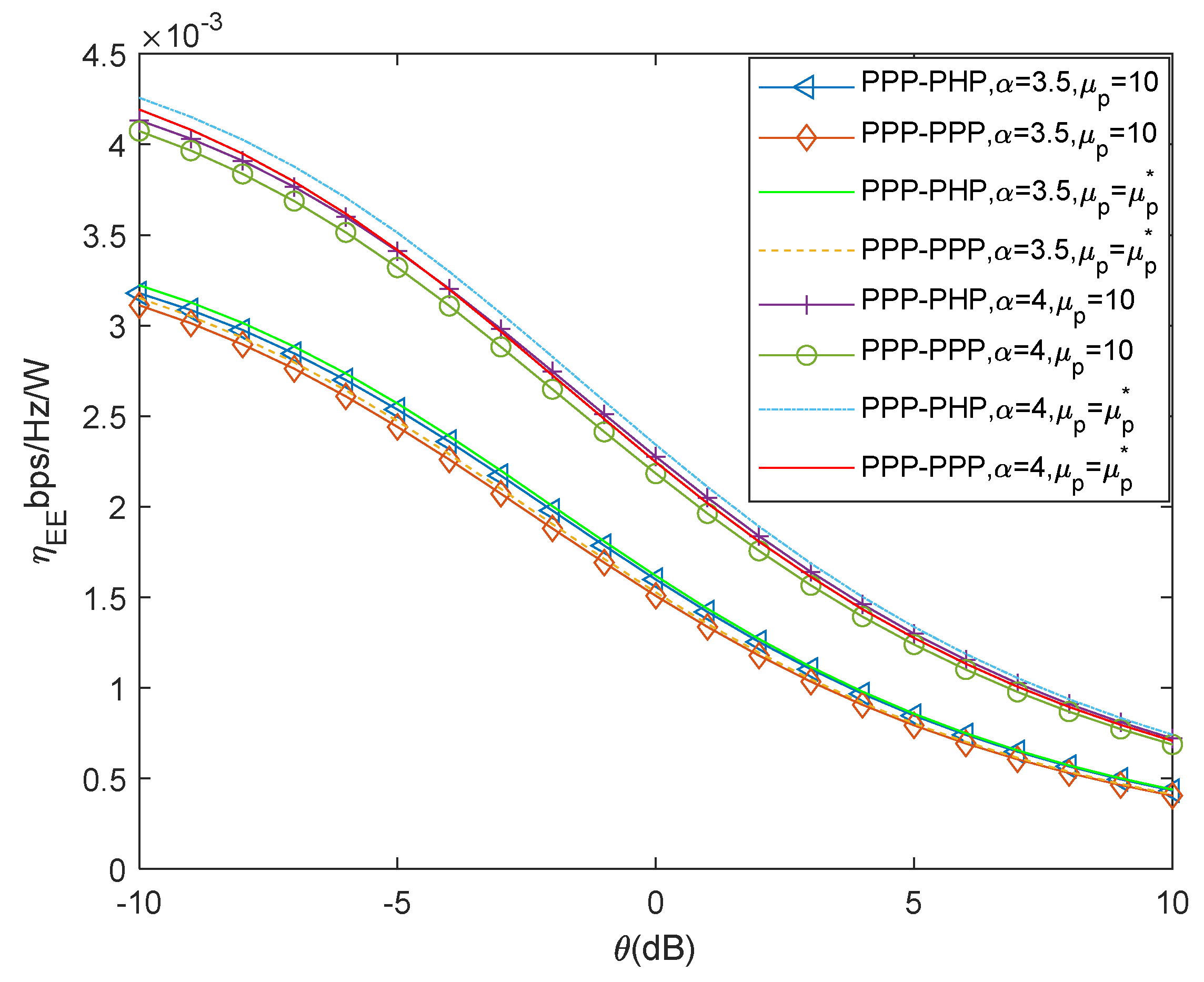
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khandekar, A.; Bhushan, N.; Ji, T.; Vanghi, V. LTE-Advanced: Heterogeneous Networks. In Proceedings of the 2010 European Wireless Conference (EW), Lucca, Italy, 12–15 April 2010. [Google Scholar]
- Kim, R.Y.; Kwak, J.S.; Etemad, K. WiMAX Femtocell: Requirements, Challenges and Solutions. IEEE Commun. Mag. 2009, 47, 84–91. [Google Scholar] [CrossRef]
- Andreev, S.; Petrov, V.; Dohler, M.; Yanikomeroglu, H. Future of Ultra-Dense Networks Beyond 5G: Harnessing Heterogeneous Moving Cells. IEEE Commun. Mag. 2019, 57, 86–92. [Google Scholar] [CrossRef]
- Gao, M.J.; Li, J.; Jayakody, D.N.K.; Chen, H.; Li, Y.H.; Shi, J.L. A Super Base Station Architecture for Future Ultra-Dense Cellular Networks: Toward Low Latency and High Energy Efficiency. IEEE Commun. Mag. 2018, 56, 35–41. [Google Scholar] [CrossRef]
- Wu, Y.; Qian, L.P.; Yang, X.; Zheng, J.; Shen, X. Dual-Connectivity Enabled Traffic Offloading via Small Cells Powered by Energy-Harvesting. In Proceedings of the IEEE Global Communications Conference, Singapore, 4–8 December 2017. [Google Scholar]
- Zhu, X.; Shen, X.; Zeng, F.; Vincent, H.; Dong, W.; Chen, W.; Li, K. Spectrum Resource Sharing in Heterogeneous Vehicular Networks: A Noncooperative Game-Theoretic Approach with Correlated Equilibrium. IEEE Trans. Veh. Technol. 2018, 67, 9449–9458. [Google Scholar]
- Slamnik, N.; Oki, A.; Muovi, J. Conceptual Radio Resource Management Approach in LTE Heterogeneous Networks using Small Cells Number Variation. In Proceedings of the IEEE XI International Symposium on Telecommunications, Sarajevo, Bosnia and Herzegovina, 24–26 October 2016. [Google Scholar]
- Kure, E.H.H.; Engelstad, P.; Maharjan, S.; Gjessing, S.; Zhang, Y. Distributed Uplink Offloading for IoT in 5G Heterogeneous Networks under Private Information Constraints. IEEE Internet Things J. 2019, 6, 6151–6164. [Google Scholar] [CrossRef]
- Vilgelm, M.; Linares, S.R.; Kellerer, W. Dynamic Binary Countdown for Massive IoT Random Access in Dense 5G Networks. IEEE Internet Things J. 2019, 6, 6896–6908. [Google Scholar] [CrossRef]
- Wang, C.X.; Haider, F.; Gao, X.; You, X.H.; Yang, Y.; Yuan, D.; Aggoune, H.; Haas, H.; Fletcher, S.; Hepsaydir, E. Cellular Architecture and Key Technologies for 5G Wireless Communication Networks. IEEE Commun. Mag. 2014, 52, 122–130. [Google Scholar] [CrossRef]
- Hossain, E.; Rasti, M.; Tabassum, H.; Abdelnasser, A. Evolution Toward 5G Multi-tier Cellular Wireless Networks: An Interference Management Perspective. IEEE Wirel. Commun. 2014, 21, 118–127. [Google Scholar] [CrossRef]
- Li, Y.Z.; Zhang, Y.; Luo, K.; Jiang, T.; Li, Z.; Peng, W. Ultra-Dense HetNets Meet Big Data: Green Frameworks, Techniques, and Approaches. IEEE Commun. Mag. 2018, 56, 56–63. [Google Scholar] [CrossRef]
- Wu, Y.; Qian, L.P.; Zheng, J.C.; Zhou, H.B.; Shen, X.S. Green-Oriented Traffic Offloading through Dual Connectivity in Future Heterogeneous Small Cell Networks. IEEE Commun. Mag. 2018, 56, 140–147. [Google Scholar] [CrossRef]
- Chen, G.; Qiu, L.; Chen, Z. Area spectral efficiency analysis of multi-antenna networks modeled by Ginibre point process. IEEE Wirel. Commun. Lett. 2017, 7, 6–9. [Google Scholar] [CrossRef]
- Zhou, Y. Simulation and Analysis of 5G Network Performance Based on Ginibre Point Process. Master’s Thesis, Shanghai Jiaotong University, Shanghai, China, 2019. [Google Scholar]
- Chen, C.; Elliott, R.C.; Krzymien, W.A. Empirical distribution of nearest-transmitter distance in wireless networks modeled by Matérn hard core point processes. IEEE Trans. Veh. Technol. 2018, 67, 1740–1749. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Q. Modeling and analysis of small cells based on clustered stochastic geometry. IEEE Commun. Lett. 2017, 21, 576–579. [Google Scholar] [CrossRef]
- Afshang, M.; Saha, C.; Dhillon, H.S. Nearest-neighbor and contact distance distributions for Matern cluster process. IEEE Commun. Lett. 2017, 21, 2686–2689. [Google Scholar] [CrossRef]
- Afshang, M.; Dhillon, H.S. Poisson cluster process based analysis of HetNets with correlated user and base station locations. IEEE Trans. Wirel. Commun. 2018, 17, 2417–2431. [Google Scholar] [CrossRef]
- Haenggi, M. User point processes in cellular networks. IEEE Wirel. Commun. Lett. 2017, 6, 258–261. [Google Scholar] [CrossRef]
- Flint, I.; Kong, H.B.; Privault, N. Analysis of heterogeneous wireless networks using Poisson hard-core hole process. IEEE Trans. Wirel. Commun. 2017, 16, 7152–7167. [Google Scholar] [CrossRef]
- Deng, N.; Zhou, W.; Haenggi, M. Heterogeneous cellular network models with dependence. IEEE J. Sel. Areas Commun. 2015, 33, 2167–2181. [Google Scholar] [CrossRef]
- Haenggi, M. The mean interference-to-signal ratio and its key role in cellular and amorphous networks. IEEE Wirel. Commun. Lett. 2014, 3, 597–600. [Google Scholar] [CrossRef]
- Ganti, R.K.; Haenggi, M. SIR asymptotics in general cellular network models. In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 14–19 June 2015. [Google Scholar]
- Haenggi, M.; Ganti, R.K. Asymptotics and Approximation of the SIR distribution in general cellular networks. IEEE Trans. Wirel. Commun. 2016, 15, 2130–2143. [Google Scholar]
- Adam, A.B.M.; Muthanna, M.S.A.; Muthanna, A.; Nguyen, T.N.; El-Latif, A.A.A. Toward Smart Traffic Management With 3D Placement Optimization in UAV-Assisted NOMA IIoT Networks. IEEE Trans. Intell. Transp. Syst. 2022, 1–11. [Google Scholar] [CrossRef]
- Chaaf, A.; Muthanna, M.; Muthanna, A.; Alhelaly, S.; Elgendy, I.A.; Iliyasu, A.M.; El-Latif, A.A.A. Energy-Efficient Relay-Based Void Hole Prevention and Repair in Clustered Multi-AUV Underwater Wireless Sensor Network. Secur. Commun. Netw. 2021, 2021, 9969605. [Google Scholar] [CrossRef]
- Rafiq, C.; Ping, W.; Min, W.; Muthanna, M.S.A. Fog Assisted 6TiSCH Tri-Layer Network Architecture for Adaptive Scheduling and Energy-Efficient Offloading Using Rank-Based Q-learning in Smart Industries. IEEE Sens. J. 2021, 21, 25489–25507. [Google Scholar] [CrossRef]
- D’Andreagiovanni, F.; Mannino, C.; Sassano, A. GUB Covers and Power-Indexed Formulations for Wireless Network Design. Manag. Sci. 2013, 59, 142–156. [Google Scholar] [CrossRef]
- Lorincz, J.; Matijevic, T. Energy-efficiency analyses of heterogeneous macro and micro base station sites. Comput. Electr. Eng. 2014, 40, 330–349. [Google Scholar] [CrossRef]
- Arshad, M.W.; Vastberg, A.; Edler, T. Energy efficiency improvement through pico base stations for a green field operator. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Paris, France, 1–4 April 2012. [Google Scholar]
- Luo, Y.; Shi, Z.; Bu, F. Joint optimization of area spectral efficiency and energy efficiency for two-tier heterogeneous ultra-dense networks. IEEE Access 2019, 7, 12073–12086. [Google Scholar] [CrossRef]
- Dong, X.; Zheng, F.C.; Zhu, X.; O’Farrell, T. On the Local Delay and Energy Efficiency of Clustered HetNets. IEEE Trans. Veh. Technol. 2019, 68, 2987–2999. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, X.; Qian, Z.H. Energy-Efficient Small Cell Cooperation in Ultra-Dense Heterogeneous Networks. IEEE Commun. Lett. 2019, 23, 1648–1651. [Google Scholar] [CrossRef]
- Lorincz, J.; Bogarelli, M. Heuristic approach for optimized energy savings in wireless access networks. In Proceedings of the 18th International Conference on Software, Telecommunications and computer networks (SoftCOM 2010), Dubrovnik, Croatia, 23–25 September 2010. [Google Scholar]
- Lorincz, J.; Capone, A.; Begušić, D. Heuristic Algorithms for Optimization of Energy Consumption in Wireless Access Networks. KSII T Internet Inf. 2011, 5, 626–648. [Google Scholar] [CrossRef]
- Lorincz, J.; Matijevic, T.; Petrovic, G. On interdependence among transmit and consumed power of macro base station technologies. Comput. Commun. 2014, 50, 10–28. [Google Scholar] [CrossRef]
- Dataesatu, A.; Boonsrimuang, P.; Mori, K.; Boonsrimuang, P. Energy Efficiency Enhancement in 5G Heterogeneous Cellular Networks Using System Throughput Based Sleep Control Scheme. In Proceedings of the 22nd International Conference on Advanced Communication Technology (ICACT), Macau, China, 23–25 November 2020. [Google Scholar]
- Li, Y.; Zhang, H.; Wang, J.; Cao, B.; Liu, Q.; Daneshmand, M. Energy-Efficient Deployment and Adaptive Sleeping in Heterogeneous Cellular Networks. IEEE Access 2019, 7, 35838–35850. [Google Scholar] [CrossRef]
- Shuvo, M.S.A.; Munna, A.R.; Adhikary, T.; Razzaque, M. An Energy-Efficient Scheduling of Heterogeneous Network Cells in 5G. In Proceedings of the International Conference on Sustainable Technologies for Industry 4.0 (STI), Dhaka, Bangladesh, 24–25 December 2019. [Google Scholar]
- Wang, Y.; Huang, C. Efficient management of interference and power by jointly configuring ABS and DRX in LTE-A HetNets. Comput. Netw. 2018, 150, 15–27. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Katsinis, G.K.; Filios, A.; Papavassiliou, S. On the problem of optimal cell selection and uplink power control in open access multi-service two-tier femtocell networks. In Proceedings of the International Conference on Ad-hoc Networks & Wireless, Benidorm, Spain, 22–27 June 2014. [Google Scholar]
- Yang, J.; Tan, Z.; Hu, H.; Chen, Y.H. Energy-efficient Microcell Base Station Power Control in Heterogeneous Cellular Network. In Proceedings of the IEEE International Conference Communication Technology, Chengdu, China, 27–30 October 2017. [Google Scholar]
- Yang, J.; Pan, Z.; Xu, H.; Hu, H. Joint Optimization of Pico-Base-Station Density and Transmit Power for an Energy-Efficient Heterogeneous Cellular Network. Future Internet 2019, 11, 208. [Google Scholar] [CrossRef]
- Chen, Y.H.; Guo, L.L.; Zhang, S.B. Energy efficiency optimization of heterogeneous cellular networks based on transmitting power of pico base station. J. Comput. Appl. 2020, 40, 1115–1118. [Google Scholar]
- Haenggi, M. ASAPPP: A simple approximative analysis framework for heterogeneous cellular networks. In Proceedings of the Workshop on Heterogeneous Small Cell Networks (HetSNets’14), Austin, TX, USA, 12 December 2014; Available online: http://www3.nd.edu/~mhaenggi/talks/hetsnets14.pdf (accessed on 26 January 2023).
- Bao, Z.Y.; Yang, J.; Hu, H. Analysis of SIR gain and approximate coverage of heterogeneous cellular networks based on Poisson hole process modeling. J. Nanjing Univ. Posts Telecommun. (Nat. Sci. Ed.) 2018, 38, 35–40. [Google Scholar]
- Kendall, D.; Mecke, W.S.; Stoyan, J. Stochastic Geometry and Its Applications, 2nd ed.; Wiley: New York, NY, USA, 1995; pp. 25–58. [Google Scholar]
- Jo, H.S.; Sang, Y.J.; Xia, P. Heterogeneous cellular networks with flexible cell association: A comprehensive downlink SINR analysis. IEEE Trans. Wirel. Commun. 2012, 11, 3484–3495. [Google Scholar] [CrossRef]
- Hamdi, K.A. A useful lemma for capacity analysis of fading interference channels. IEEE Trans. Commun. 2010, 58, 411–416. [Google Scholar] [CrossRef]
- Wei, H.; Deng, N.; Zhou, W. Approximate SIR analysis in general heterogeneous cellular networks. IEEE Trans. Commun. 2016, 64, 1259–1273. [Google Scholar] [CrossRef]
- Dhillon, H.S.; Kountouris, M.; Andrews, J.G. Downlink MIMO hetNets: Modeling, ordering results and performance analysis. IEEE Trans. Wirel. Commun. 2013, 12, 5208–5222. [Google Scholar] [CrossRef]
- Liao, L.F.; Ouyang, Z.Y. Beetle antennae search based on quadratic interpolation. Appl. Res. Comput. 2021, 38, 745–750. [Google Scholar]


| Notation | Definition |
|---|---|
| Deployment density of the MBS/PBS | |
| Point process for modeling MBS/PBS location | |
| Given threshold of the BS | |
| MBS/PBS transmit power | |
| The probability that a typical user is associated with the MBS/PBS | |
| r | Repulsion radius |
| PCm, PCp | The coverage probability of the MBS/PBS |
| The distance distribution between the service MBS/PBS and the typical user | |
| The average achievable rate of the typical user associated with the MBS/PBS | |
| The number of users served by the MBS/PBS | |
| Pm0, Pp0 | MBS/ PBS static power consumption |
| Energy efficiency |
| Parameter Symbol | Parameter Description | Parameter Value |
|---|---|---|
| Deployment density of the MBS | 10−2 m−2 | |
| Deployment density of the PBS | 0.1 m−2 | |
| Given threshold of the BS | 0 dB | |
| MBS transmit power | 40 W | |
| PBS transmit power | 10 W | |
| r | Repulsion radius | 2 m |
| Pm0 | MBS static power consumption | 1000 W |
| Pp0 | PBS static power consumption | 50 W |
| Running Time | Iterates Times | |
|---|---|---|
| The golden section method [43] | 20.37 s | 32 |
| The quadratic interpolation algorithm | 10.88 s | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Xun, L.; Zhang, S. The Energy Efficiency of Heterogeneous Cellular Networks Based on the Poisson Hole Process. Future Internet 2023, 15, 56. https://doi.org/10.3390/fi15020056
Chen Y, Xun L, Zhang S. The Energy Efficiency of Heterogeneous Cellular Networks Based on the Poisson Hole Process. Future Internet. 2023; 15(2):56. https://doi.org/10.3390/fi15020056
Chicago/Turabian StyleChen, Yonghong, Lei Xun, and Shibing Zhang. 2023. "The Energy Efficiency of Heterogeneous Cellular Networks Based on the Poisson Hole Process" Future Internet 15, no. 2: 56. https://doi.org/10.3390/fi15020056
APA StyleChen, Y., Xun, L., & Zhang, S. (2023). The Energy Efficiency of Heterogeneous Cellular Networks Based on the Poisson Hole Process. Future Internet, 15(2), 56. https://doi.org/10.3390/fi15020056






