Blockchain-Enabled Chebyshev Polynomial-Based Group Authentication for Secure Communication in an Internet of Things Network

Abstract

The utilization of Internet of Things (IoT) devices in various smart city and industrial applications is growing rapidly. Within a trusted authority (TA), such as an industry or smart city, all IoT devices are closely monitored in a controlled infrastructure. However, in cases where an IoT device from one TA needs to communicate with another IoT device from a different TA, the trust establishment between these devices becomes extremely important. Obtaining a digital certificate from a certificate authority for each IoT device can be expensive. To solve this issue, a group authentication framework is proposed that can establish trust between group IoT devices owned by different entities. The Chebyshev polynomial has many important properties, semigroup is one of the most important. These properties make the Chebyshev polynomial a good candidate for the proposed group authentication mechanism. The secure exchange of information between trusted authorities is supported by Blockchain technology. The proposed framework was implemented and tested using Python and deployed on Blockchain using Ethereum’s Goerli’s testnet. The results show that the proposed framework can reasonably use Chebyshev polynomials with degrees up to four digits in length. The values of various parameters related to Blockchain are also discussed to understand the usability of the proposed framework.

1. Introduction

The Internet of Things (IoT) plays an important role in many smart city applications, such as traffic management, public safety, environmental monitoring, smart parking, smart waste management, disaster management, and more. The IoT is crucial in many use cases in industrial IoT, such as asset management, inventory management, remote monitoring and control, supply chain management, smart manufacturing, and others [1]. Security is a significant challenge in the successful implementation of these IoT applications. The various security concerns in the IoT environment include identification, authentication, data integrity, trust, data confidentiality, access control, data privacy, and data availability. Although the generic IoT architecture addresses security concerns of perception, network, middleware, and application, trust and identity management are not given much consideration [2]. Most of the proposed security mechanisms are for IoT devices controlled by a single trusted authority (TA). However, in many use cases, the IoT device of one TA may need to communicate with the IoT device of another TA to carry out a coordinated task. A review study carried out by researchers [3] highlighted key parameters for a good authentication protocol. An authentication protocol for an IoT network should be lightweight, robust, have low overhead network traffic, have low computation cost, support the heterogeneity of the network, be scalable, and should include hardware security using physical unclonable functions (PUFs).

Keeping the suggested properties of an authentication protocol in mind, in this research, a group authentication framework to authenticate a group of IoT devices controlled by different TAs is presented. In the past, the Chebyshev polynomial has been used for public key cryptosystems and exhibits an important property of a semigroup. This property of the Chebyshev polynomial is utilized in the proposed authentication framework to authenticate the group of IoT devices. The smart contract of Blockchain technology is used for secure communication among different TAs in a distributed environment to facilitate Chebyshev polynomial-based group authentication. The presented group authentication framework provides a platform for the secure collaboration of different TAs and can help in developing future use cases of smart cities and Industrial IoT. In comparison with existing authentication protocols, the contributions of the proposed authentication scheme are as follows:

• Most authentication protocols are developed for individual device authentication and the same protocol is used for group authentication. The proposed authentication scheme is specifically proposed for group authentication.
• In the proposed scheme, the Chebyshev polynomial is used to create a shared secret so that the group can be authenticated without creating large overhead in network traffic. The Chebyshev polynomial has not been used earlier for group authentication for IoT devices.
• Blockchain technology is used to securely exchange short quick messages between various IoT devices of different entities located in different geographic locations.
• In the proposed scheme, a hardware-based identification PUF is employed.

The rest of the paper is organized as follows. A high-level overview of our system is presented in this Section 1. Section 2 discusses the work conducted by researchers in the related field. Section 3 explains the Chebyshev polynomial and its application in cryptography. In Section 4, the proposed group authentication framework is explained. In Section 5, a security analysis of the proposed authentication framework is carried out using informal security analysis methods. Section 6 discusses the analysis of the results. This section also presents results obtained by the deployment of smart contracts on Ethereum’s Goerli testnet. The paper concludes with some final remarks and future works in Section 7.

2. Related Work

Eavesdropping, malicious node injection, and distributed denial-of-service attacks are among the most common types of IoT attacks. According to the Kaspersky report [4], 1.51 billion IoT breaches were recorded between January and June 2021 using only the Telnet remote access protocol. Unsecure communications, insufficient authentication, and password hygiene are the most common reasons for IoT breaches. In the recent past, researchers have emphasized on authentication mechanisms of IoT devices. The related works section discusses the various authentication protocols for IoT devices proposed by researchers. In this section, the literature is reviewed in three parts, the first part discusses the individual authentication mechanisms for IoT devices, the second part discusses the group authentication methods, and the third part discusses the authentication methods that use Blockchain technology.

In one project, researchers presented an authentication mechanism for IoT devices and IoT servers using secure vaults. The proposed method works on multi-password shared secret-based mutual authentication [5]. Researchers in [6] used physical unclonable functions (PUFs) with elliptic curve cryptography (ECC) for device enrolment, authentication, decryption, and digital signature generation. In other research, a PUF was used along with two-factor authentication and IoT device wireless signal characteristics for secure authentication [7]. To safeguard IoT devices against cloning attacks, researchers proposed lightweight and privacy-preserving two-factor authentication for devices installed in open fields. In addition, PUFs have been utilized as authentication factors [8]. Researchers in [9] presented universal subscriber identity module (USIM)-based remote registration and group authentication for the 5G authentication and key agreement protocol (5G-AKA). Lightweight ECC was used in the proposed scheme in IoT devices in 5G cellular networks. A lightweight extensible authentication protocol (EAP) was used to develop authentication mechanisms for wireless network-connected IoT devices [10]. Researchers in [11] introduced an authentication entity between IoT sensors and receivers in a smart city environment. This authentication entity is responsible for authenticating all participating IoT devices before any data are transferred. A trusted authority-based lightweight authentication scheme using ECC and a secure element was proposed by researchers in [12] for an industrial IoT environment.

In this part of the related work, group authentication mechanisms proposed by various researchers are discussed. A group authentication scheme for IoT-enabled mobile ad hoc networks is proposed by the authors in [13]. The proposed group’s authentication mechanism is based on image hashing crosschecking of the identity image of a node that can be performed at the time of joining a group. Threshold cryptography-based group authentication (TCGA) [14] is proposed for authenticating a group of battery-constraint IoT nodes. In this mechanism, all IoT devices create their key pairs in the first phase and then a pseudorandom number is shared as a session secret in the group authentication phase. The combinatorial design is used to propose a group authentication mechanism with a fault-tolerant feature for IoT devices [15]. This authentication mechanism will operate even if some of the group members go down because of a fault. Elliptic curve cryptography and Shamir’s secret sharing-based group authentication technique were developed by researchers in [16] for resource-constraint IoT nodes. This technique can be used in both centralized and decentralized scenarios. PUF-based group authentication plus the key distribution protocol were developed using a factorial tree and the Chinese remainder theorem [17]. In this mechanism, each member of a group has to perform two encryption operations, one operation of decryption, four XOR operations, and three operations of hashing.

In this part of the related work, the use of Blockchain technology in IoT device authentication is discussed. Blockchain technology is used to store device identification information to facilitate IoT device authentication using a distributed ledger [18]. Blockchain technology is also used in registering and authenticating IoT devices in smart city applications. In this research, an API gateway is developed that can be used by IoT devices and the network gateway to sign, identify, and authorize messages [19]. The authors in [20] advocated against using centralized third-party-based identification mechanisms for IoT devices and advised to use of identity-based self-authentication algorithms using Blockchain technology. The proposed authentication method provides a cross-domain access control-oriented authentication mechanisms. Device authentication in smart dust IoT systems is difficult because it includes a very large number of devices. Hence, researchers in [21] proposed a lightweight Blockchain scheme by reorganizing the linear block structure of the conventional Blockchain. This binary tree-structured lightweight Blockchain helps to reduce the device authentication time by an average of 10%. In one research study [22], the authors proposed cluster-based authentication for IoT devices using Blockchain technology. In this authentication method, IoT devices are locally grouped and one cluster head is assigned to each group that leads the authentication mechanism for its group members. In contrast to this research, our proposed mechanism deals with global authentication of geographically distant or multi-entity controlled located IoT devices.

Researchers also used Blockchain technology with probabilistic models and random numbers to authenticate IoT devices [23]. In order to secure access to sensor data, a lightweight authentication architecture is proposed using private Blockchain technology [24]. In this method, a scalable and energy-efficient proof-of-authentication consensus algorithm is used. A cost-effective authentication mechanism using the modified Lamport–Merkle digital signature method is proposed for signature generation and verification in medical IoT for blockchain-based fog/cloud IoT network [25]. The study of related work shows that not enough work is carried out in group authentication using a decentralized approach, such as Blockchain technology. The existing group authentication protocols are proposed for the group of IoT devices that are controlled by a single entity and no framework is proposed for the scenario, such as a group of IoT devices controlled by different entities.

3. Chebyshev Polynomial

The Chebyshev polynomial introduced by mathematician Pafnuty Chebyshev is a sequence of an orthogonal polynomial and is related to trigonometric multi-angle formulae. Various characteristics of the Chebyshev polynomial make it useful in applications, such as an approximation of a function, polynomial solving, waveform synthesis, trigonometry identities, numerical analyses, and cryptography. The Chebyshev polynomial can be defined [26] as given in Equation (1).

$$T_n\left(x\right)=\left\{\begin{array}{cc}cos(n.arccos(x\left)\right)\hfill & \mathrm{if}x\in [-1,1]\hfill \\ cos\left(n\theta \right)\hfill & \mathrm{if}x=\cos \theta ,\theta \in [0,\pi ]\hfill \end{array}\right.$$

(1)

The Chebyshev polynomial can also be defined in recursive form [27], as shown in Equation (2).

$$T_{n+1}\left(x\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{n}=0\hfill \\ x\hfill & \mathrm{if}\mathrm{n}=1\hfill \\ 2x{T}_n\left(x\right)-T_{n-1}\left(x\right)\hfill & \mathrm{if}\mathrm{n}>=2\hfill \end{array}\right.$$

(2)

In both equations, n is a large integer and defines the degree of the Chebyshev polynomial. The variable x can be defined as a whole number integer if the Chebyshev value $T_n\left(x\right)$ is required to be a whole number. Alternatively, x can be defined as [−1, 1] to compute the Chebyshev values in the range of [−1, 1]. To understand more about Chebyshev polynomials, the first few polynomials are derived from Equation (2) and are shown in Equation (3) where n can be from 0 to ∞.

$$T_n\left(x\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{n}=0\hfill \\ x\hfill & \mathrm{if}\mathrm{n}=1\hfill \\ 2x^2-1\hfill & \mathrm{if}\mathrm{n}=2\hfill \\ 4x^3-3x\hfill & \mathrm{if}\mathrm{n}=3\hfill \\ 8x^4-8x^2+1\hfill & \mathrm{if}\mathrm{n}=4\hfill \\ 16x^5-20x^3+5x\hfill & \mathrm{if}\mathrm{n}=5\hfill \\ 32x^6-48x^4+18x^2-1\hfill & \mathrm{if}\mathrm{n}=6\hfill \\ \cdots \cdots \hfill \\ 1024x^{11}-2816x^9+2816x^7-1232x^5+220x^3-11x\hfill & \mathrm{if}\mathrm{n}=11\hfill \\ \cdots \cdots \hfill \end{array}\right.$$

(3)

The Chebyshev polynomial has many important properties, but for cryptography applications, the semigroup property is the most important one [27]. For two large integers, p, q, and one other integer, x, the semigroup property is given in Equation (4).

$$T_p\left(T_q\left(x\right)\right)=T_{pq}\left(x\right)$$

(4)

This semigroup property of the Chebyshev polynomial shown in Equation (4) can be used in cryptography to encrypt and decrypt the message m using ElGamal’s public key cryptosystem. To securely receive a message, Alice will generate a large integer ska, another number x, and compute $Cheb{y}_{Alice}=T_{ska}\left(x\right)$. $Cheb{y}_{Alice}$ is the Chebyshev polynomial value for Alice. For her, $(x,Cheb{y}_{Alice})$ will be her public key, whereas ska will act as her private key. Let us assume Bob wants to send a message (m) to Alice. He will generate a large integer skb, compute $Cheb{y}_{Bob}=T_{skb}\left(x\right)$, and then $T_{AliceBob}=T_{skb}\left(Cheb{y}_{Alice}\right)$. Bob will also compute M as $M=mX{T}_{AliceBob}$. Bob is now ready to send cipher text C to Alice in the form of $C=(Cheb{y}_{Bob},M)$. When Alice receives cipher text C, she computes $T_{AliceBob}$ using the formula $T_{AliceBob}=T_{ska}\left(Cheb{y}_{Bob}\right)$. She can then decrypt message m by dividing cipher text C with $T_{AliceBob}$. In the proposed group authentication mechanism, we used this Chebyshev polynomial-based cryptosystem along with Blockchain technology to facilitate the group authentication for IoT devices situated in different geographic locations under different authorities. Figure 1 shows the overall general working principle of the proposed scheme, which shows how the Chebyshev polynomial can be used for two entities. Authentication can be divided into two parts. Each entity, such as an IoT device, will use a Chebyshev polynomial with a pre-determined degree. In the first part, the degree of the Chebyshev polynomial is securely shared with corresponding entities using a smart contract as shown in Figure 1A. The second part deals with group authentication as shown in Figure 1B. The first entity computes Cheby_val1 using degree n1 previously sent to it and a generated variable var1. Entity 1 will send Cheby_val1 and var1 to the smart contract. Once the smart contract receives these values, it will send Cheby_val1 to entity 2. Upon receiving Cheby_val1, the entity will compute Cheby_val2 using Cheby_val1 and n2. Entity 2 will send Cheby_val2 to the smart contract where it will verify the group membership by comparing Cheby_val2 with its computation as shown in the figure. The same procedure can be carried out for more than two entities in a sequential manner.

4. The Proposed Group Authentication Framework

The proposed group authorization framework is inspired by the semigroup property of the Chebyshev polynomial and integrates the smart contract feature of Blockchain technology. Figure 2 shows the network diagram of one use case for the proposed group authentication framework. It shows the applicability of the security framework where there may be different industries/smart cities and some of their IoT devices want to communicate with each other. In the given example, there are three different TAs located at different geographic locations. These TAs can be as large as smart cities or as small as industrial environments. There are many IoT devices located at each premise. Each TA is also connected to one node of the Blockchain. This Blockchain can be a community Blockchain, private Blockchain, or a public Blockchain, depending on the understanding of participating TAs.

Various TAs may involve different campuses of one industry situated in different cities or even countries. The proposed framework provides a mechanism to authenticate IoT devices in case of various devices want to form a group for data sharing. Figure 3 shows a flow chart of the various processes involved in the proposed group authentication mechanism. This flow chart depicts the processes, such as storing the public key and metadata of each IoT device on the Blockchain, sharing of Chebyshev polynomial degree or exponent via the Blockchain to each IoT device, generation of Chebyshev polynomial by each IoT device in a sequential manner, and finally comparing overall Chebyshev value with the last device’s Chebyshev value to decide the success of the group authentication.

The proposed mechanism works in two different phases: group formation and group authentication. These phases are discussed as given below.

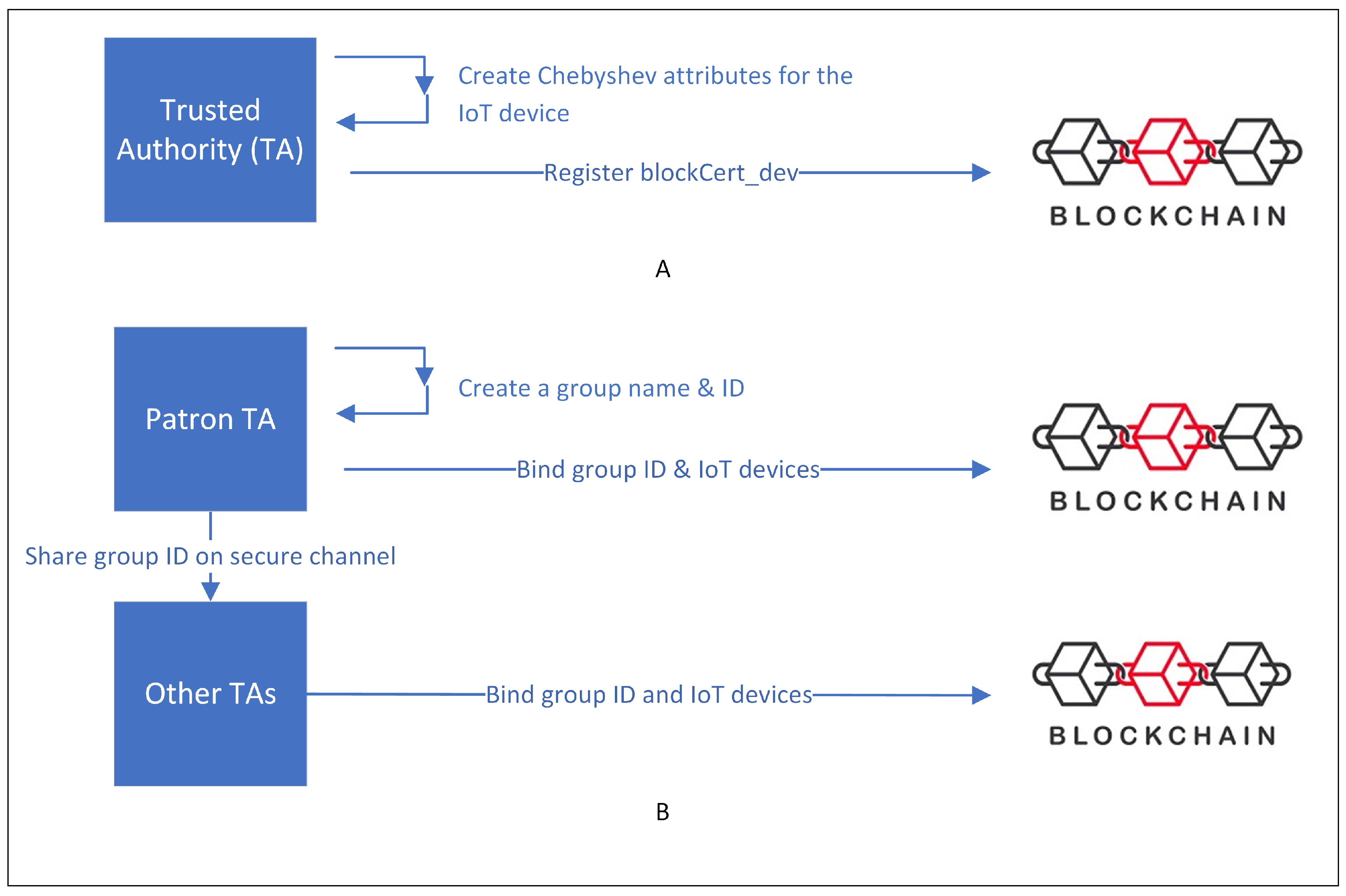
4.1. Phase 1: Group Formation

The first phase deals with preparing the IoT devices and Blockchain for group formation as shown in Figure 4. In part A of phase 1, all participating TAs will register their IoT devices on the Blockchain. In this part, a TA will generate the Chebyshev attributes, such as the required degree of the Chebyshev polynomial and the value of variable x, and compute the public key $(x,Cheb{y}_{Alice})$ as explained in the previous section. The public key of each IoT device is stored by each TA on Blockchain in the form of a digital certificate named blockCert_dev, along with other essential metadata, such as $I{D}_{puf}$, TA name, device name, device type, etc. A PUF is used to create a unique identifier (known as $I{D}_{puf}$) for an IoT device. In part B of phase 1, one TA (known as patron TA) will initiate the group formation process. The patron TA will create a group name and identifier. The patron TA then identifies the $I{D}_{puf}$ of the participating IoT devices and binds these IDs with the group ID using a function bindGroup of the smart contract. After this, the patron TA will share the group name and group ID with all the participating TAs on a secure channel. All of the remaining participating TAs will also use bindGroup of the smart contract to bind their IoT devices with the supplied group ID. After the successful execution of the first phase, the smart contract will have information, such as group name, group ID, and list of $I{D}_{puf}$ all participating IoT devices. At the end of this phase, the public keys of all participating IoT devices are also stored in Blockchain.

4.2. Phase 2: Group Authentication

Once a group is formed on a smart contract, it will initiate the authentication process. The authentication process is carried out in two steps: Chebyshev degree sharing and execution of the smart contract. Both steps are discussed in subsequent sub-sections.

4.2.1. Step 1: Sharing of Chebyshev Degree

The first step of the authentication process is to share the Chebyshev degree to be used in the Chebyshev polynomial. The smart contract will use a different Chebyshev degree for each IoT device; usually it is a large number. The smart contract will securely share the Chebyshev degree with corresponding IoT devices. To facilitate this secure sharing, the Chebyshev polynomial-based public key cryptosystem is used, as shown in Figure 5.

The process shown in the figure is used by each TA ($T{A}_i$, where i is from 1 to the total number of TAs) and smart contract to share the Chebyshev polynomial degree ($de{g}_{ij}$, for the ith TA and jth IoT device). The ith TA will initiate the process for the jth IoT device by generating a large number sdij and another number $x_{ij}$ (where $x\in (-1,1)$). The TA will compute Tdevij using the Chebyshev polynomial degree sdij and the variable $x_{ij}$. The public key of the jth IoT device will be ($x_{ij}$, Tdevij), whereas the private key will be sdij. The smart contract will use this public key to securely communicate with the IoT device. The smart contract will randomly create two large numbers, sbij and $de{g}_{ij}$. The smart contract will compute Tblockij and Tdevblockij using sbij and the IoT device’s public key ($x_{ij}$, Tdevij), as shown in the figure. The smart contract will then compute the cipher message $M_{ij}$ by multiplying $de{g}_{ij}$ with Tdevblockij. Once the cipher message is computed, the smart contract will send $M_{ij}$ to the corresponding IoT device along with Tblockij. The IoT device can recover $de{g}_{ij}$ from $M_{ij}$ by multiplying it with $T_{sdij}\left(Tblockij\right)$, which is a Chebyshev value computed using the IoT device’s private key and Tblockij. The recovery of $de{g}_{ij}$ from $M_{ij}$ is possible because of the semigroup property of the Chebyshev polynomial, which is shown in Equation (5) corresponding to the proposed authentication framework.

$$Tdevblockij=T_{sbij}\left(Tdevij\right)=T_{sdij}\left(Tblockij\right)=T_{sdij}\left(T_{sbij}\left(x_{ij}\right)\right)=T_{sbij}\left(T_{sdij}\left(x_{ij}\right)\right)$$

(5)

The smart contract follows this process with each IoT device of different TAs to securely share the associated $de{g}_{ij}$. At the end of this step, each IoT device will have its own $de{g}_{ij}$.

4.2.2. Step 2: Smart Contract Execution for Group Authentication

Before any IoT device sends data to the group, it will verify the status of the smart contract associated with a particular group ID. If the smart contract is executed, participating IoT devices deduce that group authentication is successful. To authenticate the group and execute the smart contract, the proposed framework will follow procedures given in Algorithm 1.

Algorithm 1 Group authentication algorithm.

Input: Variable $va{r}_{ij}$ and Degree $de{g}_{ij}$. Output: Smart contract: Executed or Not.   1: Smart Contract: Randomly select one IoT device by $I{D}_{puf}$. 2: Smart Contract: Initiate authentication by sending a hello message to the selected IoT device. 3: IoT Device: Generate a large integer var1, compute $chebyshev\_val=T_{de{g}_{ij}}\left(var1\right)$. 4: for Each remaining IoT device do 5:     Randomly select one IoT device and send chebyshev_val. 6:     Selected IoT Device: $new\_chebyshev\_val=T_{de{g}_{ij}}(chebyshev\_val)$. 7:     Selected IoT Device: Call smart contract function receive_value, receive_value (new_chebyshev_val). 8:     Smart Contract: chebyshev_val=new_chebyshev_val. 9: end for 10: Smart Contract: $final\_deg={\prod }_{i,j=1,1}^{n,k}de{g}_{i,j}$ 11: Smart Contract: $overall\_chebyshev\_val=T_{fina{l}_{deg}}\left(var1\right)$. 12: if overall_chebyshev_val ≈ chebyshev_val then 13: Execute Smart Contract. 14: EndIf

In order to authenticate the group, the smart contract randomly selects one IoT device and sends a special message, hello, to it. Upon receiving the hello message, the IoT device generates a large integer var1 and computes the Chebyshev value as $Chebyshev\_val=T_{de{g}_{ij}}\left(var1\right)$. The IoT device then transfers this Chebyshev value to the smart contract for further processing, using the process shown in Figure 5 to securely send the value. Once the smart contract receives the Chebyshev_val, it selects another IoT device among the remaining devices and securely transfers the value using the receive_value function to catch the new_chebyshev_val sent by Blockchain to the selected IoT device. Upon receiving Chebyshev_val, the IoT device will compute the new Chebyshev value (new_Chebyshev_val) as $new\_Chebyshev\_val=T_{de{g}_{ij}}(Chebyshev\_val)$ using its own $de{g}_{ij}$. The value of variable Chebyshev_val will be replaced by new_Chebyshev_val before it is sent to the smart contract. The smart contract will follow the same steps as all remaining IoT devices and will store the Chebyshev_val value received from the last IoT device of the group.

To authenticate the group, the smart contract will compute the product of all $de{g}_{ij}$ of all IoT devices, as shown on line 10 of the algorithm. In this equation, n is the number of TAs and k is the number of IoT devices participating in the group. The overall_Chebyshev_val will be computed using $fina{l}_{deg}$ and variable var1 (which is generated by the first IoT device) as shown in line 11 of the algorithm. If the overall_Chebyshev_val is approximately equal to the Chebyshev_val shared by the last IoT device, it means all IoT devices used their own $de{g}_{ij}$ shared by the smart contract in step 1 of phase 2. In theory, both values should be exactly equal but because we are using the approximation method to compute the Chebyshev value, the exact value may not be yielded. In this scenario, group authentication will be deemed successful and the smart contract will be executed. If any hacker replaces the IoT device with his/her own device, the overall_Chebyshev_val will never be equal to Chebyshev_val. In case of any change in the group structure, for example, an IoT device is replaced by another IoT device, or any IoT device is removed/added, the whole process needs to be carried out from the start.

5. Security Analysis

The security analysis of the proposed authentication framework is performed using the informal security analysis methods; the resilience of the proposed authentication framework against various attacks has been discussed, as in [28].

Proposition 1. 

Resilience against replay attack.

Proof. 

In the proposed authentication scheme, all communicating parties (IoT devices and Blockchain) randomly generate keys and variables, such as sdij, $x_{ij}$, sbij, $de{g}_{ij}$, and then compute variables, such as Tdevij, Tblockij, Tdevblockij, and $M_{ij}$, each time an authentication request is made. Each communication and participating variable is transferred with a timestamp. Hence, a fresh generation of variables and the usage of timestamps for each authentication request support the proposed framework against the replay attack. □

Proposition 2. 

Resilience against man-in-the-middle attack.

Proof. 

The use of Chebyshev polynomials in the authentication mechanism makes it resilient against man-in-the-middle attacks. The Blockchain and each participating IoT device share a piece of secret ($de{g}_{ij}$) in one-to-one communication. This communication is secured and no IoT device can know the piece of the secret of another IoT device. Another piece of secret (chebyshev_val is securely shared between the Blockchain and individual IoT devices in separate communications. The Blockchain will approve authentication only if all IoT devices compute their corresponding chebyshev_val using their secret. If someone successfully intercepts one communication he/she cannot recreate another valid login request method. He/she cannot even use the intercepted communication to recreate another authentication request for the same IoT device as Blockchain will securely share the next secret ($de{g}_{ij}$) using $I{D}_{purf}$ of the listed IoT device only. Hence, obtaining ($de{g}_{ij}$) of one IoT device will not help a man-in-the-middle attacker to successfully recreate another authentication request. □

Proposition 3. 

Resilience against offline guessing attacks.

Proof. 

In the proposed authentication framework, Blockchain initiates the process and sdij and $x_{ij}$ are randomly generated for each authentication request; offline guessing attack will not help an attacker to use stored sdij and $x_{ij}$ for further authentication cracking. Retrieval of sdij and $x_{ij}$ from one IoT device cannot help cracking authentication for other devices as well as further authentication for the same device; hence, we can say that the proposed framework is resilient against offline guessing attacks. □

Proposition 4. 

Resilience against device impersonation attacks and lost/stolen IoT device attacks.

Proof. 

In the group formation phase, the trusted authority uses the metadata $I{D}_{purf}$, along with other information, to create a blockCert_dev. This $I{D}_{purf}$ is a physical unclonable function that is unique to each device, and any communication can be verified to be sent only by that device. Since blockCert_dev is stored on both the Blockchain and IoT devices, even if someone changes the IoT device’s information, it can be verified from the certificate fetched from the Blockchain. This makes it difficult for anyone to impersonate an IoT device. Moreover, because the digital certificate of an IoT device can be verified from the Blockchain, it is easy to block lost/stolen devices from participating in future authentication requests. An invalidated certificate is stored on the Blockchain for the lost/stolen device, and since the Blockchain is searched from the latest-to-oldest fashion, the updated certificate will be fetched first, which will show that the device is no longer valid for that group. Hence, we can say that the proposed authentication framework is resilient against impersonation and lost/stolen device attacks. □

Proposition 5. 

Resilience against the ephemeral secret leakage (ESL) attack.

Proof. 

The security against ESL attacks depends on the long-term secret and temporal secret. In the proposed authentication framework, secrets, such as sdij, $x_{ij}$ and sbij are long-term secrets that are created and then used for many authentication requests. Temporal secrets, such as $de{g}_{ij}$ and chebyshev_val, are freshly generated for each authentication request. The generation of long-term secrets is a straightforward process that can be carried out frequently to ensure secrecy. Since temporal secrets are created for each authentication request, if these secrets are compromised for a session, it will not affect previous or future authentication requests. This aspect of the proposed framework supports forward and backward secrecy of authentication requests. Moreover, because of the use of the Chebyshev polynomial, compromise in one session of an IoT device and Blockchain communication will not affect the overall authentication requests. This is because, for successful authentication, the chebyshev_val of each IoT device should be the same as Blockchain is expecting, as explained in Figure 1. □

6. Results Discussion

The proposed framework was implemented using Python, and the smart contract was created using Solidity. The smart contract was deployed on Ethereum’s Goerli and Sepolia testnets to evaluate its performance on a near-real-size Blockchain. The Goerli testnet, which uses a proof-of-stake consensus algorithm, is a public network with a comparable Blockchain size to the Ethereum mainnet [29]. All experiments were conducted on a virtual machine running the Linux Ubuntu 18.04.6 LTS operating system, equipped with an AMD Ryzen 7 5800H with Radeon Graphics processor, 8GB of RAM, and 100 GB of allocated hard disk.

The recursive computation of the Chebyshev polynomial is a computing power-intensive process and after a certain degree, the polynomial may take months or years to compute. Instead of recursive computation, the Chebyshev polynomial value was computed using approximation methods. The Chebyshev value returned by an approximation method was not the same as the recursive method but it was close to the actual value. To better understand the time taken by the proposed authentication framework, a time analysis is carried out for various functions such as public key generation, encrypting the deg variable and then decrypting the deg value. The experiments were performed for various digit lengths of deg, with randomly generated values, and the time taken by the random number generator is also included in the time analysis. Figure 6 illustrates the time analysis for digit lengths 1 to 3.

From the figure, it is evident that as the digit length increases, the time taken to generate a public key, encrypt, and decrypt also increases. For a digit length of 1, which means a polynomial degree in a single digit (i.e., a linear equation), the times taken to generate a public key, encrypt, and decrypt are 0.502 ms, 0.226 ms, and 0.112 ms, respectively. For double-digit polynomial degrees, these times are 0.870 ms, 0.737 ms, and 0.512 ms, respectively. If the degree of the Chebyshev polynomial is increased to 3, the time taken to generate a public key, encrypt, and decrypt is found to be 9.927 ms, 8.993 ms, and 9.752 ms, respectively.

Figure 7 shows the time analysis for digit lengths of 4, 5, and 6, showing that as the digit length increases linearly, the time taken increases exponentially. The public key generation time for digit lengths 4 to 6 increases from 63.73 ms to 71,825.43 ms. Similarly, the encryption time rises from 100.88 ms for digit length 4 to 20,090.05 ms for digit length 6. The decryption time follows the same pattern and increases from 62.18 ms for digit length 4 to 68,327.17 ms for digit length 6. No further experiments are carried out for larger digit lengths because of the exponential computation time. Therefore, it is not recommended to use a Chebyshev polynomial degree greater than 6; otherwise, the authentication process will not be completed within a reasonable time.

The proposed authentication framework was also tested on Blockchain-related parameters by deploying the smart contract on Ethereum’s Goerli testnet. The results are shown in

Table 1. Performance evaluation results of the deployed blockchain.

	Use Cases	Deployment	Group Authentication Transaction
Parameters
Average Compute Units		1.4	4.1
Median Response (ms)		19	26
eth_gasPrice		102,483	101,421
eth_estimateGas		476,029	23,587
eth_getBlockByNumber: Base Fee Per Gas		91,861	115,261
eth_getBlockByNumber:Gas Used		28,623,706	19,079,703
Max Fee Per Gas		—–	1,500,230,522
Max Priority Fee Per Gas		—–	1,500,000,000
eth_getTransactionReceipt: Cumulative Gas Used		16,403,924	—–
eth_getTransactionReceipt: Effective Gas Price		102,483	—–
eth_getTransactionReceipt: Gas Used		476,029	—–

. Although it is suggested to use a permissioned private Blockchain for the proposed authentication framework where each TA maintains one Blockchain node, the results in Table 1 give an idea of the cost and performance if TAs decide to use Ethereum’s mainnet network with real Ethers. The compute units used to deploy the smart contract were 1.4, whereas it was 4.1 for authenticating the group by the deployed smart contract. The median response time for deploying the smart contract was 19 ms, and for authenticating the group, it was 26 ms. The gas price on the network at the time of deployment was 102,483 Wei, whereas it was 101,421 Wei when an experiment of group authentication was carried out. At the time of the experiment, the estimated gas required for deployment was found to be 476,029 Wei, but for group authentication transactions, the estimate was 23,587 Wei. The function eth_getBlockByNumber searches for a block and charges Ethers for the base fee and gas used. At the time of deployment of the smart contract, the base fee and gas used were 91,861 Wei and 28,623,706 Wei; at the time of the group authentication experiment, the base fee and the gas used were 115,261 Wei and 19,079,703 Wei, respectively. The parameter max fee per gas defines the absolute maximum gas price a user wants to pay to include his/her block on a Blockchain. For the experiments, the maximum gas price that could be paid by TAs for group authentication was 1,500,230,522 Wei.

The parameter max priority fee per gas is the maximum gas price set by the user, which can be paid to miners for prioritizing the addition of their blocks on the Blockchain. For the experiment, it was set to 1,500,000,000 Wei. At the time of the deployment of the smart contract, a transaction receipt was also analyzed to understand the cost involved in the transactions. The cumulative gas used shows the gas used by deployment and all the subsequent transactions in the same block, which was found to be 16,403,924 Wei. The actual value per gas deducted from the TA account to deploy the smart contract was observed as 102,483 Wei. It was also found from the transaction receipt that the actual gas used to deploy the smart contract was 476,029 Wei, which was the same as the gas estimated by the eth_estimateGas function. Based on the discussed results, users can perform a cost–benefit analysis of the proposed authentication framework and can decide on the required computation resources and Blockchain deployment type for their implementation.

7. Conclusions and Future Work

The management of trust in Internet of Things (IoT) devices controlled by different entities is an important aspect of security in IoT networks. Presently, digital certificates based on public key cryptography are utilized for secure communication, but the associated cost is substantial, particularly if every IoT device is issued a digital certificate from a certificate authority. In this research paper, a group authentication framework based on the Chebyshev polynomial and Blockchain technology is proposed. The proposed framework is capable of authenticating IoT devices situated on different entities and can facilitate secure data communication between that groups. The proposed framework was implemented in Python to understand the time analysis of the Chebyshev polynomial and was then deployed on Ethereum’s Goerli testnet using a Solidity-based smart contract. From the results, it was found that the public key generation time, encryption, and decryption time increase as the degree of the Chebyshev polynomial increases. It was also found that a Chebyshev polynomial degree of four digits can be reasonably used in the proposed framework. The public key generation time, encryption time, and decryption time of 63.73 milliseconds, 100.18 milliseconds, and 62.18 milliseconds are achieved with a four-digit long Chebyshev polynomial degree. If a three-digit length polynomial degree is used, the public key generation time, encryption time, and decryption time reduce to 9.927 milliseconds, 8.993 milliseconds, and 9.752 milliseconds, respectively. It is evident from the obtained results that a polynomial degree of digit length beyond six digits is not advised because of long key generation, encryption, and decryption time. The Blockchain results show that compute units of 1.4 and 4.1 are used for the deployment of a smart contract and one transaction on a smart contract. The median response time for deployment and transaction was 19 milliseconds and 26 milliseconds, respectively. The group authentication framework is also analyzed on various parameters of Blockchain, such as effective gas used, estimated gas, the base fee per gas, and gas used, etc.

One major issue in Blockchain-based solutions is scalability. In the future, the proposed framework could be tested for scalability. In this research, the framework was tested on the Goerli network, which is a large Blockchain and represents almost the same scalability parameter as the real Blockchain. However, there is a need to develop ideas to reduce the response time of the Blockchain for real-time group authentication. Another future direction is to modify the proposed framework to reduce the burden of Chebyshev polynomial computation over the smart contract. Smart contracts are not designed to perform large complex polynomial approximations, so the proposed framework can be modified to offload that task onto a trusted authority. It will be interesting to analyze the impact on various performance parameters with the modified mechanism.