A Novel Multi-Cell Interference-Aware Cooperative QoS-Based NOMA Group D2D System
Abstract
:1. Introduction
1.1. Related Work
1.2. Motivation and Contributions
- We propose a multi-cell cooperative relaying in Q-NOMA-enabled D2D communications. To completely analyze the device clustering and spatial separation, GPP is used to model the D2D transmitter topology, and the D2D receivers are randomly distributed around it.
- The power allocation coefficients are assigned depending upon the QoS of users.
- Furthermore, closed-form expressions of interference and the outage probability at the D2D receiver are derived. The interference approximation for cooperative Q-NOMA-aided D2D relaying is used to derive the closed-form expression of outage probability.
- Analytical and simulation results are established to validate the outage probability results and to demonstrate the dominance of Q-NOMA over conventional OMA-assisted D2D systems.
1.3. Gauss–Poisson Process
2. System Model
Power Allocation Scheme
3. Outage Probability Analysis
4. Numerical Results
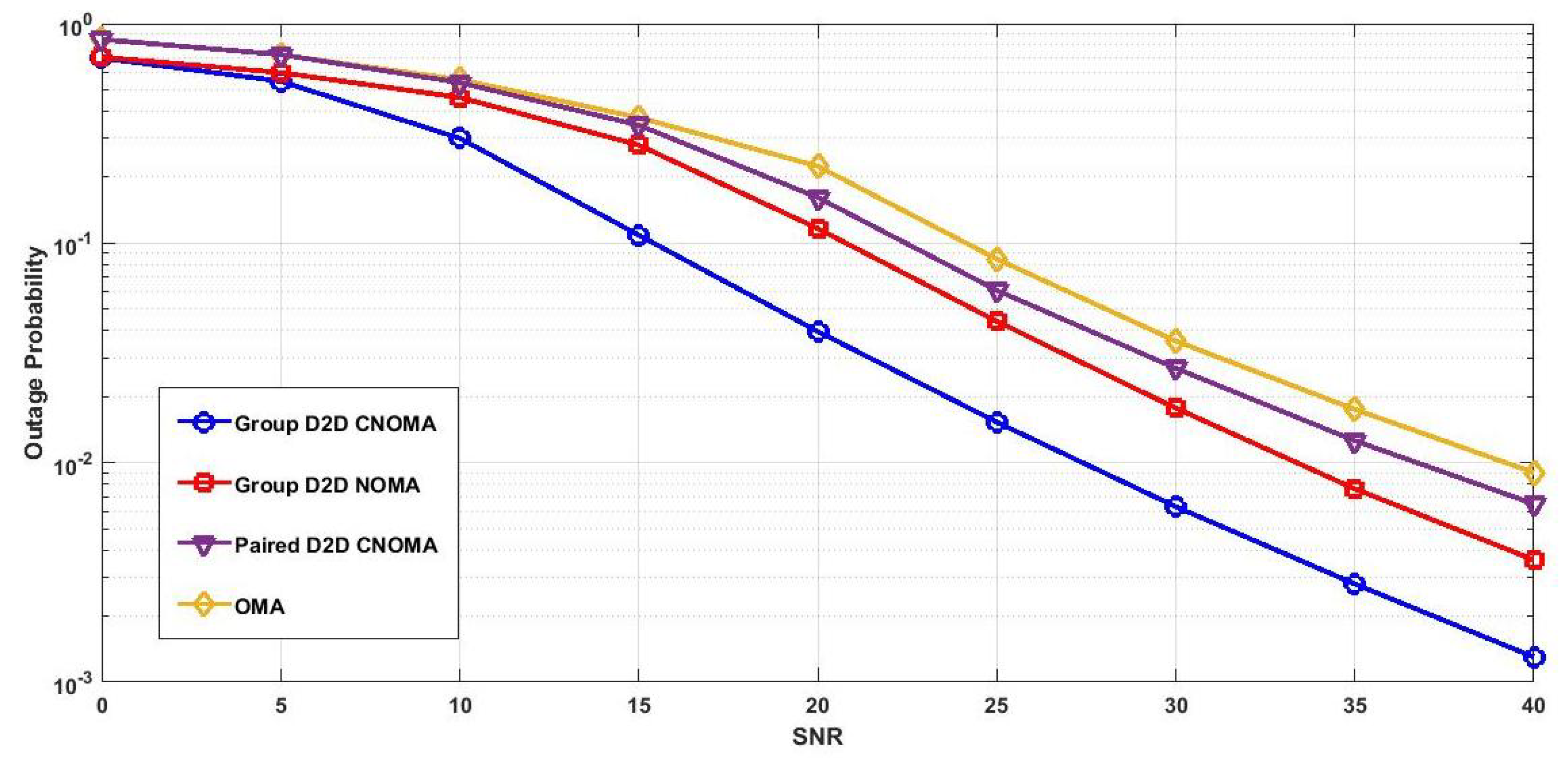
4.1. Outage Probability Comparison
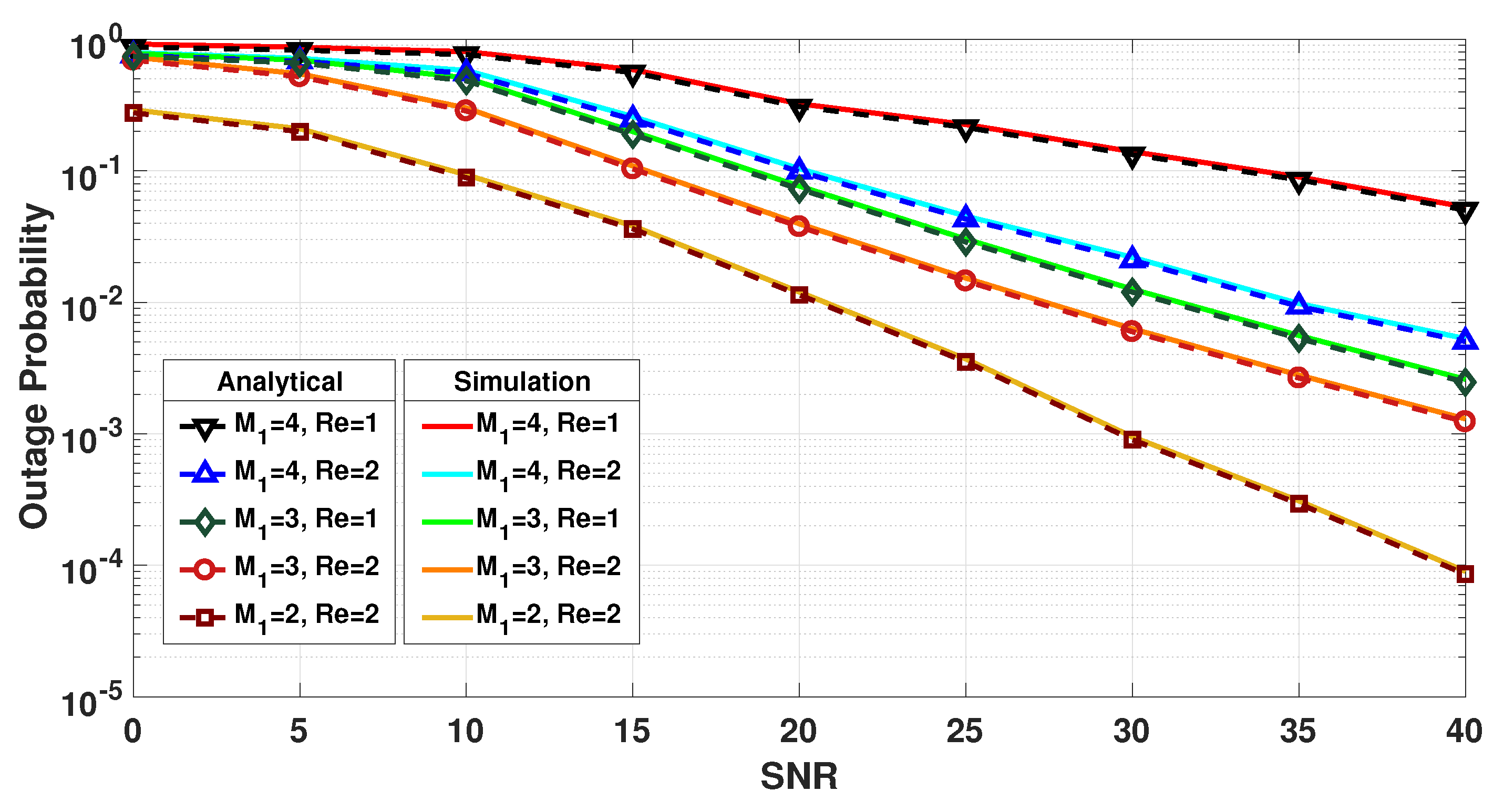
4.2. Impact of and on Outage Probability
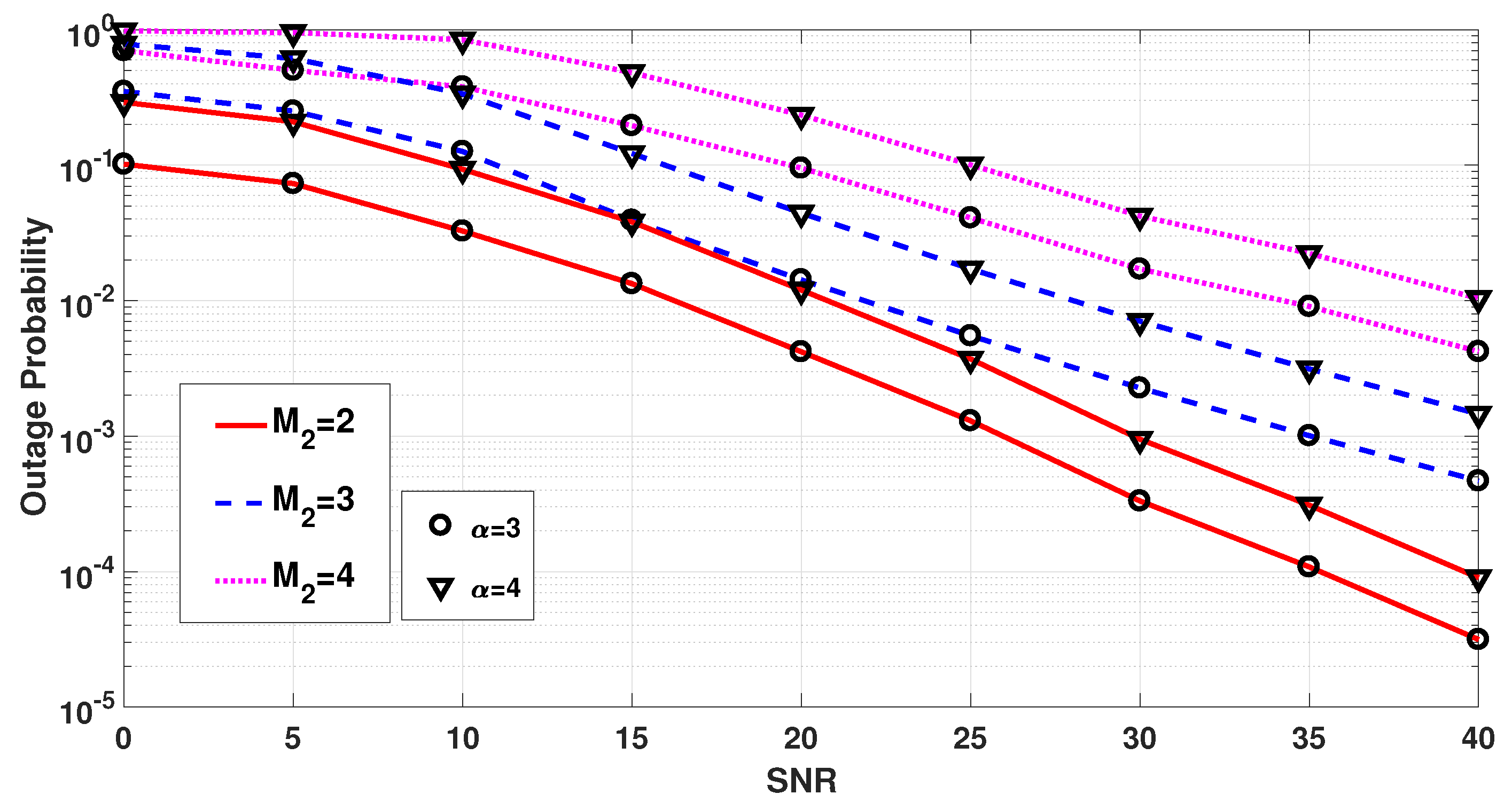
4.3. Impact of and on Outage Probability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Outage Probability in Phase II
References
- Salahdine, F.; Han, T.; Zhang, N. 5G, 6G, and Beyond: Recent advances and future challenges. Ann. Telecommun. 2023, 1–25. [Google Scholar] [CrossRef]
- Hama, Y.; Ochiai, H. Time-Frequency Domain Non-Orthogonal Multiple Access for Power Efficient Communications. IEEE Trans. Wirel. Commun. 2023, 1. [Google Scholar] [CrossRef]
- Sadat, H.; Abaza, M.; Mansour, A.; Alfalou, A. A survey of NOMA for VLC systems: Research challenges and future trends. Sensors 2022, 22, 1395. [Google Scholar] [CrossRef] [PubMed]
- Rebhi, M.; Hassan, K.; Raoof, K.; Chargé, P. Sparse code multiple access: Potentials and challenges. IEEE Open J. Commun. Soc. 2021, 2, 1205–1238. [Google Scholar] [CrossRef]
- Millar, G.; Kulhandjian, M.; Alaca, A.; Alaca, S.; D’Amours, C.; Yanikomeroglu, H. Low-Density Spreading Design Based on an Algebraic Scheme for NOMA Systems. IEEE Wirel. Commun. Lett. 2022, 11, 698–702. [Google Scholar] [CrossRef]
- Le, M.; Pham, Q.V.; Kim, H.C.; Hwang, W.J. Enhanced resource allocation in D2D communications with NOMA and unlicensed spectrum. IEEE Syst. J. 2022, 16, 2856–2866. [Google Scholar] [CrossRef]
- Qi, Y.; Vaezi, M. Signaling design for MIMO-NOMA with different security requirements. IEEE Trans. Signal Process. 2022, 70, 1389–1401. [Google Scholar] [CrossRef]
- Xiu, Y.; Zhao, J.; Sun, W.; Di Renzo, M.; Gui, G.; Zhang, Z.; Wei, N. Reconfigurable intelligent surfaces aided mmWave NOMA: Joint power allocation, phase shifts, and hybrid beamforming optimization. IEEE Trans. Wirel. Commun. 2021, 20, 8393–8409. [Google Scholar] [CrossRef]
- Anwar, A.; Seet, B.C.; Ding, Z. Non-orthogonal multiple access for ubiquitous wireless sensor networks. Sensors 2018, 18, 516. [Google Scholar] [CrossRef] [Green Version]
- Shi, W.; Sun, Y.; Liu, M.; Xu, H.; Gui, G.; Ohtsuki, T.; Adebisi, B.; Gacanin, H.; Adachi, F. Joint UL/DL resource allocation for UAV-aided full-duplex NOMA communications. IEEE Trans. Commun. 2021, 69, 8474–8487. [Google Scholar] [CrossRef]
- Jiao, R.; Dai, L.; Zhang, J.; MacKenzie, R.; Hao, M. On the performance of NOMA-based cooperative relaying systems over Rician fading channels. IEEE Trans. Veh. Technol. 2017, 66, 11409–11413. [Google Scholar] [CrossRef] [Green Version]
- Ghous, M.; Hassan, A.K.; Abbas, Z.H.; Abbas, G.; Hussien, A.; Baker, T. Cooperative Power-Domain NOMA Systems: An Overview. Sensors 2022, 22, 9652. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Zhai, C.; Zhang, X.; Liu, J. NOMA-enabled D2D adaptive relaying and transmission in cellular networks. Trans. Emerg. Telecommun. Technol. 2022, 33, e4437. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Chai, K.K.; Chen, Y.; Elkashlan, M. Joint subchannel and power allocation for NOMA enhanced D2D communications. IEEE Trans. Commun. 2017, 65, 5081–5094. [Google Scholar] [CrossRef]
- Bajpai, R.; Gupta, N. Outage trade-offs between full/half-duplex relaying for NOMA aided multicarrier cooperative D2D communications system. IETE Tech. Rev. 2022, 39, 1167–1179. [Google Scholar] [CrossRef]
- Wu, S.; He, Y.; Zhang, Y.; Zhang, Y.; Zhou, L. Performance Analysis and Relay Selection of D2D Aided Cooperative NOMA System. In Advances in Wireless Communications and Applications: Smart Wireless Communications: Algorithms and Network Technologies, Proceedings of 5th ICWCA 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 35–44. [Google Scholar]
- Zhao, J.; Liu, Y.; Chai, K.K.; Chen, Y.; Elkashlan, M.; Alonso-Zarate, J. NOMA-based D2D communications: Towards 5G. In Proceedings of the 2016 IEEE global communications conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Anwar, A.; Seet, B.C.; Li, X.J. Quality of service based NOMA group D2D communications. Future Internet 2017, 9, 73. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Ma, Z.; Xiao, M.; Ding, Z.; Fan, P. Full-duplex device-to-device-aided cooperative nonorthogonal multiple access. IEEE Trans. Veh. Technol. 2016, 66, 4467–4471. [Google Scholar]
- Madani, N.; Sodagari, S. Performance analysis of non-orthogonal multiple access with underlaid device-to-device communications. IEEE Access 2018, 6, 39820–39826. [Google Scholar] [CrossRef]
- Zheng, H.; Hou, S.; Li, H.; Song, Z.; Hao, Y. Power allocation and user clustering for uplink MC-NOMA in D2D underlaid cellular networks. IEEE Wirel. Commun. Lett. 2018, 7, 1030–1033. [Google Scholar] [CrossRef]
- Kim, J.B.; Lee, I.H.; Lee, J. Capacity scaling for D2D aided cooperative relaying systems using NOMA. IEEE Wirel. Commun. Lett. 2017, 7, 42–45. [Google Scholar] [CrossRef]
- Gandotra, P.; Jha, R.K.; Jain, S. Green NOMA with multiple interference cancellation (MIC) using sector-based resource allocation. IEEE Trans. Netw. Serv. Manag. 2018, 15, 1006–1017. [Google Scholar] [CrossRef]
- Song, Y.B.; Kang, H.S.; Kim, D.K. 5G cellular systems with D2D assisted NOMA relay. In Proceedings of the 2016 URSI Asia-Pacific Radio Science Conference (URSI AP-RASC), Seoul, Repubic of Korea, 21–25 August 2016; pp. 1–3. [Google Scholar]
- Kazmi, S.A.; Tran, N.H.; Ho, T.M.; Manzoor, A.; Niyato, D.; Hong, C.S. Coordinated device-to-device communication with non-orthogonal multiple access in future wireless cellular networks. IEEE Access 2018, 6, 39860–39875. [Google Scholar] [CrossRef]
- Afshang, M.; Dhillon, H.S. Spatial modeling of device-to-device networks: Poisson cluster process meets Poisson hole process. In Proceedings of the 2015 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; pp. 317–321. [Google Scholar]
- Dash, S.P.; Joshi, S. Performance analysis of a cooperative D2D communication network with NOMA. IET Commun. 2020, 14, 2731–2739. [Google Scholar] [CrossRef]
- Shi, Z.; Ma, S.; ElSawy, H.; Yang, G.; Alouini, M.S. Cooperative HARQ-assisted NOMA scheme in large-scale D2D networks. IEEE Trans. Commun. 2018, 66, 4286–4302. [Google Scholar] [CrossRef] [Green Version]
- Guo, A.; Zhong, Y.; Zhang, W.; Haenggi, M. The Gauss–Poisson process for wireless networks and the benefits of cooperation. IEEE Trans. Commun. 2016, 64, 1916–1929. [Google Scholar] [CrossRef]
- Yang, Z.; Ding, Z.; Wu, Y.; Fan, P. Novel relay selection strategies for cooperative NOMA. IEEE Trans. Veh. Technol. 2017, 66, 10114–10123. [Google Scholar] [CrossRef] [Green Version]
- Men, J.; Ge, J. Non-orthogonal multiple access for multiple-antenna relaying networks. IEEE Commun. Lett. 2015, 19, 1686–1689. [Google Scholar] [CrossRef]
- Zwillinger, D.; Jeffrey, A. Table of Integrals, Series, and Products; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Kuhlman, K.L. Review of inverse Laplace transform algorithms for Laplace-space numerical approaches. Numer. Algorithms 2013, 63, 339–355. [Google Scholar] [CrossRef] [Green Version]

| Parameter | Description | Value |
|---|---|---|
| Number of users in Phase I | 2 | |
| Number of users in Phase II | 2 | |
| Number of relays | 2 | |
| Users’ rates in Phase I | (0.7, 1.2) | |
| Users’ rates in Phase II | (0.5, 1.1) | |
| Radius of coverage area | 10 m | |
| Path loss exponent | 4 | |
| Intensity of group transmitters | ||
| Distance of group transmitter from relay in Phase I | 9 m | |
| Distance of group transmitter from relay in Phase II | 8 m | |
| P | Degree of Gauss–Laguerre polynomial | 5 |
| L, N, V, Q, S | Gaussian–Chebyshev parameters | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, M.A.; Ahmad, T.; Anwar, A.; Siddiq, S.; Malik, A.; Nazar, W.; Razzaq, I. A Novel Multi-Cell Interference-Aware Cooperative QoS-Based NOMA Group D2D System. Future Internet 2023, 15, 118. https://doi.org/10.3390/fi15040118
Hasan MA, Ahmad T, Anwar A, Siddiq S, Malik A, Nazar W, Razzaq I. A Novel Multi-Cell Interference-Aware Cooperative QoS-Based NOMA Group D2D System. Future Internet. 2023; 15(4):118. https://doi.org/10.3390/fi15040118
Chicago/Turabian StyleHasan, Muhammad Amish, Tanveer Ahmad, Asim Anwar, Salman Siddiq, Abdul Malik, Waseem Nazar, and Imran Razzaq. 2023. "A Novel Multi-Cell Interference-Aware Cooperative QoS-Based NOMA Group D2D System" Future Internet 15, no. 4: 118. https://doi.org/10.3390/fi15040118
APA StyleHasan, M. A., Ahmad, T., Anwar, A., Siddiq, S., Malik, A., Nazar, W., & Razzaq, I. (2023). A Novel Multi-Cell Interference-Aware Cooperative QoS-Based NOMA Group D2D System. Future Internet, 15(4), 118. https://doi.org/10.3390/fi15040118







