Benchmarking Change Detector Algorithms from Different Concept Drift Perspectives

Abstract

The stream mining paradigm has become increasingly popular due to the vast number of algorithms and methodologies it provides to address the current challenges of Internet of Things (IoT) and modern machine learning systems. Change detection algorithms, which focus on identifying drifts in the data distribution during the operation of a machine learning solution, are a crucial aspect of this paradigm. However, selecting the best change detection method for different types of concept drift can be challenging. This work aimed to provide a benchmark for four drift detection algorithms (EDDM, DDM, HDDMW, and HDDMA) for abrupt, gradual, and incremental drift types. To shed light on the capacity and possible trade-offs involved in selecting a concept drift algorithm, we compare their detection capability, detection time, and detection delay. The experiments were carried out using synthetic datasets, where various attributes, such as stream size, the amount of drifts, and drift duration can be controlled and manipulated on our generator of synthetic stream. Our results show that HDDMW provides the best trade-off among all performance indicators, demonstrating superior consistency in detecting abrupt drifts, but has suboptimal time consumption and a limited ability to detect incremental drifts. However, it outperforms other algorithms in detection delay for both abrupt and gradual drifts with an efficient detection performance and detection time performance.

1. Introduction

Concept drift refers to the phenomenon where the patterns of a dataset change with time, making it difficult to develop accurate models and predictions [1]. This is a real-life challenge that is particularly acute when dealing with data streams, where the underlying data distribution can evolve rapidly and unpredictably [2]. The problem of concept drift can arise in many different contexts, such as financial forecasting, cybersecurity [3], process mining [4,5], and environmental sensing [6,7]. In these domains, it is essential to develop algorithms and techniques that can adapt to changing data distributions and maintain high accuracy over time.

One promising approach to addressing concept drift is to use online learning methods, which update models in real time as new data become available [8]. Successful strategies for handling concept drift require a deep understanding of the underlying data-generating processes and the ability to develop flexible and adaptive algorithms, which can learn and evolve over time. Change detectors play a crucial role in addressing concept drift, as these allow for the detection of changes in the statistical properties of data streams [9]. These detectors can be used to identify when a model trained on historical data is no longer accurate due to changes in the underlying data distribution.

While the current literature on change detectors provides several established methods, selecting and tuning these techniques for specific types of concept drift can be an additional challenge. The most popular change detectors, or simply detectors, are Adaptive Windowing (ADWIN) [10], PH Page Hinkley (PH) [11], drift detection method (DDM) [12], early drift detection method (EDDM) [13], drift detection methods based on Hoeffding’s bounds with the moving average-test (HDDMA), and drift detection methods based on Hoeffding’s bounds with the moving weighted average-test (HDDMW) [14].

ADWIN and PH are both based on monitoring the statistics of a sliding window, but they use different statistical approaches. ADWIN calculates the average of the statistics in two different time intervals and compares them to detect a change. Conversely, PH uses the cumulative sum of the differences between the current and previous statistics to detect changes. Both ADWIN and PH are known to be effective in detecting gradual drifts but may struggle with abrupt and incremental drifts. EDDM, DDM, HDDMW, and HDDMA rely on the same principle of monitoring the statistics of a sliding window and detecting changes when the statistics deviate from a baseline. However, they differ in the specific statistics they use, the thresholds they apply, and the way they adapt to different types of concept drift, covering a broad range of drifts.

Detecting concept drift is an important task in machine learning applications, with a variety of change detectors available in the literature. However, selecting the most appropriate detector for a given type of concept drift can be challenging. Different detectors may perform better under specific conditions, such as different types, durations, and magnitudes of concept drift. Therefore, carefully evaluating the performances of change detectors in various contexts is critical to ensure their effectiveness in real-world applications. The most popular change detectors in the literature each have their own strengths and limitations for detecting different types of concept drifts.

There are many types of concept drift in the literature, which are categorized according to their severity and speed [15]. The most relevant categories are abrupt, gradual and incremental. Abrupt changes are characterized by a sudden and significant change in the data distribution, which can be represented in real-life examples such as an online fraud detection system or a sudden shift in sensor data distribution [16,17,18]. A gradual drift is connected with a slower rate of change and can be found, for example, in a solar power system where the weather patterns change gradually, or the dust accumulation on solar panels is reducing their efficiency with time [19]. Incremental changes occur in small increments over time. For example, this type of drift happens when stock prices change incrementally due to a shift in market conditions or investors’ behavior.

This study investigated the performance of four commonly used methods (EDDM, DDM, HDDMW, and HDDMA) across hundreds of synthetic datasets to tackle the challenge of selecting a suitable change detection algorithm in a wide range of possible scenarios. These datasets were designed using a tool developed in this work to simulate various concept drift types, with varying amplitude and duration. The number of drifts and the stream size were also manipulated to increase the scenario’s diversity. We evaluated the algorithms based on several criteria, including the detection accuracy, detection time, and detection delay. By exploring these perspectives, we aimed to provide insights into the strengths and limitations of each method, as well as their suitability for different types of concept drift scenarios.

The main contributions of this paper are as follows:

• Systematic comparison among EDDM, DDM, HDDMW, and HDDMA change detectors when processing streams with abrupt, gradual, and incremental drifts. Three different performance perspectives (accuracy, time, and delay) were analyzed;
• A free online tool to generate synthetic streams with different concept drift setups;

The remainder of this paper is organized as follows: Section 2 provides further details about stream mining and concept drift, while Section 3 presents the related work. In Section 4, we describe the steps to implement the experiment alongside the used algorithms. Section 5 presents the results, while the discussion and open issues are addressed in Section 6. Section 7 presents the main conclusions and directions for future work.

2. Problem Statement

Change detectors are techniques to identify changes in data streams that may indicate shifts in their underlying distribution. In many applications, the ability to quickly detect changes and adapt to them is critical. The problem of change detection becomes even more challenging when dealing with concept drifts, where the concept can change with time. When a concept drift occurs, the relationships between the input features and the output variable may change, leading to a shift in the data distribution. This means that the model trained on the previous data may become less accurate or even useless for making predictions on the new data. Therefore, detecting and adapting to concept drifts in a timely and effective manner is crucial for maintaining model performance and avoiding costly mistakes.

2.1. Stream Mining

A data stream refers to a continuous, potentially infinite, flow of data that arrives at high speed and rapidly and unpredictably. In contrast to traditional batch data processing, data stream processing involves analyzing data in real-time as they flow into the system. Data streams are often generated by a variety of sources, such as sensors, social media, financial transactions, network traffic, etc. Due to their continuous and high-volume nature, data streams present unique challenges for data processing, storage, and analysis. The generation of a data stream can be modeled as a random variable X, from which the objects $o\in dom\left(X\right)$ are randomly drawn. Here, $dom(·)$ represents the domain of a random variable [20]. Let $X_t$ denote a random variable representing the data stream at time t, where t is a positive integer. Each data point $x_t\in dom\left(X_t\right)$ is generated by the joint distribution $P_t(x_t,y_t)$, where $y_t$ is the corresponding class label of $x_t$. The goal is to learn a classifier $f_t:dom\left(X_1\right)\times \cdots \times dom\left(X_t\right)\to \mathcal{Y}$ that maps the current and past data instances to their respective class labels, where $\mathcal{Y}$ is the set of possible class labels.

The challenge in classification stream problems is that the joint distribution $P_t(x_t,y_t)$ may change over time, a phenomenon known as concept drift. As a result, the classifier needs to be continuously updated to adapt to the changing distribution and maintain its accuracy over time.

2.2. Concept Drift

Changes in data streams in non-stationary environments are reflected through alterations in their probability distributions, which are referred to as concept drifts. Formally, let $C_t$ denote the true concept or data distribution at time t. In a typical machine learning setting, we train a model M on a fixed dataset with the assumption that the distribution of the data will remain the same in the future. However, in a streaming scenario, the distribution of the data may shift or evolve over time, leading to a mismatch between the model and the true concept. This drift in the concept can lead to a decrease in the performance of the model over time. A concept drift can manifest in different forms, including abrupt, gradual, and incremental drift [21].

Abrupt drift occurs when there is a sudden and significant change in the underlying data distribution. The new data distribution is often very different from the old one, and the model that was previously effective may become obsolete. The main challenge with abrupt drift is to quickly detect the change and adapt the model to the new data distribution. An example of abrupt drift could be a change in the way that a sensor is calibrated, resulting in a sudden shift in the readings.

The second mentioned type is the gradual drift, which occurs when the underlying data distribution slowly changes over time. The change is often smooth, making it difficult to detect. The main challenge with gradual drift is to continuously monitor the data and update the model to reflect the new data distribution. A gradual drift could be exemplified as a change in consumer behavior over time, leading to a slow shift in product preferences.

The last one, incremental drift, occurs when the data distribution changes over time, but the rate of change increases suddenly. The main challenge with incremental drift is that of detecting the change and adapting the model quickly enough to prevent performance degradation. An example of incremental drift could be a seasonal shift in the heating system, where the shift occurs gradually over several months but accelerates rapidly during the winter.

According to [22,23], the formal representation of a concept drift between two-time points (t and $t+1$) over a given period of time is:

$$\exists X:P_t(X,y)\ne P_{t+1}(X,y)$$

(1)

In Equation (1), $P_t$ represents the joint distribution between the set of input variables X and the target variable y at time t. Similarly, $P_{t+1}$ denotes the joint distribution at time $t+1$. Concept drift is related to the covariance shift in the distribution, which means that a change in the joint probability of X and y indicates the occurrence of concept drift at time t. Hence, $P_t(X,y)$ can be defined as a composition of $P_t\left(X\right)\times P_t\left(y\right|X)$. Change detection algorithms can detect concept drift by monitoring changes in the joint distribution $P_t(X,y)$ over time. If the distribution of the input variables or the conditional distribution of the output variables change significantly over time, it can indicate the occurrence of concept drift. Change detection algorithms typically monitor the statistical properties of the data, such as the mean, variance, or distribution, to detect changes in the joint distribution. When a significant change is detected, the algorithm can trigger the retraining of the model or some other action to adapt to the new concept.

3. Related Work

Each change detection algorithm has its advantages and drawbacks, and the choice of a particular one will depend on the specific characteristics of the data stream and the requirements of the application [2,13,14]. In the context of data stream mining, monitoring the statistical properties of the data stream is one of the most commonly used strategies to detect and identify different types of concept drift. However, there is no single algorithm that works well for all types of drift, and different strategies may be more appropriate for different types of drift. For example, Adaptive Windowing (ADWIN), based on monitoring the mean and variance of the data stream, can be effective for detecting abrupt drift, where the statistical properties of the data change suddenly [10]. On the other hand, monitoring the distribution of the data stream can be more effective for detecting a gradual drift, where the statistical properties of the data change slowly over time, such as the early drift detection method (DDM) [13]. Thus, there are various types of related research on drift detection [24,25,26] with different biases and contributions.

Poenaru-Olaru et al. [27] assessed the reliability of concept drift detectors by exploring how late they were in reporting drifts and how many false alarms they signaled. The study compared the performance of the most popular drift detectors belonging to two different groups, error rate-based detectors and data distribution-based detectors, on both synthetic and real-world data, providing an insightful discussion of the methods. However, the study only covered abrupt and gradual drift, excluding incremental drift. As incremental changes are prevalent in real-world applications, especially in streaming data scenarios, their absence in the study opens the door for further investigation. Another point to consider is that one of the metrics explored to evaluate the drift detectors was latency, which ranges between 0 and 1 to show how late the detector manages to detect the drift. Using latency as a metric to evaluate drift detectors might not provide a comprehensive analysis of the detector’s delay performance. The use of latency as a metric can also overlook false alarms generated by drift detectors, as the metric only considers the time until the first alarm is raised for a given drift. Additionally, latency might not be appropriate for evaluating some types of drift detectors, such as those based on sliding window techniques. The detectors that operate on a sliding window of data are grounded on detecting the drift as soon as it occurs, regardless of how long it takes to make a prediction on the data within the window.

Gonçalves Jr. et al. [28] evaluated the performance of eight distinct concept drift detectors using artificial datasets that were subject to both abrupt and gradual concept drifts, as well as real-world datasets. The experiments compared the accuracy, evaluation time as well as false alarms and miss detection rates. As with Poenaru-Olaru et al. [27], incremental change was not considered as a type of drift to be explored. However, an important metric was used to enable a fair comparison among drift detectors—the distance to the drift point, which provides information on which method most accurately identified the position of the drift.

Considering the different applications of drift detectors, Barros and Santos [24] compared their configurations of the concept drift detectors in artificial datasets. The main goal was to adequately measure the performance of concept drift detectors and pinpoint the common challenges in detecting drifts closer to their correct positions. Furthermore, the study aimed to determine the parameters that had the most significant impact on the predictive accuracy of the methods. Following the previous surveys, the authors only considered abrupt and gradual changes, limiting the scope of the experiments.

In summary, the reviewed studies explore similar contexts and types of drift, with some variation in the metrics used to analyze performance. Because of the lack of diversity in the experimental design, their results may not cover many particularities or situations of real-world scenarios. The literature review is summarized in

Table 1. Comparison of most commonly applied, drift detectors and types of concept drift by contributions in related works.

Reference #	Drift Detectors	Types of Drift Explored
Gama et al. [2]	DDM	Abrupt; gradual
Baena-Garcıa et al. [13]	EDDM, and DDM	Abrupt; gradual
Frias-Blanco et al. [14]	HDDMW, DDM, ADWIN, and ECDD	Abrupt; gradual
Barros and Santos [24]	DDM, EDDM, ADWIN, ECDD, STEPD, SEQDRIFT, SEED, HDDMA, HDDMW, FHDDM, FTDD, RDDM, and WSTD	Abrupt; gradual
Santos et al. [25]	DDM, EDDM, ADWIN, STEPD, ECDD, SEQDRIFT, HDDMA, HDDMW, FHDDM, RDDM, and WSTD	Abrupt; gradual
Babüroğlu et al. [26]	ADWIN, DDM, EDDM, ECDD, FHDDM, FTDD, GMA, HDDMA, HDMMW, PH, RDDM, SEED, STEPD, SEQDRIFT, and WSTD	Abrupt
Poenaru-Olaru et al. [27]	DDM, EDDM, ADWIN, HDDMA, and HDDMW	Abrupt; gradual
Gonçalves et al. [28]	NB, PL, ADWIN, DOF, DDM, ECDD, EDDM, PHT, and STEPD	Abrupt; gradual

considering drift detectors and types of drift explored.

Regarding the approaches mentioned in this manuscript to deal with concept drift, they are generally applied in specific scenarios with limited comparisons among drift detectors. The detectors may exhibit different behaviors in each type of scenario. Thus, considering them in a general context, most authors do not provide useful information on specific data distributions. Therefore, this paper aims to provide further information about drift detectors using the proposed synthetic dataset technique, exploring different metrics in different contexts.

4. Material and Methods

Selecting an appropriate change detection algorithm is crucial to analyze the characteristics of the data stream in order to detect unexpected and various drift types. Our perspective is that change detectors that rely on monitoring the distribution of the data stream have the potential to detect a wider range of drifts compared to algorithms that utilize mean and variance (such as ADWIN and PH). The latter is a very good choice when it comes to a specific concept drift, such as abrupt ones.

To evaluate the performance of data stream drift detectors over several scenarios, we conducted a benchmarking study using four popular detection methods: DDM, EDDM, HDDMA, and HDDMW. We randomly generated the data streams with three concept drift types: abrupt or sudden, gradual, and incremental. The detectors were evaluated using some performance measures, including F1 score, detection time, and detection delay. To ensure fairness, the same evaluation criteria were adopted for all detectors, which had their performance compared in terms of both accuracy and speed.

Our experiments involved generating streams of three datasets of different types (i.e., abrupt, gradual, and incremental) through an automatic process, as detailed in Section 4.1. We made the tool used for this process publicly available at the following link: https://github.com/gysakurai/datastream-synthetic (accessed on 24 April 2023). Using these datasets, we evaluated four change detection algorithms from four different perspectives, as described in Section 4.2. Specifically, we assessed the algorithms using three evaluation metrics: F1 score, detection time, and detection delay, which are presented in detail in Section 4.3.

4.1. Automatic Generation of Streams

To carry out the experiments, we developed a generator of synthetic stream datasets able to create binary streams driven by several variables to simulate a wide-range of scenarios. The mentioned tool supports the definition of variables such as drift type (abrupt, gradual, or incremental), data stream size, sample range, dataset size, percentage of maximum duration, and drift divisions or amplitude. For each sample of the data stream dataset, the position of the start and end of the drift was randomly generated.

4.1.1. Algorithm for Generation of Abrupt Drifts

Abrupt concept drift is a type of drift that occurs suddenly, resulting in a significant shift in the underlying data distribution. In the context of our binary data streams, an abrupt concept drift might involve a sudden replacement of the target patterns, where a pattern was previously dominant. This type of abrupt concept drift can pose significant challenges for learning algorithms, which rely on a stable data distribution to operate effectively [22].

In Algorithm 1, used for generating streams with abrupt drift, the variables of duration and amplitude with a random number of bits are inputted. Additionally, the start and end of each drift are randomly generated. When the start bit is reached, a 0–1 bit change is made, simulating the start of an abrupt drift.

Algorithm 1 Abrupt drift type

4.1.2. Algorithm for Generation of Gradual Drifts

Detecting and adapting to gradual concept drifts can be difficult due to the smoothness of the changes. Unlike abrupt drifts, gradual drifts occur progressively over time. For this reason, they may go unnoticed until they cause a significant drop in performance. The gradual replacement of the target pattern can result in a gradual shift in the underlying data distribution. Moreover, in some cases, the number and duration of drifts may increase, leading to further challenges in detecting and adapting to changes in the data [22].

Algorithm 2 is designed to generate streams with gradual drift, and takes as input the variables of duration and amplitude, which are defined by a random number of bits. In addition, the start and end positions of each drift are randomly generated, with the duration variable being used to create a gradual pattern over time.

Algorithm 2 Gradual drift type

4.1.3. Algorithm for Generation of Incremental Drifts

Incremental drift is a type of drift that occurs slowly and incrementally, unlike the sudden and more noticeable abrupt drift. The key difference between gradual and incremental drift is the rate at which the underlying concept being learned changes over time. Gradual drift occurs slowly and progressively, while incremental drift occurs suddenly and abruptly. In our experimental data streams, a change in concept does not occur in a binary fashion. Incremental drift may not be immediately apparent, but it presents a unique challenge for detecting and adapting to changes in data streams, as the shift in concept may be subtle and occur over a longer period of time. Detecting and adapting to incremental drift may require sophisticated algorithms and monitoring techniques to identify and respond to changes in the data distribution in a timely and effective manner [22].

Algorithm 3 is designed to generate streams with incremental drift, and takes as input the variable of duration, which is defined by a random number of bits. In addition, the start and end positions of each drift are randomly generated. For each sample of the stream generated by this algorithm, there is only one drift that increments until it reaches a value of 1 bit, simulating a concept drift that changes incrementally over time.

Algorithm 3 Incremental drift type

4.2. Change Detection Algorithms

This section presents the algorithms we picked for our experiment: DDM, EDDM, HDDMA, and HDDMW. The experimental pipeline was developed in Python, using the algorithm implementations provided by the River library [29].

4.2.1. DDM

The drift detection method (DDM) uses statistical tests to determine whether a drift has occurred, based on the difference between the observed error rate and the expected error rate of a threshold [30]. The DDM algorithm assumes that the data are generated by a stationary process and that a change in the data distribution can be detected by monitoring the error rate over time. This calculates the average error rate and variance of the classifier and updates them as new data points arrive. When the error rate exceeds a certain threshold, which is calculated using the Hoeffding bound, the algorithm signals a drift. The algorithm is adaptive, meaning that it can adjust the threshold as more data points arrive, improving the detection accuracy while minimizing false alarms. DDM is computationally efficient and has been shown to perform well in practice, especially for detecting abrupt drifts.

4.2.2. EDDM

The early drift detection method (EDDM) [13] is a modified technique that enhances the DDM method. It is designed to detect drifts as early as possible, even before significant changes in the data distribution occur. EDDM has been shown to be effective in detecting both abrupt and gradual drifts.

The algorithm computes the minimum distance between the reference distribution and the observed distribution in each window and updates it as new data points arrive. When the minimum distance exceeds a certain threshold, the algorithm signals a drift. The threshold is calculated using statistical tests, such as the Student’s t-test and the Chi-squared test, which are sensitive to small changes in data distribution. EDDM uses different statistical tests than DDM and has been shown to be effective in detecting both abrupt and gradual drifts.

4.2.3. HDDMA and HDDMW

Drift detection algorithms created according to the Hoeffding Drift Detection Method (HDDM) modify the original DDM using Hoeffding’s inequality [14]. HDDMA is one of these algorithms and uses the moving average of the observed error rate to estimate the true error rate of the classifier. The algorithm calculates the average error rate over a sliding window of fixed size and compares it to Hoeffding’s bound. If the observed error rate exceeds the bound, the algorithm signals a drift.

The HDDMW algorithm is similar to the HDDMA algorithm but uses a moving weighted average of the observed error rate instead. The algorithm assigns a weight to each data point based on its recency, with more recent data points having higher weights. The weighted average is then used to estimate the true error rate of the classifier and then compared to Hoeffding’s bound. HDDMW is effective in detecting both abrupt and gradual drifts, and it outperforms DDM and HDDMA in some scenarios.

4.3. Evaluation Metrics

The drift detectors’ performances were assessed according to three main criteria: detection accuracy, detection time, and delay to detect drifts. In this section, we provide further details on how the metrics for these criteria were calculated.

4.3.1. F1 Score

F1 score was applied to evaluate the detection performance of all change detection algorithms. We used this score as the primary metric to assess each algorithm for all datasets with different types of concept drifts. F1 score, as presented in Equations (2)–(4), is derived from two other metrics, namely precision and recall [31]. Precision measures the ability of the assessed algorithm to avoid false positives. Recall expresses the capacity of the assessed algorithm to detect as many drifts as possible. By combining these two metrics, F1 score provides a broader picture of the algorithm’s accuracy.

$$Precision=\frac{\mathit{TP}}{\mathit{TP}+\mathit{FP}}$$

(2)

$$Recall=\frac{\mathit{TP}}{\mathit{TP}+\mathit{FN}}$$

(3)

$$F1=2·\frac{\mathit{Precision}·\mathit{Recall}}{\mathit{Precision}+\mathit{Recall}}$$

(4)

4.3.2. Detection Time

The notion of detection time plays a critical role in the context of data stream drift detection since it directly impacts the ability of a detector to process incoming data streams in real-time. Applications requiring the timely detection of concept drifts need the use of fast and efficient detectors. The detection time for a data stream drift detector corresponds to the time required to process each incoming instance, and it is influenced by various factors, such as data complexity, data stream size, detector implementation specifics, and available computational resources. Given the trade-off between accuracy and detection time, careful consideration of both factors is vital in selecting and optimizing the data stream drift detectors. Therefore, an evaluation of the detection time of detectors is essential to ensure their ability to operate in real-time and fulfill the requirements of the given application.

For our studies, the detection time of each algorithm was measured by assessing the amount of time it takes for the algorithm to process all the bits of each data stream.

4.3.3. Detection Delay

Detection delay is another metric related to the time that must be assessed for drift detectors. This metric refers to the time interval between the occurrence of a concept drift and its detection by the detector. Drift detectors with low detection delays enable applications to make decisions about detected changes quickly, allowing them to meet real-time constraints. On the other hand, a high detection delay may result in missed opportunities, false alarms, or incorrect decisions, which can have serious consequences in critical applications. Therefore, it is essential to evaluate the detection delay of data stream drift detectors in addition to their accuracy and detection time performance, to ensure that they can detect concept drifts in a timely and reliable manner. The detection delay depends on various factors, such as the complexity of the data, the frequency and magnitude of the drifts, the performance of the detector and the decision threshold used. The trade-off between the detection delay and accuracy is an important consideration in the selection and optimization of data stream drift detectors and may depend on the specific requirements of the intended application.

In Figure 1, the calculation of the detection delay is illustrated as the difference between the exact onset point of each drift (true detection) and the point at which it was detected by the algorithm, as described in the work by Asghari et al. [32]. Notably, when detection occurs outside of the drift area, it is disregarded and excluded from any calculations related to detection delay metrics.

5. Experimental Results

In this study, we benchmarked four drift detection algorithms—DDM, EDDM, HDDMA and HDDMW—on a synthetic data stream dataset designed to evaluate the performance of these algorithms in detecting different types of drifts: abrupt, gradual, and incremental. Our findings were based on three criteria:detection performance, detection time, and detection delay.

5.1. Detection Performance

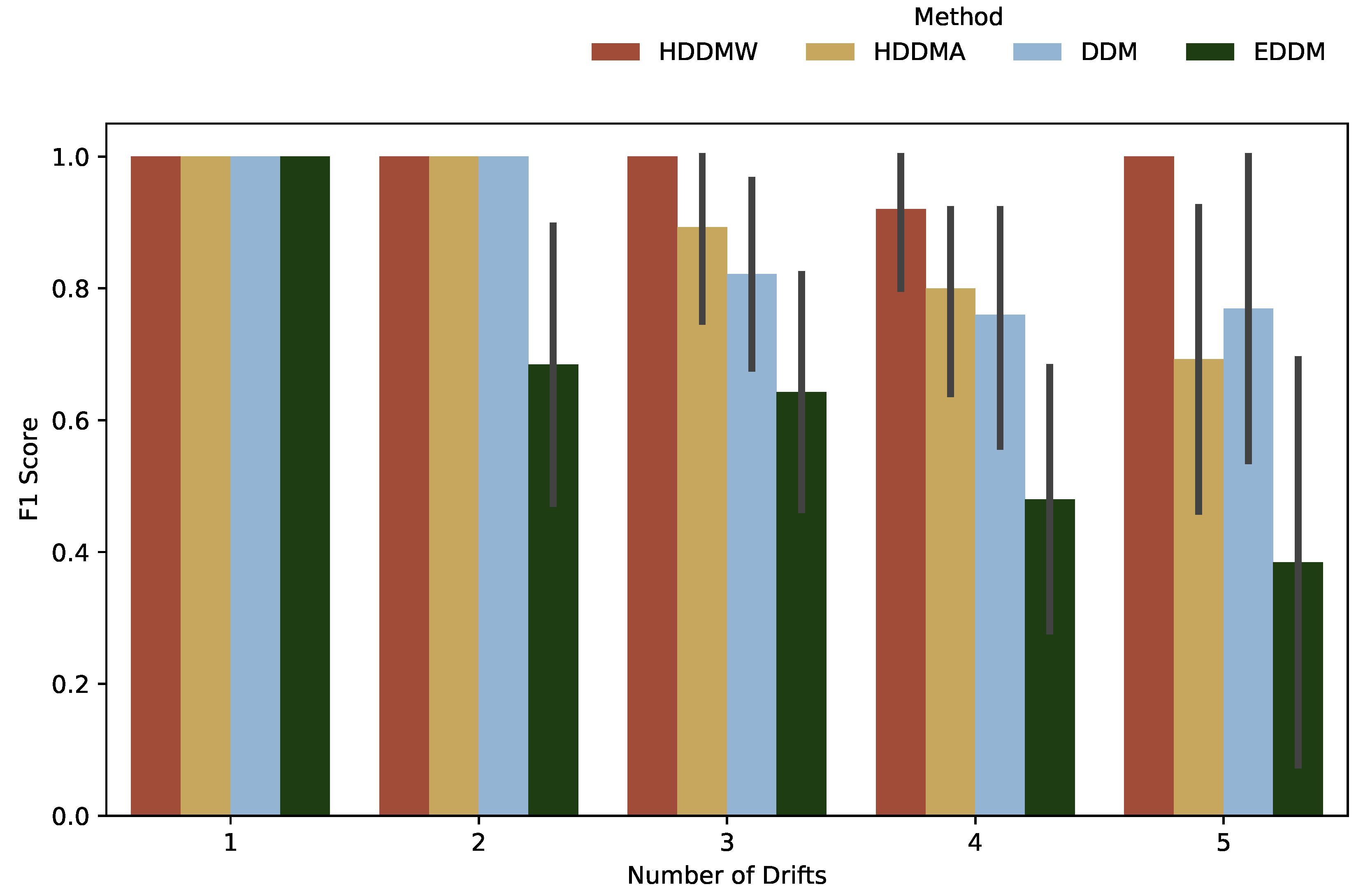
The initial results presented in this study relate to the detection of abrupt drifts. Figure 2 displays F1 score results for varying quantities of drifts, ranging from 1 to 5. It is evident that the algorithms achieved a maximum performance with an equivalent F1 score for a quantity of 1 of abrupt drifts, as shown in Figure 2. However, when the number of drifts was increased to 2, the HDDMW, HDDMA, and DDM algorithms consistently displayed reduced F1 scores, whereas the EDDM algorithm yielded a markedly inferior score. Notably, the algorithms exhibited a decreasing F1 score as the number of drifts increased. Nevertheless, the HDDMW algorithm maintained the most suitable average F1 score, while the EDDM algorithm yielded the least favorable average score.

For incremental drifts, unlike abrupt drifts, only the EDDM algorithm yielded a good result, with an F1 score close to the maximum possible. With a significant discrepancy, HDDMW had the second-best performance, while HDDMA and DDM obtained much lower and almost negligible scores. In Figure 3, it is possible to compare the algorithms’ performances regarding incremental drifts.

As we only used one incremental drift per stream, unlike abrupt drifts, the figure presents the F1 score result for only one unit of drift.

The detection performance for gradual drifts is presented in Figure 4. When the amount of drifts is 1 or 2, all algorithms yielded an identical performance, as evidenced by their respective F1 scores close to 1. However, when the number of drifts is increased to 3 or 4, the HDDMW, DDM and EDDM algorithms maintained their performance levels, while the HDDMA algorithm exhibited a decrease in its average F1 score. For five drifts, all four algorithms achieved equitable performance levels, exhibiting F1 scores of approximately 0.8. The overall results show that HDDMW, DDM, and EDDM algorithms showed equivalent performances, while the HDDMA algorithm demonstrated an inferior performance.

We evaluate the drift detection performance in terms of F1 score based on a statistical analysis grounded on the non-parametric Friedman statistical test [33] to determine any significant differences among EDDM, DDM, HDDMW, and HDDMA with 300 streams. Following the Friedman test, we performed a Nemenyi post hoc test [34] with a significance level of 0.05. The null hypothesis posits that the drift detectors’ performances are comparable based on the average F1 score per stream. If the null hypothesis is rejected, the Nemenyi post hoc test can be used. This test establishes that the performance of two detectors is significantly distinct if the average ranks differ by at least a critical difference (CD) value. Figure 5 shows the CD diagram for the F1 score. Particularly, we assume that there are no significant differences between HDDMA and DDM. All other differences are significant. In other words, EDDM was statistically the most accurate method, followed by HDDMW. HDDMA and DDM are statistically similar.

5.2. Detection Time

Regarding the algorithms’ detection time performance, our experiments revealed that the DDM algorithm achieved a notably lower detection time (y axis) compared to the others, overall. The drift detection methods based on the Hoeffding algorithms exhibited similar behavior, albeit with a higher detection time. In contrast, the EDDM algorithm displayed a marked distance from the other algorithms, with the results varying considerably throughout the analysis of each sample (identified on the x axis), as shown in Figure 6.

We made the same evaluation process as when assessing the detection performance to evaluate the detection time performance using the non-parametric Friedman statistical test to identify any significant differences among EDDM, DDM, HDDMW, and HDDMA with 300 streams. Figure 7 presents the CD diagram for detection time. According to the statistical test, there are no statistically significant differences between only HDDMA and HDDMW. Thus, we can infer that these two detectors are the fastest in comparison to the others. When selecting a drift detector, both detection time and detection performance should be considered. HDDMW is a better option than HDDMA, DDM, and EDDM since it significantly reduces the detection time while maintaining adequate predictive performance.

5.3. Detection Delay

Figure 8 presents the results for detection delay in seconds in the logarithm scale. The HDDMW algorithm had the best performance for abrupt drifts, detecting drifts in a much shorter time than the others. HDDMW is followed by HDDMA, DDM, and EDDM, respectively, but with similar times among them. For gradual drifts, HDDMW showed again a significantly shorter time than the other algorithms, followed by HDDMA, DDM, and EDDM. For incremental drifts, the HDDMA algorithm had the best detection delay performance, followed by HDDMW and EDDM with markedly different results. In none of our experiment’s samples, the DDM algorithm was able to detect an incremental drift, so there were no delay results.

6. Discussion and Open Issues

Incremental drifts proved to be the most difficult to simulate and validate. The creation of multiple samples with various random variables helped us find the best detector for this type of algorithm. Other works in the literature, such as those by Gonçalves Jr. et al. [28], Poenaru-Olaru et al. [27], and Barros and Santos [24] did not consider incremental drift in their analyses.

Our experiments have also shown that there is a significant trade-off among drift detection performance, detection time, and detection delay for the analyzed algorithms. Upon the analysis of the DDM algorithm, it demonstrated commendable proficiency in detecting abrupt and gradual drifts, as evidenced by its noteworthy average algorithm detection time. However, it was observed that the algorithm suffers from a relatively suboptimal detection delay, ranking as the second slowest algorithm in this regard. Notably, the algorithm’s most pronounced limitation lies in its capacity to identify incremental drifts, which we were unable to successfully detect during our experimental investigation.

In contrast to other algorithms, the EDDM algorithm excels in detecting incremental drifts, with a better F1 score performance than the other algorithms. However, it has a weakness in time-related criteria, such as a longer detection time and detection delay. The algorithm encounters challenges in detecting gradual drifts when the frequency of drifts increases in comparison to other algorithms. Nonetheless, it boasts the second-best performance in terms of both detection time and detection delay when it comes to detecting such drifts. However, it exhibits a notable limitation in its ability to detect incremental drifts, which are associated with an extremely low score in this regard.

The HDDMW algorithm has demonstrated superior consistency in detecting abrupt drifts, even with an increase in their frequency. However, it suffers from suboptimal detection time performance, ranking second worst in this regard. Furthermore, it exhibits a notable limitation in its ability to detect incremental drifts, as evidenced by a suboptimal detection performance and delay. On the other hand, the algorithm’s most noteworthy strength lies in its superior detection delay for both abrupt and gradual drifts, outperforming other algorithms in this regard.

Finally, our experiments have shown that choosing the best algorithm heavily depends on the objective and weaknesses we want to avoid, our prior knowledge of the data stream that will be subjected to drift detection analysis, and the type of drift. Throughout our studies, we were able to analyze the behavior of some of the most famous concept drift algorithms in detecting different types of drift, as well as their detection time and delay. Additionally, we were able to ensure replicability by varying several parameters in the construction of each type of drift using the tool developed for synthetic datasets.

Our findings have important implications for binary data stream behavior. The ability to detect drifts in real time can help adjust their strategies to better suit the changing needs of their behavior. Furthermore, the use of drift detection algorithms can help improve the overall accuracy and reliability of machine-learning models in these settings. In future research endeavors, it would be advantageous to explore more sophisticated drift detection algorithms and techniques, including ensemble methods and deep learning-based approaches. Nonetheless, it is imperative to recognize that, while deep learning-based techniques may yield promising results in detecting concept drifts across multiple domains, their efficacy is frequently constrained by the requirement for large volumes of labeled data and computational resources. Moreover, the black-box nature of these methods can impede the interpretation and understanding of their predictions, thereby restricting their utility in domains where interpretability is crucial. Therefore, efforts to enhance the precision and efficiency of drift detection in synthetic and real-world data streams would benefit from considering these limitations when assessing and selecting the appropriate techniques. Additionally, the use of more diverse and larger datasets would help increase the quality of the findings to a wider range of applications and industries.

7. Conclusions

The study’s results demonstrate significant variation in the performance of drift detection algorithms based on the type of drift. The HDDMW algorithm exhibits a superior performance for abrupt and gradual drifts, with HDDMA, DDM, and EDDM following in descending order. Conversely, the EDDM algorithm achieves the best performance for incremental drifts, with HDDMW ranking second, and HDDMA and DDM receiving notably lower scores.

As the number of drifts increases, the performance of the algorithms deteriorates, albeit with the HDDMW algorithm maintaining the most favorable average F1 score, while the EDDM algorithm exhibits the least favorable average score. In terms of detection time, the DDM algorithm achieves a significantly lower unit of time than the other algorithms, with the drift detection methods based on Hoeffding algorithms ranking next. However, the EDDM algorithm presents significant variability in terms of its detection time.

Future research may explore the potential of more advanced drift detection algorithms and techniques, such as ensemble methods or deep learning-based approaches, to enhance the accuracy and efficiency of drift detection in synthetic and real-world data streams. Additionally, the use of more diverse and larger datasets would improve the quality of the findings for various applications and industries.

In conclusion, researchers and practitioners should select the HDDMW algorithm for abrupt and gradual drifts, the EDDM algorithm for incremental drifts, and the DDM algorithm for the best detection time performance. These findings have practical implications for selecting appropriate drift detection algorithms tailored to specific needs.