4.1. Research Methodology and Applied Metric for Performance Evaluation
This subsection is concerned with the applied research methodology and metric for performance evaluation of the analyzed distributed consensus algorithms. All the experiments were carried out in Matlab2018b (Producer: MathWorks, Location: Natick, MA, USA) using built-in Matlab functions and software designed by the authors of this paper (downloadable at [
84]). As mentioned earlier in this paper, we generated random
d-regular bipartite graphs with the graph order
n = 30 and various degrees
d. Specifically,
d took the following values in our experiments:
Obviously, higher values of
d result in better connectivity of generated graphs. In our experiments, we only used connected topologies since the algorithms were unable to estimate global aggregate functions in disconnected graphs (note that data can only be separately aggregated in segregated components in disconnected topologies) [
52]. For every examined
d, we generated 100 unique regular bipartite graphs in order to ensure the high credibility of our presented contributions (executing experiments in numerous various graphs is a common procedure in top-quality papers from the field [
85,
86,
87]). Overall, we, thus, examined the algorithms in 500 unique graphs in this paper.
In order to evaluate the performance of the analyzed algorithms, we applied a commonplace metric used in top-quality papers in the field. Specifically, we quantified the algorithms’ performance using the convergence rate expressed as the number of iterations required for all the agents in MAS to achieve the consensus. In this case, the examined algorithms were bounded by a stopping criterion to border their execution time. In this paper, we applied the stopping criterion defined in (
23), where
took the values from (
24) [
65,
66].
Clearly, for lower values of
, the final estimates were assumed to be more precise but at the cost of decelerating the algorithms. Later in this paper, the precision
is referred to as a low precision,
as a medium precision, and
as a high precision. See
Figure 8, where the maximum error of an estimate (expressed in percentages %) is depicted for each applied precision. From the figure, we can see that the low precision of the applied stopping criterion ensures that the error did not exceed 30%, the medium precision guaranteed an error lower than 0.3%, and the high precision resulted in very accurate estimates since its maximum estimation error was even lower than 0.003%.
Note that we only calculated and depicted the averaged value of the applied metric for each
d and each precision of the applied stopping criterion in
Section 4.2.
In order to simulate sensor-measured initial values, we generated the initial inner states of all the agents in MAS as IID (independent and identically distributed) random scalar values with the standard Gaussian distribution, i.e., [
52]:
As stated above, both GMH and CW are easily modifiable algorithms since the entries of their weight matrices
W contain the mixing parameter
[
51]. In our experiments, it took the values from (
26) in the case of CW and (
27) if GMH was applied.
Later in this paper, we refer to
from (
26) as MD 0.1, MD 0.2, … etc., and 0.1, 0.2 … from (
27) as GMH 0.1, GMH 0.2, …, etc.
4.2. Experimental Results and Discussion about Observable Phenomena
In what follows, we focus our attention on the performance evaluation of the analyzed algorithms in regular bipartite graphs of various connectivities in order to identify whether all the algorithms can achieve the consensus and find the best-performing approach among those examined. In each connectivity graph, the algorithms were evaluated for three different precisions of the stopping criterion (the precision is provided in the right upper corner of each figure).
For
d = 2 (see
Figure 9 and
Table A1 in
Appendix A) and the low precision of the applied stopping criterion, we can see that the best performance was achieved by GMH 0.1. The second-best-performing algorithm for this precision was CW, with
= MD 0.9. Both BC and OW achieved the same performance (as for
d = 2, their matrices were identical) and were the third best among the analyzed algorithms. As further seen from the figure, the worst of the examined algorithms was MH. In the cases of the medium/high precision of the stopping criterion, GMH 0.1 outperformed all the other approaches again. Here, BC and OW were, however, better than CW and were, thus, the second best among the examined algorithms. The worst performance was observed for MH, like in the previous analysis. Moreover, it can be seen that the best performance for CW was achieved with the highest analyzed mixing parameter (i.e.,
= MD 0.9), and its performance declined with a decrease in
(this is valid for each precision of the stopping criterion). For low values of
, its performance was significantly lower than the other examined algorithms. In contrast, GMH performed the best, provided that the lowest
was applied (like for CW, this is valid for each precision of the stopping criterion). In addition, it can be seen from the figures that an increase in
resulted in performance degradation of the mentioned algorithm.
For
d = 3 (see
Figure 10 and
Table A2 in
Appendix A), OW was the best-performing approach for each precision of the used stopping criterion, unlike the previous analysis. The second-best-performing algorithm, in this case, was GMH (however, with
= 0.3), CW with
= MD 0.9 was the third best, BC was the fourth one, and MH was the worst approach once again—these statements are valid for each precision of the stopping criterion for
d = 3. In the case of CW, we can see that an increase in
resulted in better performance of the algorithm, and the highest convergence rate was obtained with
= MD 0.9, like for
d = 2. In contrast, GMH did not achieve the highest performance with the lowest
(like in the previous analysis), but with
= 0.3. In this case, we can see that an increase in
ensured the algorithm accelerated until the maximum convergence rate was achieved. Afterward, a further increase in
resulted in the deceleration of the algorithm.
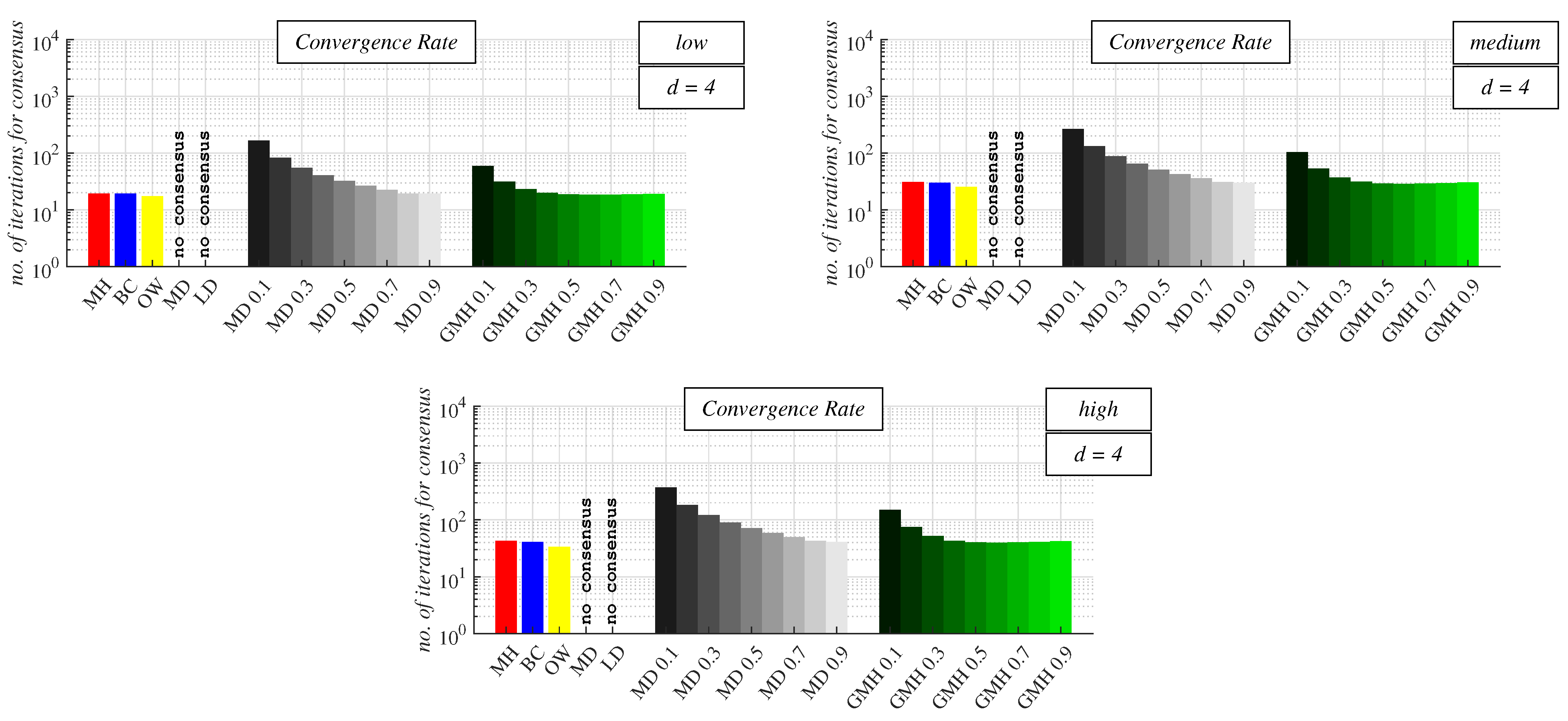
For
d = 4 (see
Figure 11 and
Table A3 in
Appendix A), the best-performing algorithm for each precision of the stopping criterion was OW again. The second-best one for each precision was GMH, but now with
= 0.6 (note that the maximum was obtained for a greater
than for
d = 3). Compared to the previous analysis, BC outperformed CW with the optimal mixing parameter (for
d = 4, CW performed the best with
= MD 0.9) if the precision of the stopping criterion was medium/high. However, if its precision was low, CW performed better than BC, like in the previous analysis. MH was also the worst algorithm regarding the number of iterations required for the consensus achievement in these graphs like before. CW achieved the highest performance with the highest examined
, like for
d = 2 and 3. However, GMH achieved the maximum convergence rate with
= 0.6; therefore, with a higher value of the mixing parameter than for
d = 3. Again, we can see that an increase in
resulted in a decrease in the number of iterations for consensus until the maximum convergence rate was achieved, like for
d = 3. Then, a further increase in
caused the performance of GMH to worsen.
In addition, for
d = 5 (see
Figure 12 and
Table A4 in
Appendix A), OW outperformed the concurrent algorithms for each precision of the stopping criterion, like for the two previously analyzed values of
d. The second-best-performing algorithm for each precision of the used stopping criterion was paradoxically MH, which was the worst approach for
d = 2, 3, and 4, as seen from
Figure 9,
Figure 10 and
Figure 11. Thus, GMH was the best performing with
= 1 (i.e., MH), which is, theoretically, the slowest initial configuration in non-regular non-bipartite topologies. For the low precision, the next in order was CW, but this algorithm performed the best with
= MD 0.8 in this case. The worst algorithm of the applied stopping criterion for the low precision was BC: the fastest algorithm with the Perron matrix. However, for the medium/high precision of the stopping criterion, BC outperformed CW with
= MD 0.8. The performance of CW increased with the growth of
until the maximum convergence rate was obtained. A further increase in
caused the algorithm to decelerate. In the case of GMH, increasing
ensured a better performance of the algorithm.
In the largest examined graphs (i.e.,
d = 10, see
Figure 13 and
Table A5 in
Appendix A), OW achieved the highest performance for each precision of the applied stopping criterion again. Here, BC performed well and was the second best performing in these graphs. The third best was CW but with
= MD 0.7 in this case. The best-performing configuration of GMH was the configuration with
= 1 (MH), which was, however, outperformed by all the other concurrent approaches. As further seen from the figures, a decrease in
caused the performance of GMH to decline. In the case of CW, an increase in
ensured acceleration of the algorithm until the maximum convergence rate was achieved (note that this maximum was achieved for lower
than for
d = 5). Afterward, a further increase in the value of
decelerated the algorithm, like in the previous analysis.
As also seen from
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13, MD and LD algorithms diverging in regular bipartite graphs were unable to achieve the consensus for each precision of the stopping criterion. One can also observe that an increase in the precision of the stopping criterion caused all the examined algorithms to decelerate. In addition, we see that an increase in
d ensured that the algorithms performed better (the only exceptions were GMH and MH).
In this paragraph, we summarize the results from
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13 for each examined algorithm to identify the best-performing approach in
d-regular bipartite graphs. We can see from the presented results that the performance of MH was the worst in many scenarios. Its high performance was only observed for
d = 5—it was the optimal initial configuration of GMH in these graphs (and also for
d = 10). However, its performance significantly degraded in the densest analyzed topologies (i.e.,
d = 10), and this algorithm was only better than the other configurations of GMH in these graphs. As further seen from the figures, BC performed poorly in many scenarios where the low precision of the stopping criterion was applied. As further seen, its performance can be generally considered average. However, for
d = 2 (when its matrix was identical to the weight matrix
W of OW) and
d = 10 (i.e., in the densest examined topologies), its performance was relatively pretty good. In both these cases, its performance was the second best among the analyzed algorithms. Overall, OW was the best-performing approach according to the presented experimental results since it outperformed all the other algorithms for each precision of the used stopping criterion except for the graphs with
d = 2 (the performance was lower if the low precision of the stopping criterion was applied). CW was one of the worst algorithms in terms of the number of iterations required for consensus achievement. In addition, it was necessary to know the value of
d to identify the optimal configuration of this algorithm, which was its other significant drawback. However, it performed relatively well in sparsely connected graphs with the low precision of the stopping criterion. GMH outperformed all its competitors in the sparsest graphs (i.e.,
d = 2), but its performance was significantly degraded with an increase in connectivity (for
d = 10, this was the worst algorithm among those examined). Similar to CW, knowing
d was also required for the optimal configuration of this algorithm. What is most important is that all the examined algorithms except for MD and LD can achieve the consensus in each
d-regular bipartite graph regardless of the precision of the applied stopping criterion. Thus, except for MD and LD, no other algorithm required the implementation of the mechanism presented in [
52] or required to be reconfigured.
4.3. Comparison with Papers Concerned with Examined Algorithms in Non-Regular Non-Bipartite Graphs
In this section, we individually compare each of the examined algorithms in
d-regular bipartite graphs with their performance in non-regular non-bipartite graphs analyzed in papers from
Section 2.2.
MH was the worst algorithm in many examined scenarios, as seen from the figures. However, for
d = 5, it was the best configuration of GMH, which does not correspond to theoretical assumptions from [
51]. In these graphs, it performed well and was the second-best-performing algorithm. It was also the optimal configuration of GMH for
d = 10; however, its performance was very low in this case (it even decreased compared to the performance in sparser graphs). This significant degradation of its performance in densely connected graphs was not seen in non-regular non-bipartite graphs [
65,
66]. In general, we can see that MH did not perform well in regular bipartite graphs, such as in non-regular non-bipartite graphs [
63,
65,
66].
BC performed well in the densest examined graphs, which confirms the conclusions in non-regular non-bipartite graphs [
66]. As identified in [
63,
65,
66], BC usually performed poorly in sparse non-regular non-bipartite graphs, but its performance was high in 2-regular bipartite graphs (i.e., in graphs of the lowest examined connectivity). As shown in [
65,
66], in non-regular non-bipartite graphs, BC performed much better if the precision of the stopping criterion was not low. This statement was partially confirmed in regular bipartite graphs. In general, this algorithm achieved an average performance, which was also identified in non-regular non-bipartite graphs [
62,
63,
65,
66].
As already mentioned, OW can be considered the best-performing distributed average consensus algorithm since it outperformed the other algorithms in almost every executed scenario. The only exception was the graphs with
d = 2, where this algorithm was beaten by GMH (for each precision of the applied stopping criterion) and even by CW (if the precision was low). This statement is supported by the conclusions from [
64,
66], where this algorithm was identified as being slow in the transient phase—the sparse connectivity of graphs caused this phase to take a longer time, and the low precision of a stopping criterion ensured that the algorithms were stopped early on. In addition, our findings in this paper correspond to the conclusions in regular bipartite graphs, where OW was mostly the best algorithm [
62,
63,
65,
66,
67,
68,
69,
70]. As shown in [
63,
65,
66], its performance was not good in sparsely connected graphs or if the stopping criterion was operating at a low precision, like in this paper.
According to the presented results, CW was one of the worst-performing algorithms, which corresponds to its performance in non-regular non-bipartite topologies [
51,
62]. Its higher performance was only seen for
d = 2 and the low precision of the stopping criterion. The theoretical assumption from [
51] that higher values of
ensure better performance of the algorithm was only valid in sparser graphs. As seen from the figures, for higher values of
d, the value of
guaranteeing its maximum performance was decreased.
Regarding GMH, this algorithm also achieved high performance, especially in sparsely connected graphs (confirmed by [
64]). Similar to CW, the theoretical assumption about the optimal value of
was not valid again—here, a lower value of
did not ensure better performance in denser regular bipartite graphs in contrast to non-regular non-bipartite topologies [
51]. As the graph connectivity grew, we can see that this algorithm did not achieve its maximum performance with the lowest examined value of
. In densely connected graphs, we can see that higher connectivity caused a greater value of
to ensure maximum performance. Thus, our finding does not correspond to the theoretical assumptions from [
51] that a lower
guarantees a better performing algorithm. In densely connected
d-regular bipartite graphs, MH, theoretically, slowest configuration of GMH, was the optimal initial configuration of this algorithm, which does not correspond to conclusions in non-regular non-bipartite graphs [
51]. As in the case of MH, the performance of this algorithm significantly decreased for
d = 10—this phenomenon was not observed in non-regular non-bipartite topologies [
51].
As seen in [
65], all the algorithms performed better in graphs of higher connectivity. This statement is also valid in regular bipartite graphs for each algorithm except for GMH and MH, whose performance was significantly degraded in the densest examined graphs compared to graphs of sparser connectivity. Furthermore, a higher precision of the applied stopping criterion resulted in a lower convergence rate, which corresponds with the conclusions in regular bipartite graphs [
65].