Neural Network Exploration for Keyword Spotting on Edge Devices
Abstract
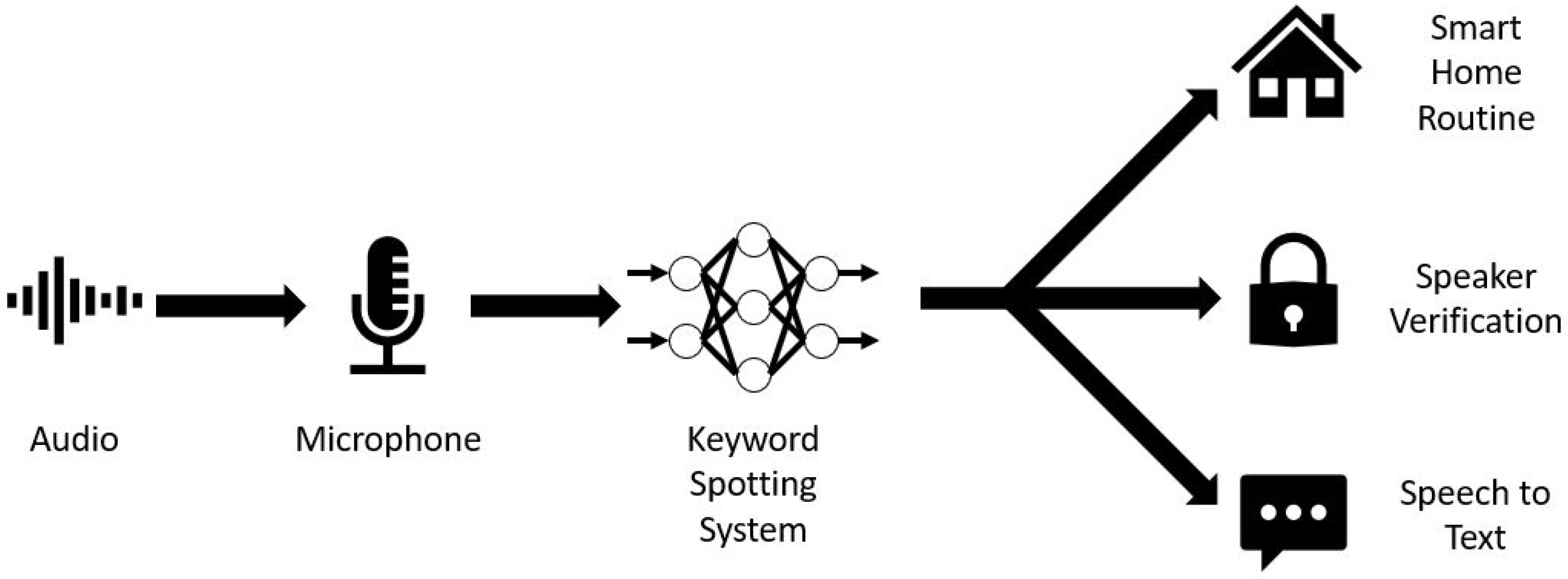
:1. Introduction
- The complete neural network development process of keyword spotting from implementation, training, quantization, evaluation, and deployment is explored. The implementation and training were carried out with TensorFlow using the well-known Google Speech Commands dataset on a Google Cloud Platform virtual machine. After training, the TensorFlow models were quantized and then converted into smaller, space-efficient FlatBuffers using TensorFlow Lite. The performance metrics, especially those pertinent to edge devices, of various quantization schemes for each neural network model were evaluated. Finally, the steps of deploying the quantized models on embedded systems such as a microcontroller board and an FGPA board were explored through the help of TensorFlow Lite Micro and CFU Playground. This process can be a useful guideline for neural network development on edge devices for keyword spotting and other similar applications.
- A total of 70 models are created, representing different model sizes of six neural network architectures well-suited for keyword spotting on embedded systems. The models are evaluated using metrics relevant to deployment on resource-constrained devices, such as model size, memory consumption, and inference latency, in addition to accuracy and parameter count. CNN-based neural network architectures are chosen for their superior performance in classifying spatial data on edge devices. They are especially fit for our keyword spotting application, as the audio input is processed into mel spectrograms that can be treated as an image-like input. This comparison is helpful for developers to find the best-performing neural network given the constraints of a target embedded system.
- The effect of four available post-training quantization methods in the TensorFlow Lite library on model performance is evaluated. In general, quantization reduces the model size while adversely affecting its performance. However, the reduction in model size and the impact on accuracy, memory consumption, and inference latency varied depending on the neural network architecture as well as the quantization method. This highlights the importance of taking multiple factors, such as network architecture, computing, and memory resources available on the edge device, as well as performance expectations, into consideration for edge computing applications such as keyword spotting.
2. Background
2.1. Audio Processing
2.2. Selected Neural Network Architectures
- FFCN: The FFCN has a simple network architecture with one input layer, one output layer, and an arbitrary number of layers in between, called hidden layers. FFCN models exhibit a noticeable leap in performance over hidden Markov model (HMM)-based approaches in keyword spotting tasks [9].
- Depthwise separable convolutional neural network (DS-CNN): The DS-CNN was designed for efficient embedded vision applications [23]. The DS-CNN effectively decreases both the number of required parameters and operations by replacing standard 3D convolution layers with depthwise separable convolution layers (i.e., 2D depthwise convolutions followed by 1D pointwise convolutions), which enables the utilization of larger architectures, even in embedded systems with limited resources.
- Deep residual network (ResNet): The ResNet architecture was conceived to combat the vanishing gradient problem, i.e., despite the neural network growing in size with each additional layer, the accuracy saturates and then degrades rapidly. Residual connections and the residual building block were devised to solve this problem. In a residual block, the output of a layer is added to another layer deeper in the block. This addition is followed by applying a nonlinear activation function to introduce nonlinearity into the block. Chaining these residual layers together (using convolution layers for the weight layers) forms a ResNet neural network. ResNet was originally proposed for image recognition [11]. It has also been applied to keyword spotting with the flexibility to adjust both the depth and width for a desired trade-off between model footprint and accuracy [24].
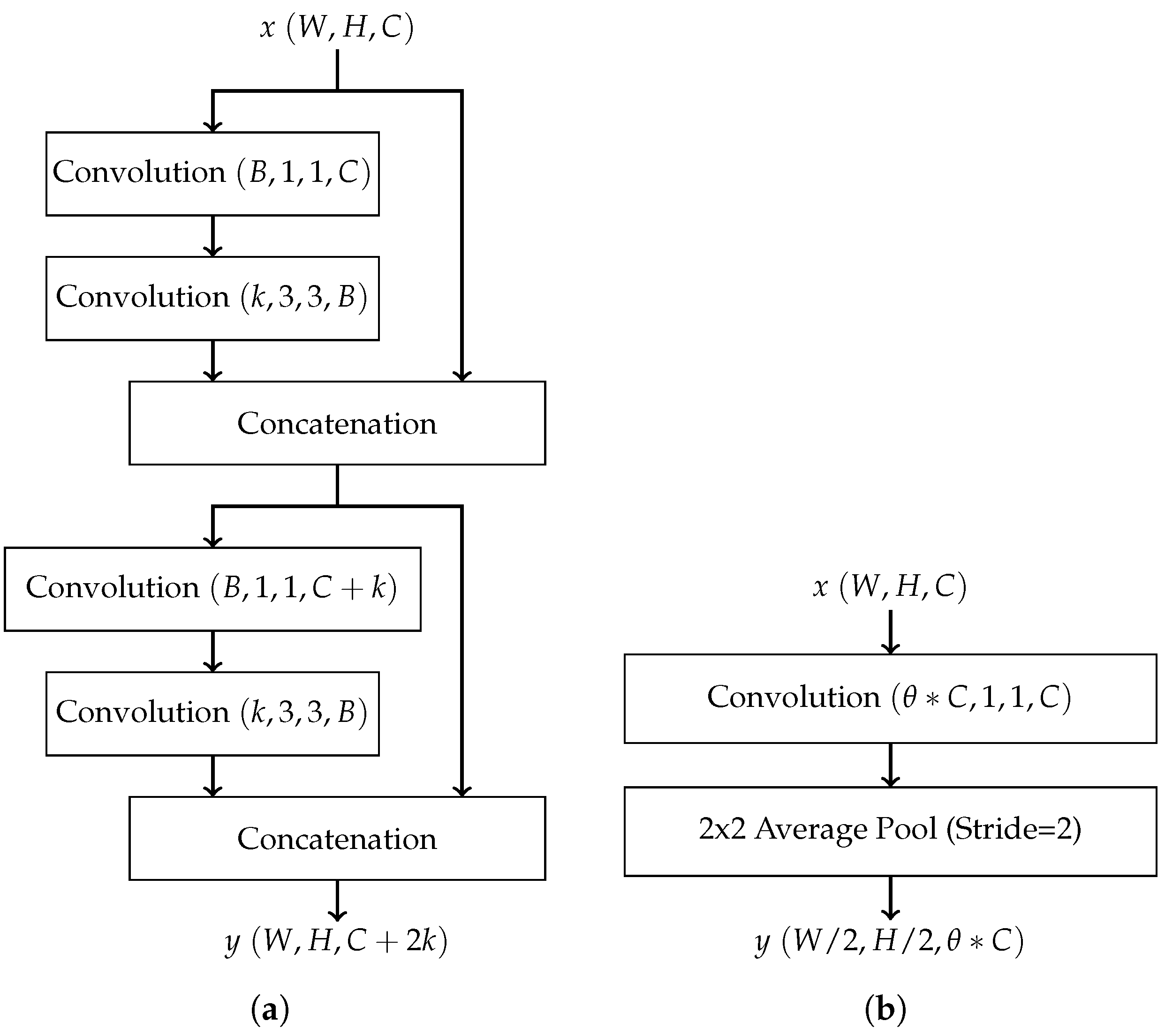
- Dense convolutional network (DenseNet): DenseNet also combats the vanishing gradient problem by promoting effective feature propagation. It requires a comparatively smaller number of parameters and fewer computations, making it well-suited for embedded applications. The DenseNet architecture implements a concept similar to residual connections with the introduction of the dense block. In short, a dense block is a series of alternating convolution and concatenation operations where the input to each convolution layer is the combined output of every preceding convolution layer [12]. Thus, each layer passes its own feature maps to all subsequent layers. Dense blocks do not reduce the dimensions of feature maps due to the presence of concatenation operations. Thus, transition layers are inserted between dense blocks, where each transition layer consists of a convolutional layer followed by pooling. The DenseNet architecture has two other variations: DenseNet-B and DenseNet-C [12]. DenseNet-B introduces bottleneck layers, which are inserted before convolution layers within dense blocks to reduce the number of feature maps and thus reduce the total number of weights. DenseNet-C introduces a compression factor as part of transition blocks to reduce the number of feature maps passed between dense blocks. DenseNet-B and DenseNet-C may be combined to form DenseNet-BC to prevent the number of parameters from ballooning. Figure 2 shows examples of a dense block and a transition block in DenseNet. In these figures, W, H, and C in represent, respectively, the width, height, and the number of channels of the input matrix x. The same notation applies to the output y. Each convolution block, e.g., Convolution , uses N convolution kernels, each with a size of width height channels , and produces N output feature maps. B in Figure 2a represents the number of feature maps produced by the bottleneck layer in DenseNet-B.
- Inception: The Inception architecture was designed to address two problems associated with increasing convolutional neural network size: the increase in the number of parameters and the amount of computational resources required to produce a result. These problems share a solution: sparsity, i.e., by replacing all fully connected layers with sparsely connected layers. However, due to limitations in modern computer architecture, sparse calculations are very inefficient. Thus, the Inception module was developed to approximate these sparse layers while maintaining reasonable efficiency on modern computers. An Inception module is composed of a series of parallel convolutional layers with different filter sizes (1 × 1, 3 × 3, 5 × 5) and a pooling layer [10]. With multiple filter sizes, the network is enhanced to capture features at different levels of abstraction. Chaining these modules together then forms an Inception neural network. The structure of an Inception module is depicted in Figure 3.Inception was originally designed for image classification and detection [10], and there is no known previous work applying it to keyword spotting. However, it is reasonable to apply Inception to the speech recognition problem, since a mel spectrogram is a pictorial representation of an audio recording.
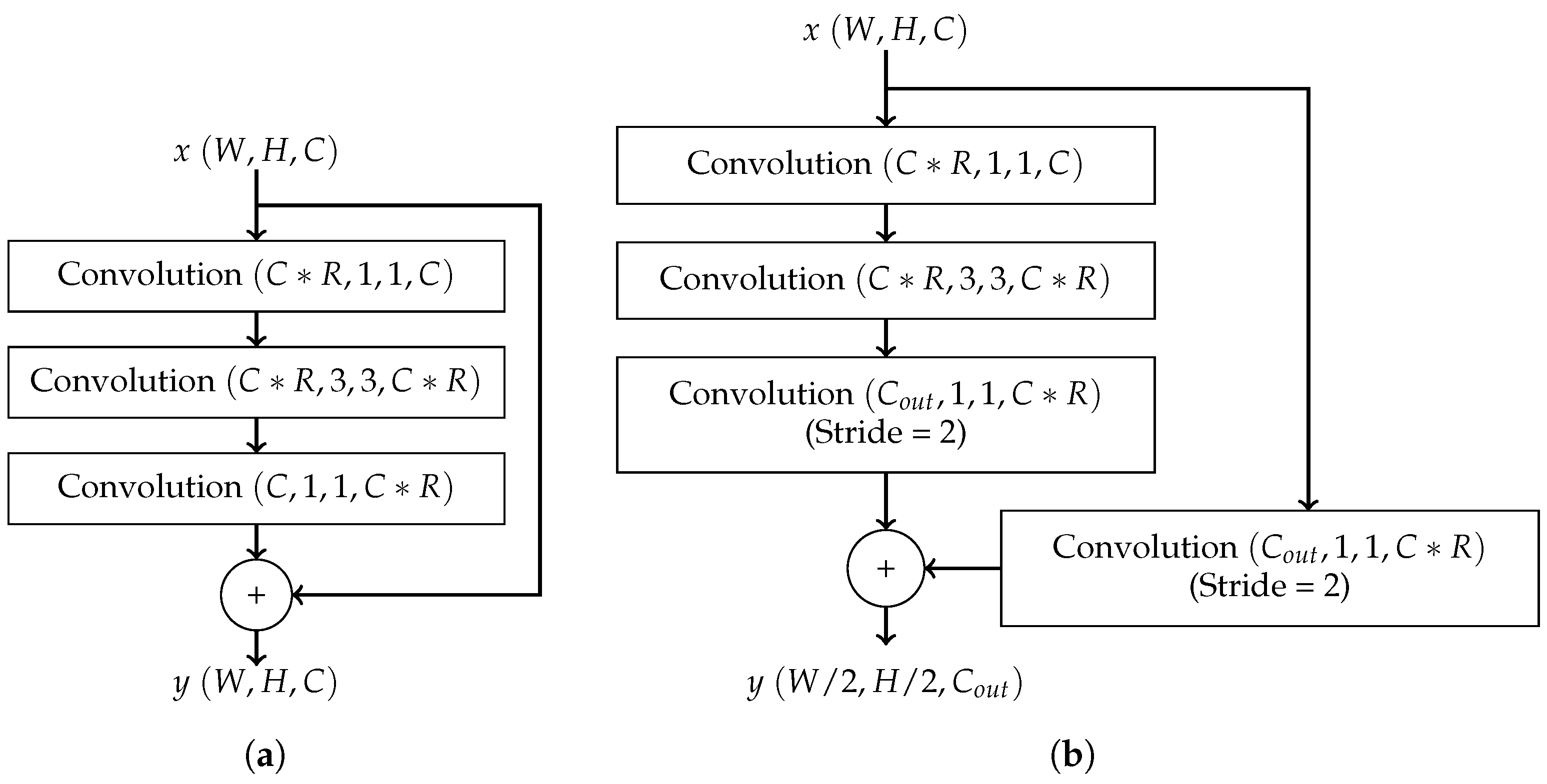
- CENet: To enable execution on embedded systems, CENet employs a residual bottleneck block. These bottleneck layers are connected to form a stage, and multiple stages can be chained together to form a complete network. As the bottleneck blocks do not decrease the size of the feature maps, a residual connection block is required to transition between stages. Each connection block decreases the number of internal feature maps by a factor of to lower resource requirements. These connection layers are inserted between stages of bottleneck blocks, forming a complete network. Figure 4 illustrates the structures of a residual bottleneck block and a residual connection block in CENet. The CENet architecture was designed explicitly to perform keyword spotting on resource-constrained devices. The proposed residual connection and bottleneck structure is compact and efficient and shown to generate superior performance [14].
2.3. Quantization
3. Method
3.1. Dataset Implementation
3.2. Architecture Implementation
3.3. Training
3.4. Quantization
- The 16-bit floating-point quantization utilizes 16-bit floating-point values for weights and 32-bit floating-point values for operations.
- Dynamic range quantization allows the model to mix integer and floating-point operations when possible (falling back to 32-bit floating-point operations when necessary) while the weights are stored as 8-bit integers. The weights are quantized post training, and the activations are quantized dynamically at inference in this method.
- Integer quantization with floating-point fallback utilizes integers for weights and operations. If an integer operation is not available, the 32-bit floating-point equivalent is substituted. This results in a smaller model and increased inference speed. For convenience, this scheme is shortened hereafter as integer-float quantization.
- Full-integer quantization utilizes only 8-bit integers for weights and operations, removing the dependency on floating-point values. This method achieves further latency improvements, reduction in peak memory usage, and compatibility with integer-only hardware devices or accelerators.
3.5. Deployment
4. Evaluation and Deployment Results
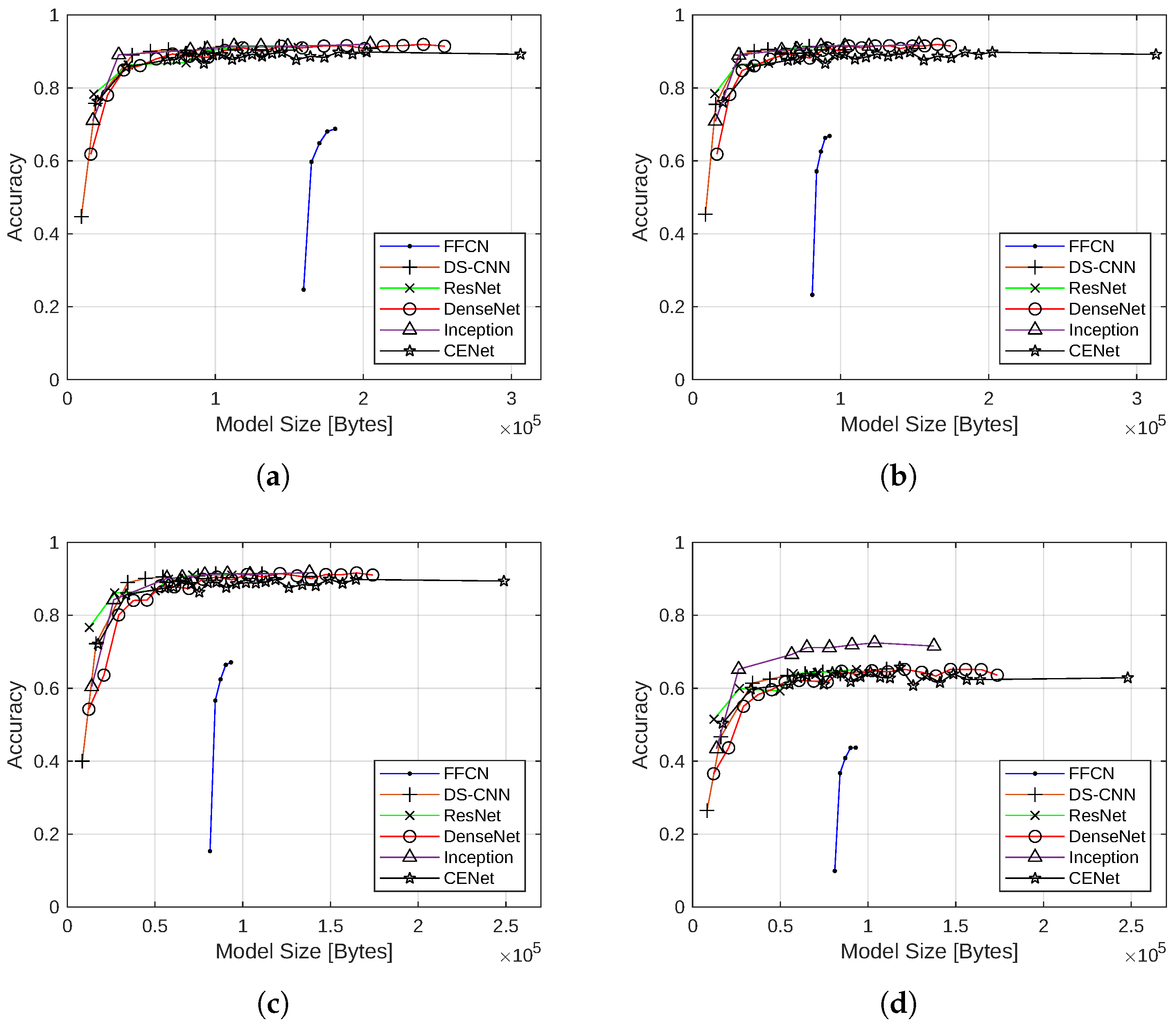
4.1. Evaluation Results
4.1.1. Performance without Quantization
4.1.2. Model Size Reduction with Quantization
4.1.3. Effect of Quantization on Accuracy
4.1.4. Effect of Quantization on Memory Consumption
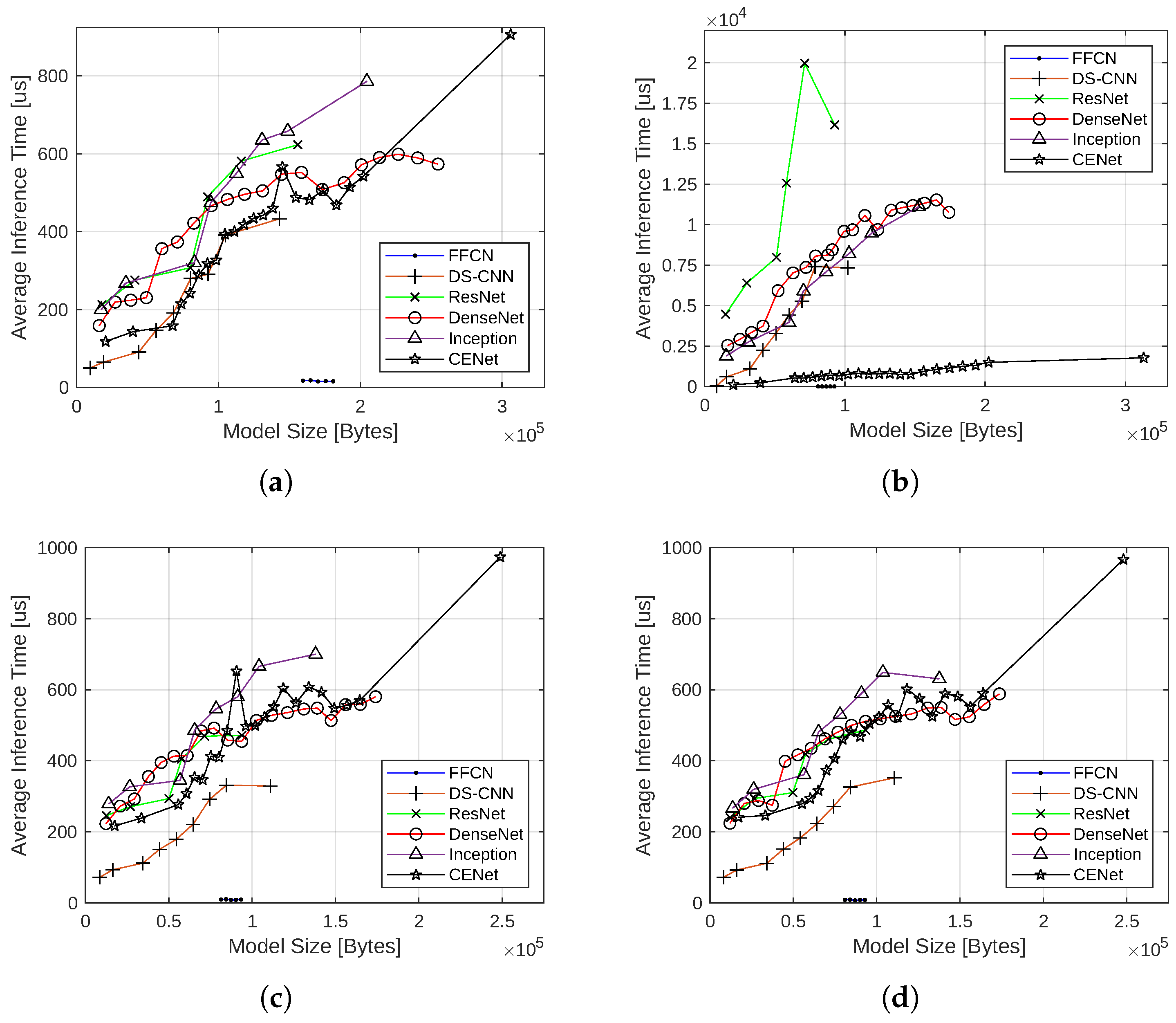
4.1.5. Effect of Quantization on Inference Latency
4.1.6. Summary
4.2. Deployment Results
4.2.1. Deployment on Arduino Nano BLE Microcontroller Board
4.2.2. Deployment on Digilent Nexys 4 FPGA Board
5. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Implemented FFCN Models
| Model | Units |
|---|---|
| 0 | [48, 48, 48, 48, 48] |
| 1 | [48, 48, 48, 48] |
| 2 | [48, 48, 48] |
| 3 | [48, 48] |
| 4 | [48] |
Appendix A.2. Implemented DS-CNN Models
| Model | Initial Features | Features | Layers |
|---|---|---|---|
| 0 | 16 | [32, 64, 128] | [1, 6, 2] |
| 1 | 16 | [32, 64, 128] | [1, 6, 1] |
| 2 | 16 | [32, 64, 128] | [1, 5, 1] |
| 3 | 16 | [32, 64, 128] | [1, 4, 1] |
| 4 | 16 | [32, 64, 128] | [1, 3, 1] |
| 5 | 16 | [32, 64, 128] | [1, 2, 1] |
| 6 | 16 | [32, 64, 128] | [1, 1, 1] |
| 7 | 16 | [32, 64] | [1, 1] |
| 8 | 16 | [32] | [1] |
Appendix A.3. Implemented ResNet Models
| Model | Initial Features | Features | Layers |
|---|---|---|---|
| 0 | 16 | [16, 24, 32] | [2, 2, 2] |
| 1 | 16 | [16, 24, 32] | [2, 2, 1] |
| 2 | 16 | [16, 24, 32] | [2, 1, 1] |
| 3 | 16 | [16, 24, 32] | [1, 1, 1] |
| 4 | 16 | [16, 24] | [1, 1] |
| 5 | 16 | [16] | [1] |
Appendix A.4. Implemented DenseNet Models
| Model | Initial Features | Blocks | Layers | Bottleneck | Growth | Compression |
|---|---|---|---|---|---|---|
| 0 | 16 | 4 | [2, 4, 8, 6] | 32 | 8 | 0.5 |
| 1 | 16 | 4 | [2, 4, 8, 5] | 32 | 8 | 0.5 |
| 2 | 16 | 4 | [2, 4, 8, 4] | 32 | 8 | 0.5 |
| 3 | 16 | 4 | [2, 4, 8, 3] | 32 | 8 | 0.5 |
| 4 | 16 | 4 | [2, 4, 8, 2] | 32 | 8 | 0.5 |
| 5 | 16 | 4 | [2, 4, 8, 1] | 32 | 8 | 0.5 |
| 6 | 16 | 4 | [2, 4, 7, 1] | 32 | 8 | 0.5 |
| 7 | 16 | 4 | [2, 4, 6, 1] | 32 | 8 | 0.5 |
| 8 | 16 | 4 | [2, 4, 5, 1] | 32 | 8 | 0.5 |
| 9 | 16 | 4 | [2, 4, 4, 1] | 32 | 8 | 0.5 |
| 10 | 16 | 4 | [2, 4, 3, 1] | 32 | 8 | 0.5 |
| 11 | 16 | 4 | [2, 4, 2, 1] | 32 | 8 | 0.5 |
| 12 | 16 | 4 | [2, 4, 1, 1] | 32 | 8 | 0.5 |
| 13 | 16 | 4 | [2, 3, 1, 1] | 32 | 8 | 0.5 |
| 14 | 16 | 4 | [2, 2, 1, 1] | 32 | 8 | 0.5 |
| 15 | 16 | 4 | [2, 1, 1, 1] | 32 | 8 | 0.5 |
| 16 | 16 | 4 | [1, 1, 1, 1] | 32 | 8 | 0.5 |
| 17 | 16 | 3 | [1, 1, 1] | 32 | 8 | 0.5 |
| 18 | 16 | 2 | [1, 1] | 32 | 8 | 0.5 |
| 19 | 16 | 1 | [1] | 32 | 8 | 0.5 |
Appendix A.5. Implemented Inception Models
| Model | Initial Features | Modules | Parameters |
|---|---|---|---|
| 0 | 16 | [2, 4, 2] | [[8, 12, 16, 2, 4, 4], [24, 12, 26, 2, 6, 8], [48, 24, 48, 6, 16, 16]] |
| 1 | 16 | [2, 4, 1] | [[8, 12, 16, 2, 4, 4], [24, 12, 26, 2, 6, 8], [48, 24, 48, 6, 16, 16]] |
| 2 | 16 | [2, 3, 1] | [[8, 12, 16, 2, 4, 4], [24, 12, 26, 2, 6, 8], [48, 24, 48, 6, 16, 16]] |
| 3 | 16 | [2, 2, 1] | [[8, 12, 16, 2, 4, 4], [24, 12, 26, 2, 6, 8], [48, 24, 48, 6, 16, 16]] |
| 4 | 16 | [2, 1, 1] | [[8, 12, 16, 2, 4, 4], [24, 12, 26, 2, 6, 8], [48, 24, 48, 6, 16, 16]] |
| 5 | 16 | [1, 1, 1] | [[8, 12, 16, 2, 4, 4], [24, 12, 26, 2, 6, 8], [48, 24, 48, 6, 16, 16]] |
| 6 | 16 | [1, 1] | [[8, 12, 16, 2, 4, 4], [24, 12, 26, 2, 6, 8]] |
| 7 | 16 | [1] | [8, 12, 16, 2, 4, 4] |
Appendix A.6. Implemented CENet Models
| Model | Initial Features | Stages | Parameters |
|---|---|---|---|
| 0 | 16 | [15, 15, 7] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 1 | 16 | [7, 7, 7] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 2 | 16 | [7, 7, 6] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 3 | 16 | [7, 7, 5] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 4 | 16 | [7, 7, 4] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 5 | 16 | [7, 7, 3] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 6 | 16 | [7, 7, 2] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 7 | 16 | [7, 7, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 8 | 16 | [7, 6, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 9 | 16 | [7, 5, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 10 | 16 | [7, 4, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 11 | 16 | [7, 3, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 12 | 16 | [7, 2, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 13 | 16 | [7, 1, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 14 | 16 | [6, 1, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 15 | 16 | [5, 1, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 16 | 16 | [4, 1, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 17 | 16 | [3, 1, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 18 | 16 | [2, 1, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 19 | 16 | [1, 1, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48], [0.25, 0.25, 64]] |
| 20 | 16 | [1, 1] | [[0.5, 0.5, 32], [0.25, 0.25, 48]] |
| 21 | 16 | [1] | [0.5, 0.5, 32] |
References
- What Is Alexa? Amazon Alexa Official Site. Available online: https://developer.amazon.com/en/alexa (accessed on 20 May 2023).
- Microsoft. Cortana. Available online: https://www.microsoft.com/en-us/cortana (accessed on 20 May 2023).
- Apple. Siri. Available online: https://www.apple.com/siri/ (accessed on 20 May 2023).
- Google Assistant, Your Own Personal Google Default. Available online: https://assistant.google.com/ (accessed on 20 May 2023).
- He, Y.; Sainath, T.N.; Prabhavalkar, R.; McGraw, I.; Alvarez, R.; Zhao, D.; Rybach, D.; Kannan, A.; Wu, Y.; Pang, R.; et al. Streaming end-to-end speech recognition for mobile devices. In Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 6381–6385. [Google Scholar]
- ESP32-WROOM-32E ESP32-WROOM-32UE Datasheet. Available online: https://www.espressif.com/sites/default/files/documentation/esp32-wroom-32e_esp32-wroom-32ue_datasheet_en.pdf (accessed on 20 May 2023).
- Han, H.; Siebert, J. TinyML: A systematic review and synthesis of existing research. In Proceedings of the 2022 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Jeju Island, Republic of Korea, 21–24 February 2022; pp. 269–274. [Google Scholar]
- Soro, S. TinyML for ubiquitous edge AI. arXiv 2021, arXiv:2102.01255. [Google Scholar]
- Chen, G.; Parada, C.; Heigold, G. Small-footprint keyword spotting using deep neural networks. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 4087–4091. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Zhang, Y.; Suda, N.; Lai, L.; Chandra, V. Hello Edge: Keyword spotting on microcontrollers. arXiv 2018, arXiv:1711.07128. [Google Scholar]
- Chen, X.; Yin, S.; Song, D.; Ouyang, P.; Liu, L.; Wei, S. Small-footprint keyword spotting with graph convolutional network. In Proceedings of the 2019 IEEE Automatic Speech Recognition and Understanding Workshop (ASRU), Sentosa, Singapore, 14–18 December 2019; pp. 539–546. [Google Scholar]
- Rybakov, O.; Kononenko, N.; Subrahmanya, N.; Visontai, M.; Laurenzo, S. Streaming keyword spotting on mobile devices. In Proceedings of the Annual Conference of International Speech Communication Association (Interspeech 2020), Shanghai, China, 25–29 October 2020; pp. 2277–2281. [Google Scholar]
- Arik, S.O.; Klieg, M.; Child, R.; Hestness, J.; Gibiansky, A.; Fougner, C.; Prenger, R.; Coates, A. Convolutional recurrent neural networks for small-footprint keyword spotting. arXiv 2017, arXiv:1703.05390. [Google Scholar]
- Warden, P. Speech Commands: A dataset for limited-vocabulary speech recognition. arXiv 2018, arXiv:1804.03209. [Google Scholar]
- David, R.; Duke, J.; Jain, A.; Reddi, V.J.; Jeffries, N.; Li, J.; Kreeger, N.; Nappier, I.; Natraj, M.; Regev, S.; et al. TensorFlow Lite Micro: Embedded machine learning on tinyML systems. arXiv 2021, arXiv:2010.08678. [Google Scholar]
- Prakash, S.; Callahan, T.; Bushagour, J.; Banbury, C.; Green, A.V.; Warden, P.; Ansell, T.; Reddi, V.J. CFU Playground: Full-stack open-source framework for tiny machine learning (tinyML) Acceleration on FPGAs. arXiv 2023, arXiv:2201.01863. [Google Scholar]
- Rabiner, L.R.; Shafer, R.W. Theory and Applications of Digital Speech Processing; Pearson: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Muda, L.; Begam, M.; Elamvazuthi, I. Voice recognition algorithms using mel frequency cepstral coefficient (MFCC) and dynamic time warping (DTW) techniques. J. Comput. 2010, 2, 138–143. [Google Scholar]
- Sainath, T.N.; Parada, C. Convolutional neural networks for small-footprint keyword spotting. In Proceedings of the Annual Conference of International Speech Communication Association (Interspeech 2015), Shanghai, China, 6–10 September 2015; pp. 1478–1482. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Tang, R.; Lin, J. Deep residual learning for small-footprint keyword spotting. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 5484–5488. [Google Scholar]
- Nagel, M.; Fournarakis, M.; Amjad, R.A.; Bondarenko, Y.; van Baalen, M.; Blankevoort, T. A white paper on neural network quantization. arXiv 2021, arXiv:2106.08295. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. In Proceedings of the USENIX Symposium on Operating Systems Design and Implementation (OSDI), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Google Cloud. Cloud Computing Services. Available online: https://cloud.google.com/ (accessed on 20 May 2023).
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- TensorFlow Lite. ML for Mobile and Edge Devices. Available online: https://www.tensorflow.org/lite (accessed on 20 May 2023).
- TensorFlow Lite. Model Optimization. Available online: https://www.tensorflow.org/lite/performance/model_optimization (accessed on 20 May 2023).
- Arduino Nano 33 BLE Sense Product Reference Manual. Available online: https://docs.arduino.cc/static/a0689255e573247c48d417c6a97d636d/ABX00031-datasheet.pdf (accessed on 20 May 2023).
- Nexys 4 FPGA Board Reference Manual. Available online: https://digilent.com/reference/_media/reference/programmable-logic/nexys-4/nexys4_rm.pdf (accessed on 20 May 2023).
- TensorFlow Lite Micro Speech Example Code Repository. Available online: https://github.com/tensorflow/tflite-micro/tree/main/tensorflow/lite/micro/examples/micro_speech (accessed on 20 May 2023).






| Parameter | Value |
|---|---|
| batch_size | 128 |
| validation_split | 0.2 |
| sample_rate | 16,000 |
| audio_length_sec | 1 |
| nfft | 512 |
| step_size | 400 |
| mel_banks | 40 |
| max_db | 80 |
| Quantization Scheme | FFCN | DS-CNN | ResNet | DenseNet | Inception | CENet |
|---|---|---|---|---|---|---|
| 16-bit floating point | 50.72% | 62.29% | 58.31% | 65.95% | 63.24% | 81.20% |
| Dynamic range | 25.81% | 48.22% | 39.51% | 52.41% | 50.55% | 39.51% |
| Integer-float | 26.01% | 50.94% | 37.23% | 47.75% | 45.36% | 66.52% |
| Full integer | 25.91% | 50.26% | 36.80% | 47.42% | 44.98% | 66.09% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bushur, J.; Chen, C. Neural Network Exploration for Keyword Spotting on Edge Devices. Future Internet 2023, 15, 219. https://doi.org/10.3390/fi15060219
Bushur J, Chen C. Neural Network Exploration for Keyword Spotting on Edge Devices. Future Internet. 2023; 15(6):219. https://doi.org/10.3390/fi15060219
Chicago/Turabian StyleBushur, Jacob, and Chao Chen. 2023. "Neural Network Exploration for Keyword Spotting on Edge Devices" Future Internet 15, no. 6: 219. https://doi.org/10.3390/fi15060219
APA StyleBushur, J., & Chen, C. (2023). Neural Network Exploration for Keyword Spotting on Edge Devices. Future Internet, 15(6), 219. https://doi.org/10.3390/fi15060219






