RIS-Assisted Fixed NOMA: Outage Probability Analysis and Transmit Power Optimization

Abstract

Reconfigurable intelligent surface (RIS)-assisted non-orthogonal multiple access (NOMA) has the ability to overcome the challenges of the wireless environment like random fluctuations, shadowing, and mobility in an energy efficient way when compared to multiple input-multiple output (MIMO)-NOMA systems. The NOMA system can deliver controlled channel gains, improved coverage, increased energy efficiency, and enhanced fairness in resource allocation with the help of RIS. RIS-assisted NOMA will be one of the primary potential components of sixth-generation (6G) networks, due to its appealing advantages. The analytical outage probability expressions for smart RIS-assisted fixed NOMA (FNOMA) are derived in this paper, taking into account the instances of RIS as a smart reflector (SR) and an access point (AP). The analytical and simulation findings are found to be extremely comparable. In order to effectively maximize the sum capacity, the formulas for optimal powers to be assigned for a two-user case are also established. According to simulations, RIS-assisted FNOMA surpasses FNOMA in terms of outage and sum capacity. With the aid of RIS and the optimal power assignment, RIS-AP-FNOMA offers ≈62% improvement in sum capacity over the FNOMA system for a signal-to-noise ratio (SNR) of 10 dB and 32 elements in RIS. A significant improvement is also brought about by the increase in reflective elements.

1. Introduction

The wireless society has begun to concentrate on connected intelligence [1]. The major focus of 6G is ultra-high rate, ultra-low latency, ultra-high dependability, and massive connectivity. The key technologies which support 6G are massive MIMO, ultra-dense networks (UDN), terahertz, and millimeter wave (mmWave) communication. The artificial intelligence (AI) and machine learning (ML)-based physical layer will pave the way for emerging applications of 6G [2]. The majority of traditional wireless research focuses on the development of algorithms, protocols, and other tools to combat the effects of radio environments. On the other hand, energy efficiency has received a lot of attention in order to secure sustainable green communication [3]. Massive MIMO employs an array of antennas at both the base station (BS) and the user equipment (UE) to provide unrivaled capacity improvements. Higher radio frequency (RF) bands, on the other hand, make electro-magnetic (EM) waves more susceptible to obstruction, particularly in metropolitan areas [4]. With today’s fifth-generation (5G) wireless technologies, universal coverage and massive connectivity are not possible. As a result, new technologies are needed to enable data-intensive and energy-intensive applications.

RIS is a new emerging hardware technology that reduces energy usage, while artificially controlling and changing the propagation environment to create a superior wireless channel. The RIS is built up of a collection of low-cost, passive reflecting components that reconfigure incident EM waves [5,6]. Using RIS, the uncontrollable wireless environment is transformed into a semi-controllable wireless environment. RIS can be simply installed on a variety of surfaces, including building facades, vehicle doors, roadside billboards, indoor walls, unmanned aerial vehicles (UAVs), pedestrian clothing, and so on. Tall buildings can obstruct the line-of-sight (LoS) between BS and UEs, reducing throughput significantly. The judicious placement of RIS can create a virtual LoS between the BS and the UEs, improving the signal-to-interference plus noise ratio (SINR). RIS can passively beamform signals collected from a transmitter to a desired receiver [7]. Unlike traditional amplify-and-forward (AF) and decode-and-forward (DF) relays, power amplifiers are not required for RIS [8,9,10]. Further, energy sources are also not required to encode, decode, retransmit, and process RF signals [4]. As a result, RIS installation is both energy efficient and environmentally benign. RIS can be integrated with other emerging technologies, such as NOMA, simultaneous wireless information and power transfer (SWIPT), UAV-aided communication, physical layer security (PLS), cognitive radios, autonomous cars, etc., due to its appealing features [11]. Power-domain NOMA can be coupled with RIS to improve spectral efficiency and the enormous connectivity. In NOMA, the signals of different users are overlaid in the power domain so that the spectrum is exploited more efficiently. Based on the channel conditions, users are explored opportunistically. Further, it is also compatible with full-duplex relays, index modulation (IM), etc. Because of these advantages, RIS provides unlimited potential to the 6G wireless technologies.

RIS can boost cell-edge users’ received signal power, while also reducing interference from nearby cells [12]. The power loss due to long haul communication can be overcome by RIS-SWIPT [13]. It helps mobile edge computing-based internet of things (IoT) networks function better in terms of latency [14]. It acts as an EM signal reflection hub, allowing the massive connectivity of device-to-device (D2D) networks [15]. It can improve PLS by intelligently canceling unauthorized transmissions using passive beamforming [16]. It can be effectively used for indoor rate-hungry applications like virtual reality (VR). The RIS-coupled visible light communications (VLC) and wireless-fidelity (Wi-Fi) ensure zero blind spots [17]. It can be utilized in vehicular ad hoc networks (VANET), autonomous vehicular networks, robotics networks [18], UAV networks [19], autonomous underwater vehicular networks, intelligent sensor networks, etc.

The following is the order in which the rest of the manuscript is presented: Related works on RIS and NOMA are discussed in Section 2. Analytical expressions for outage probability are developed in Section 3 for RIS as a smart reflector (RIS-SR)-assisted FNOMA system. Most of the traditional works integrating RIS and NOMA assume this RIS-SR-FNOMA configuration, with passive RIS installed far from the BS and UE. Because of propagation losses and shadowing, RIS may receive very weak signals and may not beamform the received signals to the intended users. As a result, RIS as an AP (RIS-AP)-assisted FNOMA configuration is proposed, in which the passive RIS is located near the AP. Analytical expressions for outage probability are developed in Section 4 for RIS-AP-FNOMA. In Section 5, analytical expressions are derived for assigning optimal powers to both the near user (NU) and far user (FU) of the NOMA system. In Section 6, extensive Monte Carlo (MC) simulations are carried through MATLAB R2023a to corroborate the developed analytical expressions. This research aimed to demonstrate that the RIS-AP-FNOMA configuration outperforms the traditional RIS-SR-FNOMA configuration in terms of outage and sum capacity. The research findings as well as future works are described in the Conclusions.

2. Related Work

Liaskos, C. et al. developed the hypersurface tile as a prototype of RIS to realize the software-controlled wireless environment [20]. Renzo, M.D. et al. highlighted the recent research progress and key challenges in RIS-assisted communication [21]. Basar, E. et al. discussed the differences between RIS and other technologies, as well as the benefits and challenges of RIS-assisted communication [22]. Wu, Q. et al. covered the issues related to RIS-assisted communication, the optimization of passive beamforming, channel estimation, and placement design [23]. Björnson, E. et al. explored the myths and overstatements concerning the RIS that have been spread in the literature [7]. Huang, C. et al. investigated the impact of using RIS with multiple antenna BS and multiple users [3]. The transmit power and phase shifts are designed to be energy efficient such that individual link budgets of the UEs are guaranteed. Two computationally efficient approaches are explored in this article. The first technique uses fractional programming for optimal transmit power allocation and gradient descent to obtain RIS phase shift coefficients. The second approach optimizes RIS phase shifts using fractional programming. The suggested algorithms’ performance is investigated in a realistic outdoor environment. When compared to typical multiple antenna AF relays, RIS-assisted resource allocation has a maximum energy efficiency improvement of 300%. Shi, W. et al. evaluated the RIS-assisted communication system under security risks [24]. The placement of RIS here is intended to increase the authorized user’s secrecy probability of outage. The theoretical secrecy probability of outage expressions is constructed by considering the discrete phase shifts at RIS. It is established that increasing the RIS elements of a discrete phase shifter by 1.6 times yields a performance comparable to that of a continuous phase shifter.

Yuan, X. et al. highlighted the three important physical layer issues, such as acquiring channel state information (CSI), passive information transfer, and low-complexity design, when incorporating RIS into wireless networks [25]. Some of the prospective RIS research directions are also highlighted, such as PLS and edge intelligence. Guo, H. et al. maximized the weighted sum capacity of all UEs by jointly designing the beamforming at BS and phase shift angles at RIS [26]. On both perfect and poor CSI conditions, the suggested scheme was tested. This approach was shown to be effective, even when the channel uncertainty is less than 10%. Agarwal, A. et al. developed closed-form outage probability expressions for ordered NOMA uplink and downlink by examining generalized fading channels [27]. The authors took into account both statistical and instantaneous CSI-based ordering schemes. Singh, S. and Bansal, M. proposed NOMA-assisted cooperative relaying for reliable communication [28]. At the first and second time slots of cooperative communication, the source and relay transmits a superimposed signal. The exact analytical closed-form outage probability formulas were developed considering Rayleigh fading channel and imperfect successive cancellation decoding. The suggested scheme’s outage probability was assessed and compared to that of the traditional cooperative relaying-assisted NOMA.

Yang, Y. et al. jointly optimized the power assignment from the BS to UEs and the phase shift matrix of RIS to maximize the SINR of all the UEs [29]. Ni, W. et al. maximized the sum capacity by jointly optimizing the power allocation, phase shift matrix, user association, decoding order, and channel assignment [30]. Zheng, B. et al. discussed the challenge of optimizing transmit power for a single input-single output (SISO) RIS-assisted NOMA system [31]. The theoretical performance of RIS-assisted orthogonal multiple access (OMA) and RIS-assisted NOMA was compared. All of the preceding works are based on static channel conditions. Guo, Y. et al. developed a joint optimization framework for resource allocation and deciding phase shift angles to maximize the sum capacity of SISO RIS-NOMA downlink [32]. The analysis was carried out under fading channels. To optimize beamforming vectors and phase shift matrices, Fu, M. et al. employed several convex algorithms [33]. The goal of this approach is to minimize the total transmit power for multiple input-single output (MISO) RIS-NOMA. Mu, X. et al. combined active beamforming at BS and passive beamforming at RIS to maximize the sum capacity [34]. Trigui, I. et al. developed the theoretical framework to analyze the outage performance of RIS-aided communication over generalized fading channels and in the existence of phase noise. It was demonstrated that when the fading channels are independent, RIS-aided communication achieves full diversity, even with the existence of phase noise [35].

Singh, S. and Bansal, M. proposed a cooperative cognitive radio NOMA, in which primary and secondary users share a secondary DF relay via NOMA [36]. The closed-form outage probability expressions were developed assuming imperfect CSI and successive interference cancellation (SIC). The influence of channel estimate inaccuracy, power allocated to individual users, and threshold for detection on outage probability was also investigated in this study. MC simulations were used to substantiate the accuracy of analytical outage expressions. Hemanth, A. et al. investigated the implications of hardware impairments on the reliability of RIS-assisted NOMA [37]. The closed-form analytical outage probability and throughput expressions were developed. The number of reflective components and power assignment factors were found to be important in enhancing the performance of RIS-assisted NOMA over OMA. Yang, L. and Yuan, Y. employed RIS-assisted NOMA for PLS [38]. The analytical expressions for secrecy outage probability were derived. When compared to traditional NOMA systems, it was observed that using RIS can improve secrecy performance.

Kumaravelu, V.B. et al. suggested the blind RIS-assisted FNOMA framework with SR and AP configurations for uplink transmission [39]. An optimization problem for power allocations was constructed to maximize the sum capacity of NU and FU. The analytical outage expressions were validated using extensive computer simulations. Blind RIS-SR-NOMA outperformed traditional NOMA by ≈38% for 32 reflective elements and a 20 dB SNR. Arslan, E. et al. examined the active RIS with virtual NOMA for uplink system [40]. Instead of using user-side controlling powers, the concept of power disparity was applied to achieve virtual NOMA. The end-to-end system model, analytical outage probability, and error probability expressions were developed and affirmed using computer simulations. Jadhav, H.K. and Kumaravelu, V.B. studied the downlink blind RIS-assisted framework for ordered NOMA, where channel gains determine user decoding order [41]. The closed-form outage probability and optimal powers to be assigned expressions were developed for stronger and weaker users. As there are more reflecting elements, the sum capacity increased accordingly. The suggested approach outperformed traditional FNOMA and ordered NOMA systems in terms of outage, bit error rate, and sum capacity. The suggested approach outperformed the ordered NOMA system by ≈33% for 20 dB SNR and 32 reflective elements. In this paper, the performance of RIS-assisted FNOMA is evaluated in light of these considerable benefits of RIS and NOMA.

The major contributions of this paper are threefold:

• Analytical outage probability expressions are developed for NU and FU in a RIS-SR-FNOMA and RIS-AP-FNOMA.
• Analytical expressions are developed for optimal power assignment to NU and FU in both RIS-SR-FNOMA and RIS-AP-FNOMA systems.
• Extensive MC simulations are used to corroborate the resulting analytical outage expressions. The accuracy of derived analytical expressions is proved using the strong correlation between the theoretical and simulation results.

3. Outage Probability Analysis of RIS-SR-FNOMA

The conceptual diagram of RIS-SR-FNOMA is illustrated in Figure 1. In this system, RIS with N reflecting elements acts as a smart reflector. The RIS elements are distributed evenly across the users. RIS is placed sufficiently far from the BS and the users. This results in a two-hop communication system. The BS, NU, and FU are considered to have a single antenna. In a two-user scenario, FU performs direct decoding while dealing with the NU signal as interference. The NU decodes the FU signal first, and the influence of that signal is eliminated through SIC. The resulting signal is then used to decode the NU signal.

The superposition-coded symbol at the BS is given by [27]

$$x_s=\sqrt{{\alpha }_{NU}{P}_s}{x}_{NU}+\sqrt{{\alpha }_{FU}{P}_s}{x}_{FU},$$

(1)

where ${\alpha }_{NU}{P}_s$ and ${\alpha }_{FU}{P}_s$ are the powers allocated to NU and FU, respectively. In FNOMA, ${\alpha }_{NU}<{\alpha }_{FU}$ and ${\alpha }_{NU}+{\alpha }_{FU}=1$. $x_{NU}$ and $x_{FU}$ are the transmit symbols corresponding to NU and FU, respectively. $P_s$ is the average transmit symbol power.

The channel condition between BS to RIS and RIS to UE are modeled as $h_i={\alpha }_i{e}^{j{\theta }_i},h_i\sim C\mathcal{N}\left(0,1\right),i=1,2,\dots ,N$ and $g_i={\beta }_i{e}^{j{\psi }_i},g_i\sim C\mathcal{N}\left(0,1\right),i=1,2,\dots ,N$ respectively. Here, ${\alpha }_i=\sqrt{(Re{\left(h_i\right)}^2+Im{\left(h_i\right)}^2)}$, ${\theta }_i=ta{n}^{-1}\left(\frac{Im\left(h_i\right)}{Re\left(h_i\right)}\right)$, ${\beta }_i=\sqrt{(Re{\left(g_i\right)}^2+Im{\left(g_i\right)}^2)}$ and ${\psi }_i=ta{n}^{-1}\left(\frac{Im\left(g_i\right)}{Re\left(g_i\right)}\right)$.

The passive RIS introduces phase shift ${\varphi }_i$ at each reflecting element, and it is given by

$${\varphi }_i=-{\theta }_i-{\psi }_i,i=1,2,\dots ,N.$$

(2)

The signal received at the FU is [42]

$$r_{FU}=\left(\sum _{\mathrm{i}=\frac{N}{2}+1}^N{g}_i{h}_i{e}^{j{\varphi }_i}\right)x_s+n_{FU},$$

(3)

where $n_{FU}$ is the additive white Gaussian noise (AWGN) at FU and $n_{FU}\in C\mathcal{N}\left(0,N_0\right)$. $N_o$ is the noise variance. Substituting the channel conditions, the received signal at the FU is

$$r_{FU}=\left(\sum _{\mathrm{i}=\frac{N}{2}+1}^N{\alpha }_i{\beta }_i\right)x_s+n_{FU}.$$

(4)

Let $B={\sum }_{\mathrm{i}=\frac{N}{2}+1}^N{\alpha }_i{\beta }_i$ be the cumulative effect of the dual-hop channel for the FU. Substituting B and (1) in (4), the received signal at FU is

$$r_{FU}=B\sqrt{{\alpha }_{NU}{P}_s}{x}_{NU}+B\sqrt{{\alpha }_{FU}{P}_s}{x}_{FU}+n_{FU}.$$

(5)

Since the cumulative dual-hop channel for the FU is weaker and ${\alpha }_{NU}$ is smaller, the first term in (5) is not more dominant than the second term. Hence, by treating the NU signal as interference, the FU signal is detected. The SINR for decoding FU signal, while treating NU signal as interference, is

$${\gamma }_{FU}^{x_{FU}}=\frac{B^2{\alpha }_{FU}{P}_s}{B^2{\alpha }_{NU}{P}_s+N_0}.$$

(6)

At the desired data rate ${\tilde{R}}_{FU}$, the outage for FU occurs when

$${\log }_2\left(1+{\gamma }_{FU}^{x_{FU}}\right)\le {\tilde{R}}_{FU}.$$

(7)

Substituting (6) in (7), the outage probability at the FU is defined as

$$P_{FU}^{o\_SR}=P\left[{\log }_2\left(1+\frac{B^2{\alpha }_{FU}{P}_s}{B^2{\alpha }_{NU}{P}_s+N_0}\right)\le {\tilde{R}}_{FU}\right].$$

(8)

Simplifying (8) gives

$$P_{FU}^{o\_SR}=P\left[B^2\le \frac{R_{FU}{N}_0}{\left({\alpha }_{FU}-{\alpha }_{NU}{R}_{FU}\right)P_s}\right],$$

(9)

where $R_{FU}=2^{{\tilde{R}}_{FU}}-1.$ Since ${\alpha }_i$ and ${\beta }_i$ are positive real, B is always positive. Hence, Equation (9) can be presented as

$$P_{FU}^{o\_SR}=P\left[B\le \sqrt{\frac{R_{FU}{N}_0}{\left({\alpha }_{FU}-{\alpha }_{NU}{R}_{FU}\right)P_s}}\right].$$

(10)

As the number of reflecting elements allocated to FU $\left(N_{FU}\right)$ is larger, according to the central limit theorem (CLT), B follows the Gaussian probability density function $f_B\left(b\right)$ with mean $m_B=\frac{N_{FU}\pi }{4}$ and variance ${\sigma }_B^2=N_{FU}\left[1-\frac{{\pi }^2}{16}\right]$. The outage probability at FU is

$$P_{FU}^{o\_SR}={\int }_0^{y_{FU}}{f}_B\left(b\right)\mathrm{d}b,$$

(11)

where $y_{FU}=\sqrt{\frac{R_{FU}{N}_0}{\left({\alpha }_{FU}-{\alpha }_{NU}{R}_{FU}\right)P_s}}.$ Substituting $f_B\left(b\right)$ and integrating within the limit yields the outage probability as

$$P_{FU}^{o\_SR}=\frac{{\sigma }_B\left\{erf\left(\frac{y_{FU}-m_B}{\sqrt{2}{\sigma }_B}\right)+erf\left(\frac{m_B}{\sqrt{2}{\sigma }_B}\right)\right\}}{2{\sigma }_B},$$

(12)

where $erf(.)$ is the error function. The signal received by the NU is

$$r_{NU}=\left(\sum _{\mathrm{i}=1}^{\frac{N}{2}}{g}_i{h}_i{e}^{j{\varphi }_i}\right)x_s+n_{NU},$$

(13)

where $n_{NU}$ is the AWGN at the NU and $n_{NU}\in C\mathcal{N}\left(0,N_0\right)$. Substituting channel conditions and (2) in (13) gives

$$r_{NU}=\left(\sum _{\mathrm{i}=1}^{\frac{N}{2}}{\alpha }_i{\beta }_i\right)x_s+n_{NU}.$$

(14)

Let $A={\sum }_{\mathrm{i}=1}^{\frac{N}{2}}{\alpha }_i{\beta }_i$ be the cumulative effect of the dual-hop channel for the NU. Substituting A and (1) in (14) gives

$$r_{NU}=A\sqrt{{\alpha }_{NU}{P}_s}{x}_{NU}+A\sqrt{{\alpha }_{FU}{P}_s}{x}_{FU}+n_{NU}.$$

(15)

Since A and ${\alpha }_{FU}$ are higher, the second term in (15) is more dominant than the first term. Hence, the FU signal is detected first by the NU. The SINR of decoding the FU signal at the NU is

$${\gamma }_{NU}^{x_{FU}}=\frac{A^2{\alpha }_{FU}{P}_s}{A^2{\alpha }_{NU}{P}_s+N_0}.$$

(16)

After decoding $x_{FU}$, its effect is removed from $r_{NU}$ using SIC.

$${\tilde{r}}_{NU}\approx A\sqrt{{\alpha }_{NU}{P}_s}{x}_{NU}+n_{NU}.$$

(17)

Then, the NU signal is detected. The SNR for decoding $x_{NU}$ at NU is given by

$${\gamma }_{NU}^{x_{NU}}=\frac{A^2{\alpha }_{NU}{P}_s}{N_0}.$$

(18)

The decoding of the FU signal fails at NU when

$${\log }_2\left(1+{\gamma }_{NU}^{x_{FU}}\right)\le {\tilde{R}}_{FU}.$$

(19)

Substituting (16) in (19), the outage probability is given by

$$P\left[{\log }_2\left(1+\frac{A^2{\alpha }_{FU}{P}_s}{A^2{\alpha }_{NU}{P}_s+N_0}\right)\right]\le {\tilde{R}}_{FU}.$$

(20)

Simplifying (20) results in

$$P\left[A^2\le \frac{R_{FU}{N}_0}{\left({\alpha }_{FU}-{\alpha }_{NU}{R}_{FU}\right)P_s}\right].$$

(21)

Since ${\alpha }_i$ and ${\beta }_i$ are positive real, A is always positive. Hence, Equation (21) can be written as

$$P\left[A\le \sqrt{\frac{R_{FU}{N}_0}{\left({\alpha }_{FU}-{\alpha }_{NU}{R}_{FU}\right)P_s}}\right].$$

(22)

As the number of reflecting elements allocated to NU is larger, according to CLT, A follows Gaussian distribution $f_A\left(a\right)$ with mean $m_A=\frac{N_{NU}\pi }{4}$ and variance ${\sigma }_A^2=N_{NU}\left[1-\frac{{\pi }^2}{16}\right]$. At the desired rate of ${\tilde{R}}_{NU}$ at NU, the decoding of the NU signal fails at NU when

$${\log }_2\left(1+{\gamma }_{NU}^{x_{NU}}\right)\le {\tilde{R}}_{NU}.$$

(23)

Substituting (18) in (23) gives

$${\log }_2\left(1+\frac{A^2{\alpha }_{NU}{P}_s}{N_0}\right)\le {\tilde{R}}_{NU}.$$

(24)

Simplifying (24), the outage probability at NU is

$$P\left[A\le \sqrt{\frac{R_{NU}{N}_0}{{\alpha }_{NU}{P}_s}}\right],$$

(25)

where $R_{NU}=2^{{\tilde{R}}_{NU}}-1$. By combining (22) and (25), the overall condition for which decoding of NU signal fails at NU is

$$A\le max\left\{\sqrt{\frac{R_{FU}{N}_0}{\left({\alpha }_{FU}-{\alpha }_{NU}{R}_{FU}\right)P_s}},\sqrt{\frac{R_{NU}{N}_0}{{\alpha }_{NU}{P}_s}}\right\}.$$

(26)

The outage probability of NU is

$$P_{NU}^{o\_SR}={\int }_0^{y_{NU}}{f}_A\left(a\right)\mathrm{d}a,$$

(27)

where

$$y_{NU}=max\left\{\sqrt{\frac{R_{FU}{N}_0}{\left({\alpha }_{FU}-{\alpha }_{NU}{R}_{FU}\right)P_s}},\sqrt{\frac{R_{NU}{N}_0}{{\alpha }_{NU}{P}_s}}\right\}.$$

(28)

After mathematical simplification, the outage probability $P_{NU}^{o\_SR}$ at the NU is given by

$$P_{NU}^{o\_SR}=\frac{{\sigma }_A\left\{erf\left(\frac{y_{NU}-m_A}{\sqrt{2}{\sigma }_A}\right)+erf\left(\frac{m_A}{\sqrt{2}{\sigma }_A}\right)\right\}}{2{\sigma }_A}.$$

(29)

4. Outage Probability Analysis of RIS-AP-FNOMA

Most traditional studies on passive RIS presume its deployment to be far from the BS and UE. As a result, the benefits claimed by the RIS may not be realized since RIS receives weaker signals. This makes RIS-SR-FNOMA unrealizable in practical environments. In practice, RIS is effective when it is placed near the transmitter or receiver [42]. In this system, RIS with N elements is installed nearest to BS/AP. Due to this, the effect of fading between the AP and RIS is negligible. As a result, RIS-AP and users communicate in a single hop. The conceptual diagram of RIS-AP-FNOMA is illustrated in Figure 2.

The signal received at the FU is

$$r_{FU}=\left(\sum _{\mathrm{i}=\frac{N}{2}+1}^N{g}_i{e}^{j{\varphi }_i}\right)x_s+n_{FU},$$

(30)

where $g_i$ is the channel condition between the i${}^{th}$ RIS element and UE. The passive RIS introduces phase shift ${\varphi }_i$ at each reflecting element, which is

$${\varphi }_i={-\psi }_i.$$

(31)

Substituting $g_i$ and (31) in (30), the received signal at the FU is

$$r_{FU}=\left(\sum _{\mathrm{i}=\frac{N}{2}+1}^N{\beta }_i\right)x_s+n_{FU}.$$

(32)

Let $C={\sum }_{\mathrm{i}=\frac{N}{2}+1}^N{\beta }_i$ be the cumulative channel effect between RIS and FU. Using steps similar to (5) to (11) discussed in Section 3, the outage probability of FU is determined as

$$P_{FU}^{o\_AP}=\frac{{\sigma }_C\left\{erf\left(\frac{y_{FU}-m_C}{\sqrt{2}{\sigma }_C}\right)+erf\left(\frac{m_C}{\sqrt{2}{\sigma }_C}\right)\right\}}{2{\sigma }_C}.$$

(33)

where $m_C=\frac{N_{FU}\pi }{4}$ is the mean and ${\sigma }_C^2=N_{FU}\left[1-\frac{{\pi }^2}{16}\right]$ is the variance of C.

The signal received by the NU is

$$r_{NU}=\left(\sum _{\mathrm{i}=1}^{\frac{N}{2}}{g}_i{e}^{j{\varphi }_i}\right)x_s+n_{NU}.$$

(34)

Substituting $g_i$ and (31) in (34), the received signal at the NU is

$$r_{NU}=\left(\sum _{\mathrm{i}=1}^{\frac{N}{2}}{\beta }_i\right)x_s+n_{NU}.$$

(35)

Let $D={\sum }_{\mathrm{i}=1}^{\frac{N}{2}}{\beta }_i$ be the cumulative channel effect between RIS and NU. Using steps similar to (15) to (28) discussed in Section 3, the outage probability of NU is determined as

$$P_{NU}^{o\_AP}=\frac{{\sigma }_D\left\{erf\left(\frac{y_{NU}-m_D}{\sqrt{2}{\sigma }_D}\right)+erf\left(\frac{m_D}{\sqrt{2}{\sigma }_D}\right)\right\}}{2{\sigma }_D}.$$

(36)

where $m_D=\frac{N_{NU}\pi }{4}$ is the mean, and ${\sigma }_D^2=N_{NU}\left[1-\frac{{\pi }^2}{16}\right]$ is the variance of D.

5. Transmit Power Optimization for Sum Capacity Maximization

In this section, optimal power allocation strategies for obtaining maximum sum capacity in RIS-SR-FNOMA and RIS-AP-NOMA systems are discussed in detail. The sum capacity of downlink RIS-SR-FNOMA for a two-user scenario is given by

$$C_{NU}+C_{FU}={\log }_2\left(1+{\gamma }_{NU}^{x_{NU}}\right)+{\log }_2\left(1+{\gamma }_{FU}^{x_{FU}}\right),$$

(37)

where $C_{NU}$ and $C_{FU}$ are the capacities of NU and FU, respectively. The optimization problem for determining the power allocation factor ${\alpha }_{NU}$ and ${\alpha }_{FU}$ of both NU and FU is formulated as maximizing the sum capacity while satisfying the quality-of-service (QoS) constraints at both NU and FU. It is defined as

$$\begin{array}{c}\max \\ {\alpha }_{NU},{\alpha }_{FU}\end{array}{C}_{NU}+C_{FU}.$$

(38)

Subject to

$${\log }_2\left(1+{\gamma }_{NU}^{x_{NU}}\right)\ge {\tilde{R}}_{NU}.$$

(39)

$${\log }_2\left(1+{\gamma }_{FU}^{x_{FU}}\right)\ge {\tilde{R}}_{FU}.$$

(40)

$${\alpha }_{NU}+{\alpha }_{FU}=1.$$

(41)

Substituting (6) and (18) in (37) gives

$$C_{NU}+C_{FU}={\log }_2\left(1+\frac{A^2{\alpha }_{NU}{P}_s}{N_0}\right)+{\log }_2\left(1+\frac{B^2{\alpha }_{FU}{P}_s}{B^2{\alpha }_{NU}{P}_s+N_0}\right).$$

(42)

Simplifying (42), it results in

$${C_{NU}+C_{FU}=\log }_2\left(\left(1+B^2\chi \right)\left(\frac{1+A^2{\alpha }_{NU}\chi }{1+B^2{\alpha }_{NU}\chi }\right)\right).$$

(43)

where $\chi =\frac{P_s}{N_0}$ is the received SNR. The term $\left(1+B^2\chi \right)$ is constant. As the term $\left(\frac{1+A^2{\alpha }_{NU}\chi }{1+B^2{\alpha }_{NU}\chi }\right)$ is a monotonically increasing function of ${\alpha }_{NU}$, the maximum sum capacity can be achieved by assigning a maximum possible value for ${\alpha }_{NU}$. By simplifying (43), the condition for ${\alpha }_{NU}$, which satisfies the QoS constraints, is given by

$$\underset{{\alpha }_{NU}^{min}}{\underbrace{\frac{R_{NU}}{A^2\chi }}}\le {\alpha }_{NU}\le \underset{{\alpha }_{NU}^{max}}{\underbrace{\frac{B^2\chi -R_{FU}}{B^2\chi \left(1+R_{FU}\right)}}}.$$

(44)

Any value between ${\alpha }_{NU}^{min}$ and ${\alpha }_{NU}^{max}$ is sub-optimal for ${\alpha }_{NU}$. In simulations, the average of ${\alpha }_{NU}^{min}$ and ${\alpha }_{NU}^{max}$ is assumed to be ${\alpha }_{NU}$. The sub-optimal power assigned to NU is

$${\alpha }_{NU}^{sub-opt}=\frac{\left({\alpha }_{NU}^{min}+{\alpha }_{NU}^{max}\right)}{2}.$$

(45)

The balance power is assigned to the FU:

$${{\alpha }_{FU}^{sub-opt}=1-\alpha }_{NU}^{sub-opt}.$$

(46)

To find the optimal value of ${\alpha }_{NU}$, the first threshold ${\alpha }_{NU}^{min}$ should be less than the second threshold ${\alpha }_{NU}^{max}$

$$\frac{R_{NU}}{A^2\chi }\le \frac{B^2\chi -R_{FU}}{B^2\chi \left(1+R_{FU}\right)}.$$

(47)

By solving (47), the minimal SNR demand to satisfy the QoS constraints of users is attained. This is called a feasible region:

$$\chi \ge \frac{R_{NU}}{A^2}+\frac{R_{NU}{R}_{FU}}{A^2}+\frac{R_{FU}}{B^2}.$$

(48)

If the condition in (48) is not met, then it is not possible to choose the value of ${\alpha }_{NU}$. The largest value of ${\alpha }_{NU}$ is the optimal value of ${\alpha }_{NU}$, which maximizes the sum capacity:

$${\alpha }_{NU}^{opt}=\frac{B^2\chi -R_{FU}}{B^2\chi \left(1+R_{FU}\right)}.$$

(49)

The balance power is assigned to FU, which is

$${{\alpha }_{FU}^{opt}=1-\alpha }_{NU}^{opt}.$$

(50)

In a similar way, the optimal powers to be assigned for the users of RIS-AP-FNOMA are derived. The optimal power assigned to the NU of RIS-AP-FNOMA system is given by

$${\alpha }_{NU}^{opt}=\frac{C^2\chi -R_{FU}}{C^2{\chi }_s\left(1+R_{FU}\right)}.$$

(51)

The balance power is assigned to the FU as in (50). The minimal SNR demand to meet the QoS constraints of the users of RIS-AP-FNOMA is given by

$$\chi \ge \frac{R_{NU}}{D^2}+\frac{R_{NU}{R}_{FU}}{D^2}+\frac{R_{FU}}{C^2}.$$

(52)

6. Simulations and Discussion

In this section, outage, and sum capacity performances of RIS-SR-FNOMA and RIS-AP-FNOMA are simulated and analyzed using MATLAB R2023a.

Table 1. Simulation parameters.

Parameter	Typical Value
Number of RIS components $\left(N\right)$	32, 64, 128, 256
Number of users	2
Mean channel gain of NU	5
Mean channel gain of FU	1
Desired rate of NU ${(\tilde{R}}_{NU})$	1 b/s/Hz
Desired rate of FU ${(\tilde{R}}_{FU})$	1 b/s/Hz
Target outage probability	${10}^{-4}$
Block length	${10}^5$

lists the parameters assessed for the simulation. The results of the MC simulation are obtained by averaging the outage probability across ${10}^5$ iterations.

The outage performance results are shown in Figure 3 for the FU and NU in RIS-SR-FNOMA and conventional FNOMA. It is assumed that ${\alpha }_{NU}=0.1$ and ${\alpha }_{FU}=0.9$. The total RIS elements of $N=64$ with 32 elements each for NU and FU are considered. In comparison with RIS-SR-FNOMA, FNOMA without RIS has poor outage performance. In the RIS-SR-FNOMA system, the SNR requirements to procure the target probability of outage are $-22$ dB and $-13$ dB for FU and NU, respectively. Since more power is allocated to FU, the outage performance of FU is better than NU for both systems. It is shown that the MC simulation curves closely or exactly match with the analytical results.

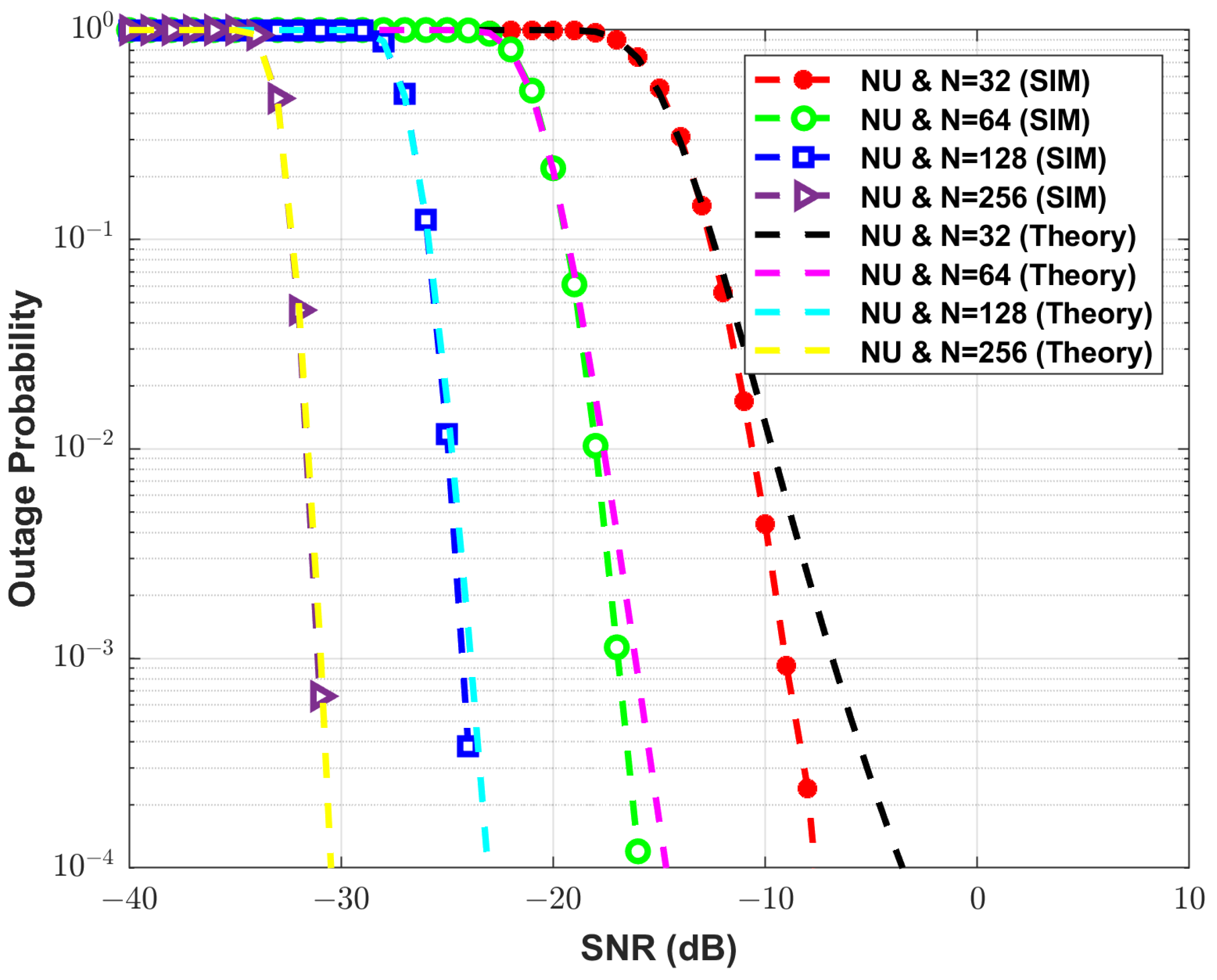
The outage performance results of the FU and NU of RIS-SR-FNOMA are indicated in Figure 4 and Figure 5, respectively, at various numbers of reflective elements with ${\alpha }_{NU}=0.2$ and ${\alpha }_{FU}=0.8$. With $N=32,$ $N=64,N=128$ and $N=256$, the FU of RIS-SR-FNOMA achieves the expected outage probability at an approximate SNR of $-8$ dB, $-21$ dB, $-28$ dB and $-35$ dB, respectively. The amount of reflecting elements in RIS is found to improve outage performance. As the CLT approximation of B holds true for higher N, at $N=128$ and $N=256$, a close match between MC simulation and analytical curves is observed compared to $N=32$ and $N=64$. On comparing the outage performance of the NU and FU in Figure 4 and Figure 5, it is evident that the FU outage performance is superior to the NU outage performance.

The sum capacity of RIS-SR-FNOMA is shown in Figure 6 for different N. The sum capacity for all N increases as the transmit SNR increases. At SNR of −10 dB, the sum capacities are approximately $6.1\mathrm{b}/\mathrm{s}/\mathrm{Hz}$, $8.1\mathrm{b}/\mathrm{s}/\mathrm{Hz}$, $10.2\mathrm{b}/\mathrm{s}/\mathrm{Hz}$ and $12.2\mathrm{b}/\mathrm{s}/\mathrm{Hz}$ when $N=32,$ $N=64,N=128$ and $N=256$ respectively. When the optimal powers are allocated, there is an improvement in the sum capacity over the sub-optimal power assignment for lower SNR. At higher SNR, the optimal and sub-optimal methods have essentially identical sum capacities.

The simulation parameters for the RIS-AP-FNOMA system are assumed to be the same as those given in Table 1. The outage performance results of RIS-AP-FNOMA and conventional FNOMA are shown in Figure 7. The desired rates and power for FU and NU, as well as N, are set as being similar to Figure 3. In comparison with RIS-AP-FNOMA, FNOMA without RIS has poor outage performance. In the RIS-AP-FNOMA system, the SNR requirements to achieve expected outage probability are $-25$ dB and $-15$ dB for FU and NU, respectively. Since more power is assigned to the FU, the outage performance of the FU is better than the NU for both systems. It is shown that the MC simulation curves closely or exactly match the analytical results. When comparing Figure 3 and Figure 7, RIS-AP-FNOMA has a modest improvement over RIS-SR-FNOMA in terms of outage performance.

The outage performance results of the FU and NU of RIS-AP-FNOMA are shown in Figure 8 and Figure 9, respectively, at various numbers of reflective elements with ${\alpha }_{NU}=0.2$ and ${\alpha }_{FU}=0.8$. With $N=32,$ $N=64,N=128$ and $N=256$, the FU of RIS-AP-FNOMA achieves the expected outage probability at approximately $-15$ dB, $-24$ dB, $-31$ dB and $-37$ dB, respectively. It is observed that increasing N in RIS enhances the outage performance. As the CLT approximation of C holds true for higher values of N, at $N=64$, $N=128$ and $N=256$, a close match between the MC simulation and analytical curves is observed compared to $N=32$. On comparing the outage performance of the NU and FU in Figure 8 and Figure 9, it is evident that the FU outage performance is superior to the NU outage performance. When comparing Figure 4 and Figure 5 with Figure 8 and Figure 9, RIS-AP-FNOMA has a modest improvement over RIS-SR-FNOMA in terms of outage performance.

The sum capacity (b/s/Hz) of the RIS-AP-FNOMA is shown in Figure 10 for different N in RIS. The sum capacity for all N increases as the transmit SNR increases. At SNR of −10 dB, the sum capacities are $6.5$ b/s/Hz, $8.5$ b/s/Hz, $10.5$ b/s/Hz and $12.5$ b/s/Hz when $N=32,$ $N=64,N=128$ and $N=256$, respectively. When optimal powers are assigned, there is an improvement in the sum capacity over the sub-optimal power assignment for lower SNR. At higher SNR, the optimal and sub-optimal methods have essentially identical sum capacities.

For optimal and sub-optimal power assignments, the sum capacities (b/s/Hz) of FNOMA, RIS-AP-FNOMA, and RIS-SR-FNOMA systems are analyzed in Figure 11. The sum capacities of the RIS-AP-FNOMA and RIS-SR-FNOMA systems are calculated for the number of passive elements $N=32$. The FNOMA system has reasonable sum capacities for positive values of SNR, whereas the RIS-SR-FNOMA and RIS-AP-FNOMA systems have good sum capacities, even for negative SNR values. The array and diversity gains via RIS-assisted communication result in an increase in capacity. With higher SNR values of RIS-AP-FNOMA and RIS-SR-FNOMA systems, the sum capacity difference between optimal and sub-optimal power assignments decreases. The RIS-AP-FNOMA system has a slightly higher sum capacity compared with the RIS-SR-FNOMA system. When optimal power allocation is employed at RIS-AP-FNOMA and FNOMA systems, the approximate sum capacities of 13.2 b/s/Hz and 5 b/s/Hz are achieved, respectively, for an SNR of 10 dB. The RIS-AP-FNOMA system has a 62% higher sum capacity than the FNOMA system.

7. Conclusions

The analytical outage probability expressions for RIS-SR-FNOMA and RIS-AP-FNOMA systems are derived in this paper. For larger numbers of reflecting elements, there is a close match between the MC simulations and analytical curves. The FU outage performance is superior to that of NU in both RIS-SR-FNOMA and RIS-AP-FNOMA systems. The outage performance for NU and FU improves as the elements in RIS increase. The optimal powers for NU and FU are also determined to maximize the sum capacity and satisfy the QoS constraints of both users. The sum capacities of RIS-SR-FNOMA and RIS-AP-FNOMA are clearly superior to FNOMA. Even with negative SNR values, the RIS-SR-FNOMA and RIS-AP-FNOMA systems can provide higher sum capacities. Over sub-optimal power assignments, the optimal power assignment maximizes the sum capacity. In terms of outage and sum capacity, RIS-AP-FNOMA is marginally better than RIS-SR-FNOMA. FNOMA paired with RIS, it may be argued, performs better in terms of outage and sum capacity. As a result, RIS-assisted NOMA will be a viable alternative for constructing next-generation networks that can handle massive connections. As a future work, the proposed model can be modified for uplink communication. The proposed system can be extended for ordered NOMA and cooperative NOMA.