SPDepth: Enhancing Self-Supervised Indoor Monocular Depth Estimation via Self-Propagation
Abstract
:1. Introduction
- We proposed an enhanced self-supervised indoor monocular depth estimation network called SPDepth. A novel depth self-propagation mechanism is innovatively proposed to address the challenge of insufficient self-supervision information. The feature self-similarities provide important cues for the propagation.
- Considering that depth self-similarities are stronger in the local range than the global, local window self-attention is introduced at the end of the network. The proposed strategy limits self-propagation in a local range so that the propagation is much more effective and saves extensive computational cost.
- The experimental results on the NYU Depth V2 dataset demonstrate the effectiveness of our proposed SPDepth. SPDepth achieves good performance in both details and object edges. The zero-shot generalization experiments on the 7-Scenes dataset provide an analysis of the characteristics of SPDepth.
2. Related Work
2.1. Monocular Depth Estimation
2.2. Self-Attention
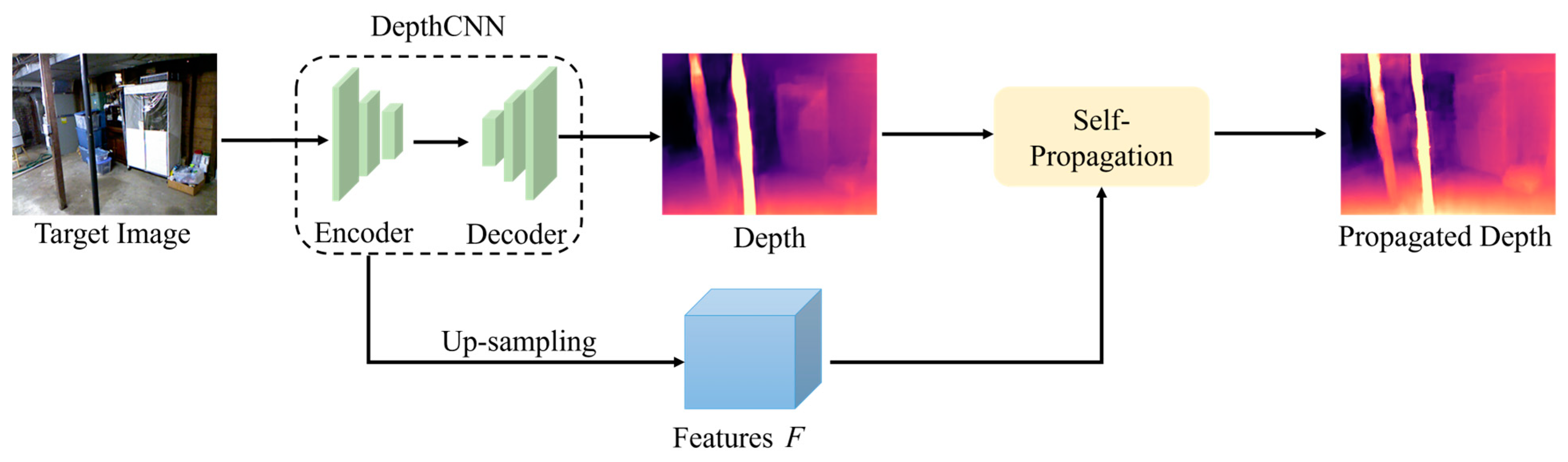
3. Methods
3.1. Overview of SPDepth
3.2. Local Window Self-Propagation
3.3. Overall Loss Functions
4. Experiments
4.1. Implementation Details
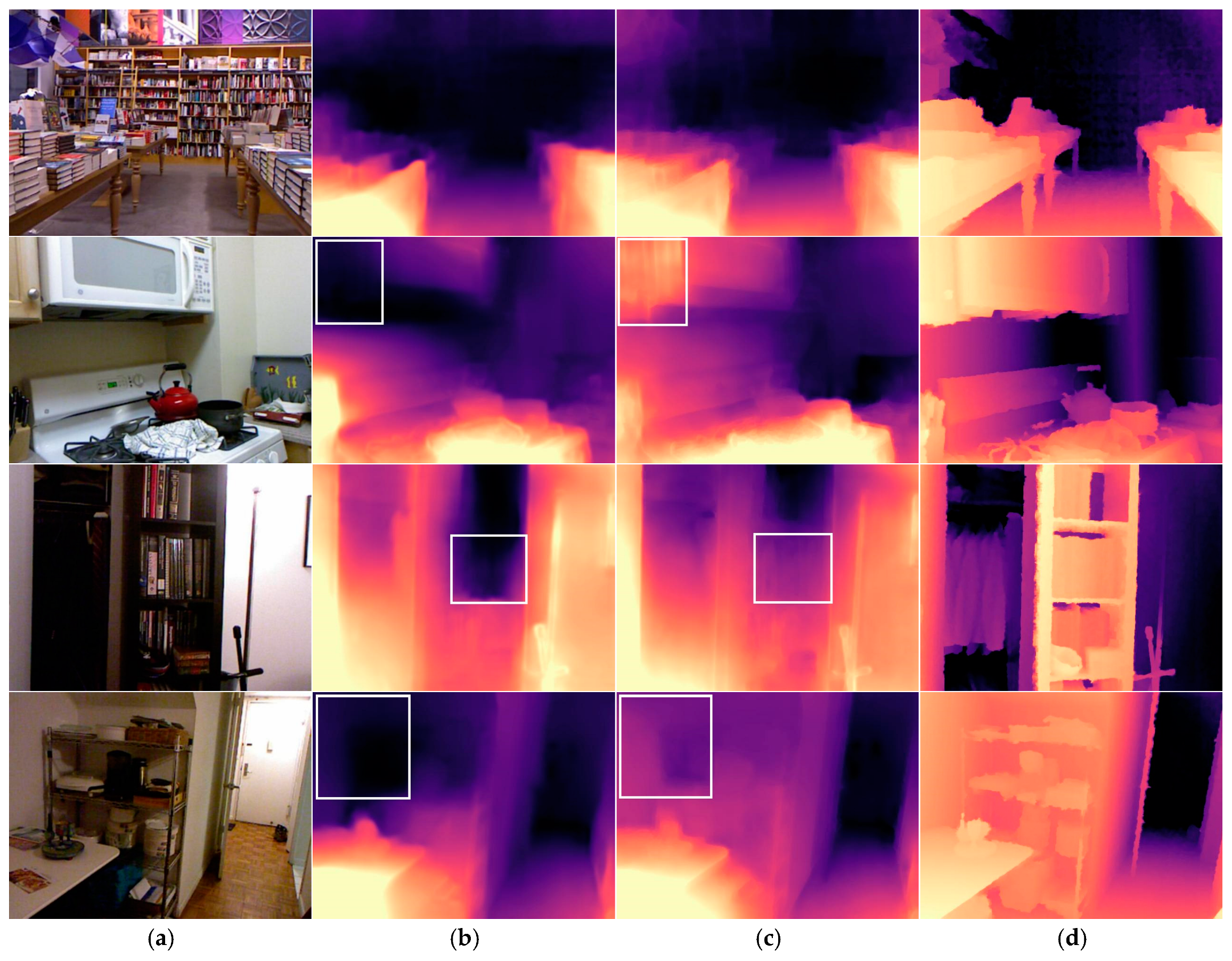
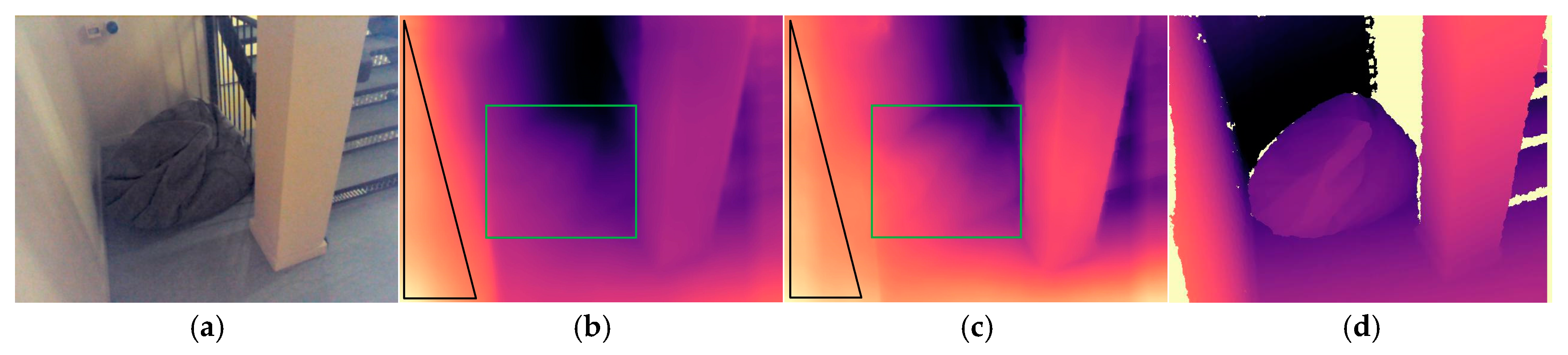
4.2. Results
4.2.1. NYU Depth V2 Results
4.2.2. 7-Scenes Results
4.2.3. Ablation Studies
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, Z.; Jin, L.; Gao, S. P2Net: Patch-match and plane-regularization for unsupervised indoor depth estimation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XXIV, 2020. pp. 206–222. [Google Scholar]
- Li, B.; Huang, Y.; Liu, Z.; Zou, D.; Yu, W. StructDepth: Leveraging the structural regularities for self-supervised indoor depth estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 12663–12673. [Google Scholar]
- Guo, X.; Zhao, H.; Shao, S.; Li, X.; Zhang, B. F2Depth: Self-supervised indoor monocular depth estimation via optical flow consistency and feature map synthesis. Eng. Appl. Artif. Intell. 2024, 133, 108391. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Y.; Qin, K.; Zeng, W. Moving Indoor: Unsupervised video depth learning in challenging environments. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8618–8627. [Google Scholar]
- Xu, H.; Zhang, J.; Cai, J.; Rezatofighi, H.; Tao, D. GMFlow: Learning optical flow via global matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8121–8130. [Google Scholar]
- Xu, H.; Zhang, J.; Cai, J.; Rezatofighi, H.; Yu, F.; Tao, D. Unifying flow, stereo and depth estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 13941–13958. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Gong, M.; Wang, C.; Batmanghelich, K.; Tao, D. Deep ordinal regression network for monocular depth estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2002–2011. [Google Scholar]
- Laina, I.; Rupprecht, C.; Belagiannis, V.; Tombari, F.; Navab, N. Deeper depth prediction with fully convolutional residual networks. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 239–248. [Google Scholar]
- Eigen, D.; Fergus, R. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2650–2658. [Google Scholar]
- Li, J.; Klein, R.; Yao, A. A two-streamed network for estimating fine-scaled depth maps from single rgb images. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3372–3380. [Google Scholar]
- Zhang, S.; Yang, L.; Mi, M.B.; Zheng, X.; Yao, A. Improving deep regression with ordinal entropy. arXiv 2023, arXiv:2301.08915. [Google Scholar]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Liu, F.; Shen, C.; Lin, G.; Reid, I. Learning depth from single monocular images using deep convolutional neural fields. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 2024–2039. [Google Scholar] [CrossRef] [PubMed]
- Shao, S.; Pei, Z.; Wu, X.; Liu, Z.; Chen, W.; Li, Z. IEBins: Iterative elastic bins for monocular depth estimation. Adv. Neural Inf. Process. Syst. 2024, 36, 53025–53037. [Google Scholar]
- Zhao, W.; Rao, Y.; Liu, Z.; Liu, B.; Zhou, J.; Lu, J. Unleashing text-to-image diffusion models for visual perception. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 5729–5739. [Google Scholar]
- Ji, Y.; Chen, Z.; Xie, E.; Hong, L.; Liu, X.; Liu, Z.; Lu, T.; Li, Z.; Luo, P. DDP: Diffusion model for dense visual prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 21741–21752. [Google Scholar]
- Hu, J.; Ozay, M.; Zhang, Y.; Okatani, T. Revisiting single image depth estimation: Toward higher resolution maps with accurate object boundaries. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019; pp. 1043–1051. [Google Scholar]
- Yin, W.; Liu, Y.; Shen, C.; Yan, Y. Enforcing geometric constraints of virtual normal for depth prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27–28 October 2019; pp. 5684–5693. [Google Scholar]
- Shao, S.; Pei, Z.; Chen, W.; Chen, P.C.; Li, Z. NDDepth: Normal-distance assisted monocular depth estimation and completion. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Shao, S.; Pei, Z.; Chen, W.; Wu, X.; Li, Z. NDDepth: Normal-distance assisted monocular depth estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 7931–7940. [Google Scholar]
- Patil, V.; Sakaridis, C.; Liniger, A.; Van Gool, L. P3Depth: Monocular depth estimation with a piecewise planarity prior. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1610–1621. [Google Scholar]
- Yu, Z.; Zheng, J.; Lian, D.; Zhou, Z.; Gao, S. Single-image piece-wise planar 3D reconstruction via associative embedding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 1029–1037. [Google Scholar]
- Liu, C.; Yang, J.; Ceylan, D.; Yumer, E.; Furukawa, Y. PlaneNet: Piece-wise planar reconstruction from a single rgb image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2579–2588. [Google Scholar]
- Zhou, T.; Brown, M.; Snavely, N.; Lowe, D.G. Unsupervised learning of depth and ego-motion from video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1851–1858. [Google Scholar]
- Godard, C.; Mac Aodha, O.; Firman, M.; Brostow, G.J. Digging into self-supervised monocular depth estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3828–3838. [Google Scholar]
- Uhrig, J.; Schneider, N.; Schneider, L.; Franke, U.; Brox, T.; Geiger, A. Sparsity invariant cnns. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 11–20. [Google Scholar]
- Wu, C.-Y.; Wang, J.; Hall, M.; Neumann, U.; Su, S. Toward practical monocular indoor depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 3814–3824. [Google Scholar]
- Ranftl, R.; Bochkovskiy, A.; Koltun, V. Vision transformers for dense prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 12179–12188. [Google Scholar]
- Ranftl, R.; Lasinger, K.; Hafner, D.; Schindler, K.; Koltun, V. Towards robust monocular depth estimation: Mixing datasets for zero-shot cross-dataset transfer. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 1623–1637. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Panahi, A.; Gao, G. FsaNet: Frequency self-attention for semantic segmentation. IEEE Trans. Image Process. 2023, 32, 4757–4772. [Google Scholar] [CrossRef] [PubMed]
- Bello, I.; Zoph, B.; Vaswani, A.; Shlens, J.; Le, Q.V. Attention augmented convolutional networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3286–3295. [Google Scholar]
- Ramachandran, P.; Parmar, N.; Vaswani, A.; Bello, I.; Levskaya, A.; Shlens, J. Stand-alone self-attention in vision models. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Agarwal, A.; Arora, C. Attention attention everywhere: Monocular depth prediction with skip attention. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 5861–5870. [Google Scholar]
- Ning, J.; Li, C.; Zhang, Z.; Wang, C.; Geng, Z.; Dai, Q.; He, K.; Hu, H. All in tokens: Unifying output space of visual tasks via soft token. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 19900–19910. [Google Scholar]
- Shao, S.; Pei, Z.; Chen, W.; Li, R.; Liu, Z.; Li, Z. URCDC-Depth: Uncertainty rectified cross-distillation with cutflip for monocular depth estimation. IEEE Trans. Multimed. 2023, 26, 3341–3353. [Google Scholar] [CrossRef]
- Piccinelli, L.; Sakaridis, C.; Yu, F. iDisc: Internal discretization for monocular depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 21477–21487. [Google Scholar]
- Li, Z.; Wang, X.; Liu, X.; Jiang, J. Binsformer: Revisiting adaptive bins for monocular depth estimation. IEEE Trans. Image Process. 2024, 33, 3964–3976. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Chen, Z.; Liu, X.; Jiang, J. Depthformer: Exploiting long-range correlation and local information for accurate monocular depth estimation. Mach. Intell. Res. 2023, 20, 837–854. [Google Scholar] [CrossRef]
- Zhao, C.; Poggi, M.; Tosi, F.; Zhou, L.; Sun, Q.; Tang, Y.; Mattoccia, S. GasMono: Geometry-aided self-supervised monocular depth estimation for indoor scenes. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 16209–16220. [Google Scholar]
- Zhang, N.; Nex, F.; Vosselman, G.; Kerle, N. Lite-Mono: A lightweight cnn and transformer architecture for self-supervised monocular depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 18537–18546. [Google Scholar]
- Johnston, A.; Carneiro, G. Self-supervised monocular trained depth estimation using self-attention and discrete disparity volume. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4756–4765. [Google Scholar]
- Kaushik, V.; Jindgar, K.; Lall, B. ADAADepth: Adapting data augmentation and attention for self-supervised monocular depth estimation. IEEE Robot. Autom. Lett. 2021, 6, 7791–7798. [Google Scholar] [CrossRef]
- Yan, J.; Zhao, H.; Bu, P.; Jin, Y. Channel-wise attention-based network for self-supervised monocular depth estimation. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 464–473. [Google Scholar]
- Jiang, S.; Campbell, D.; Lu, Y.; Li, H.; Hartley, R. Learning to estimate hidden motions with global motion aggregation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 9772–9781. [Google Scholar]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor segmentation and support inference from rgbd images. In Proceedings of the Computer Vision–ECCV 2012: 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 746–760. [Google Scholar]
- Shotton, J.; Glocker, B.; Zach, C.; Izadi, S.; Criminisi, A.; Fitzgibbon, A. Scene coordinate regression forests for camera relocalization in RGB-D images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2930–2937. [Google Scholar]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Godard, C.; Mac Aodha, O.; Brostow, G.J. Unsupervised monocular depth estimation with left-right consistency. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 270–279. [Google Scholar]
- Liu, M.; Salzmann, M.; He, X. Discrete-continuous depth estimation from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 716–723. [Google Scholar]
- Li, B.; Shen, C.; Dai, Y.; Van Den Hengel, A.; He, M. Depth and surface normal estimation from monocular images using regression on deep features and hierarchical crfs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1119–1127. [Google Scholar]
- Jun, J.; Lee, J.-H.; Lee, C.; Kim, C.-S. Depth map decomposition for monocular depth estimation. In Proceedings of the Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; Proceedings, Part II, 2022. pp. 18–34. [Google Scholar]
- Zhao, W.; Liu, S.; Shu, Y.; Liu, Y.-J. Towards better generalization: Joint depth-pose learning without posenet. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9151–9161. [Google Scholar]
- Zhang, Y.; Gong, M.; Li, J.; Zhang, M.; Jiang, F.; Zhao, H. Self-supervised monocular depth estimation with multiscale perception. IEEE Trans. Image Process. 2022, 31, 3251–3266. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Hu, H.; Liang, L.; Shi, W.; Xie, G.; Lu, X.; Hei, X. Unsupervised monocular estimation of depth and visual odometry using attention and depth-pose consistency loss. IEEE Trans. Multimed. 2023, 26, 3517–3529. [Google Scholar] [CrossRef]
- Bian, J.; Li, Z.; Wang, N.; Zhan, H.; Shen, C.; Cheng, M.-M.; Reid, I. Unsupervised scale-consistent depth and ego-motion learning from monocular video. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]




| Methods | Supervision | REL ↓ | RMS ↓ | Log10 ↓ | δ < 1.25 ↑ | δ < 1.252 ↑ | δ < 1.253 ↑ |
|---|---|---|---|---|---|---|---|
| Liu [51] | √ | 0.335 | 1.060 | 0.127 | - | - | - |
| Li [52] | √ | 0.232 | 0.821 | 0.094 | 0.621 | 0.886 | 0.968 |
| Liu [13] | √ | 0.213 | 0.759 | 0.087 | 0.650 | 0.906 | 0.976 |
| Eigen [9] | √ | 0.158 | 0.641 | - | 0.769 | 0.950 | 0.988 |
| Li [10] | √ | 0.143 | 0.635 | 0.063 | 0.788 | 0.958 | 0.991 |
| PlaneNet [23] | √ | 0.142 | 0.514 | 0.060 | 0.827 | 0.963 | 0.990 |
| PlaneReg [22] | √ | 0.134 | 0.503 | 0.057 | 0.827 | 0.963 | 0.990 |
| Laina [8] | √ | 0.127 | 0.573 | 0.055 | 0.811 | 0.953 | 0.988 |
| DORN [7] | √ | 0.115 | 0.509 | 0.051 | 0.828 | 0.965 | 0.992 |
| VNL [18] | √ | 0.108 | 0.416 | 0.048 | 0.875 | 0.976 | 0.994 |
| P3Depth [21] | √ | 0.104 | 0.356 | 0.043 | 0.898 | 0.981 | 0.996 |
| Jun [53] | √ | 0.100 | 0.362 | 0.043 | 0.907 | 0.986 | 0.997 |
| DDP [16] | √ | 0.094 | 0.329 | 0.040 | 0.921 | 0.990 | 0.998 |
| Moving Indoor [4] | × | 0.208 | 0.712 | 0.086 | 0.674 | 0.900 | 0.968 |
| TrianFlow [54] | × | 0.189 | 0.686 | 0.079 | 0.701 | 0.912 | 0.978 |
| Zhang [55] | × | 0.177 | 0.634 | - | 0.733 | 0.936 | - |
| Monodepth2 [25] | × | 0.170 | 0.617 | 0.072 | 0.748 | 0.942 | 0.986 |
| ADPDepth [56] | × | 0.165 | 0.592 | 0.071 | 0.753 | 0.934 | 0.981 |
| SC-Depth [57] | × | 0.159 | 0.608 | 0.068 | 0.772 | 0.939 | 0.982 |
| P2Net [1] | × | 0.159 | 0.599 | 0.068 | 0.772 | 0.942 | 0.984 |
| SPDepth | × | 0.159 | 0.585 | 0.067 | 0.776 | 0.946 | 0.986 |
| P2Net + PP [1] | × | 0.157 | 0.592 | 0.067 | 0.777 | 0.944 | 0.985 |
| SPDepth + PP | × | 0.157 | 0.579 | 0.066 | 0.781 | 0.947 | 0.986 |
| Methods | Our SPDepth + PP | P2Net [1] + PP | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scene | REL ↓ | RMS ↓ | Log10 ↓ | δ < 1.25 ↑ | δ < 1.252 ↑ | δ < 1.253 ↑ | REL ↓ | RMS ↓ | Log10 ↓ | δ < 1.25 ↑ | δ < 1.252 ↑ | δ < 1.253 ↑ |
| Chess | 0.190 | 0.420 | 0.082 | 0.667 | 0.939 | 0.993 | 0.183 | 0.408 | 0.081 | 0.669 | 0.940 | 0.993 |
| Fire | 0.163 | 0.305 | 0.070 | 0.741 | 0.960 | 0.995 | 0.157 | 0.291 | 0.068 | 0.767 | 0.965 | 0.994 |
| Heads | 0.187 | 0.194 | 0.079 | 0.707 | 0.927 | 0.982 | 0.187 | 0.197 | 0.079 | 0.701 | 0.924 | 0.982 |
| Office | 0.159 | 0.360 | 0.067 | 0.768 | 0.966 | 0.996 | 0.156 | 0.351 | 0.065 | 0.775 | 0.970 | 0.997 |
| Pumpkin | 0.132 | 0.361 | 0.058 | 0.831 | 0.978 | 0.996 | 0.141 | 0.380 | 0.062 | 0.797 | 0.977 | 0.995 |
| RedKitchen | 0.163 | 0.399 | 0.070 | 0.749 | 0.953 | 0.993 | 0.165 | 0.404 | 0.072 | 0.735 | 0.951 | 0.994 |
| Stairs | 0.174 | 0.486 | 0.075 | 0.748 | 0.899 | 0.964 | 0.158 | 0.454 | 0.068 | 0.767 | 0.911 | 0.971 |
| Average | 0.164 | 0.370 | 0.070 | 0.750 | 0.953 | 0.992 | 0.162 | 0.367 | 0.070 | 0.747 | 0.955 | 0.993 |
| Radius | REL ↓ | RMS ↓ | Log10 ↓ | δ < 1.25 ↑ | δ < 1.252 ↑ | δ < 1.253 ↑ | Time ↓ | Memory ↓ |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.159 | 0.585 | 0.067 | 0.776 | 0.946 | 0.986 | 15.05 h | 2.30 G |
| 2 | 0.167 | 0.621 | 0.071 | 0.757 | 0.935 | 0.983 | 24.77 h | 3.15 G |
| 3 | 0.188 | 0.661 | 0.078 | 0.717 | 0.921 | 0.977 | 120.89 h | 4.41 G |
| REL ↓ | RMS ↓ | Log10 ↓ | δ < 1.25 ↑ | δ < 1.252 ↑ | δ < 1.253 ↑ | Time ↓ | Memory ↓ | |
|---|---|---|---|---|---|---|---|---|
| (64, 144, 192) | 0.159 | 0.585 | 0.067 | 0.776 | 0.946 | 0.986 | 15.05 h | 2.30 G |
| (64, 72, 96) | 0.161 | 0.593 | 0.068 | 0.771 | 0.943 | 0.986 | 16.07 h | 2.30 G |
| (128, 36, 48) | 0.162 | 0.596 | 0.068 | 0.768 | 0.944 | 0.985 | 24.22 h | 2.90 G |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Zhao, H.; Shao, S.; Li, X.; Zhang, B.; Li, N. SPDepth: Enhancing Self-Supervised Indoor Monocular Depth Estimation via Self-Propagation. Future Internet 2024, 16, 375. https://doi.org/10.3390/fi16100375
Guo X, Zhao H, Shao S, Li X, Zhang B, Li N. SPDepth: Enhancing Self-Supervised Indoor Monocular Depth Estimation via Self-Propagation. Future Internet. 2024; 16(10):375. https://doi.org/10.3390/fi16100375
Chicago/Turabian StyleGuo, Xiaotong, Huijie Zhao, Shuwei Shao, Xudong Li, Baochang Zhang, and Na Li. 2024. "SPDepth: Enhancing Self-Supervised Indoor Monocular Depth Estimation via Self-Propagation" Future Internet 16, no. 10: 375. https://doi.org/10.3390/fi16100375
APA StyleGuo, X., Zhao, H., Shao, S., Li, X., Zhang, B., & Li, N. (2024). SPDepth: Enhancing Self-Supervised Indoor Monocular Depth Estimation via Self-Propagation. Future Internet, 16(10), 375. https://doi.org/10.3390/fi16100375






