A Multiparty Quantum Private Equality Comparison Scheme Relying on |GHZ3⟩ States
Abstract
:1. Introduction
Organization
2. Preliminary Concepts
2.1. States
- is the binary set .
- To differentiate syntactically the bit vector from the bit , the bit vector is written in boldface. A bit vector of length m is a sequence of n bits: . There is also the special zero bit vector , in which all the bits are zero; that is, .
- Each bit vector serves as the binary form of one of the basis kets that constitute the computational basis of the underlying -dimensional Hilbert space.
- As we have previously explained, to avoid ambiguity, we rely on the subscripts A, S, and T to indicate which qubits belong to Alice, Sophie, and Trent’s quantum registers, respectively.
2.2. Inner Product Modulo 2 Operation
3. The Setup
3.1. The Actors
- Always executes the protocol faithfully.
- Cannot conspire with any other player.
- Cannot be corrupted by an outside entity.
- Keeps track of all intermediate calculations and may attempt to steal information from the records.
- (A1)
- There are n players, the millionaires, who are designated by Alice0, …, Alicen−1. Each Alicei, , desires to find out whether her fortune is equal or not to the fortune of every other Alicej, , but without ever divulging her actual fortune to any other in-game player or outside eavesdropper. For the needs of the protocol, the millionaires’ fortunes are represented in binary and not in decimal. In particular, Alicei’s fortune is designated by the bit vector , . There is a catch, however, in the whole setup. The millionaires, in case their fortunes turn out to be different, must not be able to infer any additional information besides the fact that they are different, not even a single bit of the other player’s fortune.To allow for more generality, the millionaires are assumed to be in different locations.
- (A2)
- Additionally, there are two semi-honest third parties, Sophia and Trent, whose participation is essential for the correct implementation of the protocol. So, in total, this game involves players, all in different regions of space.
- (A3)
- Sophia’s role is critical as we explain now. The rationale behind the GHZ3MQPEC protocol is the following: instead of Alicei and Alicej directly comparing their fortunes and , , they both compare their fortune with a fixed but secret number . If , then , whereas if , then . Sophia is responsible for randomly choosing a secret number and embedding it into the global entanglement. It goes without saying that Sophia must never reveal her secret number to any other in-game player or outside eavesdropper.
- (A4)
- Trent’s role is also essential. First of all, he is responsible for the generation of the triplets and their distribution to the players according to the entanglement distribution scheme explained in Definition 2. Moreover, at the end of the protocol, he determines for each Alicei, , whether her fortune is equal or not to that of every other Alicej, . Trent must only announce the corresponding decision in the form of a single bit, e.g., YESi,j or NOi,j. Trent must never reveal the private measurements and records he used to arrive at his decisions to any other in-game player or outside eavesdropper.
- (A5)
- All players agree beforehand on the number m of qubits sufficient to store their fortunes , , and Sophia’s secret number .
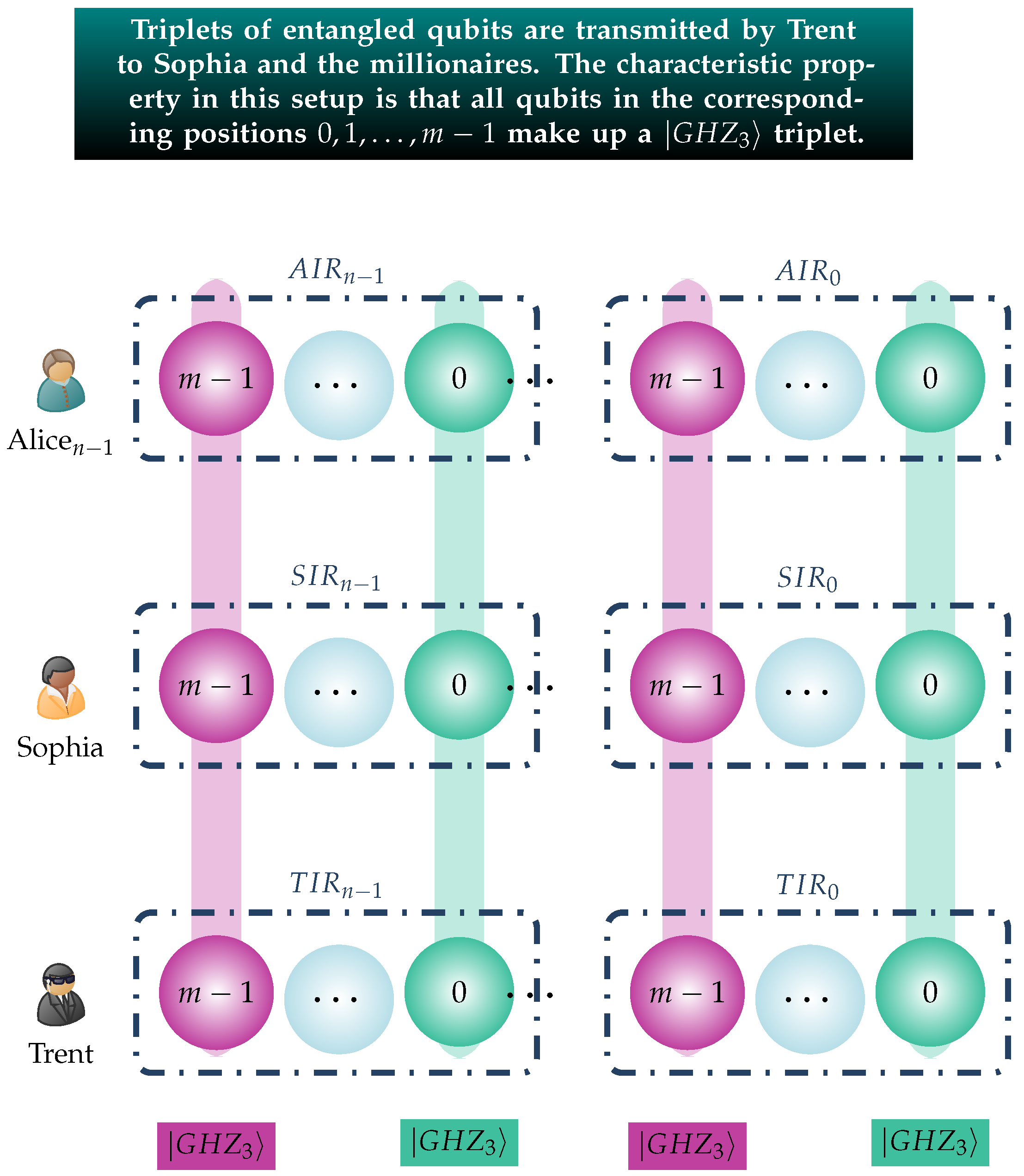
3.2. The Entanglement Distribution Scheme
- Alicei, , is endowed with an m-qubit input register .
- For every Alicei, Sophia, and Trent, each utilize an m-qubit input register corresponding to Alicei, denoted by and , , respectively.
- For every Alicei, , Trent generates triplets entangled in the state. Trent keeps the first qubit p and transmits the second and third qubits q and r to Sophia and Alicei, respectively.
4. The GHZ3MQPEC Protocol
- Ease of implementation. Besides EPR pairs, triplets are arguably the easiest maximally entangled states that can be produced by a modern quantum apparatus. The fact that, irrespective of the number n of millionaires, the GHZ3MQPEC protocol can be executed with triplets exclusively guarantees the feasibility of its implementation.
- Efficiency and scalability. The forthcoming mathematical analysis in Section 6 corroborates the efficiency of the GHZ3MQPEC protocol. Moreover, one of its most important qualitative features is that the required quantum resources scale linearly both in the number n of millionaires and the number m of qubits necessary to store their fortunes, which further enhances its potential applicability.
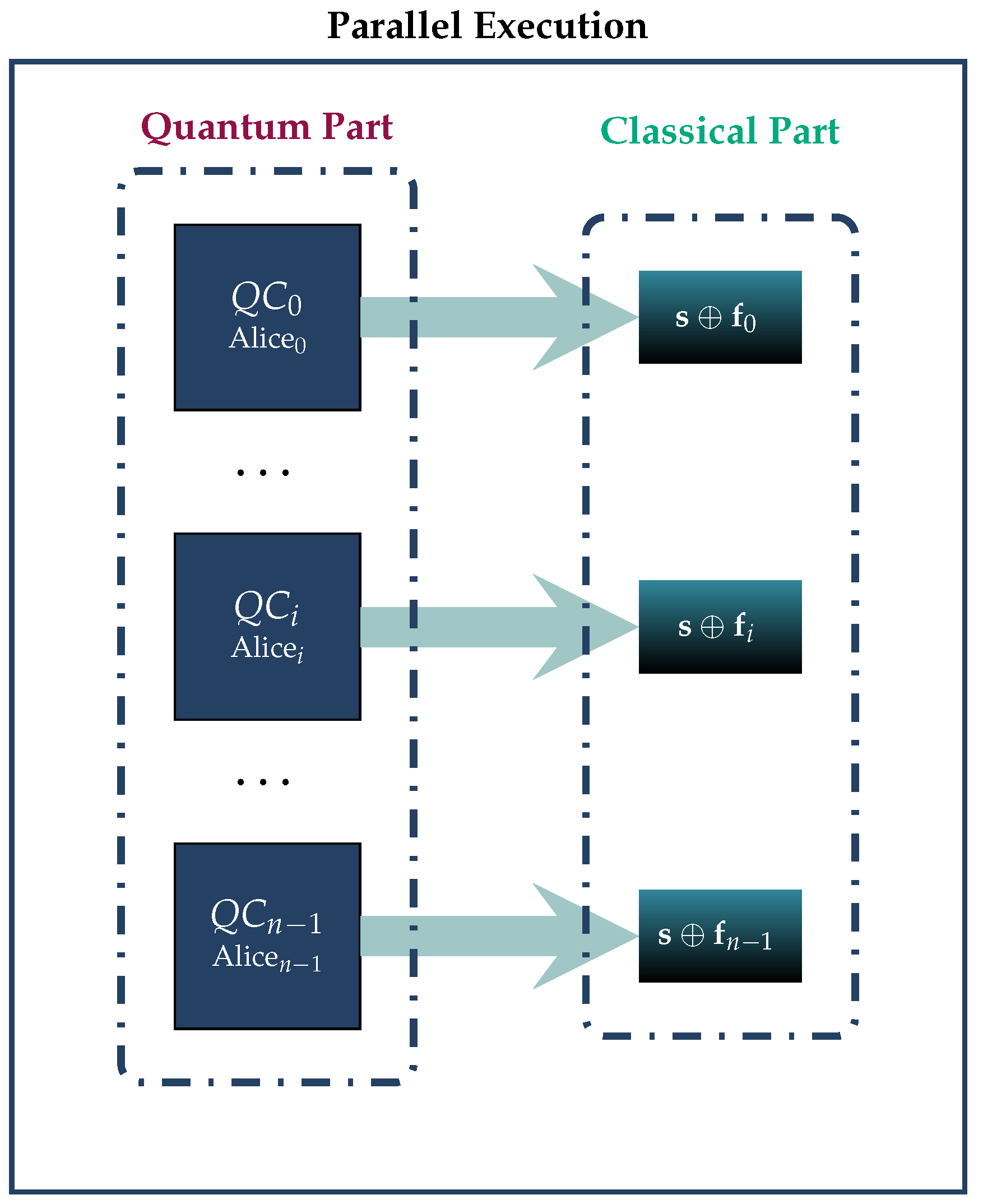
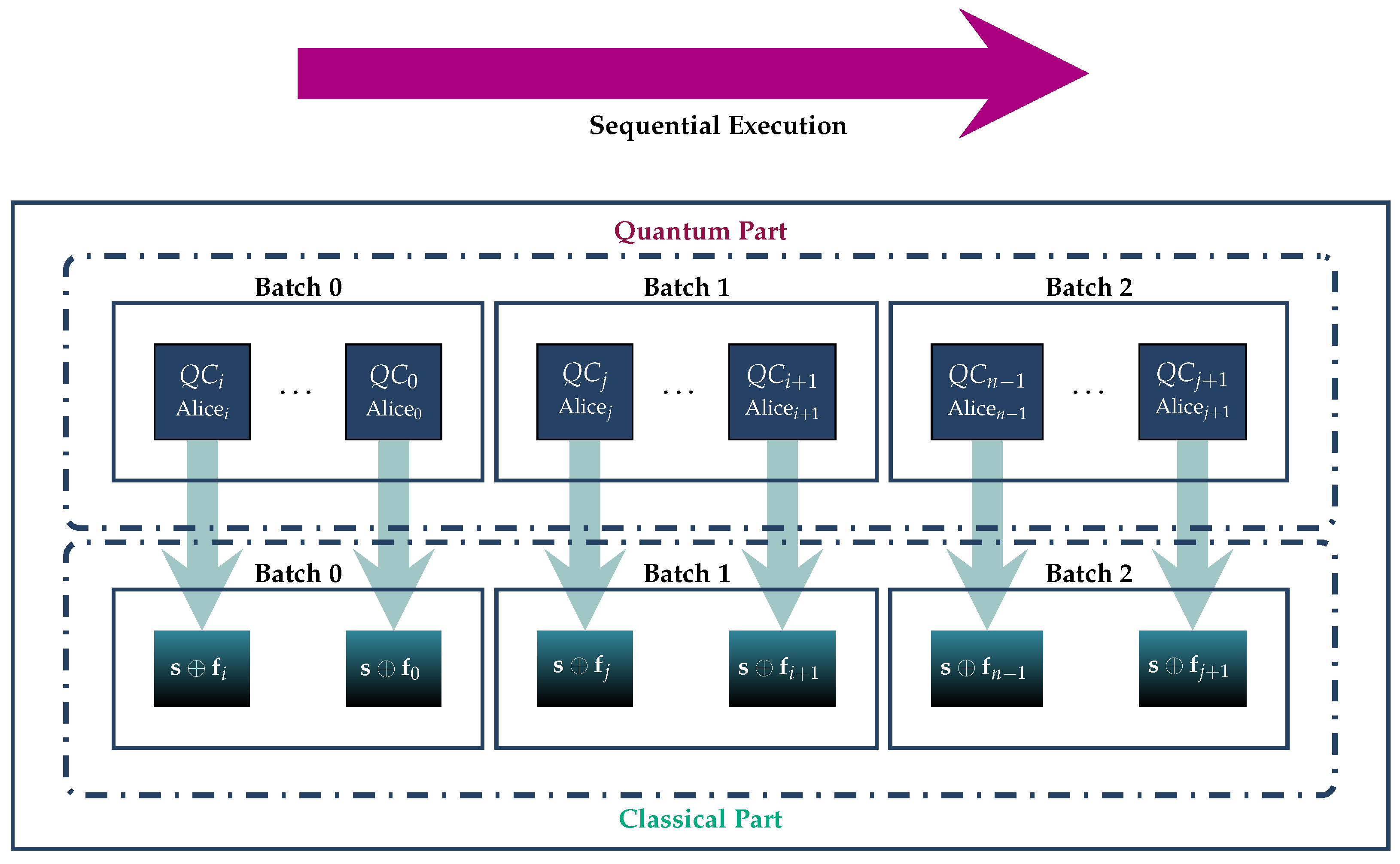
- Parallel or sequential execution. Although the execution of the quantum part of the GHZ3MQPEC protocol is envisioned to take place completely in parallel, it is also possible to be implemented sequentially. So, if the quantum resources do not suffice for the execution of the protocol in one go, it is possible to partition the n of millionaires into smaller groups and process these groups sequentially, even to the point of executing the protocol serially for one millionaire at a time.
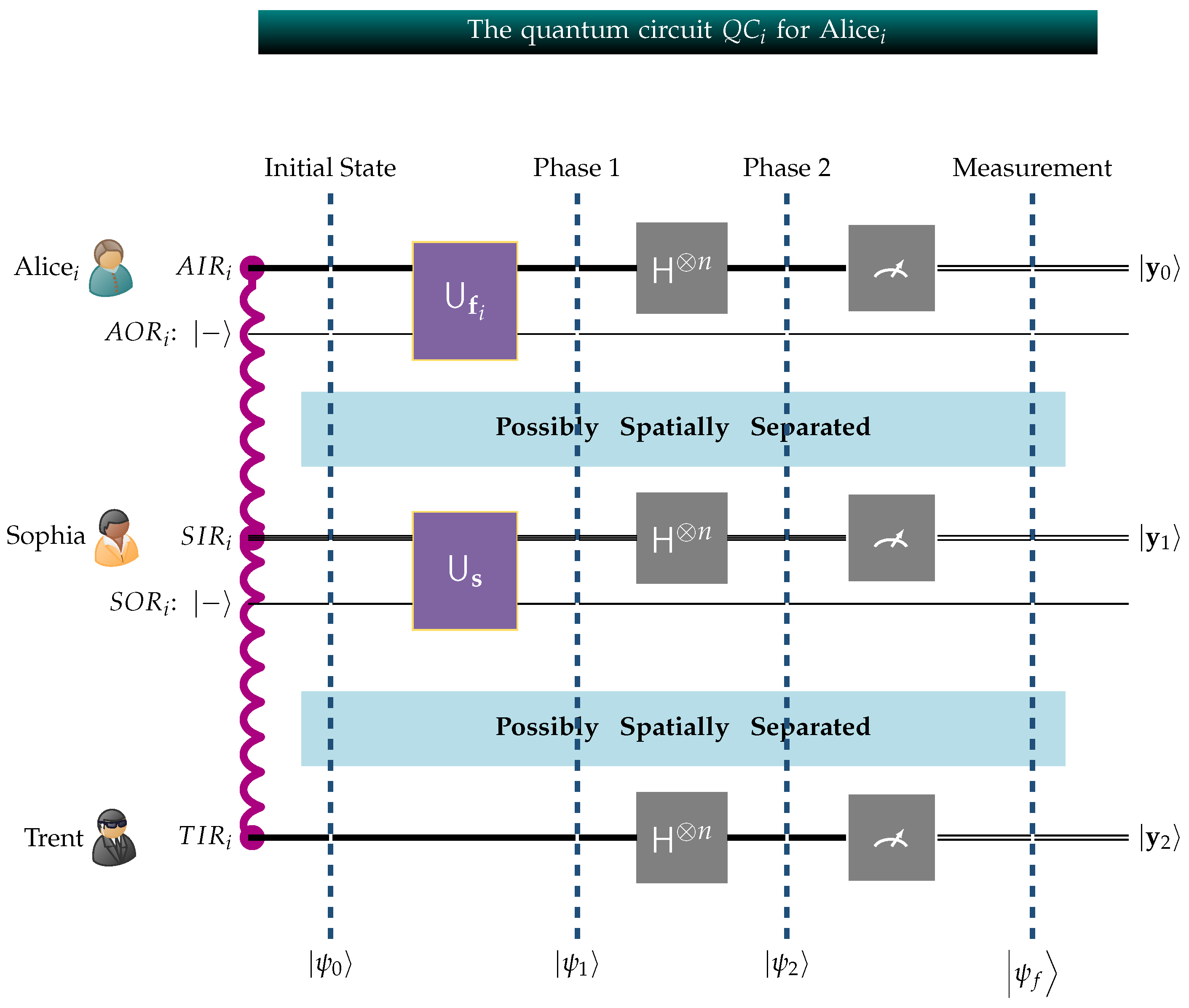
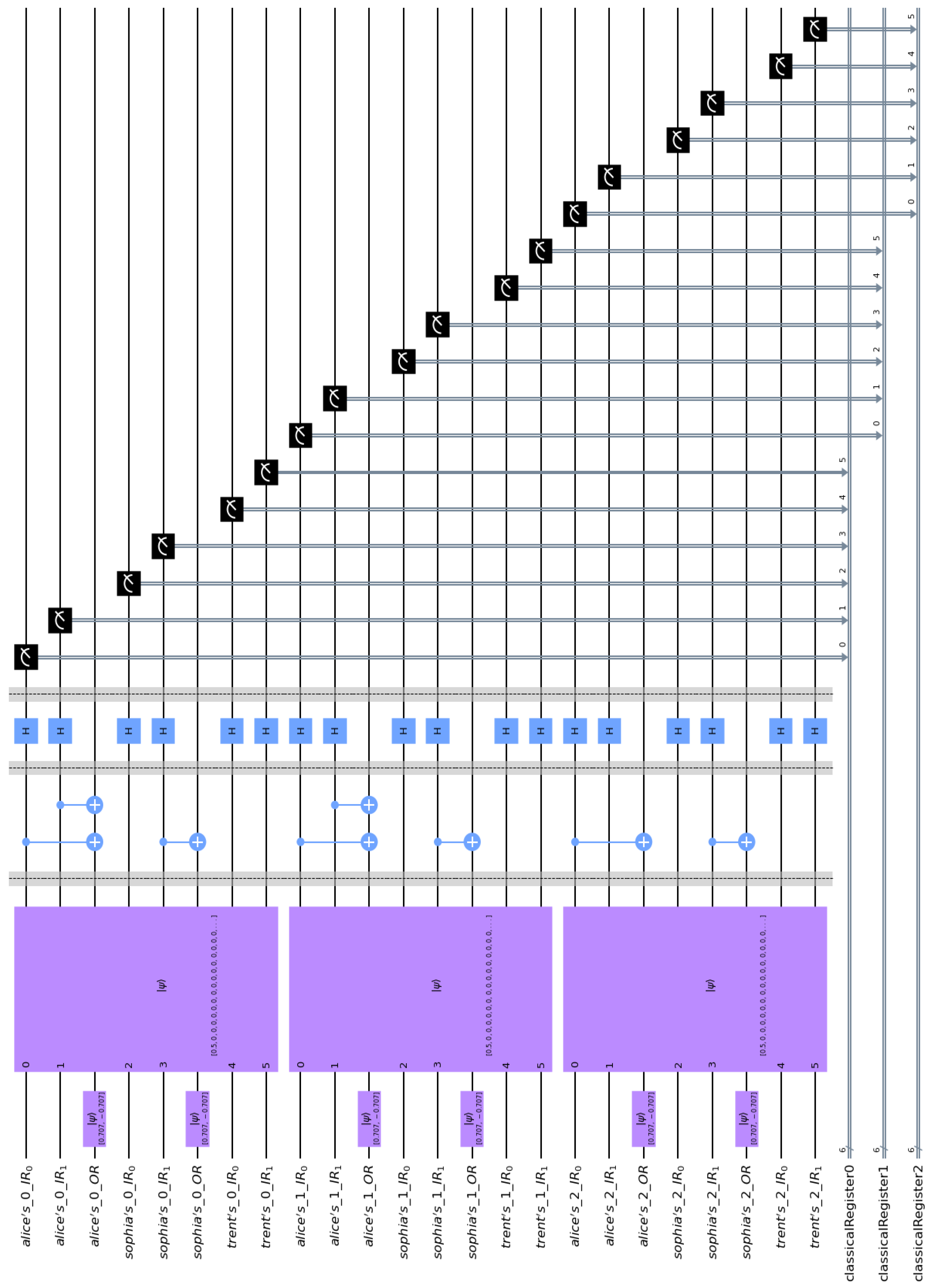
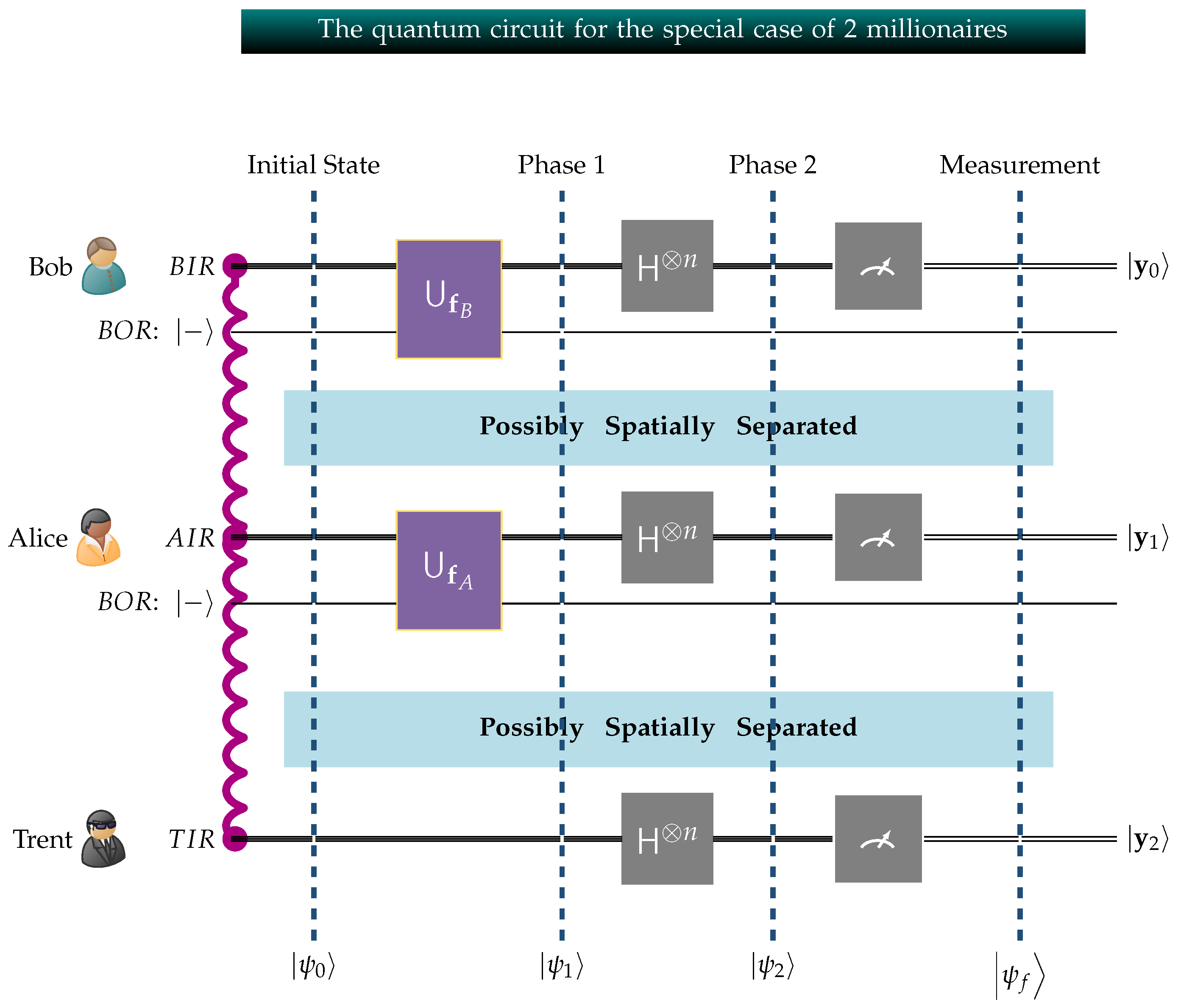
- For consistency, all quantum circuits follow the Qiskit [70] convention with respect to the order of qubits. Qiskit adheres to the little-endian qubit-indexing scheme, positioning the least significant qubit on the right side. Consequently, in the figure, the least significant qubit is placed at the top, while the most significant qubit is located at the bottom.
- is the quantum circuit corresponding to Alicei.
- , and are the input registers, each containing m qubits, in the local private circuits of Trent, Sophia, and Alicei, respectively. Their corresponding qubits are entangled, a fact that is visually indicated by the wavy red line connecting them.
- is Sophia’s single-qubit output register that is initialized to . Analogously, is Alicei’s single-qubit output register also initialized to .
- is the m-fold Hadamard transform.
- Alicei, , Sophia, and Trent act on their local circuits in a private and secret manner. Alicei’s private circuit is structurally similar to Sophia’s, but there is a critical difference. Alicei encodes her fortune into the global state of the system using an appropriate unitary transform . Similarly, Sophia embeds her secret number into the global system through her unitary transform . Since, in general, , the unitary transforms and are different.
- If , or, equivalently, ≠, the sumappearing in (14) becomes just 0.
- If , or, equivalently, =, the sumbecomes
- (D1)
- Sophia and Alicei send to Trent the measured contents of their input registers and , respectively. The communication takes place via authenticated classical channels, which means that the transmitted messages become public knowledge but cannot be modified by an adversary.
- (D2)
- Trent, as was stipulated in (A4) of Section 3.1, never divulges the measured contents of his input register to any other in-game player or outside eavesdropper. This implies that only Trent has the complete information to compute the modulo 2 sum according to (19).
- (D3)
- The same procedure is repeated for every millionaire Alice0, …, Alicen−1. This enables Trent to calculate the sequence of n modulo 2 sums , …, . We note that Trent, as was ordained in (A4), never reveals the aforementioned sequence to any other in-game player or outside eavesdropper. The following obvious identityis the key to determine whether two fortunes and , , are equal or not. Finally, Trent broadcasts through classical channels a sequence of of bits that carry the information YESi,j or NOi,j, , depending on whether or .
5. The GHZ3MQPEC Protocol in Action
- Alice0’s input register alice’s_0_IR containing two qubits.
- Alice0’s single-qubit output register alice’s_0_OR initialized at .
- Sophia’s input register sophia’s_0_IR containing two qubits.
- Sophia’s single-qubit output register sophia’s_0_OR initialized at .
- Trent’s input register trent’s_0_IR containing two qubits.
- trent’s_0_IR, sophia’s_0_IR, and alice’s_0_IR are initialized in the entangled state .
- The three classical registers (each containing two bits) used by Alice0, Sophia, and Trent to store their measurements, are collectively referred to as the classicalRegister0 with a total capacity of six bits.
- Alice1’s input register alice’s_1_IR containing two qubits.
- Alice1’s single-qubit output register alice’s_1_OR initialized at .
- Sophia’s input register sophia’s_1_IR containing two qubits.
- Sophia’s single-qubit output register sophia’s_1_OR initialized at .
- Trent’s input register trent’s_1_IR containing two qubits.
- trent’s_1_IR, sophia’s_1_IR, and alice’s_1_IR are initialized in the entangled state .
- The three classical registers (each containing two bits) used by Alice1, Sophia, and Trent to store their measurements, are collectively referred to as the classicalRegister1 with a total capacity of six bits.
- Alice2’s input register alice’s_2_IR containing two qubits.
- Alice2’s single-qubit output register alice’s_2_OR initialized at .
- Sophia’s input register sophia’s_2_IR containing two qubits.
- Sophia’s single-qubit output register sophia’s_2_OR initialized at .
- Trent’s input register trent’s_2_IR containing two qubits.
- trent’s_0_IR, sophia’s_2_IR, and alice’s_2_IR are initialized in the entangled state .
- The three classical registers (each containing two bits) used by Alice2, Sophia, and Trent to store their measurements are collectively referred to as the classicalRegister2 with a total capacity of six bits.


 . The label consists of three parts:
. The label consists of three parts:  , corresponding to the contents of classicalRegister2;
, corresponding to the contents of classicalRegister2;  , corresponding to the contents of the classicalRegister1; and
, corresponding to the contents of the classicalRegister1; and  , corresponding to the contents of the classicalRegister0. This ordering is a direct consequence of the way the quantum circuit in Figure 6 was constructed, i.e., the bits of classicalRegister2 are more significant than those of classicalRegister1, which in turn are more significant than those of classicalRegister0.
, corresponding to the contents of the classicalRegister0. This ordering is a direct consequence of the way the quantum circuit in Figure 6 was constructed, i.e., the bits of classicalRegister2 are more significant than those of classicalRegister1, which in turn are more significant than those of classicalRegister0.- classicalRegister0 is the collective name for the three classical registers (each containing two bits) used by Trent, Sophia, and Alice0 to store their measurements. Therefore, the contents of
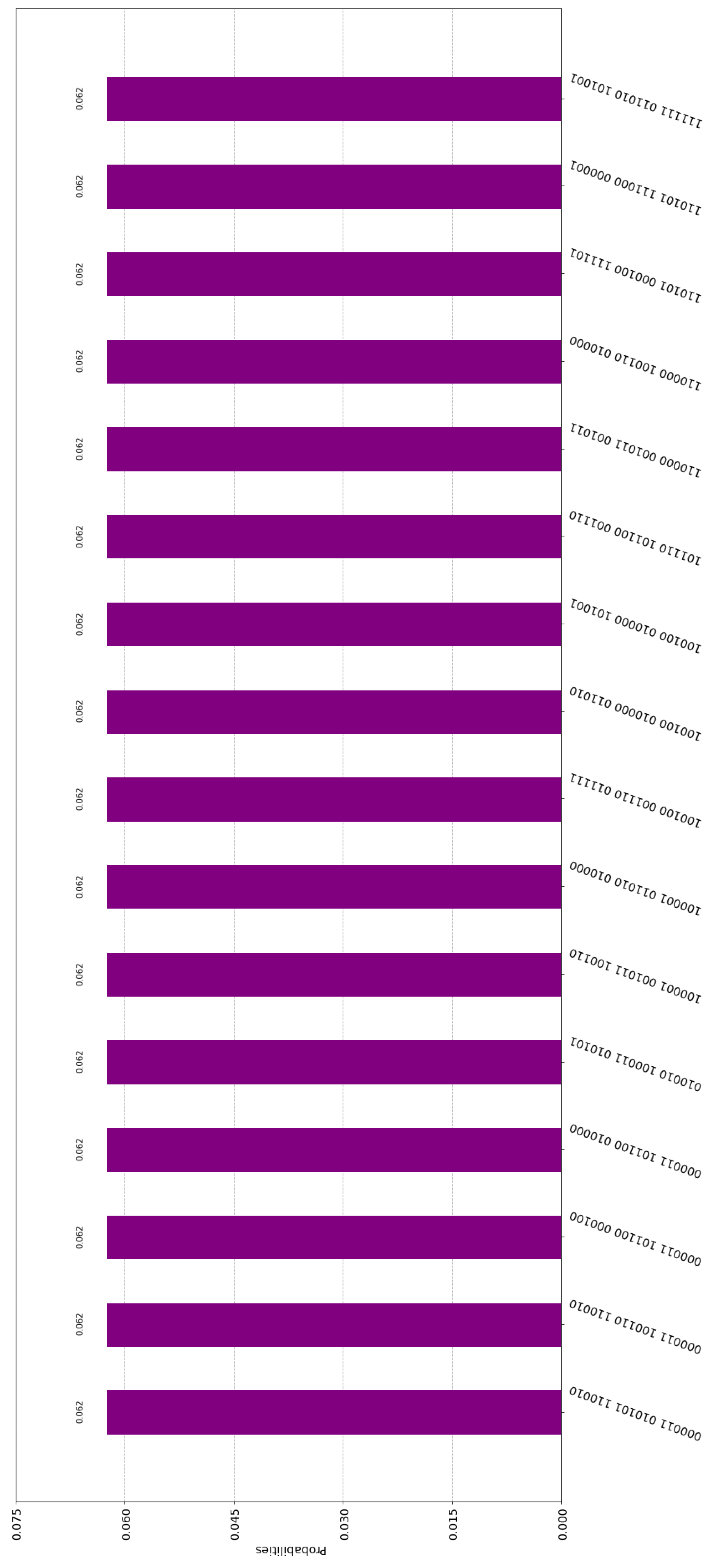
are analyzed as shown below:
This means that , , and . Sophia and Alice0 send to Trent and via authenticated classical channels. So, Trent has the complete information to compute the modulo 2 sum of , , and and conclude thataccording to (19). - Reasoning in exactly the same way for classicalRegister1 and classicalRegister2, it is straightforward to see that Trent arrives at the additional conclusions
6. Efficiency and Security Analysis
6.1. Efficiency
6.2. Security
6.2.1. External Attack
- (DT1)
- Eavesdropping detection. A typical scheme for the detection of a possible eavesdropper is to have the source responsible for the generation and distribution of the entangled particles, the triplets in our case, also produce decoy photons randomly chosen from one of the states, which are randomly embedded into the transmission sequences. Eve, by meddling with the transmission sequences, and unaware of the positions of the decoys, will invariably cause errors that are easily detectable by the legitimate players upon a typical verification check. This technique, which is referred to as the decoy technique, has been extensively studied in the literature [20,26,36,41,43,44,47,69].
- (DT2)
- Entanglement validation. The effective execution of any protocol based on entanglement relies fundamentally on the presence of entanglement itself. In the absence of assured entanglement, the operational integrity of the protocol is jeopardized. The process of validating entanglement may yield two possible results. Should entanglement be confirmed, the protocol is then able to advance and successfully fulfill its designated purpose. The inability to confirm entanglement suggests a lack of the essential entanglement itself. This situation may arise due to either the presence of noisy quantum channels or intentional disruption by an adversary. No matter what the underlying reason might be, the only appropriate course of action is to cease the current execution and restart the entire process, ensuring that corrective measures are put in place. Given its importance, the validation of entanglement has been extensively examined by numerous researchers. The GHZ3MQPEC protocol follows the advanced techniques described in previous studies, and in particular [77,78,79,80,81,82].
- (Attack1)
- Measure and Resend. Eve intercepts the qubits as they are being transmitted from Trent to Sophia, and Alicei, , measures them and then returns them to the intended recipients in this kind of attack. However, there is no information encoded in the triplets. Therefore, Eve will be unable to find any information by doing this. Additionally, the legitimate players will be able to identify a malicious presence with ease if they use the decoy technique. As a result, the protocol is immune to attacks of this kind.
- (Attack2)
- Intercept and Resend. Eve’s approach in this scenario involves intercepting the particles while they are being transmitted from Trent to Sophia and Alicei, where . Due to the no-cloning theorem, she is unable to create copies of these particles. Consequently, she opts to prepare and send new qubits to the designated recipients. Eve does not learn anything by measuring the triplets because, as we have already mentioned, they carry no information at all during the protocol’s transmission phase. Additionally, the legitimate players can deduce the existence of an eavesdropper thanks to the decoy technique. So, the GHZ3MQPEC protocol is also safe from such an attack.
- (Attack3)
- Entangle and Measure. Eve starts this kind of attack by intercepting the qubits of the triplets during their transmission. In contrast to the previous types of attack, in this case, Eve refrains from measuring these qubits; instead, she entangles them with her ancilla state before forwarding the relevant qubits to Sophia and Alicei. Following this, Eve remains inactive until the protocol concludes, at which point she measures her qubits, aiming to extract valuable information. However, the result of her efforts leads to a situation where, rather than achieving an even distribution of triplets among Trent, Sophia, and Alicei, she ends up with m quadruples distributed evenly among Trent, Sophia, Alicei, and herself. Consequently, during the classical portion of the protocol, when Sophia and Alicei relay their measurements to Trent via the public channel, Eve will be unable to compute the correct modulo 2 sum. This is due to her lack of access to Trent’s private bit vector , which Trent does not transmit through the public channel. As a result, Eve will again be unsuccessful in acquiring any information.
- (Attack4)
- PNS. One of the most potent attack methods that Eve can use against any quantum protocol at the moment is the photon number splitting attack (PNS), which was first described in [83] and subsequently examined in [84,85]. Contemporary photon sources exhibit a known flaw: at times, they might generate several identical photons rather than a single one. Consequently, Eve could intercept the pulses originating from Trent during the distribution of the triplets, retain one photon from the multiphoton pulse for her own use, and transmit the remaining photons to Sophia and Alicei without being noticed during the transmission phase. Nonetheless, this situation resembles the Entangle and Measure attack analyzed above. Again, instead of triplets evenly distributed among the three legitimate actors, there are quadruples evenly distributed among Trent, Sophia, Alicei, and Eve. Eve becomes an active fourth player in the game but fails to uncover any useful information for the reason explained above.
6.2.2. Participants’ Attack
- Alicei
- Let us assume that Alicei, , intercepts the qubits during their transmission from Trent to Sophia and another Alicej, . Alicei has the option to measure them and send them back to their intended recipients or transmit new, previously prepared qubits to their intended recipients. Taking into consideration the fact that the triplets contain no information at all, we see that, in both cases, Alicei will fail to gain any information. Moreover, the decoy technique will allow the legitimate players to infer that someone has tampered with the transmitted sequences.Another scenario for Alicei is to intercept the qubits from the triplets during their transmission from Trent to Sophia and Alicej, , and, without measuring them, entangle them with her ancilla state. Then, Alicei forwards the relevant qubits to Sophia and Alicej and waits for the quantum part of the protocol to finish. At this point, she measures her qubits in the hope of gaining useful information. The critical flaw in Alicei’s strategy is that her actions result in having quadruples evenly distributed among Trent, Sophia, Alicej, and Alicei instead of having triplets evenly distributed among Trent, Sophia, and Alicej. Ultimately, Alicei will fail to compute the correct modulo 2 sum as the classical portion of the protocol unfolds, the reason being that Alicei will not know Trent’s private bit vector . Recall that Trent never divulges or the modulo 2 sum to any other in-game player or outside eavesdropper, as ordained by (A4) and (D3). Once again, Alicei fails to gain any information. Therefore, the GHZ3MQPEC protocol is immune to attacks by Alicei, .
- Sophia
- Let us assume that Sophia intercepts the particles en route from Trent to Alicei. Sophia has the option to measure these particles and subsequently return them to Alicei, or alternatively, she may send new qubits that she has prepared in advance to Alicei. Since the triplets carry no information, Sophia will not gain any information in any of the earlier cases. Additionally, the other legitimate players will be able to identify the tampering thanks to the use of the decoy technique.Another possibility for Sophia is to intercept the qubits from the triplets during their transmission from Trent to Alicei and entangle them with her ancilla state, without measuring them. Sophia sends corresponding qubits to Alicei and waits for the protocol to finish. Then, she measures her qubits, expecting to uncover some information. The problem with this strategy is that Sophia’s tampering has resulted in having quadruples evenly distributed among Trent, Sophia, and Alicei, instead of having triplets. Ultimately, Sophia will fail to compute the correct modulo 2 sum as the classical portion of the protocol unfolds because she will not know Trent’s private bit vector . We recall that Trent never divulges or the modulo 2 sum to any other in-game player or outside eavesdropper, as dictated by (A4) and (D3). Consequently, the GHZ3MQPEC protocol is impervious to attacks by Sophia.
- Trent
- Trent cannot surmise Sophia’s secret number because Sophia, as stipulated in (A3), never reveals her secret number . Moreover, the fundamental premise of the protocol is that Alicei, , never divulges her private fortune . Hence, although Trent knows the modulo 2 sum , he can infer neither nor . Thus, the GHZ3MQPEC protocol cannot be compromised by Trent.
6.3. Comparative Assessment
7. Discussion and Conclusions
- The primary aim of this protocol is to be easily executable by modern quantum computers. This is achieved by employing only triplets, regardless of the number of participants. Though high-dimensional quantum states and more intricate multiparticle entangled states are feasible, their creation is challenging given the current state of quantum technology, leading to longer preparation times, particularly in situations involving many players. By exclusively using states, which are simpler to produce than Bell states, these issues are mitigated, advancing the practical implementation of the protocol.
- A key quantitative feature of this protocol is that the number of players and the volume of data being compared determine the required quantum resources, which scale linearly, further demonstrating its practicality. Notably, the GHZ3MQPEC protocol can be executed in both parallel and sequential modes. While the quantum operations are intended to run in parallel, sequential execution is also possible if quantum resources are insufficient, allowing the participants to be divided into smaller groups for sequential processing.
- Additionally, the protocol does not depend on a quantum signature scheme or pre-shared keys, which simplify and reduce its cost. Implementation is further streamlined as all participants use identical private quantum circuits consisting of Hadamard and CNOT gates, making it straightforward to implement on contemporary quantum computers.
- Crucially, the protocol ensures that external parties cannot access any information about the participants’ values, and participants themselves cannot learn each other’s secret numbers. The protocol is demonstrated to be information-theoretically secure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chow, J.; Dial, O.; Gambetta, J. IBM Quantum Breaks the 100-Qubit Processor Barrier. 2021. Available online: https://www.ibm.com/quantum/blog/127-qubit-quantum-processor-eagle (accessed on 2 March 2024).
- Newsroom, I. IBM Unveils 400 Qubit-Plus Quantum Processor. 2022. Available online: https://newsroom.ibm.com/2022-11-09-IBM-Unveils-400-Qubit-Plus-Quantum-Processor-and-Next-Generation-IBM-Quantum-System-Two (accessed on 2 March 2024).
- Gambetta, J. The Hardware and Software for the Era of Quantum Utility Is Here. 2023. Available online: https://www.ibm.com/quantum/blog/quantum-roadmap-2033 (accessed on 2 March 2024).
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 9–12 December 1984; pp. 175–179. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Grover, L. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Mermin, N.D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 1992, 68, 557–559. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Ampatzis, M.; Andronikos, T. QKD Based on Symmetric Entangled Bernstein-Vazirani. Entropy 2021, 23, 870. [Google Scholar] [CrossRef] [PubMed]
- Hillery, M.; Bužek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829. [Google Scholar] [CrossRef]
- Cleve, R.; Gottesman, D.; Lo, H.K. How to share a quantum secret. Phys. Rev. Lett. 1999, 83, 648. [Google Scholar] [CrossRef]
- Karlsson, A.; Koashi, M.; Imoto, N. Quantum entanglement for secret sharing and secret splitting. Phys. Rev. A 1999, 59, 162. [Google Scholar] [CrossRef]
- Ampatzis, M.; Andronikos, T. A Symmetric Extensible Protocol for Quantum Secret Sharing. Symmetry 2022, 14, 1692. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Deng, F.G.; Long, G.L.; Liu, X.S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 2003, 68, 042317. [Google Scholar] [CrossRef]
- Deng, F.G.; Long, G.L. Secure direct communication with a quantum one-time pad. Phys. Rev. A 2004, 69, 052319. [Google Scholar] [CrossRef]
- Wang, C.; Deng, F.G.; Li, Y.S.; Liu, X.S.; Long, G.L. Quantum secure direct communication with high-dimension quantum superdense coding. Phys. Rev. A 2005, 71, 044305. [Google Scholar] [CrossRef]
- Yang, Y.G.; Wen, Q.Y. An efficient two-party quantum private comparison protocol with decoy photons and two-photon entanglement. J. Phys. A Math. Theor. 2009, 42, 055305. [Google Scholar] [CrossRef]
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982), Washington, DC, USA, 3–5 November 1982. [Google Scholar] [CrossRef]
- Yao, A.C.C. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science (sfcs 1986), Toronto, ON, Canada, 27–29 October 1986. [Google Scholar] [CrossRef]
- Boudot, F.; Schoenmakers, B.; Traoré, J. A fair and efficient solution to the socialist millionaires’ problem. Discret. Appl. Math. 2001, 111, 23–36. [Google Scholar] [CrossRef]
- Chen, X.B.; Xu, G.; Niu, X.X.; Wen, Q.Y.; Yang, Y.X. An efficient protocol for the private comparison of equal information based on the triplet entangled state and single-particle measurement. Opt. Commun. 2010, 283, 1561–1565. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.B.; Jiang, Z.T. An efficient protocol for the quantum private comparison of equality with W state. Opt. Commun. 2011, 284, 3160–3163. [Google Scholar] [CrossRef]
- Tseng, H.Y.; Lin, J.; Hwang, T. New quantum private comparison protocol using EPR pairs. Quantum Inf. Process. 2011, 11, 373–384. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.B.; Jiang, Z.T.; Cao, Y.Z. A Protocol for the Quantum Private Comparison of Equality with χ-Type State. Int. J. Theor. Phys. 2011, 51, 69–77. [Google Scholar] [CrossRef]
- Jia, H.Y.; Wen, Q.Y.; Li, Y.B.; Gao, F. Quantum Private Comparison Using Genuine Four-Particle Entangled States. Int. J. Theor. Phys. 2011, 51, 1187–1194. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.B.; Jiang, Z.T.; Cao, Y.Z.; Cui, W. New Quantum Private Comparison Protocol Using χ-Type State. Int. J. Theor. Phys. 2012, 51, 1953–1960. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.B. Quantum Private Comparison Based on GHZ Entangled States. Int. J. Theor. Phys. 2012, 51, 3596–3604. [Google Scholar] [CrossRef]
- Ji, Z.X.; Ye, T.Y. Quantum Private Comparison of Equal Information Based on Highly Entangled Six-Qubit Genuine State. Commun. Theor. Phys. 2016, 65, 711–715. [Google Scholar] [CrossRef]
- Chou, W.H.; Hwang, T.; Gu, J. Semi-quantum private comparison protocol under an almost-dishonest third party. arXiv 2016, arXiv:1607.07961. [Google Scholar] [CrossRef]
- He, Z.; Lou, X. Security analysis and improvement in a semi-quantum private comparison without pre-shared key. Quantum Inf. Process. 2023, 22, 150. [Google Scholar] [CrossRef]
- Chen, X.B.; Su, Y.; Niu, X.X.; Yang, Y.X. Efficient and feasible quantum private comparison of equality against the collective amplitude damping noise. Quantum Inf. Process. 2012, 13, 101–112. [Google Scholar] [CrossRef]
- Zi, W.; Guo, F.; Luo, Y.; Cao, S.; Wen, Q. Quantum Private Comparison Protocol with the Random Rotation. Int. J. Theor. Phys. 2013, 52, 3212–3219. [Google Scholar] [CrossRef]
- Hou, M.; Wu, Y. Single-photon-based quantum secure protocol for the socialist millionaires’ problem. Front. Phys. 2024, 12, 1364140. [Google Scholar] [CrossRef]
- Liu, W.; Liu, C.; Wang, H.; Jia, T. Quantum Private Comparison: A Review. IETE Tech. Rev. 2013, 30, 439. [Google Scholar] [CrossRef]
- Jia, H.Y.; Wen, Q.Y.; Song, T.T.; Gao, F. Quantum protocol for millionaire problem. Opt. Commun. 2011, 284, 545–549. [Google Scholar] [CrossRef]
- Lin, S.; Sun, Y.; Liu, X.F.; Yao, Z.Q. Quantum private comparison protocol with d-dimensional Bell states. Quantum Inf. Process. 2012, 12, 559–568. [Google Scholar] [CrossRef]
- Zhang, W.W.; Li, D.; Zhang, K.J.; Zuo, H.J. A quantum protocol for millionaire problem with Bell states. Quantum Inf. Process. 2013, 12, 2241–2249. [Google Scholar] [CrossRef]
- Ye, C.Q.; Ye, T.Y. Multi-party quantum private comparison of size relation with d-level single-particle states. Quantum Inf. Process. 2018, 17, 252. [Google Scholar] [CrossRef]
- Cao, H.; Ma, W.; Lü, L.; He, Y.; Liu, G. Multi-party quantum privacy comparison of size based on d-level GHZ states. Quantum Inf. Process. 2019, 18, 287. [Google Scholar] [CrossRef]
- Wu, W.; Zhao, Y. Quantum private comparison of size using d-level Bell states with a semi-honest third party. Quantum Inf. Process. 2021, 20, 155. [Google Scholar] [CrossRef]
- Chang, Y.J.; Tsai, C.W.; Hwang, T. Multi-user private comparison protocol using GHZ class states. Quantum Inf. Process. 2013, 12, 1077–1088. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.B.; Wang, X.M. Multi-party Quantum Private Comparison Protocol Using d-Dimensional Basis States Without Entanglement Swapping. Int. J. Theor. Phys. 2013, 53, 1085–1091. [Google Scholar] [CrossRef]
- Huang, S.L.; Hwang, T.; Gope, P. Multi-party quantum private comparison with an almost-dishonest third party. Quantum Inf. Process. 2015, 14, 4225–4235. [Google Scholar] [CrossRef]
- Hung, S.M.; Hwang, S.L.; Hwang, T.; Kao, S.H. Multiparty quantum private comparison with almost dishonest third parties for strangers. Quantum Inf. Process. 2016, 16, 36. [Google Scholar] [CrossRef]
- Zhang, J.W.; Xu, G.; Chen, X.B.; Chang, Y.; Dong, Z.C. Improved multiparty quantum private comparison based on quantum homomorphic encryption. Phys. A Stat. Mech. Its Appl. 2023, 610, 128397. [Google Scholar] [CrossRef]
- Zhao-Xu, J.; Tian-Yu, Y. Multi-party quantum private comparison based on the entanglement swapping of d-level cat states and d-level Bell states. Quantum Inf. Process. 2017, 16, 177. [Google Scholar] [CrossRef]
- Ye, T.Y.; Hu, J.L. Multi-Party Quantum Private Comparison Based on Entanglement Swapping of Bell Entangled States within d-Level Quantum System. Int. J. Theor. Phys. 2021, 60, 1471–1480. [Google Scholar] [CrossRef]
- Colbeck, R. Impossibility of secure two-party classical computation. Phys. Rev. A 2007, 76, 062308. [Google Scholar] [CrossRef]
- Crépeau, C.; Gottesman, D.; Smith, A. Secure multi-party quantum computation. In Proceedings of the Thiry-Fourth Annual ACM Symposium on Theory of Computing, STOC02, Montreal, QC Canada, 19–21 May 2002., STOC02. [CrossRef]
- Lo, H.K. Insecurity of quantum secure computations. Phys. Rev. A 1997, 56, 1154–1162. [Google Scholar] [CrossRef]
- Sonnino, G.; Sonnino, A. Efficient Multiparty Protocols Using Generalized Parseval’s Identity and the Theta Algebra. In Proceedings of the 2022 7th International Conference on Mathematics and Computers in Sciences and Industry (MCSI), Athens, Greece, 22–24 August 2022. [Google Scholar] [CrossRef]
- Meyer, D.A. Quantum strategies. Phys. Rev. Lett. 1999, 82, 1052. [Google Scholar] [CrossRef]
- Eisert, J.; Wilkens, M.; Lewenstein, M. Quantum games and quantum strategies. Phys. Rev. Lett. 1999, 83, 3077. [Google Scholar] [CrossRef]
- Andronikos, T.; Sirokofskich, A.; Kastampolidou, K.; Varvouzou, M.; Giannakis, K.; Singh, A. Finite Automata Capturing Winning Sequences for All Possible Variants of the PQ Penny Flip Game. Mathematics 2018, 6, 20. [Google Scholar] [CrossRef]
- Andronikos, T.; Sirokofskich, A. The Connection between the PQ Penny Flip Game and the Dihedral Groups. Mathematics 2021, 9, 1115. [Google Scholar] [CrossRef]
- Andronikos, T. Conditions that enable a player to surely win in sequential quantum games. Quantum Inf. Process. 2022, 21, 268. [Google Scholar] [CrossRef]
- Kastampolidou, K.; Andronikos, T. Quantum Tapsilou—A Quantum Game Inspired by the Traditional Greek Coin Tossing Game Tapsilou. Games 2023, 14, 72. [Google Scholar] [CrossRef]
- Cruz, D.; Fournier, R.; Gremion, F.; Jeannerot, A.; Komagata, K.; Tosic, T.; Thiesbrummel, J.; Chan, C.L.; Macris, N.; Dupertuis, M.A.; et al. Efficient Quantum Algorithms for GHZ and W States, and Implementation on the IBM Quantum Computer. Adv. Quantum Technol. 2019, 2, 1900015. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Yanofsky, N.S.; Mannucci, M.A. Quantum Computing for Computer Scientists; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Wong, T.G. Introduction to Classical and Quantum Computing; Rooted Grove: Omaha, USA, 2022. [Google Scholar]
- Ampatzis, M.; Andronikos, T. Quantum Secret Aggregation Utilizing a Network of Agents. Cryptography 2023, 7, 5. [Google Scholar] [CrossRef]
- Mermin, N. Quantum Computer Science: An Introduction; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Andronikos, T.; Sirokofskich, A. One-to-Many Simultaneous Secure Quantum Information Transmission. Cryptography 2023, 7, 64. [Google Scholar] [CrossRef]
- Deng, F.G.; Li, X.H.; Zhou, H.Y. Efficient high-capacity quantum secret sharing with two-photon entanglement. Phys. Lett. A 2008, 372, 1957–1962. [Google Scholar] [CrossRef]
- Qiskit. Qiskit Open-Source Toolkit for Useful Quantum. Available online: https://www.ibm.com/quantum/qiskit (accessed on 2 March 2024).
- Tsai, C.W.; Hsieh, C.R.; Hwang, T. Dense coding using cluster states and its application on deterministic secure quantum communication. Eur. Phys. J. D 2011, 61, 779–783. [Google Scholar] [CrossRef]
- Hwang, T.; Hwang, C.C.; Tsai, C.W. Quantum key distribution protocol using dense coding of three-qubit W state. Eur. Phys. J. D 2011, 61, 785–790. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, W.F.; Zhang, S.B. Efficient multiparty quantum private comparison protocol based on single photons and rotation encryption. Quantum Inf. Process. 2023, 22, 272. [Google Scholar] [CrossRef]
- Banerjee, A.; Pathak, A. Maximally efficient protocols for direct secure quantum communication. Phys. Lett. A 2012, 376, 2944–2950. [Google Scholar] [CrossRef]
- Joy, D.; Surendran, S.P.; Sabir, M. Efficient deterministic secure quantum communication protocols using multipartite entangled states. Quantum Inf. Process. 2017, 16, 157. [Google Scholar] [CrossRef]
- Song, X.; Wen, A.; Gou, R. Multiparty Quantum Private Comparison of Size Relation Based on Single-Particle States. IEEE Access 2019, 7, 142507–142514. [Google Scholar] [CrossRef]
- Neigovzen, R.; Rodó, C.; Adesso, G.; Sanpera, A. Multipartite continuous-variable solution for the Byzantine agreement problem. Phys. Rev. A 2008, 77, 062307. [Google Scholar] [CrossRef]
- Feng, Y.; Shi, R.; Zhou, J.; Liao, Q.; Guo, Y. Quantum Byzantine Agreement with Tripartite Entangled States. Int. J. Theor. Phys. 2019, 58, 1482–1498. [Google Scholar] [CrossRef]
- Wang, W.; Yu, Y.; Du, L. Quantum blockchain based on asymmetric quantum encryption and a stake vote consensus algorithm. Sci. Rep. 2022, 12, 8606. [Google Scholar] [CrossRef]
- Yang, Z.; Salman, T.; Jain, R.; Pietro, R.D. Decentralization Using Quantum Blockchain: A Theoretical Analysis. IEEE Trans. Quantum Eng. 2022, 3, 4100716. [Google Scholar] [CrossRef]
- Qu, Z.; Zhang, Z.; Liu, B.; Tiwari, P.; Ning, X.; Muhammad, K. Quantum detectable Byzantine agreement for distributed data trust management in blockchain. Inf. Sci. 2023, 637, 118909. [Google Scholar] [CrossRef]
- Ikeda, K.; Lowe, A. Quantum protocol for decision making and verifying truthfulness among N-quantum parties: Solution and extension of the quantum coin flipping game. IET Quantum Commun. 2023, 4, 218–227. [Google Scholar] [CrossRef]
- Huttner, B.; Imoto, N.; Gisin, N.; Mor, T. Quantum cryptography with coherent states. Phys. Rev. A 1995, 51, 1863. [Google Scholar] [CrossRef]
- Lütkenhaus, N. Security against individual attacks for realistic quantum key distribution. Phys. Rev. A 2000, 61, 052304. [Google Scholar] [CrossRef]
- Brassard, G.; Lütkenhaus, N.; Mor, T.; Sanders, B.C. Limitations on practical quantum cryptography. Phys. Rev. Lett. 2000, 85, 1330. [Google Scholar] [CrossRef] [PubMed]
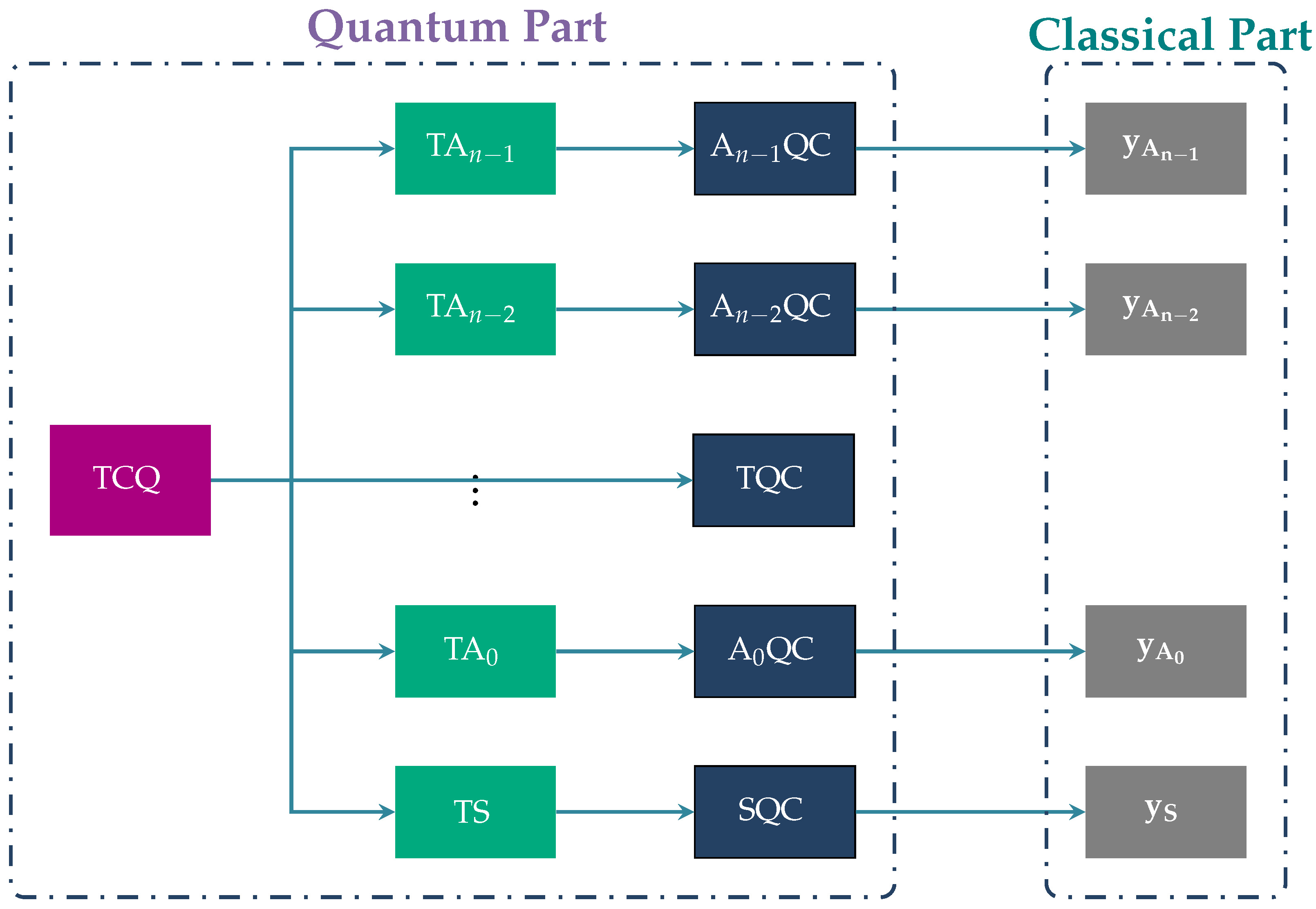
| Notations and Abbreviations | |
|---|---|
| Symbolism | Operation |
| TCQ | Trent creates triplets of qubits in the state |
| TS | Trent sends to Sophia one qubit from each triplet through a quantum channel |
| TA0 | Trent sends to Alicen−2 one qubit from each triplet via a quantum channel |
| TAn−2 | Trent sends to Alicen−2 one qubit from each triplet via a quantum channel |
| TAn−1 | Trent sends to Alicen−1 one qubit from each triplet via a quantum channel |
| SQC | Sophia applies her quantum circuit and measures her input register |
| A0QC | Alice0 applies her quantum circuit and measures her input register |
| TQC | Trent applies his quantum circuit and measures his input register |
| An−2QC | Alicen−2 applies her quantum circuit and measures her input register |
| An−1QC | Alicen−1 applies her quantum circuit and measures her input register |
| Sophia sends to Trent the bit vector through a classical public channel | |
| Alice0 sends to Bob the bit vector via a classical public channel | |
| Alicen−2 sends to Bob the bit vector via a classical public channel | |
| Alicen−1 sends to Bob the bit vector via a classical public channel | |
| # of Millionaires | Quantum State | Unitary Operations | Use of QKD | Qubit Efficiency | |
|---|---|---|---|---|---|
| [20] | 2 | EPR | ✔ | ✖ | |
| [24] | 2 | GHZ3 | ✔ | ✖ | |
| [44] | n | GHZn | ✖ | ✖ | |
| [45] | n | d-level basis states | ✔ | ✖ | |
| [49] | n | d-level states | ✔ | ✖ | |
| [50] | n | d-level Bell states | ✔ | ✖ | |
| [48] | n | Quantum Homomorphic Encryption | ✔ | ✔ | — |
| [36] | 2 | Single Photons | ✔ | ✔ | ≥50.00% |
| GHZ3MQPEC | n | GHZ3 | ✔ | ✖ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andronikos, T.; Sirokofskich, A. A Multiparty Quantum Private Equality Comparison Scheme Relying on |GHZ3⟩ States. Future Internet 2024, 16, 309. https://doi.org/10.3390/fi16090309
Andronikos T, Sirokofskich A. A Multiparty Quantum Private Equality Comparison Scheme Relying on |GHZ3⟩ States. Future Internet. 2024; 16(9):309. https://doi.org/10.3390/fi16090309
Chicago/Turabian StyleAndronikos, Theodore, and Alla Sirokofskich. 2024. "A Multiparty Quantum Private Equality Comparison Scheme Relying on |GHZ3⟩ States" Future Internet 16, no. 9: 309. https://doi.org/10.3390/fi16090309
APA StyleAndronikos, T., & Sirokofskich, A. (2024). A Multiparty Quantum Private Equality Comparison Scheme Relying on |GHZ3⟩ States. Future Internet, 16(9), 309. https://doi.org/10.3390/fi16090309