Detection of Intelligent Intruders in Wireless Sensor Networks
Abstract
:1. Introduction
1.1. Related Works and Research Motivation
1.2. Paper Organization
2. System Modeling and Definitions
2.1. Assumptions and Models
- All sensors have a sensing range of and a communication range of , both following the Boolean sensing/communication model;
- The Base Station (BS) is located in the center of A and has a communication range of ;
- Any intruder is not aware of the layout of the sensors’ placement;
- Sensors deployed in the WSN are not aware of the intrusion path or strategies adopted by any intruder;
- An intruder will enter the WSN FoI from any point along the left peripheral and move toward the right peripheral, aiming to traverse the WSN FoI and arrive at its destination outside of the FoI, as illustrated in Figure 1;
- An intruder is able to detect nearby sensor(s) within its sensing range ;
- , which ensures that an intelligent intruder is able to sense nearby sensor(s) and perform detection avoidance before being detected by the WSN;
- The terrain within the FoI will not affect sensor placement or the intruder’s intrusion path.

2.2. Problem Formulation
2.3. Performance Evaluation Metrics
- Detection probability : the probability that an intruder is detected by a connected sensor in a WSN within the maximum allowable intrusion time .
- Prevention probability : the probability that an intruder is not detected, however is prevented from reaching its destination within the maximum allowable intrusion time .
- WSN win probability : the sum of the detection probability and the prevention probability , and .
- Escape probability : the probability that an intruder manages to escape the WSN FoI and arrives at the destination within the allotted .
- Coverage: Any point in the field of interest is said to be covered if it is within the sensing range of a sensor. The network coverage is defined as the probability of a random point in A being covered by at least one sensor.
- Connectivity: Consider two random sensors and located inside A; and are connected if there exists a communication path between them. The network connectivity is defined as the probability of a random sensor that can communicate with the base station through a direct or multi-hop communication path, i.e., a connected sensor.
- Connected coverage: An intruder is considered to be detected when it enters the sensing coverage area of a connected sensor (to the BS). The network connected coverage is thus defined as the probability of a random point in A that is covered by at least one connected sensor.
3. Intrusion Algorithms
| Notation | Description |
|---|---|
| L | Side length of the field of interest |
| N | Number of sensors deployed |
| Sensing range | |
| Communication range | |
| Intruder sensing range | |
| λ | Node density |
| Detection probability | |
| Prevention probability | |
| WSN win probability | |
| Intruder escape probability |
3.1. Linear Intrusion Algorithm
3.2. Pinball Intrusion Algorithm
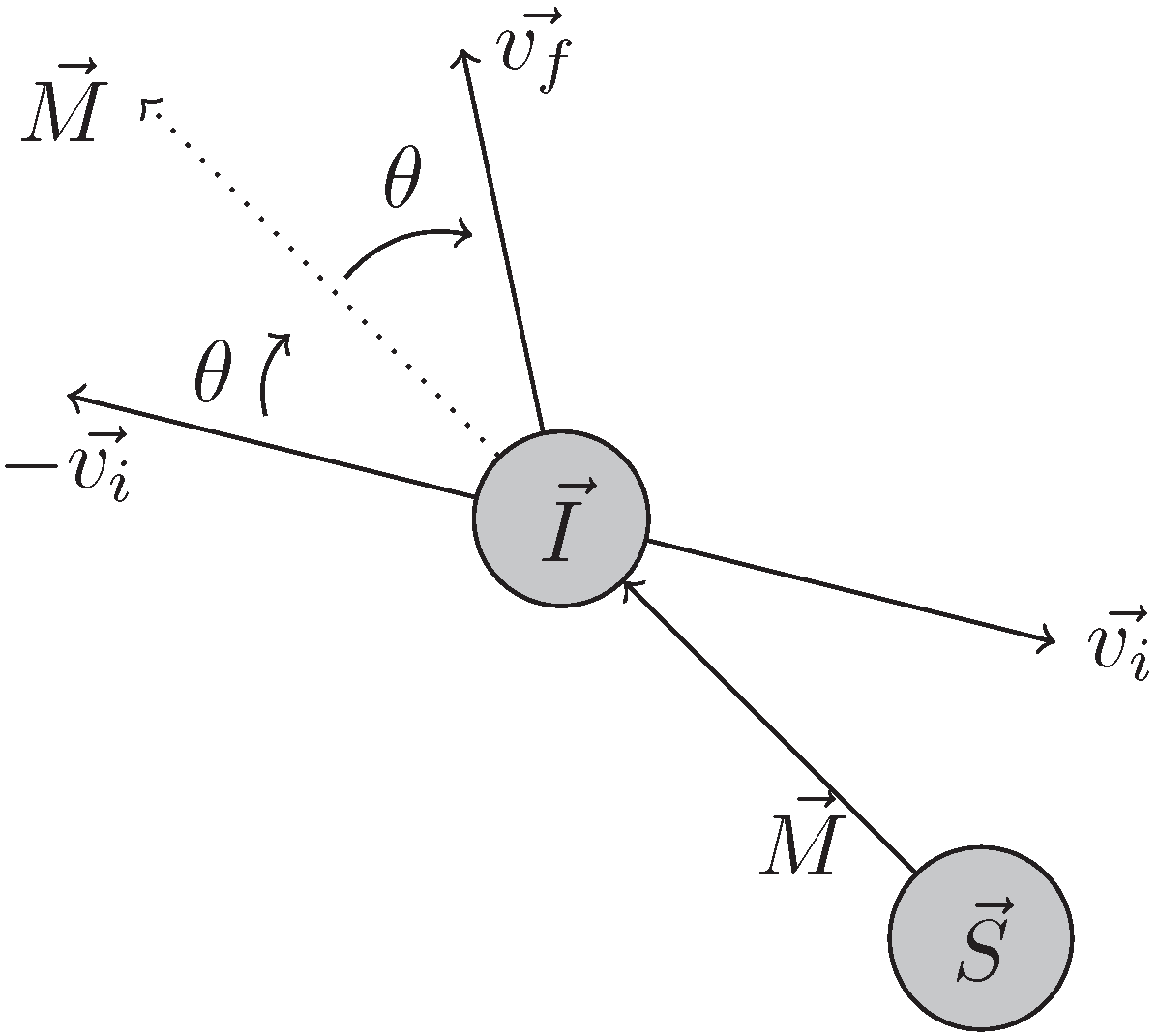
- performs vector normalization. It returns a vector that points in the same direction as the input vector, but with a length of one.
- performs sensor/wall detection between the entity’s original position and the next position against the detected (i.e., a sensor or an FoI boundary). In the case of an FoI boundary, the function will check for the intersection of two line segments. Additionally, in the case of a sensor, the function will check if lies within the sensor’s circular disk of radius .
- finds the angle between the vectors and . The resulting value will utilize the function defined in Equation (2).
- returns the result of rotated by θ around its origin.
| Algorithm 1 Pinball. | |
| 1: | while do |
| 2: | |
| 3: | |
| 4: | if collides(nextPosition, horizontalWall) then |
| 5: | |
| 6: | if collides(nextPosition, verticalWall) then |
| 7: | |
| 8: | for all sensor in sensors do |
| 9: | if collides(nextPosition, sensor) then |
| 10: | |
| 11: | |
| 12: | |
| 13: | |
3.3. Flood-Fill Intrusion Algorithm

- If a cell is fully or partially covered by a detected sensor within , then the cell receives a value of . Assume and are the locations of the cell , and the detected sensor . Cell will be considered as “unsafe” and receive a value of if . Otherwise, cell is considered “safe” and receives a value of zero.
- For a safe cell with a value of zero, the value will be incremented by one each time the intruder visits it. For instance, a cell with a value of three means the cell is visited by the intruder three times. This is because the intruder might have to backtrack under certain conditions.
- If a cell adjacent to the intruder has not been visited by the intruder before, it will check to see its coverage status first. Once the intruder has checked all adjacent cells, the intruder will proceed in the direction of the cell with the lowest value.
- If multiple cells have the same value, the intruder will decide which direction to move based on the distance from each cell to its target position. For example, if the intruder needs to travel six units along the x-axis and three units along y-axis to reach its target position, it will first attempt to travel along the x-axis.
- If that cell is not amongst those with the lowest value, then the intruder will go clockwise, checking the other cells for the lowest value, and will travel along the direction of the first lowest value cell it finds. Before the intruder leaves a cell, it will increment the value of that cell by one.
- is an array containing the four basic directions: up (), down (), left () and right ().
- is an array generated every loop containing the position of the intruder if it were to take each of the directions in
- counts the number of elements in an array
- is a data structure mapping keys (cell positions) to values (cell values). Accessing a cell’s value is expressed as .
| Algorithm 2 Flood-fill. | |
| 1: | while do |
| 2: | for do |
| 3: | |
| 4: | for do |
| 5: | if then |
| 6: | |
| 7: | for do |
| 8: | |
| 9: | |
| 10: | |
| 11: | |
| 12: | for do |
| 13: | |
| 14: | if then |
| 15: | |
| 16: | |
| 17: | |
| 18: | |
| 19: | for do |
| 20: | |
| 21: | if then |
| 22: | if then |
| 23: | |
| 24: | |
| 25: | if then |
| 26: | |
| 27: | |
4. Demonstration, Simulation and Discussion

4.1. Impact of Node Density λ

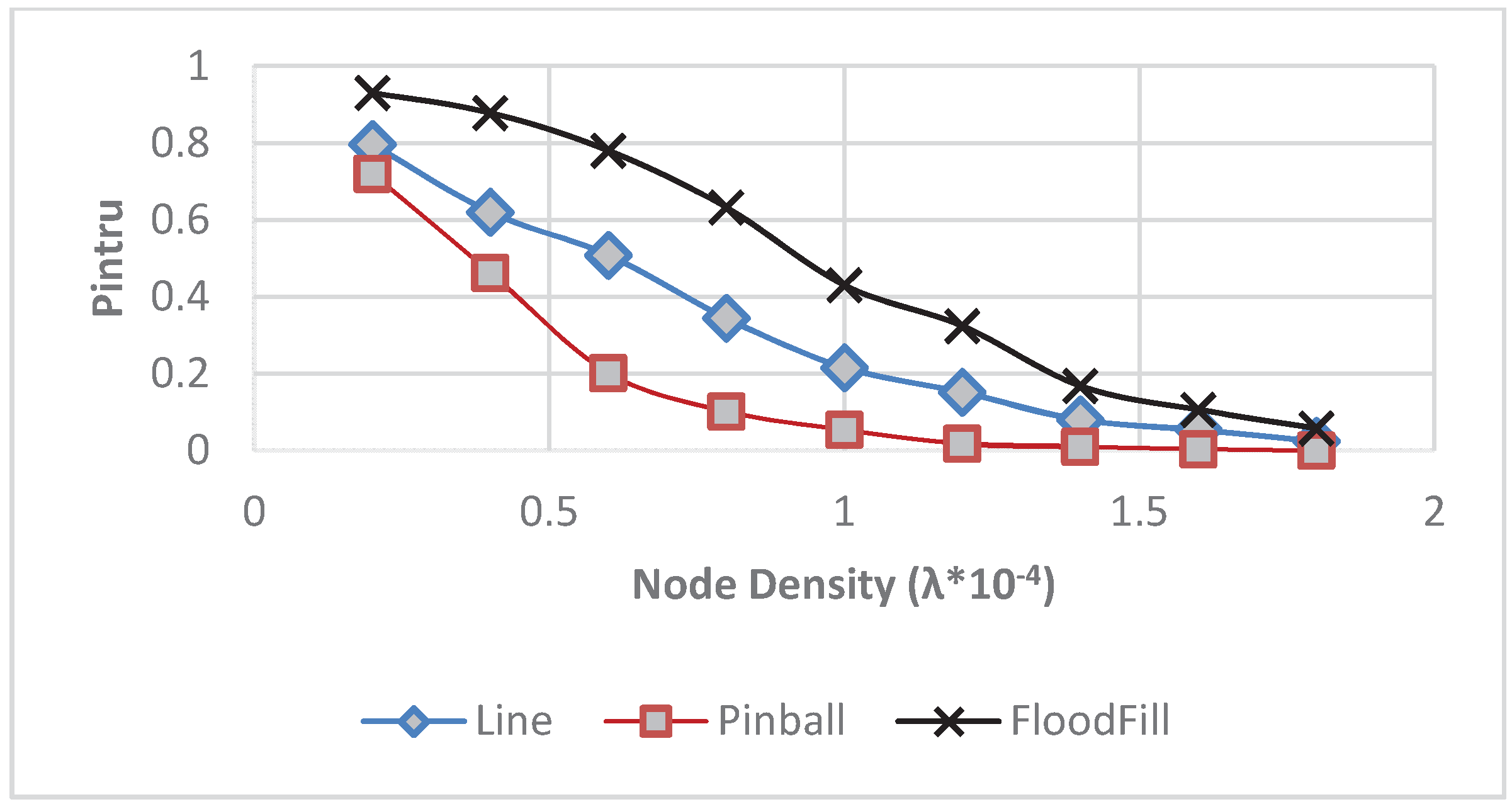


4.2. Impact of Sensing Range


4.3. Impact of Communication Range


4.4. Coverage, Connectivity, Connected Coverage versus Intruder Detection
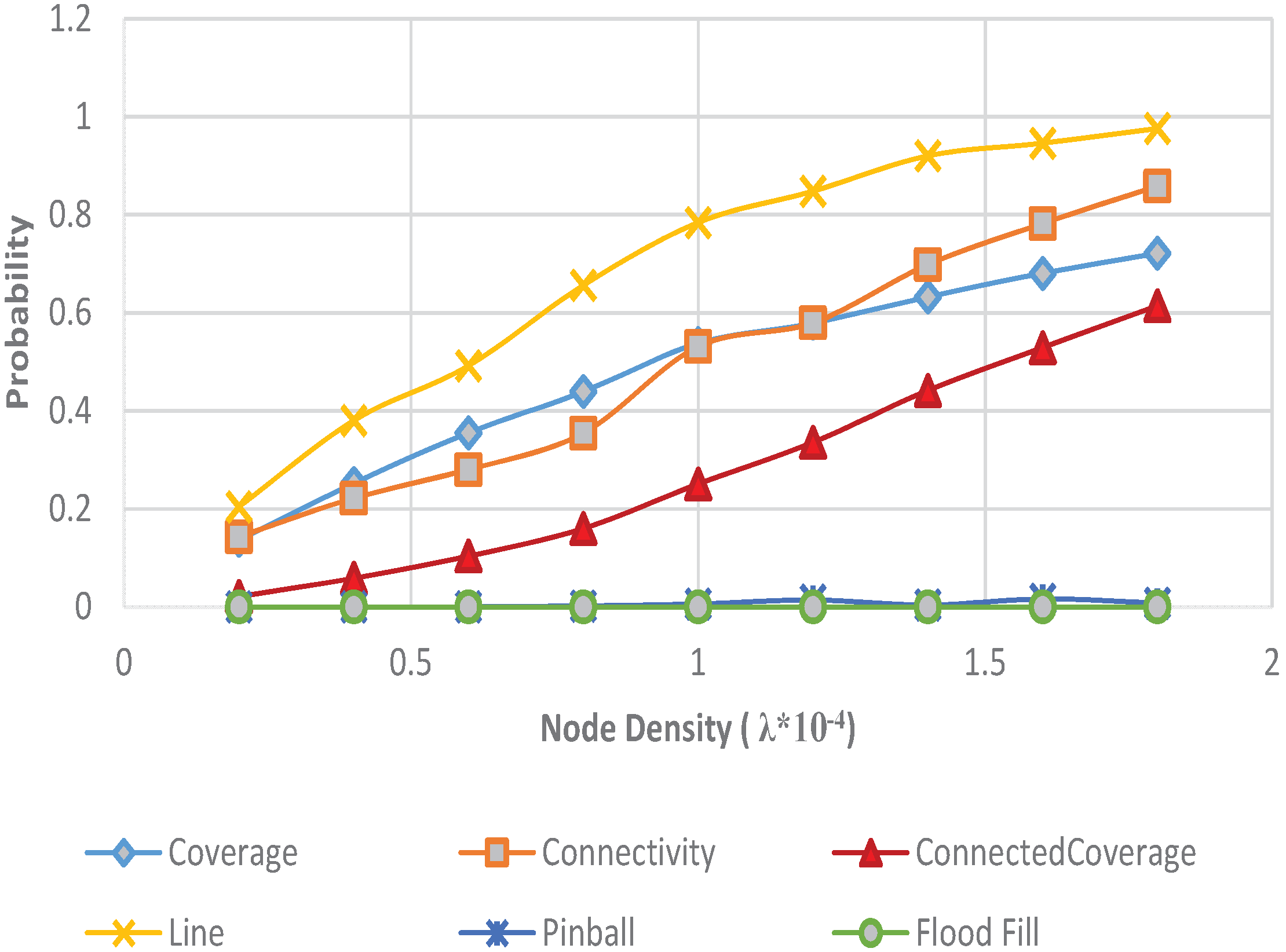
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Yang, H.; Sikdar, B. A protocol for tracking mobile targets using sensor networks. In Proceedings of the First IEEE International Workshop on Sensor Network Protocols and Applications, Anchorage, AK, USA, 11 May 2003; pp. 71–81.
- Yick, J.; Mukherjee, B.; Ghosal, D. Wireless sensor network survey. Comput. Netw. 2008, 52, 2292–2330. [Google Scholar] [CrossRef]
- Bokareva, T.; Hu, W.; Kanhere, S.; Ristic, B.; Gordon, N.; Bessell, T.; Rutten, M.; Jha, S. Wireless sensor networks for battlefield surveillance. In Proceedings of the Land Warfare Conference, Brisbane, Australia, 24-27 October 2006; pp. 1–8.
- Hamdi, M.; Boudriga, N.; Obaidat, M.S. WHOMoVeS: An optimized broadband sensor network for military vehicle tracking. Int. J. Commun. Syst. 2008, 21, 277–300. [Google Scholar] [CrossRef]
- Severino, R.; Alves, M. Engineering a search and rescue application with a wireless sensor network-based localization mechanism. In Proceedings of the IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks, WoWMoM 2007, Espoo, Finland, 18–21 June 2007; pp. 1–4.
- Sharp, C.; Schaffert, S.; Woo, A.; Sastry, N.; Karlof, C.; Sastry, S.; Culler, D. Design and implementation of a sensor network system for vehicle tracking and autonomous interception. In Proceedings of the Second European Workshop on Wireless Sensor Networks, Istanbul, Turkey, 31 January–2 February 2005; pp. 93–107.
- Tsai, H.W.; Chu, C.P.; Chen, T.S. Mobile object tracking in wireless sensor networks. Comput. Commun. 2007, 30, 1811–1825. [Google Scholar] [CrossRef]
- Bhatti, S.; Xu, J. Survey of target tracking protocols using wireless sensor network. In Proceedings of the Fifth International Conference on Wireless and Mobile Communications, ICWMC’09, Cannes, France, 23–29 August 2009; pp. 110–115.
- Dyo, V.; Ellwood, S.A.; Macdonald, D.W.; Markham, A.; Mascolo, C.; Pásztor, B.; Scellato, S.; Trigoni, N.; Wohlers, R.; Yousef, K. Evolution and sustainability of a wildlife monitoring sensor network. In Proceedings of the 8th ACM Conference on Embedded Networked Sensor Systems, Zurich, Switzerland, 3–5 November 2010; pp. 127–140.
- Lazos, L.; Poovendran, R.; Ritcey, J.A. Analytic evaluation of target detection in heterogeneous wireless sensor networks. ACM Trans. Sens. Netw. 2009, 5, 1–18. [Google Scholar] [CrossRef]
- Gui, C.; Mohapatra, P. Power conservation and quality of surveillance in target tracking sensor networks. In Proceedings of the 10th Annual International Conference on Mobile Computing and Networking, Philadelphia, PA, USA, 26 September–1 October 2004; pp. 129–143.
- Arora, A.; Dutta, P.; Bapat, S.; Kulathumani, V.; Zhang, H.; Naik, V.; Mittal, V.; Cao, H.; Demirbas, M.; Gouda, M.; et al. A line in the sand: A wireless sensor network for target detection, classification, and tracking. Comput. Netw. 2004, 46, 605–634. [Google Scholar] [CrossRef]
- Lazos, L.; Poovendran, R.; Ritcey, J.A. Probabilistic detection of mobile targets in heterogeneous sensor networks. In Proceedings of the 6th International Conference on Information Processing in Sensor Networks, Cambridge, MA, USA, 25–27 April 2007; pp. 519–528.
- Agah, A.; Das, S.K.; Basu, K.; Asadi, M. Intrusion detection in sensor networks: A non-cooperative game approach. In Proceedings of the Third IEEE International Symposium on Network Computing and Applications, (NCA 2004), Cambridge, MA, USA, 30 August–1 September 2004; pp. 343–346.
- Wang, Y.; Wang, X.; Xie, B.; Wang, D.; Agrawal, D.P. Intrusion detection in homogeneous and heterogeneous wireless sensor networks. IEEE Trans. Mob. Comput. 2008, 7, 698–711. [Google Scholar] [CrossRef]
- Wang, Y.; Leow, Y.K.; Yin, J. Is straight-line path always the best for intrusion detection in wireless sensor networks. In Proceedings of the 2009 15th International Conference on Parallel and Distributed Systems (ICPADS), Shenzhen, China, 8–11 December 2009; pp. 564–571.
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Rao, N.S.V. An algorithmic framework for navigation in unknown terrains. IEEE Comput. 1989, 22, 37–43. [Google Scholar] [CrossRef]
- Cao, Q.; Yan, T.; Stankovic, J.; Abdelzaher, T. Analysis of target detection performance for wireless sensor networks. In Distributed Computing in Sensor Systems; Springer: Berlin, Heidelberg, 2005; pp. 276–292. [Google Scholar]
- Wang, Y.; Fu, W.; Agrawal, D.P. Gaussian versus uniform distribution for intrusion detection in wireless sensor networks. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 342–355. [Google Scholar] [CrossRef]
- Camp, T.; Boleng, J.; Davies, V. A survey of mobility models for ad hoc network research. Wirel. Commun. Mob. Comput. 2002, 2, 483–502. [Google Scholar] [CrossRef]
- Liu, B.; Brass, P.; Dousse, O.; Nain, P.; Towsley, D. Mobility improves coverage of sensor networks. In Proceedings of the 6th ACM International Symposium on Mobile Ad Hoc Networking and Computing, Chicago, IL, USA, 25–28 May 2005; pp. 300–308.
- Keung, Y.; Li, B.; Zhang, Q. The intrusion detection in mobile sensor network. In Proceedings of the Eleventh ACM International Symposium on Mobile Ad Hoc Networking and Computing, Chicago, IL, USA, 20–24 September 2010; pp. 11–20.
- Morris, P. Introduction to Game Theory; Springer Science & Business Media: New York, NY, USA, 1994. [Google Scholar]
- Picker, R.C. An Introduction to Game Theory and the Law; Law School, University of Chicago: Chicago, IL, USA, 1994. [Google Scholar]
- Cutnell, J.D.; Johnson, K.W. Physics; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Kinetic Theory. Available online: http://physics.bu.edu/ duffy/py105/Kinetictheory.html (accessed on 18 April 2015).
- Unity3D. Available online: http://unity3d.com/unity (accessed on 28 March 2015).
- Blackman, S. Beginning 3D Game Development with Unity: All-in-One, Multi-Platform Game Development; Apress: New York, NY, USA, 2011. [Google Scholar]
- Wang, Y.; Leow, Y.K.; Yin, J. A novel sine-curve mobility model for intrusion detection in wireless sensor networks. Wirel. Commun. Mob. Comput. 2013, 13, 1555–1570. [Google Scholar] [CrossRef]
- Zhang, H.; Hou, J.C. Maintaining sensing coverage and connectivity in large sensor networks. Ad Hoc Sens. Wirel. Netw. 2005, 1, 89–124. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chu, W.; Fields, S.; Heinemann, C.; Reiter, Z. Detection of Intelligent Intruders in Wireless Sensor Networks. Future Internet 2016, 8, 2. https://doi.org/10.3390/fi8010002
Wang Y, Chu W, Fields S, Heinemann C, Reiter Z. Detection of Intelligent Intruders in Wireless Sensor Networks. Future Internet. 2016; 8(1):2. https://doi.org/10.3390/fi8010002
Chicago/Turabian StyleWang, Yun, William Chu, Sarah Fields, Colleen Heinemann, and Zach Reiter. 2016. "Detection of Intelligent Intruders in Wireless Sensor Networks" Future Internet 8, no. 1: 2. https://doi.org/10.3390/fi8010002
APA StyleWang, Y., Chu, W., Fields, S., Heinemann, C., & Reiter, Z. (2016). Detection of Intelligent Intruders in Wireless Sensor Networks. Future Internet, 8(1), 2. https://doi.org/10.3390/fi8010002





