A Reliability Calculation Method for Web Service Composition Using Fuzzy Reasoning Colored Petri Nets and Its Application on Supercomputing Cloud Platform

Abstract

In order to develop a Supercomputing Cloud Platform (SCP) prototype system using Service-Oriented Architecture (SOA) and Petri nets, we researched some technologies for Web service composition. Specifically, in this paper, we propose a reliability calculation method for Web service compositions, which uses Fuzzy Reasoning Colored Petri Net (FRCPN) to verify the Web service compositions. We put forward a definition of semantic threshold similarity for Web services and a formal definition of FRCPN. We analyzed five kinds of production rules in FRCPN, and applied our method to the SCP prototype. We obtained the reliability value of the end Web service as an indicator of the overall reliability of the FRCPN. The method can test the activity of FRCPN. Experimental results show that the reliability of the Web service composition has a correlation with the number of Web services and the range of reliability transition values.

1. Introduction

The Supercomputing Cloud Platform (SCP) integrates many different kinds of software including ANSYS, ABAQUS, LS-DYNA, SLURM, LSF, etc. SCP provides a simple Web interactive way for large-scale and parallel CAE simulation tasks. Our research team develops a SCP prototype of supercomputing. Specifically, we use Service-Oriented Architecture (SOA) architecture to develop the prototype. We use Petri nets to describe Web service compositions, and realized the prototype using a workflow system.

For automatic composition for Web services based on semantic technology, we introduce Ontology Web language for Services (OWL-S) to describe Web services. In order to verify the Web Service Compositions, we proposed a reliability calculation method for Web Service Composition Using Fuzzy Reasoning Colored Petri Nets (FRCPN), then we judged whether the Web service composition could meet the reliability requirements.

At present, the applications of OWL-S are well established in the engineering field. The study on web service composition has many theoretical researches and engineering practices, and the study on CPN, FRCPN has also been making progress. However, the reliability of Web service composition needs to be strengthened and studied further.

2. Related Work

Many researchers use SOA architecture, semantic technology, and workflow technology to build Colored Petri Nets (CPN) or composition system for Web services. In [1], the authors developed a platform prototype for cloud simulation named COSIM-CSP using some Web services, discovery technology, and so on. In [2,3,4,5,6,7,8], the authors also proposed models for cloud platform and designed system prototypes. In [9], the authors developed a composition system for Web services named OntoPipeliner based on semantics. At present, there are some studies underway on a cloud platform based on OWL-S semantic technology, such as [9,10,11].

It is one of the main possible directions for studying on Web service compositions base on Petri. Many researchers are dedicated to applying the improvement of Petri nets to combined Web services [12,13,14,15,16,17]. In [18], the authors proposed a CPN model. In the model, the authors added the transaction features of Web services, considered Quality of Service (QoS) and transaction, and then formed a credible composition for Web services.

In [19], the authors used CPN to design a deterministic analysis method that is used to measure the reliability and the performance. CPN can display the routing structure and apply probability theory. In addition, the authors developed a software tool called WSET, which is used for supporting QoS sensor modeling. In [20], the authors used Petri nets for orchestration with the OWL-S service, which is treated as an ontology engine to support reasoning. In [21], the authors used Hierarchical Colored Petri Net (HCPN) to formally describe Web service compositions, converted the structure of data flow information described by OWL-S, and used the CPN tool to verify the model. In [22], the authors proposed an improved HCPN namely EHCPN to describe Web service compositions. In [23], the authors proposed a method based on translation to convert the process model of OWL-S services into Petri nets. In [24], the authors proposed a method based on stochastic Petri nets for the performance analysis of OWL-S process, and used non-Markov Stochastic Petri Nets as an intermediate representation.

Some scholars have done research on the reliability of Web service compositions using Petri, CPN, or FRCPN [25,26,27,28,29]. In order to improve the reliability value of Web service compositions, [18] and [30] proposed using CPN to formalize the various properties of Web service compositions. In [16], non-Markov Stochastic Petri Nets are proposed based on a probabilistic method of reliability analysis of OWL-S Web service compositions. The authors introduce the normal completion probability of the process to calculate the reliability. In [31], the authors proposed a method to use Petri nets to build reliable Web service compositions. This method verifies the behavior of service compositions and repairs the design errors at design time or run time.

Kim, Y. et al. [32] proposed a trust model expressed by a graph. In the graph, the weights of the edges denote the weights of trust. According to the evaluated trust value, the model can choose a more suitable Web service or Web service composition. In [33], based on the analysis of the data for past services, the authors used the K-mean clustering algorithm to predict the reliability of atomic Web services. Xu, J. et al. [34] developed a model to select the most appropriate service composition. The model uses stochastic Petri nets for service compositions to create a qualitative model, which performs a quantitative analysis of the failure rate and repair rate. In [35], a method called $\mathsf{\lambda }-\mathrm{T}$ is proposed to quantify the reliability of a repairable system. The main parameters in the method are failure rate, time, and Petri nets. Many methods generate a reachable tree according to the graph, and then calculate the reliability of the tree according to the various parameters of the reachable tree as the reliability of FRCPN graph [36].

In summary, there has been some progress in terms of the reliability calculation method for Web service compositions. However, there is not yet an exact definition of semantic similarity threshold relations in the literature, nor is there a reliability calculation method for Petri nets based on the relations of semantic threshold similarity. The main contributions of this paper are as follows.

• We gradually define the concepts of reliability calculation. Based on the definition of formalized description for Web services, we define the semantic threshold similarity and semantic threshold equality for Web services. We first give the definition of FRCPN and the definition of FRCPN activity. Then, we propose the conditions of the activity. We analyze the reliability calculation of some elements in five kinds of production rules in FRCPN. According to the requirements of reliability calculation for FRCPN, we redefine the formalized definition of transition and the formalized definition of Web services.
• A reliability calculation method for FRCPN is proposed. Firstly, the method calculates the reliability values of the transitions in FRCPN, and uses an algorithm to generate a Sequential Linked List for Filling Reliability Value (SLLFRV) linked list. According to the SLLFRV linked list, we propose an algorithm to calculate the reliability values of all Web services. Finally, we use the reliability value of the end Web service in FRCPN as the reliability value of FRCPN.
• We apply and analyze the reliability calculation method. The reliability value of a FRCPN graph is calculated as an example. We analyze the execution process of the method. We analyze the implementation effect of the method for different size FRCPNs and obtain some rules. We give the application description for the method in SCP.

3. Related Definition

3.1. Definition of Semantic Threshold Similarity and Definition of Semantic Threshold Equality

Definition 1.

Formal description of Web services [9]. A Web service can be formally described as

$$W{S}_i(I_i,O_i,P_i,Q_i),$$

where $I_i$ is the input parameter set of Web service $W{S}_i, O_i$ is the output parameter set of Web service $W{S}_i, P_i$ is the precondition set of Web service $W{S}_i, and Q_i$ is the QoS set of Web service $W{S}_i$.

Definition 2.

Semantic threshold similarity for two ontologies and semantic threshold equality for two ontologies. There are two ontology concepts, $c_i$ and $c_j$. By calculating their semantic similarity, we can obtain the value of $sim(c_i,c_j)$. We set a semantic similarity threshold, $k(0\le k\le 1)$. If $sim(c_i,c_j)\ge k$, then the relation of semantic threshold similarity is built between $c_i$ and $c_j$, denoted as $c_i\beth c_j$. If $c_i\beth c_j$, and $c_j\beth c_i$, then the relation of semantic threshold equality is built between $c_i$ and $c_j$, denoted as $c_i\cong c_j$.

Definition 3.

Semantic threshold similarity for two ontology sets and semantic threshold equality for two ontology sets. There are two concept sets $C_i\{c_i\}$ and $C_j\{c_j\}$. We set a semantic similarity threshold, $k(0\le k\le 1)$. If any concept $c_i$ in $C_i$ exists corresponding $c_j$ in $C_j$ to satisfy $c_i\beth c_j$, then the relation of semantic threshold similarity is built between $C_i$ and $C_j$, denoted as $C_i\beth C_j$. If $C_i\beth C_j$, and $C_j\beth C_i$, then the relation of semantic threshold equality is built between $C_i$ and $C_j$, denoted as $C_i\cong C_j$.

Definition 4.

Semantic threshold similarity for Web service preconditions and semantic threshold similarity for Web services QoS. There are two Web services, $W{S}_i(I_i,O_i,P_i,Q_i)$ and $W{S}_j(I_j,O_j,P_j,Q_j)$; if any logical expression $p_i$ in $P_i$ exists corresponding $p_j$ in $P_j$, and $p_i$ is true, then $p_j$ is true, the relation of semantic threshold similarity is built between $P_i and P_j$, denoted as $P_i\beth P_j$. If any logical expression of QoS $q_i$ in $Q_i$ exists corresponding $q_j$ in $Q_j$, and $q_i$ is true, then $q_j$ is true, the relation of semantic threshold similarity is built between $Q_i$ and $Q_j$, denoted as $Q_i\beth Q_j$.

Definition 5.

Semantic threshold similarity for two Web services and semantic threshold equality for two Web services. There are two Web services, $W{S}_i(I_i,O_i,P_i,Q_i)$ and $W{S}_j(I_j,O_j,P_j,Q_j)$. We set a semantic similarity threshold $k(0\le k\le 1)$, if $I_i\beth I_j$, $O_i\beth O_j$, $P_i\beth P_j$ and $Q_i\beth Q_j$, then the relation of semantic threshold similarity is built between $W{S}_i and W{S}_j$, denoted as $W{S}_i\beth W{S}_j$. If $W{S}_i\beth W{S}_j$ and $W{S}_j\beth W{S}_i$, then the relation of semantic threshold equality is built between $W{S}_i and W{S}_j$, denoted as $W{S}_i\cong W{S}_j$.

3.2. Definition of FRCPN and Definition of FRCPN Activity

Definition 6.

Formal definition of FRCPN based on semantic similarity for Web service composition [16]:

$$FRCPN=(P,T,F,\mu ,PR,Q).$$

(1)

$P=\{P_1,P_2,\cdots ,P_n\}$ represents the place set, and each place represents a Web service.

(2)

$T=\{T_1,T_2,\cdots ,T_m\}$ represents the transition set, and each transition represents the matching relationships among Web services.

(3)

F is a dependence relation set, represented as an If-Then form.

(4)

$\mathsf{\mu }$ is a function of $T$, and the function’s value is in the range of [0,1], which is the triggered threshold of the transition. The function is also the semantic similarity threshold for Web services, and we can control the minimum triggered threshold using the function.

(5)

$PR$ is the precondition set defined on the $P$, which represents all preconditions being satisfied before the transitions are triggered.

(6)

$Q$ is the QoS set defined on the $P$; it indicates all QoS of the Web services that need to be satisfied before the transitions are triggered.

We can measure the matching degree using semantic similarity between the interfaces of two Web services, and then establish the dependence relation. There are five kinds of dependence relations in FRCPN. The semantic similarity calculation considers some factors, including I/O interfaces P, Q, etc., so we adopt semantic similarity as reliability. It is necessary that the reliability value of the transition achieve semantic threshold $k$ as a trigger.

Definition 7.

FRCPN activity. In FRCPN, if $t\in T$, and a transition sequence exists, the transition sequence is triggered in sequence, and in semantic threshold $k(0\le k\le 1)$, the reliability value Γ of each transition t is satisfied with $\Gamma \ge k$, then transition t is triggered, we consider that transition t is active in semantic threshold k. According to the dependence relations in FRCPN, we can calculate the reliability values of the Web services and the transitions. We use the reliability value of the end Web service in FRCPN as the reliability value ω of FRCPN. In the reliability threshold $a(0\le a\le 1)$, all of the transitions in FRCPN are active in semantic threshold k, and the reliability value ω of FRCPN satisfies $\omega \ge a$, so FRCPN is activity in semantic threshold k and reliability threshold a.

3.3. Production Rule of FRCPN

Next, we discuss five production rules of FRCPN. According to the reliability values of Web services, we can verify the FRCPN activity, and obtain better quality FRCPN.

3.3.1. The First Production Rule

$\mathbf{\text{If}} W{S}_i \mathbf{\text{Then}} W{S}_j$ (The semantic similarity threshold k)

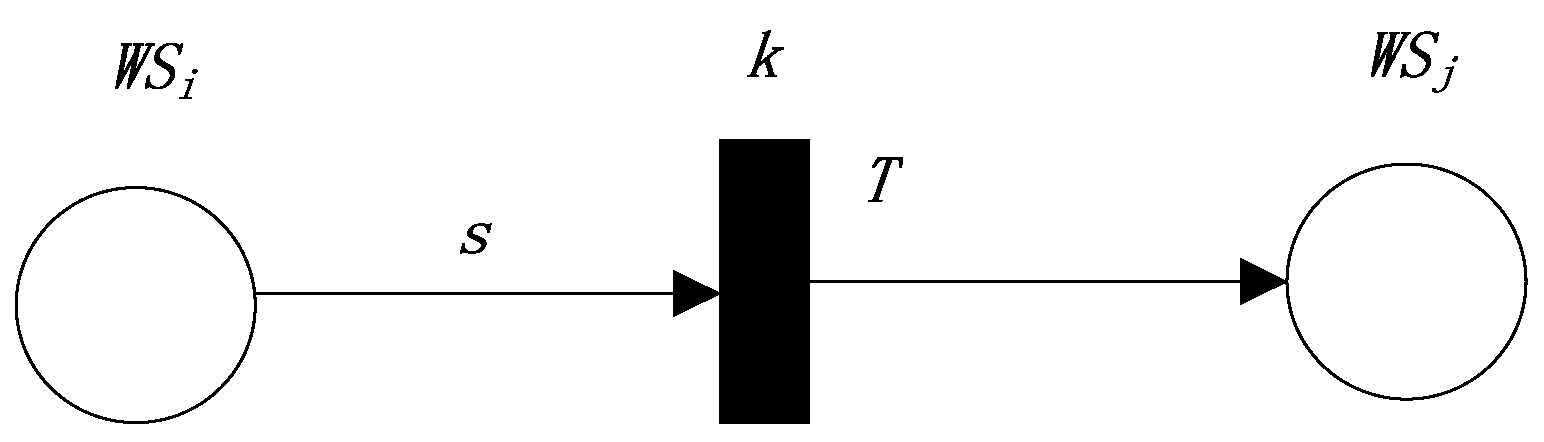
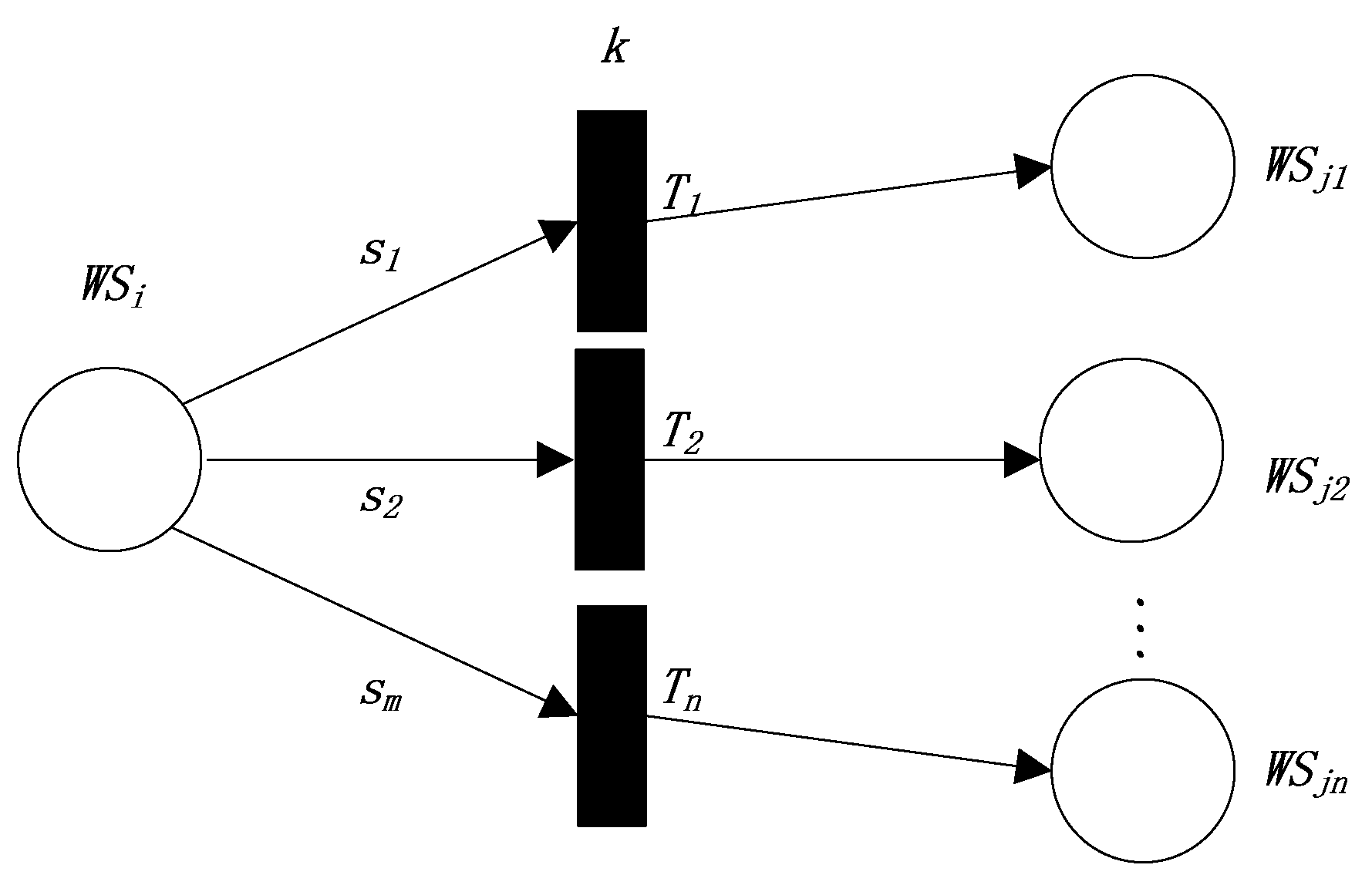
The first production rule represents a dependence relation $W{S}_i\to W{S}_j$ (the semantic similarity threshold k). The FRCPN based on semantic similarity for Web service compositions is shown in Figure 1.

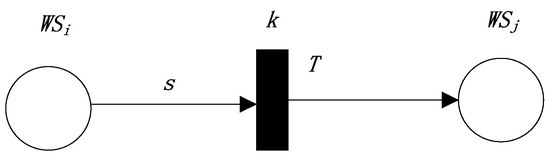
Figure 1. The FRCPN (Fuzzy Reasoning Colored Petri Net) expression of the first production rule.

The above rule indicates the dependence relationship $W{S}_i\to W{S}_j$. Here, s is the semantic similarity value between the outputs of $W{S}_i$ and the inputs of $W{S}_j$. The above rule needs to satisfy some conditions including $s\ge k$, $O_i\beth I_j$, and all of the conditions in $P_i,Q_i$. Therefore,

$$s=m_1\times \text{sim}(O_i,I_j)+m_2, m_1+m_2=1.$$

(1)

In Equation (1), $\text{sim}(O_i,I_j)$ represents the semantic similarity between the outputs of $W{S}_i$ and the inputs of $W{S}_j$. $m_1$ is the weight that represents the attention degree of matching between the outputs of $W{S}_i$ and the inputs of $W{S}_j$. $m_2$ is the weight that represents the attention degree of satisfying all conditions in $P_i$ and $Q_i$.

According to the above definition, we define the reliability value ${\Gamma }_t$ of the transition T by the semantic similarity between the interfaces of $W{S}_i$ and the interfaces of $W{S}_j$, as follows:

$${\Gamma }_t=s.$$

(2)

We can define the reliability value of $W{S}_j$ in this dependence relation as follows:

$${\Gamma }_j={\Gamma }_i\times {\Gamma }_t={\Gamma }_i\times s.$$

(3)

3.3.2. The Second Production Rule

$\mathbf{\text{If}} W{S}_{i1} \mathbf{\text{and}} W{S}_{i2} \cdots \mathbf{\text{and}} W{S}_{in} \mathbf{\text{Then}} W{S}_j$ (The semantic similarity threshold k)

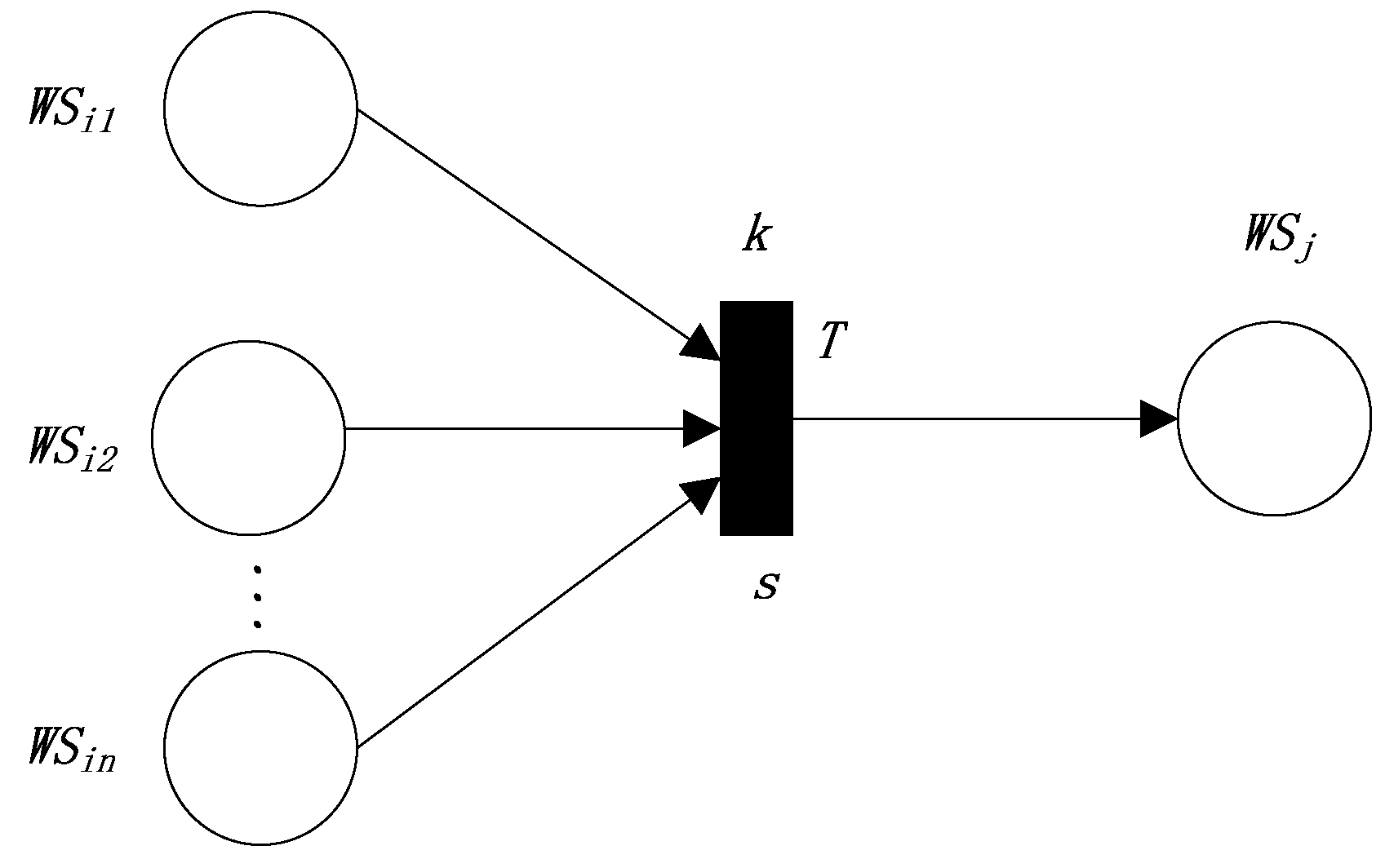
The second production rule represents a dependence relation “$W{S}_{i1} \mathbf{\text{and}} W{S}_{i2} \cdots \mathbf{\text{and}} W{S}_{in}\to W{S}_j$” (the semantic similarity threshold k). The FRCPN based on semantic similarity for Web service compositions is shown in Figure 2.

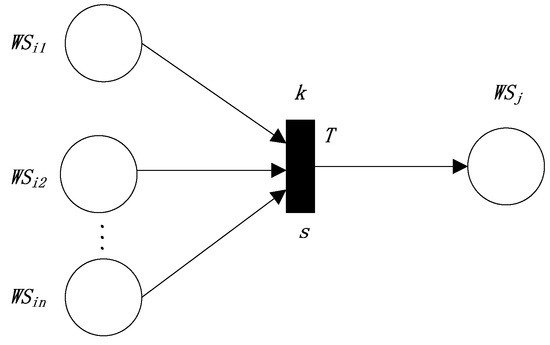
Figure 2. The FRCPN expression of the second production rule.

s is the semantic similarity between $O_{i1}\cup O_{i2}\cup \cdots \cup O_{in}$ (the union of the outputs of “$W{S}_{i1},W{S}_{i2},\cdots ,W{S}_{in}$”) and the inputs of $W{S}_j$. The above rule needs to satisfy some conditions, including $s\ge k$, $(O_{i1}\cup O_{i2}\cup \cdots \cup O_{in})\beth I_j$, all of the conditions in “$P_{i1},P_{i2},\cdots ,P_{in}$”, and all of the conditions in “$Q_{i1},Q_{i2},\cdots ,Q_{in}$”. Therefore,

$$s=m_1\times \text{sim}(O_{i1}\cup O_{i2}\cup \cdots \cup O_{in},I_j)+m_2, m_1+m_2=1.$$

(4)

In Equation (4), $\text{sim}(O_{i1}\cup O_{i2}\cup \cdots \cup O_{in},I_j)$ represents the semantic similarity between $O_{i1}\cup O_{i2}\cup \cdots \cup O_{in}$ and the inputs of $W{S}_j$. $m_1$ is the weight that represents the attention degree of matching between $O_{i1}\cup O_{i2}\cup \cdots \cup O_{in}$ and the inputs of $W{S}_j$. $m_2$ is the weight that represents the attention degree of satisfying all the conditions in “$P_{i1},P_{i2},\cdots ,P_{in}$” and “$Q_{i1},Q_{i2},\cdots ,Q_{in}$”.

According to the above definition, we define the reliability value ${\Gamma }_t$ of the transition T in terms of the semantic similarity between the interfaces of “$W{S}_{i1},W{S}_{i2},\cdots ,W{S}_{in}$” and the interfaces of $W{S}_j$ as follows:

$${\Gamma }_t=s.$$

(5)

We can define the reliability value of $W{S}_j$ as follows:

$${\Gamma }_j=\mathbf{\text{min}}\{{\Gamma }_{i1},{\Gamma }_{i2},\cdots ,{\Gamma }_{in}\}\times {\Gamma }_t=\mathbf{\text{min}}\{{\Gamma }_{i1},{\Gamma }_{i2},\cdots ,{\Gamma }_{in}\}\times s.$$

(6)

3.3.3. The Third Production Rule

$\mathbf{\text{If}} W{S}_{i1} \mathbf{\text{or}} W{S}_{i2} \cdots \mathbf{\text{or}} W{S}_{in} \mathbf{\text{Then}} W{S}_j$ (The semantic similarity threshold k)

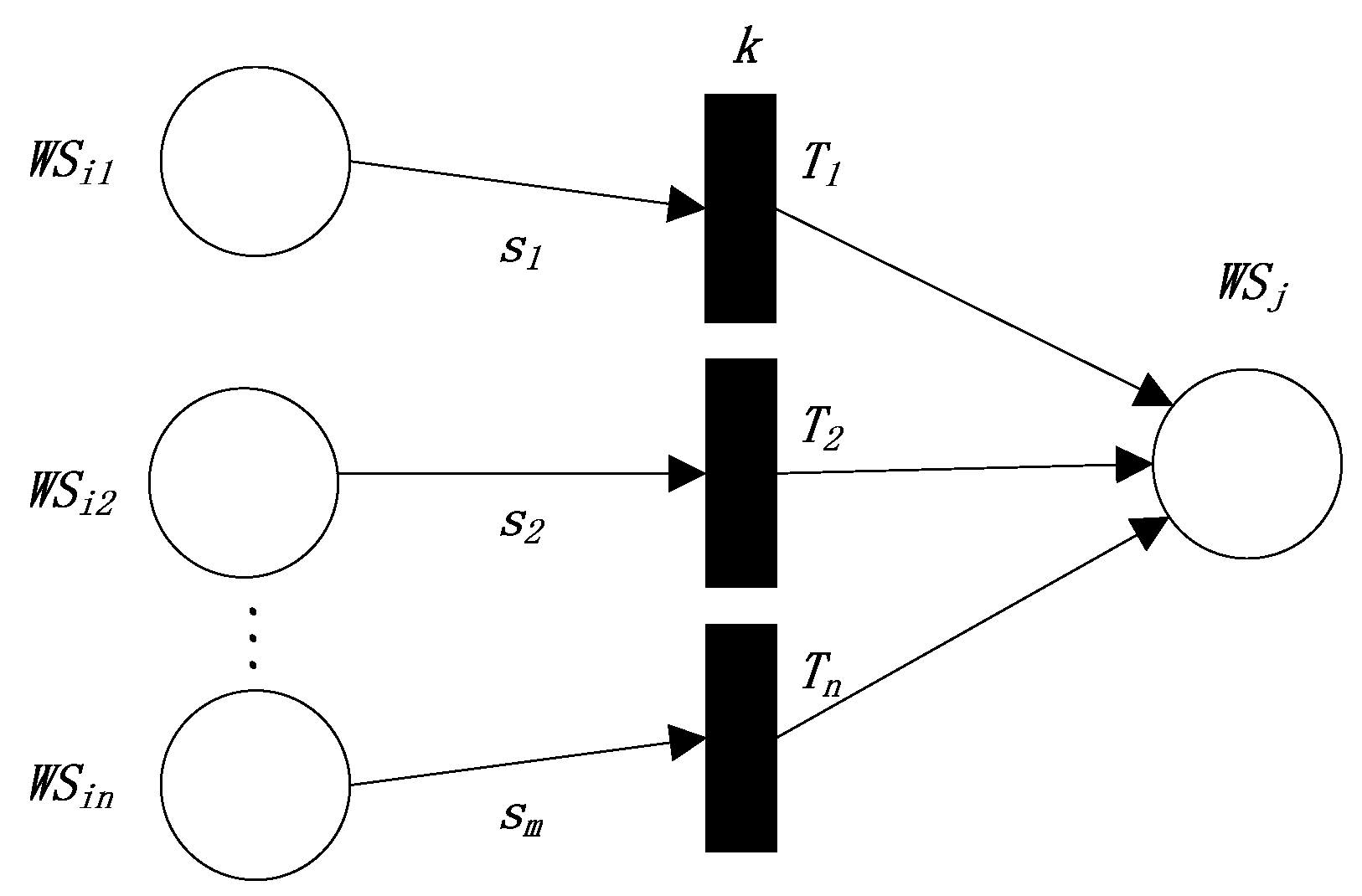
This production rule represents a dependence relation “$W{S}_{i1} \mathbf{\text{or}} W{S}_{i2} \cdots \mathbf{\text{or}} W{S}_{in}\to W{S}_j$” (the semantic similarity threshold k). The FRCPN based on semantic similarity for Web service compositions is shown in Figure 3.

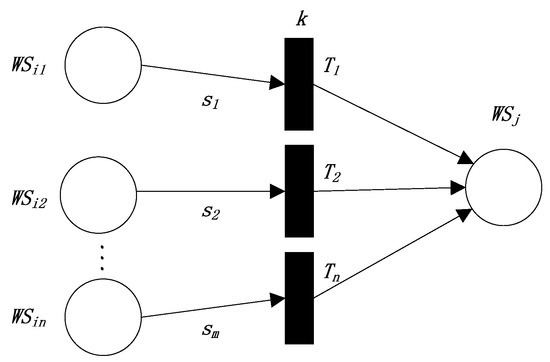
Figure 3. The FRCPN expression of the third production rule.

“$s_1$, $s_2$, $\cdots$, $s_m$” are the values of the semantic similarity between the outputs of “$W{S}_{i1},W{S}_{i2},\cdots ,W{S}_{in}$,” respectively, and the inputs of $W{S}_j$. The above rule needs to satisfy some conditions, including $s_1\ge k,s_2\ge k,\cdots ,s_m\ge k$, $(O_{i1}\beth I_j)\vee (O_{i2}\beth I_j)\vee \cdots (O_{in}\beth I_j)$, all of the conditions in “$P_{i1},P_{i2},\cdots ,P_{in}$”, and those in “$Q_{i1},Q_{i2},\cdots ,Q_{in}$”.

$$\begin{array}{c}{s}_1=m_{11}\times \text{sim}(O_{i1},I_j)+m_{21}, m_{11}+m_{21}=1\\ s_2=m_{12}\times \text{sim}(O_{i2},I_j)+m_{22}, m_{12}+m_{22}=1\\ \dots ,\\ s_n=m_{1n}\times sim(O_{in},I_j)+m_{2n}, m_{1n}+m_{2n}=1\end{array}$$

(7)

In Equation (7), $\text{sim}(O_{i1},I_j)$ represents the semantic similarity between the outputs of $W{S}_{i1}$ and the inputs of $W{S}_j$; $\text{sim}(O_{i2},I_j)$ represents the semantic similarity between the outputs of $W{S}_{i2}$ and the inputs of $W{S}_j$, and so on. $m_{11}$ is the weight that represents the attention degree of matching between the outputs of $W{S}_{i1}$ and the inputs of $W{S}_j$; $m_{12}$ is the weight that represents the attention degree of matching between the outputs of $W{S}_{i2}$ and the inputs of $W{S}_j$, and so on. $m_{21}$ is the weight that represents the attention degree of satisfying all the conditions in $P_1$ and $Q_1$; $m_{22}$ is the weight that represents the attention degree of satisfying all the conditions in $P_2$ and $Q_2$, and so on.

According to the above definition, we define the reliability values “${\Gamma }_1,{\Gamma }_2,\cdots ,{\Gamma }_n$” of the transitions “$T_1,T_2,\cdots ,T_n$” as the semantic similarities between the interfaces of “$W{S}_{i1},W{S}_{i2},\cdots ,W{S}_{in},$” respectively, and the interfaces of $W{S}_j$, as follows:

$${\Gamma }_1=s_1,{\Gamma }_2=s_2,\cdots ,{\Gamma }_n=s_n.$$

(8)

We can define the reliability of $W{S}_j$ as follow,

$${\Gamma }_j=\mathbf{\text{max}}\{{\Gamma }_{i1}\times {\Gamma }_1,{\Gamma }_{i2}\times {\Gamma }_2,\cdots ,{\Gamma }_{in}\times {\Gamma }_n\}=\mathbf{\text{max}}\{{\Gamma }_{i1}\times s_1,{\Gamma }_{i2}\times s_2,\cdots ,{\Gamma }_{in}\times s_n\}.$$

(9)

3.3.4. The Fourth Production Rule

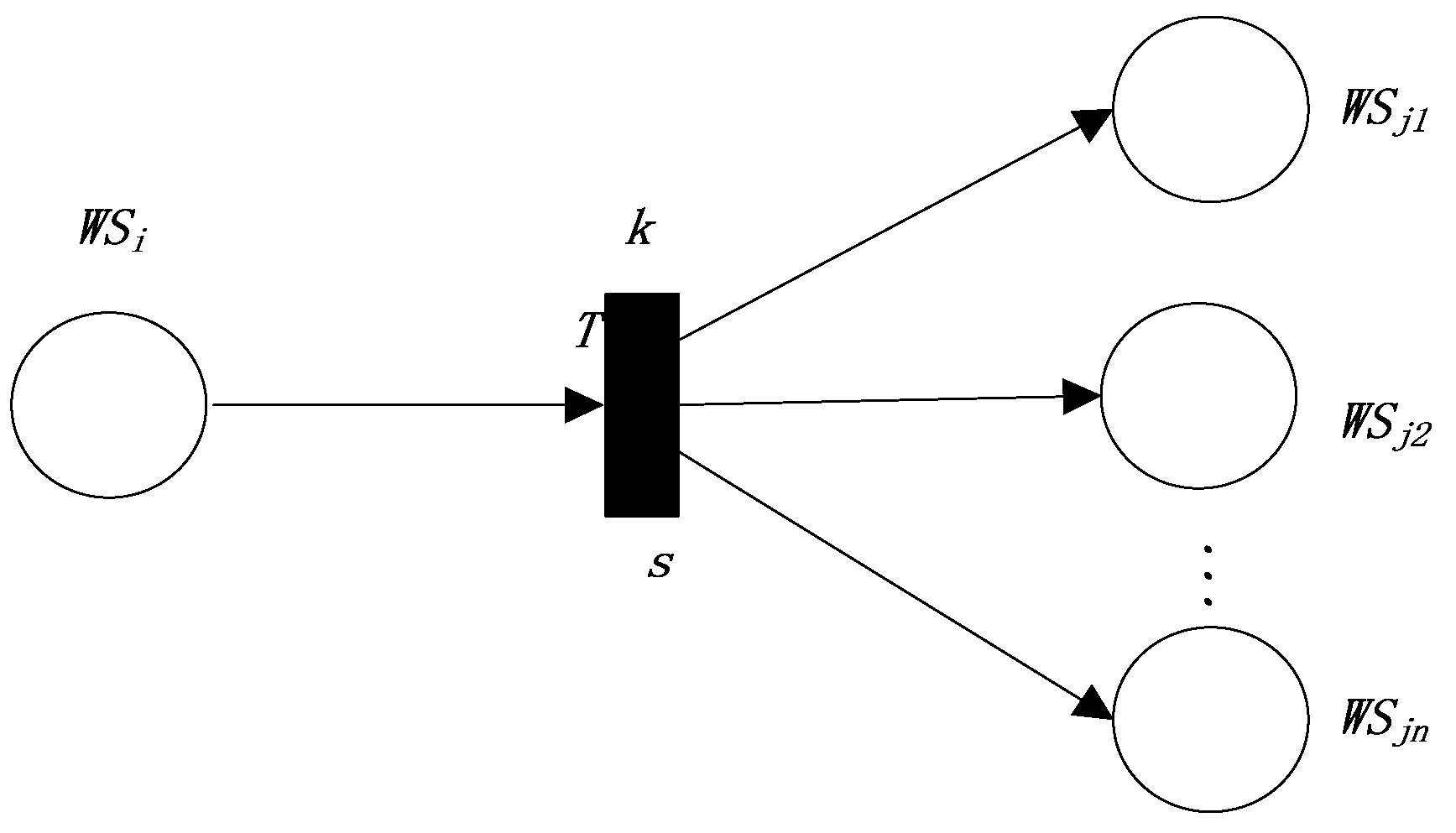
$\mathbf{\text{If}} W{S}_i \mathbf{\text{then}} W{S}_{j1} \mathbf{\text{and}} W{S}_{j2} \cdots \mathbf{\text{and}} W{S}_{jn}$ (The semantic similarity threshold k)

This fourth production rule represents a dependence relation “$W{S}_i\to W{S}_{j1} \mathbf{\text{and}} W{S}_{j2} \cdots \mathbf{\text{and}} W{S}_{jn}$” (the semantic similarity threshold k). The FRCPN based on semantic similarity for Web service compositions is shown in Figure 4.

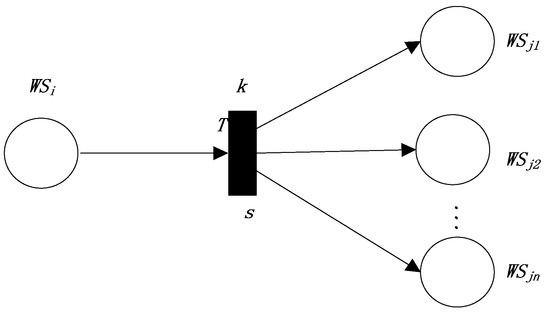
Figure 4. The FRCPN expression of the fourth production rule.

s is the semantic similarity between the outputs of $O_i$ and $I_{j1}\cup I_{j2}\cup \cdots \cup I_{jn}$ (union of inputs of “$W{S}_{j1},W{S}_{j2},\cdots ,W{S}_{jn}$”). The above rule needs to satisfy some conditions, including $s\ge k$, $O_i\beth (I_{j1}\cup I_{j2}\cup \cdots \cup I_{jn})$, and all of the conditions in $P_i,Q_i$. Therefore,

$$s=m_1\times \text{sim}(O_i,I_{j1}\cup I_{j2}\cup \cdots \cup I_{jn})+m_2, m_1+m_2=1.$$

(10)

In Equation (10), $\text{sim}(O_i,I_{j1}\cup I_{j2}\cup \cdots \cup I_{jn})$ represents the semantic similarity between the outputs of $W{S}_i$ and $I_{j1}\cup I_{j2}\cup \cdots \cup I_{jn}$. $m_1$ is the weight that represents the attention degree of matching between the outputs of $W{S}_i$ and $I_{j1}\cup I_{j2}\cup \cdots \cup I_{jn}$. $m_2$ is the weight that represents the attention degree of matching meeting all the conditions in $P_i$ and $Q_i$.

According to the above definition, we define the reliability value ${\Gamma }_t$ of the transition $T$ in terms of the semantic similarity between the interfaces of $W{S}_i$ and the interfaces of $W{S}_{j1},W{S}_{j2},\cdots ,W{S}_{jn}$, as follows:

$${\Gamma }_t=s.$$

(11)

We can define the reliability values of “$W{S}_{j1},W{S}_{j2},\cdots ,W{S}_{jn}$” in this dependence relation as follows:

$${\Gamma }_{j1}={\Gamma }_{j2}=\cdots ={\Gamma }_{jn}={\Gamma }_i\times {\Gamma }_t={\Gamma }_i\times s.$$

(12)

3.3.5. The Fifth Production Rule

$\mathbf{\text{If}} W{S}_i \mathbf{\text{then}} W{S}_{j1} \mathbf{\text{or}} W{S}_{j2} \cdots \mathbf{\text{or}} W{S}_{jn}$ (The semantic similarity threshold k)

This fifth production rule represents a dependence relation “$W{S}_i\to W{S}_{j1} \mathbf{\text{or}} W{S}_{j2} \cdots \mathbf{\text{or}} W{S}_{jn}$” (the semantic similarity threshold k). The FRCPN based on semantic similarity for Web service compositions is shown in Figure 5.

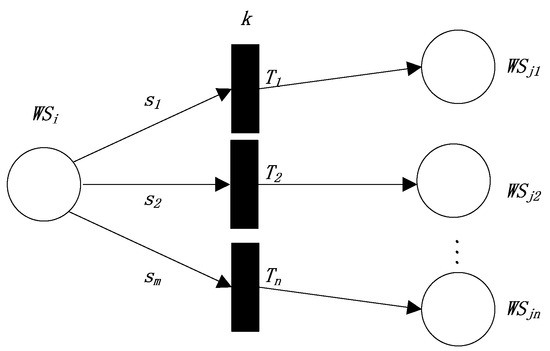
Figure 5. The FRCPN expression of the fifth production rule.

$s_1$, $s_2$, $\cdots$, $s_n$ are the semantic similarity between the outputs of $W{S}_i$ and the inputs of “$W{S}_{j1},W{S}_{j2},\cdots ,W{S}_{jn}$,” respectively. The above rule needs to satisfy some conditions, including $s_1\ge k,s_2\ge k,\cdots ,s_n\ge k$, $(O_i\beth I_{j1})\vee (O_i\beth I_{j2})\vee \cdots (O_i\beth I_{jn})$, and all of the conditions in $P_i$, $Q_i$. Therefore,

$$\begin{array}{c}{s}_1=m_{11}\times \text{sim}(O_i,I_{j1})+m_{21}, m_{11}+m_{21}=1\\ s_2=m_{12}\times \text{sim}(O_i,I_{j2})+m_{22}, m_{12}+m_{22}=1\\ \dots \\ s_n=m_{1n}\times \text{sim}(O_i,I_{jn})+m_{2n}, m_{1n}+m_{2n}=1.\end{array}$$

(13)

In Equation (13), $\text{sim}(O_i,I_{j1})$ represents the semantic similarity between the outputs of $W{S}_i$ and the inputs of $W{S}_{j1}$; $\text{sim}(O_i,I_{j2})$ represents the semantic similarity between the outputs of $W{S}_i$ and the inputs of $W{S}_{j2}$, and so on. $m_{11}$ is the weight that represents the attention degree of matching between the outputs of $W{S}_i$ and the inputs of $W{S}_{j1}$; $m_{12}$ is the weight that represents the attention degree of matching between the outputs of $W{S}_i$ and the inputs of $W{S}_{j2}$, and so on. $m_{21}$ is the weight that represents the attention degree of satisfying all the conditions in $P_i$, $Q_i$ in $s_1$, ${\mathrm{m}}_{22}$ is the weight that represents the attention degree of satisfying all the conditions in $P_i$, $Q_i$ in $s_2$, and so on.

According to the above definition, we define the reliability values “${\Gamma }_1,{\Gamma }_2,\cdots ,{\Gamma }_{\mathrm{n}}$” of the transitions “$T_1,T_2,\cdots ,T_n$” to equal the semantic similarities between the interfaces of $W{S}_i$ and the interfaces of “$W{S}_{j1},W{S}_{j2},\cdots ,W{S}_{jn}$”, respectively, as follows:

$${\Gamma }_1=s_1,{\Gamma }_2=s_2,\cdots ,{\Gamma }_n=s_n.$$

(14)

We can further define the reliability values of $W{S}_{j1},W{S}_{j2},\cdots ,W{S}_{jn}$. This production rule needs only one Web service $W{S}_i$, we can trigger “$W{S}_{j1},W{S}_{j2},\cdots ,W{S}_{jn}$”, so,

$$\begin{array}{c}{\Gamma }_{j1}={\Gamma }_i\times {\Gamma }_1={\Gamma }_i\times s_1\\ {\Gamma }_{j2}={\Gamma }_i\times {\Gamma }_2={\Gamma }_i\times s_2\\ \dots \\ {\Gamma }_{jn}={\Gamma }_i\times {\Gamma }_n={\Gamma }_i\times s_n.\end{array}$$

(15)

The five kinds of production rule, above have some common points; the points can be summed up with some general rules:

(1)

In the first, fourth, and fifth production rules, the reliability value of the postpositional Web service of the transition equals the product of the reliability of the prepositional Web service of the transition and the reliability value of the transition.

(2)

In the second production rule, the reliability value of the postpositional Web service of the transition equals the minimum reliability value of all the prepositional Web services multiplied by the reliability value of the transition.

(3)

In the third production rule, the reliability value of the postpositional Web service of the transitions equals the maximum value of the reliability values of the respective prepositional Web services multiplied by the reliability values of the transitions.

In order to calculate the reliability of Web services and the reliability values of transitions, we make formal definitions of Web services and transitions in FRCPN.

Definition 8.

Formal definition of Web service in FRCPN.

$$WS(IRS,PRTS,POTS,PIRS,ReliabilityValue)$$

(1)

WS, Web Service represents a Web service in FRCPN.

(2)

IRS, Immediate Reachability Set. For a current Web service WS, if there exists a transition t satisfying some conditions, including $WS\in I(t)$ and $W{S}_i\in O(t)$, then we call $W{S}_i$ the immediate reachability Web service of WS. All of the immediate reachability Web services of WS are called an immediate reachability set of WS, denoted as IRS.

(3)

PRTS, PRepositional Transition Set. For a current Web service WS, if there exists a transition t satisfying $WS\in O(t)$, we call t the prepositional transition of WS. All of the prepositional transitions of WS are called a prepositional transition set of WS, denoted as PRTS.

(4)

POTS, POstpositional Transition Set. For a current Web service WS, if there exists a transition t satisfying $WS\in I(t)$, we call t the postpositional transition of WS. All of the postpositional transitions of WS are called a postpositional transition set of WS, denoted as POTS.

(5)

PIRS, Prepositional Immediate Reachability Set. For a current Web service WS, if there exists a transition t satisfying some conditions, including $WS\in O(t)$ and $W{S}_i\in I(t)$, we call $W{S}_{\mathrm{i}}$ the prepositional immediate reachability Web service of WS. All of the prepositional immediate reachability Web services of WS are called a prepositional immediate reachability Web service set, denoted as PIRS.

(6)

$ReliabilityValue$, the reliability value of the current Web service. Before calculating the reliability value of all Web services in the graph, we set the initial Web service’s reliability to 1, and the reliability value of other Web services to 0.

Definition 9.

Formal definition of transition in FRCPN.

$$T(PRWSS,POWSS,Type,Reliability Value)$$

(1)

T, Transition, represents a transition in FRCPN.

(2)

PRWSS, PRepositional Web Service Set. For a current transition t, if there exists a Web service WS satisfying $WS\in I(t)$, we call WS the prepositional Web service of t. All of the prepositional Web services of t are called the prepositional Web service set of t, denoted as PRWSS.

(3)

POWSS, POstpositional Web Service Set. For a current transition t, if there exists a Web service WS satisfying $WS\in O(t)$, we call WS s the postpositional Web Service of t. All of the postpositional Web Services of t are called the postpositional Web Service set of t, denoted as POWSS.

(4)

Type, the type of current transition. There are five types of transition. The first type of transition is shown in Figure 1, the second type of transition is shown in Figure 2, the third type of transition is shown in Figure 3, the fourth type of transition is shown in Figure 4, and the fifth type of transition is shown in Figure 5.

(5)

$ReliabilityValue$, the reliability value of the current transition.

4. Reliability Calculation Method for FRCPN

Here we propose a reliability calculation method for Web service compositions in FRCPN, as shown in Figure 6. Firstly, we calculated the reliability values of all the transitions in FRCPN, then we generated the SLLFRV linked list. Finally, according to the reliability values of all the transitions and the SLLFRV linked list, we calculated the reliability value of FRCPN.

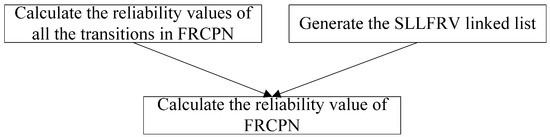
Figure 6. The procedure of the reliability calculation method.

4.1. Reliability Calculation Algorithm for All the Transitions in FRCPN

The time complexity of Algorithm 1 is O(n). After getting the transition set of the graph, the algorithm uses a cycle “for” to set the reliability values of the transitions. The reliability values of the transitions are related to the type of transition. If the type of the current transition is the first type, the third type, or the fifth type, and the PRWSS of the current transition and the POWSS of the current transition have only a Web service, the reliability value of the current transition is $m_1\times \text{sim}(O_{wsi},I_{wsj})+m_2$. If the type of the current transition is the second type, then the PRWSS has many Web services, but the POWSS of the current transition only has a Web service, so the reliability value of the current transition is $m_1\times \text{sim}(O_{preWSS1}\cup O_{preWSS2}\cup \cdots \cup O_{preWSSn},I_{wsj})+m_2$. If the type of the current transition is the fourth type, then the POWSS of the current transition has many Web services, but the PRWSS only has a Web service, so the reliability value of the current transition is $m_1\times \text{sim}(O_{wsi},I_{postWSS1}\cup I_{postWSS2}\cup \cdots \cup I_{postWSSn})+m_2$.

Algorithm 1 TSet fillTransitionValue(FRCPN frcpn)

Algorithm’s name: The reliability calculation algorithm for all the transitions in FRCPN

Input parameter: FRCPN graph frcpn

Output parameter: TSet, The transition set filled with reliability values in FRCPN

//Get the transition set of FRCPN graph frcpn

1  TSet tSet = frcpn.getTransitionSet()

//Set successively the reliability values of all the transitions in frcpn using a loop

2  for int k = 0 to |tSet| − 1 step 1

3    Transition t = tSet.get(k)

//Get the type of the transition

4    int type = t.getType()

//Set the reliability value of the transition according to the type of the transition

//If the type of the transition is the first type, the third type or the fifth type

5    if type = 1 or type = 3 or type = 5 then

//The PRWSS has only a Web service

6      WS wsi = t.getPRWSS.get(0)

//The POWSS has only a Web service

7      WS wsj = t.getPOWSS.get(0)

//Set the reliability value of the transition. In the expression, $m_1+m_2=1$

8      t.setReliablityValue($m_1\times \text{sim}(O_{wsi},I_{wsj})+m_2$)

9    end if

//If the type of the transition is the second type

10   if type = 2 then

//Get the PRWSS of current transition

11     WSSet preWSS = t.getPRWSS()

//The POWSS has only a Web service

12     WS wsj = t.getPOWSS.get(0)

//Set the reliability value of the transition. In the expression, $m_1+m_2=1$

//|preWSS| = n

//The elements in preWSS are represented as preWSS1, preWSS2,…, preWSSn

13     t.setReliablityValue($m_1\times \text{sim}(O_{preWSS1}\cup O_{preWSS2}\cup \cdots \cup O_{preWSSn},I_{wsj})+m_2$)

14   end if

// If the type of the transition is the fourth type

15   if type = 4 then

//The PRWSS has only a Web service

16     WS wsi = t.getPRWSS.get(0)

//Get the POWSS of current transition

17     WSSet postWSS = t.getPOWSS ()

// Set the reliability value of the transition. In the expression, $m_1+m_2=1$

//|postWSS| = n

//The elements in postWSS are represented as postWSS1, postWSS2,…, postWSSn

18     t.set Reliablity Value($m_1\times \text{sim}(O_{wsi},I_{postWSS1}\cup I_{postWSS2}\cup \cdots \cup I_{postWSSn})+m_2$)

19   end if

20 end for

21 return tSet

4.2. Generation Algorithm for SLLFRV Linked List

We set the reliability value of the starting Web service in FRCPN as 1. The call to the Web service is always backward, and a FRCPN is a directed acyclic graph, so we can successively calculate the reliability values of the Web services in FRCPN according to the transitions. When we calculate the last Web service, the reliability value of the last Web service is used as the reliability value of FRCPN. There are the following problems when we set the reliability values of Web services.

(1)

If the reliability values of some Web services in the PIRS of current Web service are not set, this situation will lead to non-generation of the reliability value for the current Web service.

(2)

A transition has several possible postpositional Web Services, and different transitions may have the same postpositional Web Service, so we need to consider the situation for setting the reliability value of Web service many times.

Regarding the first problem, we propose a SLLFRV linked list. According to the sequence of transitions in SLLFRV, we can successively set the reliability values in the POWSS of the current transition. Certainly, this solves the first problem, because the reliability values in PIRS of the current transition have not been generated.

Regarding the second problem, we propose a reliability calculation algorithm for Web services in FRCPN. In the algorithm, we consider the situation for setting the reliability value of Web service many times. If we arrive at the current Web service from multiple different paths, we select a higher reliability value among multiple paths as the reliability value of the current Web service.

The data structure of SLLFRV is a simple Singly Linked List, denoted as LinkT. The algorithm for generating SLLFRV is given below.

Algorithm 2 uses the recursive idea. Each time, the algorithm performs a double cycle “for” and continues recursion, so the time complexity of the algorithm is O(n³).

Algorithm 2 LinkT generateLinkT(FRCPN frcpn, Transition t, LinkT linkT)

Algorithm’s name: The generation algorithm for SLLFRV

Input parameters: FRCPN graph frcpn, current transition t, SLLFRV linked list linkT. When the algorithm is called first, we set the input parameter t is ∅, and set the input parameter linkT is ∅.

Output parameter: the SLLFRV linked list generated

//If t is ∅ and linkT is ∅, then it is the first time to call this algorithm

1  if t is ∅ and linkT is ∅ then

2     linkT = newLinkT()

//Get starting Web service of frcpn

3     WS ws = frcpn.getStartWebService()

//Get the POTS of starting Web service

4     TSet postTSet = ws.getPOTS()

5     for int i = 0 to|postTSet| − 1 step 1

6       if i = 0 then

7         linkT = postTSet.get(0)

8         linkT.top = postTSet.get(0)

9         linkT.last = postTSet.get(0)

10      else

11    linkT.last.next = postTSet.get(i)

12    linkT.last = postTSet.get(i)

13      end if

14    end for

//Continue to iterative generate linkT

15    for int i = 0 to|postTSet| − 1 step 1

16      generateLinkT(fcpn,postTSet.get(i),linkT)

17    end for

18 else //It is not first time to call generateLinkT()

// Generate linkT and return to the superior function

19    if t is ∅ then

20    return linkT

21    end if

//Get the POWSS of the current transition

22    WSSet wsSet = t.getPOWSS ()

23    for int i = 0 to |wsSet| − 1 step 1

24      WS ws = wsSet.get(i)

//Get the POTS of the current Web service

25      TSet postTSet = ws.getPOTS()

//Get the PRTS of the current Web service

26      TSet preTSet = ws.getPRTS()

//If PRTS of the current Web service is not in linkT

27      if preTSet not in linkT then

28    break

29    end if

//If the current Web service does not have a postpositional transition

30      if postTSet is ∅ then

31    break

32    end if

33      for int j = 0 to |postTSet| − 1 step 1

34        Transition ct = postTSet.get(j)

//Get the union of POWSS of all the transitions in linkT

35        WSSet linkTPreWSSet = ${\cup }_{k=0}^{\left|linkT\right|}linkT.\text{get}(k).\text{getPOWSS}()$

//Set the initial value of the judgment flag to false

/*The judgment flag indicates whether the PRWSS of the current transition is included in preWSSet*/

36        boolean flag = false

37        WSSet tPreWSSet = ct.getPRWSS()

// If tPreWSSet is a subset of linkTPreWSSet, then set the flag to true

38        if tPreWSSet in linkTPreWSSet then

39        flag = true

40        end if

/*If the current transition is not included in linkT, and the judgment flag is

true*/

41        if ct not in linkT and flag is true then

42      linkT.last.next = ct

43      linkT.last = ct

44        end if

45      end for

// Continue to iterative generate linkT

46      for int i = 0 to |postTSet| − 1 step 1

47        generateLinkT(fcpn,postTSet.get(i),linkT)

48    end for

49    end for

50    end if

51    return linkT

When the algorithm is first time to be called, t and linkT are ∅, so the algorithm creates a new linkT, and begins to inspect from the starting Web service of the graph. The algorithm puts the POTS of the starting Web service into linkT, and then continues the recursion.

If the algorithm is not first time to be called, then the algorithm must judge some things. If the current transition t is ∅, then it indicates that recursion is completed and the algorithm can return to the superior function. If the transition t is not empty, then the algorithm gets the POWSS of the current transition and uses a cycle “for” to inspect the elements in POWSS.

Next, the algorithm gets the POTS postTSet of the current Web service and the PRTS preTSet of the current Web service. If preTSet is not in linkT, it shows that the reliability values of the prepositional transitions of the current Web service and the reliability values of the postpositional transitions of the current Web service have not all been generated, so the algorithm does not continue to inspect the candidate transitions, and uses “break” to exit inspection. If the current Web service does not have an immediate postpositional transition, postTSet is empty and the algorithm does not continue to follow the transition in the future, so also uses “break” to exit inspection.

Next, the algorithm uses a cycle “for” to traverse the transitions in postTSet. In the ideas of the algorithm, if the transitions are already in linkT, then the reliability values of all the immediate postpositional web services of the transitions can be calculated. The algorithm first gets the union of POWSS of all the transitions in linkT, and then executes set operations. If the PRWSS of the current transition is a subset of linkTPreWSSet, then it indicates that the reliability values of all the immediate postpositional Web services of the current transition can be calculated. If the current transition is not in linkT, the algorithm puts the current transition into linkT and then continues recursion.

In summary, if the transition is in linkT, the reliability values of all the prepositional Web services of the transition can be calculated according to the order in linkT before the reliability values of the postpositional Web services of the transition are calculated. Therefore, the algorithm can confirm that the reliability values of the immediate postpositional Web services of the transition can be calculated.

4.3. Reliability Calculation Algorithm for All the Web Services in FRCPN

Algorithm 3 was used to calculate the reliability values of Web Services according to SLLFRV linkT in sequence. According to the content of the algorithm, the time complexity of the algorithm is O(n²).

Algorithm 3 FRCPN fillWSValue(FRCPN frcpn, LinkT linkT)

Algorithm’s name: the reliability calculation algorithm for FRCPN frcpn

Input parameters: FRCPN graph frcpn, SLLFRV linked list linkT

Output parameter: FRCPN graph frcpn that the graph has generated the reliability values of Web services

//According to SLLFRV linkT, generate successively the reliability values of Web services

1  for Transition t = linkT.top to t = null step t = t.next

//If the current transition is of the first, fourth, or fifth type

2   if t.getType() = 1 or t.getType() = 4 or t.getType() = 5 then

/*Get the reliability value of the prepositional Web service of the current transition*/

3    float trustValue = t.getPRWSS().get(0).getTrustValue() × t.getTrustValue()

//Get the POWSS of the transition t

4    WSSet postWSSet = t.$\text{getPOWSS} ()$

//Set the reliability values of the Web services in POWSS of transition t

5    for int i = 0 to |postWSSet| − 1 step 1

6     WS ws = postWSSet.get(i)

7     ws.setTrustValue( Max{ ws.getTrustValue, trustValue} )

8    end for

9   end if

//If the current transition is of the second type

10   if t.getType() = 2 then

//Get the PRWSS of the current transition

11    WSSet preWSSet = t.getPRWSS()

/*The reliability value of the postpositional Web service of the transition equals the minimum value of reliability values of all the prepositional Web services of the transition*/

//|preWSSet| =

12    float trustValue = Min( preWSSet.get(0).getTrustValue(),

preWSSet.get(1).getTrustValue(), …,preWSSet.get(n).getTrustValue())

×t.getTrustValue()

//The POWSS of the current transition has only one Web service

13    WS ws = t.getPOWSS.get(0)

14    ws.setTrustValue( Max{ ws.getTrustValue, trustValue} );

15   end if

// If the current transition is of the third type

16   if t.getType() = 3 then

//The POWSS of the current transition only has one Web service

17   WS ws = t.getPOWSS().get(0)

//Get the PRTS of the current transition

18   TSet tSet = ws.getPRTS()

//Get the reliability value of ws, |tSet| = n

19   float trustValue = Max(

tSet.get(0).getPRWSS().get(0).getTrustValue()×tSet.get(0).getTrustVale(),

tSet.get(1).getPRWSS().get(0).getTrustValue()×tSet.get(1).getTrustVale(),

…,

tSet.get(n).getPRWSS().get(0).getTrustValue()×tSet.get(n).getTrustVale());

20   ws.setTrustValue( Max{ ws.getTrustValue, trustValue} );

21   end if

22  end for

23  return frcpn

The algorithm traverses the transitions in SLLFRV linkT, in order to calculate the reliability values of the direct subsequent Web services of the transitions in SLLFRV linkT according to the type of transition. If the current transition t is of the first, fourth, or fifth type, it only has one immediate prepositional Web service, and the reliability values of immediate postpositional Web services are t.getPRWSS().get(0).getTrustValue()×t.getTrustValue(). In order to prevent conflict between the reliability values of multiple transitions, the algorithm executes the operation “Max”, so as to always get the highest reliability value as the final reliability value of a Web service.

If the current transition t is of the second type, the current transition has multiple immediate prepositional Web services, so the algorithm must take the minimum reliability value of the immediate prepositional Web services as the basis for calculating the reliability values of the postpositional Web services of the current transition. The calculation formula is Min(preWSSet.get(0).getTrustValue(),preWSSet.get(1).getTrustValue(),…,preWSSet.get(n).getTrustValue())×t.getTrustValue().

If the current transition t is of the third type, the current transition has only one immediate postpositional Web service, so the algorithm must take the operation “Max” after the reliability values of the immediate prepositional Web Services and the reliability value of the current transition are multiplied. The algorithm can obtain the reliability value of the immediate postpositional Web service. The calculation formula is

Max(tSet.get(0).getPRWSS().get(0).getTrustValue() × tSet.get(0).getTrustValue(),_

tSet.get(1).getPRWSS().get(0).getTrustValue() × tSet.get(1).getTrustValue(),…,_

tSet.get(n).getPRWSS().get(0).getTrustValue() × tSet.get(n).getTrustValue(),).

5. An Example of the Application of the Method

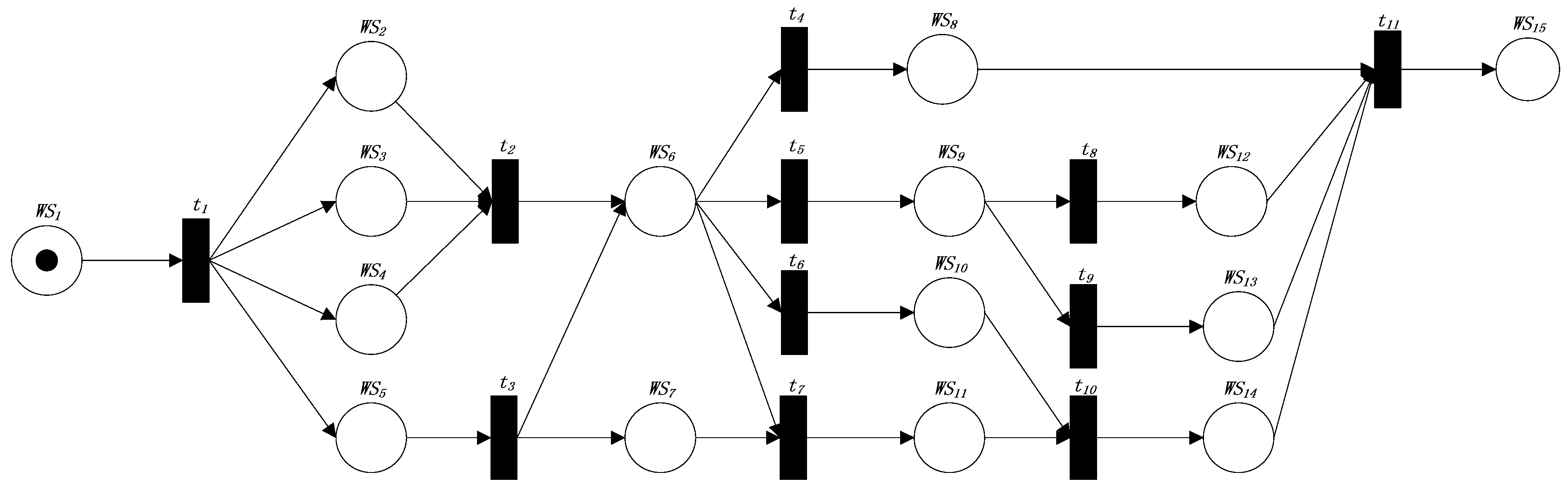
Assume that we have generated a service composition expressed by FRCPN for the calculation process for CAE simulation in SCP prototype, as shown in Figure 7. According to the reliability calculation method, we will calculate the reliability value of the FRCPN.

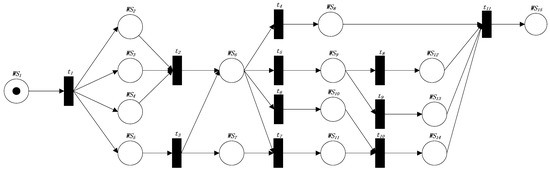
Figure 7. The FRCPN generated.

We get all kinds of parameters of Web services, as shown in Table 1. The reliability value ReliabilityValue is required for the calculation, so we use the method in this paper to calculate the reliability value.

Table 1. The parameters of Web services in FRCPN (Fuzzy Reasoning Colored Petri Net).

Web Services’ Name	IRS (Immediate Reachability Set)	PRTS (PRepositional Transition Set)	POTS (POstpositional Transition Set)	PIRS (Prepositional Immediate Reachability Set)
WS1	{WS2, WS3, WS4, WS5}	∅	{t1}	∅
WS2	{WS6}	{t1}	{t2}	{WS1}
WS3	{WS6}	{t1}	{t2}	{WS1}
WS4	{WS6}	{t1}	{t2}	{WS1}
WS5	{WS6, WS7}	{t1}	{t3}	{WS1}
WS6	{WS4, WS5, WS6, WS7}	{t2,t3}	{t4,t5,t6,t7}	{WS2,WS3,WS4,WS5}
WS7	{WS11}	{t3}	{t7}	{WS5}
WS8	{WS15}	{t4}	{t11}	{WS6}
WS9	{WS12, WS13}	{t5}	{t8,t9}	{WS6}
WS10	{WS14}	{t6}	{t10}	{WS6}
WS11	{WS14}	{t7}	{t10}	{WS6,WS7}
WS12	{WS15}	{t8}	{t11}	{WS9}
WS13	{WS15}	{t9}	{t11}	{WS9}
WS14	{WS15}	{t10}	{t11}	{WS10,WS11}
WS15	$\varnothing$	{t11}	$\varnothing$	{WS8,WS12,WS13,WS14}

Firstly, we use Algorithm 1 to get the reliability values of the transitions in the FRCPN. We use frcpn.getTransitionSet() to get the transition sequence, which is {t₄,t₇,t₅,t₆,t₈,t₁₁,t₉,t₁₀,t₃,t₂,t₁}. We set the semantic similarity threshold k = 0.8, m₁ = 0.8, and m₂ = 0.2 in all the formulas. All of the conditions in P, Q are satisfied. All the transitions in the FRCPN are shown in Table 2.

Table 2. The parameters of the transitions in the FRCPN.

Transition’s Name	Known Similarity	PRWSS	POWSS	Type
t1	$sim(O_{WS1},I_{WS2}\cup I_{WS3}\cup I_{WS4}\cup I_{WS5})=0.94$	{WS1}	{WS2,WS3,WS4,WS5}	fourth
t2	$sim(O_{WS2}\cup O_{WS3}\cup O_{WS4},I_{WS6})=0.92$	{WS2,WS3,WS4}	{WS6}	second
t3	$sim(O_{WS5},I_{WS6}\cup I_{WS7})=0.9$	{WS5}	{WS6,WS7}	fourth
t4	$sim(O_{ws6},I_{ws8})=0.98$	{WS6}	{WS8}	fifth
t5	$sim(O_{ws6},I_{ws9})=0.88$	{WS6}	{WS9}	fifth
t6	$sim(O_{ws6},I_{ws10})=0.92$	{WS6}	{WS10}	fifth
t7	$sim(O_{WS6}\cup O_{WS7},I_{ws11})=0.9$	{WS6,WS7}	{WS11}	second
t8	$sim(O_{ws9},I_{ws12})=0.94$	{WS9}	{WS12}	fifth
t9	$sim(O_{ws9},I_{ws13})=0.94$	{WS9}	{WS13}	fifth
t10	$sim(O_{WS10}\cup O_{WS11},I_{ws14})=0.9$	{WS10,WS11}	{WS14}	second
t11	$sim(O_{WS8}\cup O_{WS12}\cup O_{WS13}\cup O_{WS14},I_{15})=0.92$	{WS8,WS12,WS13,WS14}	{WS15}	second

According to the sequence {t₄,t₇,t₅,t₆,t₈,t₁₁,t₉,t₁₀,t₃,t₂,t₁} and Algorithm 1, we calculate the reliability values of the transitions. Let us start with a look at the calculation of t₄’s reliability value. We know from Table 2 that t₄ is of the fifth type. According to Algorithm 1, wsi and wsj are WS₆ and WS₈, respectively, and we can calculate the reliability value of t₄ as follows:

$$ReliabilityValue(t_4)=m_1\times \text{sim}(O_{wsi},I_{wsj})+m_2=m_1\times \text{sim}(O_{WS6},I_{WS8})+m_2=0.8\times 0.98+0.2=0.984.$$

According to Algorithm 1, we can calculate the reliability value of each transition in order as follows:

$$ReliabilityValue(t_7)=m_1\times \text{sim}(O_{preWSS1}\cup O_{preWSS2}\cup \cdots \cup O_{preWSSn},{\mathrm{I}}_{\mathrm{wsj}})+m_2=m_1\times \text{sim}(O_{WS6}\cup O_{WS7},I_{WS11})+m_2=0.8\times 0.9+0.2=0.92$$

$$ReliabilityValue(t_5)=m_1\times \text{sim}(O_{wsi},I_{wsj})+m_2=m_1\times \text{sim}(O_{WS6},I_{WS9})+m_2=0.8\times 0.88+0.2=0.904$$

$$ReliabilityValue(t_6)= m_1\times \text{sim}(O_{wsi},I_{wsj})+m_2=m_1\times \text{sim}(O_{WS6},I_{WS10})+m_2=0.8\times 0.92+0.2=0.936$$

$$ReliabilityValue(t_8)= m_1\times \text{sim}(O_{wsi},I_{wsj})+m_2=m_1\times \text{sim}(O_{WS9},I_{WS12})+m_2=0.8\times 0.94+0.2=0.952$$

$$ReliabilityValue(t_{11})=m_1\times \text{sim}(O_{preWSS1}\cup O_{preWSS2}\cup \cdots \cup O_{preWSSn},I_{wsj})+m_2=m_1\times \text{sim}(O_{WS8}\cup O_{WS12}\cup O_{WS13}\cup O_{WS14},I_{15})+m_2=0.8\times 0.92+0.2=0.936$$

$$ReliabilityValue(t_9)=m_1\times \text{sim}(O_{wsi},I_{wsj})+m_2=m_1\times \text{sim}(O_{WS9},I_{WS13})+m_2=0.8\times 0.94+0.2=0.952$$

$$ReliabilityValue(t_{10})=m_1\times \text{sim}(O_{preWSS1}\cup O_{preWSS2}\cup \cdots \cup O_{preWSSn},I_{wsj})+m_2=m_1\times \text{sim}(O_{WS10}\cup O_{WS11},I_{WS14})+m_2=0.8\times 0.9+0.2=0.92$$

$$ReliabilityValue(t_3)=m_1\times \text{sim}(O_{wsi},I_{postWSS1}\cup I_{postWSS2}\cup \cdots \cup I_{postWSSn})+m_2=m_1\times \text{sim}(O_{WS5},I_{WS6}\cup I_{WS7})+m_2=0.8\times 0.9+0.2=0.92$$

$$ReliabilityValue(t_2)=m_1\times \text{sim}(O_{preWSS1}\cup O_{preWSS2}\cup \cdots \cup O_{preWSSn},I_{wsj})+m_2=m_1\times \text{sim}(O_{WS2}\cup O_{WS3}\cup O_{WS4},I_{WS6})+m_2=0.8\times 0.92+0.2=0.936$$

$$ReliabilityValue(t_1)=m_1\times \text{sim}(O_{wsi},I_{postWSS1}\cup I_{postWSS2}\cup \cdots \cup I_{postWSSn})+m_2=m_1\times \text{sim}(O_{WS1},I_{WS2}\cup I_{WS3}\cup I_{WS4}\cup I_{WS5})+m_2=0.8\times 0.94+0.2=0.952$$

We continue to use Algorithm 2 to generate the SLLFRV linked list. When the algorithm is first time to be called, we can use generateLinkT(frcpn,$\varnothing ,\varnothing$). Therefore, we get $postTSet=\{t_1\}$, and the algorithm puts $t_1$ in the to SLLFRV linked list linkT. Next, the algorithm calls recursively generateLinkT(frcpn,$t_1,linkT$).

When the algorithm is called by generateLinkT(frcpn,$t_1,linkT$), we get $wsSet=\{W{S}_2,W{S}_3,W{S}_4,W{S}_5\}$. Next, according to the cycle “for” to wsSet in the algorithm, we get $postTSet=\{t_2\}$, $preTSet=\{t_1\}$, and know that the value of “pretest not in linkT” is false. In the cycle “for” to postTSet in the algorithm, we can get $ct=t_2$ and the following results:

$$linkTPreWSSet={\displaystyle \underset{k=0}{\overset{\left|linkT\right|}{\cup }}}linkT.\text{get}(k).\text{getPOWSS}()=\{W{S}_2,W{S}_3,W{S}_4,W{S}_5\}$$

$$tPreWSSet=ct.\text{getPRWSS}( )=\{W{S}_2,W{S}_3,W{S}_4\}.$$

According to the above analysis, tPreWSSet is a subset of linkTPreWSSet, the value of flag is true. “ct not in linkT” indicates that the current transition is not in linkT, and the value of flag is true, so the algorithm puts $t_2$ into the tail of linkT.

Next, the algorithm is called recursively generateLinkT(frcpn,$t_2,linkT$). Through continuous recursive calls, the algorithm produces the SLLFRV linkT as follows:

$$t_1\to t_2\to t_3\to t_4\to t_5\to t_7\to t_8\to t_9\to t_{10}\to t_{11}$$

According to the sequence in the SLLFRV linkT, we use Algorithm 3 to get the reliability values of all the Web services as follows:

$$TrustValue(W{S}_1)=1.0$$

$$Type(t_1)=4, TrustValue(W{S}_2)=\mathbf{\text{Max}}(1.0\times 0.952,0)=0.952,$$

$$Type(t_1)=4, TrustValue(W{S}_2)=\mathbf{\text{Max}}(1.0\times 0.952,0)=0.952,$$

$$TrustValue(W{S}_3)=\mathbf{\text{Max}}(1.0\times 0.952,0)=0.952,$$

$$TrustValue(W{S}_4)=\mathbf{\text{Max}}(1.0\times 0.952,0)=0.952$$

$$TrustValue(W{S}_5)=\mathbf{\text{Max}}(1.0\times 0.952,0)=0.952$$

$$Type(t_2)=2, TrustValue(W{S}_6)=\mathbf{\text{Max}}(\mathrm{Min}(0.952,0.952,0.952)\times 0.936,0)=0.891$$

$$Type(t_3)=4,TrustValue(W{S}_6)=\mathbf{\text{Max}}(0.952\times 0.92,0.891)=0.891$$

$$TrustValue(W{S}_7)=\mathbf{\text{Max}}(0.952\times 0.92,0)=0.876$$

$$Type(t_4)=5, TrustValue(W{S}_8)=\mathbf{\text{Max}}(0.891\times 0.984,0)=0.877$$

$$Type(t_5)=5, TrustValue(W{S}_9)=\mathbf{\text{Max}}(0.891\times 0.904,0)=0.805$$

$$Type(t_6)=5, TrustValue(W{S}_{10})=\mathbf{\text{Max}}(0.891\times 0.936,0)=0.834$$

$$Type(t_7)=2,TrustValue(W{S}_{11})=\mathbf{\text{Max}}(\mathrm{Min}(0.891,0.876)\times 0.92,0)=0.806$$

$$Type(t_8)=5, TrustValue(W{S}_{12})=\mathbf{\text{Max}}(0.805\times 0.952,0)=0.766$$

$$Type(t_9)=5, TrustValue(W{S}_{13})=\mathbf{\text{Max}}(0.805\times 0.952,0)=0.766$$

$$Type(t_{10})=2, TrustValue(W{S}_{14})=\mathbf{\text{Max}}(\mathbf{\text{Min}}(0.834,0.806)\times 0.92,0)=0.791$$

$$Type(t_{11})=2, TrustValue(W{S}_{15})=\mathbf{\text{Max}}(\mathbf{\text{Min}}(0.877,0.766,0.766,0.791)\times 0.936,0)=0.717.$$

The last Web service is $W{S}_{15}$ in the FRCPN graph, so the reliability of the FRCPN graph is the reliability value of $W{S}_{15}$. The reliability value of the FRCPN graph is 0.717.

6. Simulated Experiments

In order to analyze the effect of the method proposed in this paper, we used the SCP prototype to conduct simulated experiments. Due to the uncertainty of the Web services, under the premise of the validity of experiment, we made the following settings for the experimental conditions and related parameters.

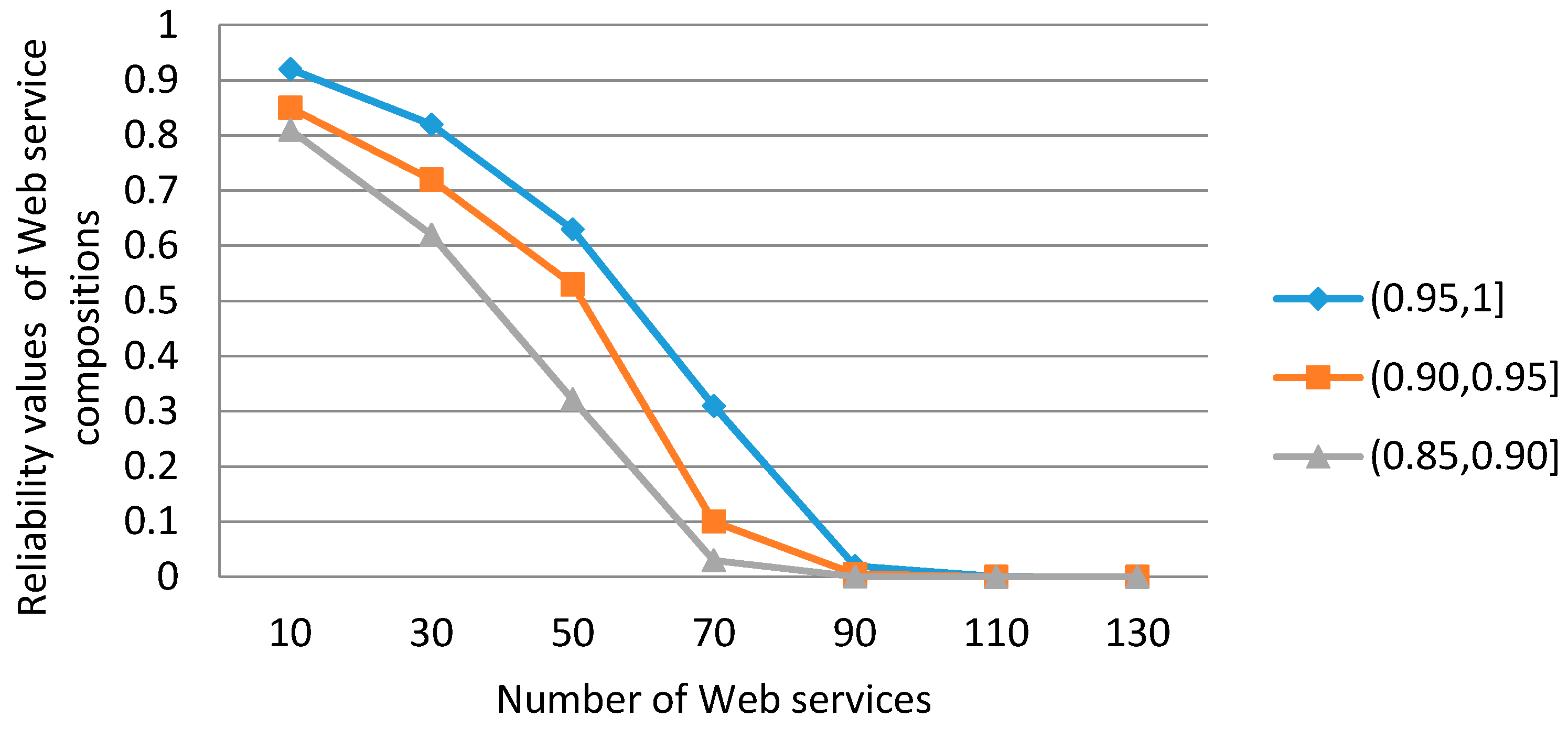
We used seven FRCPN graphs to simulate the Web service compositions; the number of Web services in the FRCPN graphs is 10, 30, 50, 70, 90, 110, and 130, respectively. We used five kinds of production rules to represent FRCPN, but kept the ratio between Web services and transitions is 1:5, so the length of SLLFRV is respectively 2, 6, 10, 14, 18, 22. The similarity threshold of all the transitions is set to the same value. After Algorithm 1 is finished, we assumed that the reliability values of transitions are divided into three ranges, i.e., $(0.95, 1.0],(0.90, 0.95],\text{and} (0.85, 0.90]$. According to the three ranges, we can get three sets of data; the similarity thresholds of the three sets are 0.95, 0.90, and 0.85, respectively.

The purpose of the experiment was to simulate the reliability values of FRCPN in different reliability ranges of transitions. The reliability values of Web service compositions were unlimited. The experimental results are shown in Figure 8. In the figure, the horizontal axis represents the number of Web services in FRCPN; the vertical axis represents the reliability values of Web service compositions.

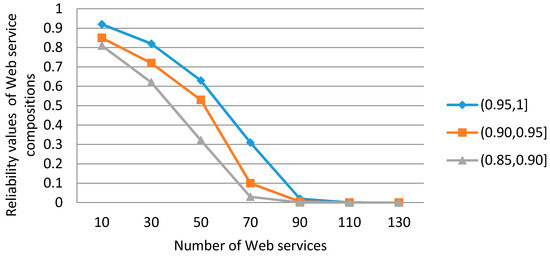
Figure 8. The results of the simulated experiment.

According to Figure 8, we can know the relationships among the reliability values of Web service compositions, the number of Web services, and the reliability ranges of transitions. The following relationships can be obtained:

(1)

Under the same reliability range of transitions, if the number of Web services is greater, then the length of SLLFRV is longer and the reliability values of the Web service compositions are smaller.

(2)

Under different reliability ranges of transitions, if the minimum range is smaller, then as the number of Web services increases, the reliability values of the service compositions decrease more rapidly.

(3)

We should proper control the scale of Web services in FRCPN. For example, if we set the reliability threshold of Web service compositions as 0.6, then in the reliability range (0.95, 1.0] of transitions, the number of Web services should be controlled below 30 and the length of SLLFRV is below 6.

7. Application in SCP

The SCP prototype uses Eclipse as a development tool, Java as a development language, OWL-S as a Web service description language, Tuscany as the Web services’ container, WSDL2OWLS as conversion tool, and OWL-S API as an interface tool.

The Web services in the SCP prototype are implemented by POJO Java class, and we use Web Service Description Language (WSDL) to describe the Web services. The software of the SCP prototype generates semantic Web service descriptions after filling QoS content according to WSDL, and then gets OWL documents.

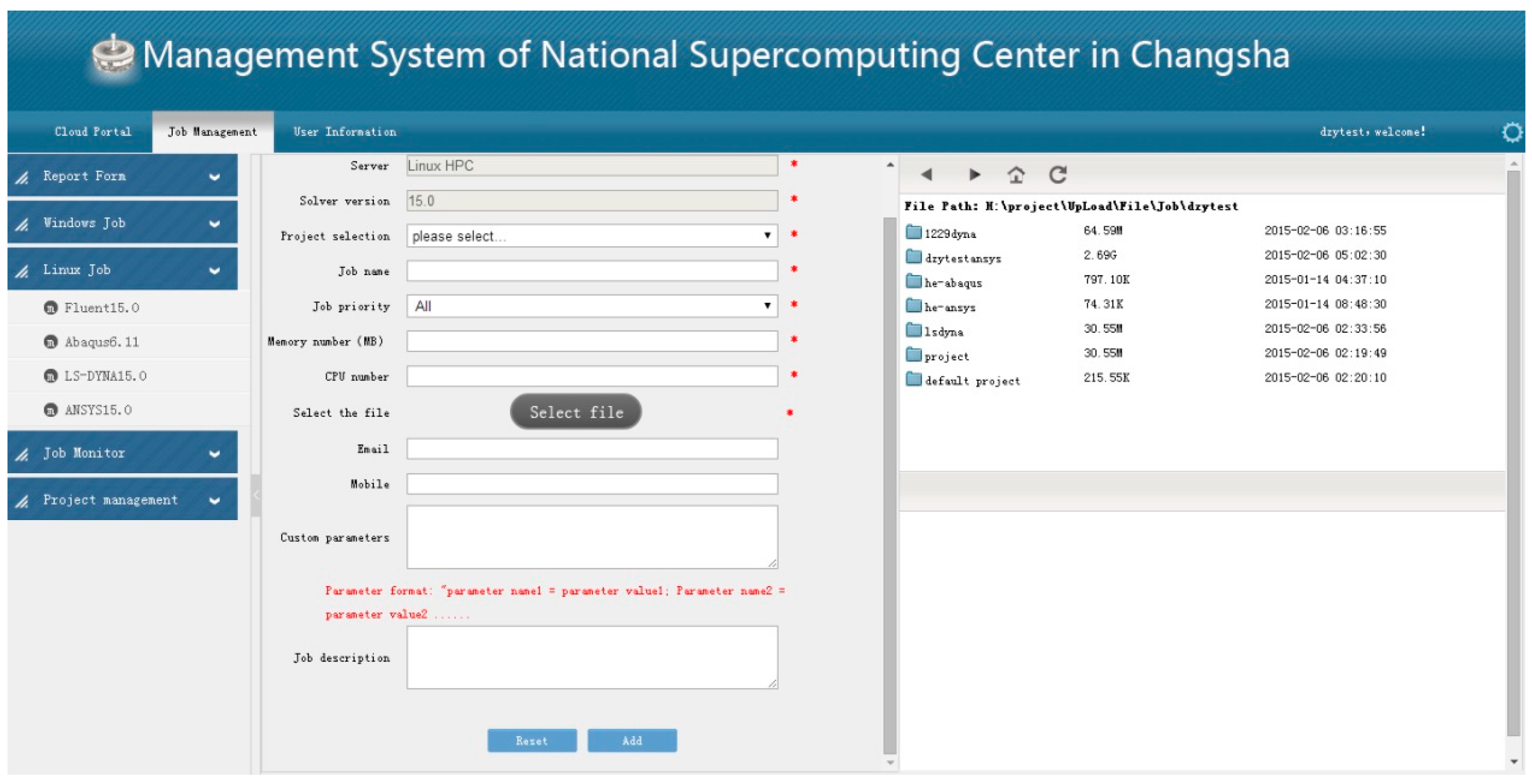
The users of the SCP prototype submit their computing requirements for CAE simulation through the Web system, as shown in Figure 9. After the SCP prototype receives the user’s request, the SCP prototype generates the request ontology, and then generates FRCPN. Therefore, we used the method in this paper to calculate the reliability value, then screen and get the best FRCPN.

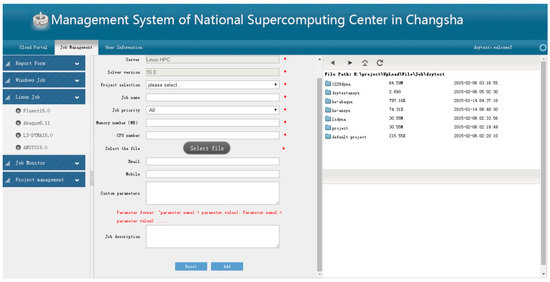
Figure 9. The interface for submitting a job in the SCP (Supercomputing Cloud Platform) prototype.

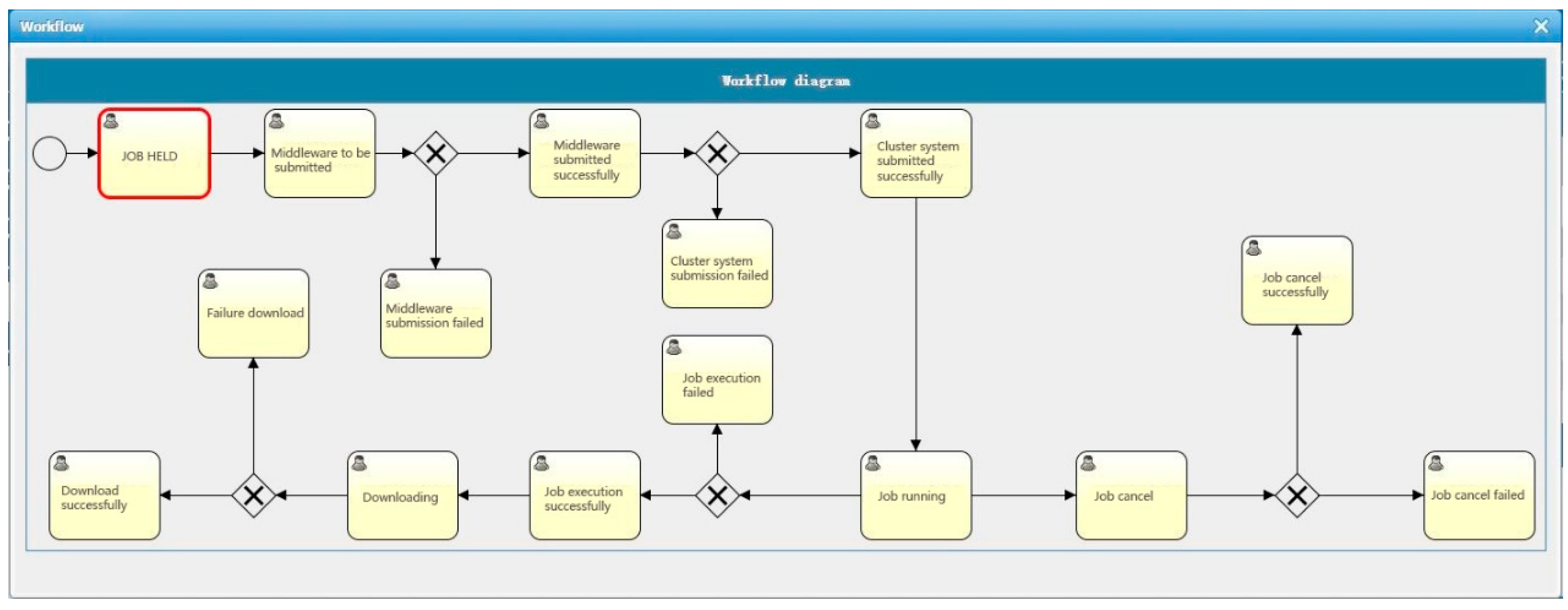
After the SCP prototype generates FRCPN graphs for CAE simulation, many FRCPN graphs are selected. The SCP prototype then calculates the reliability value of FRCPN graphs. We set k = 0.95, a = 0.9, and the number of Web services as not more than 30. We chose the highest reliability of FRCPN as the final business flow chart. Then we used Activiti to implement FRCPN. An example Activiti workflow for a computing job is shown in Figure 10.

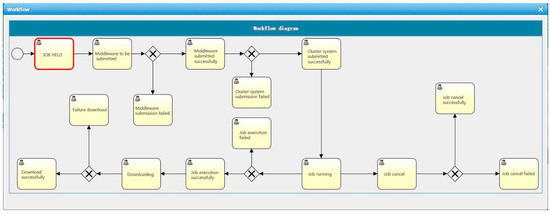
Figure 10. An example Activiti workflow for a computing job in the SCP prototype.

8. Conclusions and Further Work

When we use SOA architecture to develop an SCP prototype, we need to verify FRCPN after the prototype automatically generates FRCPN, and calculate the reliability value of FRCPN for further screening. We proposed a series of definitions, including semantic threshold similarity for Web services, formal definition of transition in FRCPN, etc. We proposed a reliability calculation method for Web service compositions using FRCPN. Firstly, the method calculates the reliability values of all the transitions in FRCPN. Then, the method generates the SLLFRV linked list. Finally, according to the reliability values of all the transitions and SLLFRV linked list, the method calculates the reliability value of FRCPN.

The experiment shows that the reliability values of Web service compositions have some regularity with the number of Web services and the reliability range of transitions. If the FRCPN scale is larger and the minimum value of the reliability range of transitions is smaller, then the reliability value of FRCPN is smaller, so we need to proper control the scale of Web services in FRCPN, and improve the reliability of a single transition. Next, we can carry out further research in the following areas:

(1)

Study the transaction model of Web service compositions and the exception recovery mechanism of Web service compositions, to facilitate the fallback handling for the jobs in the SCP prototype.

(2)

Carry out research into the structural verification algorithm of FRCPN to verify the validity of the structure.

(3)

Create a comprehensive summary of existing research works to form the theory and application system behind service compositions in the cloud platform, including modeling, searching, matching, automatic composition, validation, transaction handling, exception handling, etc.