Evaluation of the Magnetic Field Leakage from Two Wireless Power Transfer Systems for EV/PHV Driven Simultaneously
Abstract
:1. Introduction
2. Analysis Method and Conditions
2.1. Outline of Analysis Method
2.2. Analysis Conditions
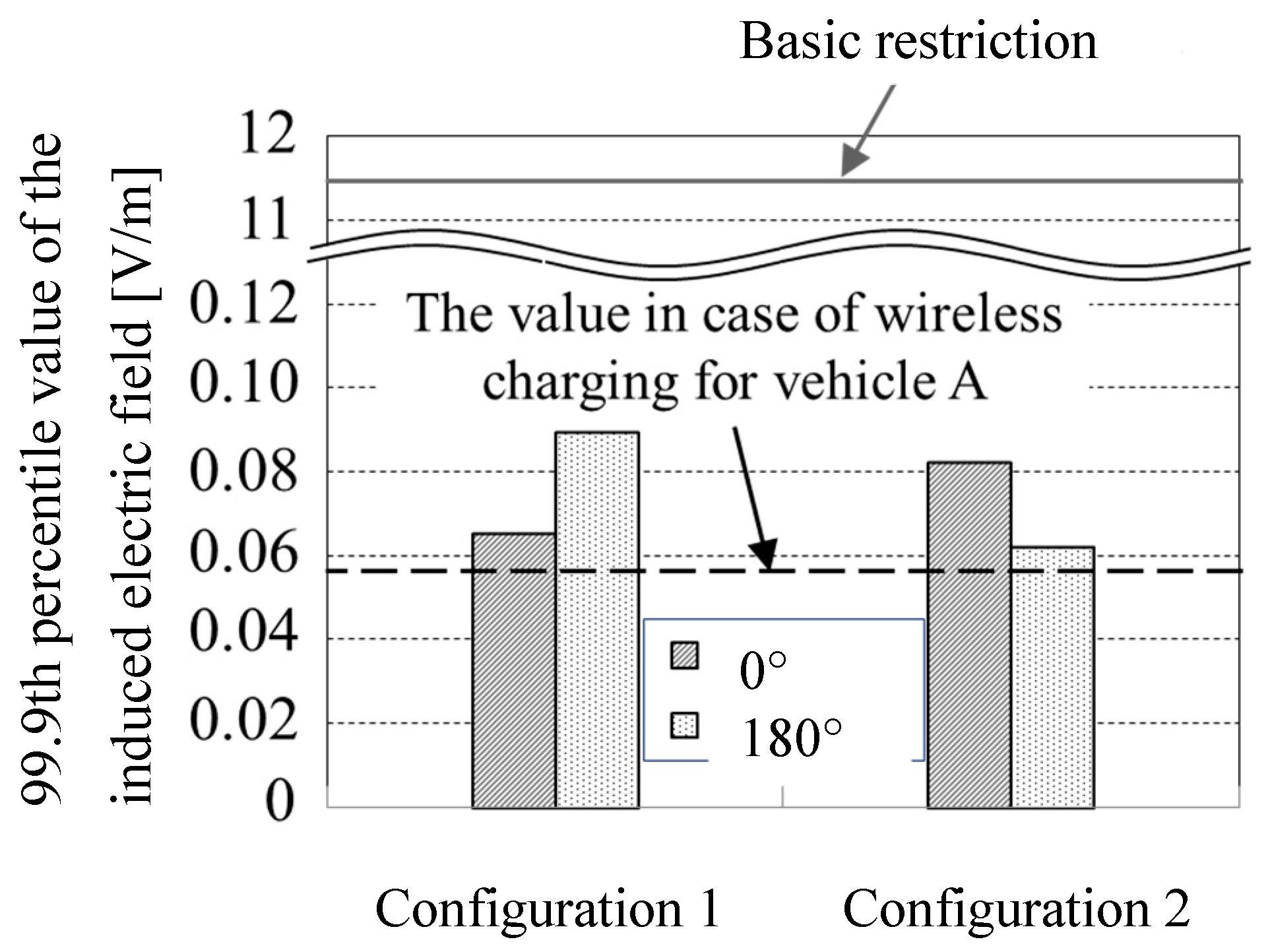
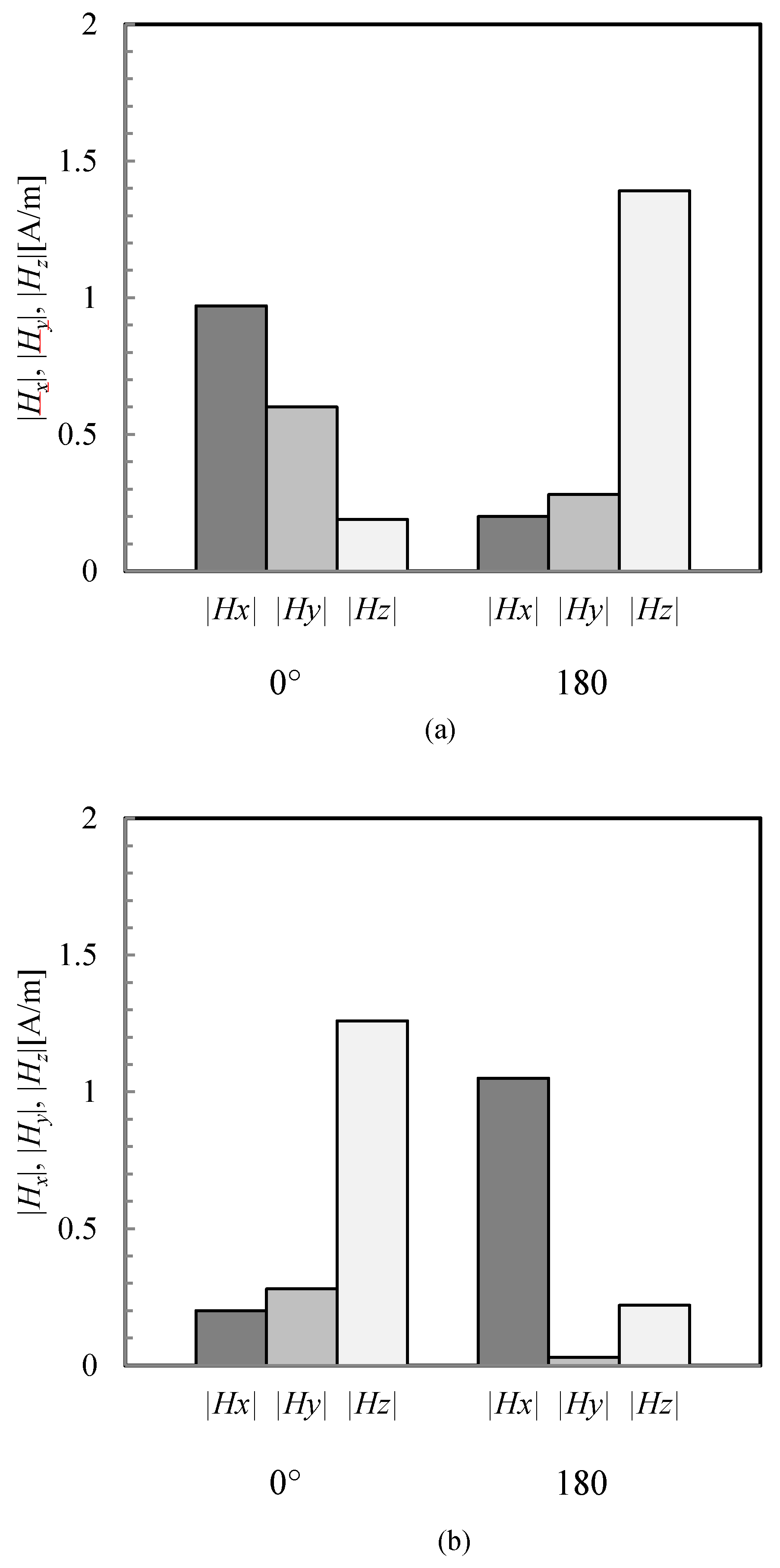
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soliačić, M. Wireless power transfer via strongly coupled magnetic resonances. Sci. Express 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Imura, T.; Uchida, T.; Hori, Y. Basic experimental study on helical antennas of contactless power transfer for electric vehicles by using magnetic resonant couplings. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 936–940. [Google Scholar] [CrossRef]
- Bushia, M.; Covic, G.A.; Boys, J. A new IPT magnetic coupler for electric vehicle charging systems. In Proceedings of the IECON 2010 36th Annual Conference on IEEE Industrial Electronics Societyemph, Glendale, AZ, USA, 7–10 November 2010; pp. 2481–2486. [Google Scholar] [CrossRef]
- Takahashi, H.; Kaneko, Y.; Abe, S.; Yasuda, T. A large air gap 3kW wireless power transfer system for electric vehicles. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 269–274. [Google Scholar] [CrossRef]
- Covic, G.A.; Boys, J.T. Inductive Power Transfer. Proc IEEE. 2013, 101, 1276–1289. [Google Scholar] [CrossRef]
- ICNIRP GUIDELINES for Limiting Exposure to Time-Varying Electric and Magnetic Fields (1 Hz–100 kHz). Health Phys. 2010, 99, 818–836.
- Laakso, I.; Hirata, A. Evaluation of induced electric field and compliance procedure for a wireless power transfer system in an electrical vehicle. Phys. Med. Biol. 2013, 58, 7583–7593. [Google Scholar] [CrossRef] [PubMed]
- Shimamoto, T.; Laakso, I.; Hirarta, A. In-situ electric field in human body model in differnt postures for wireless power transfer system in an electrical vehicle. Phys. Med. Biol. 2014, 60, 163–173. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, T.; Ishida, M. Study on the Influence of the Magnetic Field and the Induced Electric Field in Human Bodies by EV/PHV Wireless Charging System. SAE Tech. Paper 2016. [Google Scholar] [CrossRef]
- Hakuta, Y.; Watanabe, T.; Matsuzawa, S. Evaluation of the Induced Electric Field in Human Body by Exposure to Leaked Magnetic Field from Wireless Power Transfer System for EV and PHV. IEICE Tech. Rep. 2016, 116, 7–12. [Google Scholar]
- Hirata, A.; Yamazaki, K.; Hamada, S.; Kamimura, Y.; Tarao, H.; Wake, K.; Suzuki, Y.; Hayashi, N.; Fujiwara, O. Intercomparison of induced fields in Japanese male model for ELF magnetic field exposures. Radiat. Prot. Dosim. 2010, 138, 237–244. [Google Scholar] [CrossRef]
- Nagaoka, T.; Watanabe, T.; Sakurai, K.; Kunieda, E.; Taki, M.; Yamanaka, Y. Development of realistic high-resolution whole-body voxel models of Japanese adult males and females of average height and weight, and application of models to radio-frequency electromagnetic-field dosimetry. Phys. Med. Biol. 2004, 49, 1–15. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef] [Green Version]
- ANSYS HFSS: High Frequency Electromagnetic Field Simulation. Available online: https://www.ansys.com/products/electronics/ansys-hfss (accessed on 7 June 2019).





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watanabe, T.; Hakuta, Y. Evaluation of the Magnetic Field Leakage from Two Wireless Power Transfer Systems for EV/PHV Driven Simultaneously. World Electr. Veh. J. 2019, 10, 41. https://doi.org/10.3390/wevj10020041
Watanabe T, Hakuta Y. Evaluation of the Magnetic Field Leakage from Two Wireless Power Transfer Systems for EV/PHV Driven Simultaneously. World Electric Vehicle Journal. 2019; 10(2):41. https://doi.org/10.3390/wevj10020041
Chicago/Turabian StyleWatanabe, Toshiaki, and Yusuke Hakuta. 2019. "Evaluation of the Magnetic Field Leakage from Two Wireless Power Transfer Systems for EV/PHV Driven Simultaneously" World Electric Vehicle Journal 10, no. 2: 41. https://doi.org/10.3390/wevj10020041
APA StyleWatanabe, T., & Hakuta, Y. (2019). Evaluation of the Magnetic Field Leakage from Two Wireless Power Transfer Systems for EV/PHV Driven Simultaneously. World Electric Vehicle Journal, 10(2), 41. https://doi.org/10.3390/wevj10020041




