Investigation of Thermal Effects in Different Lightweight Constructions for Vehicular Wireless Power Transfer Modules
Abstract
1. Introduction
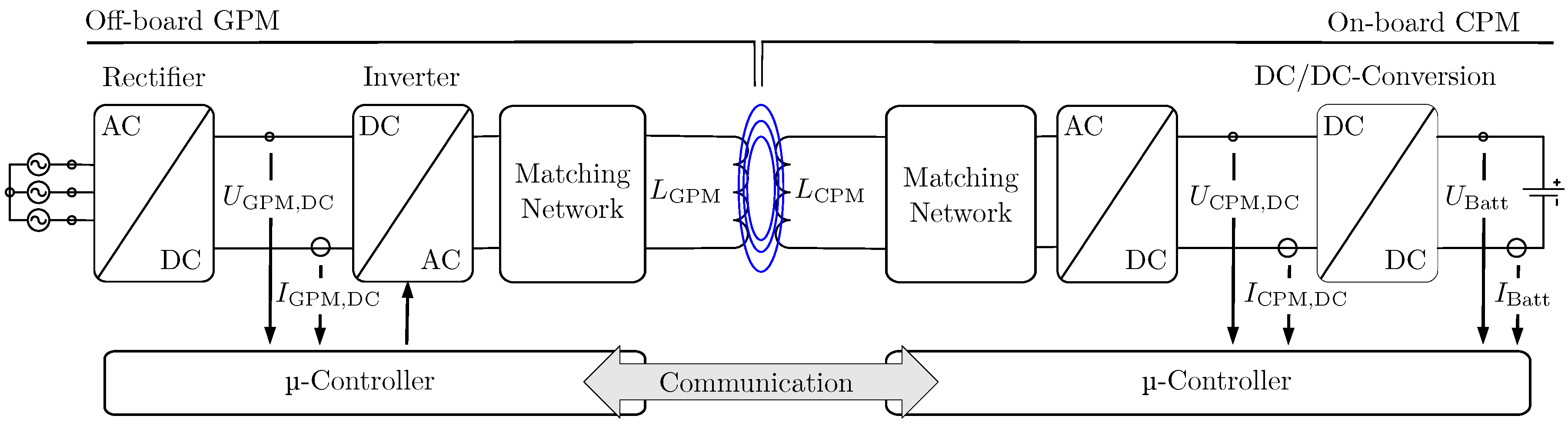
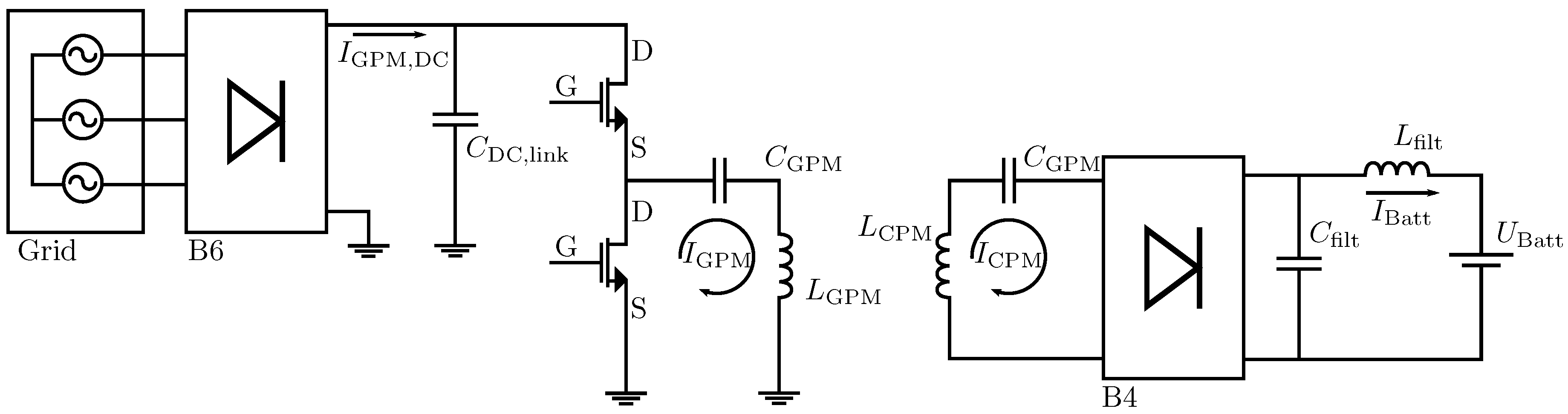
2. Exemplary Wireless Power Transfer System
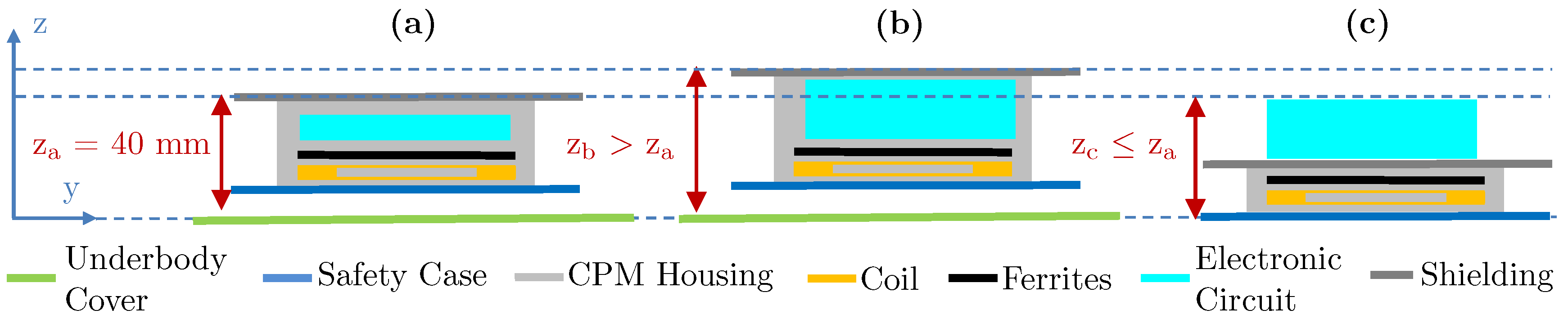
3. Description of Proposed CPM Concepts
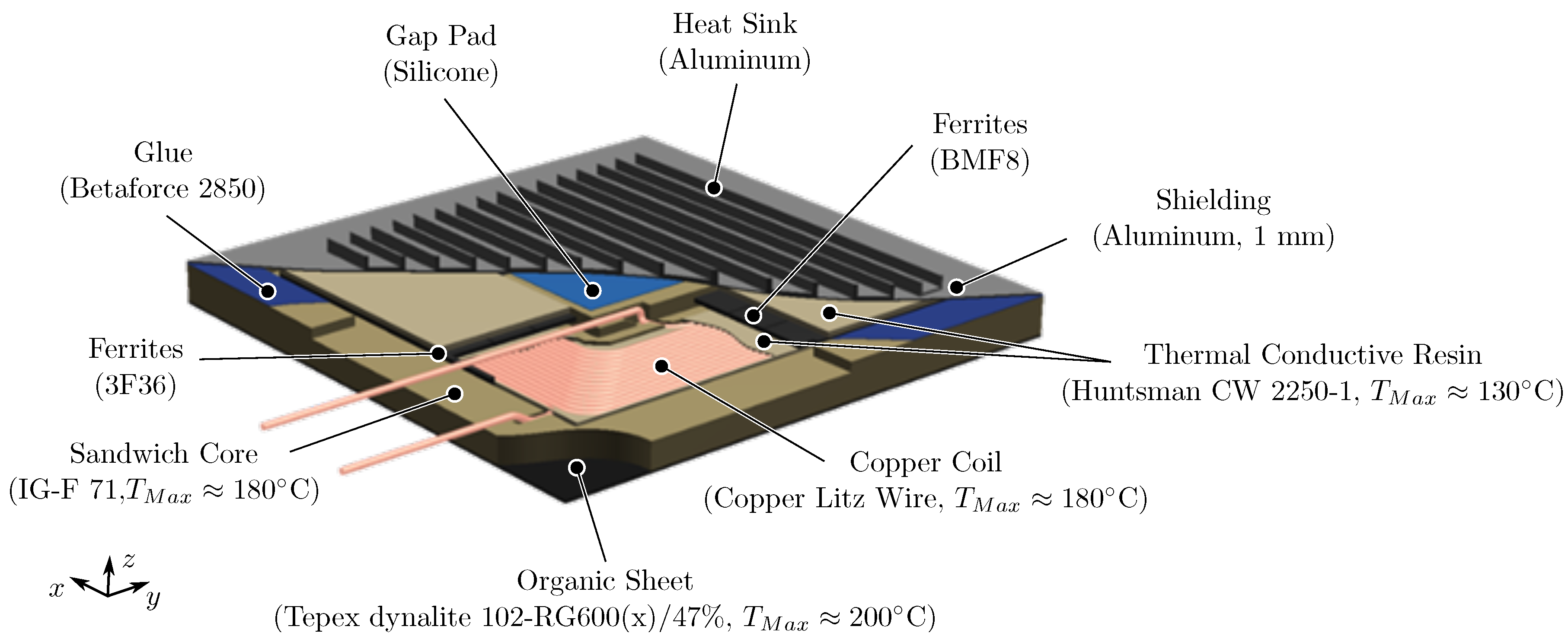
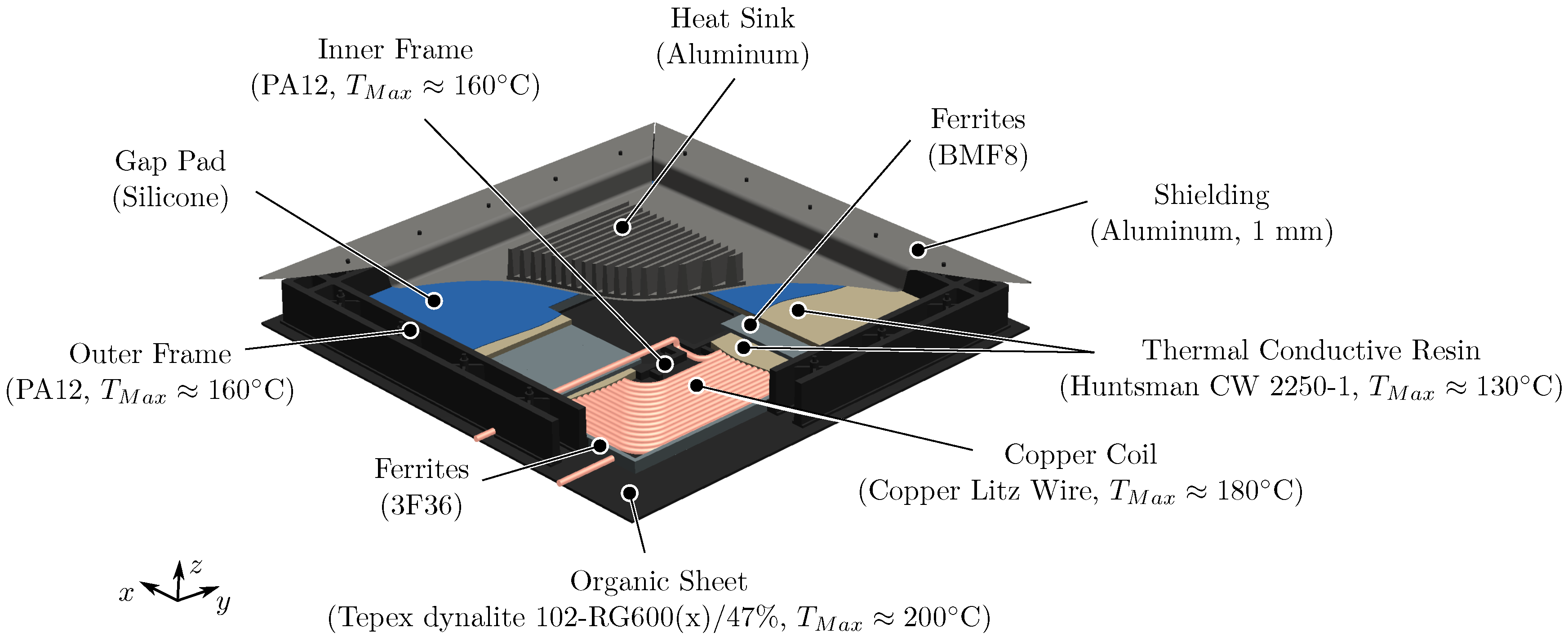
3.1. Sandwich Concept
3.2. Space-Frame Concept
4. Thermal Model
4.1. Calculation of Power Losses
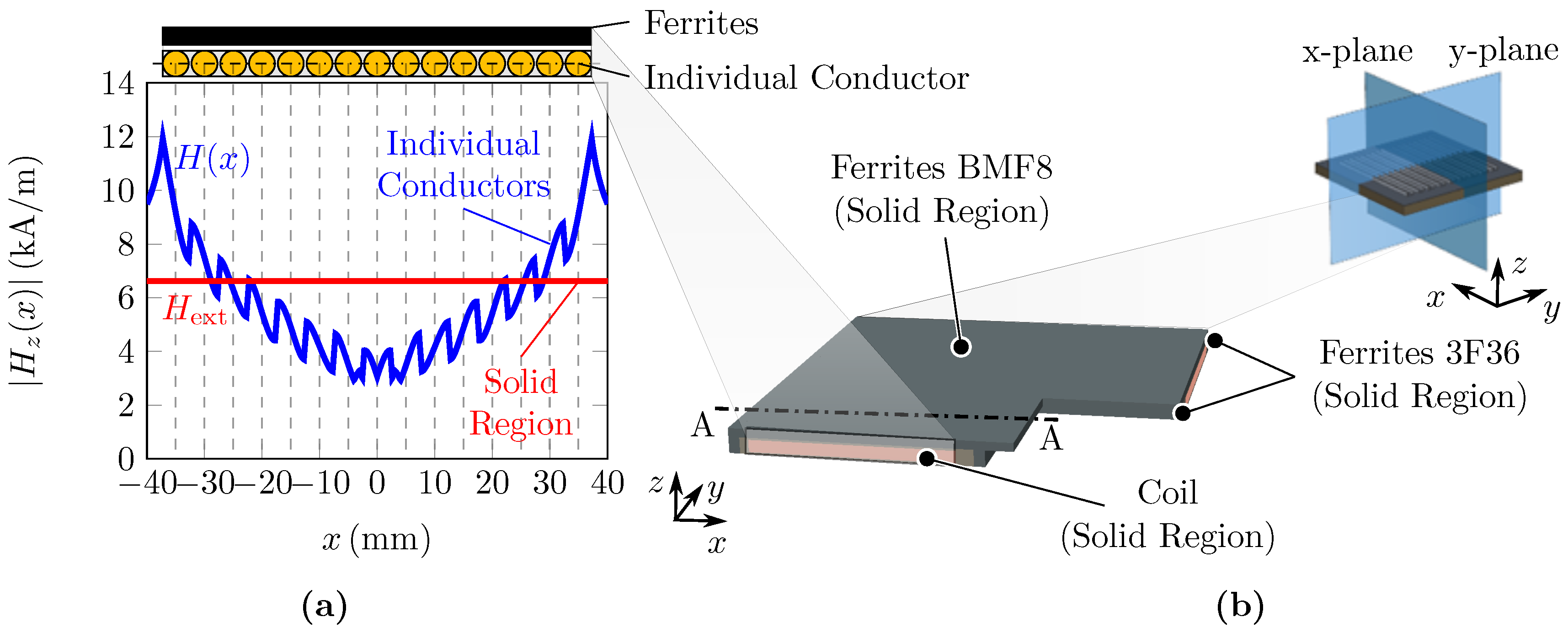
4.1.1. Coil Losses
4.1.2. Core Losses
4.1.3. Eddy Current Losses
4.2. Thermal Simulation Model
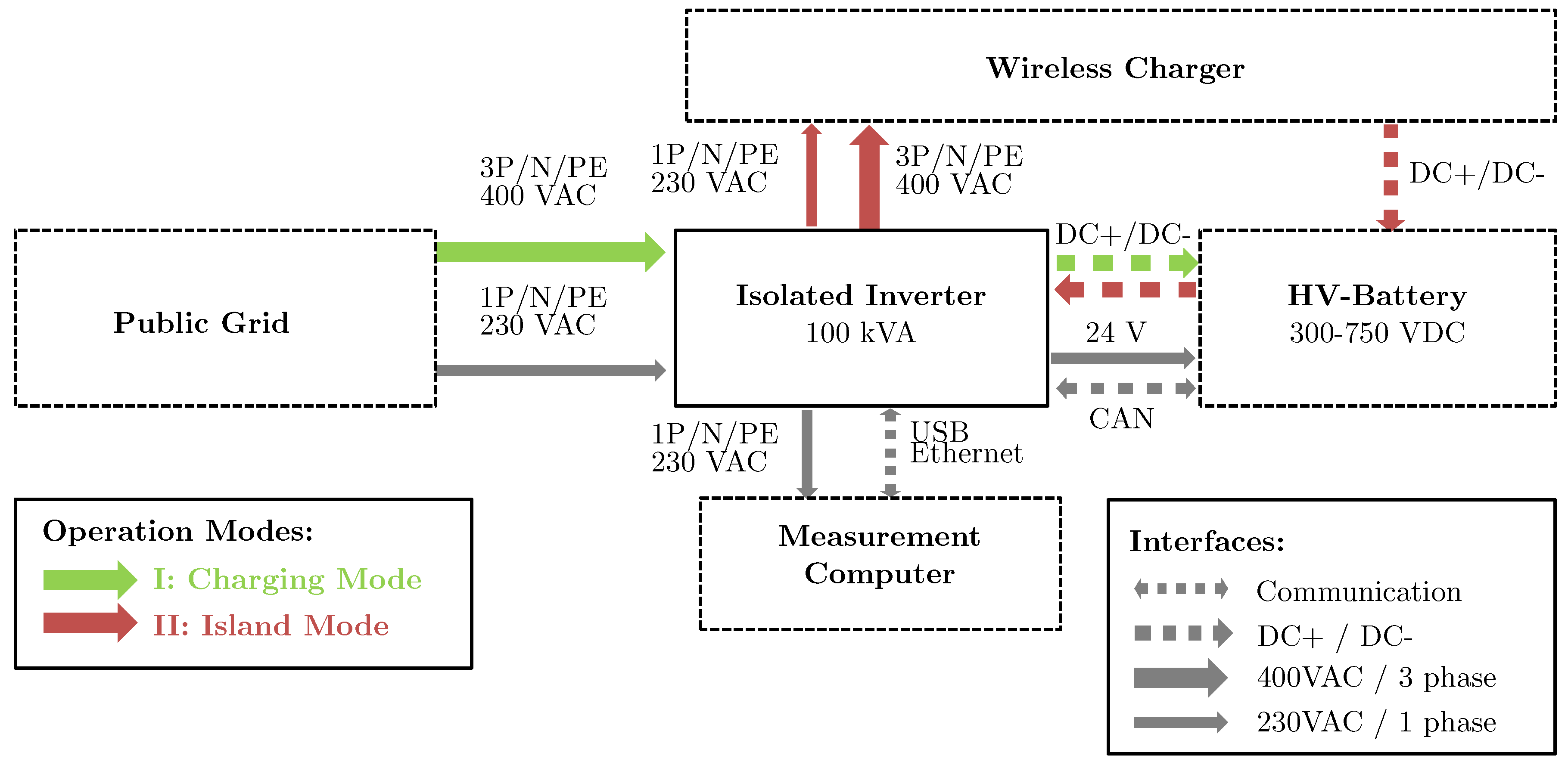
5. Experimental Setups
5.1. Component Level Testing
5.2. System Level Testing
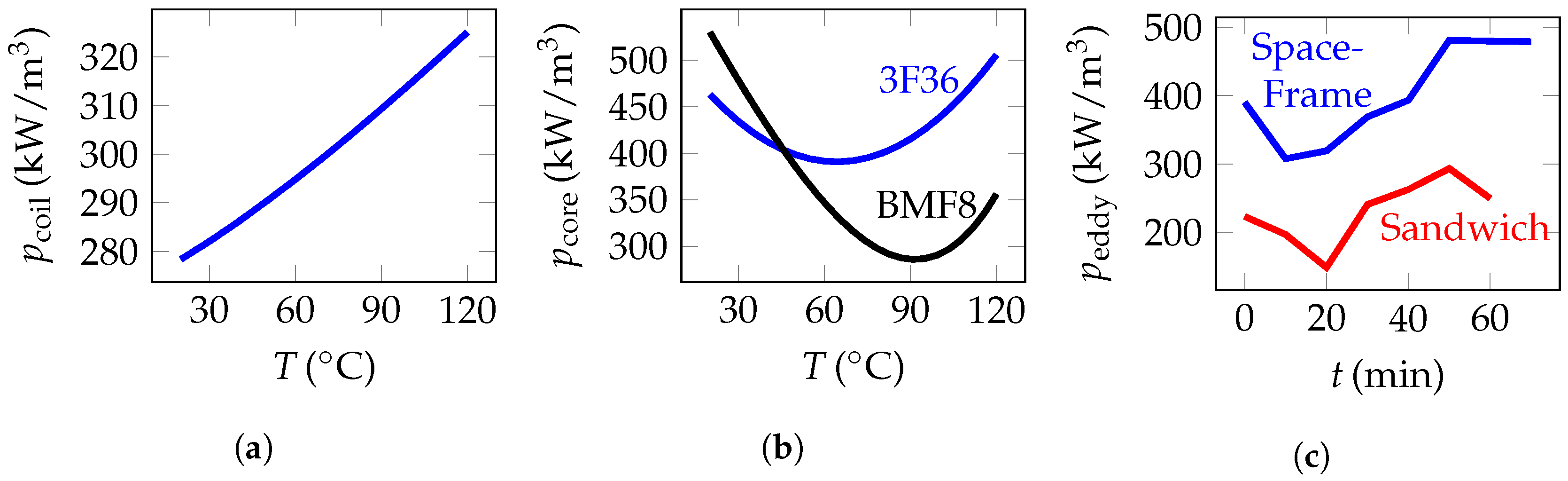
6. Results
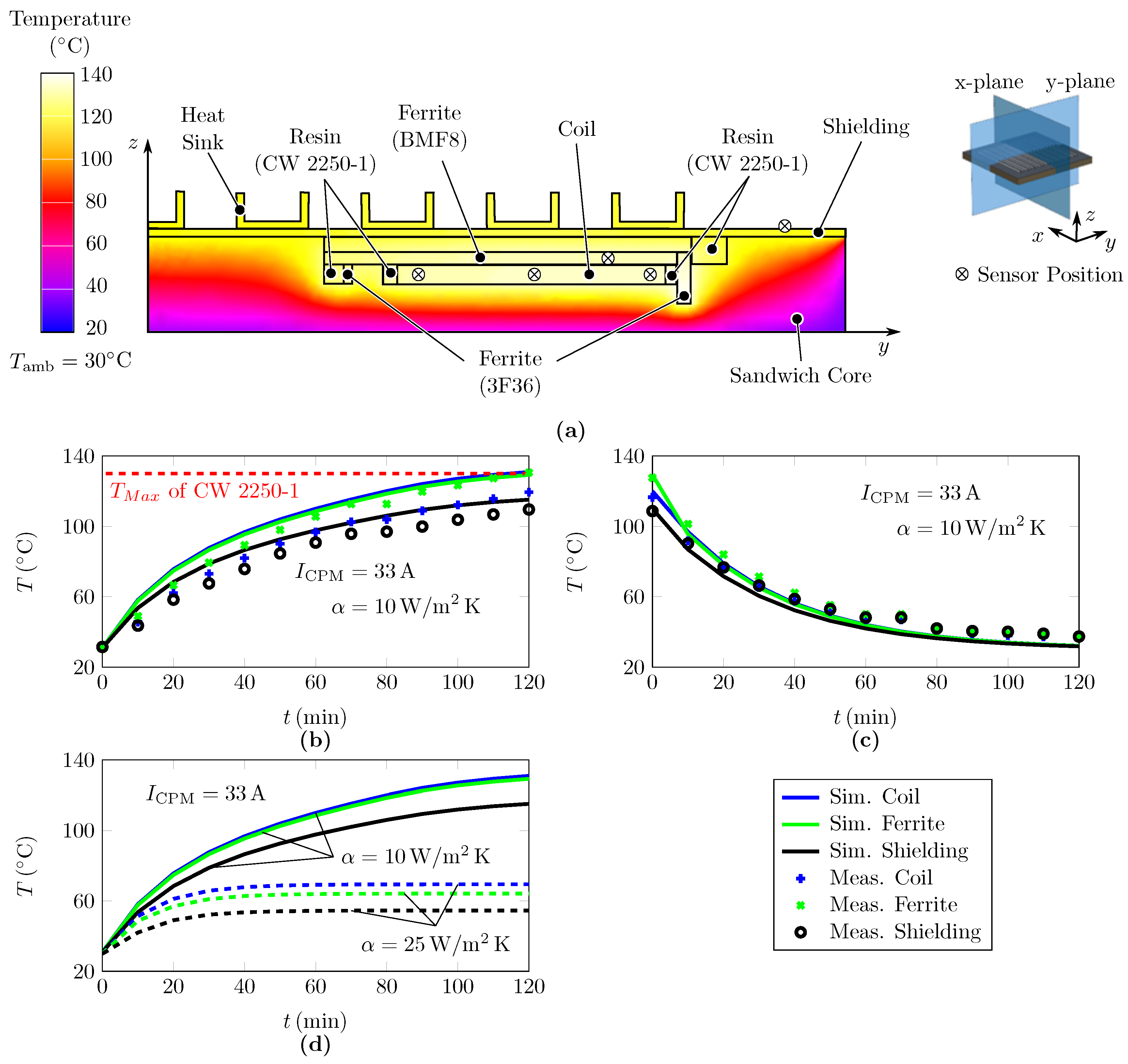
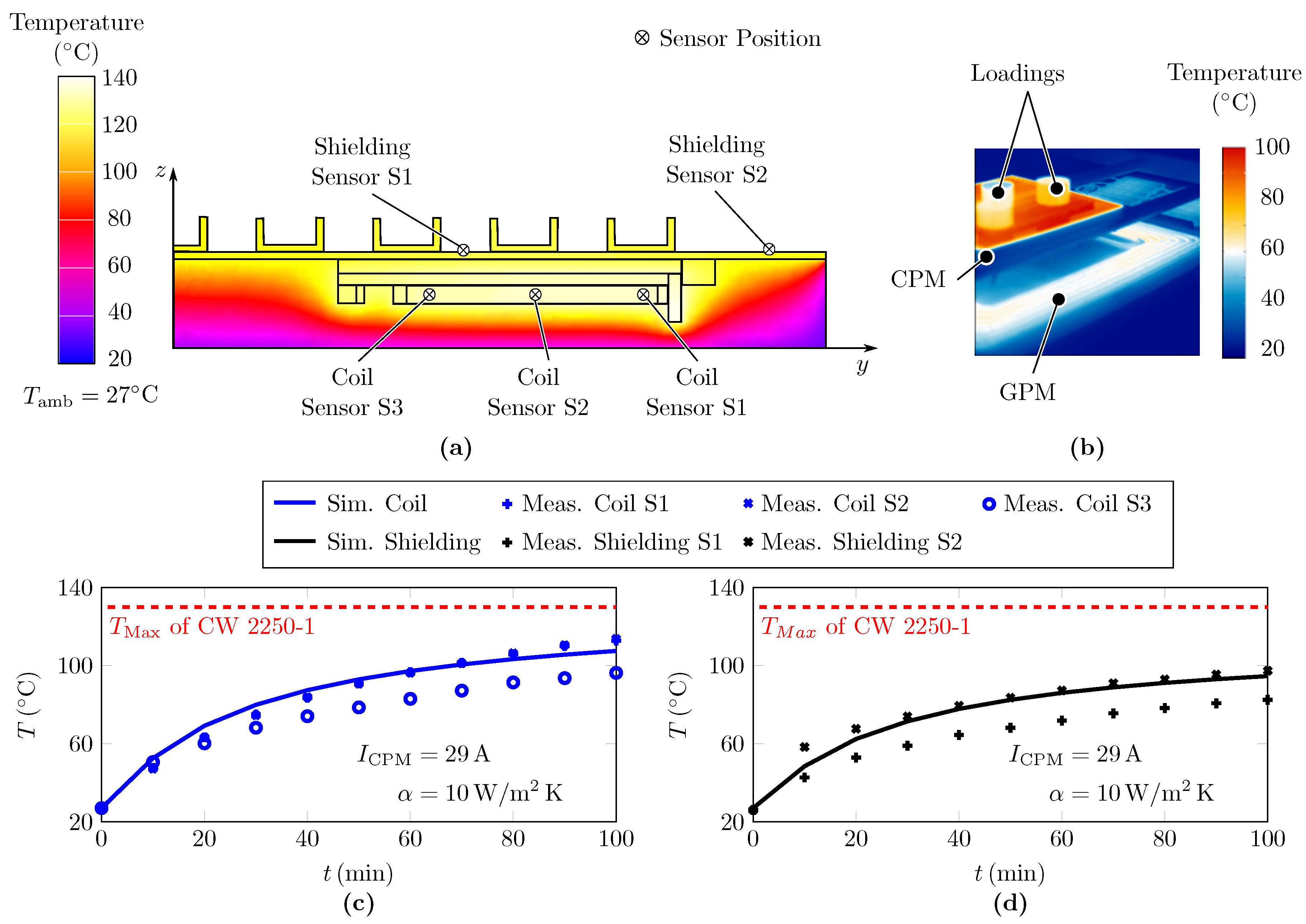
6.1. Sandwich Concept
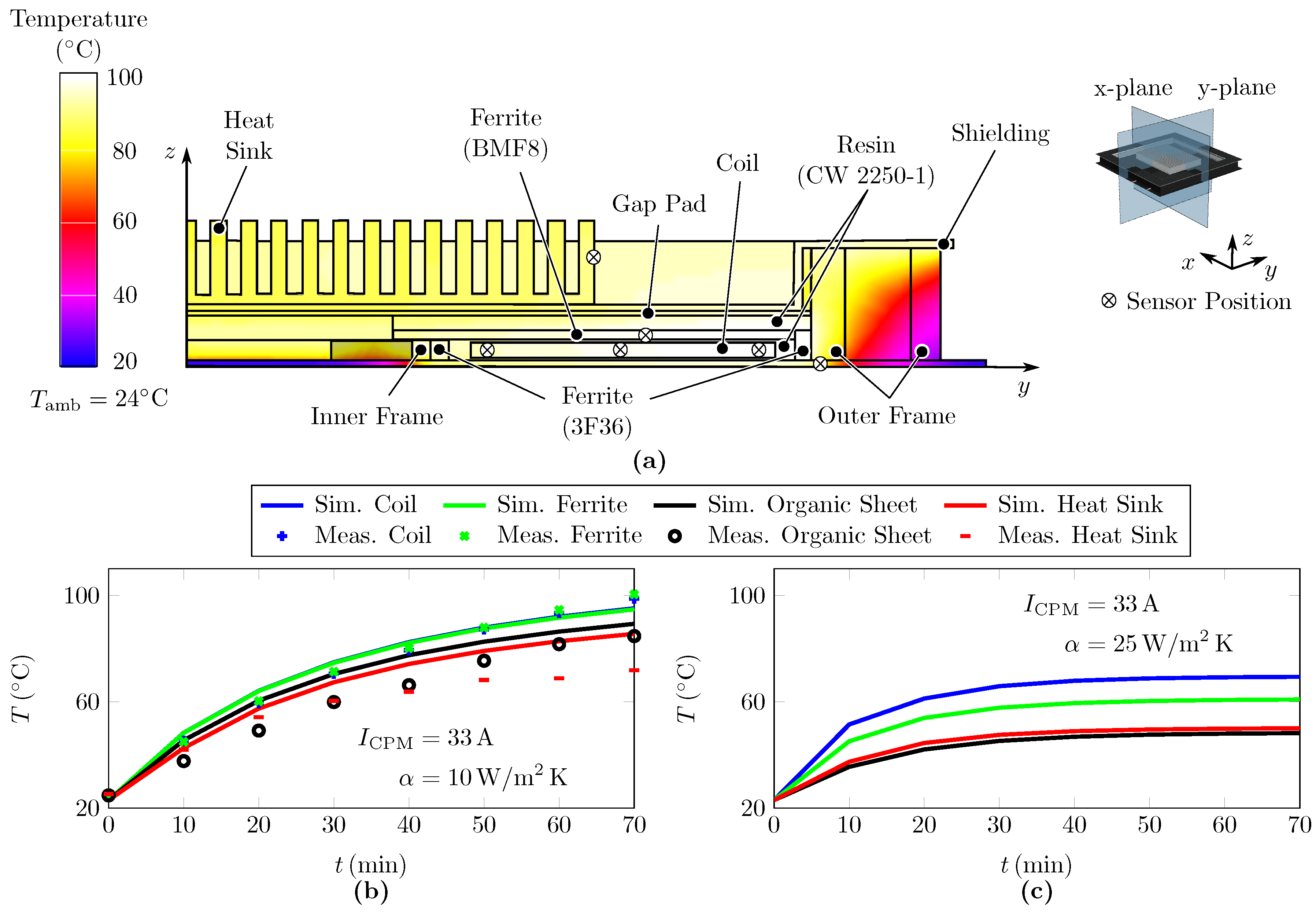
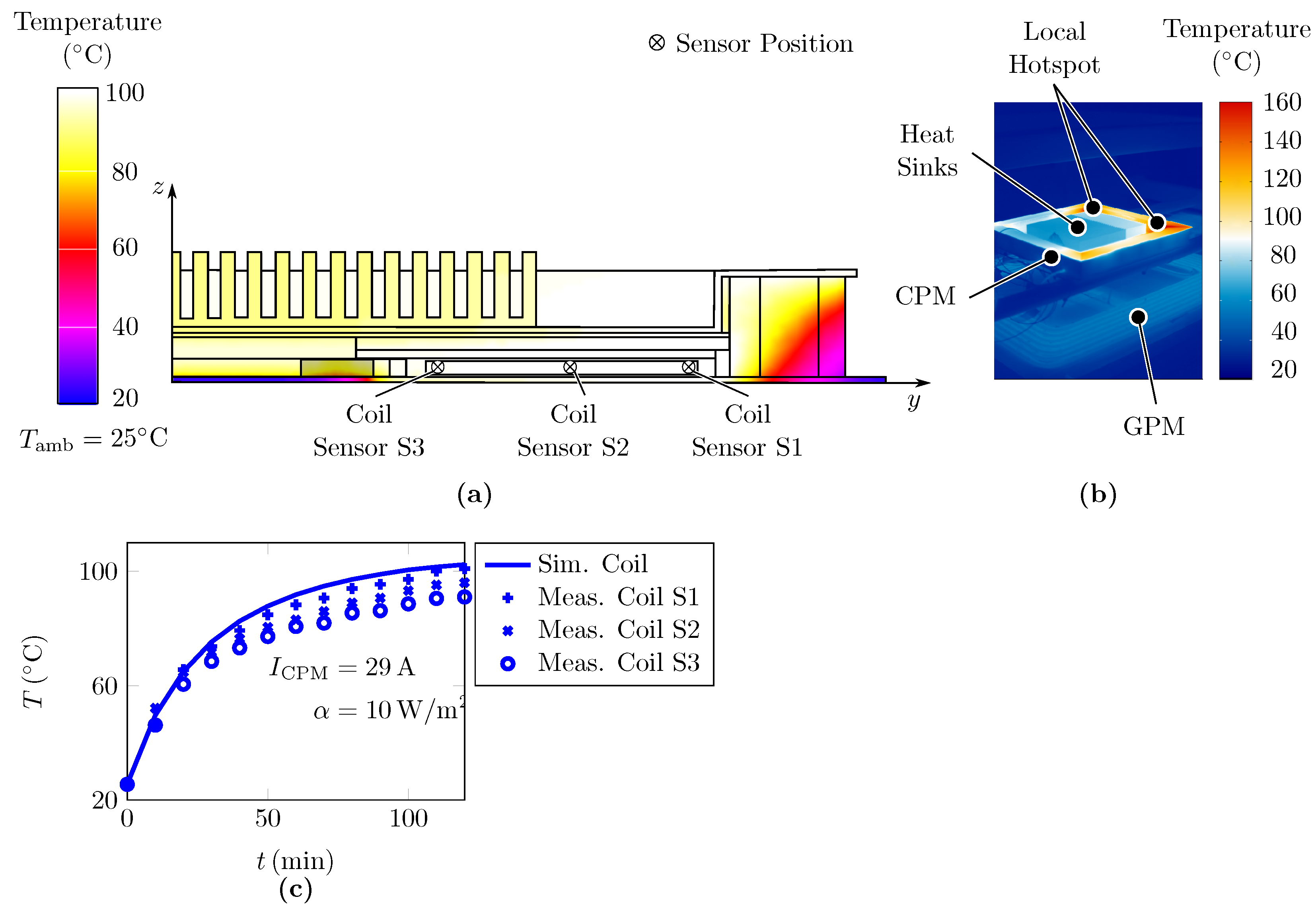
6.2. Space-Frame Concept
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| CPM | Car Pad Module |
| DC | Direct current |
| EVs | Electric vehicles |
| FE | Finite elements |
| FOM | Figure-of-Merit |
| GPM | Ground Pad Module |
| HF | High frequency |
| HiL | Hardware-in-the-Loop |
| MOSFET | Metal–oxide–semiconductor field-effect transistor |
| PFC | Power factor correction |
| RMS | Root Mean Square |
| WPTS | Wireless power transfer systems |
References
- Fett, D.; Ensslen, A.; Jochem, P.; Fichtner, W. A Survey on User Acceptance of Wireless Electric Vehicle Charging. World Electr. Veh. J. 2018, 9, 36. [Google Scholar] [CrossRef]
- Khutwad, S.R.; Gaur, S. Wireless charging system for electric vehicle. In Proceedings of the 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES), Odisha, India, 3–5 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 441–445. [Google Scholar] [CrossRef]
- Vilathgamuwa, D.M.; Sampath, J.P.K. Wireless Power Transfer (WPT) for Electric Vehicles (EVs)—Present and Future Trends. In Plug In Electric Vehicles in Smart Grids; Rajakaruna, S., Shahnia, F., Ghosh, A., Eds.; Power Systems; Springer: Singapore, 2015; pp. 33–60. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, L.; Huang, Z. Studies on the different assembles of magnetic shielding pieces in electromagnetic induction-type wireless charging system. Appl. Phys. A 2019, 125, 1413. [Google Scholar] [CrossRef]
- Society of Automotive Engineers. (R) Wireless Power Transfer for Light-Duty Plug-In/Electric Vehicles and Alignment Methodology; Society of Automotive Engineers: Warrendale, PA, USA, 2017. [Google Scholar]
- Aditya, K.; Peschiera, B.; Youssef, M.; Williamson, S.S. Modelling and calculation of key design parameters for an Inductive Power Transfer system using Finite Element Analysis—A comprehensive discussion. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 14–17 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Barth, D.; Klaus, B.; Leibfried, T. Litz wire design for wireless power transfer in electric vehicles. In Proceedings of the 2017 IEEE Wireless Power Transfer Conference (WPTC), Taipei, Taiwan, 10–12 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, S.; Dorrell, D.G. Copper Loss Analysis of EV Charging Coupler. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.; Kong, S.; Kim, H.; Suh, I.S.; Suh, N.P.; Cho, D.H.; Kim, J.; Ahn, S. Coil Design and Shielding Methods for a Magnetic Resonant Wireless Power Transfer System. Proc. IEEE 2013, 101, 1332–1342. [Google Scholar] [CrossRef]
- Chen, W.; Liu, C.; Lee, C.; Shan, Z. Cost-Effectiveness Comparison of Coupler Designs of Wireless Power Transfer for Electric Vehicle Dynamic Charging. Energies 2016, 9, 906. [Google Scholar] [CrossRef]
- Bosshard, R.; Kolar, J.W.; Wunsch, B. Accurate finite-element modeling and experimental verification of inductive power transfer coil design. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1648–1653. [Google Scholar] [CrossRef]
- Dolara, A.; Leva, S.; Longo, M.; Castelli-Dezza, F.; Mauri, M. Coil design and magnetic shielding of a resonant wireless power transfer system for electric vehicle battery charging. In Proceedings of the 2017 IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 200–205. [Google Scholar] [CrossRef]
- Lin, H.N.; Wu, C.H.; Huang, J.F.; Tseng, W.D.; Lin, J.Y.T.; Lin, M.S. Near-and far-field shielding effectiveness analysis of magnetic materials and their effect on wireless power charger. In Proceedings of the 2018 IEEE International Symposium on Electromagnetic Compatibility and 2018 IEEE Asia-Pacific Symposium on Electromagnetic Compatibility (EMC/APEMC), Singapore, 14–18 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1071–1076. [Google Scholar] [CrossRef]
- Wielandt, S.; De Strycker, L.; Goemaere, J.P.; Stevens, N. Influence of shielding materials on coil characteristics in inductive wireless power systems. In Proceedings of the International Symposium on Electromagnetic Compatibility (EMC Europe), Brugge, Belgium, 2–6 September 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Lu, M.; Ngo, K.D.T. Comparison of passive shields for coils in inductive power transfer. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 6–30 March 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1419–1424. [Google Scholar] [CrossRef]
- Bosshard, R.; Kolar, J.W. Multi-Objective Optimization of 50 kW/85 kHz IPT System for Public Transport. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1370–1382. [Google Scholar] [CrossRef]
- Bosshard, R.; Muhlethaler, J.; Kolar, J.W.; Stevanovic, I. The η-α-Pareto front of inductive power transfer coils. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 4270–4277. [Google Scholar] [CrossRef]
- Lu, M.; Ngo, K.D.T. Pareto fronts for coils’ efficiency versus stray magnetic field in inductive power transfer. In Proceedings of the 2016 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Knoxville, TN, USA, 4–6 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 140–144. [Google Scholar] [CrossRef]
- Bosshard, R. Multi-Objective Optimization of Inductive Power Transfer Systems for EV Charging. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 2015. [Google Scholar]
- Zimmer, S.; Rothenberg, S.; Tattko, B.; Baumer, T.; Baier, k.; Glöggler, C. Vehicle Integration of wireless power transfer systems: An experimental safety investigation of underfloor impact scenarios. In Proceedings of the 31th International Electric Vehicle Symposium & Exhibition (EVS31), Kobe, Japan, 30 November–3 October 2018. [Google Scholar]
- Barth, H.; Jung, M.; Braun, M.; Schmuelling, B.; Reker, U. Concept Evaluation of an Inductive Charging System for Electric Vehicles. In Smart Grids and E-mobility; Stoa, P., Günther, E., Eds.; Ostbayerisches Technologie-Transfer-Institut (OTTI): Regensburg, Germany, 2011. [Google Scholar]
- Onar, O.C.; Campbell, S.L.; Seiber, L.E.; White, C.P.; Chinthavali, M. Vehicular integration of wireless power transfer systems and hardware interoperability case studies. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Ombach, G. Technische Herausforderungen bei der Suche nach einer optimalen Lösung für die drahtlose Energieübertrage für Kraftfahrzeuge. In Proceedings of the Elektronik im Fahrzeug 2013, Baden-Baden, Germany, 16–17 October 2013; VDI Wissensforum GmbH, Ed.; VDI Wissensforum GmbH: Düsseldorf, Germany, 2013. [Google Scholar]
- Nestler, M.; Hensel, S.; Müller, R.; Drossel, W.G. Process design for the shaping of sandwich sheets with sensor and actuator functionality. Procedia Eng. 2017, 207, 872–877. [Google Scholar] [CrossRef]
- Pascual, C.; de Castro, J.; Schueler, A.; Vassilopoulos, A.P.; Keller, T. Total light transmittance of glass fiber-reinforced polymer laminates for multifunctional load-bearing structures. J. Compos. Mater. 2013, 48, 3591–3604. [Google Scholar] [CrossRef]
- Winter, J. Fahrdrahtlose Energieübertragung bei Schienenfahrzeugen des Vollbahnverkehrs; Deutsches Zentrum für Luft- und Raumfahrt e.V.: Stuttgart, Germany, 2014. [Google Scholar]
- Moghaddami, M.; Sarwat, A. Time-Dependent Multi-Physics Analysis of Inductive Power Transfer Systems. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 130–134. [Google Scholar] [CrossRef]
- Blinzinger Elektronik GmbH. Data Sheet: Ferrite Core BMF8; Blinzinger Elektronik GmbH: Forchtenberg, Germany, 2020. [Google Scholar]
- Digi-Key Electronics Germany Gmbh. Data Sheet: PLT32/20/3.2/R-3F36; Digi-Key Electronics Germany Gmbh: Munich, Germany, 2020. [Google Scholar]
- Evonik Resource Efficiency GmbH. Product Information: ROHACELL’IG-F; Evonik Resource Efficiency GmbH: Marl, Germany, 2020. [Google Scholar]
- Huntsman International LLC. Advanced Materials: Araldite’CW 2250-1; Huntsman International LLC: Salt Lake City, UT, USA, 2020. [Google Scholar]
- LANXESS Deutschland GmbH. Material Data Sheet: Tepex dynalite 102-RG600(x)/47%: Roving Glass—PA6 Consolidated Composite Laminate; Lanxess: Cologne, Germany, 2020. [Google Scholar]
- Huntsman International LLC. Betaforce; Huntsman International LLC: Salt Lake City, UT, USA, 2020. [Google Scholar]
- ARCTIC GmbH. Thermal Pad: High Performance Gap Filler; ARCTIC GmbH: Freienbach, Switzerland, 2020. [Google Scholar]
- ACC Silicones Ltd. SILCOTHERM’: Werkstoffe zur Wärmeleitung; ACC Silicones Ltd.: Bridgwater, UK, 2020. [Google Scholar]
- Conrad Electronic SE. Fischer Elektronik SK 42 150 SA Strangkühlkörper 0.75 K/W (L × B × H) 200 × 150 × 25 mm; Conrad Electronic SE: Hirschau, Germany, 2020. [Google Scholar]
- Klaus, B. Aspekte zur Praxisnahen Auslegung Induktiver Energieübertragungssysteme für Elektrofahrzeuge. Ph.D. Thesis, Karlsruher Institut für Technologie (KIT), Karlsruhe, Germany, 2018. [Google Scholar]
- Biela, J. Wirbelstromverluste in Wicklungen Induktiver Bauelemente; Skriptum, ETH Zürich: Zürich, Germany, 2012. [Google Scholar]
- Mühletaler, J. Modeling and Multi-Objective Optimization of Inductive Power Components. Ph.D. Thesis, ETH Zürich, Zürich, Germany, 2012. [Google Scholar]
- Weißgerber, W. Elektrotechnik für Ingenieure–Formelsammlung: Elektrotechnik Kompakt, 5th ed.; Durchgesehene Aufl. 2015; Lehrbuch; Springer Vieweg: Wiesbaden, Germany, 2015. [Google Scholar]
- Ashby, M.F. Materials Selection in Mechanical Design, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Groth, C.; Müller, G. FEM für Praktiker, 5th ed.; Edition Expertsoft; Expert-Verl.: Renningen, Germany, 2009; Volume 45. [Google Scholar]
- VDI-Wärmeatlas: Mit 320 Tabellen; VDI-Buch, Springer Vieweg: Berlin, Germany, 2013.
- Alsayegh, M.; Saifo, M.; Clemens, M.; Schmuelling, B. Magnetic and Thermal Coupled Field Analysis of Wireless Charging Systems for Electric Vehicles. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Deutsches Kupferinstitut: Düsseldorf, Germany, 2020. Cu-ETP. Available online: http://te-x-te.de/images/DA_DKI.pdf (accessed on 23 September 2020).
- Ferroxcube. Soft Ferrites: Ferrite Material Survey; Ferroxcube: Hong Kong, China, 2020. [Google Scholar]
- Kern GmbH. Polyamid 6 (PA 6); Kern GmbH: Großmaischeid, Germany, 2020. [Google Scholar]
- Schwarzwälder Metallhandel GmbH. Werkstoffdatenblatt: EN AW 5754 [EN AW-Al Mg3]; Schwarzwälder Metallhandel GmbH: Trossingen, Germany, 2020. [Google Scholar]
- Cosinus Messtechnik GmbH. Data Sheet: CWT Mini; Cosinus Messtechnik GmbH: Taufkirchen, Germany, 2020. [Google Scholar]
- Weidmann Technologies Deutschland GmbH. TS2: Fiber Optic Temperature Sensor; Weidmann Technologies Deutschland GmbH: Dresden, Germany, 2020. [Google Scholar]
- InfraTec GmbH. VarioCAM’HD Head: Infrarot-Thermografiesystem für den Industrie—und Laboreinsatz; InfraTec GmbH: Dresden, Germany, 2020. [Google Scholar]



| Parameter | Variable | Value | Unit |
|---|---|---|---|
| Output Power | 11 | kW | |
| GPM DC-Link Voltage | 0–540 | V | |
| CPM DC-Link Voltage | 300–470 | V | |
| Battery Voltage | 300–470 | V | |
| Air Gap | z | 100–210 | mm |
| Misalignment longitudinal | ±75 | mm | |
| Misalignment transversal | ±150 | mm | |
| Transmission Frequency | 81.38–90 | kHz | |
| Area of CPM coil | 300 × 300 | mm2 |
| Parameter | Variable | Value | Unit |
|---|---|---|---|
| Coil length | 600 | mm | |
| 300 | mm | ||
| Coil width | 750 | mm | |
| 300 | µm | ||
| Number of windings | 7 | ||
| 15 | |||
| Self-Inductance | 77 | µH | |
| 112 | µH | ||
| Mutual Inductance | M | 7.4–18.6 | µH |
| Magnetic Coupling | k | 0.08–0.2 | |
| AC-Resistance | <40 | m | |
| 100 | m | ||
| RMS-Current | 35–100 | A RMS | |
| 23–36 | A RMS |
| Name | Parameter | Value | Unit |
|---|---|---|---|
| Transmission frequency | f | 85 | kHz |
| Peak coil current | 33 | A | |
| Magnitude of external magnetic field | 6.62 | kA | |
| Number of strands in the litz wire | N | 15 | |
| Total length of litz wire | 12.7 | m | |
| Outer diameter of the litz wire | 4.5 | mm | |
| Specific resistance of litz wire material at 20 °C [40] | 0.018 | mm | |
| Specific temperature coefficent of litz wire material at 20 °C [40] | 0.004 |
| Density | Heat Capacity | Thermal Expansion Coeffient | Thermal Conductivity | |
|---|---|---|---|---|
| Copper [45] | 8.92 | 385 | 17 | 381 |
| BMF8 [46] | 4.8 | 750 | 1 | 4.2 |
| 3F36 [46] | 4.8 | 750 | 1 | 4.2 |
| IG-F 71 [30] | 0.075 | 200 | 38 | 0.03 |
| CW 2250-1 [31] | 1.58 | 1800 | 65 | 0.76 |
| PA [47] | 1.14 | 1700 | 80 | 0.23 |
| Organic sheet | 1.35 | 1280 | 16 | 0.28 |
| Silicone [35] | 3.2 | 710 | 200 | 6 |
| Aluminium [48] | 2.66 | 900 | 25 | 117 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zimmer, S.; Helwig, M.; Lucas, P.; Winkler, A.; Modler, N. Investigation of Thermal Effects in Different Lightweight Constructions for Vehicular Wireless Power Transfer Modules. World Electr. Veh. J. 2020, 11, 67. https://doi.org/10.3390/wevj11040067
Zimmer S, Helwig M, Lucas P, Winkler A, Modler N. Investigation of Thermal Effects in Different Lightweight Constructions for Vehicular Wireless Power Transfer Modules. World Electric Vehicle Journal. 2020; 11(4):67. https://doi.org/10.3390/wevj11040067
Chicago/Turabian StyleZimmer, Steve, Martin Helwig, Peter Lucas, Anja Winkler, and Niels Modler. 2020. "Investigation of Thermal Effects in Different Lightweight Constructions for Vehicular Wireless Power Transfer Modules" World Electric Vehicle Journal 11, no. 4: 67. https://doi.org/10.3390/wevj11040067
APA StyleZimmer, S., Helwig, M., Lucas, P., Winkler, A., & Modler, N. (2020). Investigation of Thermal Effects in Different Lightweight Constructions for Vehicular Wireless Power Transfer Modules. World Electric Vehicle Journal, 11(4), 67. https://doi.org/10.3390/wevj11040067





