Design and Performance Analysis of Misalignment Tolerant Charging Coils for Wireless Electric Vehicle Charging Systems
Abstract
:1. Introduction
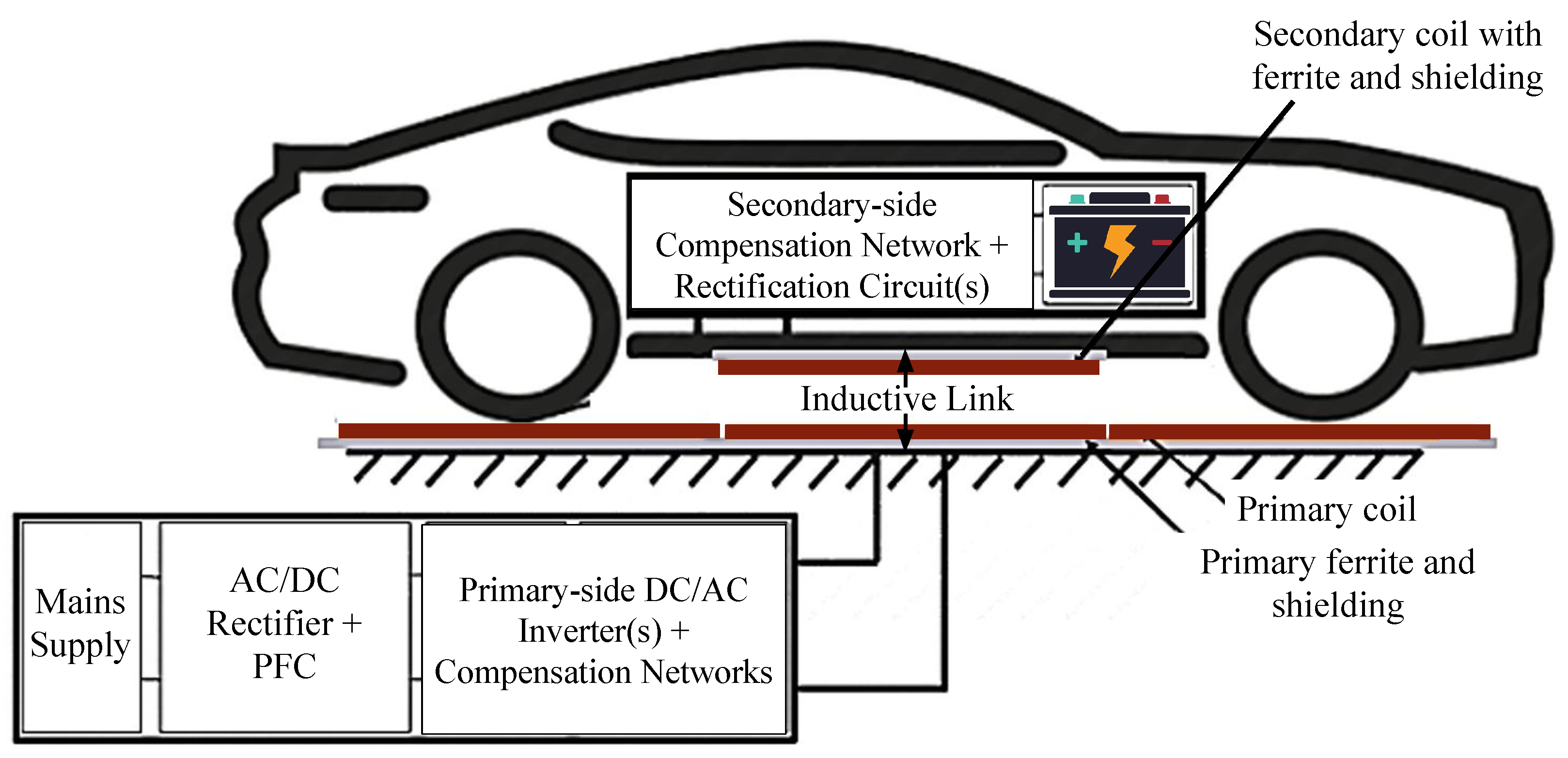
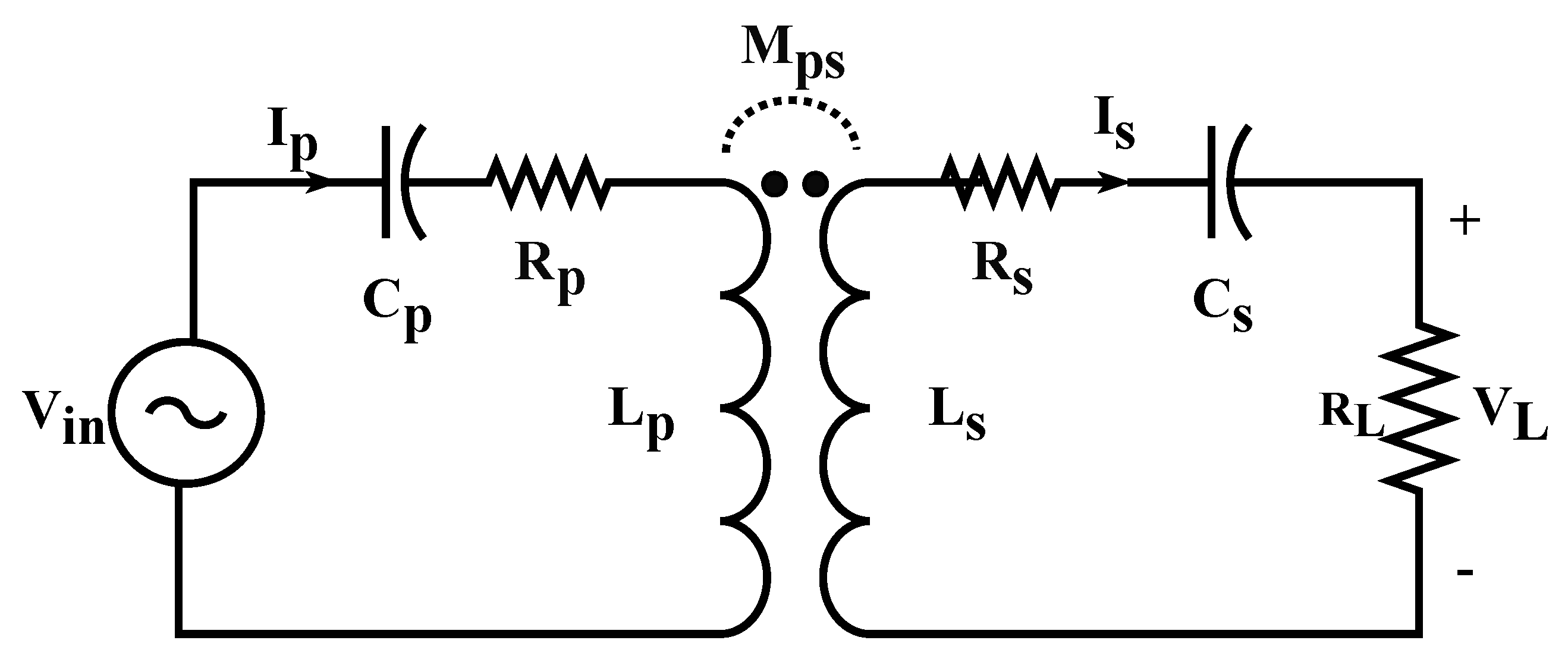
2. Inductive Link Modeling
3. Charging Coil Geometries
- Non-polarized geometries, such as circular and rectangular coils, in which the perpendicular component of the magnetic flux is responsible for the wireless power transfer process.
- Polarized geometries, such as DD, DDQ and bipolar coils, in which the parallel component of the magnetic flux dominates and becomes responsible for the wireless power transfer process.
- In non-polarized coil geometries, perpendicular magnetic field lines provide satisfactory coupling at perfect alignment conditions, and the coupling strength is impacted by the vertical air gap between the primary and secondary coils.
- For effective coupling between circular charging coils, the vertical separation between the coils should be proportional to a quarter of the coil diameter [34]. Hence, significantly large circular coil diameters are required to improve the coupling performance in WEVC systems due to the large EV-to-ground clearance distance, i.e., the large air gap between the primary and secondary charging pads.
- Parallel field patterns, on the other hand, are not as significantly affected by increasing the air gap, thereby they are expected to provide better coupling performance for large air gap applications such as WEVC systems, in comparison with non-polarized charging pads of equal dimensions.
- For similar-sized charging pads, the flux path height of DD coils is double that of circular coils, which significantly reduces the flux leakage and enhances the coupling factor.
- For symmetric DD-DD inductive link structures, as the secondary coil is displaced from the perfect alignment position, the flux linkage of the parallel fields experiences a significant degradation [35]. This motivates the addition of a quadrature coil, forming a DDQ charging pad, that utilizes parallel fields in perfect alignment conditions and benefits from the perpendicular field lines coupling with the quadrature coil during misalignments [26].
- The key drawback of using DDQ coils is the added system weight, cost and complexity, due to the need to connect the DD and the quadrature portions of the charging pad to separate power management circuitry. This, on the receiver’s side, means that two separate compensation and rectification circuits are required to capture the maximum amount of transferred power during perfect alignment as well as when misalignments occur.
- Bipolar charging pads leverage on the advantages of DDQ coils with 25–30% less copper in comparison with DDQ charging pads [36]. However, separate compensation, rectification and control circuits are also required for each coil constituting the bipolar charging pad.
4. Design Strategy
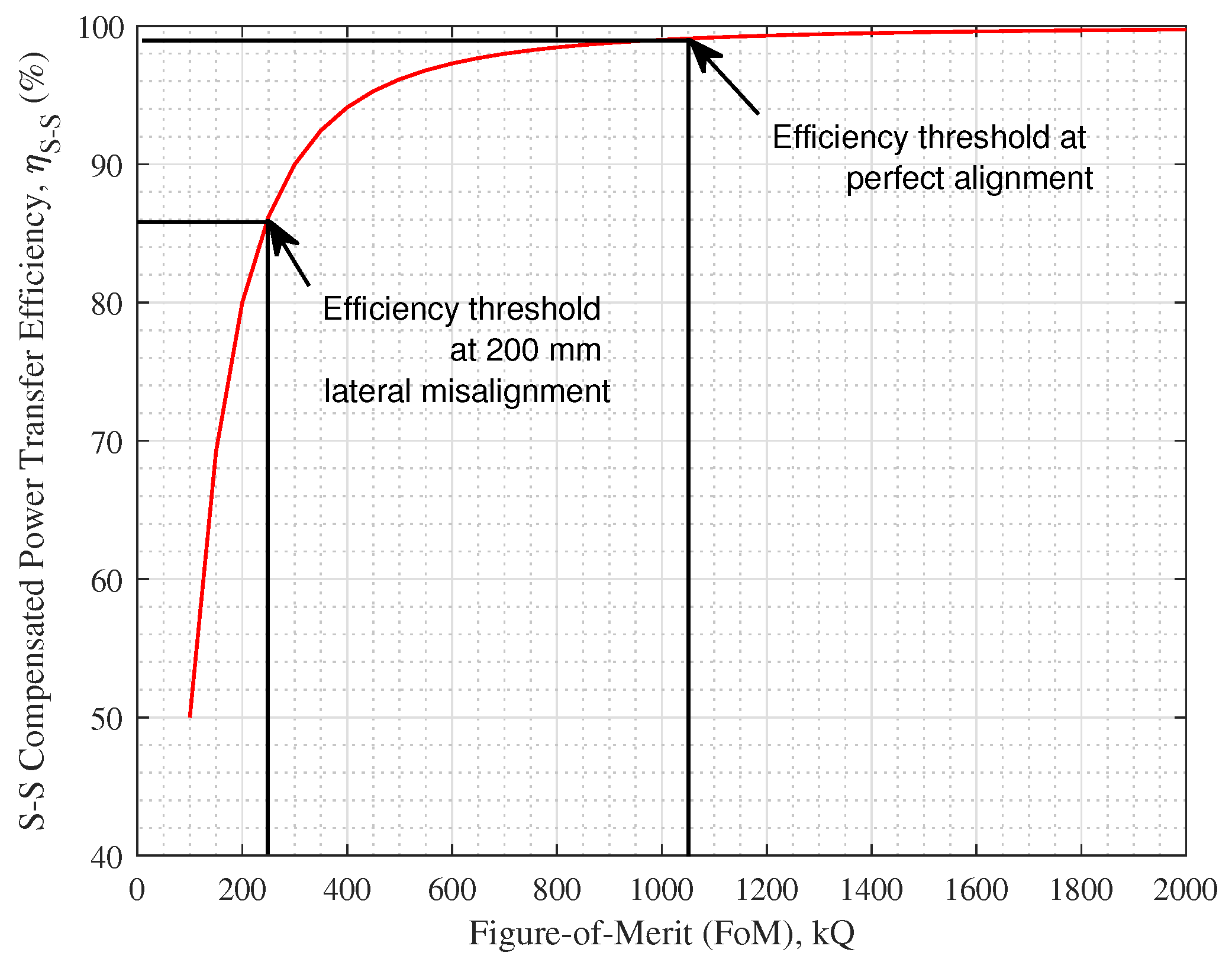
4.1. Definition of Efficiency Thresholds
4.2. Definition of Constant Coil Parameters
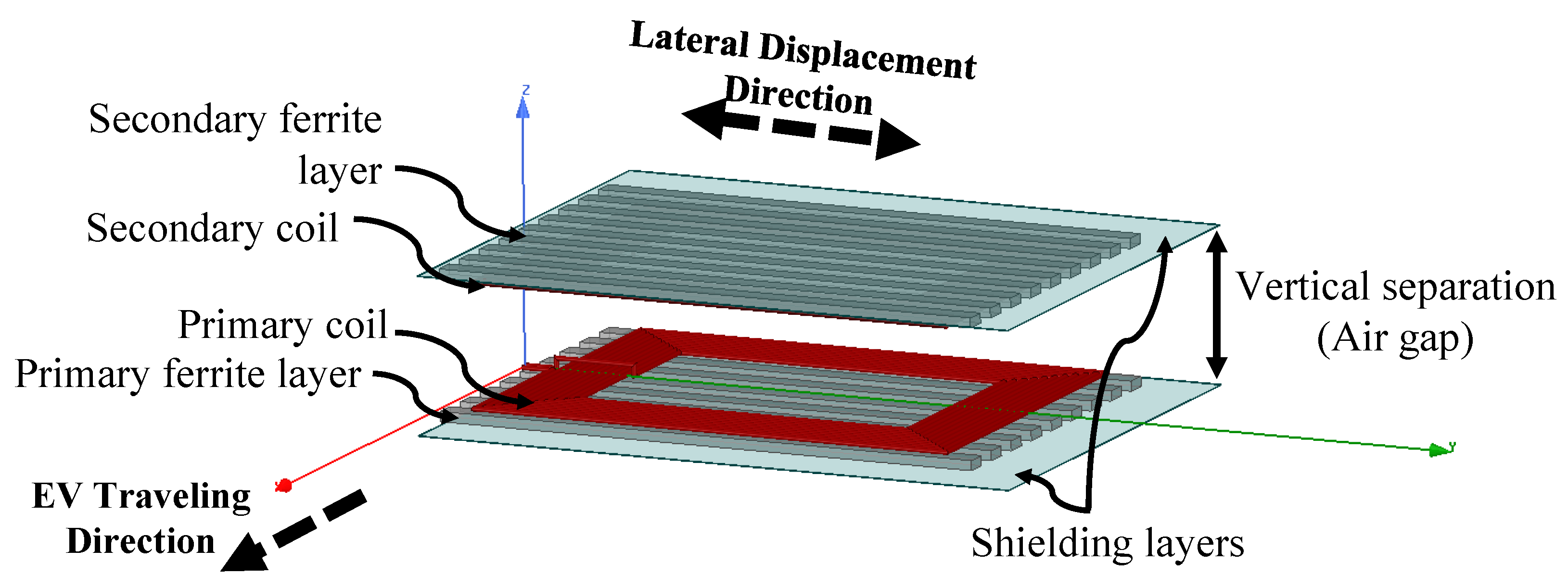
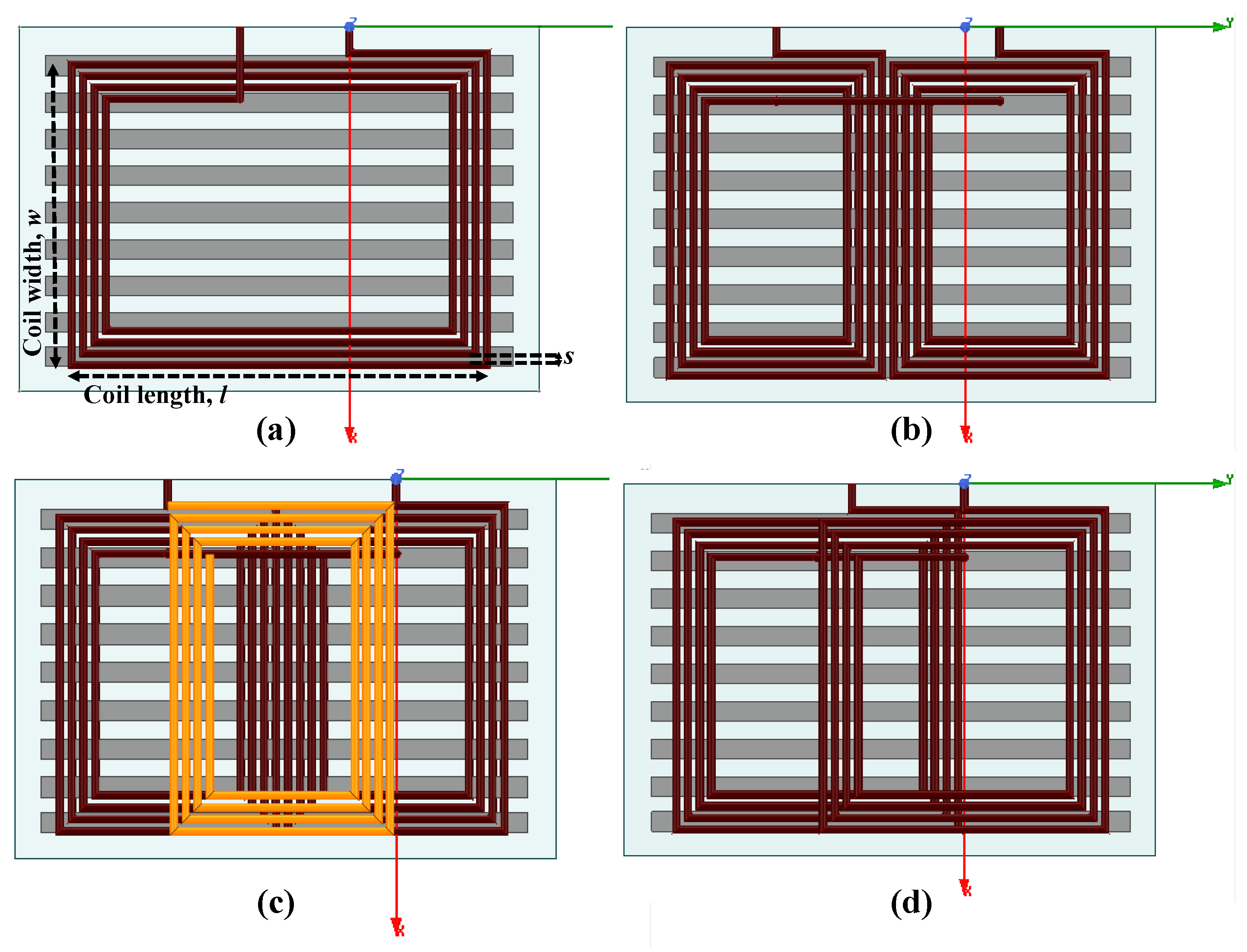
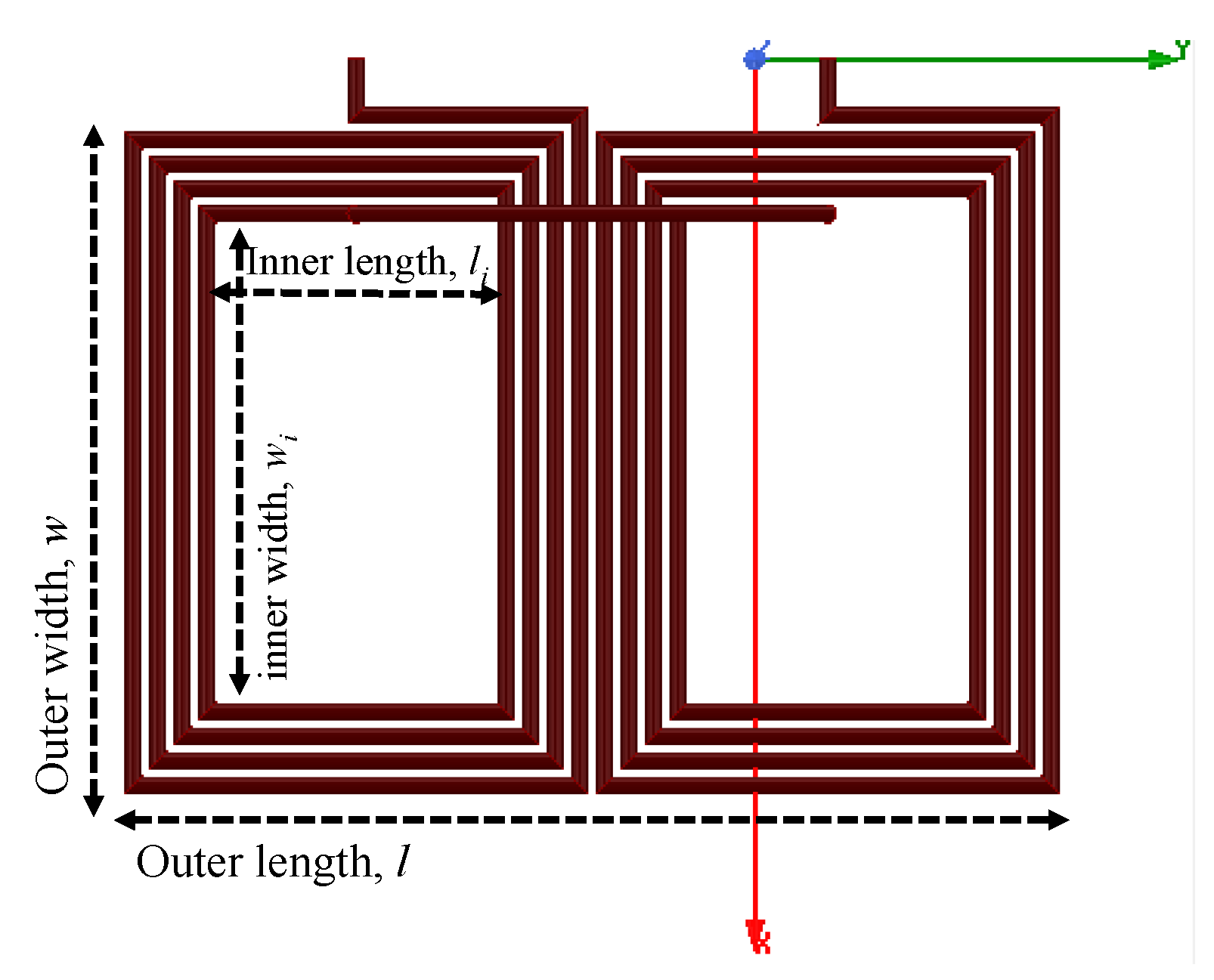
- Outer coil surface area, : Acknowledging the space restrictions in the placement of the charging coils at the bottom of EVs, the outer coil area is determined given a set of considerations and is eliminated from the conducted parametric optimization process. According to [37], a reasonable secondary coil occupancy is around 480,000 mm for a typical sedan EV, while the outer charging pad dimensions need to be larger to ensure effective shielding. In addition, according to [38], the optimal value of the width of a rectangular coil is three times the vertical separation between the primary and the secondary coils. The average vehicle-to-ground clearance of a typical EV is estimated to be ∼200 mm, based on which the outer coil width is selected to be 600 mm. Accordingly, for a total coil area of 480,000 mm, the coil dimensions are selected to be mm.
- Wire diameter, d: Stranded copper wires are utilized for all the simulations conducted in this work to reduce eddy current losses, effectively replicating the performance of Litz wires. According to [39], the current carrying capacity of a Litz wire is 4 A/mm. Assuming the current through the coils is around 50 A for a 25 kW/500 V wireless EV charging system, the wire diameter is selected to 4 mm with a cross-sectional area of ∼12.5 mm.
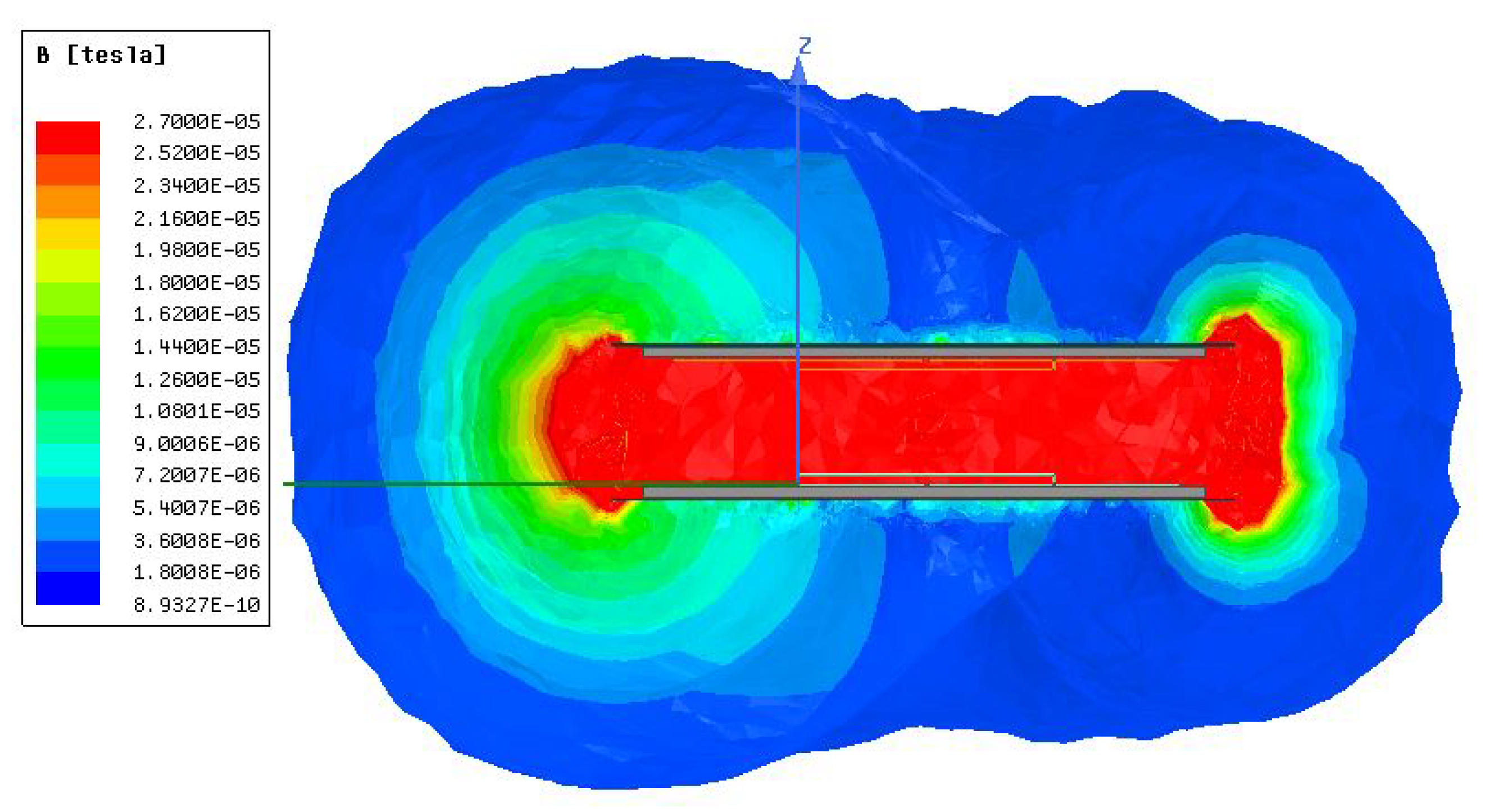
- Ferrite and shielding layers: Since this work focuses on analyzing the performance of different coil geometries, identical ferrite and shielding layers are used for all the FEM simulations, as shown in Figure 4. The specifications of these layers are detailed in the authors’ earlier works in [11,23,40] and are summarized in Table 1.
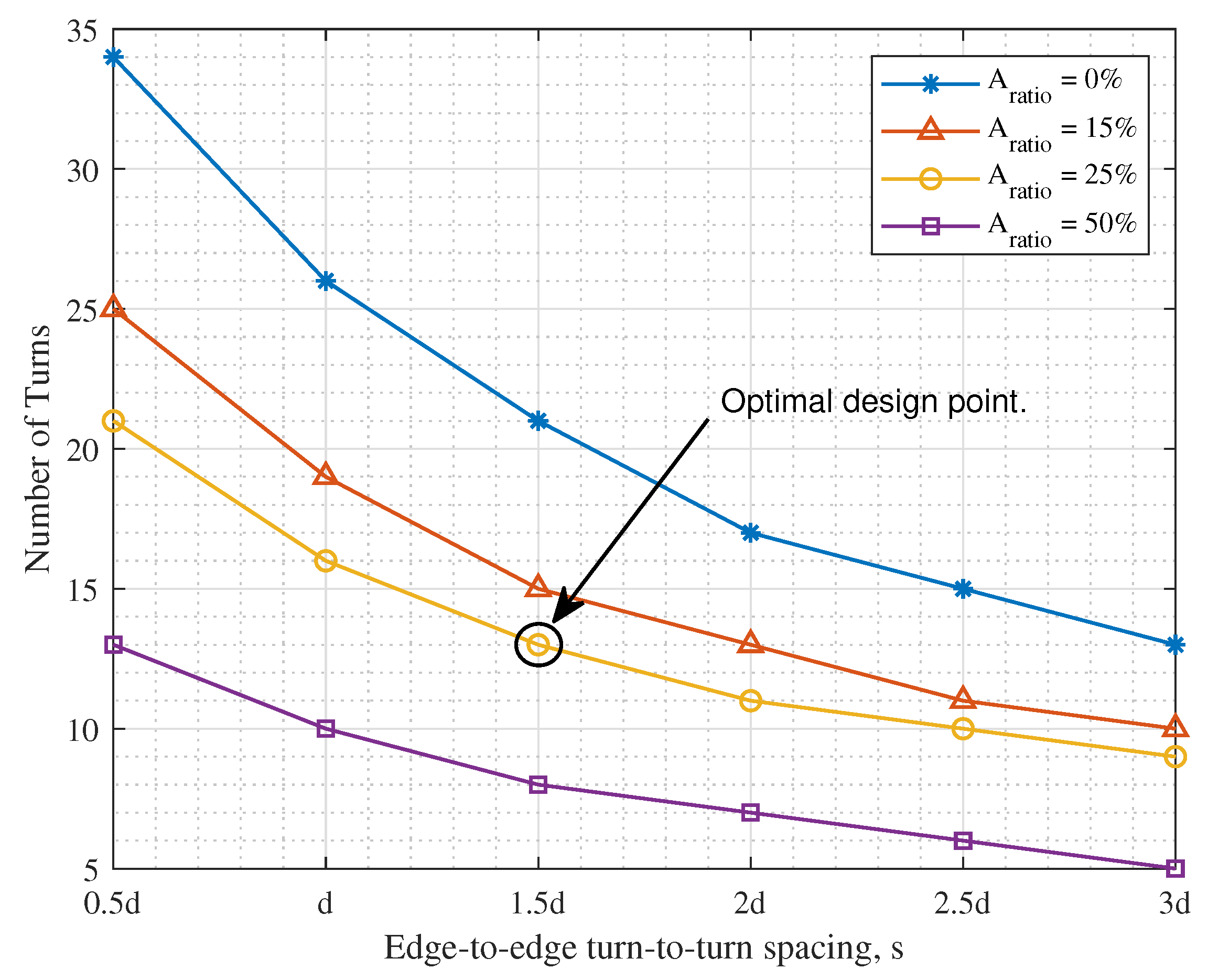
4.3. Identification of Design Variables
- The number of turns of the coils, N.
- The corresponding spacing between adjacent turns, s.
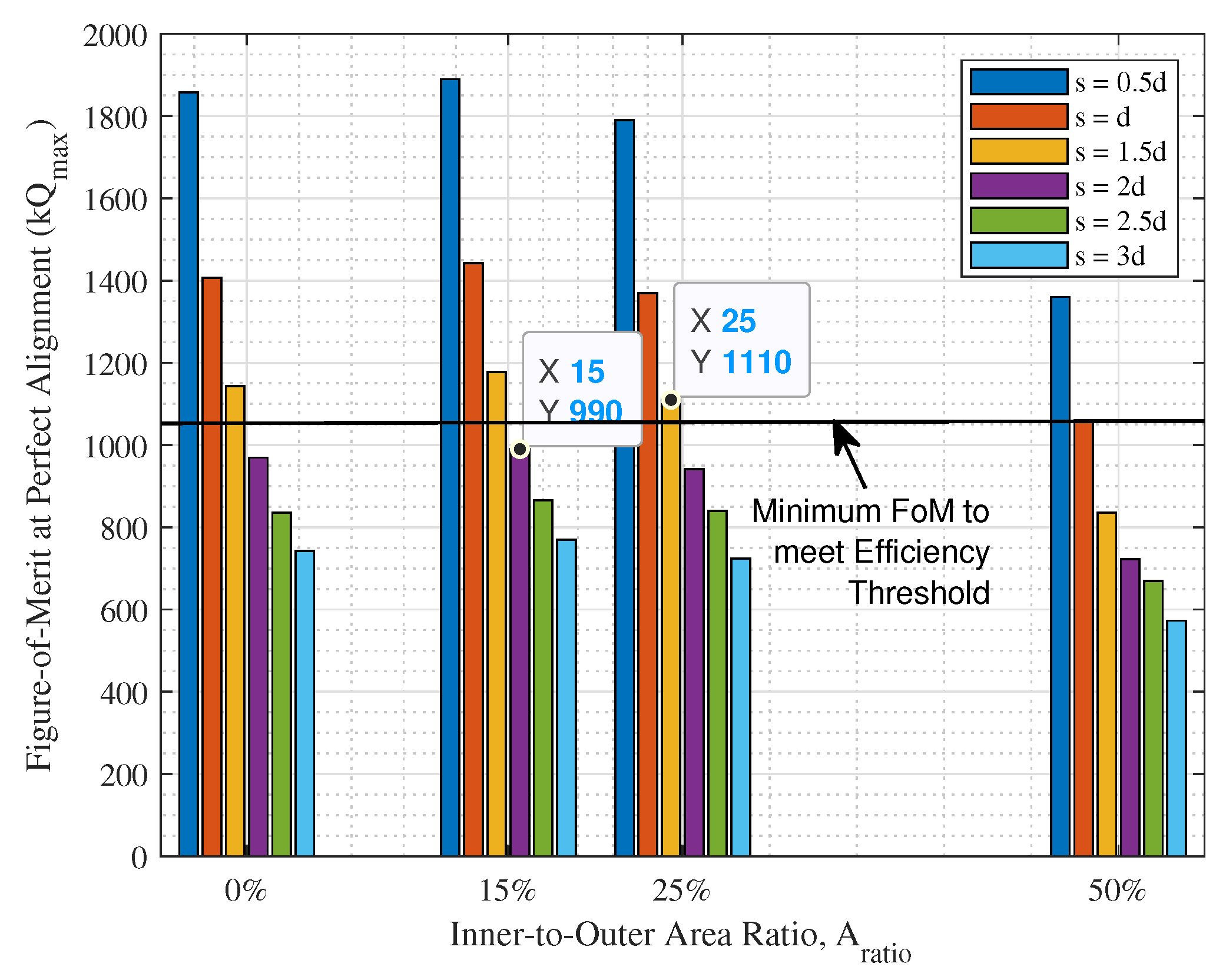
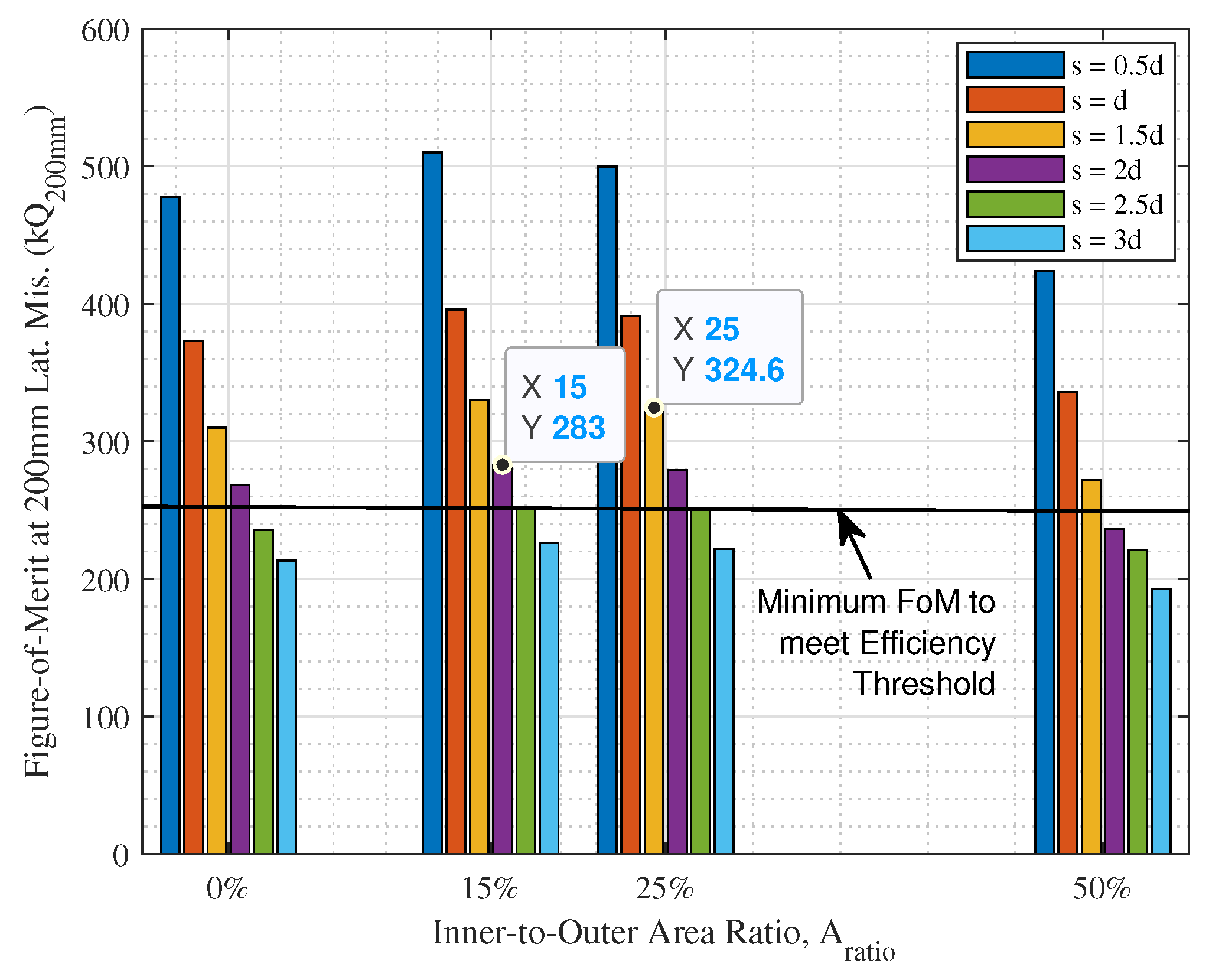
4.4. Parametric Optimization Using FEM Simulations
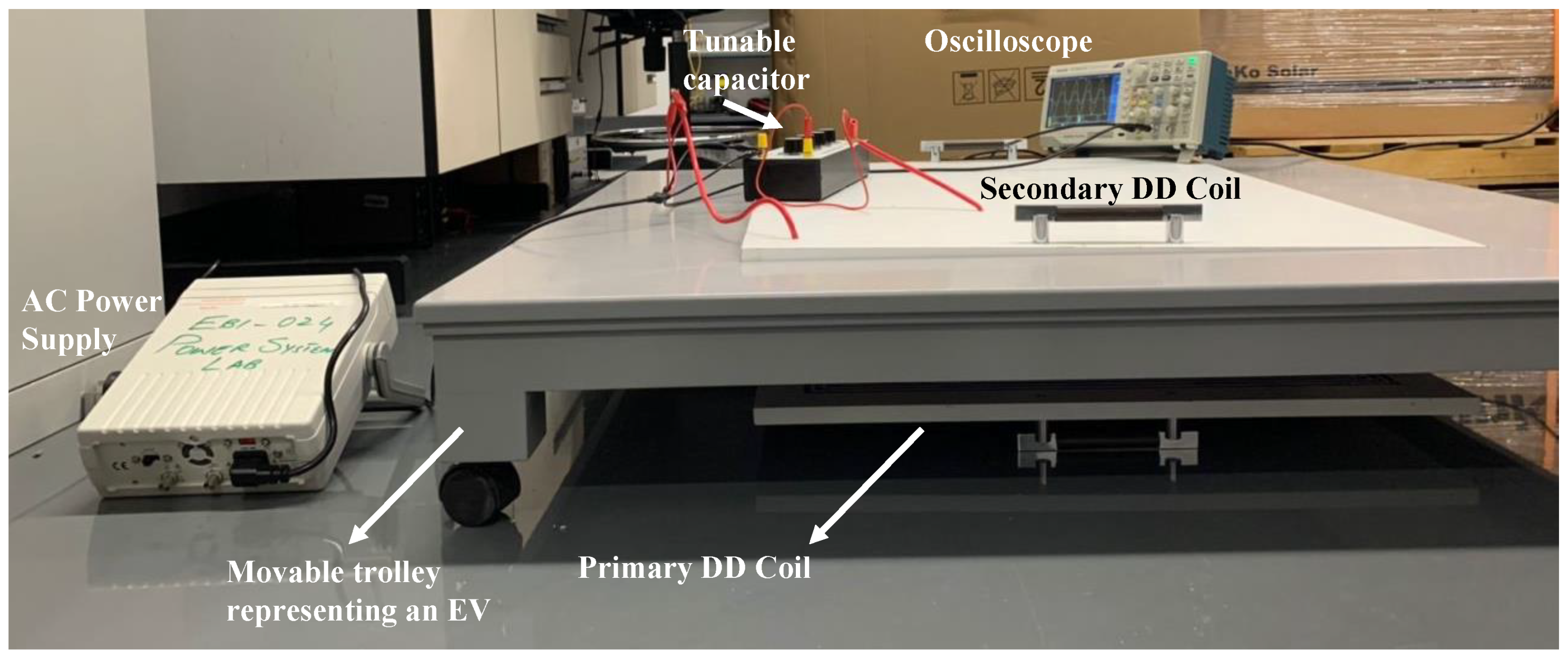
5. Simulation Results and Experimental Verification
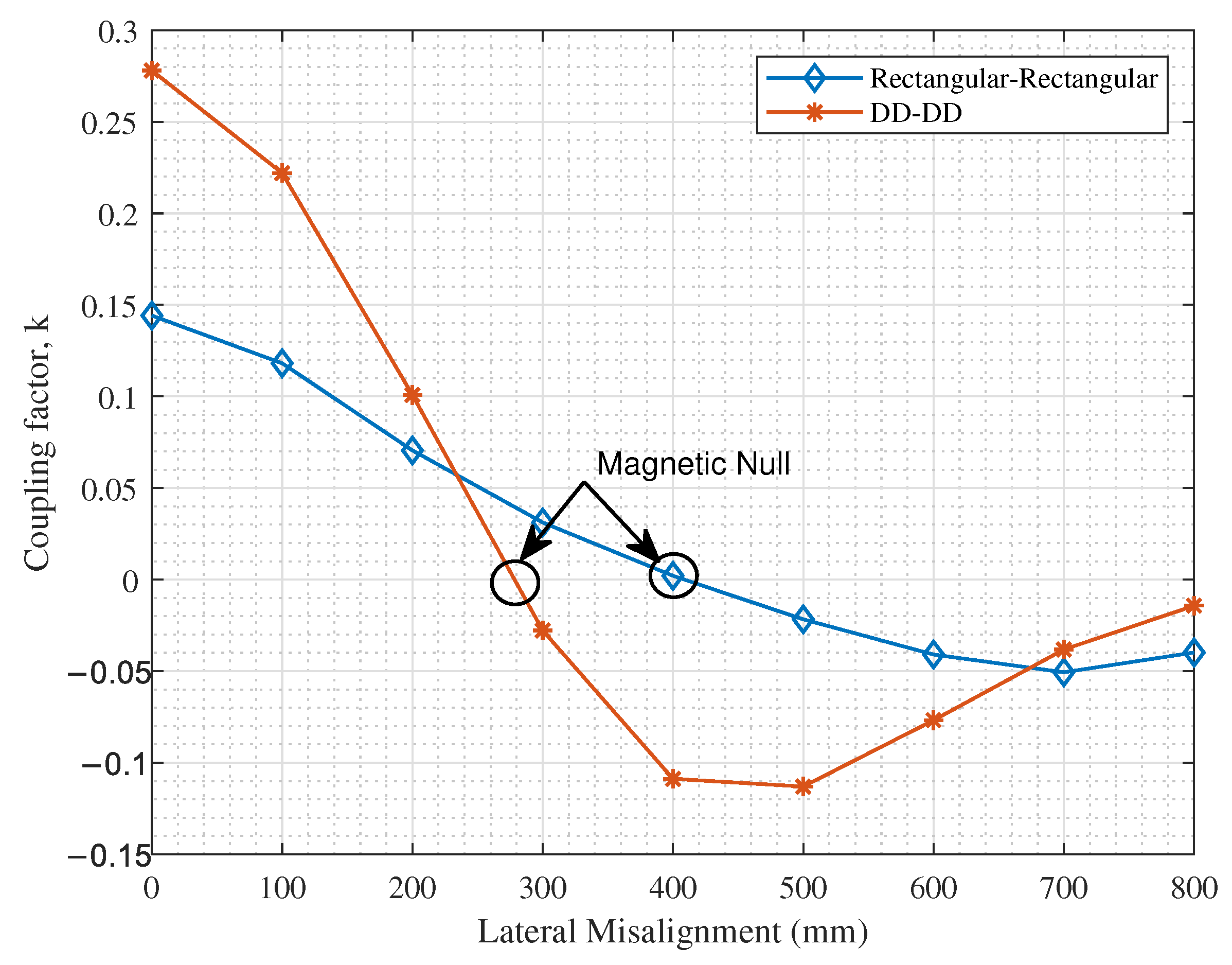
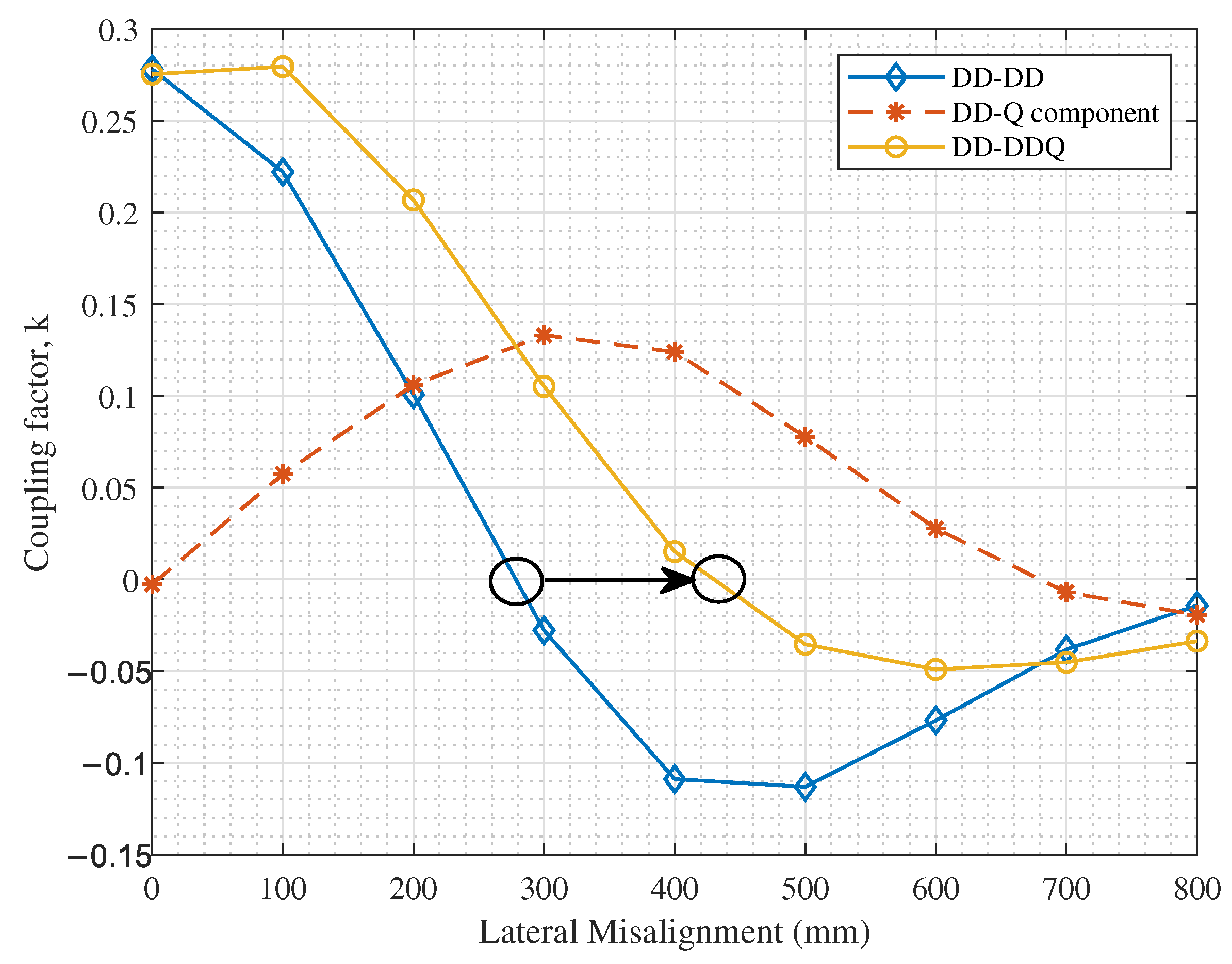
6. Rectangular, DD and DDQ Charging Coils
- The coupling performance at 200 mm lateral misalignment.
- The magnetic null point.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Patil, D.; McDonough, M.K.; Miller, J.M.; Fahimi, B.; Balsara, P.T. Wireless Power Transfer for Vehicular Applications: Overview and Challenges. IEEE Trans. Transp. Electrif. 2018, 4, 3–37. [Google Scholar] [CrossRef]
- Jayakumar, A. Review of prospects for adoption of fuel cell electric vehicles in New Zealand. IET Electr. Syst. Transp. 2017, 7, 259–266. [Google Scholar] [CrossRef]
- Wu, H.H.; Gilchrist, A.; Sealy, K.D.; Bronson, D. A High Efficiency 5 kW Inductive Charger for EVs Using Dual Side Control. IEEE Trans. Ind. Inform. 2012, 8, 585–595. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, A.; Alam, M.S.; Chabaan, R. A Comprehensive Review of Wireless Charging Technologies for Electric Vehicles. IEEE Trans. Transp. Electrif. 2018, 4, 38–63. [Google Scholar] [CrossRef]
- IEEE Approved Draft Standard for Safety Levels with Respect to Human Exposure to Electric, Magnetic and Electromagnetic Fields, 0 Hz to 300 GHz; IEEE PC95.1/D3.5, October 2018; IEEE: Piscataway, NJ, USA, 2019; pp. 1–312.
- ICNIRP. Guidelines for Limiting Exposure to Time-Varying Electric and Magnetic Fields (1 Hz–100 kHz). Health Phys. 2010, 99, 818–836. [Google Scholar] [CrossRef] [PubMed]
- Tavakoli, R.; Pantic, Z. Analysis, Design, and Demonstration of a 25-kW Dynamic Wireless Charging System for Roadway Electric Vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1378–1393. [Google Scholar] [CrossRef]
- Shin, J.; Shin, S.; Kim, Y.; Ahn, S.; Lee, S.; Jung, G.; Jeon, S.; Cho, D. Design and Implementation of Shaped Magnetic-Resonance-Based Wireless Power Transfer System for Roadway-Powered Moving Electric Vehicles. IEEE Trans. Ind. Electron. 2014, 61, 1179–1192. [Google Scholar] [CrossRef]
- Feng, H.; Cai, T.; Duan, S.; Zhao, J.; Zhang, X.; Chen, C. An LCC-Compensated Resonant Converter Optimized for Robust Reaction to Large Coupling Variation in Dynamic Wireless Power Transfer. IEEE Trans. Ind. Electron. 2016, 63, 6591–6601. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, L.; Guo, Y.; Liao, C.; Li, F. Applying LCC Compensation Network to Dynamic Wireless EV Charging System. IEEE Trans. Ind. Electron. 2016, 63, 6557–6567. [Google Scholar] [CrossRef]
- ElGhanam, E.; Hassan, M.; Osman, A. Design of a High Power, LCC-Compensated, Dynamic, Wireless Electric Vehicle Charging System with Improved Misalignment Tolerance. Energies 2021, 14, 885. [Google Scholar] [CrossRef]
- Jeong, S.; Jang, Y.J.; Kum, D. Economic Analysis of the Dynamic Charging Electric Vehicle. IEEE Trans. Power Electron. 2015, 30, 6368–6377. [Google Scholar] [CrossRef]
- Vaidehi, S.; Dhar, S.; Jayakumar, A.; Lavanya, R.; Dinesh Kumar, M. Techno-economic assessment of various motors for three-wheeler E-auto rickshaw: From Indian context. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Green, P.; Cullinane, B.; Zylstra, B.; Smith, D. Typical Values for Driving Performance with Emphasis on the Standard Deviation of Lane Position: A Summary of the Literature. In Safety Vehicles Using Adaptive Interface Technology(Task 3A); U.S. Department of Transportation: Cambridge, MA, USA, 2004. [Google Scholar]
- Ramezani, A.; Farhangi, S.; Iman-Eini, H.; Farhangi, B.; Rahimi, R.; Moradi, G.R. Optimized LCC-Series Compensated Resonant Network for Stationary Wireless EV Chargers. IEEE Trans. Ind. Electron. 2019, 66, 2756–2765. [Google Scholar] [CrossRef]
- Lassioui, A.; Fadil, H.E.; Rachid, A.; Belhaj, F.Z.; Tarkany, O.; Bajit, A. Characterestics Analysis of Wireless Power Transfer System for Electric Vehicle Charging Applications. In Proceedings of the 2018 International Symposium on Advanced Electrical and Communication Technologies (ISAECT), Rabat, Morocco, 21–23 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Tan, L.; Zhao, W.; Ju, M.; Liu, H.; Huang, X. Research on an EV Dynamic Wireless Charging Control Method Adapting to Speed Change. Energies 2019, 12, 2214. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Wong, S.; Tse, C.K.; Chen, Q. An Optimized Track Length in Roadway Inductive Power Transfer Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 598–608. [Google Scholar] [CrossRef]
- Liang, X.; Chowdhury, M.S.A. Emerging Wireless Charging Systems for Electric Vehicles - Achieving High Power Transfer Efficiency: A Review. In Proceedings of the 2018 IEEE Industry Applications Society Annual Meeting (IAS), Portland, OR, USA, 23–27 September 2018; pp. 1–14. [Google Scholar] [CrossRef]
- Liu, H.; Tan, L.; Huang, X.; Zhang, M.; Zhang, Z.; Li, J. Power Stabilization based on Switching Control of Segmented Transmitting Coils for Multi Loads in Static-Dynamic Hybrid Wireless Charging System at Traffic Lights. Energies 2019, 12, 607. [Google Scholar] [CrossRef] [Green Version]
- Mazharov, N.; Hristov, S.; Dichev, D.; Zhelezarov, I. Some Problems of Dynamic Contactless Charging of Electric Vehicles. Acta Polytech. Hung. 2017, 14, 7–26. [Google Scholar] [CrossRef]
- Ahmad, A.; Alam, M.S.; Mohamed, A.A.S. Design and Interoperability Analysis of Quadruple Pad Structure for Electric Vehicle Wireless Charging Application. IEEE Trans. Transp. Electrif. 2019, 5, 934–945. [Google Scholar] [CrossRef]
- ElGhanam, E.A.; Hassan, M.S.; Osman, A. Design and Finite Element Modeling of The Inductive Link in Wireless Electric Vehicle Charging Systems. In Proceedings of the 2020 IEEE Transportation Electrification Conference Expo (ITEC), Chicago, IL, USA, 23–26 June 2020; pp. 389–394. [Google Scholar]
- Ongayo, D.; Hanif, M. Comparison of Circular and Rectangular Coil Transformer Parameters for Wireless Power Transfer based on Finite Element Analysis. In Proceedings of the 2015 IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), Fortaleza, Brazil, 29 November–2 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Bosshard, R.; Iruretagoyena, U.; Kolar, J.W. Comprehensive Evaluation of Rectangular and Double-D Coil Geometry for 50 kW/85 kHz IPT System. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1406–1415. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Venugopal, P.; Dong, J.; Bauer, P. Comparison of Magnetic Couplers for IPT-Based EV Charging Using Multi-Objective Optimization. IEEE Trans. Veh. Technol. 2019, 68, 5416–5429. [Google Scholar] [CrossRef]
- Zargham, M.; Gulak, P.G. Maximum Achievable Efficiency in Near-Field Coupled Power-Transfer Systems. IEEE Trans. Biomed. Circ. Syst. 2012, 6, 228–245. [Google Scholar] [CrossRef] [PubMed]
- Wireless Power Transfer for Light-Duty Plug-in/Electric Vehicles and Alignment Methodology; SAE J2954, April 2019; SAE International: Warrendale, PA, USA, 2019.
- Lu, J.; Zhu, G.; Wang, H.; Lu, F.; Jiang, J.; Mi, C.C. Sensitivity Analysis of Inductive Power Transfer Systems with Voltage-Fed Compensation Topologies. IEEE Trans. Veh. Technol. 2019, 68, 4502–4513. [Google Scholar] [CrossRef]
- Abou Houran, M.; Yang, X.; Chen, W. Magnetically Coupled Resonance WPT: Review of Compensation Topologies, Resonator Structures with Misalignment, and EMI Diagnostics. Electronics 2018, 7, 296. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Zhao, H.; Deng, J.; Li, S.; Mi, C.C. Comparison Study on SS and Double-Sided LCC Compensation Topologies for EV/PHEV Wireless Chargers. IEEE Trans. Veh. Technol. 2016, 65, 4429–4439. [Google Scholar] [CrossRef]
- Lin, F.Y.; Covic, G.A.; Boys, J.T. Evaluation of Magnetic Pad Sizes and Topologies for Electric Vehicle Charging. IEEE Trans. Power Electron. 2015, 30, 6391–6407. [Google Scholar] [CrossRef]
- Liu, Y.; Mai, R.; Yue, P.; Li, Y.; He, Z. Efficiency optimization for wireless dynamic charging system with overlapped DD coil arrays. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 1439–1442. [Google Scholar] [CrossRef]
- Marco, D.; Dolara, A.; Longo, M.; Yaici, W. Design and Performance Analysis of Pads for Dynamic Wireless Charging of EVs using the Finite Element Method. Energies 2019, 12, 4139. [Google Scholar] [CrossRef] [Green Version]
- Zaheer, A.; Hao, H.; Covic, G.A.; Kacprzak, D. Investigation of Multiple Decoupled Coil Primary Pad Topologies in Lumped IPT Systems for Interoperable Electric Vehicle Charging. IEEE Trans. Power Electron. 2015, 30, 1937–1955. [Google Scholar] [CrossRef]
- Lin, F.Y.; Kim, S.; Covic, G.A.; Boys, J.T. Effective Coupling Factors for Series and Parallel Tuned Secondaries in IPT Systems Using Bipolar Primary Pads. IEEE Trans. Transp. Electrif. 2017, 3, 434–444. [Google Scholar] [CrossRef]
- Nguyen, T.; Li, S.; Li, W.; Mi, C.C. Feasibility Study on Bipolar Pads for Efficient Wireless Power Chargers. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 1676–1682. [Google Scholar] [CrossRef]
- Sallan, J.; Villa, J.L.; Llombart, A.; Sanz, J.F. Optimal Design of ICPT Systems Applied to Electric Vehicle Battery Charge. IEEE Trans. Ind. Electron. 2009, 56, 2140–2149. [Google Scholar] [CrossRef]
- Tan, L.; Zhao, W.; Liu, H.; Li, J.; Huang, X. Design and Optimization of Ground-Side Power Transmitting Coil Parameters for EV Dynamic Wireless Charging System. IEEE Access 2020, 8, 74595–74604. [Google Scholar] [CrossRef]
- Elghanam, E.A.; Hassan, M.S.; Osman, A. Modeling, Simulation and Comparison of Different Ferrite Layer Geometries for Inductive Wireless Electric Vehicle Chargers. In Modelling, Simulation and Intelligent Computing. MoSICom 2020. Lecture Notes in Electrical Engineering; Goel, N., Hasan, S., Kalaichelvi, V., Eds.; Springer: Singapore, 2020; Volume 659, pp. 411–418. [Google Scholar]
- Kim, H.; Song, C.; Kim, D.; Jung, D.H.; Kim, I.; Kim, Y.; Kim, J.; Ahn, S.; Kim, J. Coil Design and Measurements of Automotive Magnetic Resonant Wireless Charging System for High-Efficiency and Low Magnetic Field Leakage. IEEE Trans. Microw. Theory Tech. 2016, 64, 383–400. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Gross ferrite surface area | mm |
| Bar dimensions | mm |
| No. of ferrite bars | 9 |
| Ferrite thickness | 16 mm |
| Relative permeability | |
| Ferrite material | T-type ferrite |
| Gross aluminum surface area | mm |
| Aluminum shield thickness | mm |
| Aluminum 1050A alloy Conductivity | MS/m |
| Parameters | Value |
|---|---|
| Coil surface area | mm |
| Number of turns, N | 13 |
| Wire diameter, d | 4 mm |
| Edge-to-edge spacing, s | 6 mm |
| Equipment | Part No. | Rating |
|---|---|---|
| AC supply | BK PRECISION 4017A | 1 Hz–10 MHz, up to 250 V |
| Oscilloscope | TBS1052B-EDU | Up to 50 MHz |
| LCR meter | GW Instek LCR-916 | kHz, 20 μH–20 kH |
| Tunable capacitor | Cropico CM5-N | 100 pF–10 F |
| Tunable resistor load | AEMC BR07 | 1 –1 M |
| PVC Insulated Cables | – | BS6231, V |
| Parameters | Prim. Coil Prototype | Sec. Coil Prototype | FEM Simulations |
|---|---|---|---|
| Self inductance, L | μH | μH | μH |
| Series resistance, R | 605 m | 574 m | m |
| Quality factor, Q | 190 | 2220 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
ElGhanam, E.; Hassan, M.; Osman, A.; Kabalan, H. Design and Performance Analysis of Misalignment Tolerant Charging Coils for Wireless Electric Vehicle Charging Systems. World Electr. Veh. J. 2021, 12, 89. https://doi.org/10.3390/wevj12030089
ElGhanam E, Hassan M, Osman A, Kabalan H. Design and Performance Analysis of Misalignment Tolerant Charging Coils for Wireless Electric Vehicle Charging Systems. World Electric Vehicle Journal. 2021; 12(3):89. https://doi.org/10.3390/wevj12030089
Chicago/Turabian StyleElGhanam, Eiman, Mohamed Hassan, Ahmed Osman, and Hanin Kabalan. 2021. "Design and Performance Analysis of Misalignment Tolerant Charging Coils for Wireless Electric Vehicle Charging Systems" World Electric Vehicle Journal 12, no. 3: 89. https://doi.org/10.3390/wevj12030089
APA StyleElGhanam, E., Hassan, M., Osman, A., & Kabalan, H. (2021). Design and Performance Analysis of Misalignment Tolerant Charging Coils for Wireless Electric Vehicle Charging Systems. World Electric Vehicle Journal, 12(3), 89. https://doi.org/10.3390/wevj12030089









