Day-Ahead Forecast of Electric Vehicle Charging Demand with Deep Neural Networks †
Abstract
:1. Introduction
2. Literature Review
Research Gap and Contribution
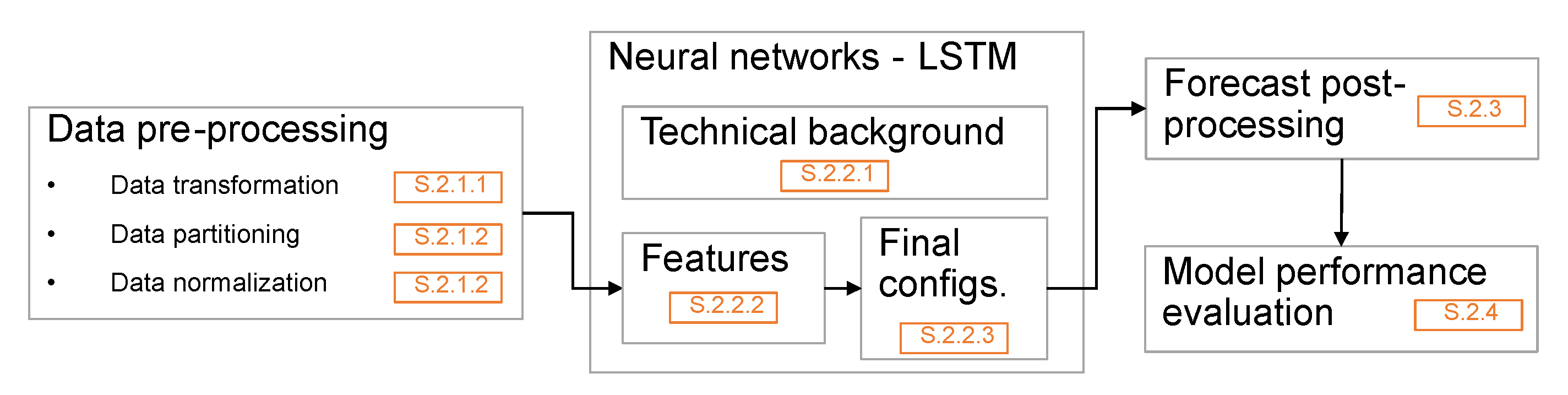
3. Materials and Methods
3.1. Data Pre-Processing
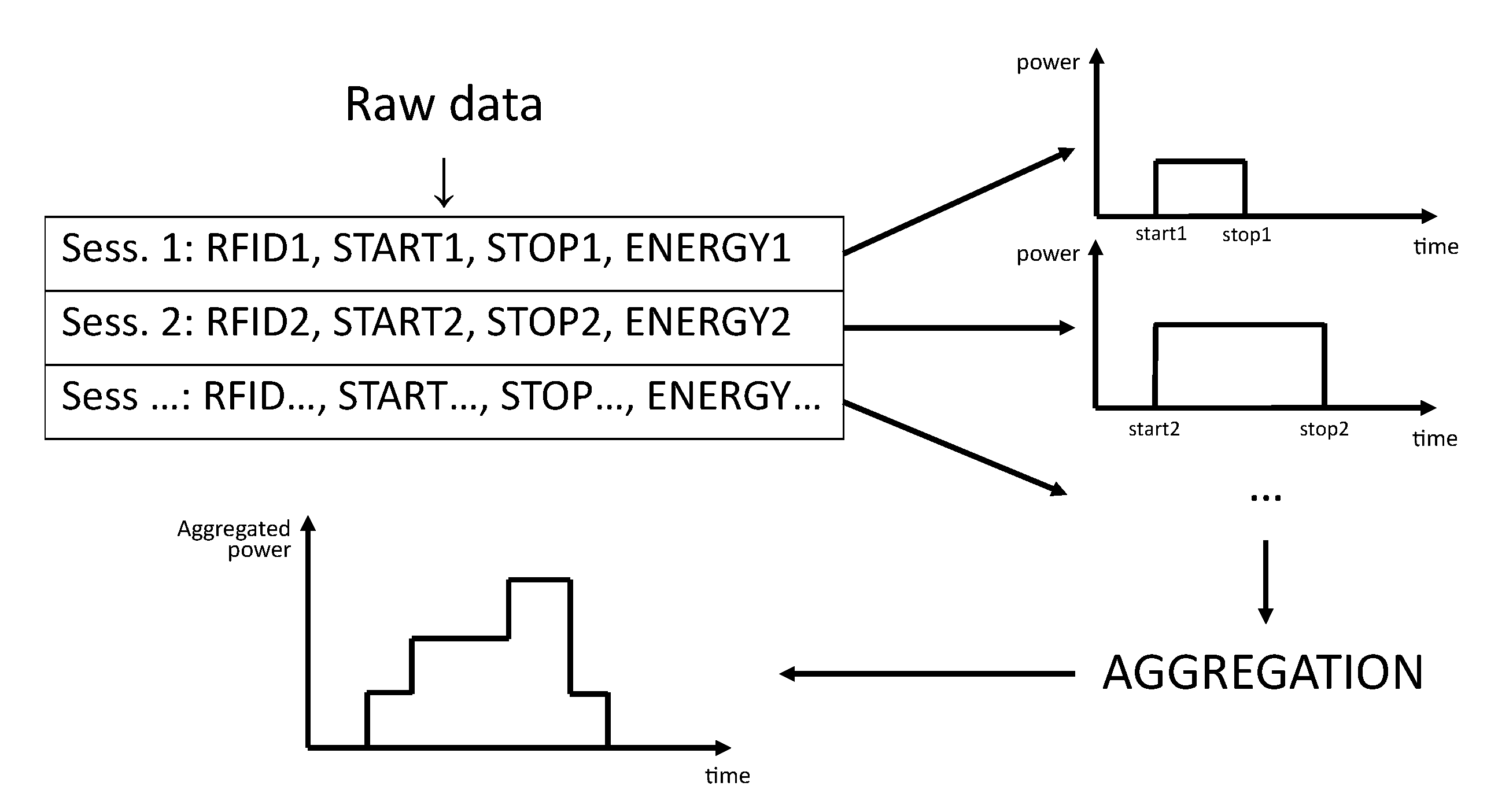
3.1.1. Data Transformation
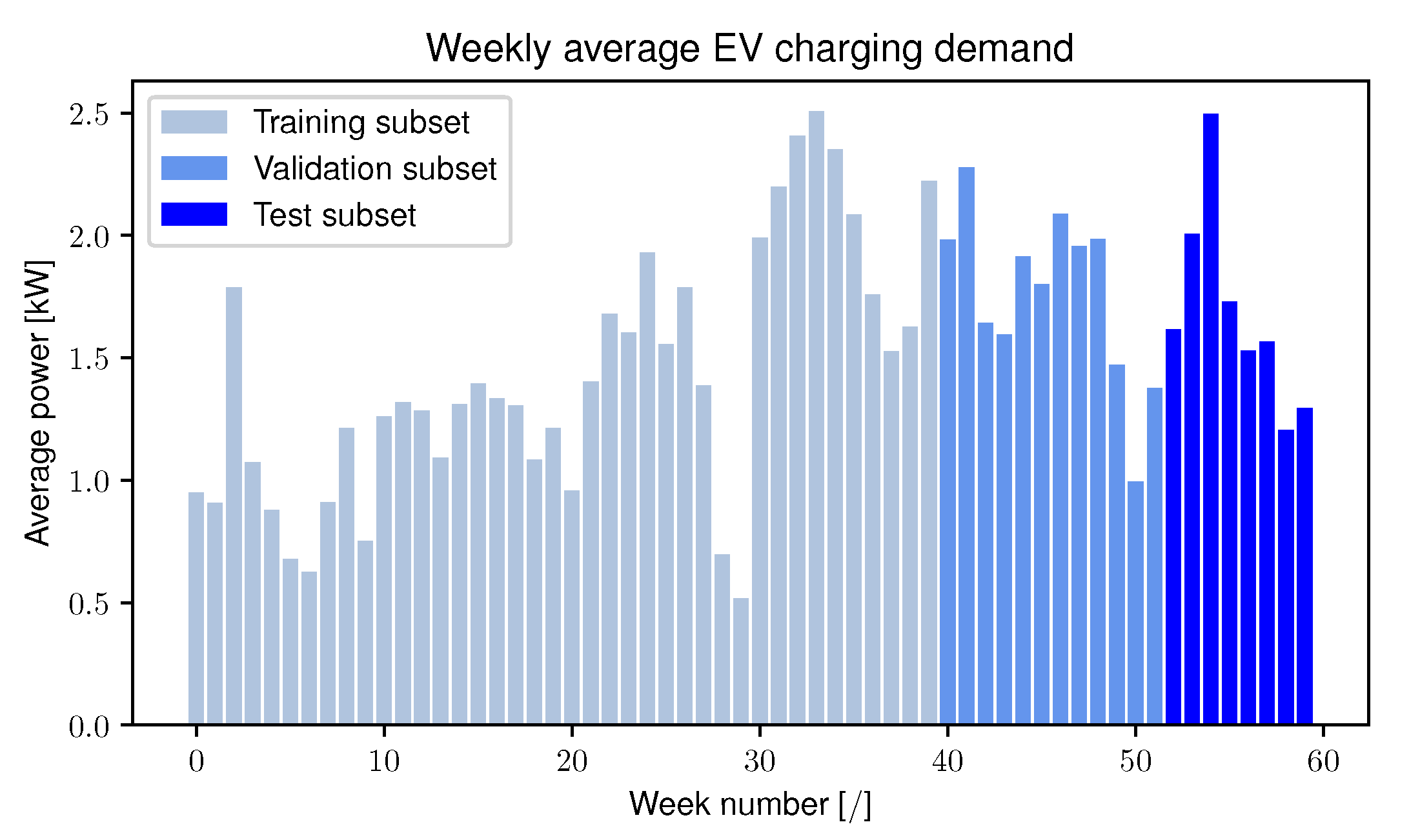
3.1.2. Data Partitioning and Normalization
3.2. Neural Networks
3.2.1. Technical Background
3.2.2. Features
3.2.3. Final Configuration
3.3. Forecast Post-Processing
3.4. Model Performance Evaluation
4. Results and Discussions
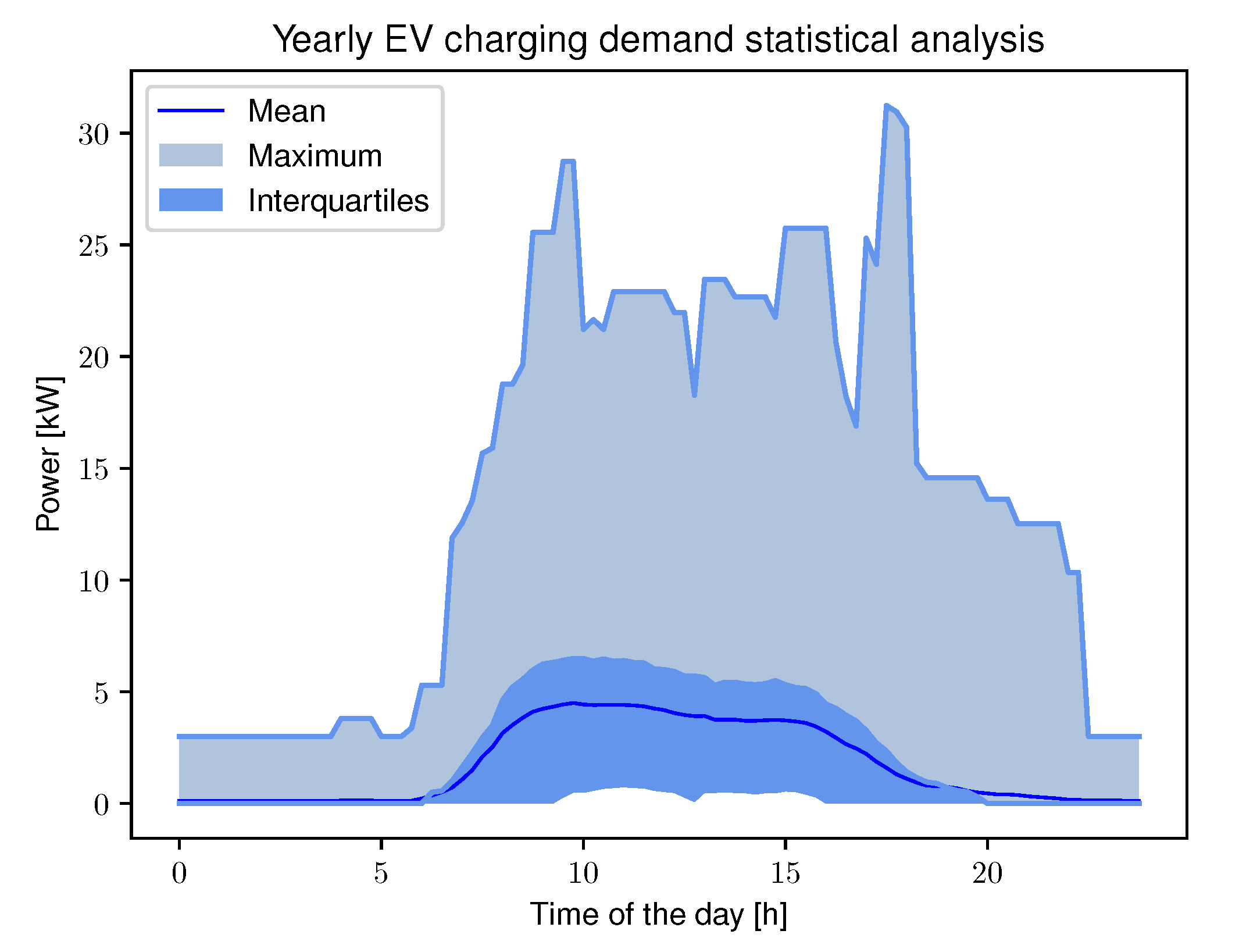
4.1. Use Case and Data Analysis
4.2. Simulation Results
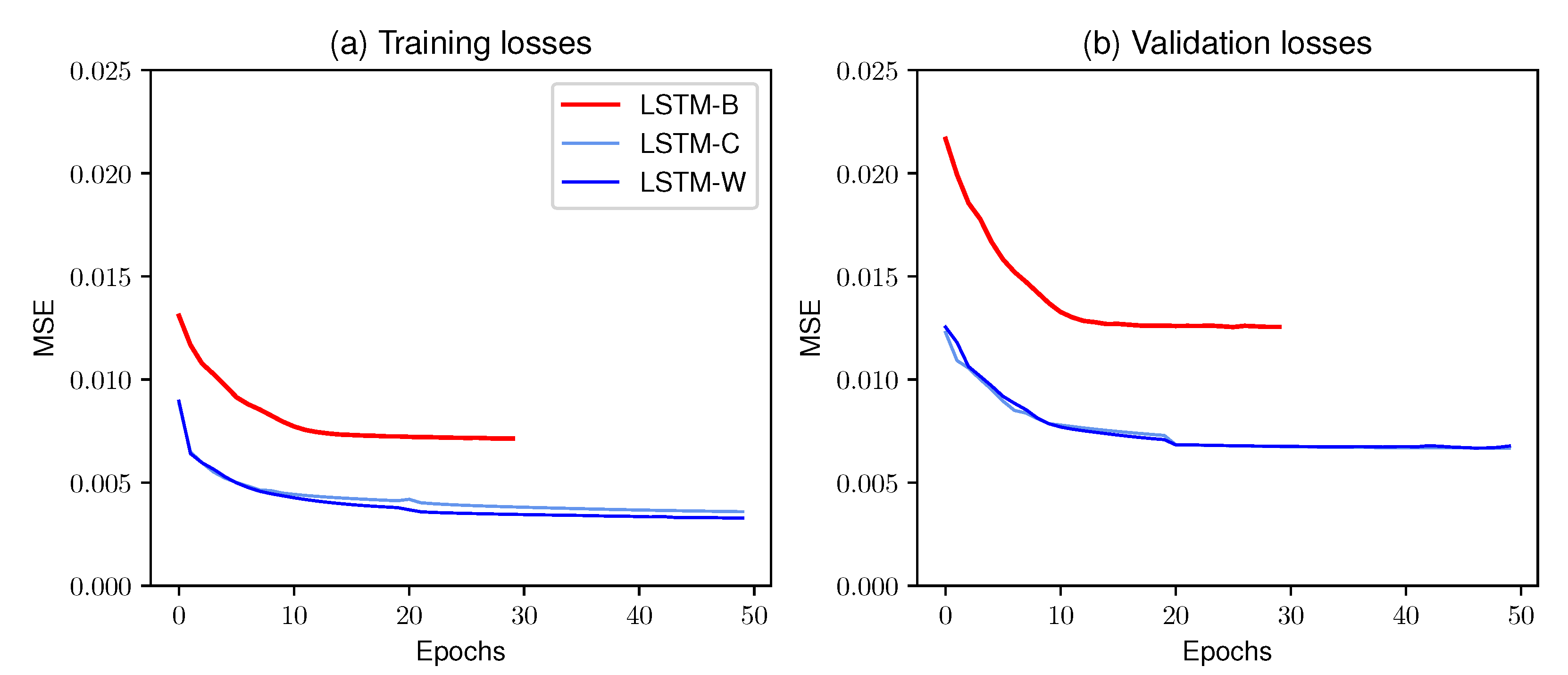
4.2.1. Neural Network Convergence Analysis
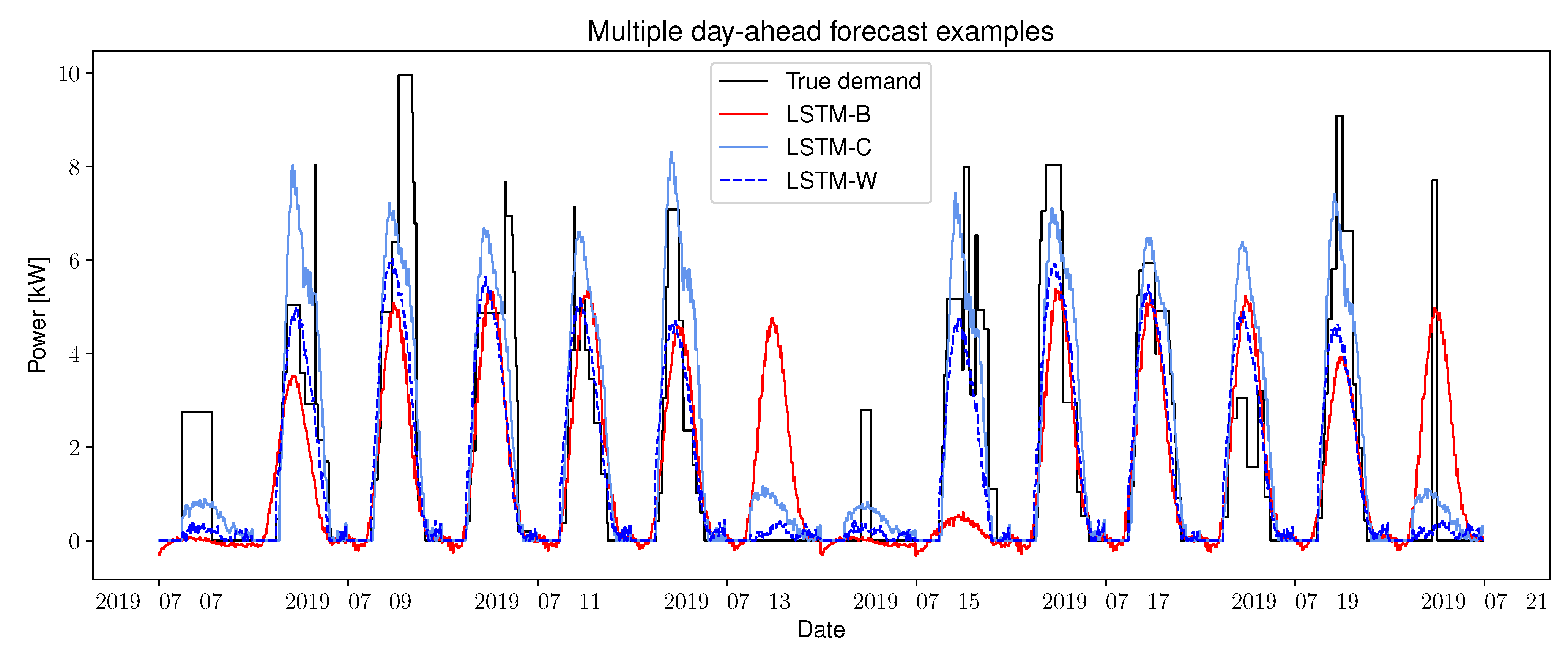
4.2.2. Two-Weeks Period Forecast Example
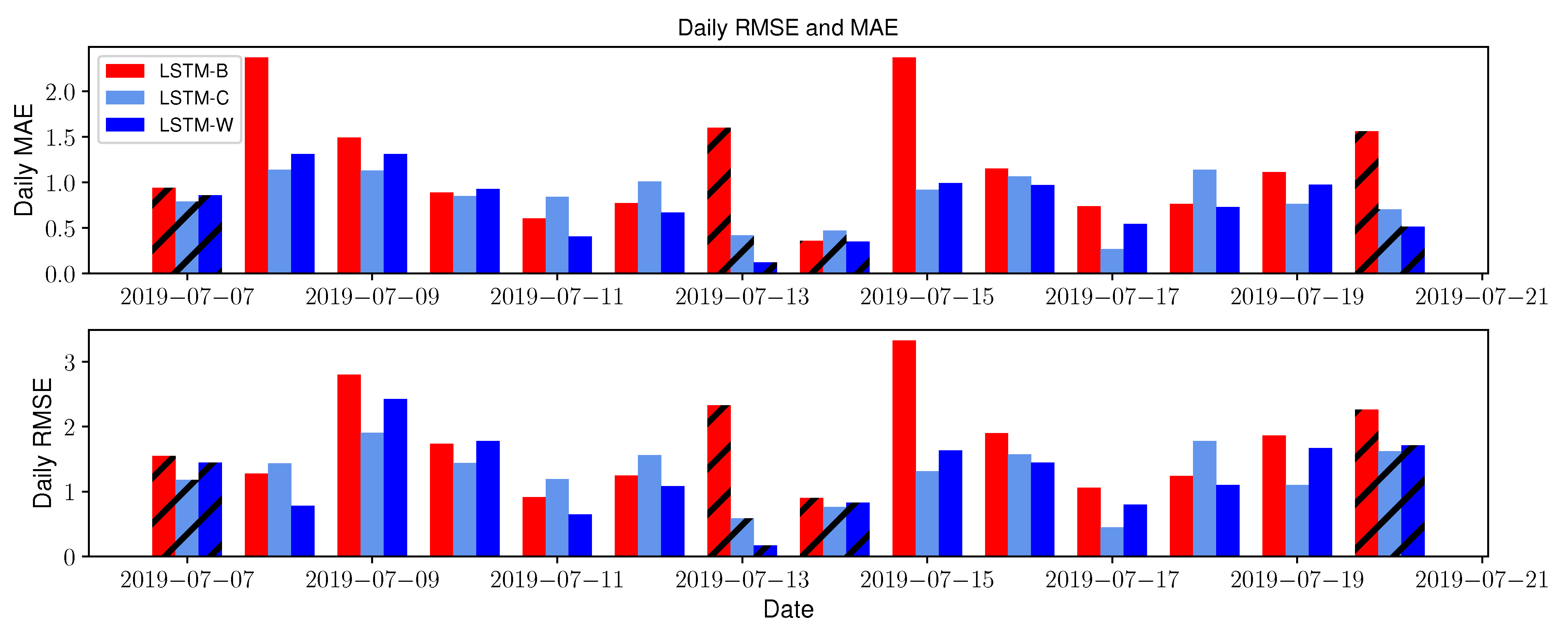
4.2.3. Test Subset Performances
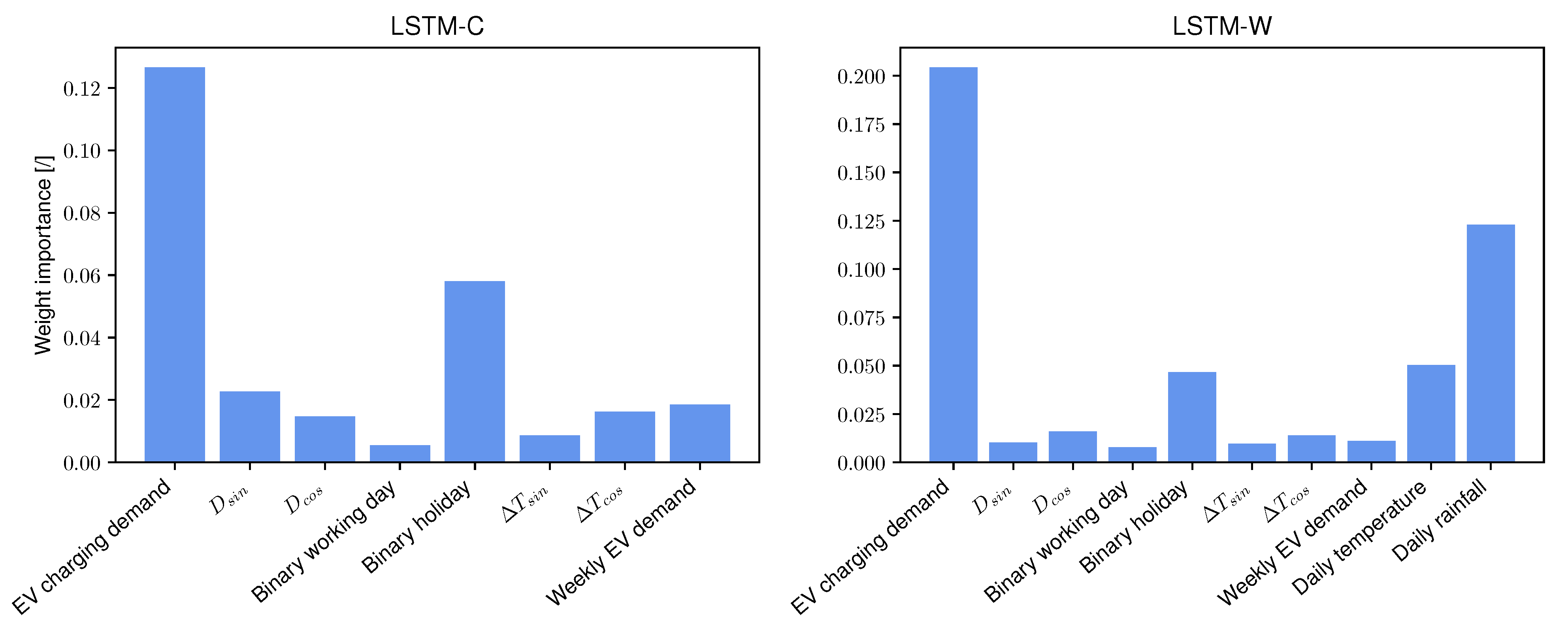
4.2.4. Feature Importance
4.3. Forecast Timing and Real-Time Capabilities
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EMS | Energy management system |
| EV | Electric vehicle |
| MAE | Mean-absolute error |
| MSE | Mean-square error |
| LSTM | Long short-term memory |
| LSTM-B | Long short-term memory-Base |
| LSTM-C | Long short-term memory-Calendar |
| LSTM-W | Long short-term memory-Weather |
| Relu | Rectified linear unit |
| RMSE | Root-mean-square error |
| RNN | Recurrent neural network |
| Tanh | Hyperbolic tangent |
| VIANN | Variance-based feature Importance in Artificial Neural Networks |
References
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; et al. (Eds.) Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Technical Report; IPCC: Geneva, Switzerland, 2021. [Google Scholar]
- IEA. Electric Vehicles. Available online: https://www.iea.org/reports/electric-vehicles (accessed on 3 August 2020).
- Dubey, A.; Santoso, S. Electric Vehicle Charging on Residential Distribution Systems: Impacts and Mitigations. IEEE Access 2015, 3, 1871–1893. [Google Scholar] [CrossRef]
- Jiang, R.; Zhang, Z.; Li, J.; Zhang, Y.; Huang, Q. A coordinated charging strategy for electric vehicles based on multi-objective optimization. In Proceedings of the 2017 2nd International Conference on Power and Renewable Energy, ICPRE 2017, Chengdu, China, 20–23 September 2018; pp. 823–827. [Google Scholar] [CrossRef]
- Liang, H.; Liu, Y.; Li, F.; Shen, Y. Dynamic Economic/Emission Dispatch Including PEVs for Peak Shaving and Valley Filling. IEEE Trans. Ind. Electron. 2019, 66, 2880–2890. [Google Scholar] [CrossRef]
- Neofytou, N.; Blazakis, K.; Katsigiannis, Y.; Stavrakakis, G. Modeling vehicles to grid as a source of distributed frequency regulation in isolated grids with significant RES penetration. Energies 2019, 12, 720. [Google Scholar] [CrossRef] [Green Version]
- Tomura, Y.; Nakagawa, T. Effective utilization system of renewable energy through the use of vehicle. Energy Procedia 2019, 158, 3000–3007. [Google Scholar] [CrossRef]
- Tan, K.M.; Ramachandaramurthy, V.K.; Yong, J.Y. Integration of electric vehicles in smart grid: A review on vehicle to grid technologies and optimization techniques. Renew. Sustain. Energy Rev. 2016, 53, 720–732. [Google Scholar] [CrossRef]
- Xydas, E.S.; Marmaras, C.E.; Cipcigan, L.M.; Hassan, A.S.; Jenkins, N. Forecasting Electric Vehicle charging demand using Support Vector Machines. In Proceedings of the Universities Power Engineering Conference, Dublin, Ireland, 2–5 September 2013. [Google Scholar] [CrossRef]
- Amini, M.H.; Kargarian, A.; Karabasoglu, O. ARIMA-based decoupled time series forecasting of electric vehicle charging demand for stochastic power system operation. Electr. Power Syst. Res. 2016, 140, 378–390. [Google Scholar] [CrossRef]
- Su, W.; Wang, J.; Zhang, K.; Huang, A.Q. Model predictive control-based power dispatch for distribution system considering plug-in electric vehicle uncertainty. Electr. Power Syst. Res. 2014, 106, 29–35. [Google Scholar] [CrossRef]
- Buzna, L.; De Falco, P.; Ferruzzi, G.; Khormali, S.; Proto, D.; Refa, N.; Straka, M.; van der Poel, G. An ensemble methodology for hierarchical probabilistic electric vehicle load forecasting at regular charging stations. Appl. Energy 2020, 283. [Google Scholar] [CrossRef]
- Buzna, L.; De Falco, P.; Khormali, S.; Proto, D.; Straka, M. Electric vehicle load forecasting: A comparison between time series and machine learning approaches. In Proceedings of the 2019 IEEE 1st International Conference on Energy Transition in the Mediterranean Area (SyNERGY MED), Cagliari, Italy, 28–30 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Jewell, N.; Turner, M.; Naber, J.; McIntyre, M. Analysis of forecasting algorithms for minimization of electric demand costs for electric vehicle charging in commercial and industrial environments. In Proceedings of the 2012 IEEE Transportation Electrification Conference and Expo, ITEC 2012, Dearborn, MI, USA, 18–20 June 2012; pp. 4–9. [Google Scholar] [CrossRef]
- Majidpour, M.; Qiu, C.; Chu, P.; Gadh, R.; Pota, H.R. Modified pattern sequence-based forecasting for electric vehicle charging stations. In Proceedings of the 2014 IEEE International Conference on Smart Grid Communications, SmartGridComm 2014, Venice, Italy, 3–6 November 2014; Volume 2, pp. 710–715. [Google Scholar] [CrossRef]
- Majidpour, M.; Qiu, C.; Chu, P.; Pota, H.R.; Gadh, R. Forecasting the EV charging load based on customer profile or station measurement? Appl. Energy 2016, 163, 134–141. [Google Scholar] [CrossRef] [Green Version]
- Majidpour, M.; Qiu, C.; Chu, P.; Gadh, R.; Pota, H.R. A novel forecasting algorithm for electric vehicle charging stations. In Proceedings of the 2014 International Conference on Connected Vehicles and Expo, ICCVE 2014, Vienna, Austria, 3–7 November 2014; pp. 1035–1040. [Google Scholar] [CrossRef]
- Shao, H.; Deng, X.; Jiang, Y. A novel deep learning approach for short-term wind power forecasting based on infinite feature selection and recurrent neural network. J. Renew. Sustain. Energy 2018, 10, 043303. [Google Scholar] [CrossRef]
- Shen, M.L.; Lee, C.F.; Liu, H.H.; Chang, P.Y.; Yang, C.H. Effective multinational trade forecasting using LSTM recurrent neural network. Expert Syst. Appl. 2021, 182, 115199. [Google Scholar] [CrossRef]
- Ali, M.; Prasad, R.; Xiang, Y.; Sankaran, A.; Deo, R.C.; Xiao, F.; Zhu, S. Advanced extreme learning machines vs. deep learning models for peak wave energy period forecasting: A case study in Queensland, Australia. Renew. Energy 2021, 177, 1031–1044. [Google Scholar] [CrossRef]
- Anagnostis, A.; Papageorgiou, E.; Dafopoulos, V.; Bochtis, D. Applying Long Short-Term Memory Networks for natural gas demand prediction. In Proceedings of the 2019 IEEE 10th International Conference on Information, Intelligence, Systems and Applications (IISA), Patras, Greece, 15–17 July 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Rahman, A.; Srikumar, V.; Smith, A.D. Predicting electricity consumption for commercial and residential buildings using deep recurrent neural networks. Appl. Energy 2018, 212, 372–385. [Google Scholar] [CrossRef]
- Zhang, C.; Li, R.; Shi, H.; Li, F. Deep learning for day-ahead electricity price forecasting. IET Smart Grid 2020, 3, 462–469. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, Z.; Guo, Y.; Zhang, J.; Yang, H. Short-term load forecasting for electric vehicle charging stations based on deep learning approaches. Appl. Sci. 2019, 9, 1723. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Yang, Z.; Mourshed, M.; Guo, Y.; Zhou, Y.; Chang, Y.; Wei, Y.; Feng, S. Electric Vehicle Charging Load Forecasting: A Comparative Study of Deep Learning Approaches. Energies 2019, 12, 2692. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Wu, D.; Boulet, B. Ensemble learning for charging load forecasting of electric vehicle charging stations. In Proceedings of the 2020 IEEE Electric Power and Energy Conference, (EPEC 2020), Edmonton, AB, Canada, 9–10 November 2020; Volume 3. [Google Scholar] [CrossRef]
- Skansi, S. Introduction to Deep Learning; Undergraduate Topics in Computer Science; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Hochreiter, S. The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions. Int. J. Uncertain. Fuzziness-Knowl.-Based Syst. 1998, 06, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. Available online: https://www.tensorflow.org/ (accessed on 1 August 2021).
- Wang, J.b.; Liu, K.; Yamamoto, T.; Morikawa, T. Improving Estimation Accuracy for Electric Vehicle Energy Consumption Considering the Effects of Ambient Temperature. Energy Procedia 2017, 105, 2904–2909. [Google Scholar] [CrossRef]
- De Cauwer, C.; Verbeke, W.; Van Mierlo, J.; Coosemans, T. A Model for Range Estimation and Energy-Efficient Routing of Electric Vehicles in Real-World Conditions. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2787–2800. [Google Scholar] [CrossRef]
- Li, Y.; Huang, Y.; Zhang, M. Short-term load forecasting for electric vehicle charging station based on niche immunity lion algorithm and convolutional neural network. Energies 2018, 11, 1253. [Google Scholar] [CrossRef] [Green Version]
- Xydas, E.S.; Marmaras, C.E.; Cipcigan, L.M.; Hassan, A.S.; Jenkins, N. Electric vehicle load forecasting using data mining methods. IET Conf. Publ. 2013, 2013. [Google Scholar] [CrossRef]
- Skomski, E.; Lee, J.Y.; Kim, W.; Chandan, V.; Katipamula, S.; Hutchinson, B. Sequence-to-sequence neural networks for short-term electrical load forecasting in commercial office buildings. Energy Build. 2020, 226, 110350. [Google Scholar] [CrossRef]
- Kandel, I.; Castelli, M. The effect of batch size on the generalizability of the convolutional neural networks on a histopathology dataset. ICT Express 2020, 6, 312–315. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Smith, L.N. Cyclical Learning Rates for Training Neural Networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 464–472. [Google Scholar] [CrossRef] [Green Version]
- de Sá, C.R. Variance-Based Feature Importance in Neural Networks; Springer International Publishing: Cham, Switzerland, 2019; pp. 306–315. [Google Scholar]
- de Sá, C.R. Variance-based Feature Importance in Neural Networks—Github. Available online: https://github.com/rebelosa/feature-importance-neural-networks (accessed on 1 September 2021).
- Liu, J.; Danait, N.; Hu, S.; Sengupta, S. A leave-one-feature-out wrapper method for feature selection in data classification. In Proceedings of the 2013 IEEE 6th International Conference on Biomedical Engineering and Informatics, Hangzhou, China, 16–18 December 2013; pp. 656–660. [Google Scholar] [CrossRef]

| Class | Feature | LSTM-B | LSTM-C | LSTM-W |
|---|---|---|---|---|
| Load | EV charging demand [kW] | X | X | X |
| Average weekly EV demand [kW] | X | X | ||
| Calendar | Quarter-hour number [/] | X | X | |
| Day number [/] | X | X | ||
| Binary working day [0 or 1] | X | X | ||
| Binary Holiday [0 or 1] | X | X | ||
| Weather | Daily temperature [] | X | ||
| Daily rainfall [mm/h] | X |
| Parameters | LSTM-B | LSTM-C | LSTM-W |
|---|---|---|---|
| Epochs | 30 | 50 | 50 |
| Batch size | 512 | 192 | 192 |
| Optimizer | RMSprop | Adam | Adam |
| Loss function | MAE | MSE | MSE |
| Learning rate | 0.001 | 0.001 * | 0.001 * |
| Hidden neurons | 16 | 25 ** | 30 ** |
| Activation function | Tanh | Tanh ** | Tanh ** |
| Dropout | 0.3 | 0 ** | 0.3 ** |
| Metrics | LSTM-B | LSTM-C | LSTM-W |
|---|---|---|---|
| MAE | 1.25 kW | 0.96 kW (−23.2%) | 0.89 kW (−28.8%) |
| RMSE | 2.29 kW | 1.85 kW (−19.22%) | 1.92 kW (−16.16%) |
| Neural Networks | Training and Validation [min] | Testing 50 Days [s] | Average Time for a Day-Ahead Forecast [s] |
|---|---|---|---|
| LSTM-B | 3.88 | 3.17 | 0.063 |
| LSTM-C | 11.47 | 3.42 | 0.068 |
| LSTM-W | 15.04 | 3.28 | 0.065 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Kriekinge, G.; De Cauwer, C.; Sapountzoglou, N.; Coosemans, T.; Messagie, M. Day-Ahead Forecast of Electric Vehicle Charging Demand with Deep Neural Networks. World Electr. Veh. J. 2021, 12, 178. https://doi.org/10.3390/wevj12040178
Van Kriekinge G, De Cauwer C, Sapountzoglou N, Coosemans T, Messagie M. Day-Ahead Forecast of Electric Vehicle Charging Demand with Deep Neural Networks. World Electric Vehicle Journal. 2021; 12(4):178. https://doi.org/10.3390/wevj12040178
Chicago/Turabian StyleVan Kriekinge, Gilles, Cedric De Cauwer, Nikolaos Sapountzoglou, Thierry Coosemans, and Maarten Messagie. 2021. "Day-Ahead Forecast of Electric Vehicle Charging Demand with Deep Neural Networks" World Electric Vehicle Journal 12, no. 4: 178. https://doi.org/10.3390/wevj12040178
APA StyleVan Kriekinge, G., De Cauwer, C., Sapountzoglou, N., Coosemans, T., & Messagie, M. (2021). Day-Ahead Forecast of Electric Vehicle Charging Demand with Deep Neural Networks. World Electric Vehicle Journal, 12(4), 178. https://doi.org/10.3390/wevj12040178







