Hierarchical Model Predictive Control for Autonomous Collision Avoidance of Distributed Electric Drive Vehicle with Lateral Stability Analysis in Extreme Scenarios
Abstract
:1. Introduction
2. Distributed Drive Vehicle Model
2.1. Vehicle Kinematics Model
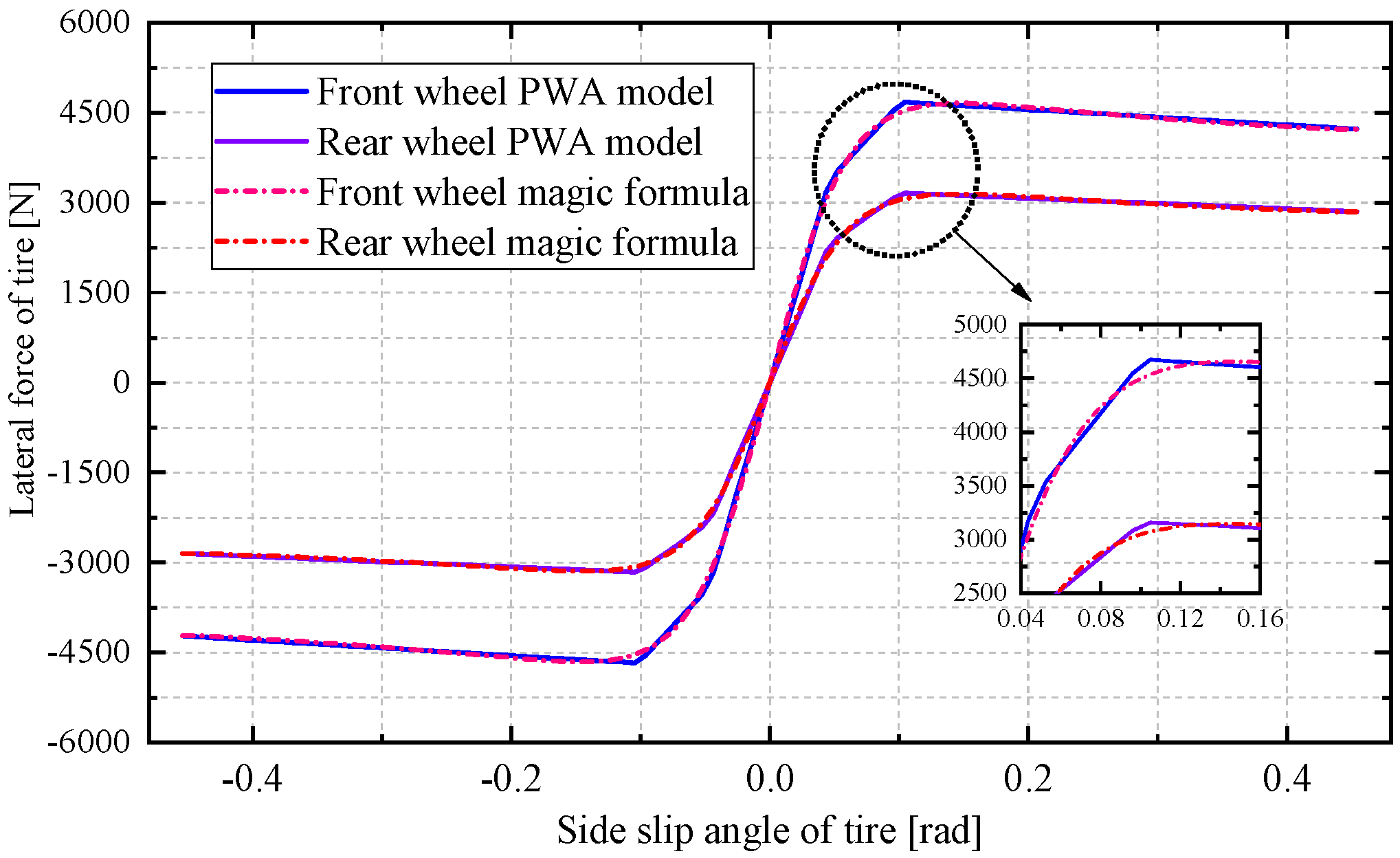
2.2. Piecewise Affine Vehicle Lateral Dynamics Model
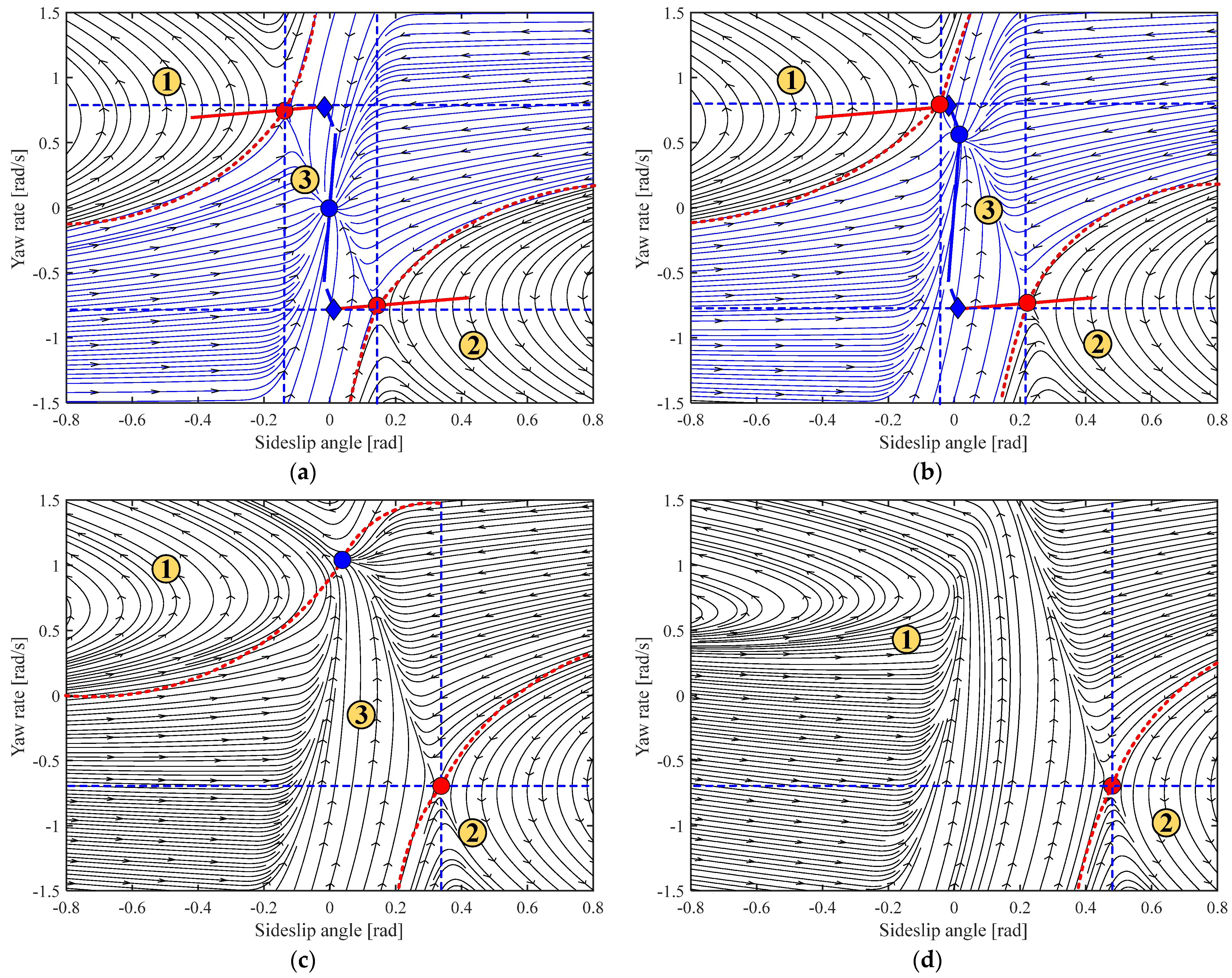
2.3. Stability Region Analysis Based on Phase Portrait
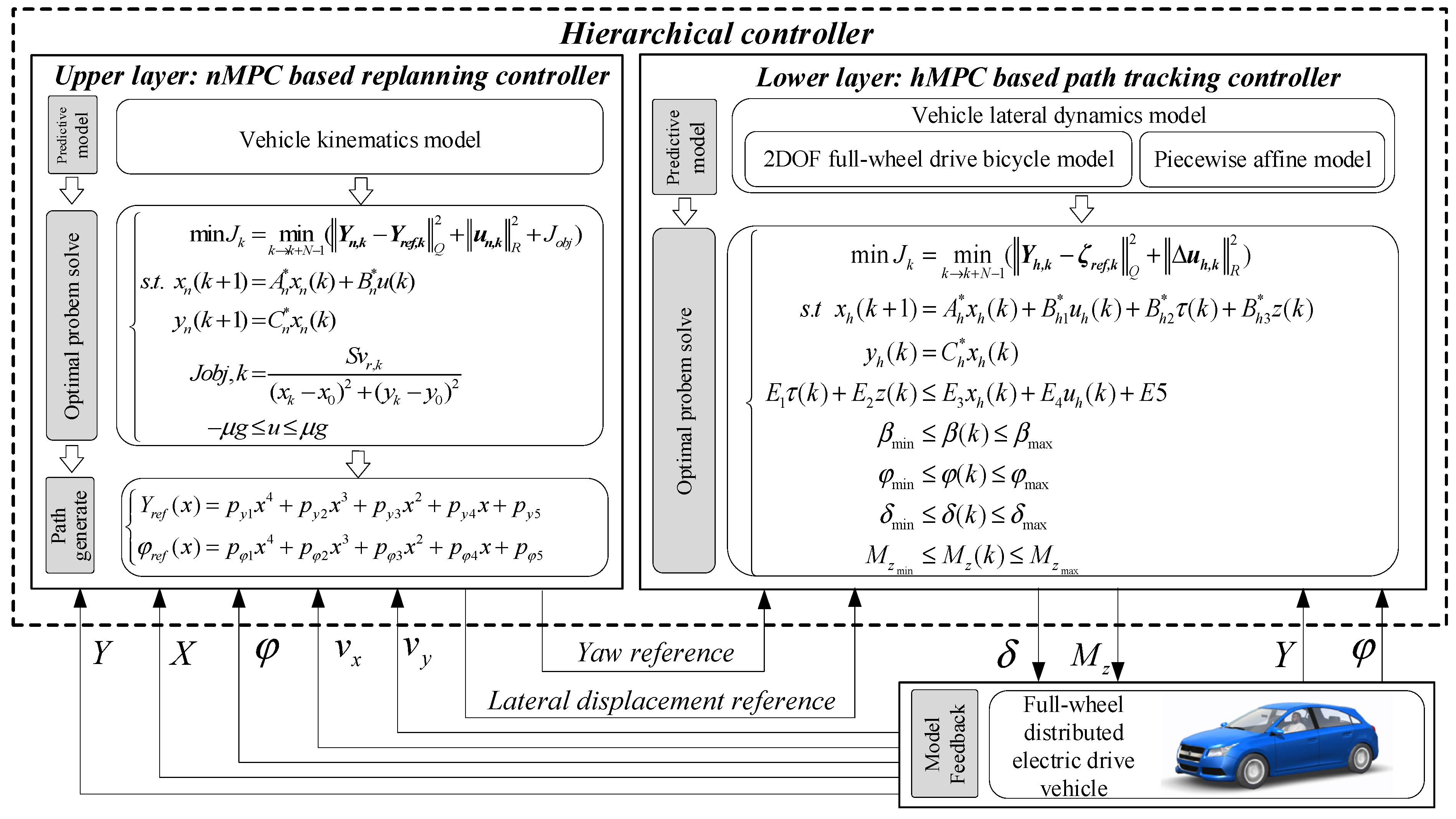
3. Hierarchical Controller Design
3.1. Path Planning Controller Based on Nonlinear MPC
3.2. Path Tracking Controller Based on Hybrid MPC
4. Simulation and Results Analysis
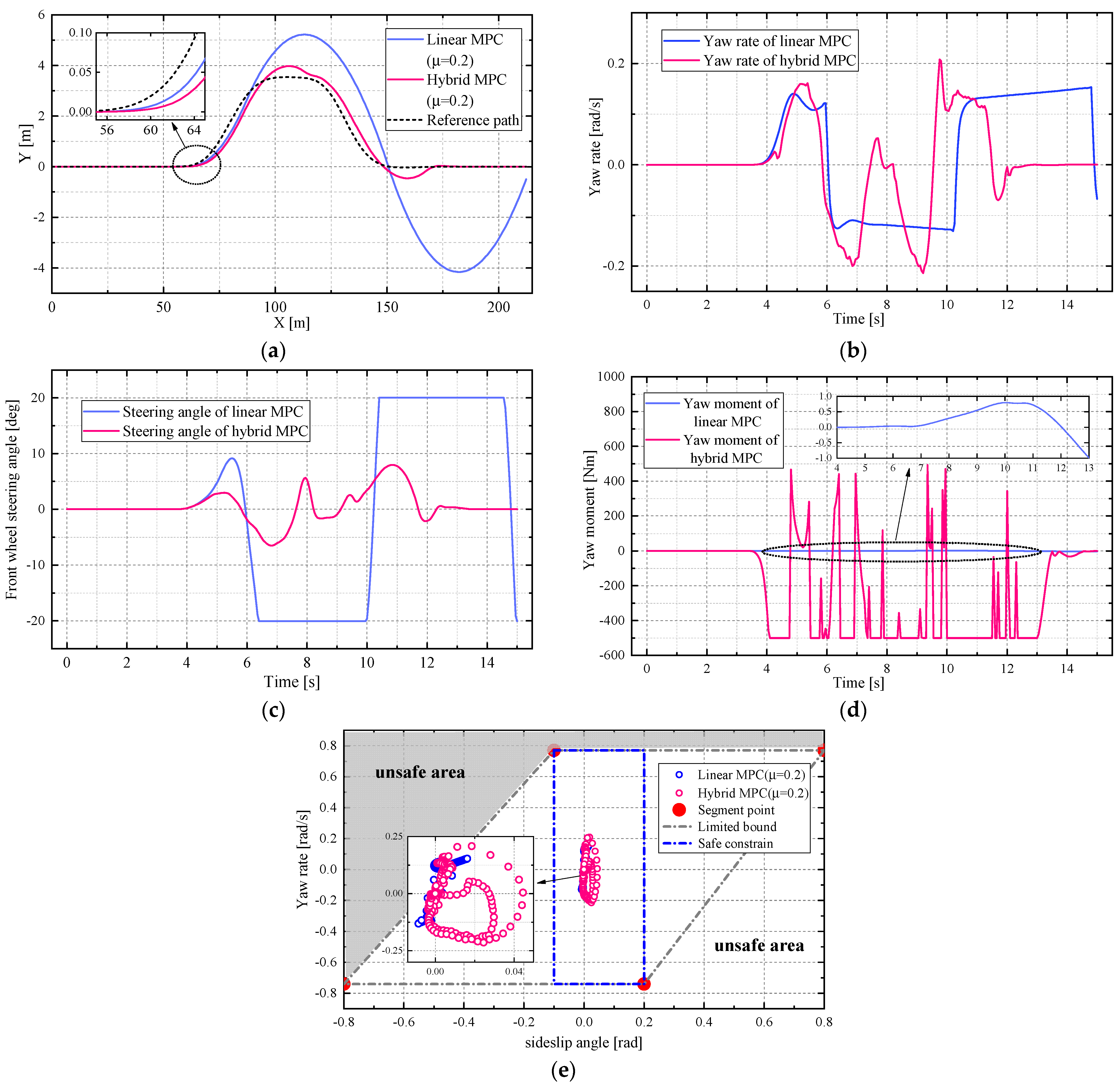
4.1. Simulation in a DLC Scenario
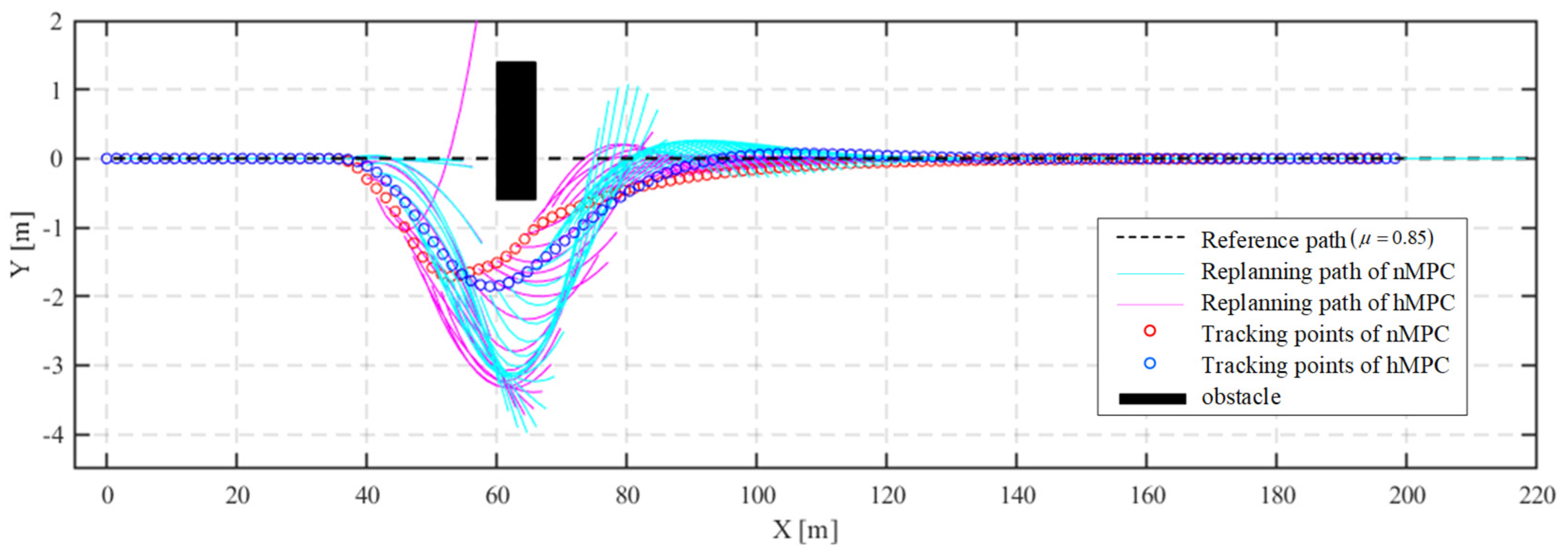
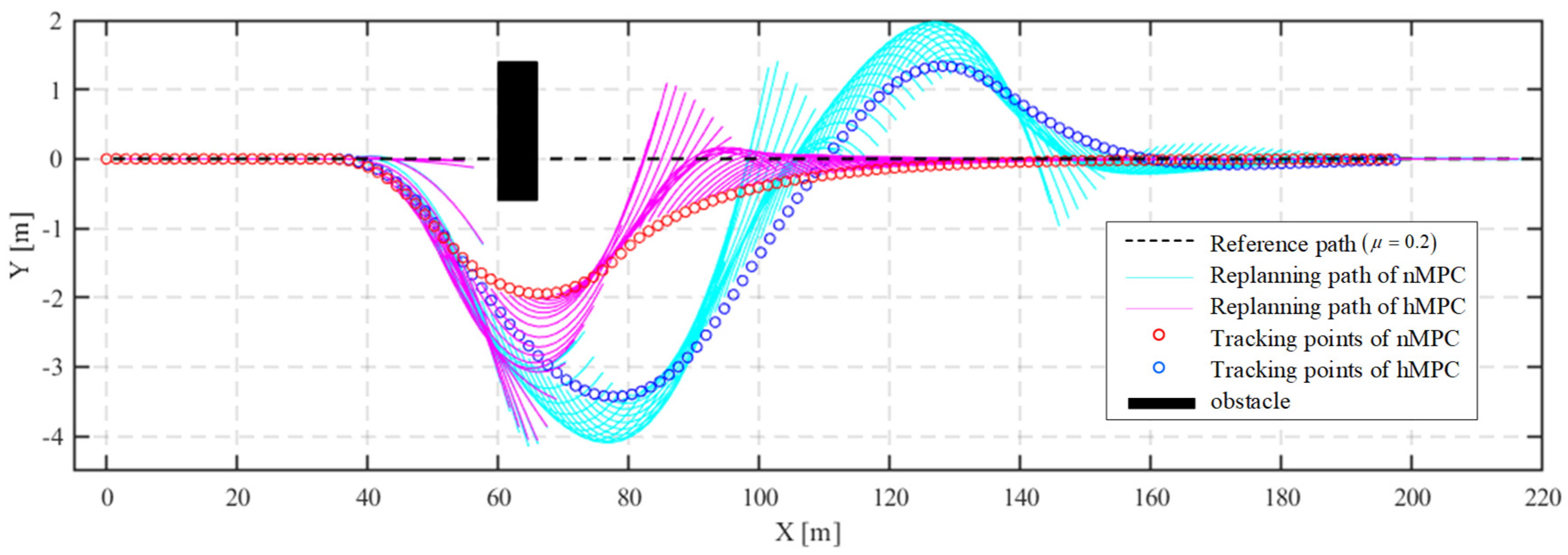
4.2. Simulation in a collIsion Avoidance Scenario
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Hang, P.; Chen, X.; Luo, F. LPV/H∞ Controller Design for Path Tracking of Autonomous Ground Vehicles Through Four-Wheel Steering and Direct Yaw-Moment Control. Int. J. Automot. Technol. 2019, 20, 679–691. [Google Scholar] [CrossRef]
- Lin, C.; Liang, S.; Chen, J.; Gao, X. A Multi-Objective Optimal Torque Distribution Strategy for Four In-Wheel-Motor Drive Electric Vehicles. IEEE Access 2019, 7, 64627–64640. [Google Scholar] [CrossRef]
- Zhao, B.; Xu, N.; Chen, H.; Guo, K.; Huang, Y. Design and Experimental Evaluations on Energy-Efficient Control for 4WIMD-EVs Considering Tire Slip Energy. IEEE Trans. Veh. Technol. 2020, 69, 14631–14644. [Google Scholar] [CrossRef]
- Zhang, C.; Chang, B.; Zhang, R.; Wang, R.; Wang, J. Observation of Dynamic State Parameters and Yaw Stability Control of Four-Wheel-Independent-Drive EV. World Electr. Veh. J. 2021, 12, 105. [Google Scholar] [CrossRef]
- Huang, Y.; Ding, H.; Zhang, Y.; Wang, H.; Cao, D.; Xu, N.; Hu, C. A Motion Planning and Tracking Framework for Autonomous Vehicles Based on Artificial Potential Field Elaborated Resistance Network Approach. IEEE Trans. Ind. Electron. 2020, 67, 1376–1386. [Google Scholar] [CrossRef]
- Lu, B.; He, H.; Yu, H.; Wang, H.; Li, G.; Shi, M.; Cao, D. Hybrid Path Planning Combining Potential Field with Sigmoid Curve for Autonomous Driving. Sensors 2020, 20, 7197. [Google Scholar] [CrossRef] [PubMed]
- Wahid, N.; Zamzuri, H.; Amer, N.H.; Dwijotomo, A.; Saruchi, S.A.; Mazlan, S.A. Vehicle collision avoidance motion planning strategy using artificial potential field with adaptive multi-speed scheduler. IET Intell. Transp. Syst. 2020, 14, 1200–1209. [Google Scholar] [CrossRef]
- Lim, W.; Lee, S.; Sunwoo, M.; Jo, K. Hierarchical Trajectory Planning of an Autonomous Car Based on the Integration of a Sampling and an Optimization Method. IEEE Trans. Intell. Transp. Syst. 2018, 19, 613–626. [Google Scholar] [CrossRef]
- Zhang, X.; Liniger, A.; Borrelli, F. Optimization-Based Collision Avoidance. IEEE Trans. Control. Syst. Technol. 2021, 29, 972–983. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Jayakumar, P.; Stein, J.L.; Ersal, T. Combined Speed and Steering Control in High-Speed Autonomous Ground Vehicles for Obstacle Avoidance Using Model Predictive Control. IEEE Trans. Veh. Technol. 2017, 66, 8746–8763. [Google Scholar] [CrossRef]
- Chen, L.; Ma, Y.; Zhang, Y.; Liu, J. Obstacle Avoidance and Multitarget Tracking of a Super Redundant Modular Manipulator Based on Bezier Curve and Particle Swarm Optimization. Chin. J. Mech. Eng. 2020, 33, 1–19. [Google Scholar] [CrossRef]
- Li, H.; Luo, Y.; Wu, J. Collision-Free Path Planning for Intelligent Vehicles Based on Bézier Curve. IEEE Access 2019, 7, 123334–123340. [Google Scholar] [CrossRef]
- Huang, C.; Huang, H.; Hang, P.; Gao, H.; Wu, J.; Huang, Z.; Lv, C. Personalized Trajectory Planning and Control of Lane-Change Maneuvers for Autonomous Driving. IEEE Trans. Veh. Technol. 2021, 70, 5511–5523. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, L.; Chen, J.; Shen, S. Safe Trajectory Generation for Complex Urban Environments Using Spatio-Temporal Semantic Corridor. IEEE Robot. Autom. Lett. 2019, 4, 2997–3004. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Lu, B.; Li, J.; Liu, T.; Xing, Y.; Lv, C.; Cao, D.; Li, J.; Zhang, J.; Hashemi, E. Risk Assessment and Mitigation in Local Path Planning for Autonomous Vehicles With LSTM Based Predictive Model. IEEE Trans. Autom. Sci. Eng. 2021, 1–12. [Google Scholar] [CrossRef]
- Hang, P.; Lv, C.; Huang, C.; Cai, J.; Hu, Z.; Xing, Y. An Integrated Framework of Decision Making and Motion Planning for Autonomous Vehicles Considering Social Behaviors. IEEE Trans. Veh. Technol. 2020, 69, 14458–14469. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, C.; Wang, J. Motion Planning with Velocity Prediction and Composite Nonlinear Feedback Tracking Control for Lane-Change Strategy of Autonomous Vehicles. IEEE Trans. Intell. Veh. 2020, 5, 63–74. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, Q.; Zhou, J.; Zheng, H.; Chen, H. Longitudinal and lateral control of autonomous vehicles in multi-vehicle driving environments. IET Intell. Transp. Syst. 2020, 14, 924–935. [Google Scholar] [CrossRef]
- Zheng, L.; Zeng, P.; Yang, W.; Li, Y.; Zhan, Z. Bézier curve-based trajectory planning for autonomous vehicles with collision avoidance. IET Intell. Transp. Syst. 2020, 14, 1882–1891. [Google Scholar] [CrossRef]
- Hang, P.; Han, Y.; Chen, X.; Zhang, B. Design of an Active Collision Avoidance System for a 4WIS-4WID Electric Vehicle. In Proceedings of the 5th IFAC Conference on Engine and Powertrain Control, Simulation and Modeling, Changchun, China, 20–22 September 2018; pp. 771–777. [Google Scholar]
- Hang, P.; Xia, X.; Chen, X. Handling Stability Advancement With 4WS and DYC Coordinated Control: A Gain-Scheduled Robust Control Approach. IEEE Trans. Veh. Technol. 2021, 70, 3164–3174. [Google Scholar] [CrossRef]
- Li, X.; Xu, N.; Guo, K.; Huang, Y. An adaptive SMC controller for EVs with four IWMs handling and stability enhancement based on a stability index. Veh. Syst. Dyn. 2020, 59, 1509–1532. [Google Scholar] [CrossRef]
- Yang, K.; Dong, D.; Ma, C.; Tian, Z.; Chang, Y.; Wang, G. Stability Control for Electric Vehicles with Four In-Wheel-Motors Based on Sideslip Angle. World Electr. Veh. J. 2021, 12, 42. [Google Scholar] [CrossRef]
- He, Z.; Nie, L.; Yin, Z.; Huang, S. A Two-Layer Controller for Lateral Path Tracking Control of Autonomous Vehicles. Sensors 2020, 20, 3689. [Google Scholar] [CrossRef]
- Tang, L.; Yan, F.; Zou, B.; Wang, K.; Lv, C. An Improved Kinematic Model Predictive Control for High-Speed Path Tracking of Autonomous Vehicles. IEEE Access 2020, 8, 51400–51413. [Google Scholar] [CrossRef]
- Choi, M.; Choi, S.B. Model Predictive Control for Vehicle Yaw Stability with Practical Concerns. IEEE Trans. Veh. Technol. 2014, 63, 3539–3548. [Google Scholar] [CrossRef]
- Li, S.E.; Chen, H.; Li, R.; Liu, Z.; Wang, Z.; Xin, Z. Predictive lateral control to stabilise highly automated vehicles at tire-road friction limits. Veh. Syst. Dyn. 2020, 58, 768–786. [Google Scholar] [CrossRef]
- Di Cairano, S.; Tseng, H.E.; Bernardini, D.; Bemporad, A. Vehicle Yaw Stability Control by Coordinated Active Front Steering and Differential Braking in the Tire Sideslip Angles Domain. IEEE Trans. Control. Syst. Technol. 2012, 21, 1236–1248. [Google Scholar] [CrossRef]
- Ataei, M.; Khajepour, A.; Jeon, S. Model Predictive Control for integrated lateral stability, traction/braking control, and rollover prevention of electric vehicles. Veh. Syst. Dyn. 2019, 58, 49–73. [Google Scholar] [CrossRef]
- Yuan, K.; Shu, H.; Huang, Y.; Zhang, Y.; Khajepour, A.; Zhang, L. Mixed local motion planning and tracking control framework for autonomous vehicles based on model predictive control. IET Intell. Transp. Syst. 2019, 13, 950–959. [Google Scholar] [CrossRef]
- Ji, J.; Khajepour, A.; Melek, W.W.; Huang, Y. Path Planning and Tracking for Vehicle Collision Avoidance Based on Model Predictive Control With Multiconstraints. IEEE Trans. Veh. Technol. 2017, 66, 952–964. [Google Scholar] [CrossRef]
- Sazgar, H.; Azadi, S.; Kazemi, R. Trajectory planning and combined control design for critical high-speed lane change manoeuvres. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 234, 823–839. [Google Scholar] [CrossRef]
- Gao, Y.; Gordon, T.; Lidberg, M. Optimal control of brakes and steering for autonomous collision avoidance using modified Hamiltonian algorithm. Veh. Syst. Dyn. 2019, 57, 1224–1240. [Google Scholar] [CrossRef]
- Liu, J.; Jayakumar, P.; Stein, J.L.; Ersal, T. Improving the robustness of an MPC-based obstacle avoidance algorithm to parametric uncertainty using worst-case scenarios. Veh. Syst. Dyn. 2019, 57, 874–913. [Google Scholar] [CrossRef]
- Borri, A.; Bianchi, D.; Di Benedetto, M.; Di Gennaro, S. Optimal workload actuator balancing and dynamic reference generation in active vehicle control. J. Frankl. Inst. 2017, 354, 1722–1740. [Google Scholar] [CrossRef]
- Bianchi, D.; Borri, A.; Toledo, B.C.; Di Benedetto, M.D.; Di Gennaro, S. Smart management of actuator saturation in integrated vehicle control. In Proceedings of the 2011 5th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 2529–2534. [Google Scholar]
- Bobier, C.G.; Gerdes, J.C. Staying within the nullcline boundary for vehicle envelope control using a sliding surface. Veh. Syst. Dyn. 2013, 51, 199–217. [Google Scholar] [CrossRef]
- Alberto Bemporad, M.M. Control of systems integrating logic, dynamics, and constraints. Automatica 1999, 39, 407–427. [Google Scholar] [CrossRef]
- Torrisi, F.; Bemporad, A. HYSDEL—A Tool for Generating Computational Hybrid Models for Analysis and Synthesis Problems. IEEE Trans. Control. Syst. Technol. 2004, 12, 235–249. [Google Scholar] [CrossRef]




| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| 1.015 | m | 1270 | kg | ||
| 1.885 | m | 9.8 | m/s2 | ||
| 15 | m/s | 1536.7 | Kg·m2 |
| Path Tracking Controller | RMSE of Tracking Errors | Computing Time Radio |
|---|---|---|
| Hybrid MPC | 0.20067 | 8.42104 |
| Linear MPC | 1.36947 | 7.52817 |
| Path Tracking Controller | RMSE of Tracking Error | Computing Time Radio |
|---|---|---|
| Hybrid MPC () | 0.44925 | 27.8171 |
| Hybrid MPC () | 0.58644 | 25.2747 |
| Linear MPC () | 0.49850 | 26.5447 |
| Linear MPC () | 1.09053 | 23.4518 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Lin, C.; Liang, S.; Gong, X.; Tao, Z. Hierarchical Model Predictive Control for Autonomous Collision Avoidance of Distributed Electric Drive Vehicle with Lateral Stability Analysis in Extreme Scenarios. World Electr. Veh. J. 2021, 12, 192. https://doi.org/10.3390/wevj12040192
Wang B, Lin C, Liang S, Gong X, Tao Z. Hierarchical Model Predictive Control for Autonomous Collision Avoidance of Distributed Electric Drive Vehicle with Lateral Stability Analysis in Extreme Scenarios. World Electric Vehicle Journal. 2021; 12(4):192. https://doi.org/10.3390/wevj12040192
Chicago/Turabian StyleWang, Bowen, Cheng Lin, Sheng Liang, Xinle Gong, and Zhenyi Tao. 2021. "Hierarchical Model Predictive Control for Autonomous Collision Avoidance of Distributed Electric Drive Vehicle with Lateral Stability Analysis in Extreme Scenarios" World Electric Vehicle Journal 12, no. 4: 192. https://doi.org/10.3390/wevj12040192
APA StyleWang, B., Lin, C., Liang, S., Gong, X., & Tao, Z. (2021). Hierarchical Model Predictive Control for Autonomous Collision Avoidance of Distributed Electric Drive Vehicle with Lateral Stability Analysis in Extreme Scenarios. World Electric Vehicle Journal, 12(4), 192. https://doi.org/10.3390/wevj12040192






