Optimization of TSPWM for Common-Mode Voltage Reduction in Vehicular Electric Drive System

Abstract

Common-mode voltage can be reduced effectively by optimized modulation methods without increasing additional costs. However, the existing methods cannot satisfy the requirements of the vehicular electric-drive application. This paper optimizes the tri-state voltage modulation method to reduce the common-mode voltage for vehicular electric drive system applications. Firstly, the discontinuous switching issue during sector transition is analyzed. Under the limit of two switching times in one period, multiple alignments combination is proposed to address that issue. Secondly, the zero-voltage time intervals in different modulation ranges are explored. This paper proposes an unsymmetric translation method to reconstruct the voltage vector, and then the minimum zero-voltage time interval is controlled to enough value for safe switching. Finally, the proposed methods have been validated through experiments on a vehicular electric drive system. The results show that the common-mode voltage can be reduced effectively in the whole range with the optimized tri-state voltage modulation method.

1. Introduction

The conventional space vector pulse width modulation (SVPWM) has been widely applied to the vehicular electric drive system, as it performs well in terms of voltage linearity, current harmonics, and system efficiency [1,2]. However, since the introduction of the zero vectors of 000 and 111, the corresponding amplitude of the common-mode voltage (CMV) is equal to V_dc/2 (the DC bus voltage) [3]. On the one hand, the excessively high CMV will lead to poor electromagnetic compatibility (EMC) performance [4]. On the other hand, the common-mode voltage will break down the bearing oil film and generate shaft currents, which can corrode the bearing and seriously affect the noise, vibration, and harshness (NVH) and safety performance of the electric drive system [5].

The CMV fluctuation can be reduced by hardware or software methods. The hardware solutions, such as adding filters or adopting complex topologies, will increase the cost and size of the electric drive system [6]. On the contrary, the software solutions adjusting the voltage modulation strategies are more flexible and applied widely [7,8]. According to the selection of voltage space vectors, the reduction of common-mode voltage (RCMV) methods include the active zero state PWM (AZSPWM1, AZSPWM2, AZSPWM3) [9], remote state PWM (RSPWM) [10], near state PWM (NSPWM [11]), TSPWM [12,13]. Both these RCMV methods can reduce the maximum CMV of conventional SVPWM from V_dc/2 to V_dc/6, and then decrease the negative effect of CMV on the EMC and shaft corrosion. However, most RCMV methods have bipolar line-to-line voltage patterns, require simultaneous switching, and cause significant voltage harmonics, which is not suitable for practical application. Among those RCMV methods, the TSPWM performs best in the whole modulation range, harmonic proportion, and system efficiency [14]. Thus, this paper will optimize the TSPWM method and apply it to the CMV reduction of the vehicular electric drive system.

The main contributions of this paper are shown as follows:

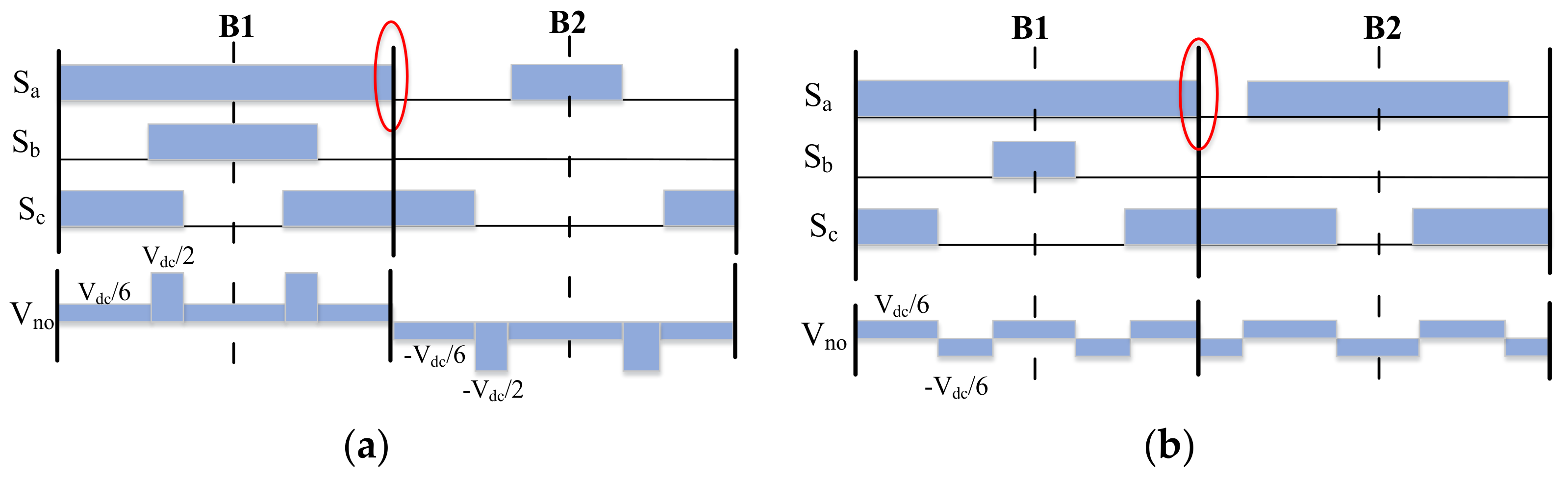
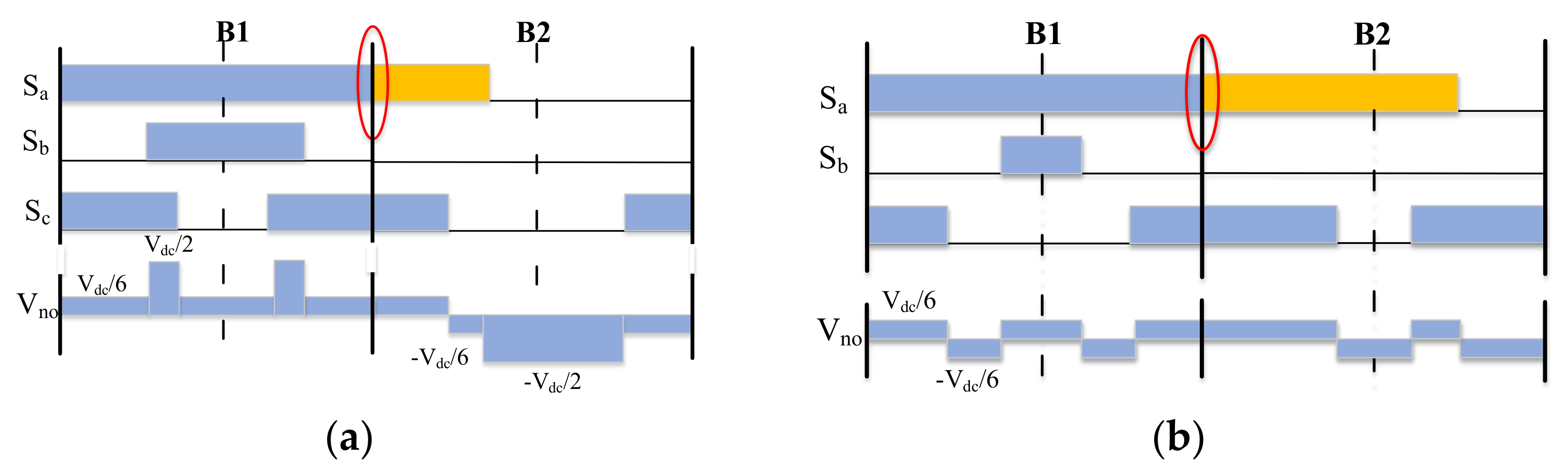
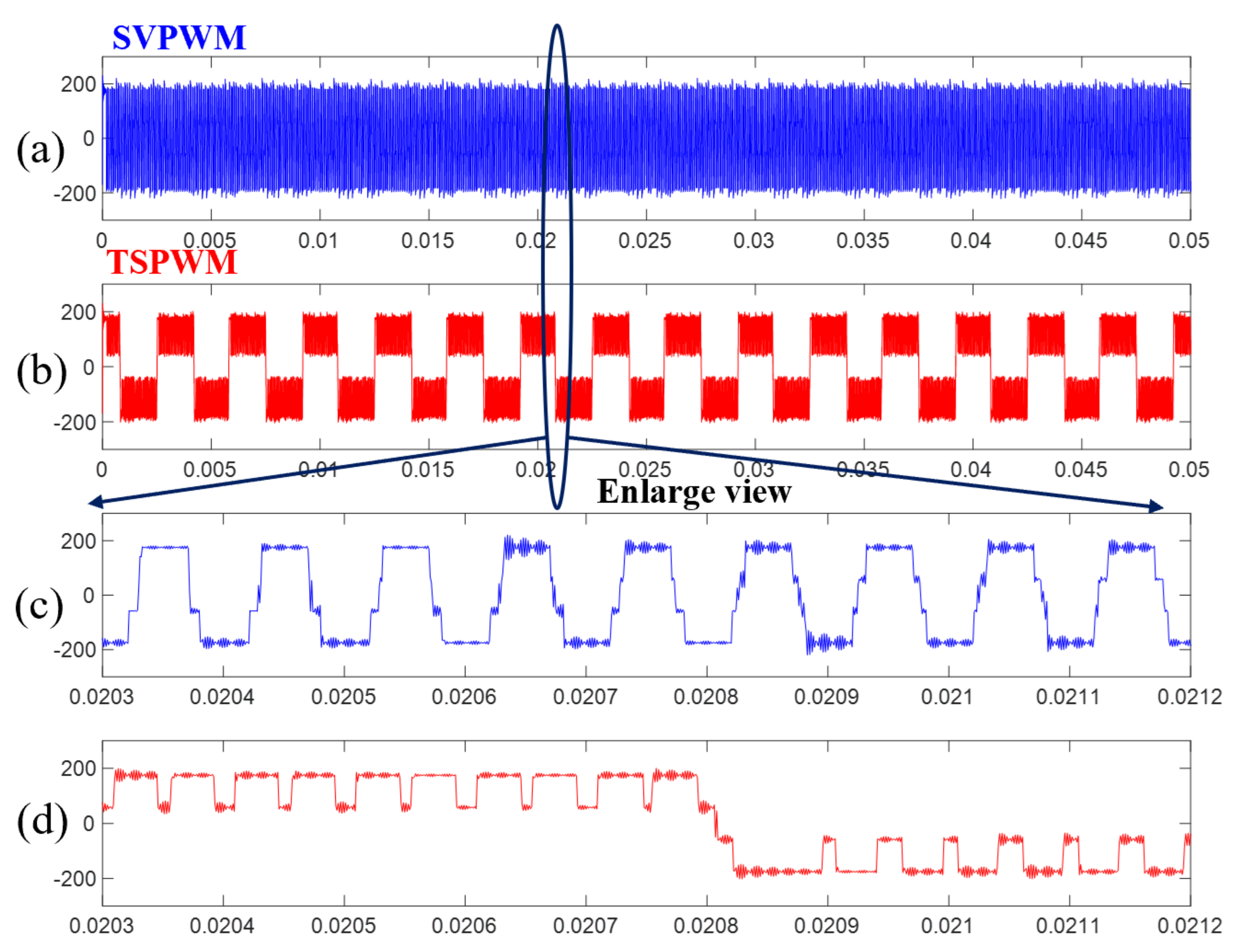
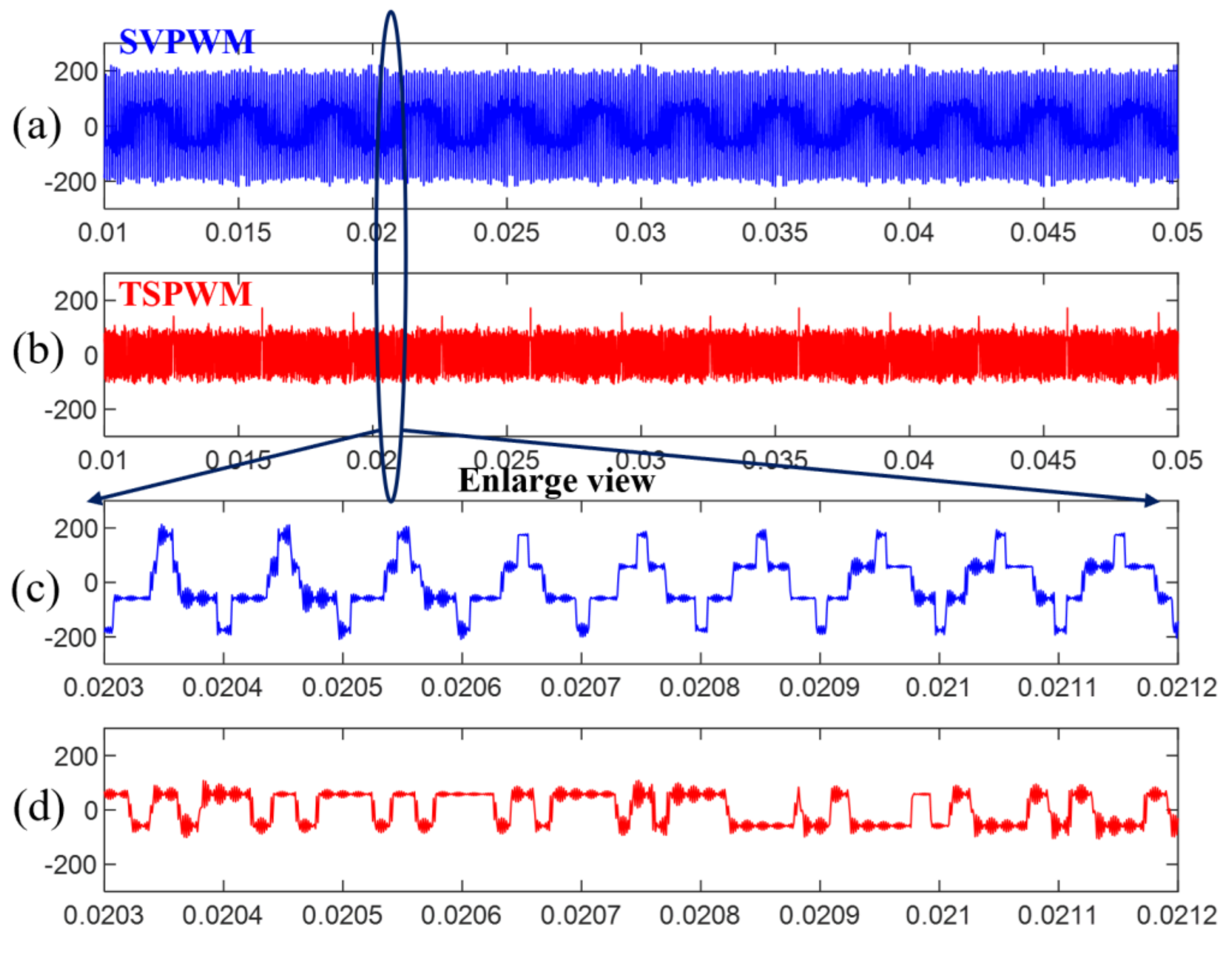
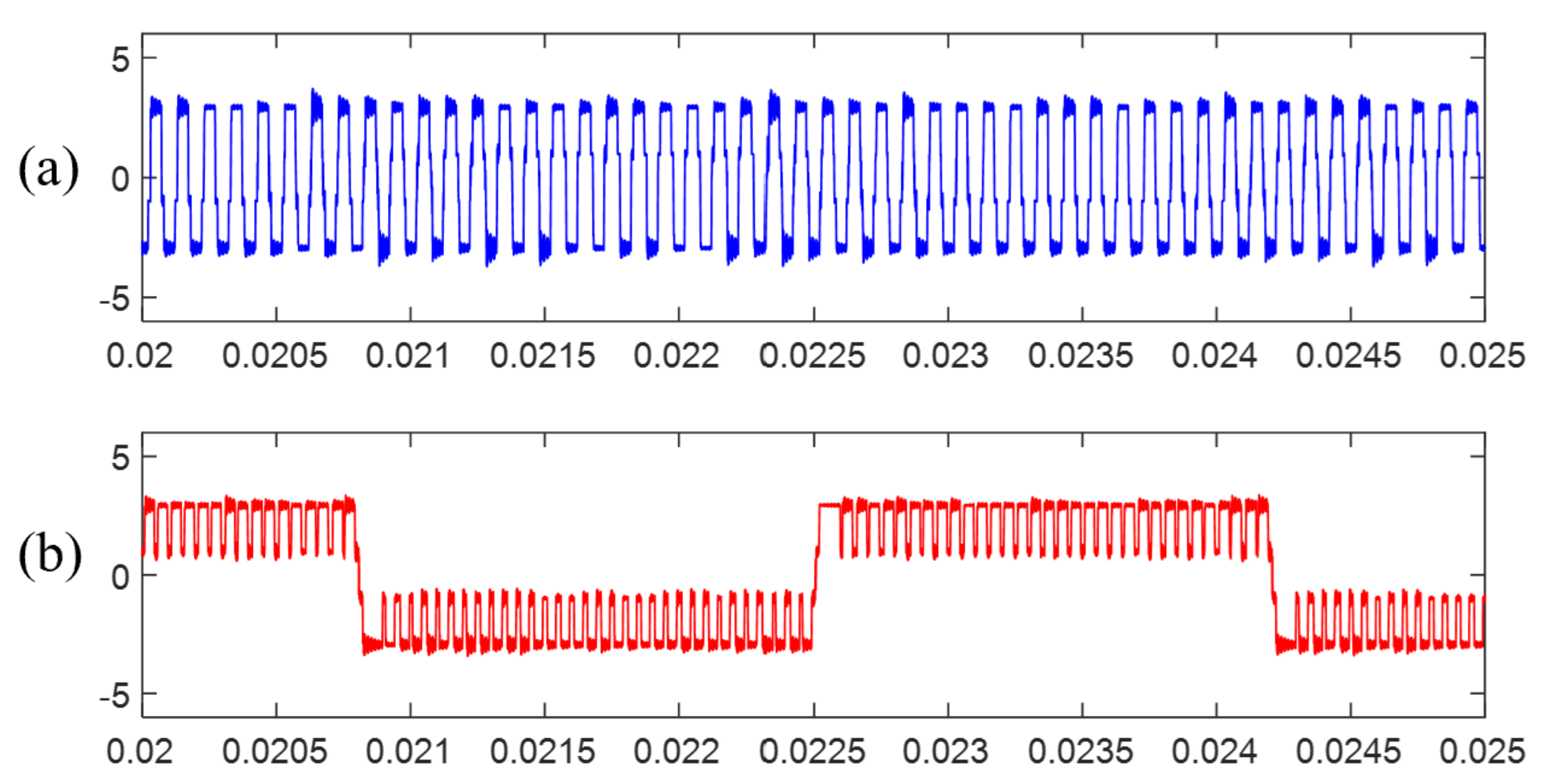
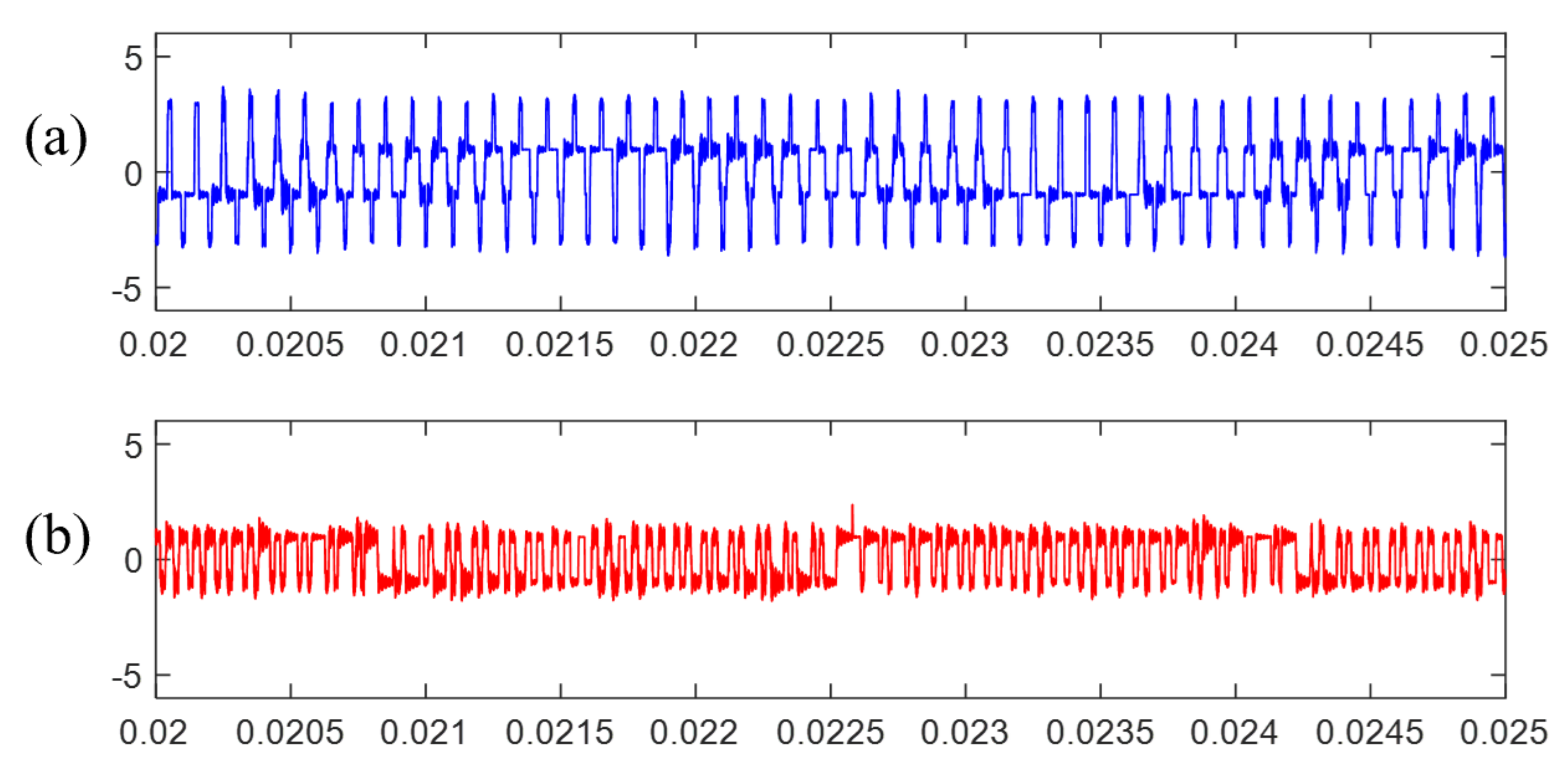
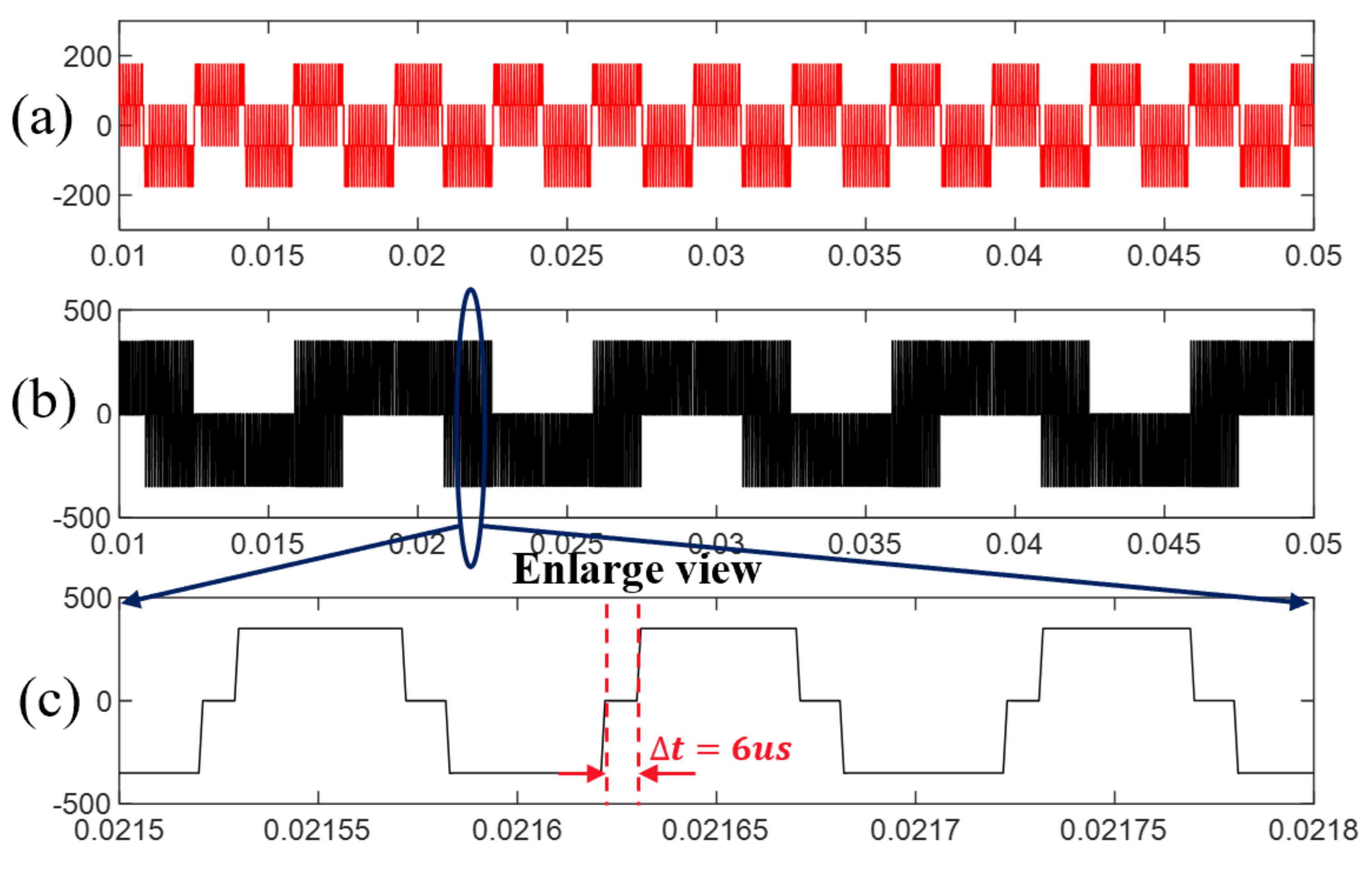
• The standard TSPWM needs to switch three times in one period when the voltage vector transit from one sector to another, which is not suitable for vehicular electric drive applications. This paper combines different alignment technology in the sector transition process. The switch times are reduced to one while the CMV can keep low in the whole control range.
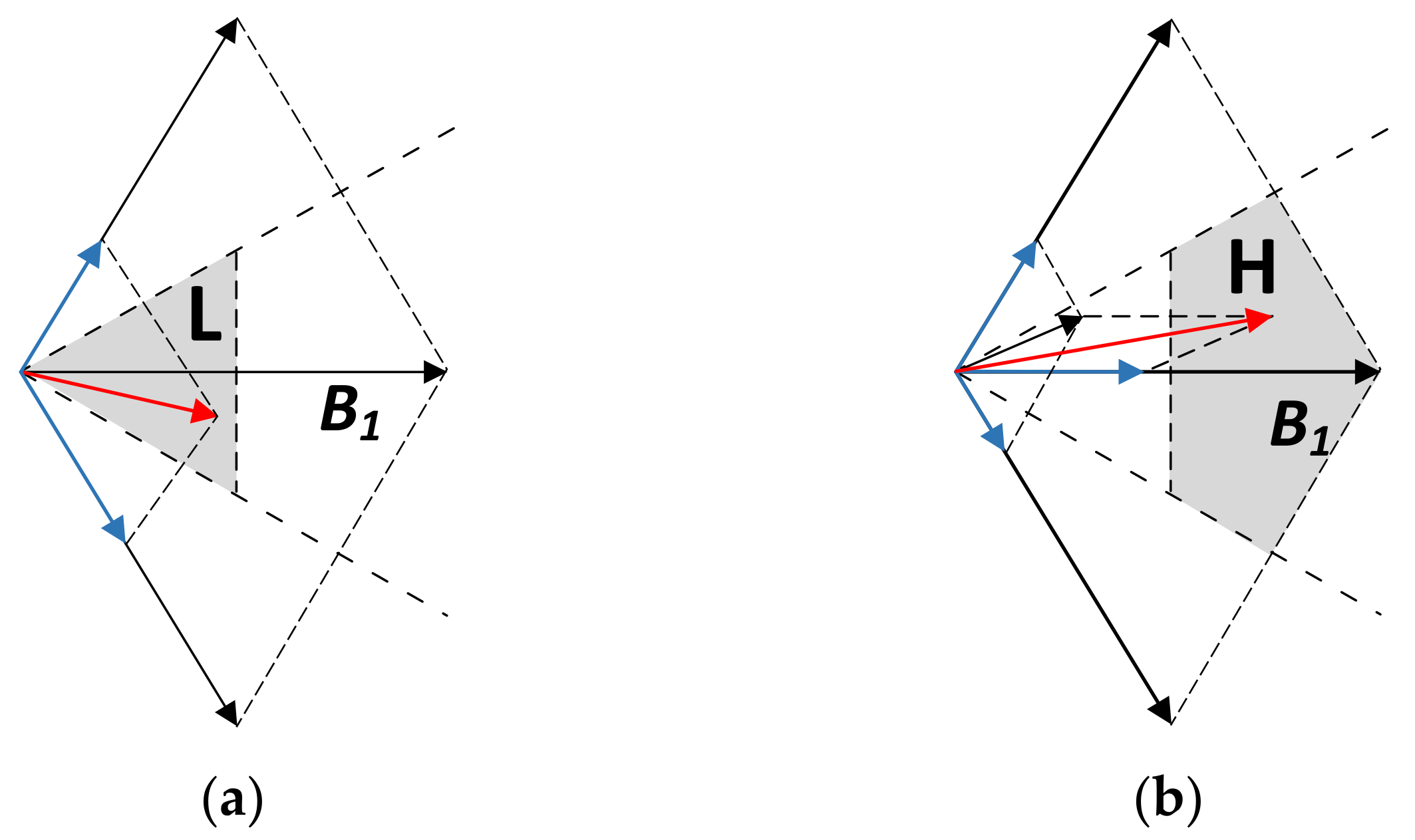
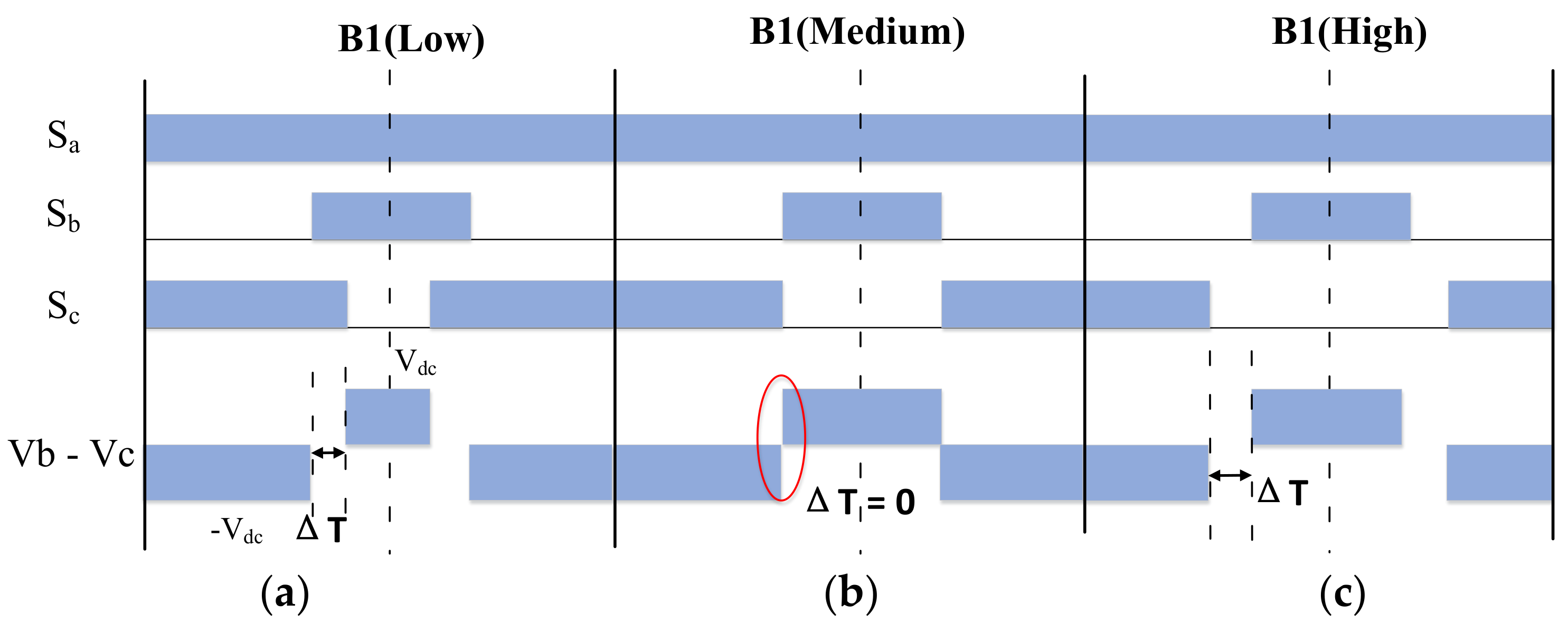
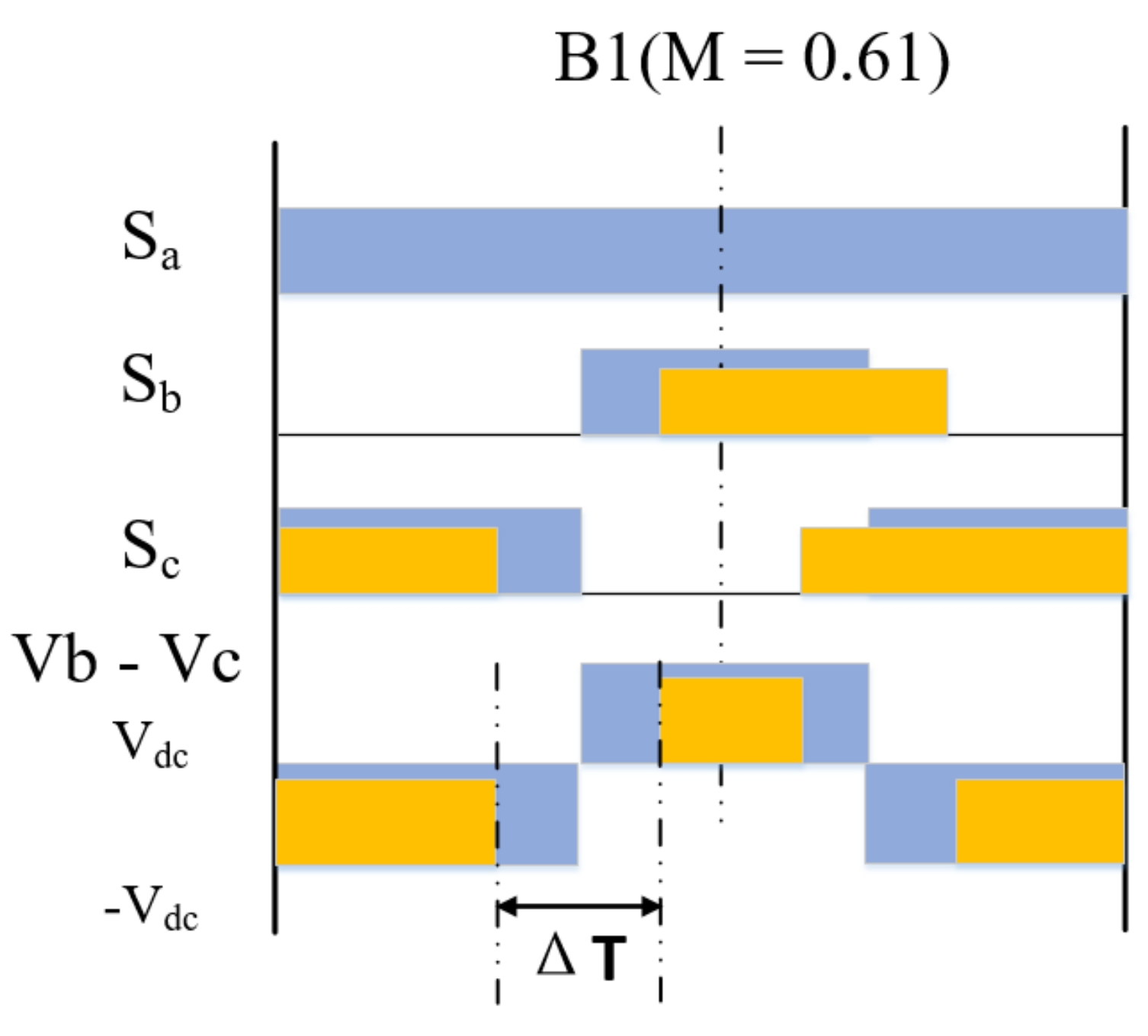
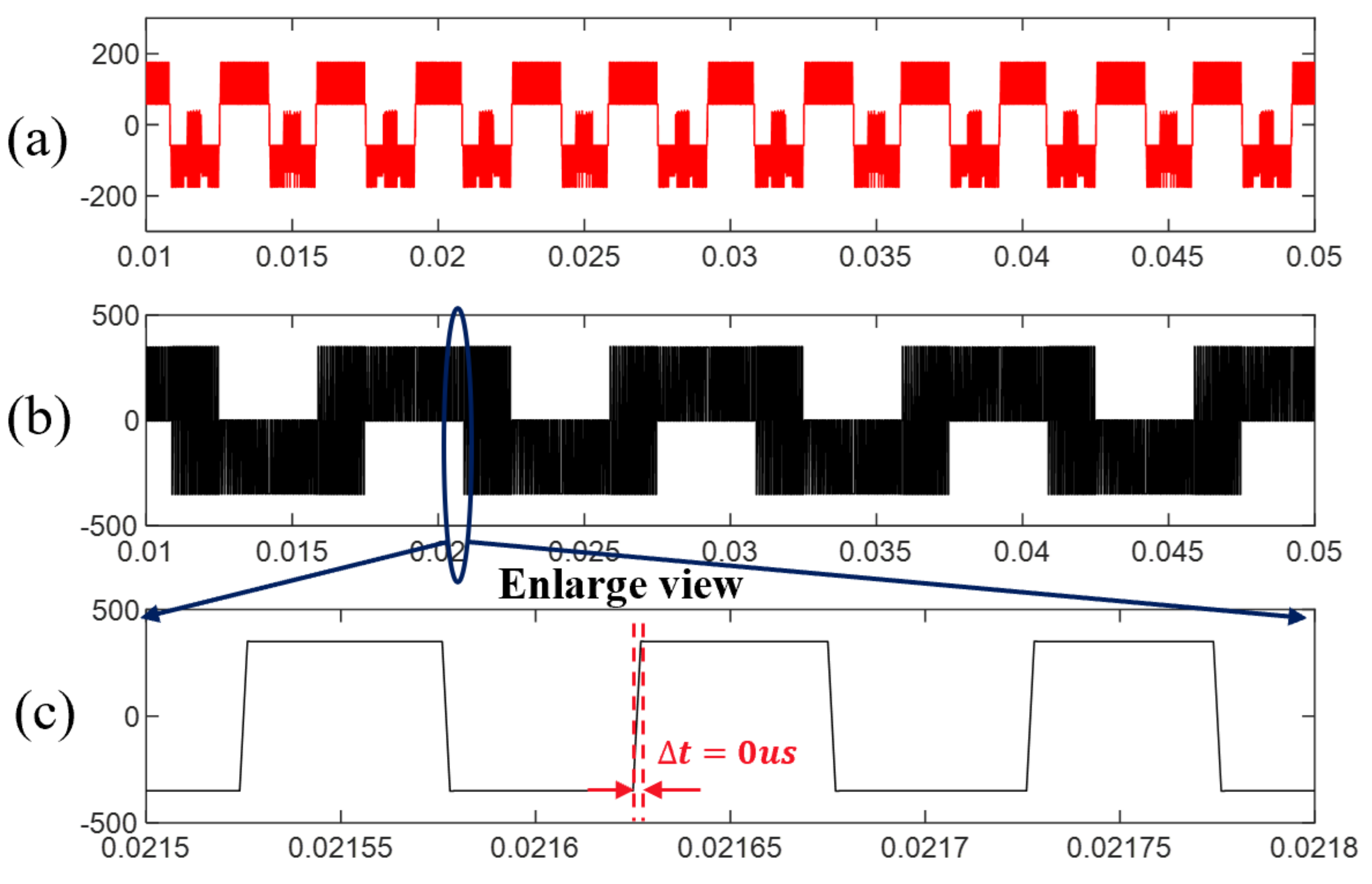
• In the standard TSPWM, the minimum zero-voltage time interval between line-to-line voltage pulse reversals is close to zero in the border between the high and low region of TSPWM, which causes overvoltage and can be dangerous in a vehicular electric drive application. This paper proposes an unsymmetric translation method to reconstruct the voltage vector, and then the minimum zero-voltage time interval is controlled to a safe lower limit.

The rest of this paper is as follows: Section 2 makes a simple review of the existing TSPWM technology; Section 3 analyzes two issues of the standard TSPWM, and then proposes the corresponding solutions for each issue respectively; Section 4 compares the experimental results with or without the proposed methods; Section 5 discusses the work of this paper and makes a further research plan.

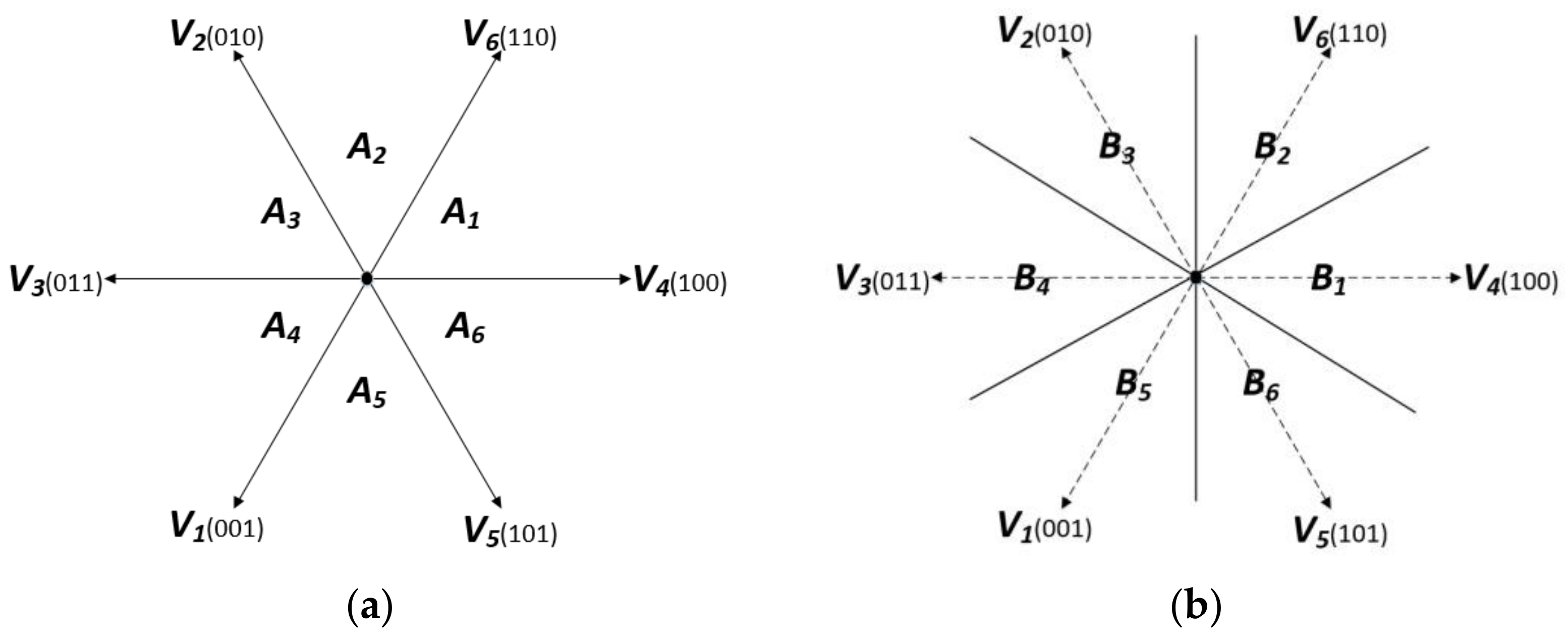
2. Review of the Existing TSPWM Technology

The topology of the conventional three-phase electric drive system is shown in Figure 1. CMV of the system is defined as the voltage difference between the neutral point of the electric machine (n) and the midpoint of dc voltage (o); the phase voltages can represent this:

$$V_{no}=\frac{V_{ao}+V_{bo}+V_{co}}{3}$$

(1)

When the conventional SVPWM is applied, the output voltages can be divided into six different voltage sectors depending on the selected primary voltage vectors. As shown in Figure 2a, in the voltage sector A1, the output voltages are generated by combing the basic voltage vectors V₄ (100) and V₆ (110). While in the TSPWM method, all the voltage sectors have 30 degrees ahead compared to the conventional SVPWM, as shown in Figure 2b.

In the standard TSPWM technology, the switch patterns can be divided based on the modulation factor. As shown in Figure 3, in the B1 voltage sector, the desired output voltage vector is constructed by two primary voltage vectors and the zero-voltage vector in the low modulation region. While in the high modulation region, three nearest voltage vectors are applied together to construct the desired output voltage vector.

The CMV of SVWPM and TSPWM in different regions are compared in Figure 4. The fluctuation amplitude of CMV with conventional SVPWM is much larger than the TSPWM, with V_dc and V_dc/3, respectively. Besides, although the maximum CMV value with the TSPWM in the low region reaches V_dc/2, the minimum CMV is V_dc/6. The whole fluctuation of CMV in the B1 voltage sector can remain under V_dc/3. The more considerable CMV fluctuation will only occur in the sector switching time. Moreover, the maximum CMV and CMV fluctuation keep low for the CMV with TSPWM in the high region. In short, with the TSPWM method, the CMV can be reduced to a relatively low range, which is beneficial for suppressing EMC and shaft corrosion.

However, in the standard TSPWM strategy, three switching times in one period are needed when the voltage vector transitions from one sector to another. Besides, the zero-voltage time interval between line-to-line voltage pulse reversals can be too small when the modulation factor is close to the boundary between the high and low regions. Both these two aspects cannot satisfy the requirements of the electric drive system. Thus, in the following parts of this paper, these two problems of TSPWM are discussed, and the corresponding optimization solution is developed to address these issues.

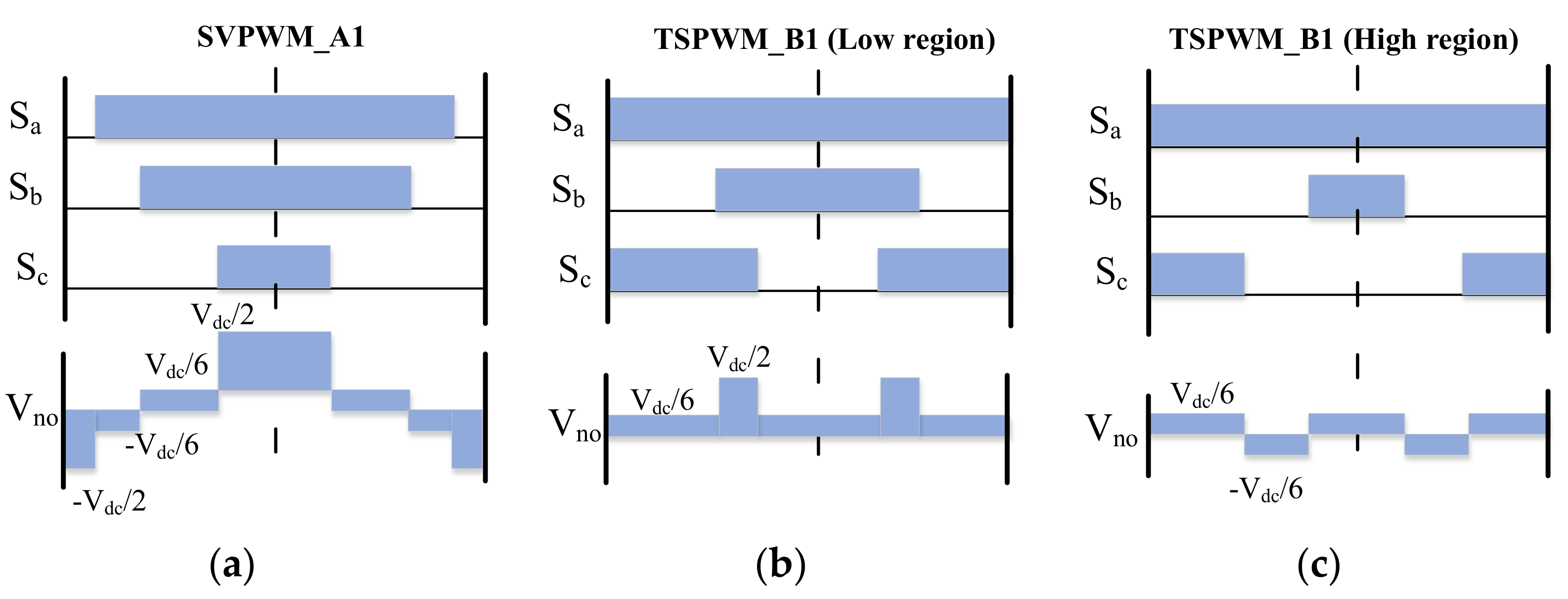
3. Optimization of TSPWM

3.1. Discontinuous Switching between Different Sectors

In Figure 5a, the discontinuous switching phenomenon of TSPWM in the low region is represented. In the standard TSPWM, the switch state of S_a at the end of sector B1 is high, but it changes to low at the beginning of sector B2. When the voltage vector changes to sector B2, the state of S_a should switch to low immediately and then switches on and off by following the regular instructions. Thereby, three switch times are needed in one period, leading to additional switching loss and voltage spike, and the actual output voltage vector also has a slight deviation from the desired output voltage. Similarly, the discontinuous switching phenomenon will occur in the high region with the standard TSPWM method, as shown in Figure 5b.

In Figure 6, the left-alignment configuration of Sa is applied in the sector transition time to solve this issue. Then only one switch time is needed in sector B2, and as the switch on the duty of S_a is the same as the standard central-alignment configuration, the average output voltage has no deviation to the desired voltage. Simultaneously, the fluctuation of the CMV is as slight as the standard TSPWM. Please notice that only in the transition time, the left-alignment configuration is utilized, and then for the following voltage vector in the B2 sector, the standard central alignment will be reused to achieve better harmonic performance. Besides, the right alignment should also be applied for the transit between another voltage sector.

3.2. Increase Zero-Voltage Time Interval

For the conventional SVPWM, the zero-voltage time interval between line-to-line voltage pulse reversals can always stay at a relatively large value. As shown in Figure 7, the line-to-line voltage pulse reversal only occurs between two dependent PWM periods. Moreover, since the maximum switch-on time of every phase is smaller than one period, the $\Delta T$ in Figure 6 is much larger than zero. Thereby, for the conventional SVPWM, the zero-voltage time interval will not occur, which is also an essential advantage of that modulation method.

As for the TSPWM, the voltage-time interval $\Delta T$ can keep large in both the low and high modulation factor region, which is shown in Figure 8a,c. However, the $\Delta T$ can be zero when the modulation factor equals 0.61. The overvoltage caused by the zero-voltage time interval is dangerous for the vehicular electric drive system.

To address this problem, a novel switch configuration is developed. As shown in Figure 9, the on–off switch time of S_b is moved in the right direction, while the on–off switch time of S_c is moved in the left direction. Moreover, in the moving process, the switch-on time of S_b and S_c are not changed to guarantee the output voltage is the same as the desired voltage. Then, the voltage time interval $\Delta T$ can be about twice the moving time length. The $\Delta T$ is determined by the dead time and switch characteristics of electric drive, and its value can be calibrated in practical application.

4. Experiment

To validate these two optimization methods of TSPWM, a simulation platform including modulation strategy, inverter model, standard voltage model, and bearing voltage model is established in MATLAB/Simulink. The shaft voltage model is constructed through some equivalent capacitances, in which the C_sf denotes the capacitance between stator winding and machine housing, the C_sr denotes the capacitance between stator winding and rotor, the C_rf denotes the capacitance between the rotor and machine housing. The C_b and R_b denote the capacitance and resistance of bearing oil film. The corresponding parameters of the simulation platform are shown in

Table 1. Parameters of the simulation platform.

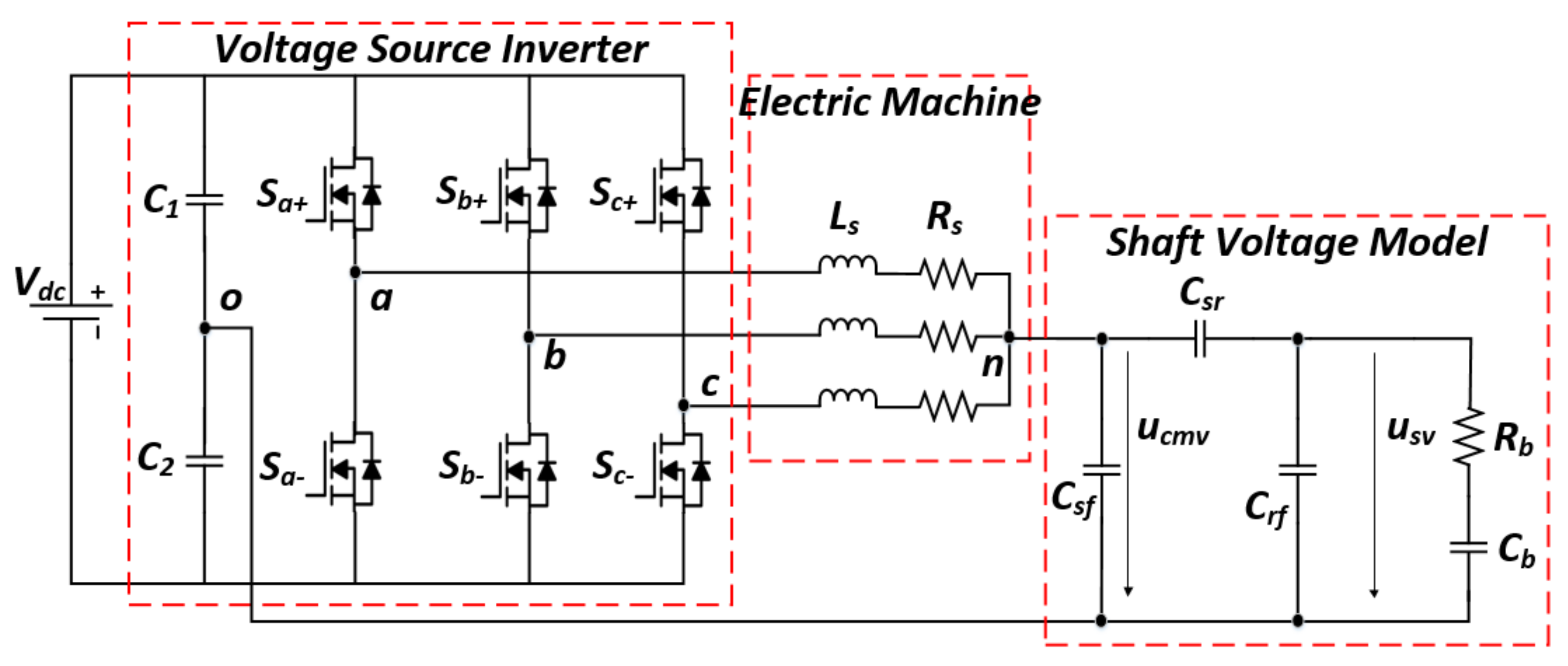
Parameters	Value	Parameters	Value
DC link voltage	360 V	Csf	11 nf
Switching frequency	10 kHz	Csr	33 pf
Machine speed	6000 rpm	Crf	1.65 nf
Phase current	200 A	Cb	300 pf
Simulation step	1 × 10−6 s	Rb	3.2 Ω

.

Firstly, the optimization for discontinuous switching between different sectors has been validated. In Figure 10, the CMV of the conventional SVPWM and optimized TSPWM in low modulation factor (0.2) are compared. By combing the left-alignment, central-alignment, right-alignment, the switching times in one period can be controlled equal to or less than two. At the same time, the CMV of the optimized TSPWM has the same performance as the standard TSPWM, with only 1/3 of the conventional SVPWM. Besides, the CMV performance in high modulation factor (0.8) is also demonstrated, as shown in Figure 11. The CMV fluctuation has been suppressed effectively from ±180 V to about ±60 V.

Secondly, the bearing voltage with different modulation methods is also obtained via the bearing voltage equivalent model. The bearing voltage is about 1/60 of the CMV. The wave of bearing voltage has the same change law as the CMV. Thus, as shown in Figure 12 and Figure 13, the bearing voltage fluctuation with the optimized TSPWM method is about 1/3 of the bearing voltage with the SVPWM, and the corresponding values are ±3 V and ±1 V, respectively.

At last, the optimization for zero-voltage time intervals with the TSPWM method has been validated. In Figure 14, the line–line voltage V_ab wave when the modulation factor is 0.6 is shown. From the enlarged view, we can notice that the minimum voltage pulse reversals can be zero at some points, which is extremely dangerous for the vehicular electric drive system. Then, the V_ab with an optimized TSPWM strategy is tested. Setting the moving time length for each phase to 5 μs, the minimum voltage pulse reversals are expanded to about 6 μs, as shown in Figure 15.

5. Conclusions

This paper focuses on the application problem of TSPWM to the vehicular electric drive system. It then optimizes the standard TSPWM to address two issues: discontinuous switching between different sectors and the zero-voltage time interval between voltage pulse reversals. The validation of the proposed methods is carried out in a simulation platform. The results show that with the proposed strategies in this paper, the CMV can be reduced to one-third of the SVPWM without additional switching and the zero-voltage time interval. Thus, the methods effectively promote the TSPWM on vehicular applications by reducing EMC and improving bearing life. Further work will be implemented to test the proposed strategies in a practical test bench and explore the efficiency and harmonic characteristics of TSPWM.