Torque Distribution Based on Dynamic Programming Algorithm for Four In-Wheel Motor Drive Electric Vehicle Considering Energy Efficiency Optimization

Abstract

The improvement of both the stability and economy of the four in-wheel motor drive (4IWMD) electric vehicle under complex drive cycles is currently a difficult problem in this field. A torque distribution method with the comprehensive goals of optimal torque distribution and energy efficiency, considering economy through energy efficiency for the 4IWMD electric vehicle, is proposed in this paper. Each component of the 4IWMD electric vehicle is modelled. The dynamic programming (DP) control algorithm is utilized for torque distribution between the front and rear in-wheel motors to obtain optimal torque distribution and energy efficiency in the 4IWMD electric vehicle. The simulation is performed on a co-simulation platform with the software of AVL Cruise and MATLAB/Simulink, considering a straight road. Compared to the fuzzy logic control algorithm, the simulation results are very promising, as the energy consumption of the electric vehicle was reduced by 22.68%, 20.73% and 21.84% under the WLTC, NEDC and customized IM240 driving cycle conditions, respectively, with the proposed DP control algorithm. The hardware-in-the loop (HIL) experimental results also indicate that the effectiveness of the proposed DP algorithm is verified under the NEDC, WLTC and IM240 driving cycles, when a straight road is considered. The proposed DP control algorithm not only reduces the vehicle energy consumption and guarantees the optimization of torque distribution, but also increases the driving range of the vehicle.

1. Introduction

Over the years, owing to the increasingly severe energy crisis and environmental pollution, there has been an increase in the demand and manufacture of electric vehicles. Researchers have carried out extensive research on electric vehicles, especially on in-wheel motor drive (IWMD) electric vehicles. Amongst electric vehicles, IWMD electric vehicles possess distinct advantages, some of which are a simple and compact structure, flexible maneuverability and steering, high transmission efficiency and easy control including the independent torque control of each wheel.

The possibility for individual torque control has led to ample research in this area, including research focus on torque distribution, with a large focus on safety. Safety-based torque distribution utilizes torque vector/torque distribution to improve traction, handling and stability performances in vehicles. Li et al. [1] proposed an optimal torque distribution approach for the improvement of vehicle handling and stability in spite of slippery road conditions. Joa et al. [2] presented an integrated chassis control method for front/rear torque distribution and four-wheel independent braking based on tire slip which improves handling performance. A novel torque vectoring algorithm was proposed by Park et al. [3] to improve cornering performance in electronic-four-wheel drive vehicles, meanwhile Deng et al. [4] and Chatzikomis et al. [5] studied a torque vectoring algorithm, with a consideration of stability and economy, as well as safety and energy efficiency improvement, respectively. The total longitudinal slip of an electric vehicle can also be reduced through novel torque distribution strategies to improve the vehicle safety [6]. When considering safety, results from a torque distribution study indicate that the improved stability of the vehicle can be derived when a greater weight coefficient is applied to the rear wheels, as this causes the rear axle to bear a larger weight [7]. Four IWMD electric vehicles which have four in-wheel motors positioned inside each of the vehicle wheel possess several advantages as stated earlier, including the delivery of the desired torque directly to each wheel [8], providing increased possibilities for economy management and improvement. Based on the vehicle requirement for propulsion, the torque distributed to each motor has to be well controlled and distributed to ensure the in-wheel motor functions efficiently and prevents energy loss. Furthermore, part of the efficiently distributed energy can be saved through regenerative braking, ensuring maximal energy saving [9,10,11].

Considering vehicle economy, methods for acquiring optimal torque distribution are diverse, and this includes utilizing motor loss models for gaining optimal torque distribution [12,13]. The motor loss model has the possibility of increasing system efficiency by some margin. However, the boundary conditions, such as motor parameters and control algorithms, could affect the possibility of getting the desired positive results [14,15]. The steering controlled by the driver and longitudinal forces restricted from yaw result in the increase in the vehicle’s maximum acceleration ability [16]. Furthermore, mathematical models and quadratic programming methods are used to provide driving force [17,18,19]. Additionally, energy management strategies, such as strategies based on optimal driving torque distribution, can be considered to reduce electric energy consumption [20]. Braking torque distribution between the front and the rear wheels in an electric vehicle can also significantly improve energy regeneration efficiency [21].

It is necessary to investigate the torque distribution approach of the 4IWMD electric vehicle considering the coordinated control of stability and economy [22]. However, there are few scholars working from this perspective. Deng et al. proposed a novel torque vectoring algorithm based on a novel type of mechanical elastic electric wheel, which ensures the stability of the vehicle and reduces the energy consumption of the powertrain.

An optimized torque distribution method considering energy efficiency optimization based on DP strategy for a 4IWMD EV is proposed in this paper. This was considered under the constraint of straight-line driving. The main contributions made by this research are stated as follows:

(1)

A torque distribution method with the comprehensive goals of optimal torque distribution and energy efficiency considering economy through energy efficiency is proposed in this paper.

(2)

The DP control algorithm is utilized for toque distribution between the front and rear in-wheel motors to obtain optimal torque distribution and energy efficiency in the 4IWMD EV.

(3)

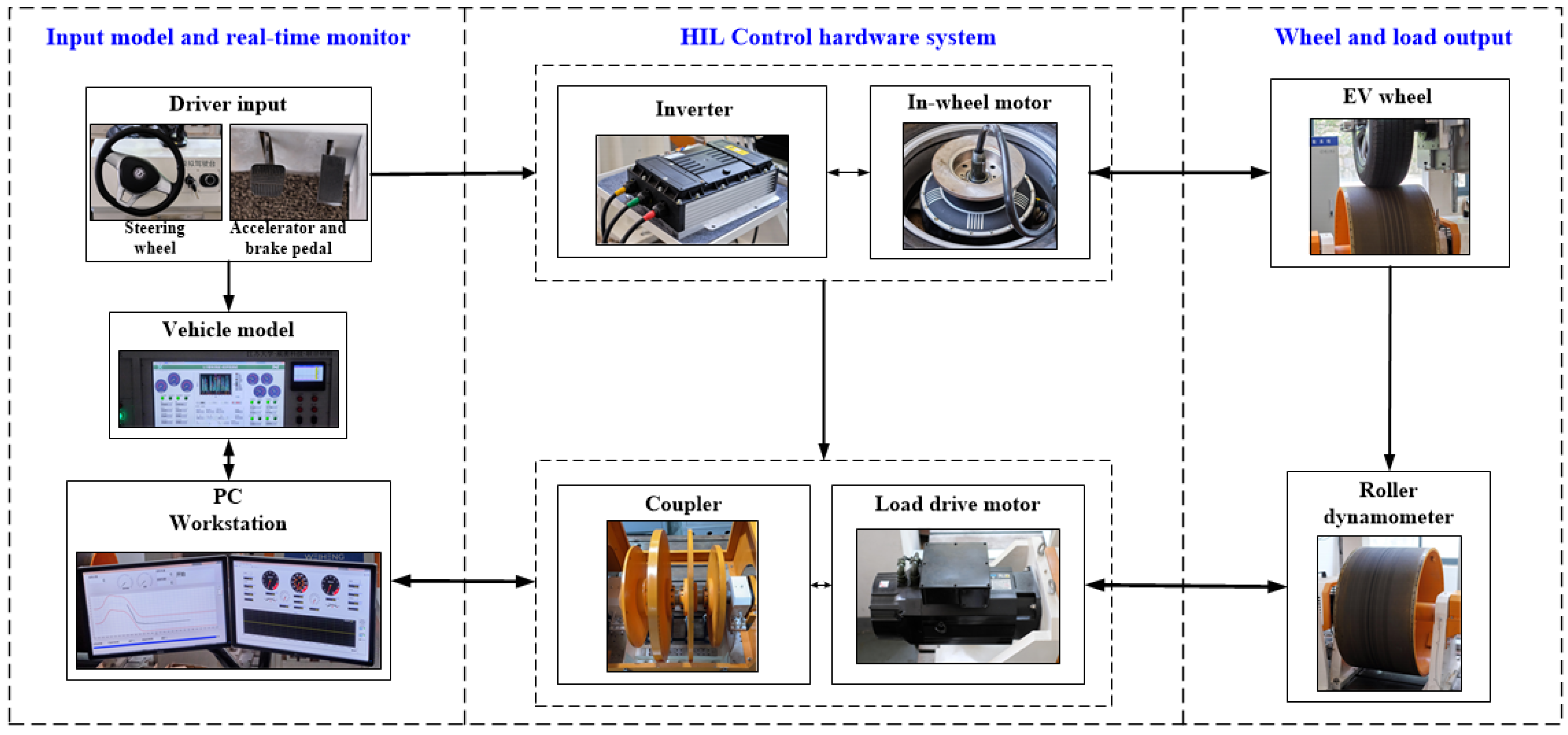
The proposed torque distribution based on the DP algorithm for the 4IWMD electric vehicle considering energy efficiency optimization is effectively verified through simulation and experiment under the NEDC, WLTC and IM240 driving cycles.

The rest of the paper is organized as follows. First, in Section 2, the four in-wheel electric vehicle model is discussed, meanwhile Section 3 exposes the torque distribution strategies applied in the study, followed by Section 4 and Section 5 which detail the simulation results and the experimental validation results, respectively, and in Section 6, the conclusion of the study is drawn and considerations for future studies are presented.

2. IWMD Electric Vehicle Model

A four-in-wheel motor drive (4IWMD) electric vehicle model is built to verify the effectiveness of the proposed strategies under various driving cycles. The AVL Cruise and MATLAB/Simulink platforms are utilized in building the co-simulation model. The complete vehicle model consists of the vehicle, in-wheel motor and battery model established in the AVL Cruise software, meanwhile the vehicle dynamics model and the torque distribution control models are built in the MATLAB/Simulink software.

2.1. Vehicle Dynamics Model

The vehicle model consists of four electric motors located inside each wheel of the electric vehicle. The total vehicle mass can be expressed using the following equation:

$$M_v=m_c+m_{em}+m_{bat}$$

(1)

where $m_{em}=m_{fl}+m_{fr}+m_{rl}+m_{rr}$, m_c is vehicle curb weight, m_em is total mass of the in-wheel motors, m_bat is battery mass, m_fl is the mass of the front left in-wheel motor, m_fr is the mass of the front right in-wheel motor, m_rl is the mass of the rear left in-wheel motor and m_rr is the mass of the rear right in-wheel motor [23].

Table 1. Vehicle parameters for four IWMD electric vehicles.

Vehicle Parameter	Symbol	Value (Unit)
Curb weight	M	1270 kg
Coefficient of rolling friction	Cr	0.017
Cross-sectional area	A	1.97 m2
Aerodynamic drag coefficient	CD	0.35
Rolling radius	R	0.31 m

shows the parameters of the four IWMD electric vehicles modelled in this study.

The vehicle torque calculation is carried out in MATLAB/Simulink, in which the input variables are vehicle speed u and acceleration a_x. Figure 1 shows the free body diagram of the 4IWMD electric vehicle on a slope, with the resistance forces that act on the vehicle [24,25].

The total driving torque (F_t) is derived through the following equations:

$$F_t=F_a+F_G+F_r+F_w$$

(2)

The forces that make up the necessary overall total driving force can be expressed as follows:

$$F_a=M\dot{v}$$

(3)

$$F_G=Mg\sin \theta$$

(4)

$$F_r=C_{r}Mg\cos \theta$$

(5)

$$F_w=\frac{1}{2}\rho A{C}_a{v}^2$$

(6)

where F_a is the acceleration resistance, F_G is the grade resistance, F_r is the vehicle rolling resistance, F_w is the aerodynamic resistance, C_r represents the rolling resistance coefficient, C_a represents the aerodynamic resistance coefficient, ρ is the density of air and A is the frontal area of the 4IWMD electric vehicle.

The power consumption of the 4IWMD electric vehicle can be calculated through the following equation:

$$P_{EV}=F_{t}v={\displaystyle \sum _{j=1}^{2}2\eta (j)P_{motor}(j)}$$

(7)

where $P_{motor}=T\omega$ and it represents the power of a single in-wheel motor, meanwhile η represents the in-wheel motor efficiency, v is the vehicle speed and j represents the polynomial order number. T represents torque, and ω represents the angular velocity of the in-wheel motor.

The torque required on the drive wheel can be calculated as follows:

$$T=F_t\times r_{wheel}$$

(8)

where r_wheel is radius of the drive wheel.

2.2. In-Wheel Motor Model

The efficiency map of the in-wheel motor is shown in Figure 2. The output power of the in-wheel motor is bounded by the output torque and motor speed conditions, which can be defined as:

$$T_m(t)\in \left[T_{m,\min }({\omega }_m(t)),T_{m,\max }({\omega }_m(t))\right]$$

(9)

$${\omega }_m(t)\in \left[0,{\omega }_{m,\max }(t)\right]$$

(10)

Where P_m is the output power of the in-wheel motor, T_m is the output torque of the in-wheel motor and ω_m is the speed of the in-wheel motor.

The in-wheel motor power demanded by the 4IWMD electric vehicle need to be supplied by the battery through the following equation:

$$P_{dem}=P_m+P_{loss.m}$$

(11)

where P_dem represents the power demanded by the power system of the 4IWMD electric vehicle, and P_loss.m is the power loss of the in-wheel motor, especially as a result of motor heat losses and mechanical losses.

The efficiency η of the in-wheel motor can be calculated by the formula:

$$\eta =P_{out}/P_{in}$$

(12)

where P_out and P_in are the output and input power of the in-wheel motor, respectively [26].

Table 2. Parameters of the in-wheel motor utilized for the experimental test bench studies.

In-Wheel Motor Parameter	Value (Unit)
Rated voltage	72 V
Rated current	110 A
Maximum speed	1200 rpm
Rated power	8 kW
Rated frequency	50 Hz
Maximum torque	250 Nm

shows the parameters of the in-wheel motor used for the test bench experimental study.

2.3. Battery Model

The battery pack is made up of rows and columns of battery cells modelled as voltage sources with resistance. The total power of the battery can be described as follows:

$$P_{em,tot}=P_{dem}+P_{aux}$$

(13)

where P_aux is the auxiliary power demanded by the vehicle.

The simplified battery equivalent circuit model utilized by theoretically deriving the state of charge (SOC) of the EV is shown in Figure 3 below.

The simplified equation of the battery SOC is shown as follows:

$$\stackrel{·}{SOC}=-\frac{I\left(k\right)}{Q_{bat}}$$

(14)

$$\stackrel{·}{SOC}=-{\eta }_{SOC}\frac{U_{OCV}(SOC)-\sqrt{U_{OCV}^2\left(SOC\right)-4\left(R_{int}\left(SOC\right)+R_t\right)P_m\left(k\right)}}{2\left(R_{int}\left(SOC\right)+R_t\right)Q_{bat}}$$

(15)

where I represents the battery current, Q_bat represents the battery capacity, η_SOC represents the coulomb efficiency, U_OCV represents the battery’s open circuit voltage, R_int represents the battery’s polarization internal resistance, R_t represents the battery’s ohmic internal resistance and P_m represents the required power of the in-wheel motor. R_int and U_OCV are the function of the battery’s SOC as a variable [27]. Equation (15) is the broadened expression of Equation (14).

3. Torque Distribution Strategies

3.1. Torque Optimization Approach

Torque distribution and energy saving can be achieved by the proper control allocation method [28]. The overall framework for torque distribution control is illustrated in Figure 4. Torque can be allocated utilizing different control allocation methods. In this study, the DP algorithm is proposed for optimizing the torque distributed to the in-wheel motors. Meanwhile, the fuzzy logic control (FLC) algorithm, based on the fuzzy set theory which operates very precisely and responds rapidly, ascertained by other studies, is used in comparison. The triangular membership function with the input variables of vehicle speed, vehicle acceleration and output variable being the coefficient of torque distribution k, were utilized for the fuzzy logic controller. Additionally, the simulated FLC algorithm is designed considering equal torque distribution between front and rear axles under a straight-line driving scenario. The optimal operation of the in-wheel motor is improved by the optimal distribution of the required drive torque, so as to ensure that the in-wheel motor operates in high efficiency areas during operation at specified motor working speeds. As a result, optimal torque distribution control can be expressed as a problem of determining the torque distribution coefficient k of the front wheels and rear wheels. The coefficient k is described as the torque distribution characteristic between the front wheels and rear wheels, which can be expressed by the following Equation:

$$k=\frac{T_f}{T_f+T_r}$$

(16)

The boundary conditions guiding the above equation are shown below:

$$\left\{\begin{array}{l}{T}_f+T_r=T_{req}\\ 0\le T_f\le T_{req}\\ 0\le T_r\le T_{req}\\ 0\le k\le 1\end{array}\right.$$

(17)

where T_f represents the torque of the front axle motor, T_r represents the torque of the rear axle motor and T_req represents the torque demand of the 4IWMD electric vehicle.

Figure 4. Framework of torque distribution control scheme.

Figure 4. Framework of torque distribution control scheme.

Note that k can express different driving modes. When k = 1, it expresses a separate front wheel drive. When k = 0, it expresses a separate rear wheel drive. When k = 0.5, it expresses a four-wheel average torque distribution mode [18,29].

The driving energy utilization efficiency under the in-wheel motor driving condition can be defined by Equation (18).

$$\max \eta =\left[\frac{k}{{\eta }_f\left(k{T}_{dem},n\right)}+\frac{\left(1-k\right)}{{\eta }_r\left(\left(1-k\right)T_{dem},n\right)}\right]$$

(18)

where η_f represents the efficiency of the front axle motor, η_r represents the efficiency of the rear axle motor and n represents the equivalent speed of the axle motor.

$$\left\{\begin{array}{l}n<n_{\max }\\ 0<T_f<T_{dem}\\ 0<T_r<T_{dem}\\ T_{dem}<T_{\max }\end{array}\right.$$

(19)

The boundary condition that satisfies the above equation is shown above.

Considering the interference of other factors, the overall efficiency of the system η can be acquired. Then, the energy consumption of the of the in-wheel motor drive system under driving cycles can be simplified as below:

$$E={\displaystyle {\int }_0^t\left(P_{dem}\times \eta \right)dt}$$

(20)

The torque distribution coefficient k is the output value derived by the control allocation method and used for optimal torque distribution to ensure high working efficiency of the front and rear in-wheel motors, in straight line driving conditions as considered in this study [30].

3.2. Torque Distribution Based on DP

To derive a better efficiency optimizing effect, the torque distribution by DP is utilized to solve the torque optimization problem.

Torque distribution through DP optimization involves the establishment of the constrained optimization problem and solving the numerical solution [31]. The utilization of the mathematical optimization and computer programming method developed by Richard Bellman in the 1950s for torque distribution in an electric vehicle requires utilizing the DP algorithm to solve and derive an optimal shorter path for the working points of the in-wheel motor, in such a way that it brings about increased in-wheel motor and vehicle efficiency.

The DP computational technique extends the decision-making concept to sequences of decisions, which as a whole define an optimal policy and trajectory. To determine the optimal trajectory and enable the in-wheel motors to work in high efficiency regions, the DP algorithm is defined by these mathematical equations:

$$C_{a{x}_{i}h}^{\ast }=J_{a{x}_i}+J_{x_{i}h}^{\ast }$$

(21)

$$J_{\alpha h}^{\ast }=\min \{C_{a{x}_{1}h}^{\ast },C_{a{x}_{2}h}^{\ast },\dots ,C_{a{x}_{i}h}^{\ast },\dots \}$$

(22)

where α is the current state, u_i is an allowable decision elected at the state α, x_i is the state adjacent to α that is replaced by the application of u_i at α, h is the final state, $J_{a{x}_i}$ is the cost to move from α to x_i, $J_{x_{i}h}^{\ast }$ is the minimum cost to reach the final state h from x_i, $C_{a{x}_{i}h}^{\ast }$ is the minimum cost to go from α to h via x_i, $J_{\alpha h}^{\ast }$ is the minimum cost to go from α to h (by any allowable path), $u^{\ast }(\alpha )$ is the optimal decision (control) at α.

The principle of optimality utilized to find an optimal policy, represented by Equation (23), can be represented by the state equation of the 4IWMD electric vehicle presented in Equation (24).

$$u^{\ast }(t)=f(x(t),t)$$

(23)

where f is a functional relationship referred to as the optimal control law or the optimal policy, and t is the time.

The vehicle speed u and torque T_dem of the 4IWMD electric vehicle are the state variables in the range of actual domain [t₀, t_f] of power system of the 4IWMD. The speed of the 4IWMD electric vehicle can be determined according to the driving cycle utilized for the optimization. Therefore, the state variable is noted as x(t) = [T_dem(t), n]′, meanwhile the vehicle demand power is utilized as the control variable, which is noted as u(t) = [P_dem(t)] discrete state. The powertrain of the 4IWMD electric vehicle can then be described by the following Equation (24).

$$\frac{dx}{dt}=f\left(x\left(k\right),u\left(k\right)\right)$$

(24)

where f is the equation of the power system of the 4IWMD electric vehicle, consisting of the vehicle dynamics Equations (2)–(7) and (11),

$$\begin{array}{l}0\le P_{dem}\le P_{dem,max}\\ T_{m,min}\le T_{dem}\left(t\right)\le T_{m,max}\\ n_{m,min}\le n\left(t\right) \le n_{m,max}\end{array}$$

(25)

where T_dem represents the in-wheel motor torque, T_m,min represents the minimum torque, T_m,max represents the maximum torque of the in-wheel motor, n_m,min and n_m,max represent the minimum and maximum speed of the in-wheel motor, respectively, P_dem,max represents the maximum output power of the in-wheel motor.

The energy efficiency of the in-wheel motor drive system that is necessary for the optimal energy consumption is taken as the objective function in this study. Additionally, the objective function is shown as follows:

$$J=\min {\displaystyle \sum _{i=0}^N\left[\frac{n{T}_f}{{\eta }_f\left(T_f,n\right)}+\frac{n{T}_r}{{\eta }_r\left(T_r,n\right)}\right]}=\min {\displaystyle \sum _{i=0}^N\left[\frac{nk{T}_{dem}}{{\eta }_f\left(k{T}_{dem},n\right)}+\frac{n\left(1-k\right)T_{dem}}{{\eta }_r\left(\left(1-k\right)T_{dem},n\right)}\right]}$$

(26)

where T_f represents the output torque value of the front axle in-wheel motor, T_r represents the output torque value of the rear axle in-wheel motor, η_f (T_f,n) represents the efficiency of the front axle in-wheel motor and η_r (T_r,n) represents the efficiency of the rear axle in-wheel motor [32].

The dynamics model of the 4IWMD electric vehicle needs to be represented in terms of change of state for the investigation of DP. The procedure needs to be performed in a discrete format, rather than in a continuous format. Therefore, the discretization needs to be carried out due to the numerical solution of DP. The time and system state are firstly discretized, and then the calculation grid of the torque distribution ratio state is divided along the time direction of the vehicle driving cycle.

According to the drive cycle, the vehicle model is utilized to calculate the power demand and speed of the drive cycle along the time direction. Considering the constraints of the in-wheel motor, the system’s reachable boundary of the entire driving cycle is acquired from the initial state and the termination state. The system constraints are met within the reachable boundary range. Additionally, the forward function is calculated according to the designed objective function. Through the recursive call method, the final state is reversed to the initial state when the torque distribution ratio state matrix of the in-wheel motor for the entire drive cycle is obtained.

The transversal optimization process is completed when the optimal torque distribution trajectory of the in-wheel motor is obtained. The calculation approach of the DP method is shown in Figure 5, and it can be seen that the backward recursion process of the dynamic program is used to calculate the minimal cost for torque distribution along the entire drive cycle by proceeding backward. This is done in order to output the dynamic and optimal path for the calculation process, in such a way that the optimal torque distribution coefficient can be derived for every time step of the state space of the dynamic programming algorithm [33].

The process of utilizing the DP method to conduct the torque distribution of the in-wheel motor is shown in Figure 6. For the simulation’s implementation, the inputs for the DP optimization are the calculated total torque and wheel speeds for the front and rear in-wheel motors, while the output is the coefficient of torque distribution. Considering the in-wheel motor, stator resistance, rated motor power, wheel speed and loss model, the in-wheel motor efficiency map is linearly interpolated and the distribution coefficient are greatly utilized to find the optimal outputs. The output is the optimal torque for each in-wheel motor, with the utilized distribution coefficient [34].

The equations for the calculation of the output are expressed as follows:

$$\begin{array}{l}M{T}_1=\frac{T_{toll}\times K_r}{2};\\ M{T}_2=M{T}_1;\\ M{T}_3=\frac{T_{toll}\times (1-K_r)}{2};\\ M{T}_4=M{T}_3\end{array}$$

(27)

where MT_i represents the in-wheel motor torque and i = 1, 2, 3, 4 represent each of the four motors (front left, front right, rear left, rear right), respectively. T_toll represents the required total torque for propulsion and braking and K_r is the torque distribution coefficient.

The discretized dynamic model produces the output indicated by the above equations to provide the front left, front right, rear left and rear right total motor torque utilized by the in-wheel motor when the in-wheel motor torque is greater than T₁ (at T_toll > T₁). Meanwhile, at other instances of T_toll < T₁, the torque is distributed to the in-wheel motors as indicated below:

$$\begin{array}{l}M{T}_1=0;\\ M{T}_2=0;\\ M{T}_3=\frac{T_{toll}}{2};\\ M{T}_4=\frac{T_{toll}}{2}\end{array}$$

(28)

The vehicle dynamic model may optimally distribute no torque to the front electric motors when the vehicle torque is lower than T₁. However, it only distributes the total required torque to the vehicle by the rear wheels, as it enhances the optimal performance of the in-wheel motor and electric vehicle overall, as the in-wheel motor operates with a higher torque.

For the vehicle torque to be optimally controlled, the dynamic programming model utilizes the above mode for the derivation of the vehicle torque. This is further indicated as below,

$$M{T}_i(k+1)=M{T}_3=\frac{T_{toll}(k)}{2}=M{T}_4=\frac{T_{toll}(k)}{2}$$

(29)

where k represents the index of the current node, MT_i (k + 1) represents the motor torque for the next node and T_toll (k) is the required motor torque.

4. Simulation Results and Analysis

To compare the effectiveness of the proposed DP-based torque distribution strategies for the 4IWMD electric vehicle, simulations were carried out using the co-simulation platform of MATLAB/Simulink and AVL Cruise. The simulations ran under the WLTC driving cycle, the NEDC driving cycle and the IM240 driving cycle to simulate the driving. The simulation results of the torque distribution based on DP control algorithm carried out under these different driving cycle conditions are compared with the torque distribution based on the FLC strategy. This comparison documents a comprehensive energy saving analysis of both torque distribution strategies.

The FLC distribution strategy is developed considering the equal distribution of torque, as well as the effective torque distribution to both sets of in-wheel motors of the front and rear axle [35]. When the required torque is low, the rear in-wheel motors supply most of the torque. When the required torque is supposed to increase and enlarge, the front in-wheel motors will supply more torque and compensate for the remaining required torque. The DP controller is developed considering maximum in-wheel motor efficiency, in which both of the rear in-wheel motors handle the vehicle propulsion request when the calculated total required torque is less than 300 Nm. When the required torque is over 300 Nm, both of the front in-wheel motors assist the rear in-wheel motors and supply the left-over share of the required torque that is needed to propel the vehicle. The simulations are carried out under the assumption that the 4IWMD electric vehicle drives on a straight line without cornering. The low-speed–low-torque characteristic of the in-wheel motor keeps the electric vehicle within a maximum speed under 60 km/h. The main parameters of the 4IWMD electric vehicle utilized in the co-simulation studies are shown in Table 1.

4.1. WLTC Driving Cycle

The worldwide harmonized light vehicle test cycle (WLTC) with a distance of 23,266 m, a duration of 1800s and a maximum speed around 130 km/h is utilized, as it is the classified test cycle for a broader category of vehicles and diverse electric powertrain vehicles. The speed profile of the WLTC drive cycle is shown in Figure 7.

The required total torque under the WLTC drive cycle is shown in Figure 8, as the control distribution method controls the amount of torque that is needed to navigate through the entire driving cycle. The torque that is individually distributed to the pair of front and rear motors when FLC is utilized for torque distribution is shown in Figure 9a. The torque that is individually distributed to the pair of front and rear motors when the DP algorithm is utilized for torque distribution is depicted in Figure 9b. It can be noted that the calculated required torque by vehicle dynamics (T_toll) is different from the required total torque to navigate through the driving cycles, as the latter is the total torque which the control algorithm utilizes to navigate through the driving cycle, considering the control parameters, constraints and objectives. Therefore, it is the result calculated by the torque distribution control algorithm, using the total desired torque by vehicle dynamics and in–wheel motor speed for the front and rear in-wheel motors.

Figure 10 shows a section of the torque distribution figure in Figure 9b, from 0 s to 500 s. Figure 10 shows that the rear in-wheel motors work all through the drive cycle, while the front in-wheel motors assist the rear motors as intended, when the calculated required total torque is over 300 Nm. At other time periods of lower torque, the front in-wheel motors remain inactive and do not engage in torque distribution. It is noted that both the front and rear in-wheel motors engage in energy recuperation, as the negative torque recorded shows. It is also visible in Figure 9 that the torque distribution using the proposed DP algorithm is well coordinated, efficient in distribution and better in comparison to the FLC method. The results indicate that a lesser amount of torque with a maximum of 109.3 Nm is utilized to achieve the torque distribution task in comparison with FLC with the maximum of 160.927 Nm. Good regenerative braking/energy recuperation is also visible, as the above figures indicate.

The DP controller works with the in-wheel motor to ensure it works within its designated operation capacity, while working with the end goal of improving torque distribution to the front and rear axle through maximum in-wheel motor efficiency.

The in-wheel motor operation points for both front in-wheel motors and both rear in-wheel motors in the WLTC driving cycle are shown in Figure 11a,b, respectively. The figures show a comparison of operating points between the FLC and the proposed DP torque distribution strategy.

As the operating points have significantly shown in Figure 11, important efforts are being undertaken by the front and rear in-wheel electric motors. The in-wheel motors work effectively as required in very high efficiency working regions. The proposed DP-based torque distribution strategy ensures the in-wheel motor works in higher efficiency regions than that with the FLC-based torque distribution strategy. Therefore, compared to the FLC-based torque distribution method, the proposed DP-based torque distribution method achieves a better efficiency optimizing effect, as both of the front and rear in-wheel motors work mostly in highly efficient regions. The proposed DP-based method always works in high efficiency regions effectively, even when only the front motor is in operation. The WLTC driving cycle motor operating points with the proposed DP-based torque distribution strategy presents better results in comparison to the motor operating points with the FLC-based torque distribution strategy, as depicted especially by the WLTC driving cycle motor operating point map in Figure 11a,b.

4.2. NEDC Driving Cycle

The new European driving cycle (NEDC) with a total distance of about 11,017 m, a duration of 1180 s and a maximum speed of 120 km/h, is the one used for the determination of a vehicle’s consumption and emission values. The speed profile of the NEDC driving cycle is shown in Figure 12.

The required total torque utilized by the 4IWMD electric vehicle to navigate through the entire NEDC cycle is shown in Figure 13. Meanwhile, shown in Figure 14a,b is the torque individually distributed to the pair of front and rear motors when FLC and the proposed DP strategy are utilized for torque distribution, respectively. Figure 15 shows one section, from 0 s to 430 s of the torque distribution result presented in Figure 14.

The rear in-wheel motor works all through the NEDC driving cycle, while the front in-wheel motor assists the rear motor as intended. It can be visibly seen in Figure 14 from 830 s to 1100 s that the front in-wheel motors remain inactive and do not engage in torque distribution at other time periods of lower torque, where the front in-wheel motors’ torque becomes idle after assisting the vehicle in reaching the higher acceleration from low torque. The rear in-wheel motor is able to provide sufficient torque to sustain the vehicle at the attained desired vehicle speed. The in-wheel motor works as a generator at deceleration periods, enabling energy recuperation through regenerative braking.

The in-wheel motor operating points for both of the front motors and rear motors in the NEDC driving cycle are shown in Figure 16. The figures show a comparison between the operating points, when torque distribution is based on FLC and the proposed DP strategy.

The in-wheel motors effectively work as required in higher efficiency working regions of the electric motors when the DP-based torque distribution strategy is applied. Therefore, the proposed DP-based torque distribution method achieves a better efficiency optimization effect than that with the FLC-based torque distribution method, as both the front and rear in-wheel motors work mostly in highly efficient regions. The motor operating points in the NEDC driving cycle, under the proposed DP-based torque distribution strategy, clearly shows that the rear in-wheel motor provides more torque for vehicle propulsion than the front in-wheel motor.

4.3. Customized IM240 Driving Cycle

A customized driving cycle called the custom IM240 drive cycle based on the inspection and maintenance driving cycle with a total distance of about 3100 km, a duration of 240 s and maximum speed of 56.7 km/h is also utilized in this study as it is a representation of a low-speed driving cycle, which represents the driving pattern in urban areas with traffic and low speed limitations. The speed profile of the custom IM240 driving cycle is shown in Figure 17. The required total torque with the entire custom IM240 drive cycle is presented in Figure 18. The torque individually distributed to the front and rear motors based on FLC and the proposed DP algorithm strategy are shown in Figure 19a,b. The torque requirement with the IM240 drive cycle is low and the rear in-wheel motor supplies most of the required torque throughout the driving cycle. This has the benefit of reducing the battery consumption, as only the rear in-wheel motor supplies the needed torque, therefore increasing the final SOC of the battery, which can be used to cover more travel range.

The motor operating points for both the front and rear in-wheel motors in the custom IM240 driving cycle are shown in Figure 20. The figures show a comparison between the motor operating points, when torque distribution based on FLC and on the proposed DP are utilized for torque distribution.

The motor operating points under the custom IM240 driving cycles shown in Figure 20 indicate that the in-wheel motors work in high efficiency working areas when the proposed DP-based torque distribution is utilized. The custom IM240 driving cycle operating points confirm that an increase in vehicle speed will lead to an increase in torque, which allows the in-wheel motor to work at higher efficiency regions. The in-wheel motor contributes to the high motor efficiency, with a maximum efficiency of approximately 96.48% by the front motors and 96.52% by the rear motors, which is obtained by the proposed DP-based torque distribution method in the 4IWMD electric vehicle.

4.4. Energy Saving Analysis

The energy consumption of the 4IWMD electric vehicle with FLC and the proposed DP strategy for torque distribution under different drive cycles are shown in

Table 3. Energy consumption of the 4IWDEV over the studied driving cycles.

	FLC-Based Torque Distribution Energy Consumption (kWh/100 km)	DP-Based Torque Distribution Energy Consumption (kWh/100 km)	Improvement in Energy Consumption (%)
WLTC	10.01	7.74	22.68
NEDC	9.89	7.84	20.73
Custom IM240	9.11	7.12	21.84

. From Table 3, it can be seen that the energy consumption of the 4IWMD electric vehicle with FLC and the proposed DP strategy for torque distribution under the WLTC drive cycle are 10.01 kWh/100 km and 7.74 kWh/100 km, respectively. It can be seen that the energy consumption with the proposed DP strategy is less than that with the FLC strategy, in which the energy consumption is reduced by 22.68%. The energy consumption of the vehicle with FLC and the proposed DP strategy for torque distribution under the NEDC drive cycle are 9.89 kWh/100 km and 7.84 kWh/100 km, respectively. It also can be seen that the energy consumption with the proposed DP strategy is less than that with the FLC strategy, in which the energy consumption is reduced by 20.73%. The energy consumption with FLC and the proposed DP strategy for torque distribution under the custom IM240 drive cycle are 9.11 kWh/100 km and 7.12 kWh/100 km, respectively. We see that the energy consumption is reduced by 21.84% with the proposed DP strategy compared to the FLC strategy.

The energy consumption with FLC and the proposed DP strategy for torque distribution under different drive cycles is clearly shown in Figure 21.

It can be seen that the proposed DP-based torque distribution method functions with high motor efficiency capability, which enables the in-wheel motor to work maximally in highly efficient working regions. The rear in-wheel motors supply most of the required torque, while the front in-wheel motors assist the rear in-wheel motors as designed.

The proposed DP-based torque distribution method brings an improvement in the torque distribution of the 4IWMD electric vehicle, resulting in reduced energy consumption, good energy recuperation and an increase in vehicle travel range.

5. Experimental Validation

Experimental studies were carried out to verify the effectiveness of the proposed DP-based torque distribution strategy, which is achieved on a NI Veristand IWMD electric vehicle test bench. The above-mentioned three drive cycles are used for experimental studies. Figure 22 shows the utilized experimental test bench setup.

5.1. WLTC Drive Cycle

A comparison of both the experimental and simulation results of torque distribution for the front and rear in-wheel motors with the FLC and the proposed DP strategy under the WLTC drive cycle are shown in Figure 23 and Figure 24, respectively. It can be seen that the experimental results of torque distribution track most of the simulation results. The torque distribution results obtained by the proposed DP strategy follow those obtained by the FLC strategy, in which the track accuracy is improved and the fluctuation is reduced. It is confirmed that the proposed DP strategy is a better option for torque distribution than the FLC strategy in the 4IWMD electric vehicle.

5.2. NEDC Drive Cycle

Figure 25 and Figure 26 show the comparison between simulation and experimental results of torque distribution with FLC and the proposed DP strategy under the NEDC driving cycle. It is noted that the NEDC cycle requires less torque for acceleration to the required vehicle speed in comparison to the WLTC cycle, as the WLTC experiment results show in Figure 23 and Figure 24. The experimental result validates the simulation results of torque distribution in the NEDC driving cycle.

5.3. Customized IM240 Driving Cycle

Figure 27 and Figure 28 highlight the torque distribution results for the experiment in the custom IM240 driving cycle in comparison with the simulation results in the custom IM240 driving cycle for torque distribution based on the FLC and DP algorithm, respectively. The experimental results of the custom IM240 driving cycle for the torque distribution, similar to the NEDC driving cycle, tracks the simulation results, with high torque exerted during deceleration.

5.4. Energy Saving Analysis

Energy saving analysis is conducted in line with the energy consumption during the experimental studies. The quantitative analysis of the vehicle energy consumption during the experiment was derived based on the torque distribution coefficient, for torque distribution based on the FLC algorithm and the DP algorithm, respectively. The total energy consumed by the in-wheel motor during the experiment based on the FLC algorithm and the DP algorithm in the WLTC driving cycle is 359.714 kJ and 273.765 kJ, respectively. Meanwhile, in the NEDC driving cycle, the in-wheel motor consumed an energy of 528.834 kJ and 406.549 kJ during the experiment based on the FLC algorithm and the DP algorithm, respectively. For the custom IM240 driving cycle, the in-wheel motor consumed an energy of 163.051 kJ and 125.527 kJ during the experiment based on the FLC algorithm and the DP algorithm, respectively. As is shown from Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28, the WLTC urban driving experiment covered 0–500 s of the WLTC driving cycle, while that of NEDC covered 0–438 s of the NEDC driving cycle; meanwhile, the custom IM240 experiment covers the entire 240 s of the custom IM240 driving cycle.

The energy consumption in Kilowatt-hour per 100 km, calculated from the Watt-hour calculation, is assumed to showcase the consumption per km for the three driving cycles, for torque distribution methods with FLC and the proposed DP algorithm. The percentage of improvement in energy consumption during the experiments based on the FLC and DP torque distributions is shown in

Table 4. In-wheel Motor Energy Consumption during Experimental Studies.

	Energy Consumption with FLC Algorithm (kWh/100 km)	Energy Consumption with DP Algorithm (kWh/100 km)	Improvement in Energy Consumption (%)
WLTC	9.992	7.605	23.89
NEDC	14.690	11.293	23.12
Custom IM240	4.529	3.487	23.01

.

The IM240 driving cycle during the experiments based on the FLC and DP torque distributions is presented in Figure 29. Compared to the FLC-based strategy, it can be seen that there is a reduction in energy consumption with the DP-based torque distribution strategy.

The energy consumed in the WLTC, NEDC and custom IM240 driving cycles during the experiment clearly verifies that DP-based torque distribution is a more optimal torque distribution method than the FLC strategy, for which less energy is consumed when the DP-based torque distribution is applied in the 4IWMD EV.

6. Conclusions

Centered on the aim of improving energy saving, the economy-based torque distribution strategy is proposed in this paper. Upon the building of a complete four-in-wheel motor drive electric vehicle model, featuring a comprehensive vehicle model, a motor model and a battery model, torque distribution methods based on the FLC algorithm and a proposed DP algorithm are investigated through co-simulation studies carried out in AVL Cruise and MATLAB/Simulink software. Additionally, further experimental studies were implemented to verify the simulation results. These were performed considering a straight-line road.

This article produces very interesting results, as shown by the simulation and experimental results. The simulation results show that the torque distribution based on the DP algorithm is the optimal option for optimized front and rear torque distribution, as it effectively reduces the vehicle’s energy consumption by 2.27 kWh, 2.05 kWh and 1.99 kWh for every 100 km of distance travelled in the WLTC, NEDC and custom IM240 driving cycle conditions, respectively, when compared to the torque distribution based on the FLC algorithm. Furthermore, compared to the FLC algorithm, the experimental results show that the energy consumption under the WLTC, NEDC and IM240 drive cycles is reduced by 23.89%, 23.12% and 23.01% with the proposed DP algorithm, respectively. Hence, the proposed DP algorithm produces an optimized front and rear torque distribution that effectively reduces vehicle energy consumption, which leads to an improved energy saving and overall vehicle efficiency in four-in-wheel motor drive electric vehicles. The online global optimization method with the proposed DP algorithm which can be monitored in real-time during simulation and the vehicle experiment studies may assist in optimization and real time control, enabling better simulation results and even experimental results to be obtained with minimal or negligible errors.

It should be noted that DP is an exhaustive search that requires more time and space for its computation. Future work will focus on the algorithm and the reduction of the computation load.