Research on Cascaded Single Phase PFC Based on Predictive PI Control
Abstract
:1. Introduction
2. Structure of Cascaded Single Phase PFC System
- (1)
- The common duty cycle control strategy is adopted, and the difference of switching function caused by CPS-SPWM is ignored, that is, m1 ≈ m2 ≈ … ≈ mi; and
- (2)
- The capacitance and resistance of the DC side are the same, which are C and R, respectively.
3. Design of Cascade Single Phase PFC Control System
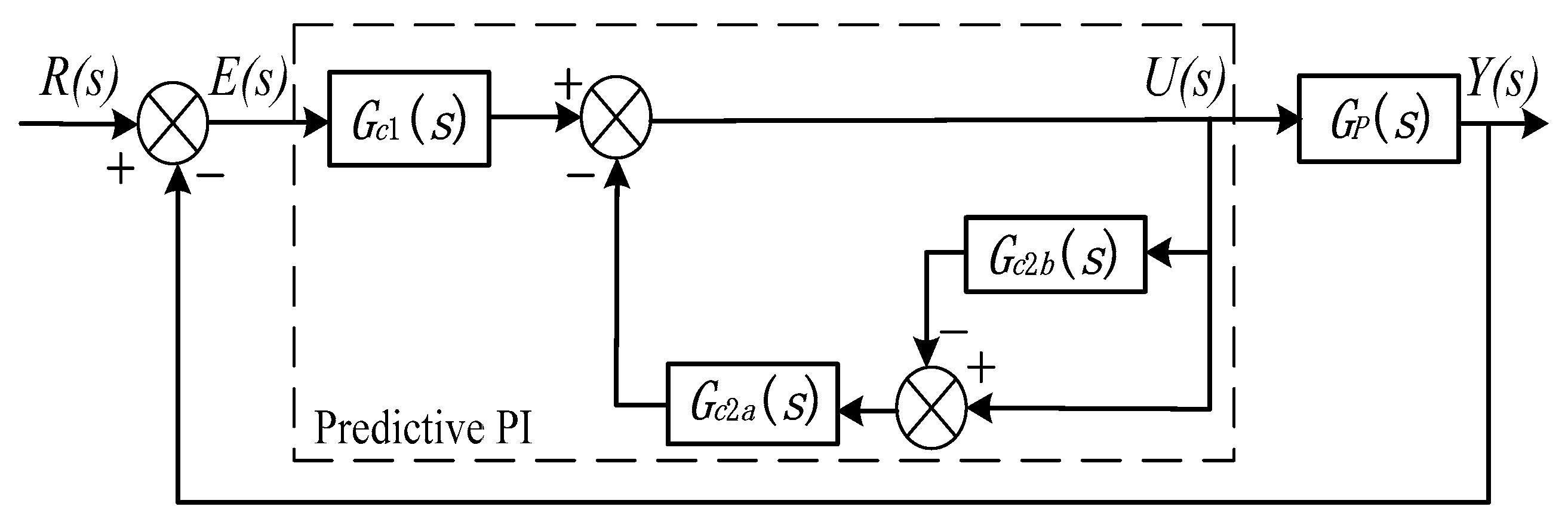
3.1. Predictive PI Control
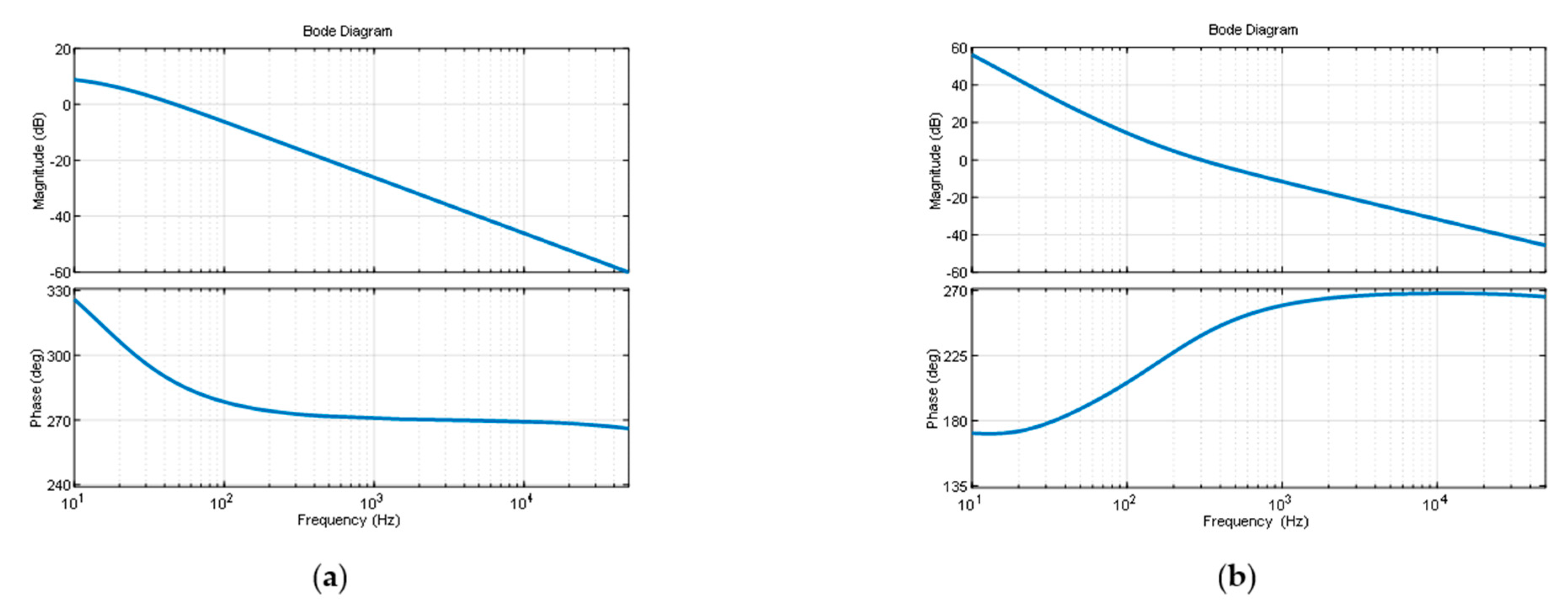
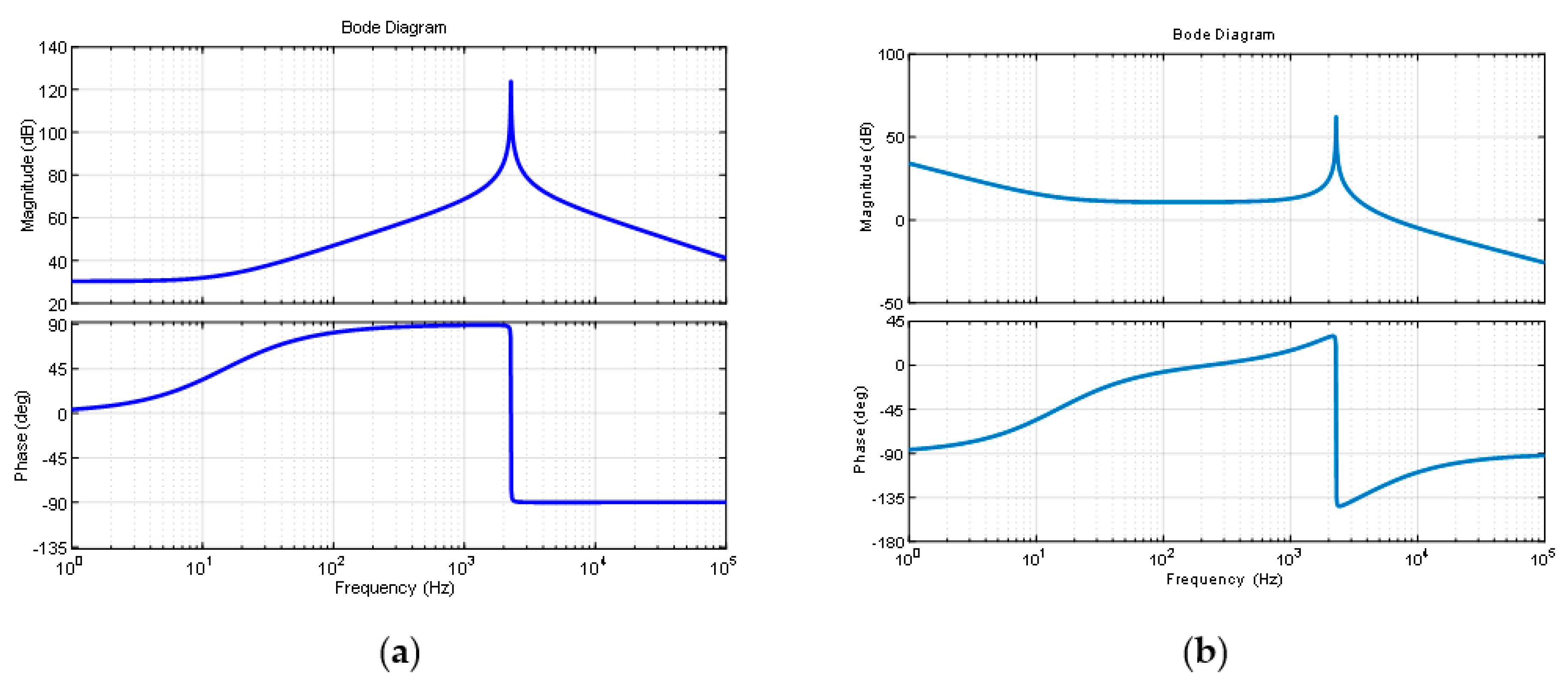
3.1.1. The Determination of Parameter K
3.1.2. Determination of Parameters T and τ
3.2. Current Inner Loop Control
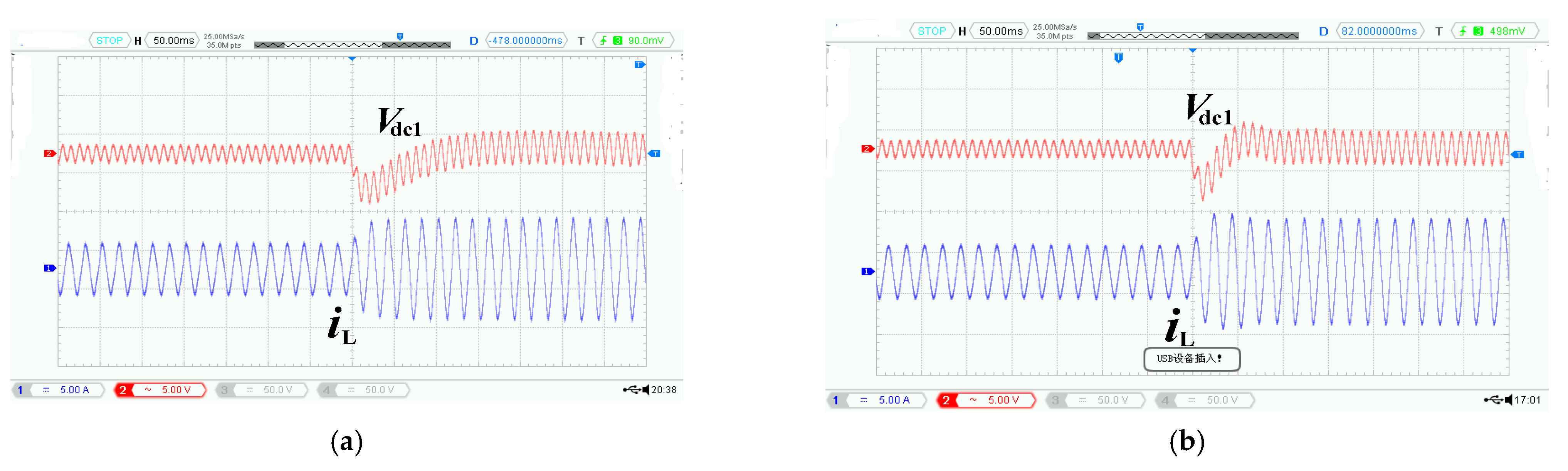
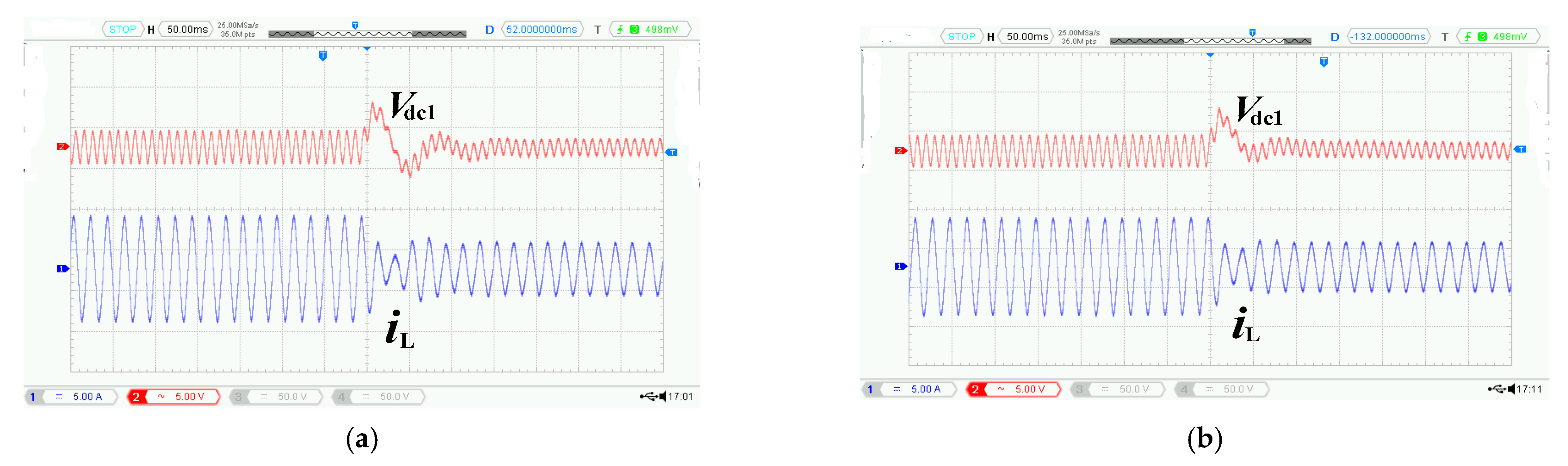
4. System Experimental Analysis
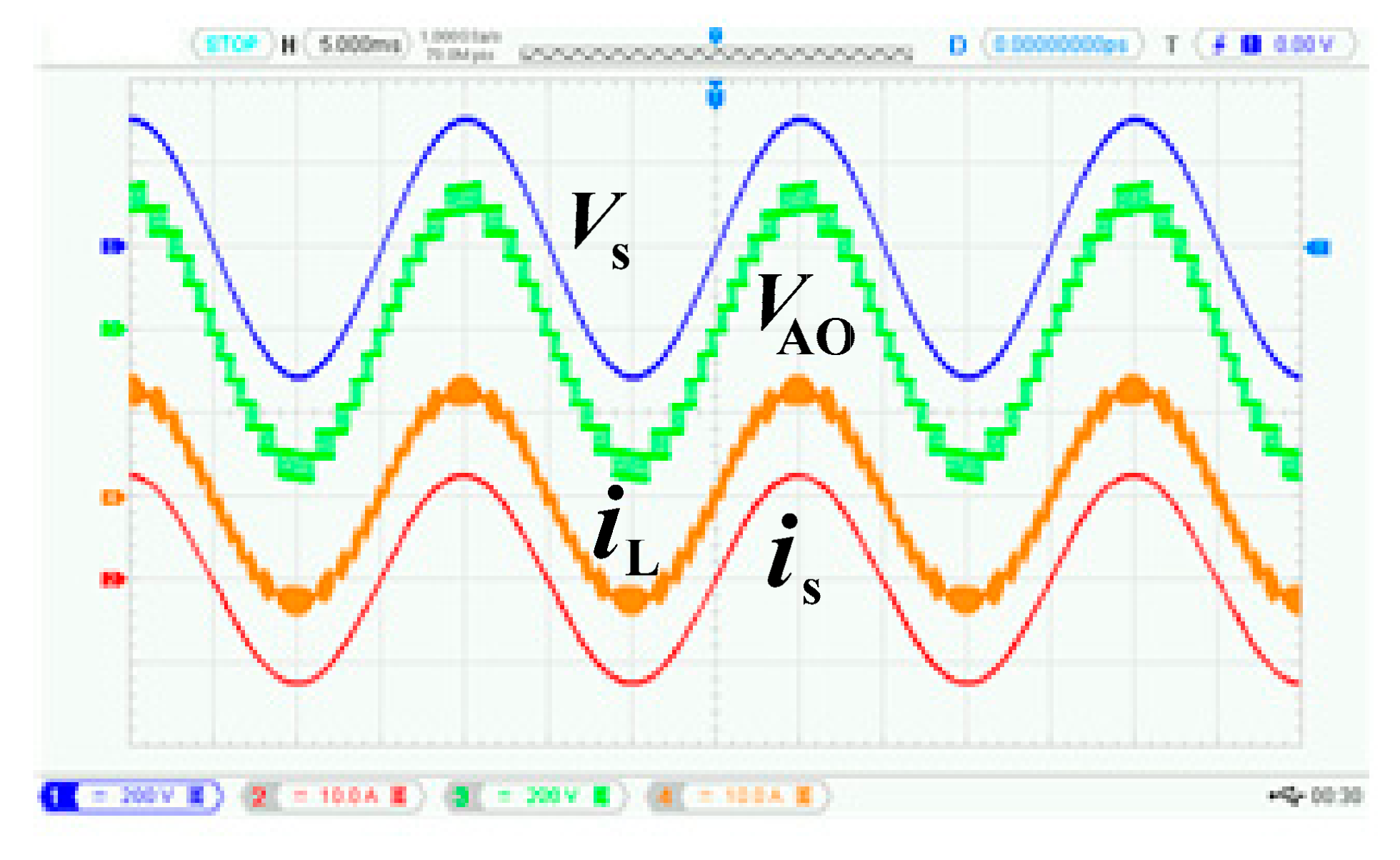
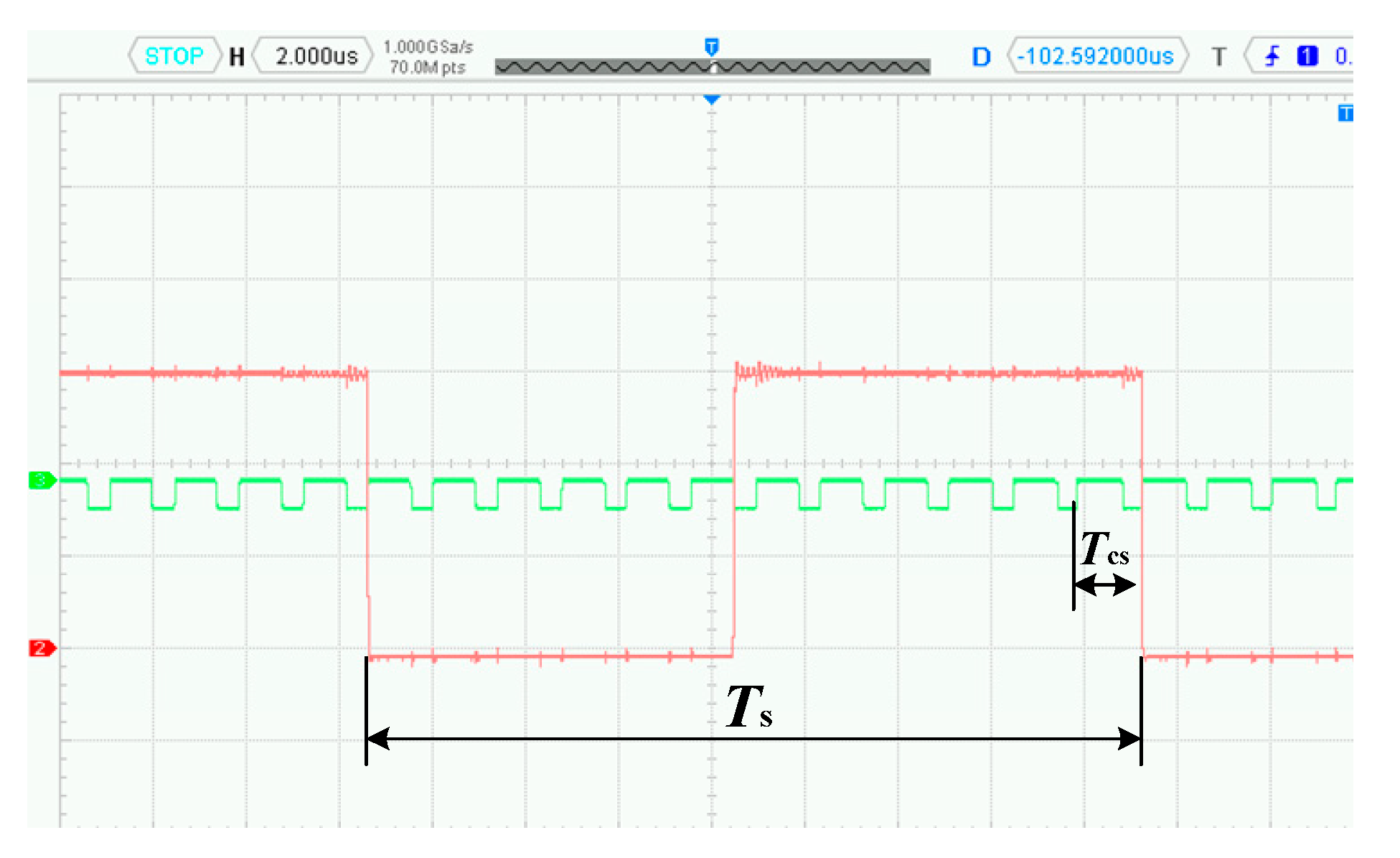
4.1. System Steady-State Experimental Analysis
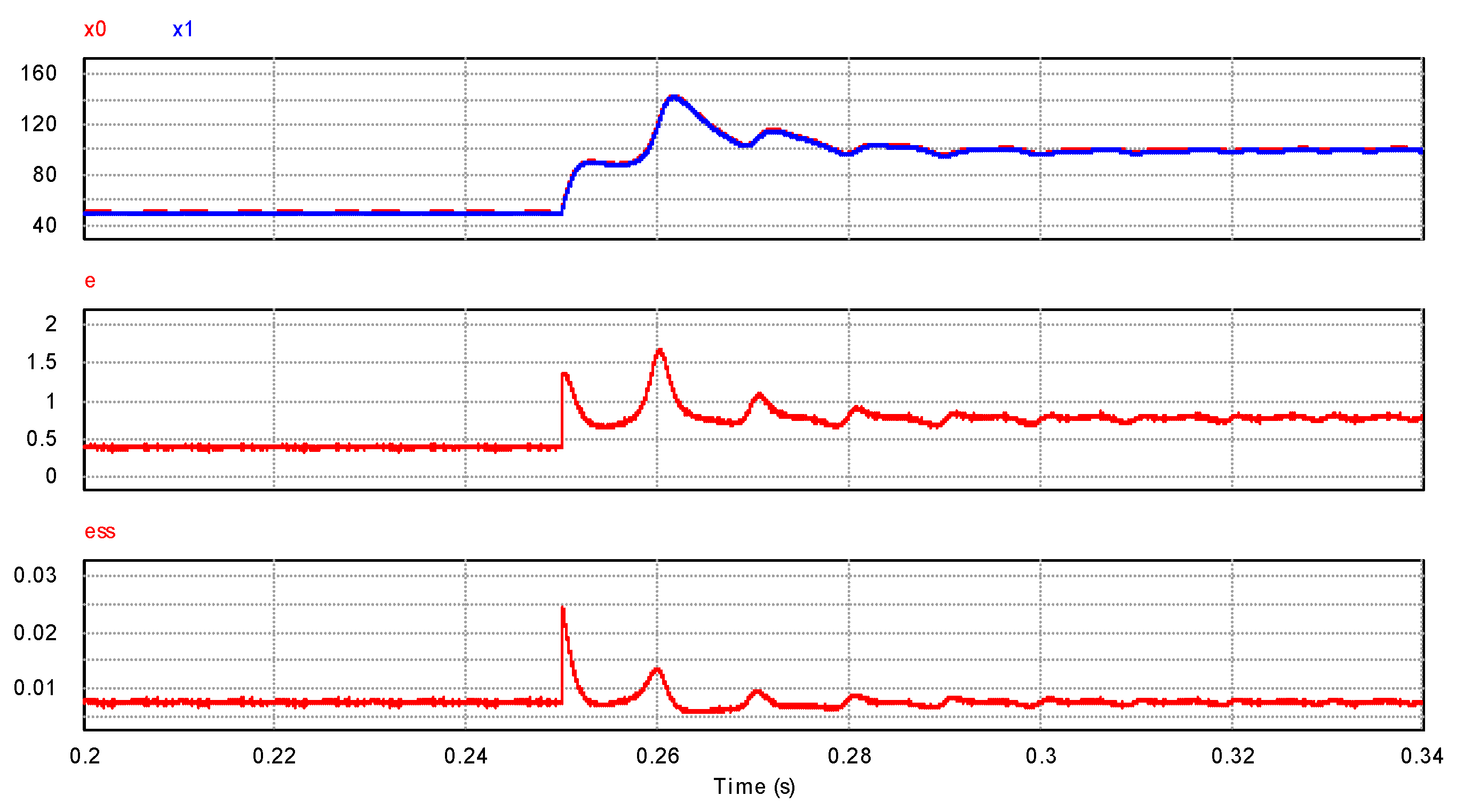
4.2. System Dynamic Experimental Analysis
5. Conclusions
- (1)
- The cascaded multilevel structure can effectively improve the system power density of the charger, reduce the voltage drop borne by a single switch, and improve the power factor of the system output.
- (2)
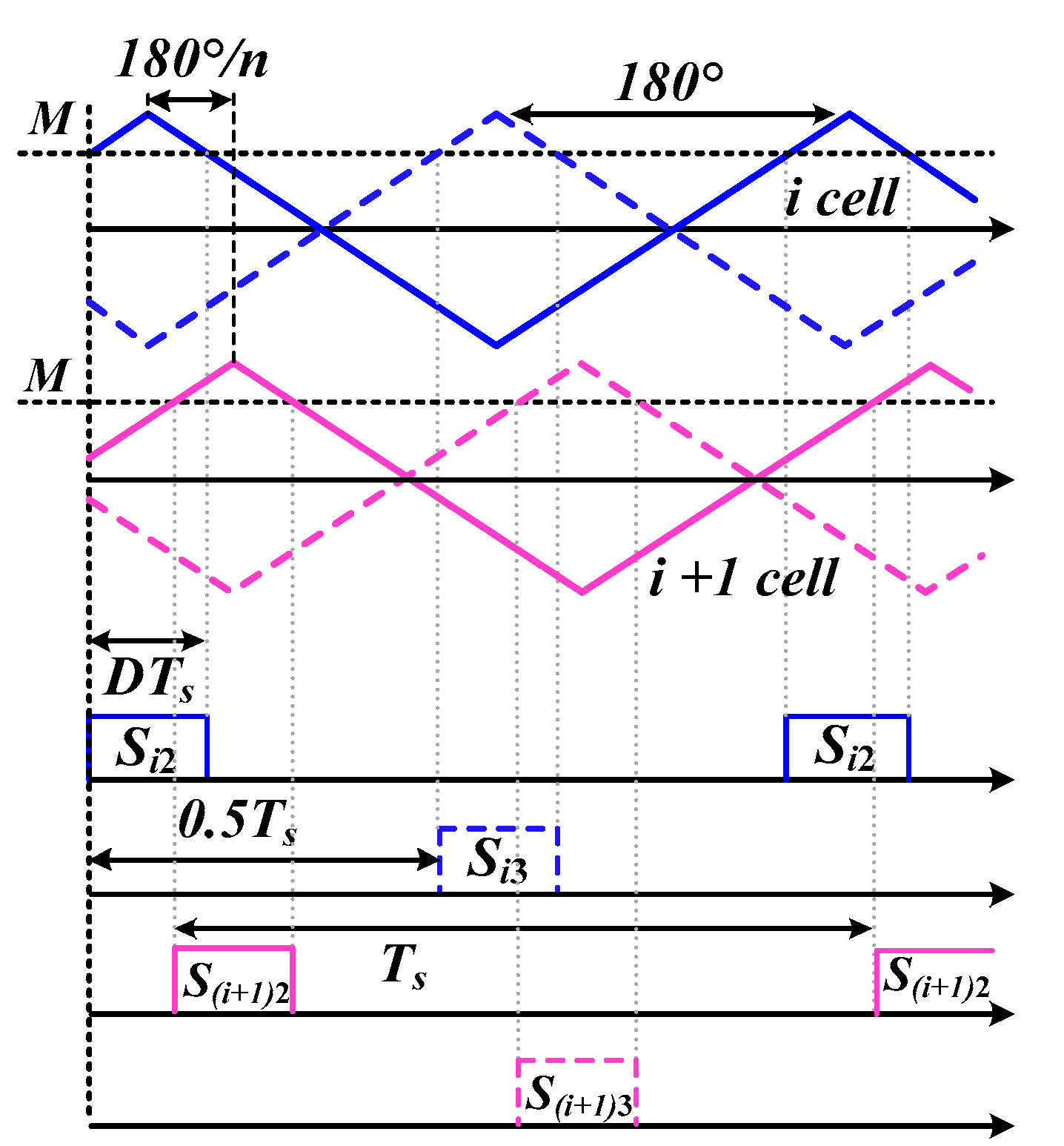
- The carrier phase shift control strategy was adopted to greatly increase the system switching frequency to reduce the burden of each switch and reduce the switching loss.
- (3)
- Predictive PI control was adopted in the voltage loop to effectively improve the dynamic stability of the system.
Author Contributions
Funding
Conflicts of Interest
References
- IEA. Global-ev-Outlook-2018. Available online: https://webstore.iea.org/global-ev-outlook-2018 (accessed on 2 February 2022).
- Bortis, D.; Neumayr, D.; Kolar, J.W. ηρ-Pareto optimization and comparative evaluation of inverter concepts considered for the GOOGLE Little Box Challenge. In Proceedings of the 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016; pp. 1–5. [Google Scholar]
- Chou, D.; Fernandez, K.; Pilawa-Podgurski, R.C.N. An Interleaved 6-Level GaN Bidirectional Converter for Level II Electric Vehicle Charging. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Phoenix, AZ, USA, 14–17 June 2021; pp. 594–600. [Google Scholar]
- Liu, Z.; Li, B.; Lee, F.C.; Li, Q. High-Efficiency High-Density Critical Mode Rectifier/Inverter for WBG-Device-Based on-Board Charger. IEEE Trans. Ind. Electron. 2017, 64, 9114–9123. [Google Scholar] [CrossRef]
- Maheswaria, K.T.; Bharanikumara, R.; Arjunb, V.; Amrishb, R.; Bhuvanesh, M. A comprehensive review on cascaded H-bridge multilevel inverter for medium voltage high power applications. Mater. Today Proc. 2021, 45, 2666–2670. [Google Scholar] [CrossRef]
- Hurley, W.G.; Wölfle, W.H. Transformers and Inductors for Power Electronics: Theory, Design and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Babu, J.J.; Thirumavalavan, V. Variable Duty Cycle Control with PSO-PI Controller for Power Factor Correction and Fast Regulation. J. Inst. Eng. India Ser. B 2021, 1–9. [Google Scholar] [CrossRef]
- Cai, Y.; Xu, J.; Yang, P.; Liu, G. Design of double-line-frequency ripple controller for quasi-single-stage AC/DC converter with audio susceptibility model. IEEE Trans. Ind. Electron. 2019, 66, 9226–9237. [Google Scholar] [CrossRef]
- Villarroel, F.A.; Espinoza, J.R.; Pérez, M.A.; Ramírez, R.O.; Baier, C.R.; Sbárbaro, D.; Silva, J.J.; Reyes, M.A. Stable Shortest Horizon FCS-MPC Output Voltage Control in Non-Minimum Phase Boost-Type Converters Based on Input-State Linearization. IEEE Trans. Energy Convers. 2021, 36, 1378–1391. [Google Scholar] [CrossRef]
- Su, Y.; Ge, X.; Xie, D.; Wang, K. An Active Disturbance Rejection Control-Based Voltage Control Strategy of Single-Phase Cascaded H-Bridge Rectifiers. IEEE Trans. Ind. Appl. 2020, 56, 5182–5193. [Google Scholar] [CrossRef]
- Ming, W.L.; Zhong, Q.C.; Zhang, X. A Single-Phase Four-Switch Rectifier With Significantly Reduced Capacitance. IEEE Trans. Power Electron. 2015, 31, 1618–1632. [Google Scholar] [CrossRef] [Green Version]
- Bai, L.; Ren, X.; Hui, Q.; Wu, Y.; Li, K.; Guo, Z.; Zhang, Y. Dynamic response optimization forinterleaved boost PFC converter with improved dual feedforward control. In Proceedings of the 2017 IEEE Energy Conversion Congress & Exposition, Cincinnati, OH, USA, 1–5 October 2017; pp. 5280–5286. [Google Scholar]
- Leung, K.H.; Loo, K.H.; Lai, Y.M. A Family of Ripple Estimation-Cancellation Methods Based on Switched-Resistor Circuits and Their Application in Fast-Response PFC Preregulator. IEEE Trans. Power Electron. 2017, 32, 2608–2621. [Google Scholar] [CrossRef]
- Yao, C.; Zhang, Y.; Chen, H. Adaptive Constant Power Control of MHz GaN-Based AC/DC Converters for Low Power Applications. IEEE Trans. Ind. Appl. 2018, 54, 2525–2533. [Google Scholar] [CrossRef]
- Mallik, A.; Lu, J.; Khaligh, A. Sliding Mode Control of Single-Phase Interleaved Totem-Pole PFC for Electric Vehicle Onboard Chargers. IEEE Trans. Veh. Technol. 2018, 67, 8100–8109. [Google Scholar] [CrossRef]
- Li, S.; Lu, W.; Yan, S.; Zhao, Z. Improving Dynamic Performance of Boost PFC Converter Using Current-Harmonic Feed forward Compensation in Synchronous Reference Frame. IEEE Trans. Ind. Electron. 2020, 67, 4857–4866. [Google Scholar] [CrossRef]
- Xiao, D.; Alam, K.S.; Norambuena, M.; Rahman, M.F.; Rodriguez, J. Modified Modulated Model Predictive Control Strategy for a Grid-Connected Converter. IEEE Trans. Ind. Electron. 2021, 68, 575–585. [Google Scholar] [CrossRef]
- Kwak, S. Model predictive direct power control with vector preselection technique for highly efficient active rectifiers. IEEE Trans. Ind. Inform. 2015, 11, 44–52. [Google Scholar] [CrossRef]
- He, T.; Lu, D.D.-C.; Li, L.; Zhang, J.; Zheng, L.; Zhu, J. Model-Predictive Sliding-Mode Control Three-Phase AC/DC Converters. IEEE Trans. Power Electron. 2018, 33, 8982–8993. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model predictive control for power converters and drives: Advances and trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef] [Green Version]
- Qi, C.; Chen, X.; Tu, P.; Wang, P. Cell-by-Cell-Based Finite-Control-Set Model Predictive Control for a Single-Phase Cascaded H-Bridge Rectifier. IEEE Trans. Power Electron. 2018, 33, 4857–4866. [Google Scholar] [CrossRef]
- Leung, K.H.; Loo, K.H.; Lai, Y.M. Unity-power-factor control based on precise ripple cancellation for fast-response PFC preregulator. IEEE Trans. Power Electron. 2016, 31, 3324–3337. [Google Scholar] [CrossRef]
- Zheng, D.; Ren, Z.Y.; Fang, J.A. Stability analysis of multiple time-delayed system. ISA Trans. 2008, 47, 439–447. [Google Scholar] [CrossRef]
- Airikka, P. Stability analysis of a predictive PI controller. In Proceedings of the 2013 21st Mediterranean Conference on Control and Automation, Platanias, Greece, 25–28 June 2013; pp. 1380–1385. [Google Scholar]


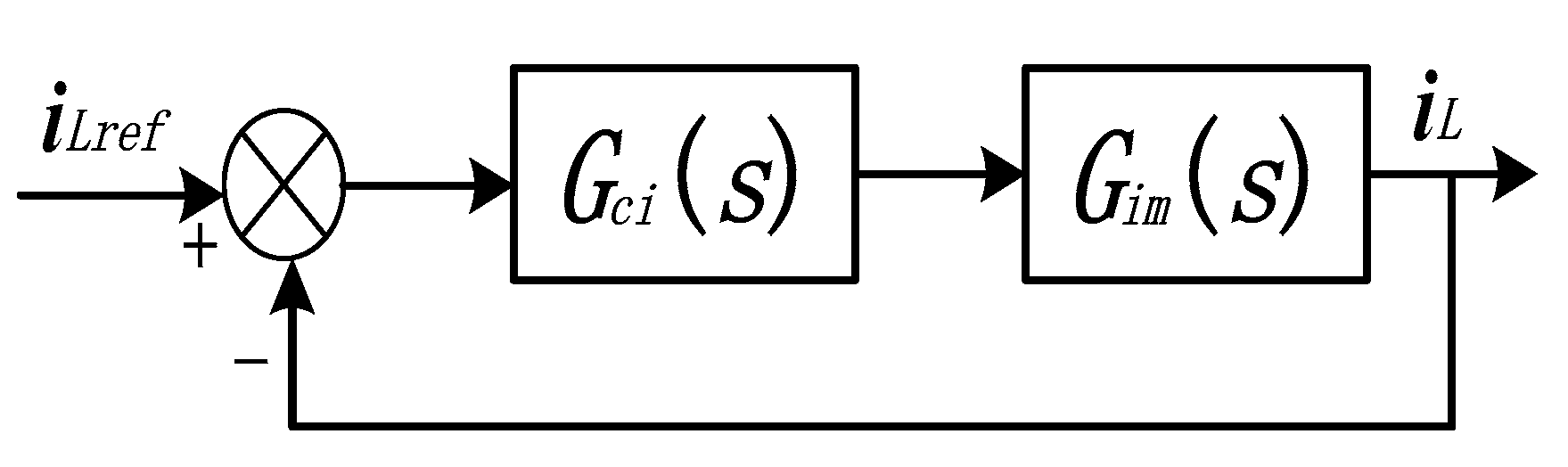

| Component | Model |
|---|---|
| Switch tube | EPC2032 |
| Isolator | ISOW7840 |
| Driver | LMG1205 |
| Driver power supply | TPS60150 |
| Current sensor | ACS723 |
| DSP | TMS320F28069 |
| FPGA | AL3S10NG88 |
| Parameter | Values |
|---|---|
| Main inductance | 5 μH |
| Filter inductance | 8 μH |
| Filter capacitor | 620 nF |
| Unit bus capacitance | 1800 μF |
| Unit resistive load | 12 Ω |
| Switching frequency | 60 kHz |
| AC side phase voltage | 220 V |
| DC side voltage | 360 V |
| Rated power | 2 kW |
| Power density | 1500 W/in3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, G.; Qian, Y. Research on Cascaded Single Phase PFC Based on Predictive PI Control. World Electr. Veh. J. 2022, 13, 48. https://doi.org/10.3390/wevj13030048
Shi G, Qian Y. Research on Cascaded Single Phase PFC Based on Predictive PI Control. World Electric Vehicle Journal. 2022; 13(3):48. https://doi.org/10.3390/wevj13030048
Chicago/Turabian StyleShi, Guoping, and Yece Qian. 2022. "Research on Cascaded Single Phase PFC Based on Predictive PI Control" World Electric Vehicle Journal 13, no. 3: 48. https://doi.org/10.3390/wevj13030048
APA StyleShi, G., & Qian, Y. (2022). Research on Cascaded Single Phase PFC Based on Predictive PI Control. World Electric Vehicle Journal, 13(3), 48. https://doi.org/10.3390/wevj13030048







