State of Health Estimation for Lithium-Ion Batteries Using IAO–SVR
Abstract
:1. Introduction
2. IAO–SVR
2.1. Aquila Optimizer
2.1.1. Expanded Exploration
2.1.2. Narrow Exploration
2.1.3. Expanded Exploitation
2.1.4. Narrow Exploitation
2.2. Improved Aquila Optimizer
2.2.1. Population Initialization Method by Logistic-Sin–Cos Chaotic Mapping
2.2.2. Adaptive t-Distribution Variation
2.2.3. Support Vector Regression
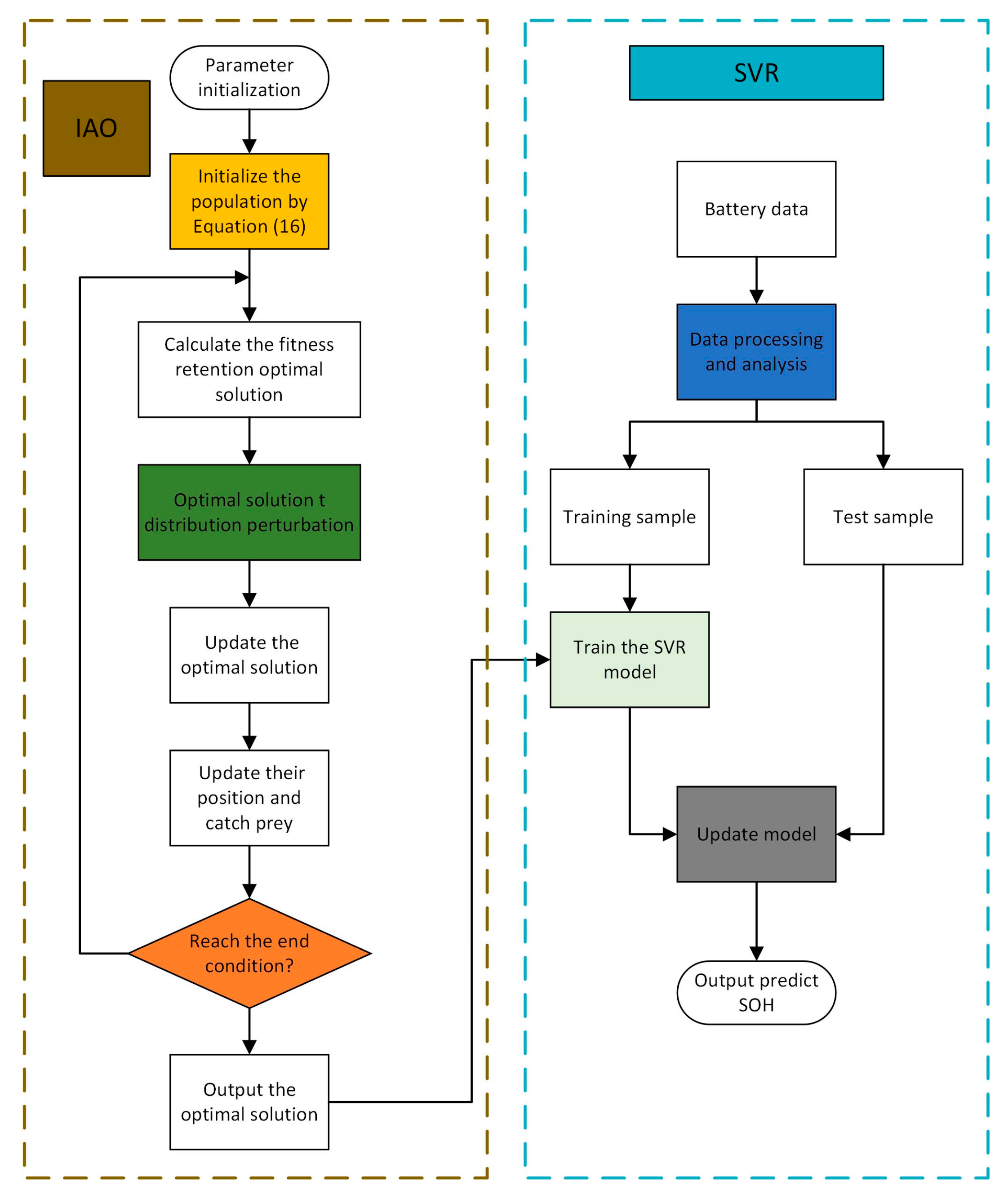
2.3. IAO–SVR Model
- Data pre-processing: Sample data is normalized, which allows the pre-processed data to be limited to a certain range, eliminates the influence of abnormal feature vectors, and places each data in the same order of magnitude; then, we can divide the data into training and test samples. The expression is shown in Equation (24) as follows:where and , respectively, are the characteristic values of the sample before and after normalization of the training data, and and , respectively, are the minimum and maximum values of the sample characteristic data.
- SVR parameter settings: The SVR parameter settings include the dimension of the individuals , the maximum number of iterations , the upper bound for individual values and lower bound for individual values , and the number of populations .
- Define fitness function: We define the two parameters as the individuals of the IAO algorithm; during the training process, each individual will be verified in the SVR. We propose the root mean square error (RMSE) as the fitness function, and the optimal individual is selected by the principle of minimum mean square error as follows:where is the predicted value of the test samples, is the actual value of the test samples, and is the number of test samples.
3. Experiment and Analysis of Health Features
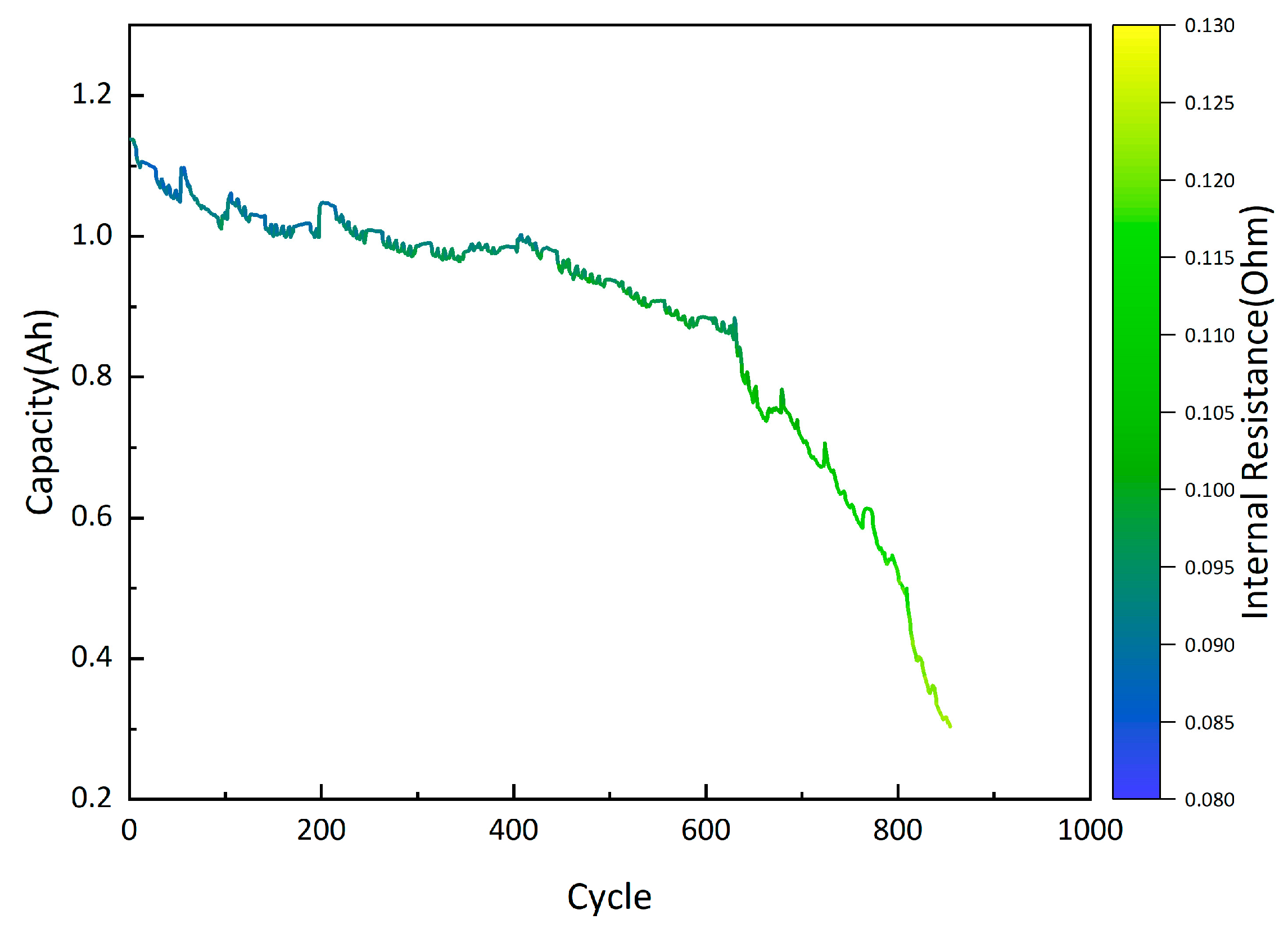
3.1. Definition of SOH
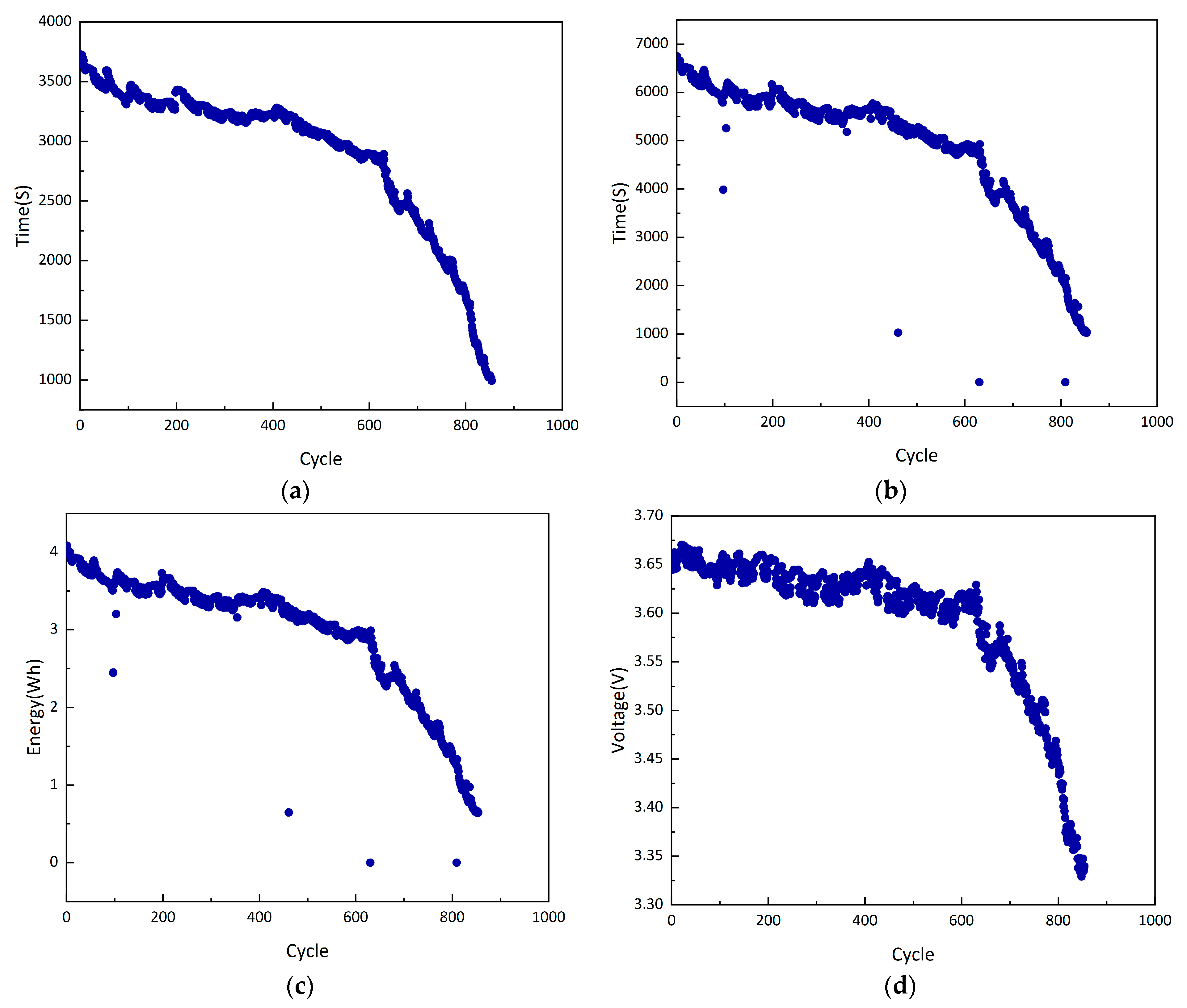
3.2. Battery Experiment
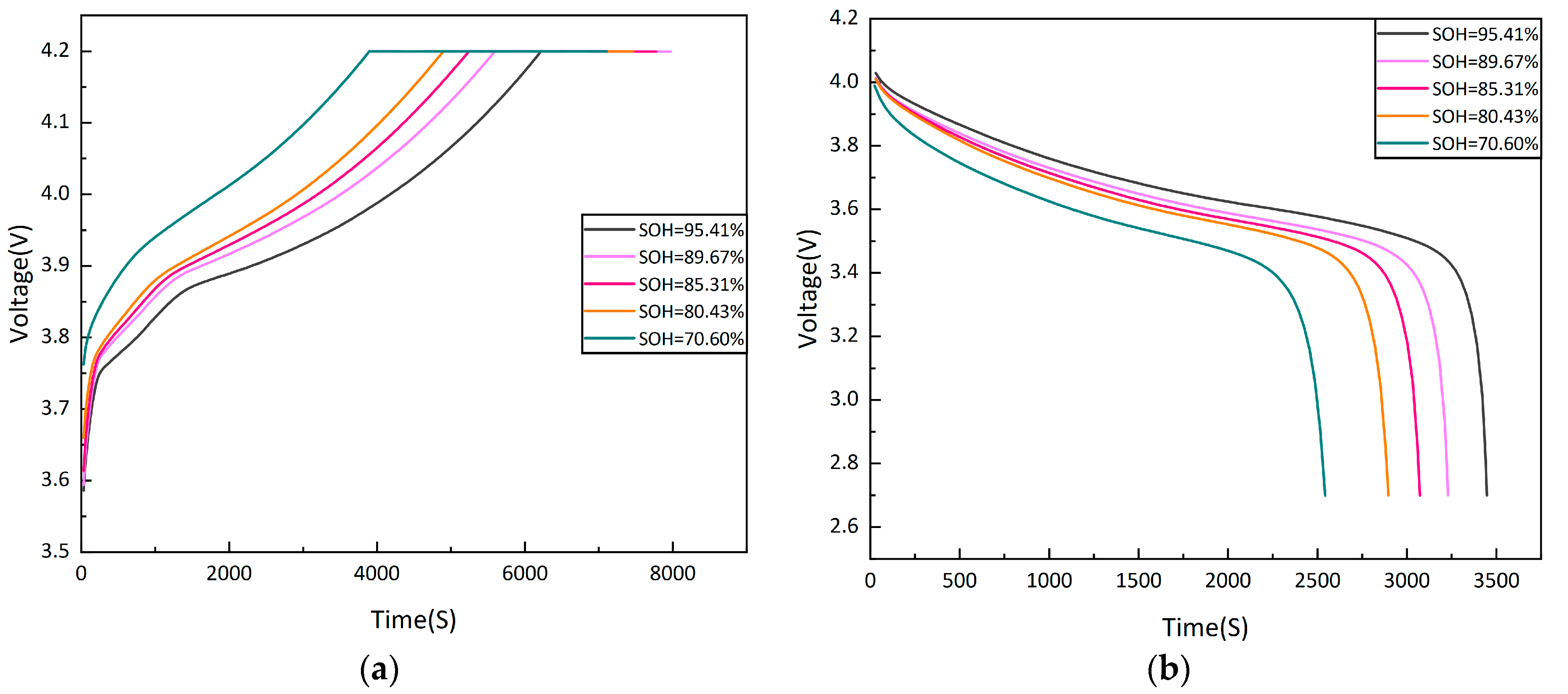
3.3. Selection of Health Features
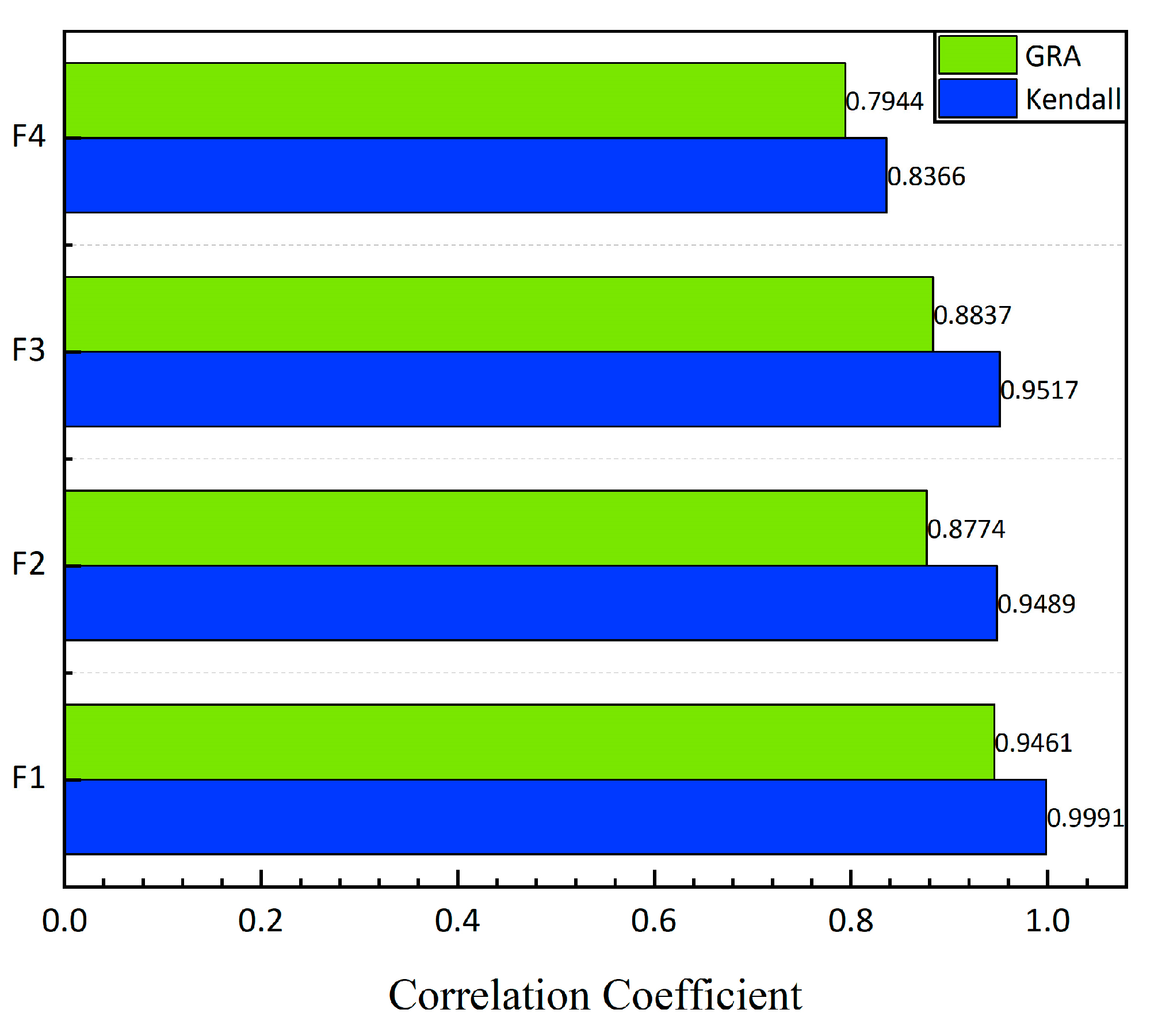
3.4. Correlation Analysis
- (1)
- Set the reference sequence and the comparison sequence ;
- (2)
- Pre-process the variables to simplify calculations by reducing the range of variables;
- (3)
- Calculate the correlation coefficient between the comparison series and the reference series, where it is a constant value and is taken as 0.5. The specific formula is expressed as follows:
4. The SOH Estimation and Result Analysis
4.1. Experimental Environment
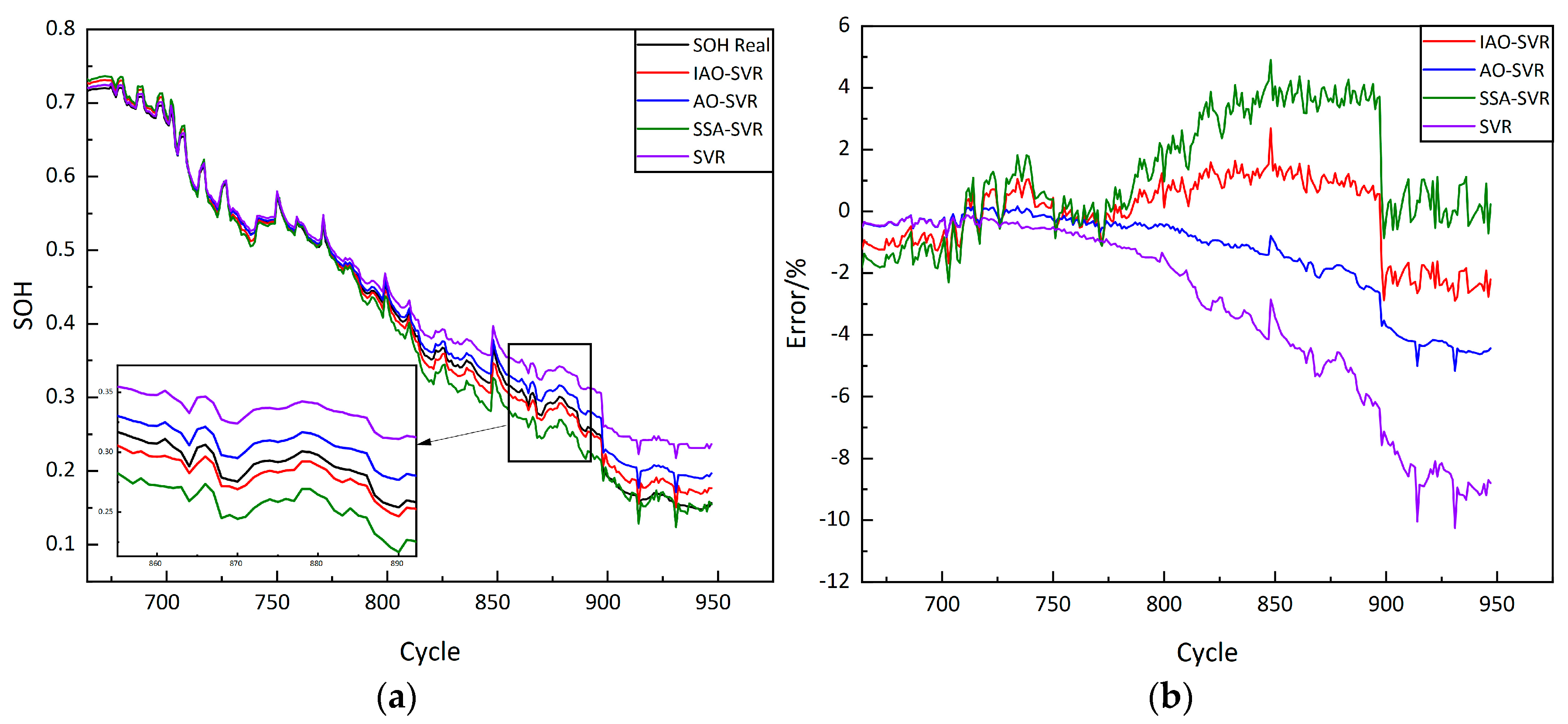
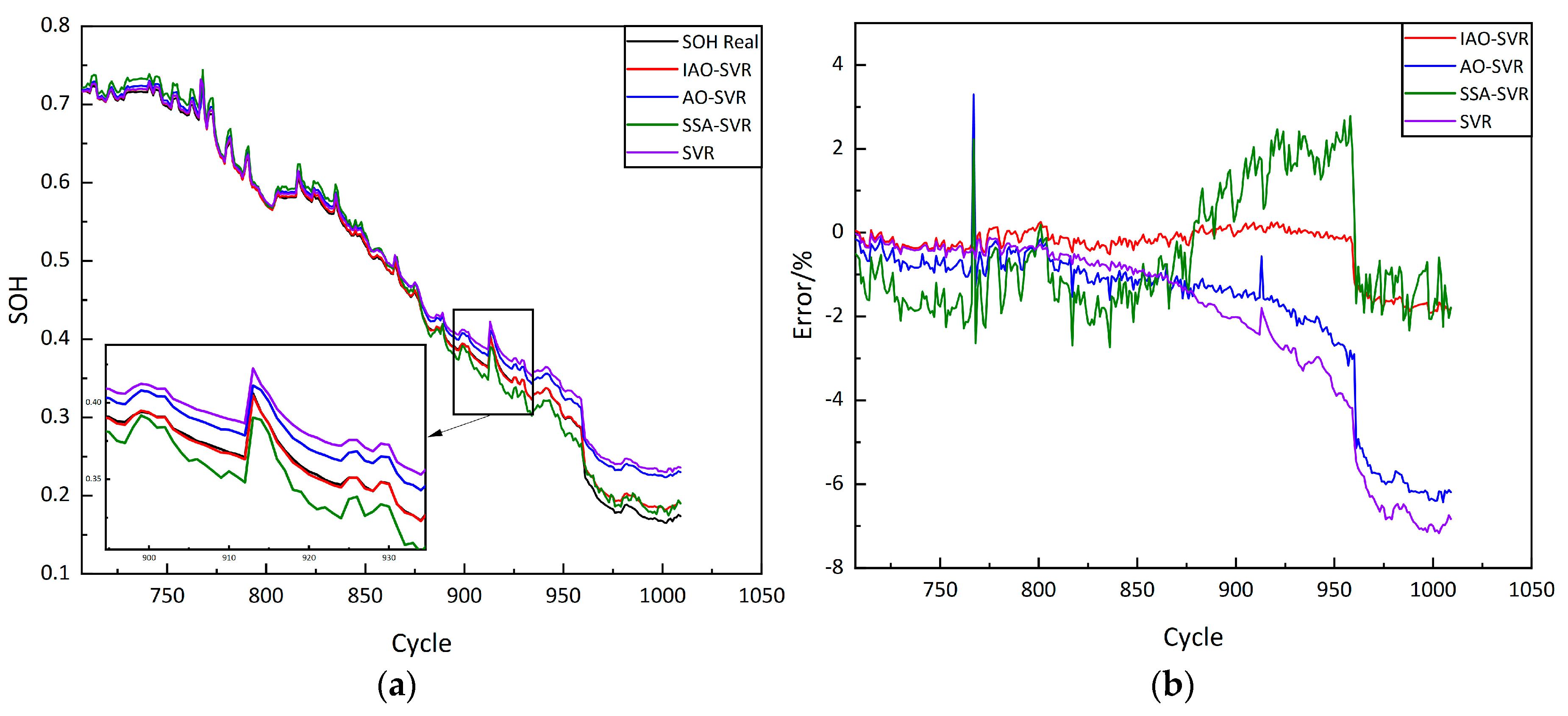
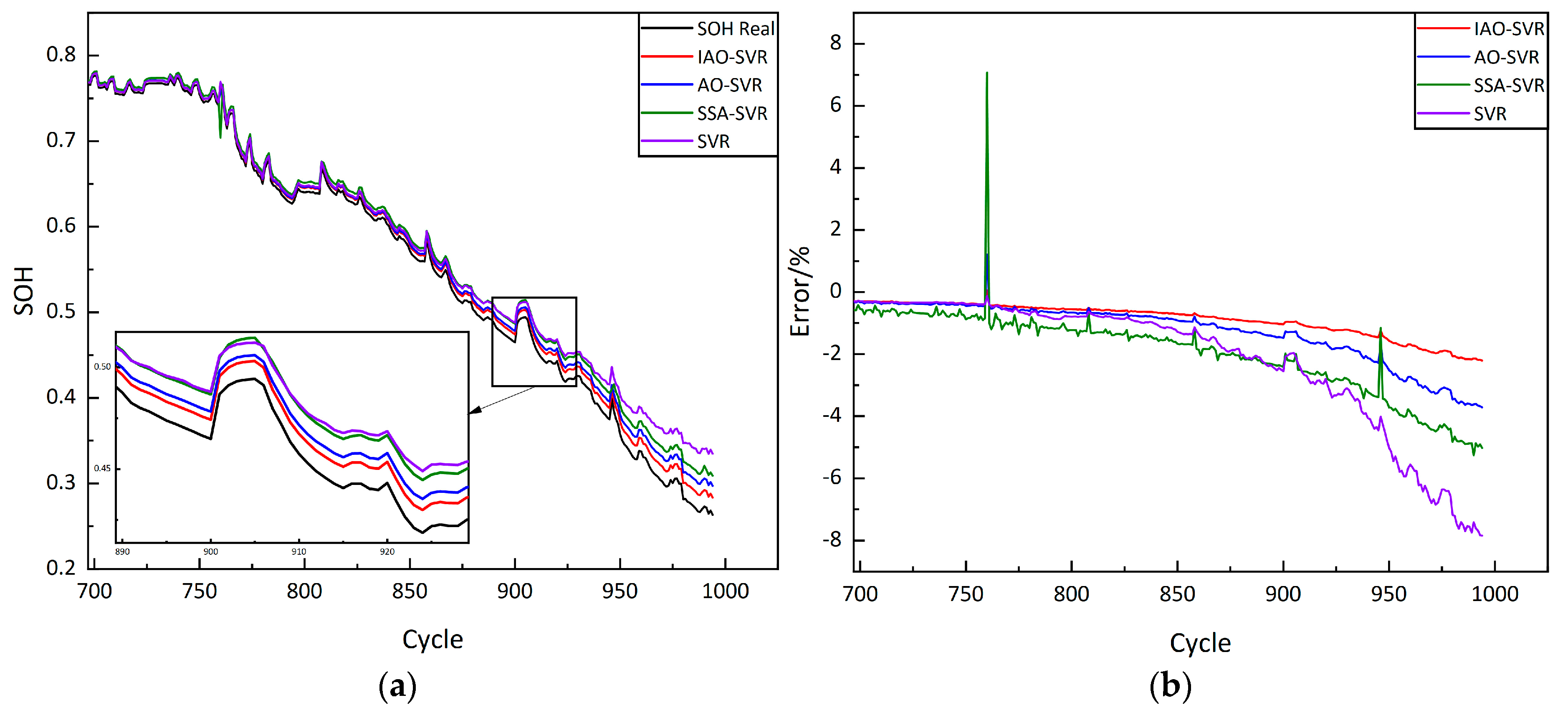
4.2. Analysis of Estimation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, L.; Xu, S.; Tang, A.; Zhou, F.; Hou, J.; Xiao, Y.; Fu, Z. A review of lithium-ion battery state of health estimation and prediction methods. World Electr. Veh. J. 2021, 12, 113. [Google Scholar] [CrossRef]
- Ghalkhani, M.; Habibi, S. Review of the Li-Ion Battery, Thermal Management, and AI-Based Battery Management System for EV Application. Energies 2023, 16, 185. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, C.; Jiang, J.; Zhang, W.; Zhang, L.; Wang, Y. Review on state-of-health of lithium-ion batteries: Characterizations, estimations and applications. J. Clean. Prod. 2021, 314, 128015. [Google Scholar] [CrossRef]
- Li, J.; Adewuyi, K.; Lotfi, N.; Landers, R.G.; Park, J. A single particle model with chemical/mechanical degradation physics for lithium ion battery State of Health (SOH) estimation. Appl. Energy 2018, 212, 1178–1190. [Google Scholar] [CrossRef]
- Golla-Schindler, U.; Zeibig, D.; Prickler, L.; Behn, S.; Bernthaler, T.; Schneider, G. Characterization of degeneration phenomena in lithium-ion batteries by combined microscopic techniques. Micron 2018, 113, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Li, K.; Xiao, E.; Xiao, E.; Wong, C.-K. Joint SoC and SoH estimation for zinc-nickel single-flow batteries. IEEE Trans. Ind. Electron. 2020, 67, 8484–8494. [Google Scholar] [CrossRef]
- Hu, X.; Feng, F.; Liu, K.; Zhang, L.; Xie, J.; Liu, B. State estimation for advanced battery management: Key challenges and future trends. Renew. Sustain. Energy Rev. 2019, 114, 109334. [Google Scholar] [CrossRef]
- Feng, H. An Online Prediction System of Lithium-ion Battery Safety. In Proceedings of the 2021 IEEE International Conference on Advances in Electrical Engineering and Computer Applications, AEECA 2021, Dalian, China, 27–28 August 2021; pp. 399–404. [Google Scholar]
- Oji, T.; Zhou, Y.; Ci, S.; Kang, F.; Chen, X.; Liu, X. Data-Driven Methods for Battery SOH Estimation: Survey and a Critical Analysis. IEEE Access 2021, 9, 126903–126916. [Google Scholar] [CrossRef]
- Li, C.; Xiao, F.; Fan, Y.; Yang, G.; Tang, X. An Approach to Lithium-Ion Battery SOH Estimation Based on Convolutional Neural Network SOH. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2020, 35, 4106–4119. [Google Scholar]
- Lin, M.; Yan, C.; Zeng, X. State of Health Estimation Method for Lithium-Ion Batteries via Generalized Additivity Model and Transfer Component Analysis. World Electr. Veh. J. 2023, 14, 14. [Google Scholar] [CrossRef]
- Shen, S.; Liu, B.; Zhang, K.; Ci, S. Toward Fast and Accurate SOH Prediction for Lithium-Ion Batteries. IEEE Trans. Energy Convers. 2021, 36, 2036–2046. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Chen, G.; Lyu, C.; Wu, Y.; Xu, L.; Ma, S. Research on Feature Extraction and SOH Evaluation Methods for Retired Power Battery. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2022, 42, 1332–1346. [Google Scholar]
- Bustos, R.; Gadsden, S.A.; Malysz, P.; Al-Shabi, M.; Mahmud, S. Health Monitoring of Lithium-Ion Batteries Using Dual Filters. Energies 2022, 15, 2230. [Google Scholar] [CrossRef]
- Wu, T.; Liu, S.; Wang, Z.; Huang, Y. SOC and SOH Joint Estimation of Lithium-Ion Battery Based on Improved Particle Filter Algorithm. J. Electr. Eng. Technol. 2022, 17, 307–317. [Google Scholar] [CrossRef]
- Wei, J.; Chen, C. State of Charge and Health Estimation for Lithium-Ion Batteries Using Recursive Least Squares. In Proceedings of the 5th IEEE International Conference on Advanced Robotics and Mechatronics, ICARM 2020, Shenzhen, China, 18–21 December 2020; pp. 686–689. [Google Scholar]
- Chen, Y.; He, Y.; Li, Z.; Chen, L.; Zhang, C. Remaining useful life prediction and state of health diagnosis of lithium-ion battery based on second-order central difference particle filter. IEEE Access 2020, 8, 37305–37313. [Google Scholar] [CrossRef]
- Zeng, M.; Zhang, P.; Yang, Y.; Xie, C.; Shi, Y. SOC and SOH joint estimation of the power batteries based on fuzzy unscented Kalman filtering algorithm. Energies 2019, 12, 3122. [Google Scholar] [CrossRef]
- Pang, B.; Chen, L.; Dong, Z. Data-Driven Degradation Modeling and SOH Prediction of Li-Ion Batteries. Energies 2022, 15, 5580. [Google Scholar] [CrossRef]
- Sun, H.; Sun, J.; Zhao, K.; Wang, L.; Wang, K. Data-Driven ICA-Bi-LSTM-Combined Lithium Battery SOH Estimation. Math. Probl. Eng. 2022, 2022, 1–8. [Google Scholar] [CrossRef]
- You, G.-W.; Park, S.; Lee, S. Data-driven SOH prediction for EV batteries. In Proceedings of the 2015 IEEE International Conference on Consumer Electronics, ICCE 2015, Las Vegas, NV, USA, 9–12 January 2015; pp. 577–578. [Google Scholar]
- Li, Q.; Li, D.; Zhao, K.; Wang, L.; Wang, K. State of health estimation of lithium-ion battery based on improved ant lion optimization and support vector regression. J. Energy Storage 2022, 50, 104215. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, W.; Yin, J.; Feng, T. Lithium Battery Health Factor Extraction Based on Improved DouglasPeucker Algorithm and SOH Prediction Based on XGboost. Energies 2022, 15, 5981. [Google Scholar] [CrossRef]
- Deng, Y.; Ying, H.; E, J.; Zhu, H.; Wei, K.; Chen, J.; Zhang, F.; Liao, G. Feature parameter extraction and intelligent estimation of the State-of-Health of lithium-ion batteries. Energy 2019, 176, 91–102. [Google Scholar] [CrossRef]
- Wen, J.; Chen, X.; Li, X.; Li, Y. SOH prediction of lithium battery based on IC curve feature and BP neural network. Energy 2022, 261, 125234. [Google Scholar] [CrossRef]
- Shen, S.; Sadoughi, M.; Li, M.; Wang, Z.; Hu, C. Deep convolutional neural networks with ensemble learning and transfer learning for capacity estimation of lithium-ion batteries. Appl. Energy 2020, 260, 114296. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-qaness, M.A.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Inf. Sci. 2019, 480, 403–419. [Google Scholar] [CrossRef]
- Mao, Q.; Wang, Y. Adaptive T-distribution seagull optimization algorithm combining improved logistics chaos and Sine-cosine operator. J. Chin. Comput. Syst. 2022, 43, 2271–2277. (In Chinese) [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, Z.; Zhai, Z.; Shang, Z.; Yan, R.; Chen, X. Explainability-driven model improvement for SOH estimation of lithium-ion battery. Reliab. Eng. Syst. Saf. 2023, 232, 109046. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.-L.; Pecht, M. An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 811–820. [Google Scholar] [CrossRef]

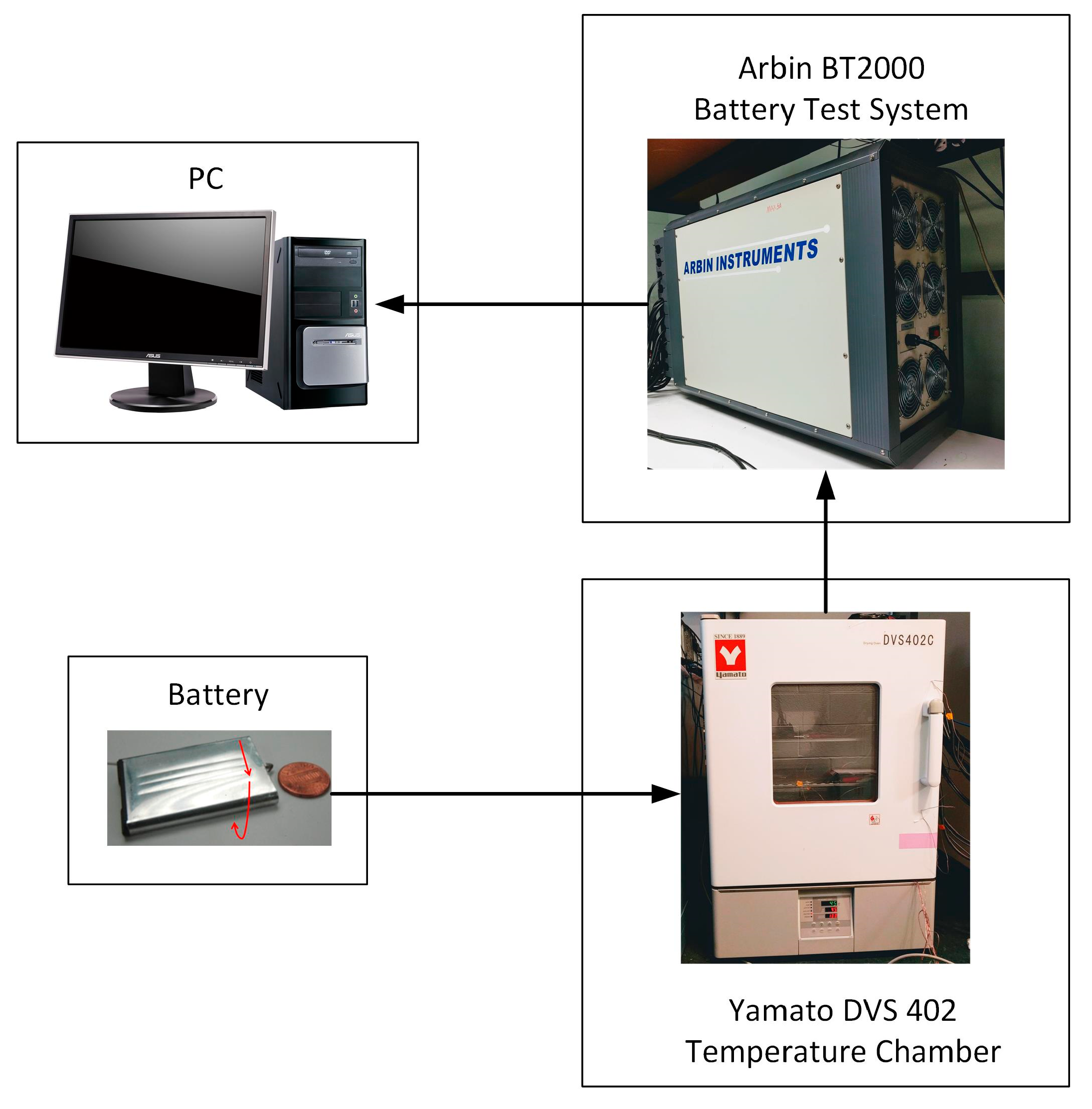


| Parameters | Specifications |
|---|---|
| Shape | Prismatic |
| Capacity | 1100 mAH |
| Weight | 21.1 g |
| Dimensions | 5.4 × 33.6 × 50.6 mm |
| Battery | Method | MAE | RMSE | |
|---|---|---|---|---|
| CS2-35 | IAO–SVR | 0.9976 | 0.0052 | 0.0081 |
| AO–SVR | 0.9926 | 0.0111 | 0.0141 | |
| SSA–SVR | 0.9918 | 0.0109 | 0.0148 | |
| SVR | 0.9781 | 0.0226 | 0.0334 | |
| CS2-36 | IAO–SVR | 0.9960 | 0.0103 | 0.0124 |
| AO–SVR | 0.9915 | 0.0133 | 0.0180 | |
| SSA–SVR | 0.9877 | 0.0169 | 0.0217 | |
| SVR | 0.9502 | 0.0316 | 0.0437 | |
| CS2-37 | IAO–SVR | 0.9987 | 0.0042 | 0.0071 |
| AO–SVR | 0.9822 | 0.0192 | 0.0267 | |
| SSA–SVR | 0.9943 | 0.0138 | 0.0150 | |
| SVR | 0.9764 | 0.0211 | 0.0307 | |
| CS2-38 | IAO–SVR | 0.9965 | 0.0088 | 0.0102 |
| AO–SVR | 0.9917 | 0.0126 | 0.0156 | |
| SSA–SVR | 0.9810 | 0.0200 | 0.0238 | |
| SVR | 0.9691 | 0.0215 | 0.0304 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, L.; Liu, X.; Luo, W.; Wu, L. State of Health Estimation for Lithium-Ion Batteries Using IAO–SVR. World Electr. Veh. J. 2023, 14, 122. https://doi.org/10.3390/wevj14050122
Xing L, Liu X, Luo W, Wu L. State of Health Estimation for Lithium-Ion Batteries Using IAO–SVR. World Electric Vehicle Journal. 2023; 14(5):122. https://doi.org/10.3390/wevj14050122
Chicago/Turabian StyleXing, Likun, Xiao Liu, Wenfei Luo, and Long Wu. 2023. "State of Health Estimation for Lithium-Ion Batteries Using IAO–SVR" World Electric Vehicle Journal 14, no. 5: 122. https://doi.org/10.3390/wevj14050122
APA StyleXing, L., Liu, X., Luo, W., & Wu, L. (2023). State of Health Estimation for Lithium-Ion Batteries Using IAO–SVR. World Electric Vehicle Journal, 14(5), 122. https://doi.org/10.3390/wevj14050122





