Research on the Multiple Capacitor Current Sharing of High-Current Receiving Coils in a Series–Series Wireless Charging System
Abstract
:1. Introduction
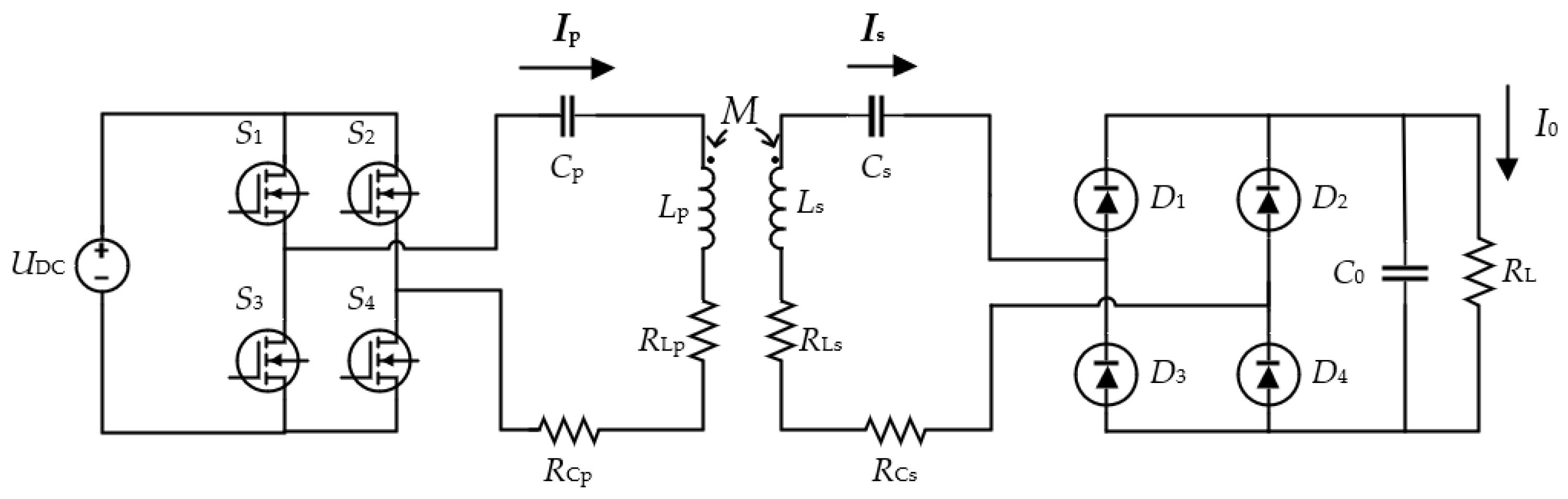
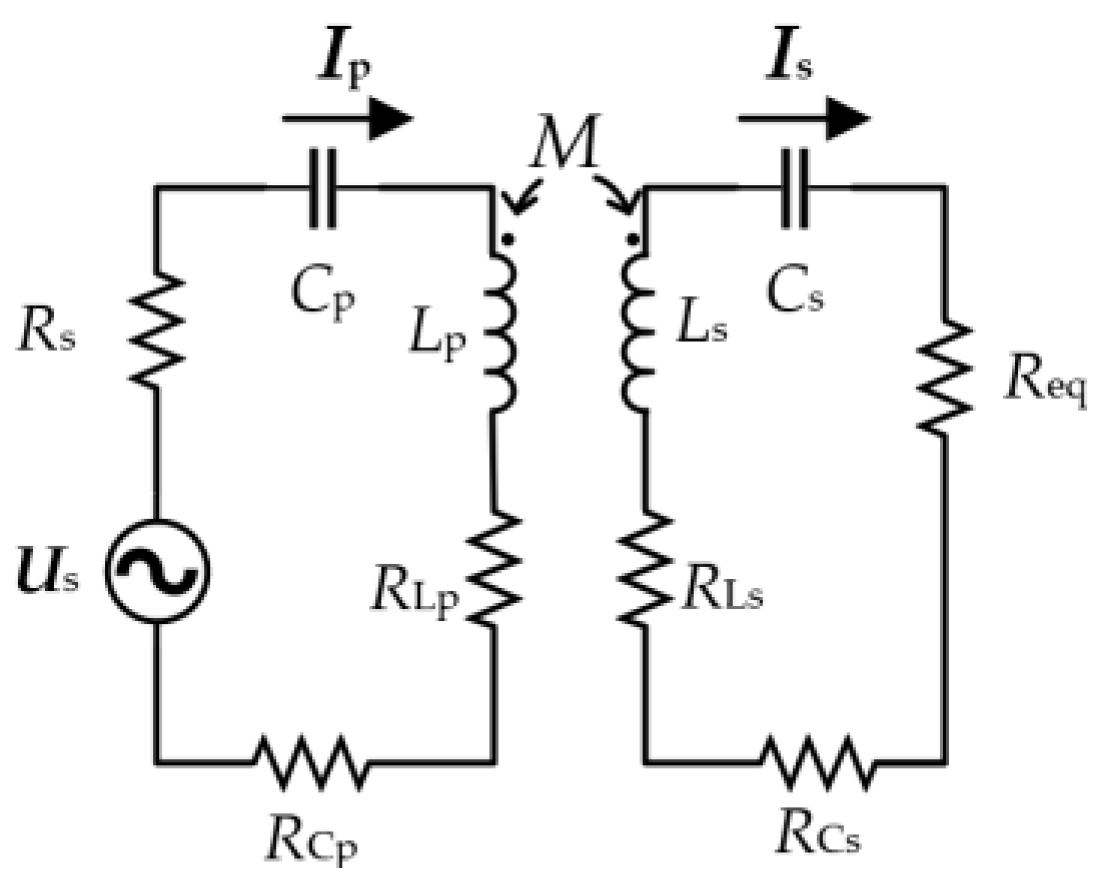
2. Principle of Wireless Power Transmission in a SS Structure
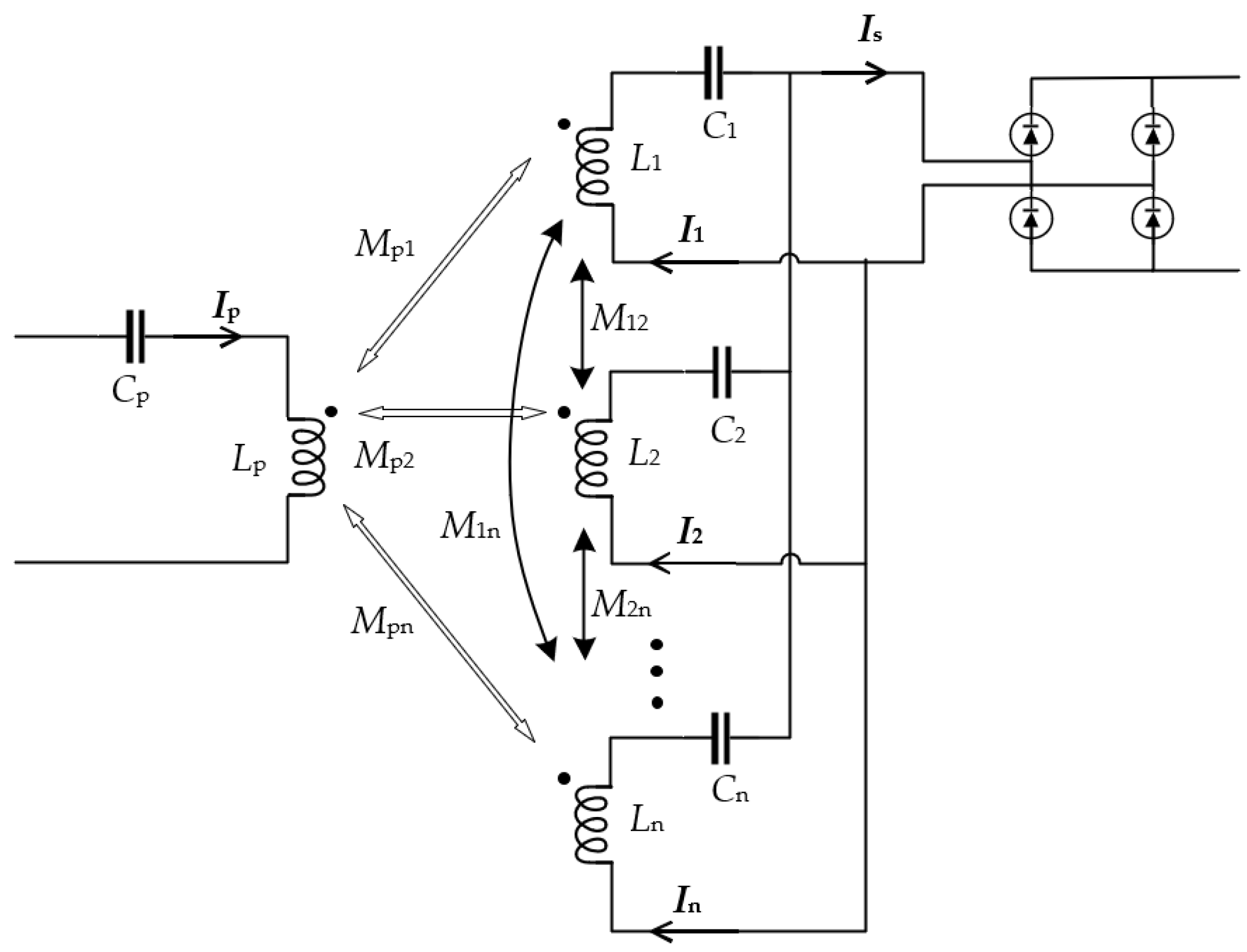
3. Model of the Current Sharing of Coils and Efficiency Analysis
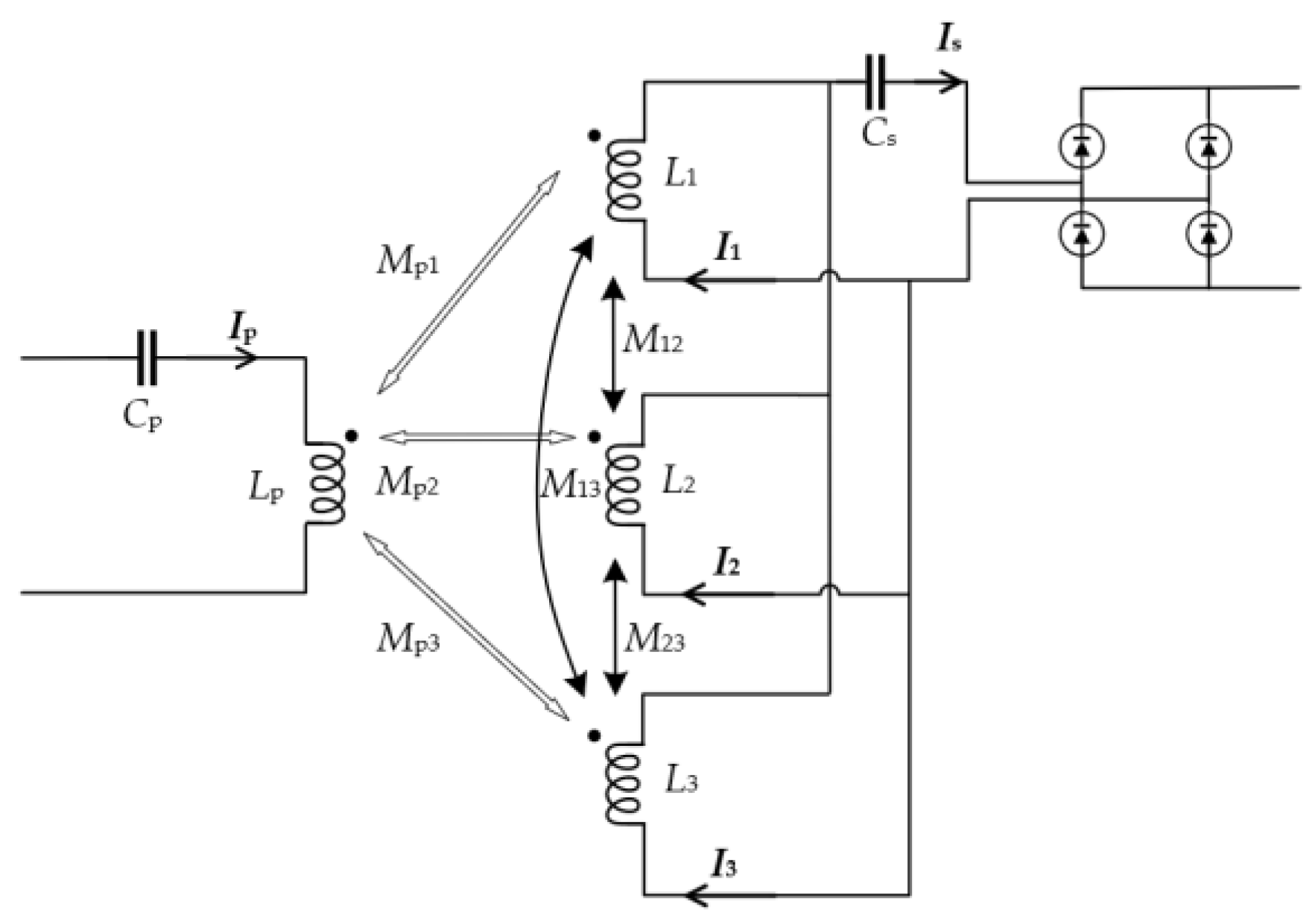
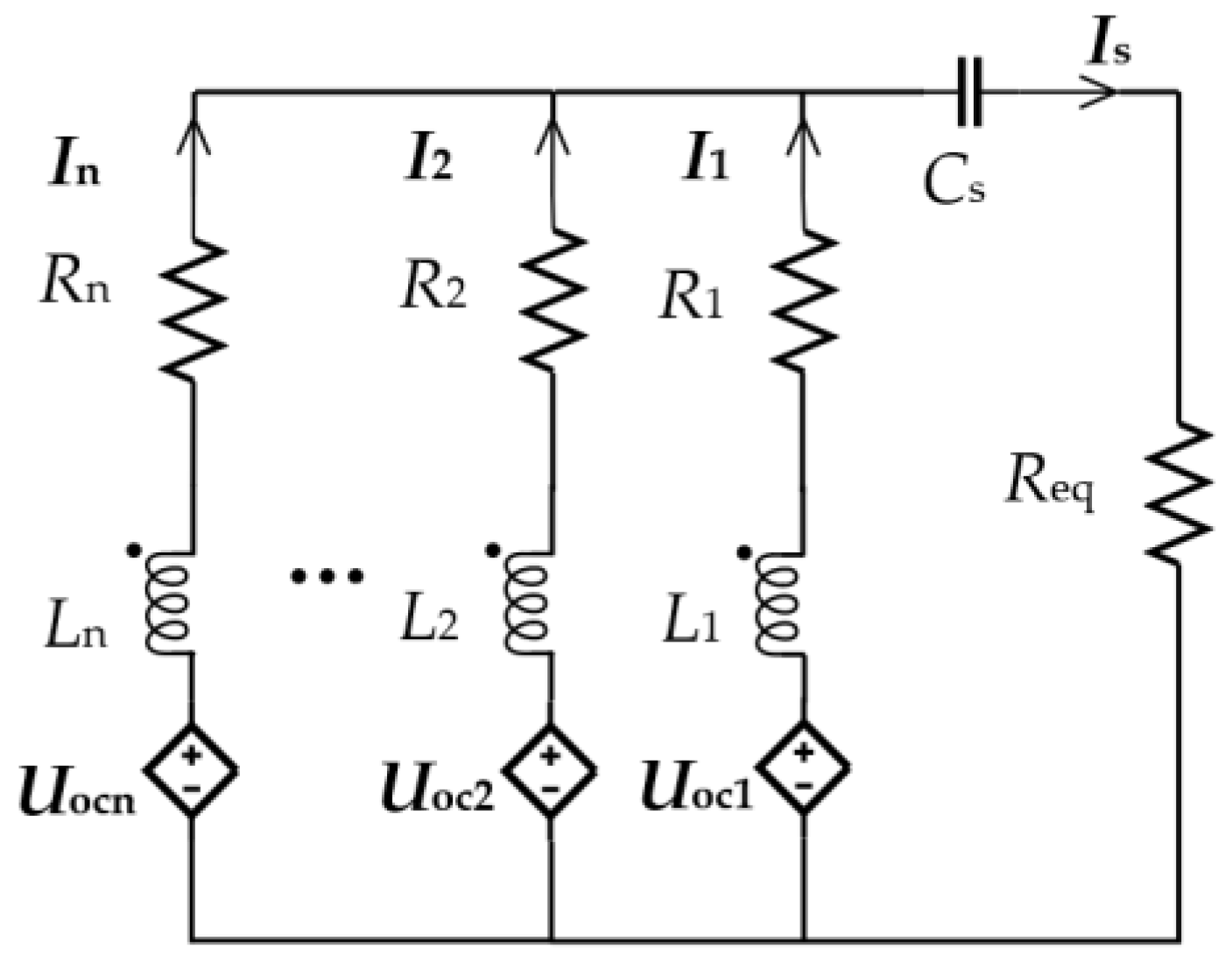
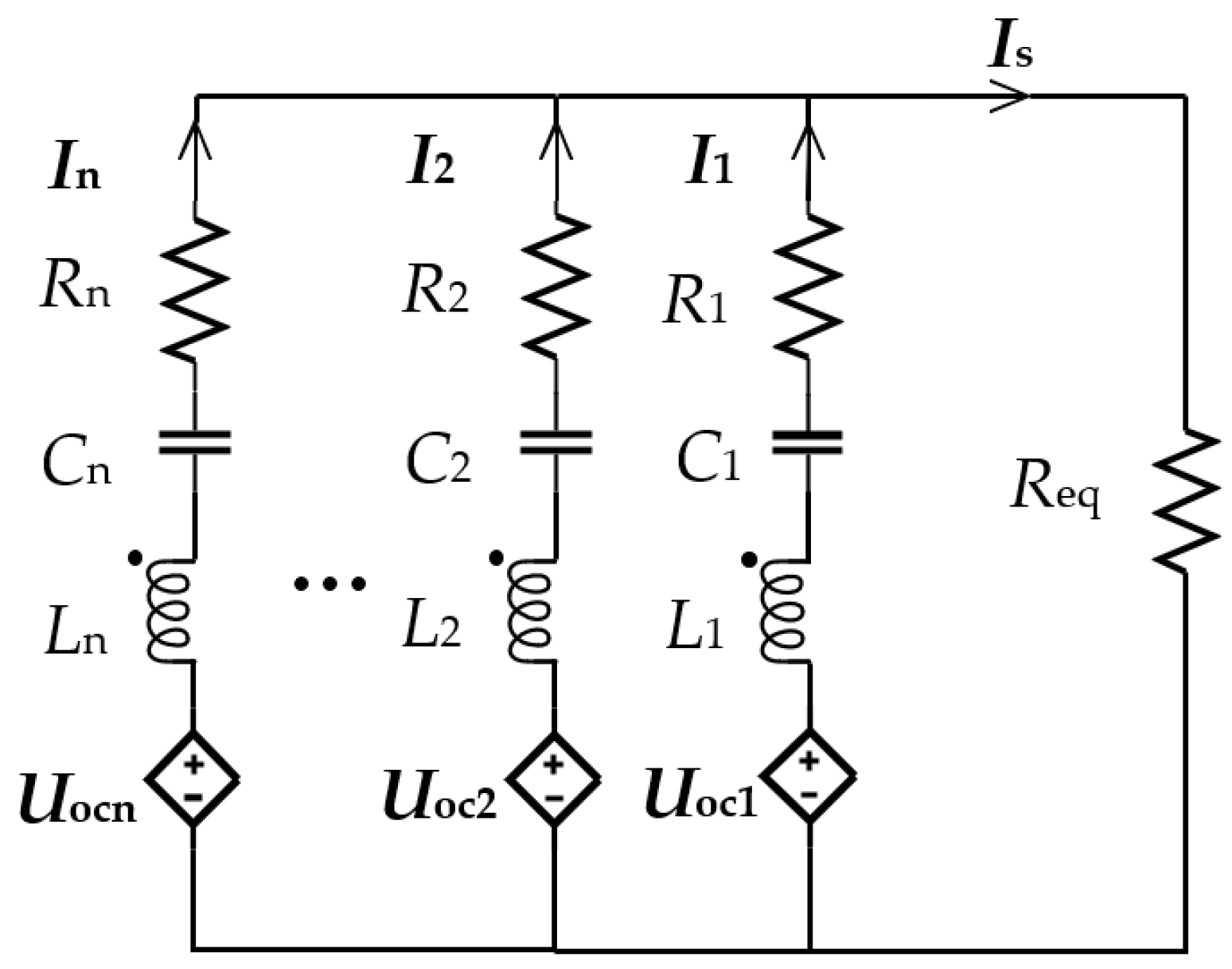
3.1. Analysis of n Branches Parallel to One Capacitor
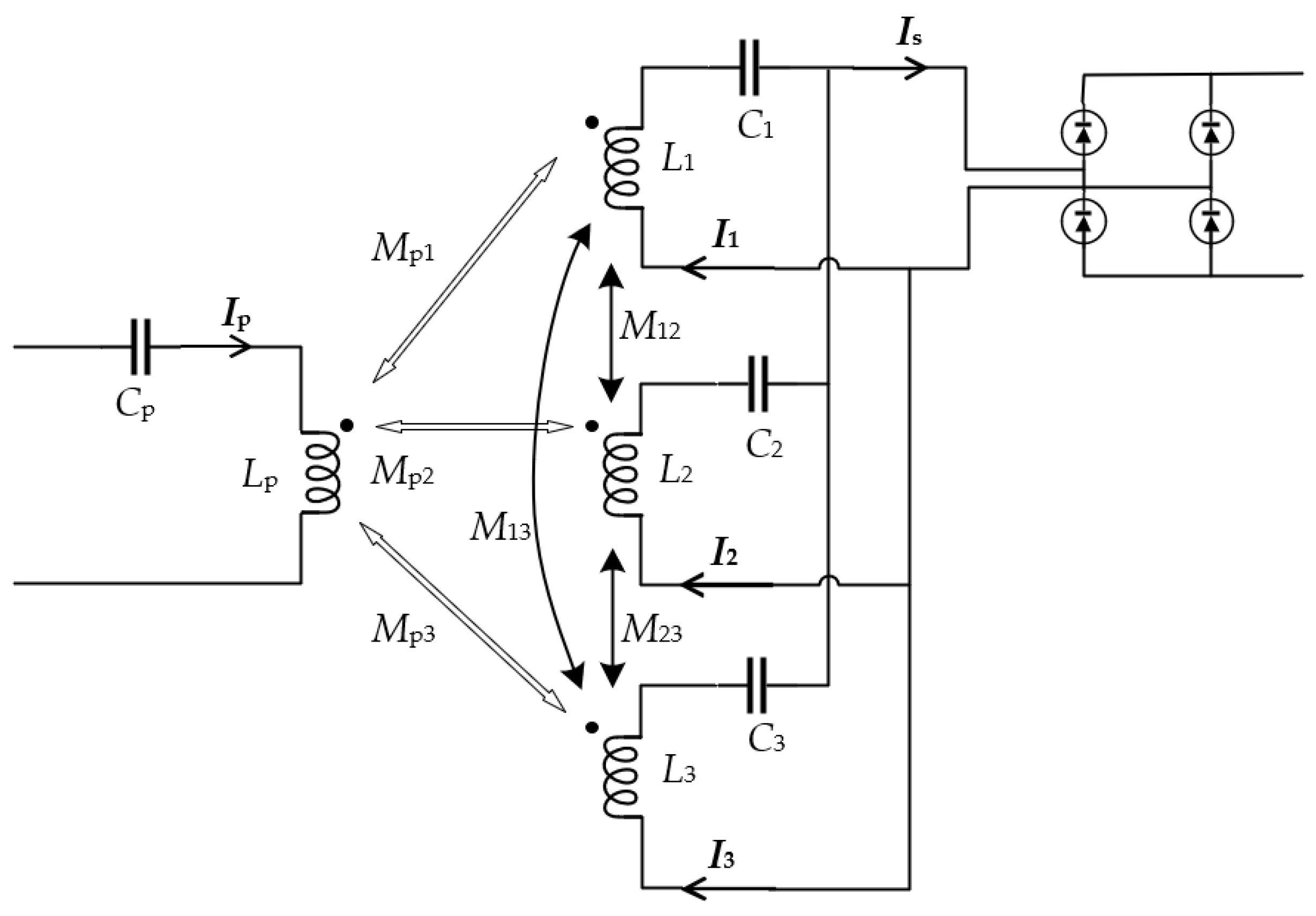
3.2. Analysis of n Branches Parallel to Three Capacitors
3.3. Analysis of Efficiency
3.4. Analysis of Three Parallel Branches
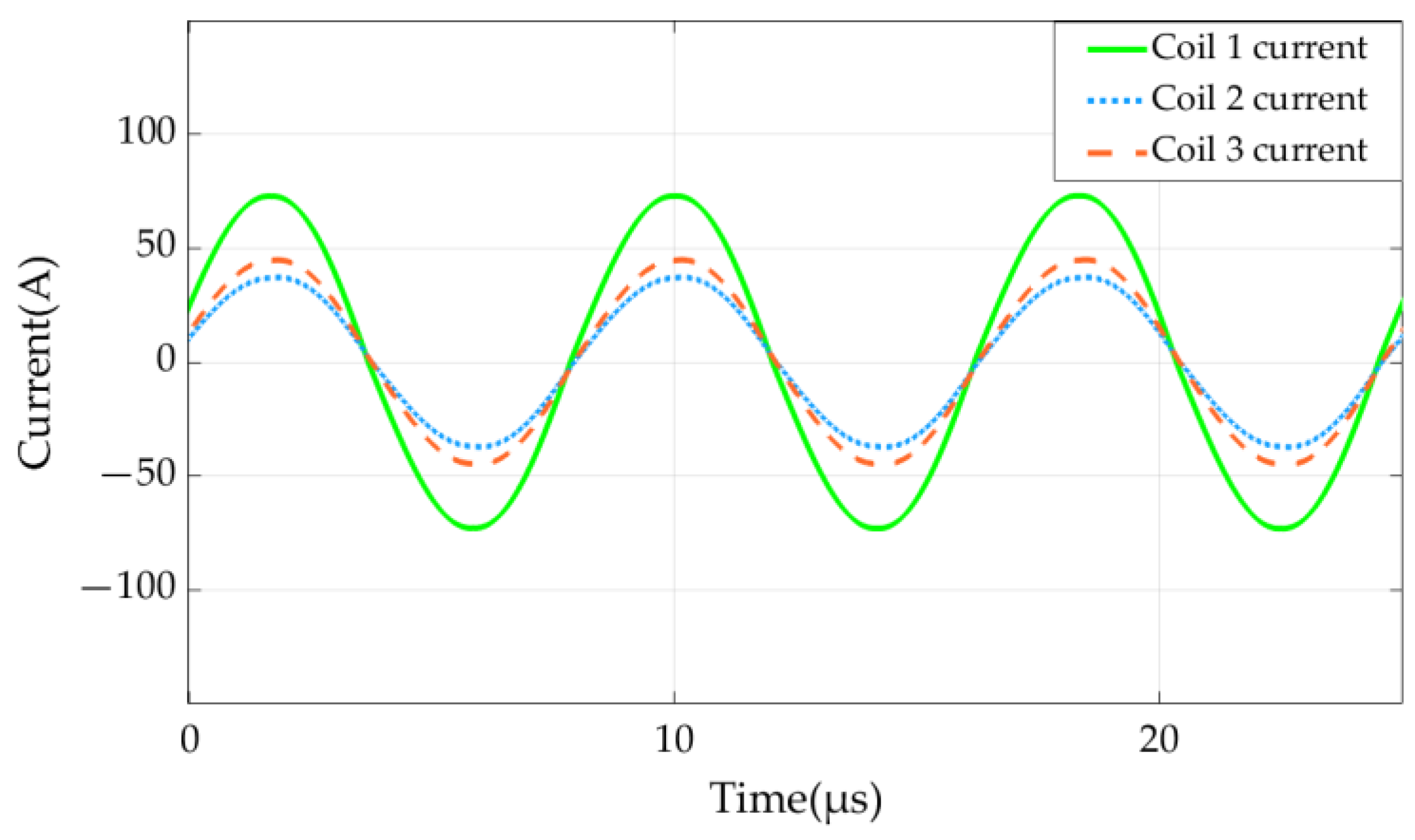
4. Simulation Verification of Parallel Current Sharing
5. Analysis of the Effect of Current Sharing Optimization
5.1. Efficiency Comparison of Three Branches in Parallel
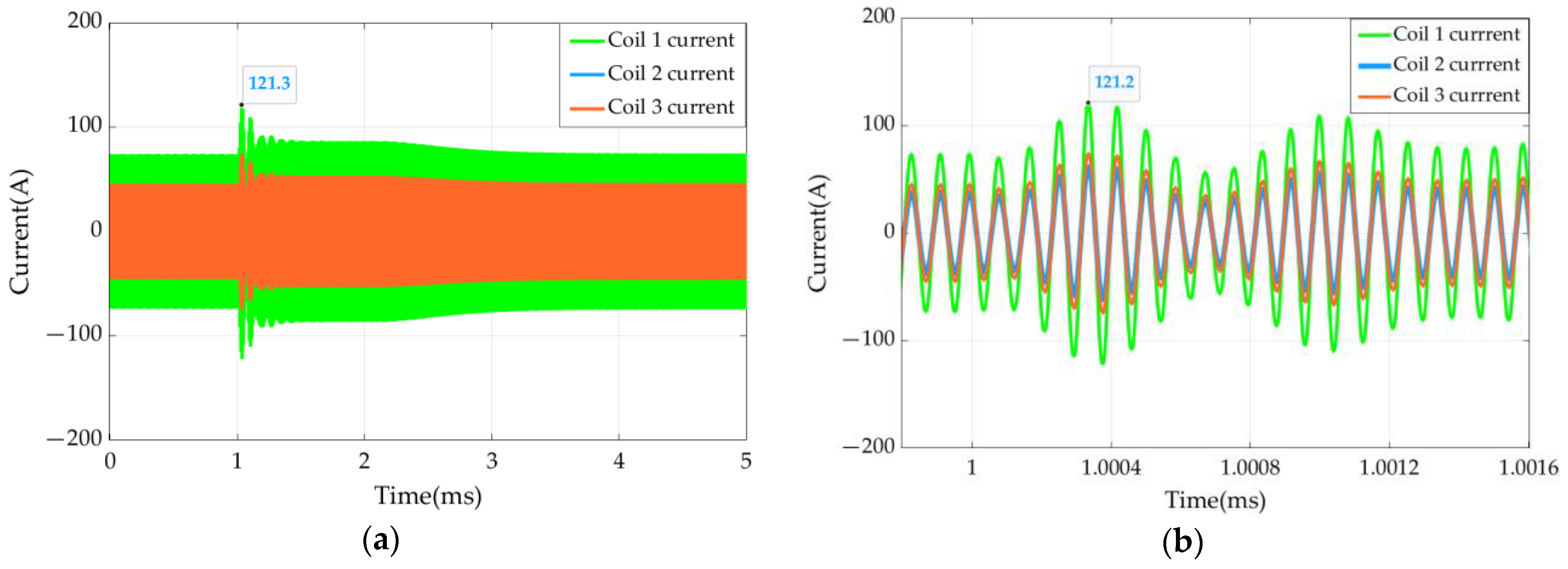
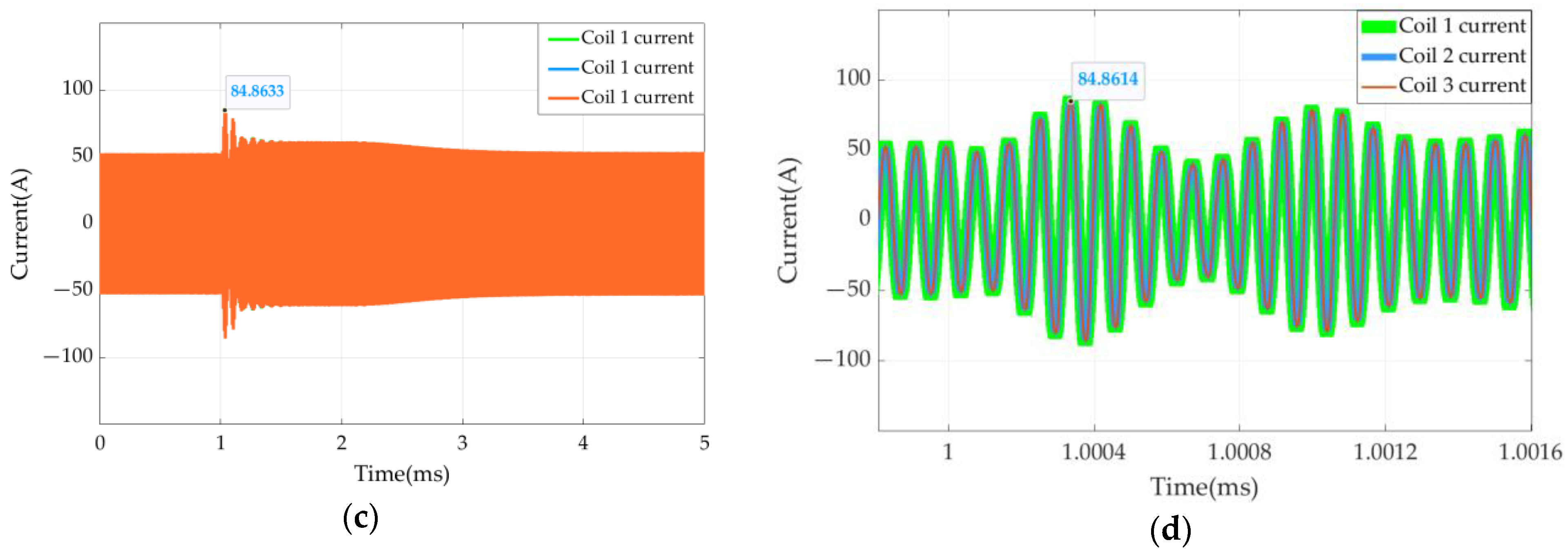
5.2. System Disturbance Analysis
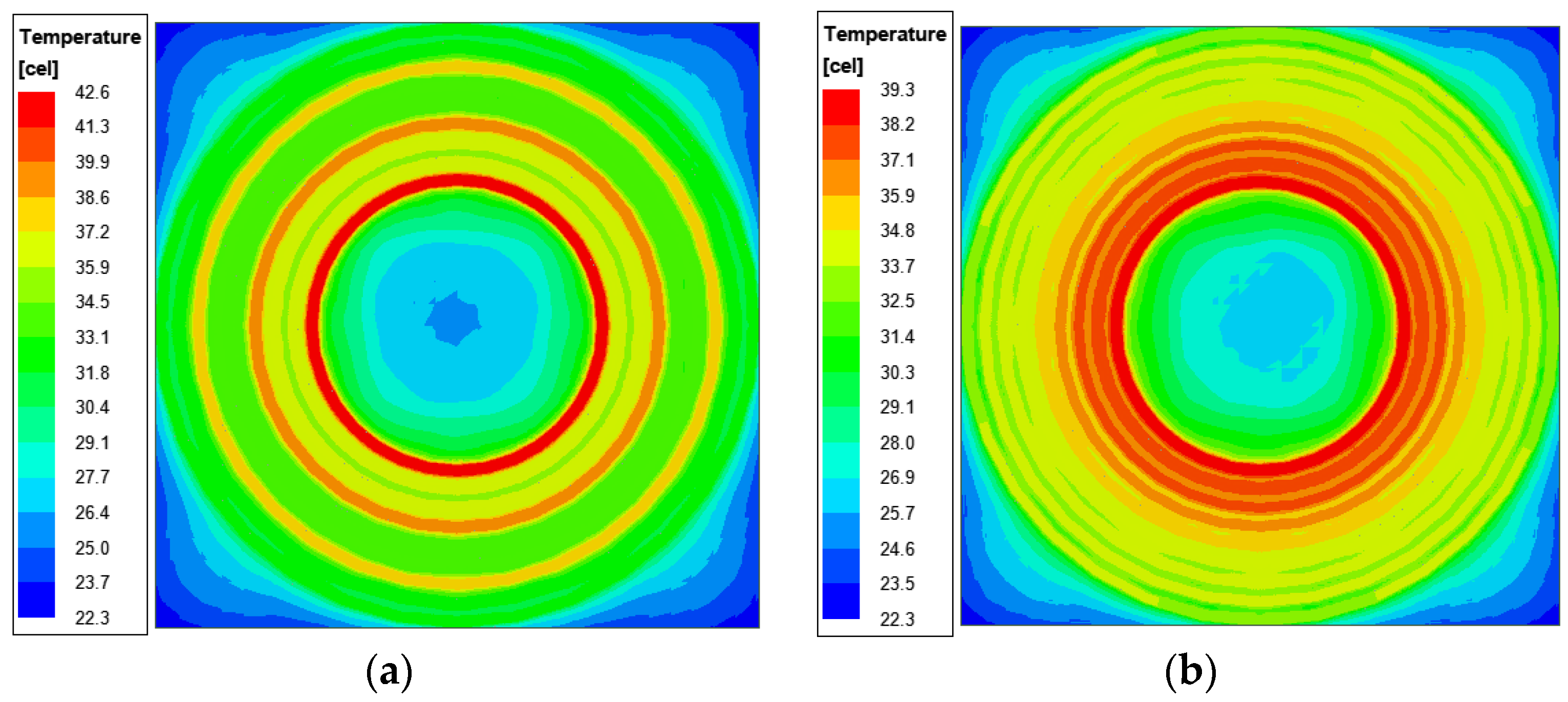
5.3. Temperature Simulation Comparison
6. Experimental Verification
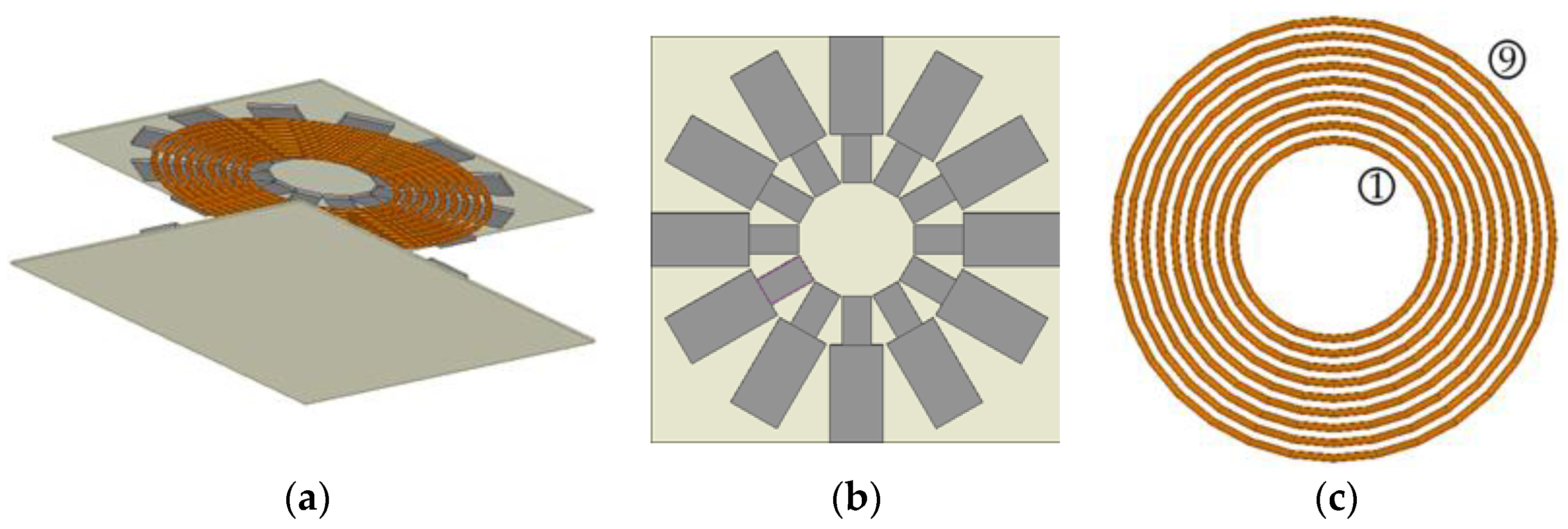
6.1. Experimental Prototype
6.2. Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, J.H.; Lee, B.; Lee, J.; Lee, S.; Park, C.; Jung, S.; Lee, S.; Yi, K.; Baek, J. Development of 1-MW Inductive Power Transfer System for a High-Speed Train. IEEE Trans. Ind. Electron. 2015, 62, 6242–6250. [Google Scholar] [CrossRef]
- Covic, G.A.; Boys, J.T. Modern Trends in Inductive Power Transfer for Transportation Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 28–41. [Google Scholar] [CrossRef]
- Elliott, G.A.J.; Covic, G.A.; Kacprzak, D.; Boys, J.T. A New Concept: Asymmetrical Pick-Ups for Inductively Coupled Power Transfer Monorail Systems. IEEE Trans. Magn. 2006, 42, 3389–3391. [Google Scholar] [CrossRef]
- Luo, B.; Long, T.; Guo, L.; Dai, R.; Mai, R.; He, Z. Analysis and Design of Inductive and Capacitive Hybrid Wireless Power Transfer System for Railway Application. IEEE Trans. Ind. Appl. 2020, 56, 3034–3042. [Google Scholar] [CrossRef]
- Shin, J.; Shin, S.; Kim, Y.; Ahn, S.; Lee, S.; Jung, G.; Jeon, S.; Cho, D. Design and Implementation of Shaped Magnetic-Resonance-Based Wireless Power Transfer System for Roadway-Powered Moving Electric Vehicles. IEEE Trans. Ind. Electron. 2014, 61, 1179–1192. [Google Scholar] [CrossRef]
- Li, W.; Zhao, H.; Li, S.; Deng, J.; Kan, T.; Mi, C.C. Integrated LCC Compensation Topology for Wireless Charger in Electric and Plug-in Electric Vehicles. IEEE Trans. Ind. Electron. 2015, 62, 4215–4225. [Google Scholar] [CrossRef]
- Kumar, K.; Chowdary, V.V.S.R.; Mali, V.; Kumar, R. Analysis of Output Power Variation in Dynamic Wireless Charging System for Electric Vehicles. In Proceedings of the 2021 IEEE 2nd International Conference on Smart Technologies for Power, Energy and Control (STPEC), Bilaspur, India, 19–22 December 2021; pp. 1–6. [Google Scholar]
- Kavitha, M.; Bobba, P.B.; Prasad, D. Comprehensive mathematical modelling and experimental analysis of a wireless power transfer system for neighborhood electric vehicles. In Proceedings of the 2015 IEEE International WIE Conference on Electrical and Computer Engineering (WIECON-ECE), Dhaka, Bangladesh, 19–20 December 2015; pp. 275–279. [Google Scholar]
- Liu, F.; Zhang, Y.; Chen, K.; Zhao, Z.; Yuan, L. A comparative study of load characteristics of resonance types in wireless transmission systems. In Proceedings of the 2016 Asia-Pacific International Symposium on Electromagnetic Compatibility (APEMC), Shenzhen, China, 17–21 May 2016; pp. 203–206. [Google Scholar]
- Zaheer, A.; Kacprzak, D.; Covic, G.A. A bipolar receiver pad in a lumped IPT system for electric vehicle charging applications. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 283–290. [Google Scholar]
- Takanashi, H.; Sato, Y.; Kaneko, Y.; Abe, S.; Yasuda, T. A large air gap 3 kW wireless power transfer system for electric vehicles. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 269–274. [Google Scholar]
- Deng, Q.; Liu, J.; Czarkowski, D.; Kazimierczuk, M.K.; Bojarski, M.; Zhou, H.; Hu, W. Frequency-Dependent Resistance of Litz-Wire Square Solenoid Coils and Quality Factor Optimization for Wireless Power Transfer. IEEE Trans. Ind. Electron. 2016, 63, 2825–2837. [Google Scholar] [CrossRef]
- Acero, J.; Hernandez, P.J.; Burdio, J.M.; Alonso, R.; Barragdan, L.A. Simple resistance calculation in litz-wire planar windings for induction cooking appliances. IEEE Trans. Magn. 2005, 41, 1280–1288. [Google Scholar] [CrossRef]
- Li, H.; Wang, K.; Huang, L.; Li, J.; Yang, X. Coil structure optimization method for improving coupling coefficient of wireless power transfer. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 2518–2521. [Google Scholar]
- Lu, M.; Ngo, K.D.T. Systematic Design of Coils in Series–Series Inductive Power Transfer for Power Transferability and Efficiency. IEEE Trans. Power Electron. 2018, 33, 3333–3345. [Google Scholar] [CrossRef]
- Cheng, Y.; Shu, Y. A New Analytical Calculation of the Mutual Inductance of the Coaxial Spiral Rectangular Coils. IEEE Trans. Magn. 2014, 50, 7026806. [Google Scholar] [CrossRef]
- Sun, Y.; Xia, C.; Dai, X.; Su, Y. Analysis and optimization of mutual inductance for inductively coupled power transfer system. Proc. CSEE 2010, 30, 44–50. [Google Scholar]
- Bosshard, R.; Kolar, J.W.; Wunsch, B. Accurate finite-element modeling and experimental verification of inductive power transfer coil design. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 1648–1653. [Google Scholar]
- Wang, C.S.; Stielau, O.H.; Covic, G.A. Design Considerations for a Contactless Electric Vehicle Battery Charger. IEEE Trans. Ind. Electron. 2005, 52, 1308–1314. [Google Scholar] [CrossRef]
- Kurs, A.; Moffatt, R.; Soljačić, M. Simultaneous mid-range power transfer to multiple devices. Appl. Phys. Lett. 2010, 96, 044102. [Google Scholar] [CrossRef]
- Ahn, D.; Hong, S. Effect of Coupling Between Multiple Transmitters or Multiple Receivers on Wireless Power Transfer. IEEE Trans. Ind. Electron. 2013, 60, 2602–2613. [Google Scholar] [CrossRef]
- Shen, H.; Liu, X.; Yan, C.; Chen, X. Analysis and Optimization of High-Power MCR Bidirectional WPT System with High Distance-Diameter Ratio. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar]
- Niu, S.; Yu, H.; Niu, S.; Jian, L. Power loss analysis and thermal assessment on wireless electric vehicle charging technology: The over-temperature risk of ground assembly needs attention. Appl. Energy 2020, 275, 115344. [Google Scholar] [CrossRef]
- Hwang, K.; Chung, S.; Yoon, U.; Lee, M.; Ahn, S. Thermal analysis for temperature robust wireless power transfer systems. In Proceedings of the 2013 IEEE Wireless Power Transfer (WPT), Perugia, Italy, 15–16 May 2013; pp. 52–55. [Google Scholar]
- Zhu, C.; Fu, C.; Wang, D.; Huang, X.; Zhang, H.; Dong, S.; Wei, G.; Song, K. Thermal Simulation and Optimization Study for Magnetic Coupler of Static Electric Vehicle Wireless Power Transfer Systems. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–4. [Google Scholar]
- Duerbaum, T. First harmonic approximation including design constraints. In Proceedings of the INTELEC—Twentieth International Telecommunications Energy Conference (Cat. No.98CH36263), San Francisco, CA, USA, 4–8 October 1998; pp. 321–328. [Google Scholar]
- Feng, A.; Mao, Z.; Qin, H. Bifurcation Phenomena and Phase Shift Control Strategy in Loosely Coupled Inductive Power Transfer System. J. Shanghai Dianji Univ. 2010, 13, 17–21. [Google Scholar]
- Bagchi, A.C.; Kamineni, A.; Zane, R. Analytical Optimization of a Litz Wire Spiral Coil Based Underwater IPT System. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 2456–2463. [Google Scholar]
- Xie, Y.; Liu, Z.; Hou, Y.; Luo, X.; Sun, S.; Ding, R. Optimal Design of Magnetic Cores for the Circular Coil in Wireless Power Transfer System. In Proceedings of the 2023 International Conference on Power System Technology (PowerCon), Jinan, China, 21–22 September 2023; pp. 1–5. [Google Scholar]
- Shijo, T.; Ogawa, K.; Obayashi, S. Optimization of thickness and shape of core block in resonator for 7 kW-class wireless power transfer system for PHEV/EV charging. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3099–3102. [Google Scholar]
- Sampath, J.P.K.; Alphones, A.; Shimasaki, H. Coil design Guidelines for High Efficiency of Wireless Power Transfer (WPT). In Proceedings of the 2016 IEEE Region 10 Conference (Tencon), Singapore, 22–25 November 2016; pp. 726–729. [Google Scholar]





| Parameters | Values | Parameters | Values |
|---|---|---|---|
| primary AC equivalent voltage (V) | 500 | primary Litz wire | 0.05 × 3000 |
| side length of primary /secondary aluminum plate (cm) | 54/50 | secondary Litz wire | 0.05 × 10,000 |
| total inductance of receiving coil (μH) | 5 | primary /secondary pitch (mm) | 4.5/7.5 |
| Lp (μH) | 152 | k | 0.2 |
| Cp (nF) | 11.57 | load voltage (V) | 48 |
| frequency (kHz) | 120 | load current (A) | 100 |
| Cs (nF) | 352 | RL (Ω) | 0.48 |
| distance between the primary coil and the magnetic core (mm) | 5.5 | distance between the secondary coil and the magnetic core(mm) | 2.5 |
| Parameters | Values | ||
|---|---|---|---|
| primary side | first ring | radius (mm) | 80–150 |
| length/width (mm) | 70/40 | ||
| second ring | radius (mm) | 150–270 | |
| length/width (mm) | 120/70 | ||
| secondary side | first ring | radius (mm) | 70–130 |
| length/width (mm) | 60/35 | ||
| second ring | radius (mm) | 130–250 | |
| length/width (mm) | 120/65 | ||
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Mp1 (μH) | 6.6 | Rp (mΩ) | 83.9 |
| Mp2 (μH) | 6.9 | R1 (mΩ) | 8.6 |
| Mp3 (μH) | 7.0 | R2 (mΩ) | 9.9 |
| R3 (mΩ) | 10.8 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| L1 (μH) | 5.6 | M12 (μH) | 4.6 |
| L2 (μH) | 6.0 | M13 (μH) | 4.4 |
| L3 (μH) | 6.1 | M23 (μH) | 4.8 |
| Parameters | Values |
|---|---|
| I1 (A) | 41 |
| I2 (A) | 36 |
| I3 (A) | 34 |
| Parameters | Without Current Sharing Measure | With Current Sharing Measure |
|---|---|---|
| Maximum current fluctuation(A) | 121.3 | 84.86 |
| Rise range | 65% | 62% |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| L1 (μH) | 5.67 | M12 (μH) | 4.27 |
| L2 (μH) | 6.69 | M13 (μH) | 4.32 |
| L3 (μH) | 7.48 | M23 (μH) | 5.02 |
| Parameters | Values |
|---|---|
| C1 (μF) | 123 |
| C2 (μF) | 110 |
| C3 (μF) | 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Cai, S.; Li, G.; Liu, Z.; Zhao, Y.; Qiao, G.; Li, X. Research on the Multiple Capacitor Current Sharing of High-Current Receiving Coils in a Series–Series Wireless Charging System. World Electr. Veh. J. 2024, 15, 58. https://doi.org/10.3390/wevj15020058
Xie Y, Cai S, Li G, Liu Z, Zhao Y, Qiao G, Li X. Research on the Multiple Capacitor Current Sharing of High-Current Receiving Coils in a Series–Series Wireless Charging System. World Electric Vehicle Journal. 2024; 15(2):58. https://doi.org/10.3390/wevj15020058
Chicago/Turabian StyleXie, Yuxin, Shengkun Cai, Guangye Li, Zhizhen Liu, Yuandi Zhao, Gangjie Qiao, and Xianglin Li. 2024. "Research on the Multiple Capacitor Current Sharing of High-Current Receiving Coils in a Series–Series Wireless Charging System" World Electric Vehicle Journal 15, no. 2: 58. https://doi.org/10.3390/wevj15020058
APA StyleXie, Y., Cai, S., Li, G., Liu, Z., Zhao, Y., Qiao, G., & Li, X. (2024). Research on the Multiple Capacitor Current Sharing of High-Current Receiving Coils in a Series–Series Wireless Charging System. World Electric Vehicle Journal, 15(2), 58. https://doi.org/10.3390/wevj15020058





