Design and Optimization of External Rotor Consequent Pole Permanent Magnet Motor with Low Iron Loss and Low Torque Ripple
Abstract
:1. Introduction
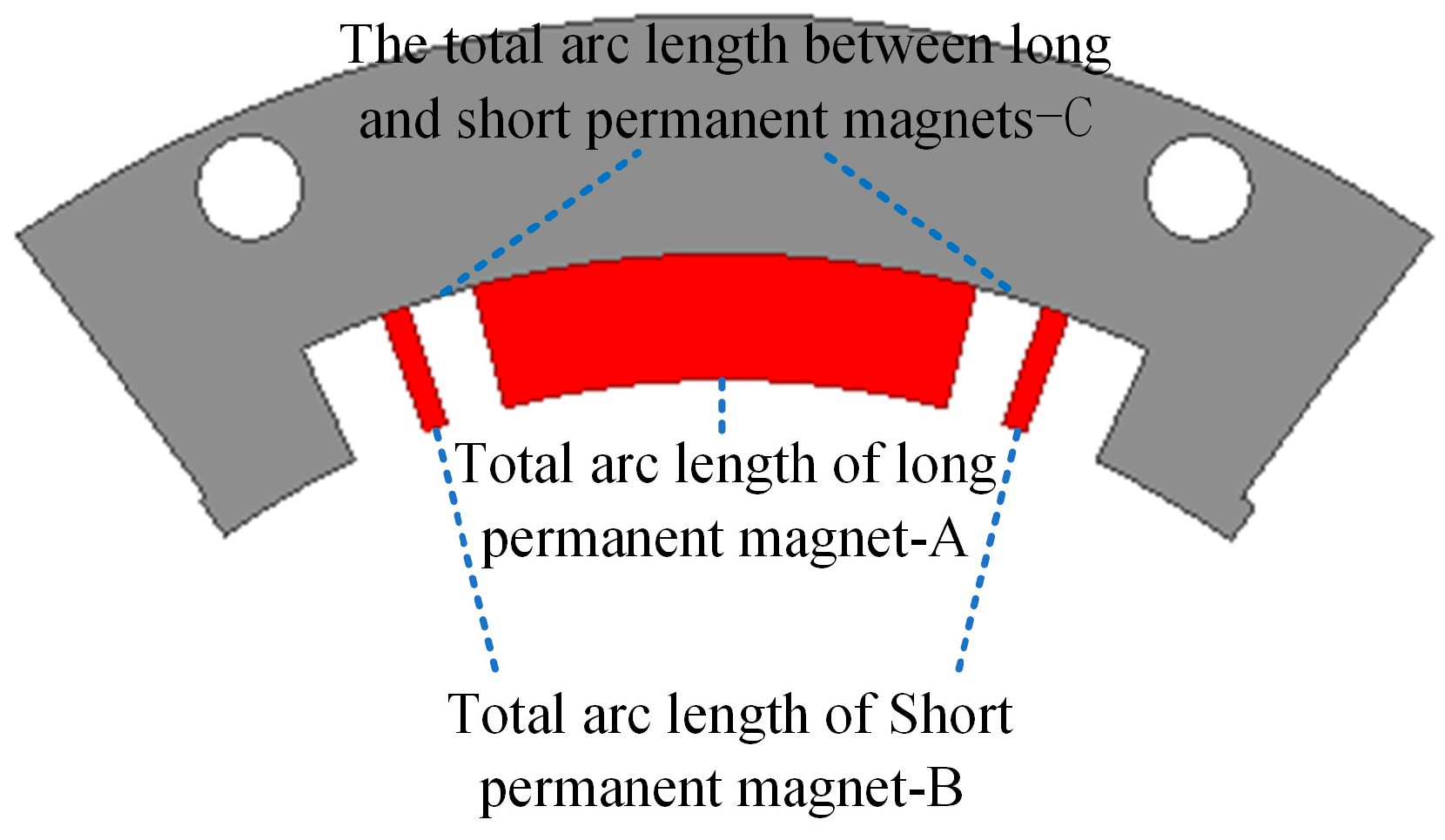
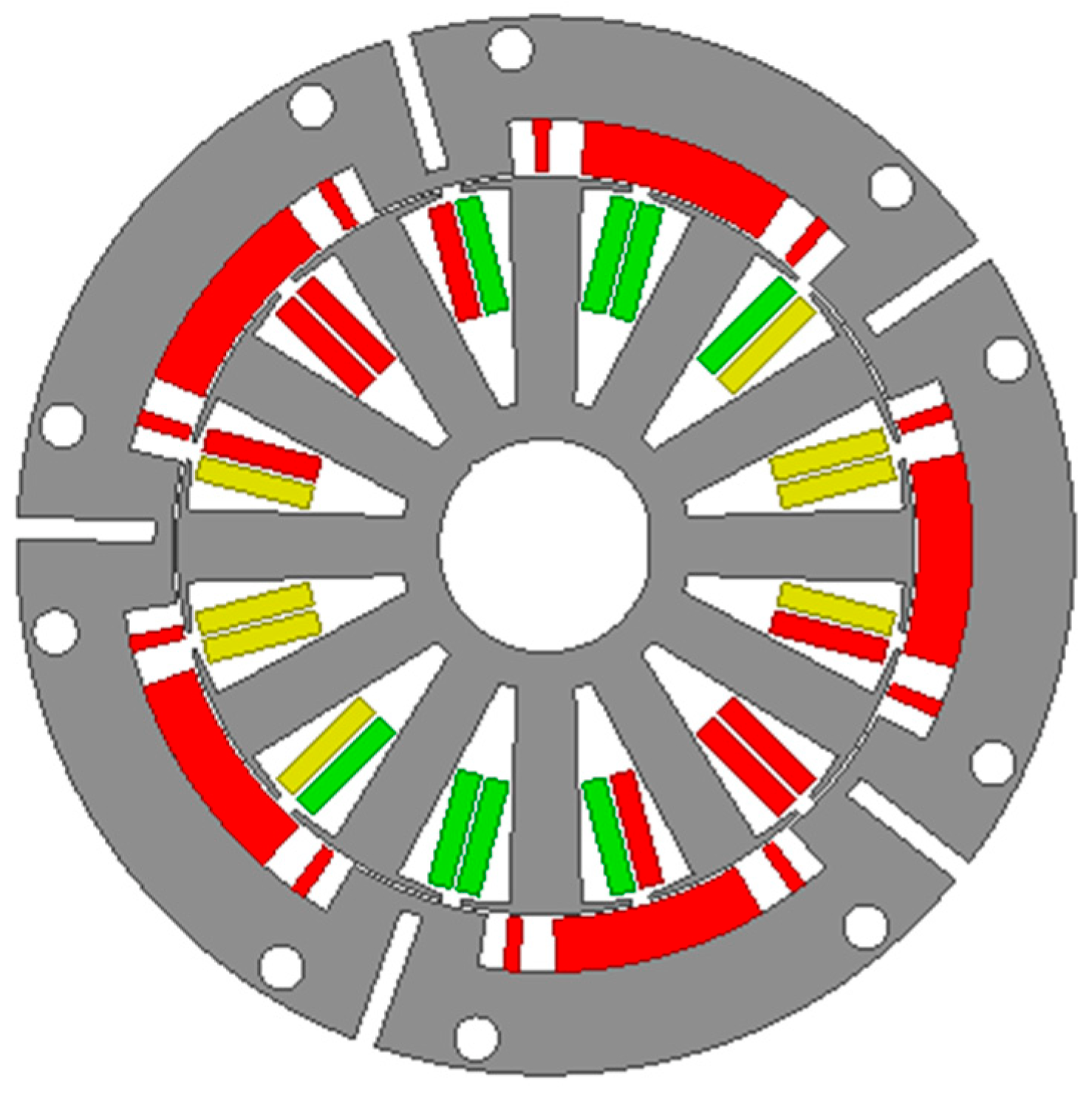
2. Design and Analyses of Unequal Piecewise Consequent Pole Structure
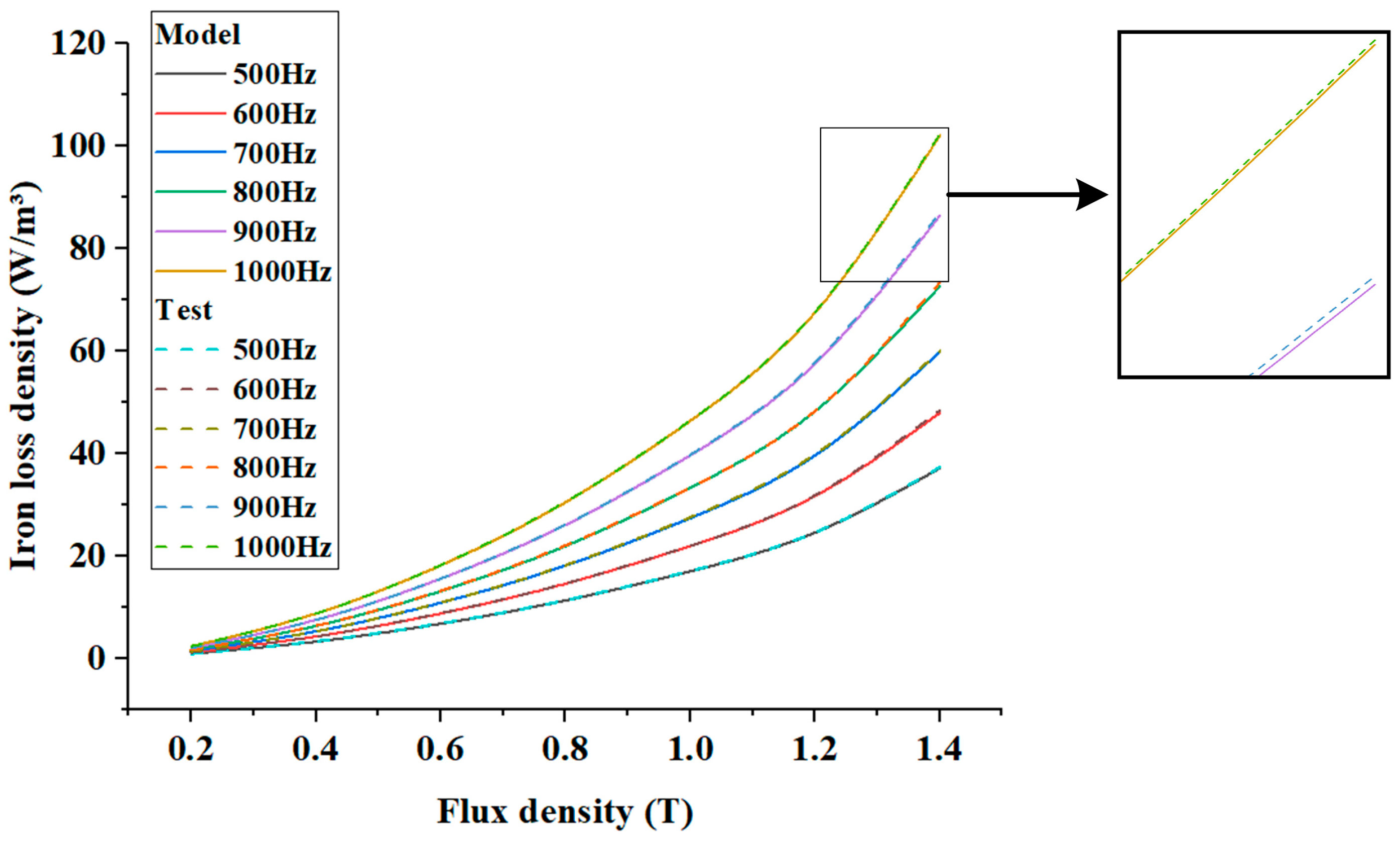
2.1. Calculation Method of Motor Iron Loss
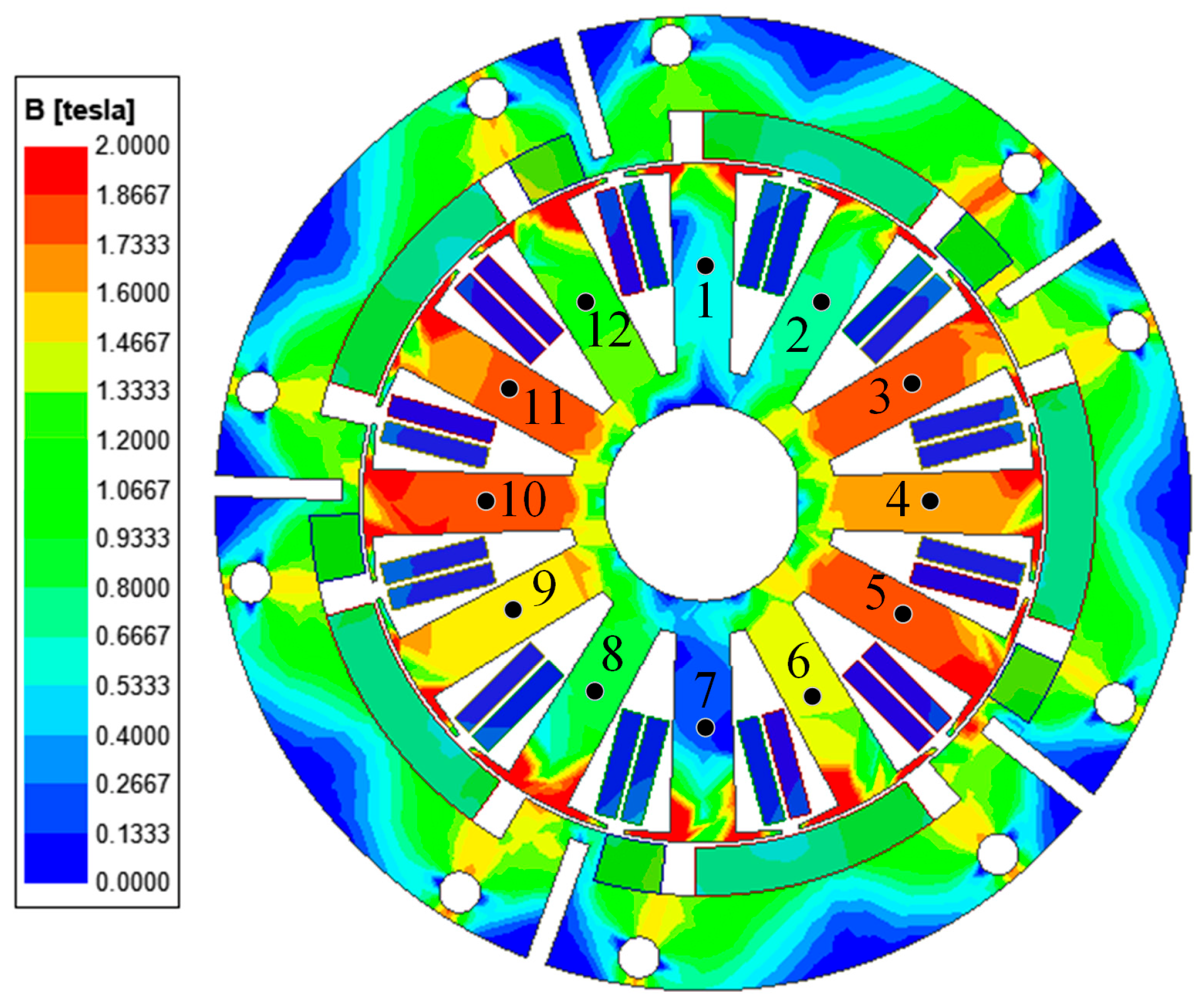
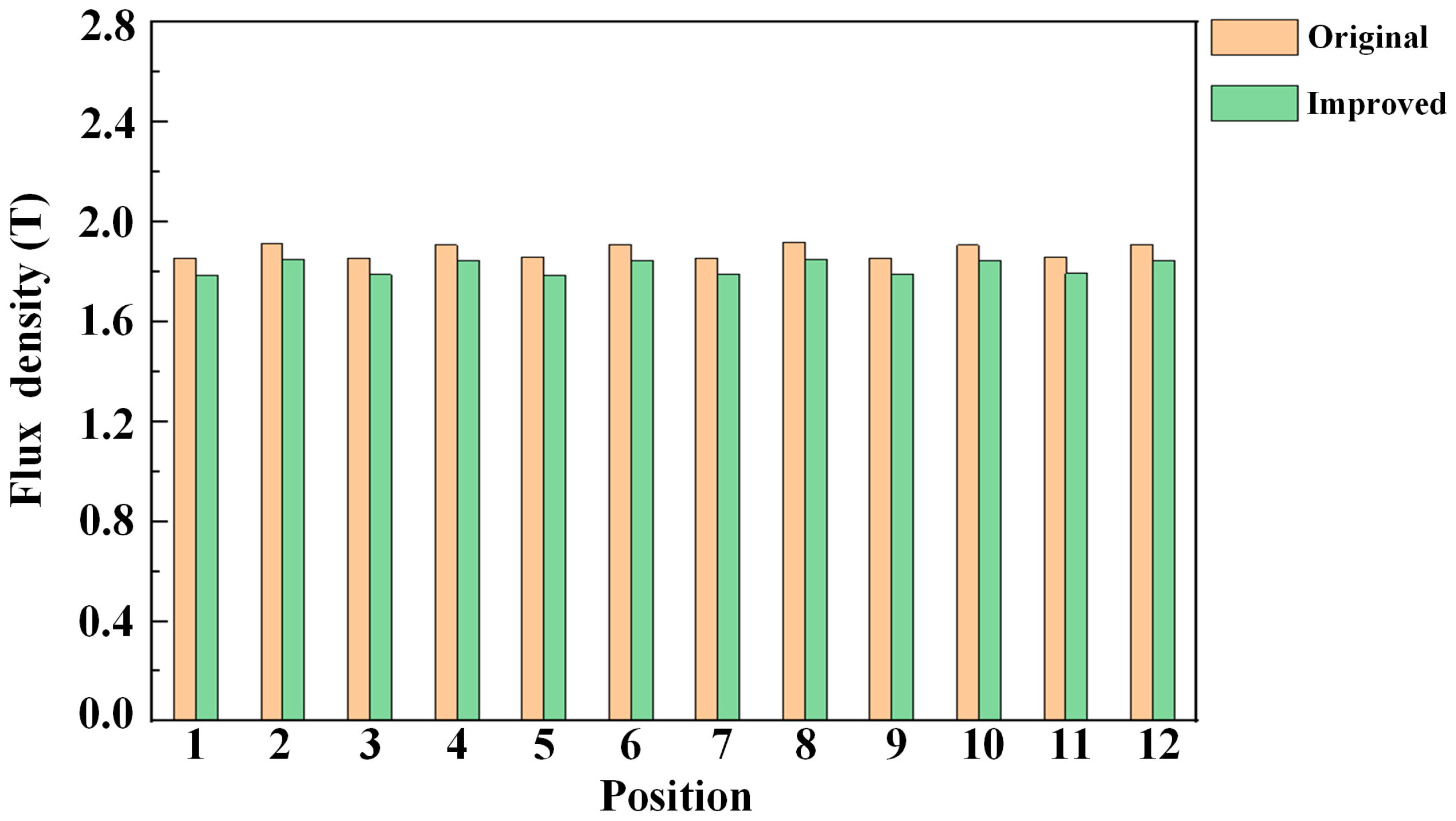
2.2. Performance Comparison between the Original Motor and the Preliminary Improved Motor
3. Optimization Design Based on the Taguchi Method
3.1. Orthogonal Test Design
3.1.1. Average Value Analysis
3.1.2. Variance Analysis
3.2. Determination of the Final Optimized Design Scheme
4. The Performance of the Final Improved Motor
4.1. Structure of the Final Improved Motor
4.2. Performance of the Final Improved Motor
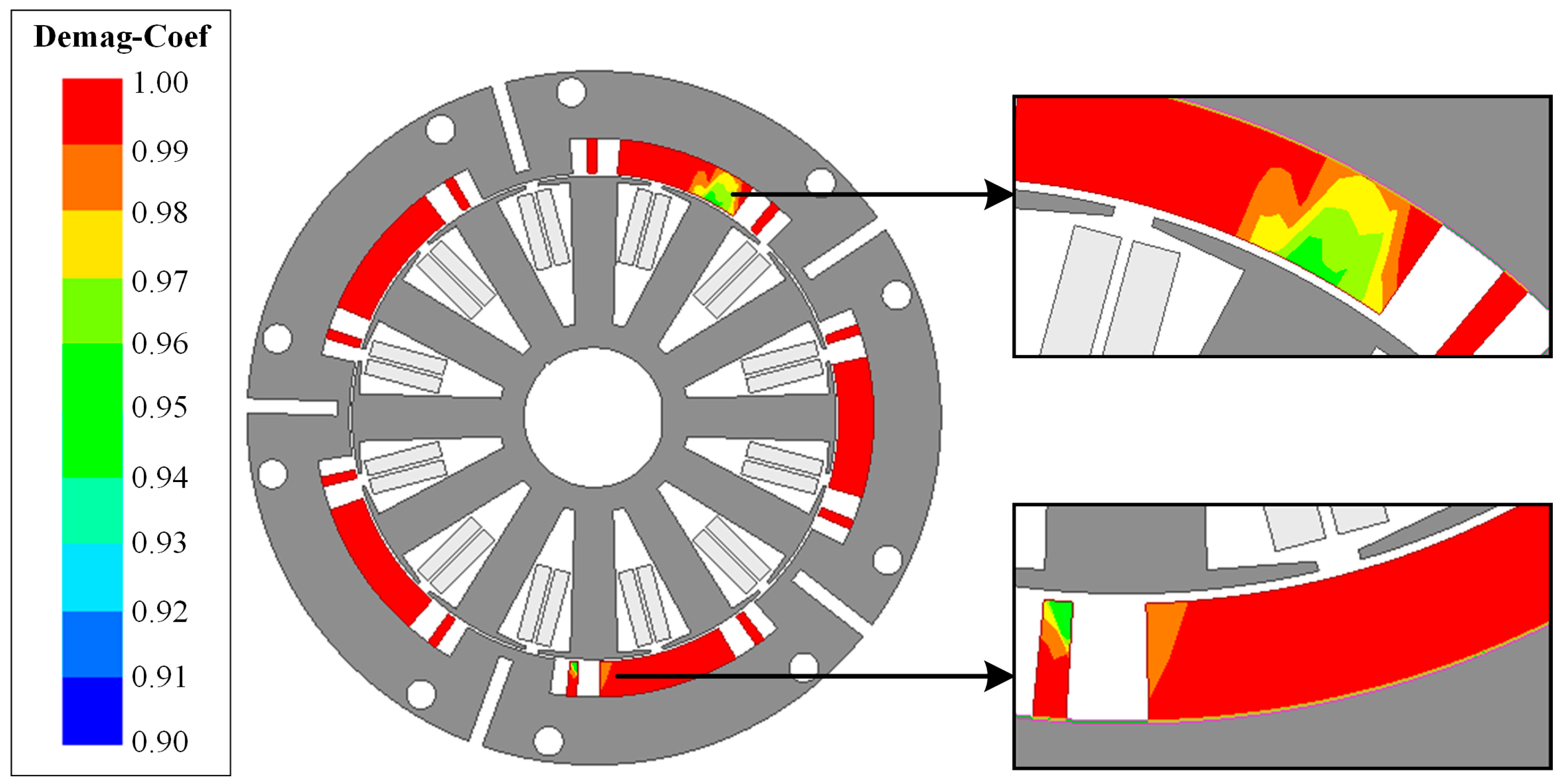
4.3. Demagnetization Analysis of the Final Improved Motor
5. Conclusions
- Compared with the original motor, the iron loss of the motor with the final optimization scheme is reduced from 54.834 W to 37.22 W, which is a reduction of 32.12%;
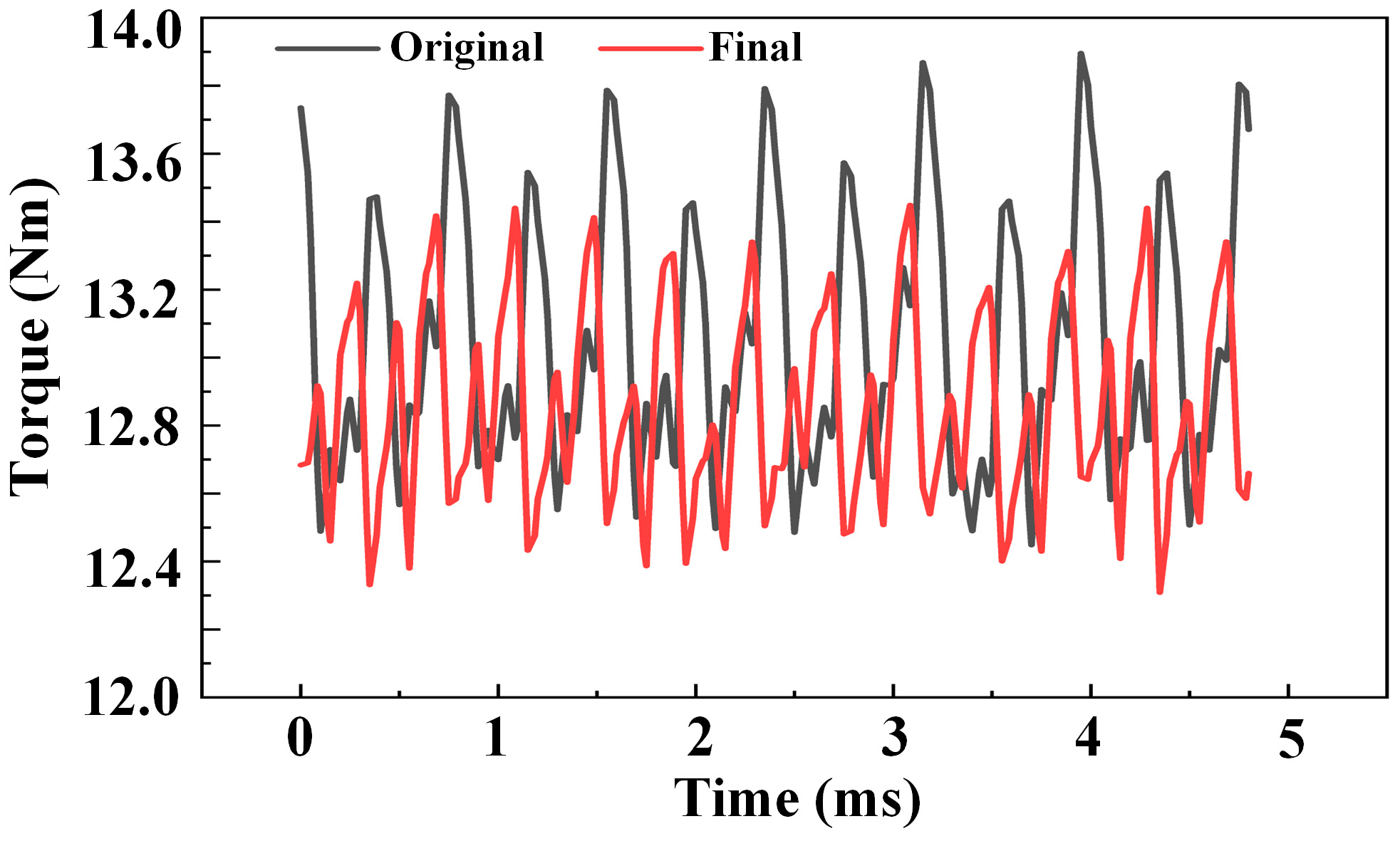
- Compared with the original motor, the average torque of the motor with the final optimization scheme is reduced from 13.05 Nm to 12.95 Nm, which is only 0.77% lower than that of the original motor. The torque ripple is reduced from 5.5% to 3.89%, which is a reduction of 25.09%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Li, B.; Gerada, D.; Huang, K.; Stone, I.; Worrall, S.; Yan, Y. A critical review on thermal management technologies for motors in electric cars. Appl. Therm. Eng. 2022, 201, 117758. [Google Scholar] [CrossRef]
- Jiang, Y.; Ji, B.; Zhang, J.; Yan, J.; Li, W. An Overview of Diagnosis Methods of Stator Winding Inter-Turn Short Faults in Permanent-Magnet Synchronous Motors for Electric Vehicles. World Electr. Veh. J. 2024, 15, 165. [Google Scholar] [CrossRef]
- Wang, P.; Wang, X.; Wang, Y. End-to-End Differentiable Physics Temperature Estimation for Permanent Magnet Synchronous Motor. World Electr. Veh. J. 2024, 15, 174. [Google Scholar] [CrossRef]
- Ruoho, S.; Kolehmainen, J.; Ikaheimo, J.; Arkkio, A. Interdependence of demagnetization, loading, and temperature rise in a permanent-magnet synchronous motor. IEEE Trans. Magn. 2009, 46, 949–953. [Google Scholar] [CrossRef]
- Chung, S.U.; Kim, J.W.; Chun, Y.D.; Woo, B.C.; Hong, D.K. Fractional slot concentrated winding PMSM with consequent pole rotor for a low-speed direct drive: Reduction of rare earth permanent magnet. IEEE Trans. Energy Convers. 2015, 30, 103–109. [Google Scholar] [CrossRef]
- Li, J.; Wang, K. A parallel hybrid excited machine using consequent pole rotor and AC field winding. IEEE Trans. Magn. 2019, 55, 8101605. [Google Scholar] [CrossRef]
- Li, J.; Wang, K.; Liu, C.; Xu, B.F. Elimination of unipolar leakage flux in consequent-pole PM machines by employing novel pole sequence. IEEE Trans. Magn. 2018, 54, 8106105. [Google Scholar] [CrossRef]
- Huang, X.; Liang, J.; Zhou, B.; Zhang, C.; Li, L.; Gerada, D. Suppressing the thrust ripple of the consequent-pole permanent magnet linear synchronous motor by two-step design. IEEE Access 2018, 6, 32935–32944. [Google Scholar] [CrossRef]
- Li, J.; Wang, K.; Zhang, H. Comparative analysis of spoke-type, consequent-pole and hybrid-pole permanent magnet machines. IET Electr. Power Appl. 2020, 14, 648–657. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, C.; Song, Z.; Liu, S. A consequent-pole PM magnetic-geared double-rotor machine with flux-weakening ability for hybrid electric vehicle application. IEEE Trans. Magn. 2019, 55, 8202507. [Google Scholar] [CrossRef]
- Ueda, Y.; Takahashi, H.; Ogawa, A.; Akiba, T.; Yoshida, M. Cogging-torque reduction of transverse-flux motor by skewing stator poles. IEEE Trans. Magn. 2016, 52, 8203504. [Google Scholar] [CrossRef]
- Chung, S.U.; Kim, J.W.; Woo, B.C.; Hong, D.K.; Lee, J.Y.; Koo, D.H. A novel design of modular three-phase permanent magnet vernier machine with consequent pole rotor. IEEE Trans. Magn. 2011, 47, 4215–4218. [Google Scholar] [CrossRef]
- Zivotic-Kukolj, V.; Soong, W.L.; Ertugrul, N. Iron loss reduction in an interior PM automotive alternator. IEEE Trans. Ind. Appl. 2006, 42, 1478–1486. [Google Scholar] [CrossRef]
- Yamazaki, K.; Ohki, S.; Nezu, A.; Ikemi, T. Development of interior permanent magnet motors reduction of harmonic iron losses by optimizing rotor structures. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007; pp. 489–494. [Google Scholar]
- Yamazaki, K.; Ishigami, H. Rotor-shape optimization of interior-permanent-magnet motors to reduce harmonic iron losses. IEEE Trans. Ind. Electron. 2010, 57, 61–69. [Google Scholar] [CrossRef]
- Zhiyong, M.; Hu, Y.; Can, C. Reduction of iron loss in a V-shaped IPM machine for traction applications. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–6. [Google Scholar]
- Barcaro, M.; Bianchi, N.; Magnussen, F. Rotor flux-barrier geometry design to reduce stator iron losses in synchronous IPM motors under FW operations. IEEE Trans. Ind. Appl. 2010, 46, 1950–1958. [Google Scholar] [CrossRef]
- Frias, A.; Pellerey, P.; Lebouc, A.K.; Chillet, C.; Lanfranchi, V.; Friedrich, G.; Albert, L.; Humbert, L. Rotor and stator shape optimization of a synchronous machine to reduce iron losses and acoustic noise. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference, Seoul, Republic of Korea, 9–12 October 2012; pp. 98–103. [Google Scholar]
- Li, F.; Wang, K.; Li, J.; Zhang, H.J. Suppression of Even-Order Harmonics and Torque Ripple in Outer Rotor Consequent-Pole PM Machine by Multilayer Winding. IEEE Trans. Magn. 2018, 54, 8108605. [Google Scholar] [CrossRef]
- Xu, L.; Fan, W.; Zheng, S.; Wu, J.; Hua, Y.; Zhou, S. Investigation of a Partitioned-stator Hybrid-excited Flux-switching Permanent Magnet Machine with Consequent Poles. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar]
- Jian, L.; Kai, W.; Chuang, L. Torque Improvement and Cost Reduction of Permanent Magnet Machines with Dovetailed Consequent-Pole Rotor. IEEE Trans. Energy Convers. 2018, 33, 1628–1640. [Google Scholar]
- Chung, S.U.; Moon, S.H.; Kim, D.J.; Kim, J.M. Development of a 20Pole-24Slot SPMSM with Consequent Pole Rotor for In-Wheel Direct Drive. IEEE Trans. Ind. Electron. 2015, 63, 302–309. [Google Scholar] [CrossRef]
- Wu, Z.Z.; Zhu, Z.Q. Partitioned Stator Flux Reversal Machine with Consequent-Pole PM Stator. IEEE Trans. Energy Convers. 2015, 30, 1472–1482. [Google Scholar] [CrossRef]
- Guo, L.; Xiao, S.; Wu, S.; Wang, H. Optimal design of hybrid consequent-pole permanent magnet motor to reduce torque ripple. Int. J. Appl. Electromagn. Mech. 2022, 70, 149–174. [Google Scholar] [CrossRef]
- Rens, J.; Vandenbossche, L.; Dorez, O. Iron Loss Modelling of Electrical Traction Motors for Improved Prediction of Higher Harmonic Losses. World Electr. Veh. J. 2020, 11, 24. [Google Scholar] [CrossRef]







| Parameters | Value | Unit |
|---|---|---|
| Rotor inner diameter | 84 | mm |
| Rotor cooling diameter | 119 | mm |
| Stator inner diameter | 24 | mm |
| Stator cooling diameter | 83 | mm |
| Magnet thickness | 5.95 | mm |
| N-pole total arc length | 9.92 | ° |
| S-pole total arc length | 37.2 | ° |
| Rotor slot arc length | 57.12 | ° |
| Iron pole total arc length | 9.25 | ° |
| Rated speed | 2500 | r/min |
| Rated current | 16.33 | A |
| Performance | Value | Unit |
|---|---|---|
| Rated power | 3.5 | kW |
| Current density | 5.35 | A/mm2 |
| Torque ripple | 5.5 | % |
| Average torque | 13.05 | Nm |
| Iron loss | 54.834 | W |
| Copper loss | 160 | W |
| Eddy current loss | 9.26 | W |
| Efficiency | 93.79 | % |
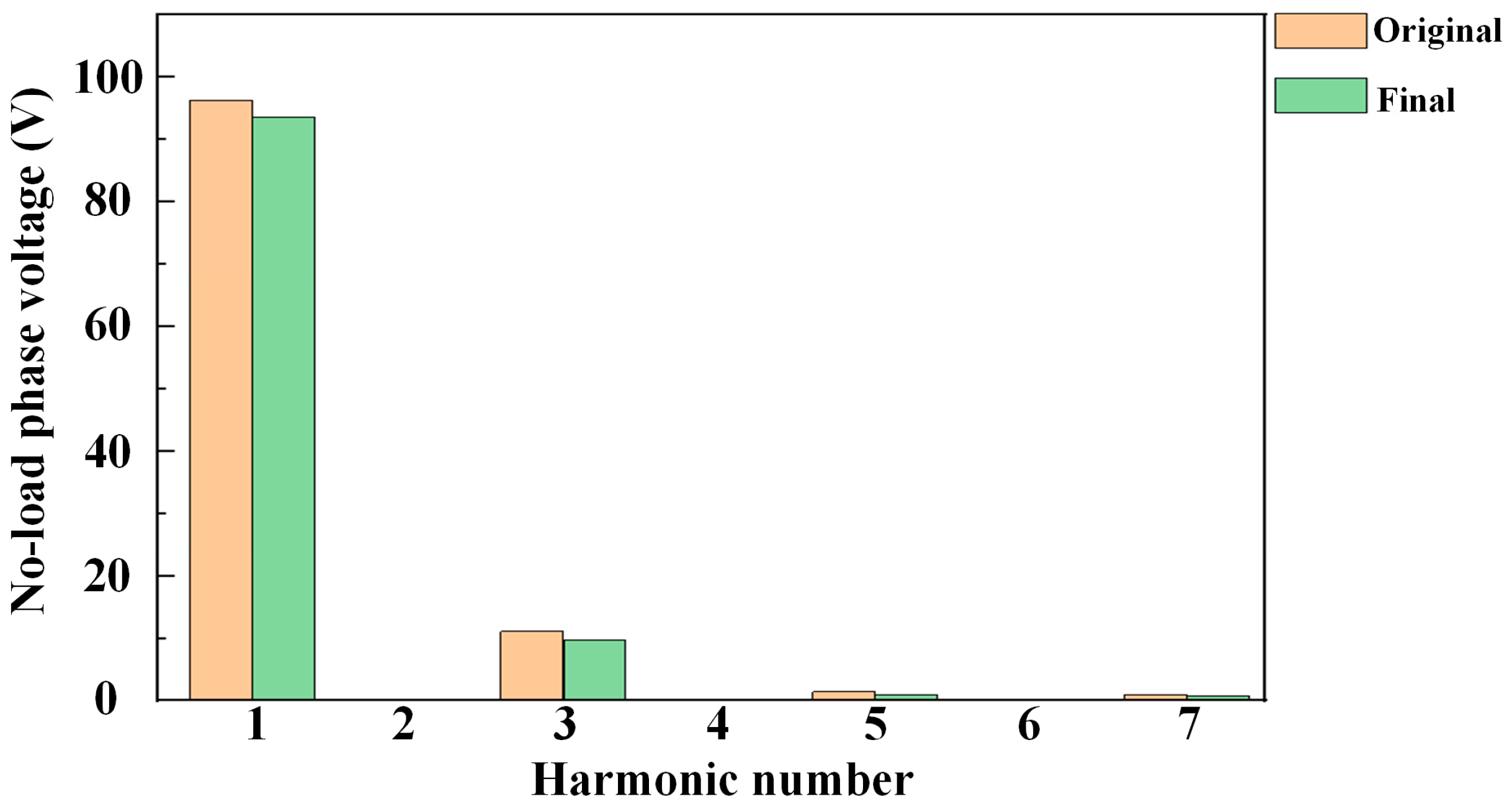
| No-load phase voltage | 106 | V |
| No-load phase voltage THD | 12.45 | % |
| Parameters | Value | Unit |
|---|---|---|
| Rotor inner diameter | 84 | mm |
| Rotor cooling diameter | 119 | mm |
| Stator inner diameter | 24 | mm |
| Stator cooling diameter | 83 | mm |
| Magnet thickness | 5.95 | mm |
| Long S-pole arc length | 29.12 | ° |
| Short S-pole arc length | 3.0 | ° |
| Magnet interval | 4.0 | ° |
| Rotor slot arc length | 50.12 | ° |
| Iron pole arc length | 18.5 | ° |
| Harmonic Number | Harmonic Amplitude (Original Motor) | Harmonic Amplitude (Preliminary Improved Motor) |
|---|---|---|
| 1 | 1.01 | 0.96 |
| 2 | 0.23 | 0.14 |
| 3 | 0.24 | 0.16 |
| 4 | 0.20 | 0.09 |
| 5 | 0.03 | 0.08 |
| 6 | 0.07 | 0.05 |
| THD | 49.62% | 45.32% |
| Parameters | Original Motor | Preliminary Improved Motor |
|---|---|---|
| Average torque | 13.05 Nm | 13.03 Nm |
| Torque ripple | 5.50% | 7.53% |
| Iron loss | 54.834 W | 39.75 W |
| Factor Level | A | B | C |
|---|---|---|---|
| I | 21.12° | 3° | 6° |
| II | 23.12° | 4° | 8° |
| III | 25.12° | 5° | 10° |
| IV | 27.12° | 6° | 12° |
| V | 29.12° | 7° | 14° |
| Test Times | A | B | C |
|---|---|---|---|
| 1 | I | I | I |
| 2 | I | II | III |
| 3 | I | III | V |
| 4 | I | IV | II |
| 5 | I | V | IV |
| 6 | II | I | V |
| 7 | II | II | II |
| 8 | II | III | IV |
| 9 | II | IV | I |
| 10 | II | V | III |
| 11 | III | I | IV |
| 12 | III | II | I |
| 13 | III | III | III |
| 14 | III | IV | V |
| 15 | III | V | II |
| 16 | IV | I | III |
| 17 | IV | II | V |
| 18 | IV | III | II |
| 19 | IV | IV | IV |
| 20 | IV | V | I |
| 21 | V | I | II |
| 22 | V | II | IV |
| 23 | V | III | I |
| 24 | V | IV | III |
| 25 | V | V | V |
| Test Times | Iron Loss (W) | Average Torque (Nm) | Torque Ripple (%) |
|---|---|---|---|
| 1 | 31.74 | 11.88 | 11.78% |
| 2 | 32.12 | 11.46 | 11.12% |
| 3 | 32.68 | 11.47 | 5.45% |
| 4 | 32.69 | 11.72 | 4.15% |
| 5 | 34.38 | 12.44 | 9.4% |
| 6 | 33.08 | 11.85 | 6.98% |
| 7 | 34.38 | 12.03 | 9.19% |
| 8 | 34.86 | 11.73 | 5.85% |
| 9 | 36.77 | 11.87 | 7.9% |
| 10 | 36.81 | 12.69 | 5.08% |
| 11 | 37.14 | 12.63 | 8.42% |
| 12 | 36.84 | 12.04 | 8.31% |
| 13 | 38.79 | 12.75 | 2.67% |
| 14 | 36.29 | 13.28 | 7.33% |
| 15 | 39.33 | 12.90 | 6.45% |
| 16 | 37.31 | 12.88 | 3.95% |
| 17 | 36.71 | 12.91 | 8.97% |
| 18 | 39.56 | 12.72 | 4.76% |
| 19 | 37.44 | 14.08 | 10.17% |
| 20 | 41.81 | 13.94 | 9.82% |
| 21 | 39.75 | 13.03 | 7.53% |
| 22 | 38.82 | 13.04 | 3.06% |
| 23 | 42.24 | 12.69 | 4.26% |
| 24 | 40.27 | 14.24 | 6.22% |
| 25 | 37.598 | 14.52 | 6.51% |
| Iron Loss (W) | Average Torque (Nm) | Torque Ripple (%) | |
|---|---|---|---|
| Overall average value | 36.78 | 12.67 | 7.01 |
| Factor | Level | Iron Loss (W) | Average Torque (Nm) | Torque Ripple (%) |
|---|---|---|---|---|
| A | I | 32.722 | 11.794 | 8.38 |
| II | 35.180 | 12.034 | 7.00 | |
| III | 37.678 | 12.720 | 6.64 | |
| IV | 38.566 | 13.306 | 7.53 | |
| V | 39.736 | 13.504 | 5.52 | |
| B | I | 35.804 | 12.454 | 7.73 |
| II | 35.774 | 12.296 | 8.13 | |
| III | 37.626 | 12.272 | 4.60 | |
| IV | 36.692 | 13.038 | 7.15 | |
| V | 37.986 | 13.298 | 7.45 | |
| C | I | 37.880 | 12.484 | 8.41 |
| II | 37.142 | 12.480 | 6.42 | |
| III | 37.060 | 12.804 | 5.81 | |
| IV | 36.528 | 12.784 | 7.38 | |
| V | 35.272 | 12.806 | 7.05 |
| Factor | Iron Loss | Average Torque | Torque Ripple |
|---|---|---|---|
| A | 6.352 | 0.4549 | 0.9 |
| B | 0.8284 | 0.1749 | 1.5588 |
| C | 0.7516 | 0.024 | 0.7772 |
| Parameters | Value | Unit |
|---|---|---|
| Rotor inner diameter | 84 | mm |
| Rotor cooling diameter | 119 | mm |
| Stator inner diameter | 24 | mm |
| Stator cooling diameter | 83 | mm |
| Magnet thickness | 5.95 | mm |
| Long S-pole arc length | 29.12 | ° |
| Short S-pole arc length | 4.0 | ° |
| Magnet interval | 5.0 | ° |
| Rotor slot arc length | 50.12 | ° |
| Iron pole arc length | 18.5 | ° |
| Performance | Value | Unit |
|---|---|---|
| Average torque | 12.95 | Nm |
| Torque ripple | 3.89 | % |
| Iron loss | 37.22 | W |
| Copper loss | 160 | W |
| Eddy current loss | 8.64 | W |
| Efficiency | 94.29 | % |
| No-load phase voltage | 104 | V |
| No-load phase voltage THD | 11.36 | % |
| Iron Loss (W) | Average Torque (Nm) | Torque Ripple (%) | |
|---|---|---|---|
| Original motor | 54.834 | 13.05 | 5.50 |
| Final improved motor | 37.22 | 12.95 | 3.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, L.; Yu, H.; Wang, H. Design and Optimization of External Rotor Consequent Pole Permanent Magnet Motor with Low Iron Loss and Low Torque Ripple. World Electr. Veh. J. 2024, 15, 232. https://doi.org/10.3390/wevj15060232
Guo L, Yu H, Wang H. Design and Optimization of External Rotor Consequent Pole Permanent Magnet Motor with Low Iron Loss and Low Torque Ripple. World Electric Vehicle Journal. 2024; 15(6):232. https://doi.org/10.3390/wevj15060232
Chicago/Turabian StyleGuo, Liyan, Hubin Yu, and Huimin Wang. 2024. "Design and Optimization of External Rotor Consequent Pole Permanent Magnet Motor with Low Iron Loss and Low Torque Ripple" World Electric Vehicle Journal 15, no. 6: 232. https://doi.org/10.3390/wevj15060232






