Decoupled Adaptive Motion Control for Unmanned Tracked Vehicles in the Leader-Following Task
Abstract
:1. Introduction
- Geometric relations are utilized to parse the leader-following task as motion control for tracked vehicles.
- By effective transformations, the motion control of tracked vehicles is decoupled into the speed closed-loop control subsystem and the curvature closed-loop control subsystem. This decoupling ensures that both subsystems satisfy the mathematical conditions of model reference adaptive control, and corresponding reference models are designed.
- For each subsystem, a reasonable parameter adaptive algorithm is designed. This ensures stable closed-loop system control under conditions where the rolling resistance and steering resistance coefficients are unknown and frequently changing. The actual speed and curvature outputs effectively converge to the reference model’s output, achieving stable control of the speed and curvature. This approach enhances the vehicle’s steering performance and minimizes the following distance, ultimately achieving the expected outcomes that align with the leader-following motion.
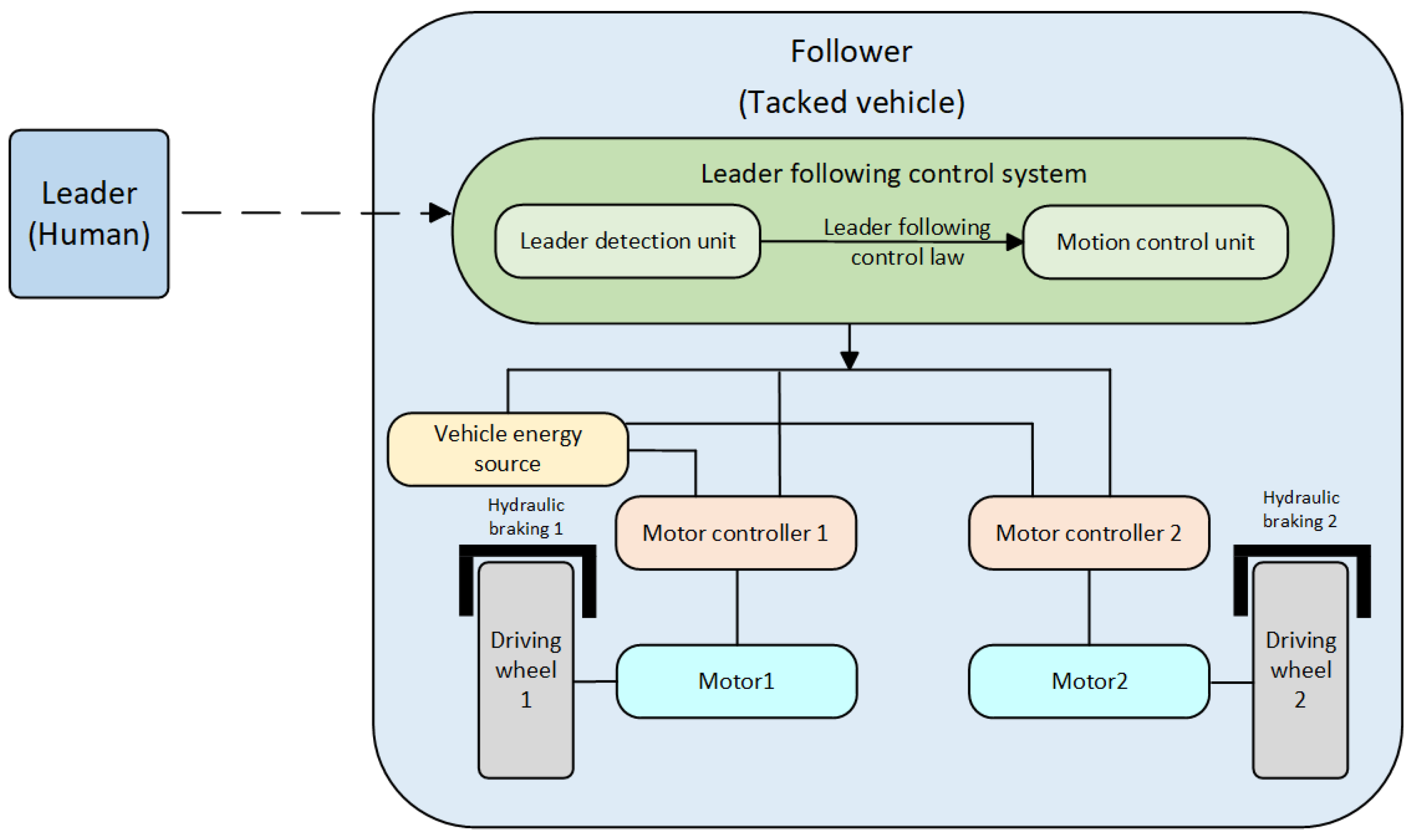
2. Modeling for Leader-Following of Tracked Vehicles
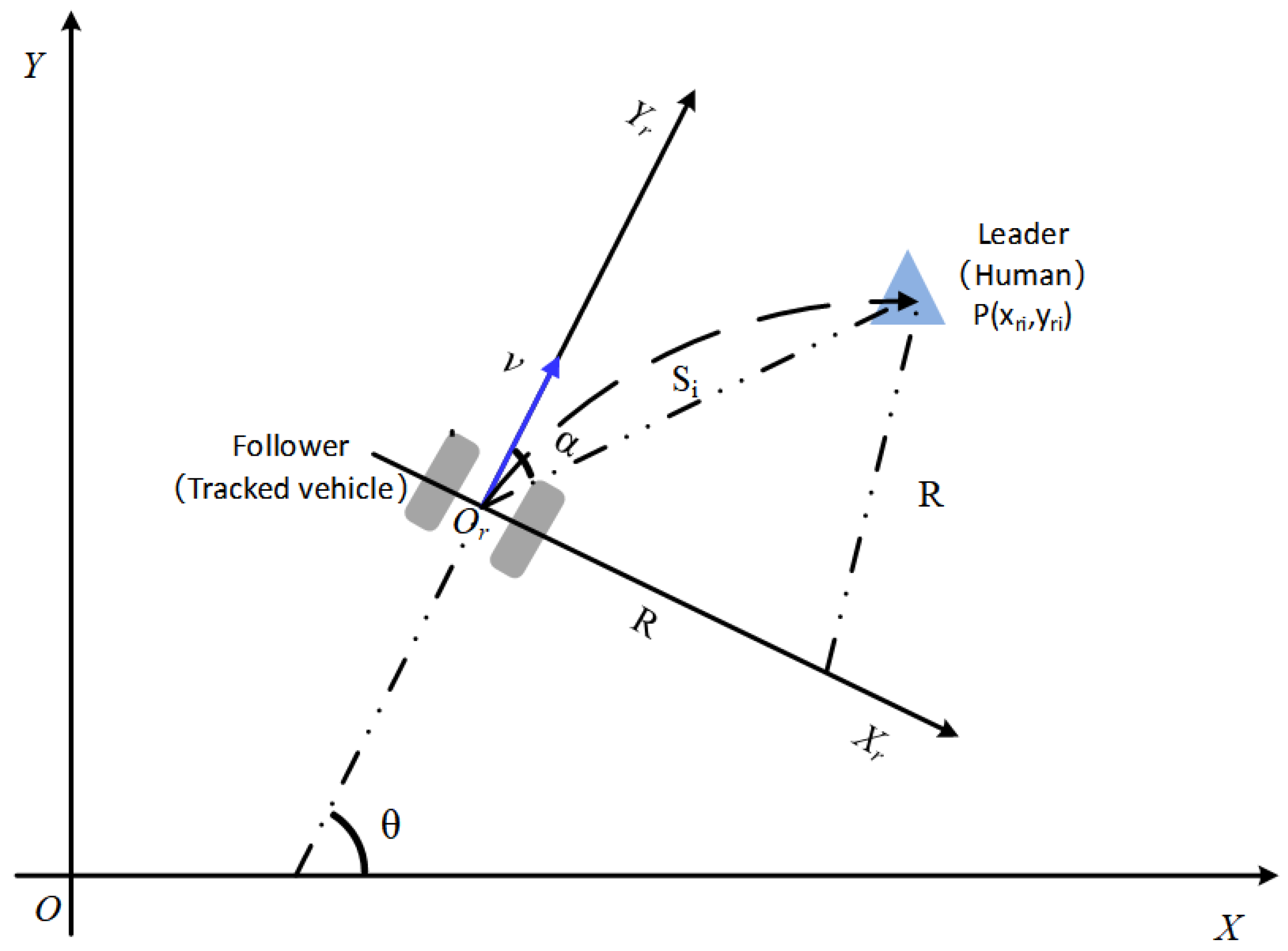
2.1. Leader-Following Model
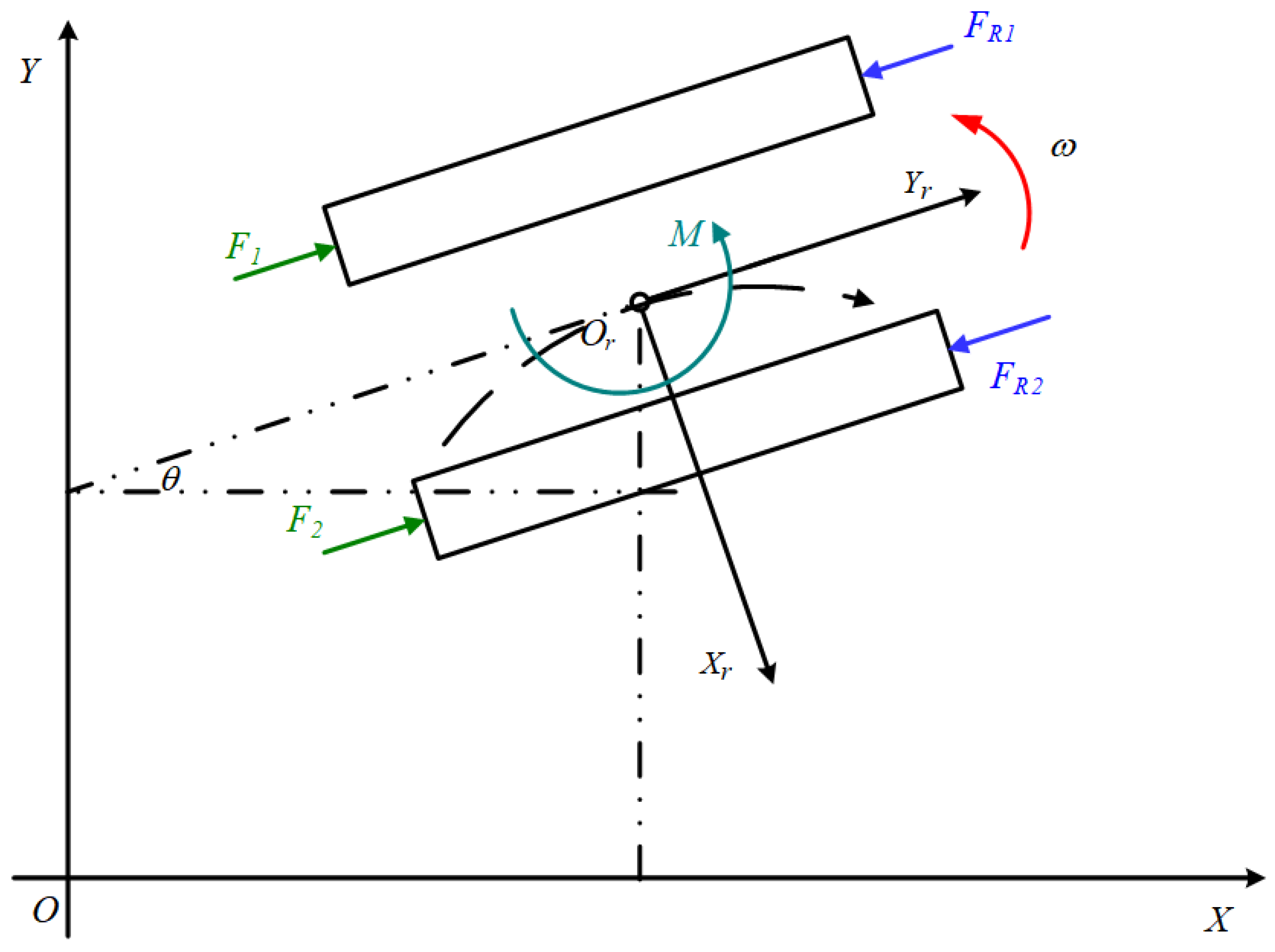
2.2. Dynamics Model of the Tracked Vehicle
2.3. Linear Equivalent Model
3. Control Strategy
3.1. Integrated Control Algorithm Structure
- The interaction mechanism between the tracks and the ground is highly complex, leading to such characteristics as indefinite inertia, unknown parameters, nonlinearity, and multiple-input multiple-output (MIMO) in the dynamics model of the tracked vehicles;
- Human behavior often exhibits significant uncertainties, such as sudden changes in speed and direction, so highly adaptive control algorithms are required;
- The strong coupling between v and results in mutual influences on the closed-loop control over the two parameters.
3.2. Leader-Following Control Law
3.3. Reference Model
3.4. Motion Adaptive Control Law
3.5. Proof of Control System Stability
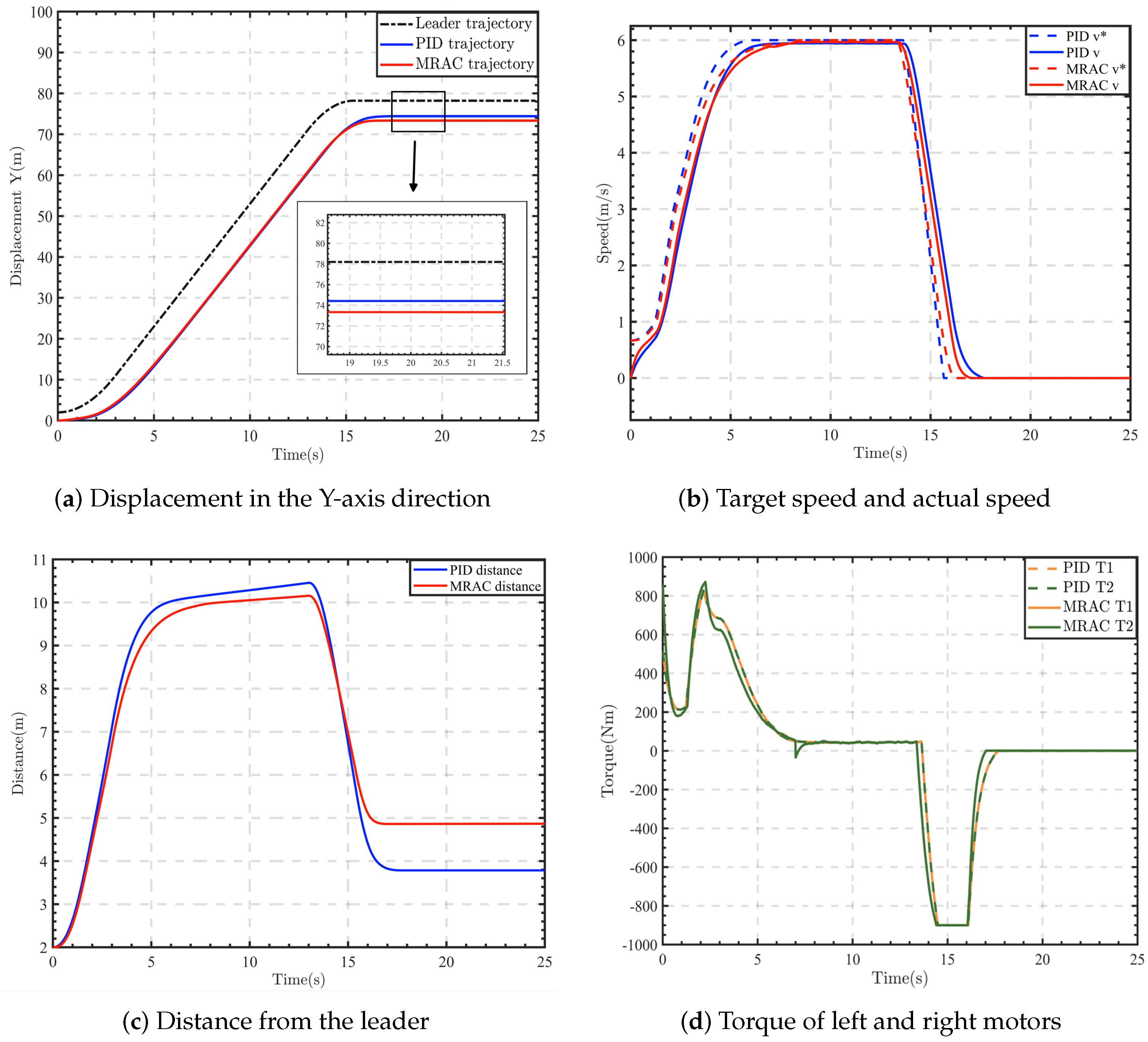
4. Experimental Results
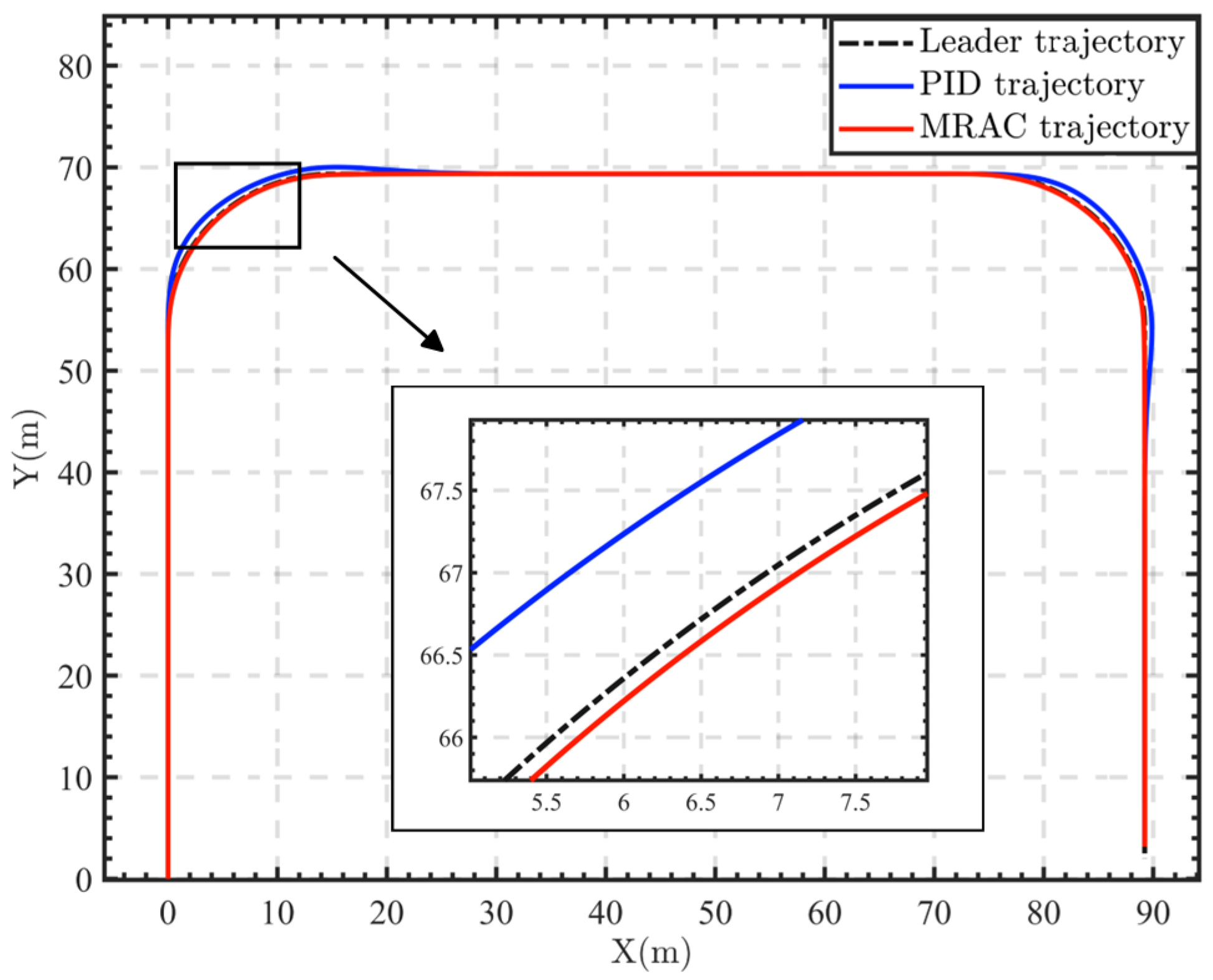
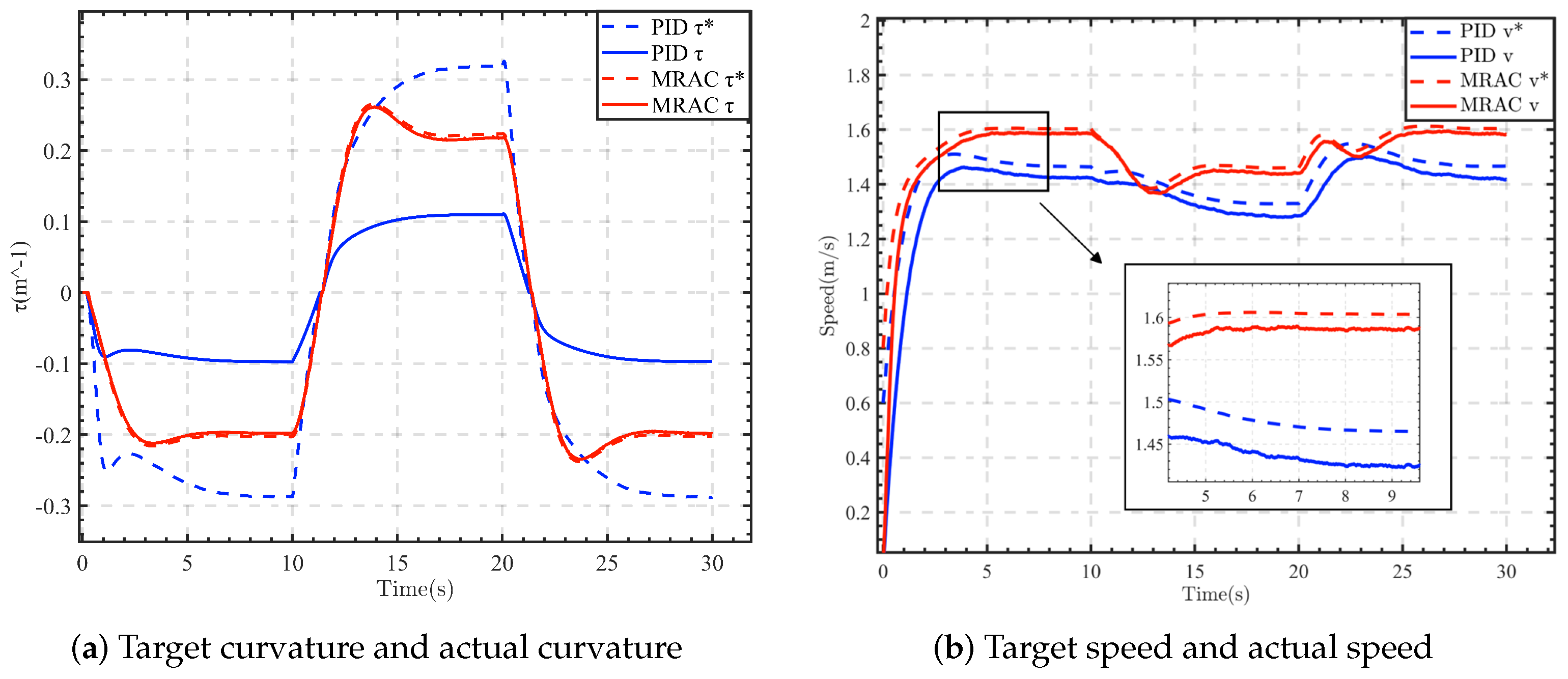
4.1. Simulation Validation
4.1.1. Condition 1
4.1.2. Condition 2
4.1.3. Condition 3
4.2. Experimental Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amer, N.H.; Zamzuri, H.; Hudha, K.; Kadir, Z.A. Modelling and control strategies in path tracking control for autonomous ground vehicles: A review of state of the art and challenges. J. Intell. Robot. Syst. 2017, 86, 225–254. [Google Scholar]
- Nguyen, V.L.; Kim, D.H.; Le, V.S.; Jeong, S.K.; Lee, C.H.; Kim, H.K.; Kim, S.B. Positioning and trajectory tracking for caterpillar vehicles in unknown environment. Int. J. Control Autom. Syst. 2020, 18, 3178–3193. [Google Scholar]
- Sabiha, A.D.; Kamel, M.A.; Said, E.; Hussein, W.M. Dynamic modeling and optimized trajectory tracking control of an autonomous tracked vehicle via backstepping and sliding mode control. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2022, 236, 620–633. [Google Scholar]
- Li, R.; Fan, J.J.; Han, Z.D.; Guan, S.; Qin, Z.B. Configuration design and control of hybrid tracked vehicle with three planetary gear sets. J. Cent. South Univ. 2021, 28, 2105–2119. [Google Scholar] [CrossRef]
- Hu, K.; Cheng, K. Trajectory Planning for an Articulated Tracked Vehicle and Tracking the Trajectory via an Adaptive Model Predictive Control. Electronics 2023, 12, 1988. [Google Scholar] [CrossRef]
- Li, R.; Xiang, C.; Wang, C.; Fan, J.; Liu, C. Robust Adaptive Trajectory Tracking Control Approach for Autonomous Tracked Vehicles. Acta Armamentarii 2021, 42, 1128–1137. [Google Scholar]
- Zhao, Z.; Liu, H.; Chen, H.; Hu, J.; Guo, H. Kinematics-aware model predictive control for autonomous high-speed tracked vehicles under the off-road conditions. Mech. Syst. Signal Process. 2019, 123, 333–350. [Google Scholar] [CrossRef]
- Wang, P.; Rui, X.; Yu, H. Study on dynamic track tension control for high-speed tracked vehicles. Mech. Syst. Signal Process. 2019, 132, 277–292. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, L.; Fan, J.; Xu, B.; Hu, M.; Chen, X. An improved real-time slip model identification method for autonomous tracked vehicles using forward trajectory prediction compensation. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Kang, Y.; Zhang, Y.; Zeng, R. Path Tracking Control of Tracked Vehicles Considering Skid-steer Characteristic on Uneven Terrain. J. Cent. South Univ. 2022, 53, 491–501. [Google Scholar]
- Lu, J.; Liu, H.; Guan, H.; Li, D.; Chen, H.; Liu, L. Trajectory Tracking Control of Unmanned Tracked Vehicles Based on Adaptive Dual-Parameter Optimization. Acta Armamentarii 2023, 44, 960–971. [Google Scholar]
- Gai, J.; Liu, C.; Ma, C.; Shen, H. Steering control of electric drive tracked vehicle considering tracks’ skid and slip. Acta Armamentarii 2021, 42, 2092–2101. [Google Scholar]
- Wang, B.Y.; Gong, J.W.; Gao, T.Y.; Zhang, R.Z.; Chen, H.Y.; Xi, J.Q. Longitudinal and lateral path following coordinated control method of tracked vehicle based on double-layer driver model. Acta Armamentarii 2018, 39, 1675–1682. [Google Scholar]
- Tang, Z.; Liu, H.; Xue, M.; Chen, H.; Gong, X.; Tao, J. Trajectory Tracking Control of Dual Independent Electric Drive Unmanned Tracked Vehicle Based on MPC-MFAC. Acta Armamentarii 2023, 44, 129–139. [Google Scholar]
- Hu, J.; Hu, Y.; Chen, H.; Liu, K. Research on trajectory tracking of unmanned tracked vehicles based on model predictive control. Acta Armamentarii 2019, 40, 456–563. [Google Scholar]
- Sebastian, B.; Ben-Tzvi, P. Active disturbance rejection control for handling slip in tracked vehicle locomotion. J. Mech. Robot. 2019, 11, 021003. [Google Scholar] [CrossRef]
- Han, J.; Wang, F.; Wang, Y. A control method for the differential steering of tracked vehicles driven independently by a dual hydraulic motor. Appl. Sci. 2022, 12, 6355. [Google Scholar] [CrossRef]
- Mahalingam, I.; Padmanabhan, C. An integrated three-dimensional powertrain-vehicle dynamics model for tracked vehicle analysis. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 3353–3366. [Google Scholar] [CrossRef]
- Dasgupta, S.; Raghuraman, V.; Choudhury, A.; Teja, T.N.; Dauwels, J. Merging and splitting maneuver of platoons by means of a novel PID controller. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence, Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Akopov, A.S.; Beklaryan, L.A.; Thakur, M. Improvement of Maneuverability within a Multiagent Fuzzy Transportation System with the Use of Parallel Biobjective Real-Coded Genetic Algorithm. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12648–12664. [Google Scholar] [CrossRef]
- Liang, J.; Li, Y.; Yin, G.; Xu, L.; Lu, Y.; Feng, J.; Shen, T.; Cai, G. A MAS-Based Hierarchical Architecture for the Cooperation Control of Connected and Automated Vehicles. IEEE Trans. Veh. Technol. 2023, 72, 1559–1573. [Google Scholar] [CrossRef]
- Cosgun, A.; Florencio, D.A.; Christensen, H.I. Autonomous person following for telepresence robots. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4335–4342. [Google Scholar]
- Satake, J.; Chiba, M.; Miura, J. A SIFT-based person identification using a distance-dependent appearance model for a person following robot. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, 11–14 December 2012; pp. 962–967. [Google Scholar]
- Evseev, K.B.; Kositsyn, B.B.; Kotiev, G.O.; Stadukhin, A.A.; Smirnov, I.A.; Godzhaev, Z.A. Design of the double-jointed multi-tracked vehicle steering control law providing its motion along a reference trajectory. J. Phys. Conf. Ser. 2021, 2032, 012064. [Google Scholar] [CrossRef]
- Cui, D.; Wang, G.; Zhao, H.; Wang, S. Research on a Path-Tracking Control System for Articulated Tracked Vehicles. Stroj. Vestn. J. Mech. Eng. 2020, 66, 311–324. [Google Scholar] [CrossRef]
- Shentu, S.; Xie, F.; Liu, X.J.; Gong, Z. Motion Control and Trajectory Planning for Obstacle Avoidance of the Mobile Parallel Robot Driven by Three Tracked Vehicles. Robotica 2021, 39, 1037–1050. [Google Scholar] [CrossRef]
- Chunming, L.; Ke, B. Modeling and Analysis of Multi-level Coupling Dynamics of Tracked Vehicle Based on Load Transfer Path. J. Mech. Eng. 2023, 59, 157–174. [Google Scholar]
- Xiong, H.; Chen, Y.; Li, Y.; Zhu, H.; Yu, C.; Zhang, J. Dynamic model-based back-stepping control design for-trajectory tracking of seabed tracked vehicles. J. Mech. Sci. Technol. 2022, 36, 4221–4232. [Google Scholar] [CrossRef]
- Zou, T.; Angeles, J.; Hassani, F. Dynamic modeling and trajectory tracking control of unmanned tracked vehicles. Robot. Auton. Syst. 2018, 110, 102–111. [Google Scholar] [CrossRef]
- Zheng, Q.; Tian, Y.; Deng, Y.; Zhu, X.; Chen, Z.; Liang, B. Reinforcement Learning-Based Control of Single-Track Two-Wheeled Robots in Narrow Terrain. Actuators 2023, 12, 109. [Google Scholar] [CrossRef]
- Amokrane, S.B.; Laidouni, M.Z.; Adli, T.; Madonski, R.; Stanković, M. Active disturbance rejection control for unmanned tracked vehicles in leader–follower scenarios: Discrete-time implementation and field test validation. Mechatronics 2024, 97, 103114. [Google Scholar] [CrossRef]
- Wang, S.; Guo, J.; Mao, Y.; Wang, H.; Fan, J. Research on the model predictive trajectory tracking control of unmanned ground tracked vehicles. Drones 2023, 7, 496. [Google Scholar] [CrossRef]
- Wan, Q.; Li, Z.; Li, Y.; Ge, Z.; Wang, Y.; Wu, D. Target following method of mobile robot based on improved YOLOX. Acta Autom. Sin. 2023, 49, 1558–1572. [Google Scholar]
- Zeng, G.; Wang, W.; Gai, J.; Ma, C.; Li, X.; Li, H. Steering on Ramp Control Strategy of Double Motor Coupling Drive Transmission for Tracked Vehicle. Acta Armamentarii 2021, 42, 2189–2195. [Google Scholar]
- Zhang, L.; Liu, Q.; Wang, Z. Research on Electro-hydraulic Composite ABS Control for Four-wheel-independent-drive Electric Vehicles Based on Robust Integral Sliding Mode Control. J. Mech. Eng. 2022, 58, 243–252. [Google Scholar]









| Vehicle Parameters | |
|---|---|
| Weight/kg | 8000 |
| Track contact length/m | 2.12 |
| Driving wheel radius/m | 0.26 |
| Center track distance/m | 1.78 |
| Moment of inertia/kg·m2 | 1000 |
| Gear ratio | 9.83 |
| Vehicle Parameters | |
|---|---|
| Weight/kg | 8000 |
| Track contact length/m | 2.12 |
| Driving wheel radius/m | 0.26 |
| Center track distance/m | 1.78 |
| Gear ratio | 9.83 |
| Motor Parameters | |
| Rated voltage/V | 550 |
| Rated rotational speed/rpm | 1500 |
| Peak rotational speed/rpm | 4500 |
| Rated torque/Nm | 525 |
| Peak torque/Nm | 900 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, J.; Yan, P.; Li, R.; Liu, Y.; Wang, F.; Liu, Y.; Chen, C. Decoupled Adaptive Motion Control for Unmanned Tracked Vehicles in the Leader-Following Task. World Electr. Veh. J. 2024, 15, 239. https://doi.org/10.3390/wevj15060239
Fan J, Yan P, Li R, Liu Y, Wang F, Liu Y, Chen C. Decoupled Adaptive Motion Control for Unmanned Tracked Vehicles in the Leader-Following Task. World Electric Vehicle Journal. 2024; 15(6):239. https://doi.org/10.3390/wevj15060239
Chicago/Turabian StyleFan, Jingjing, Pengxiang Yan, Ren Li, Yi Liu, Falong Wang, Yingzhe Liu, and Chang Chen. 2024. "Decoupled Adaptive Motion Control for Unmanned Tracked Vehicles in the Leader-Following Task" World Electric Vehicle Journal 15, no. 6: 239. https://doi.org/10.3390/wevj15060239
APA StyleFan, J., Yan, P., Li, R., Liu, Y., Wang, F., Liu, Y., & Chen, C. (2024). Decoupled Adaptive Motion Control for Unmanned Tracked Vehicles in the Leader-Following Task. World Electric Vehicle Journal, 15(6), 239. https://doi.org/10.3390/wevj15060239





