An Automatic Emergency Braking Control Method for Improving Ride Comfort
Abstract
:1. Introduction
1.1. Motivations
1.2. State of the Art
1.3. Contributions
1.4. Structure Overview
2. AEB Control Algorithms
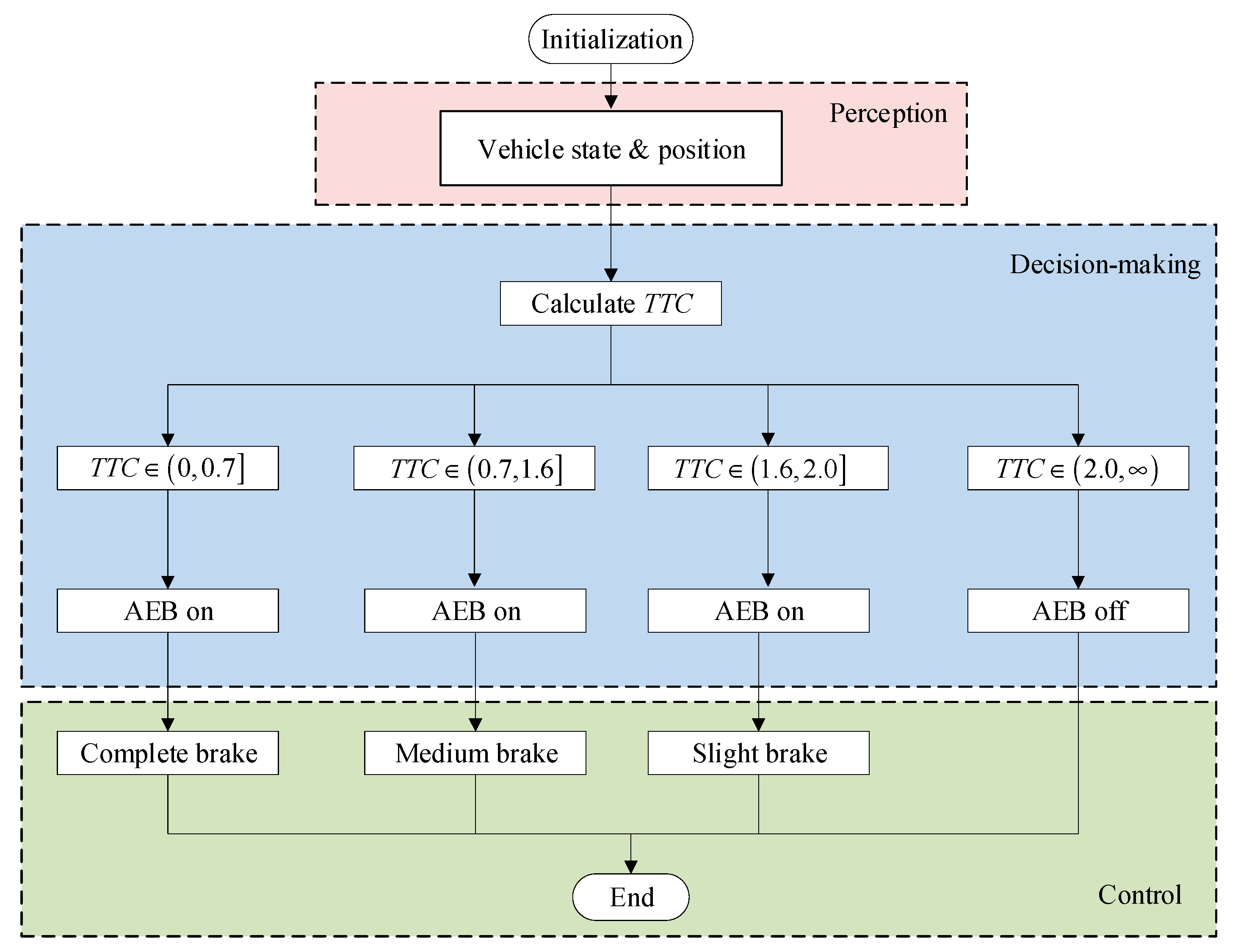
2.1. TTC Control Algorithm
2.2. Quadratic Curve Deceleration Control Algorithm
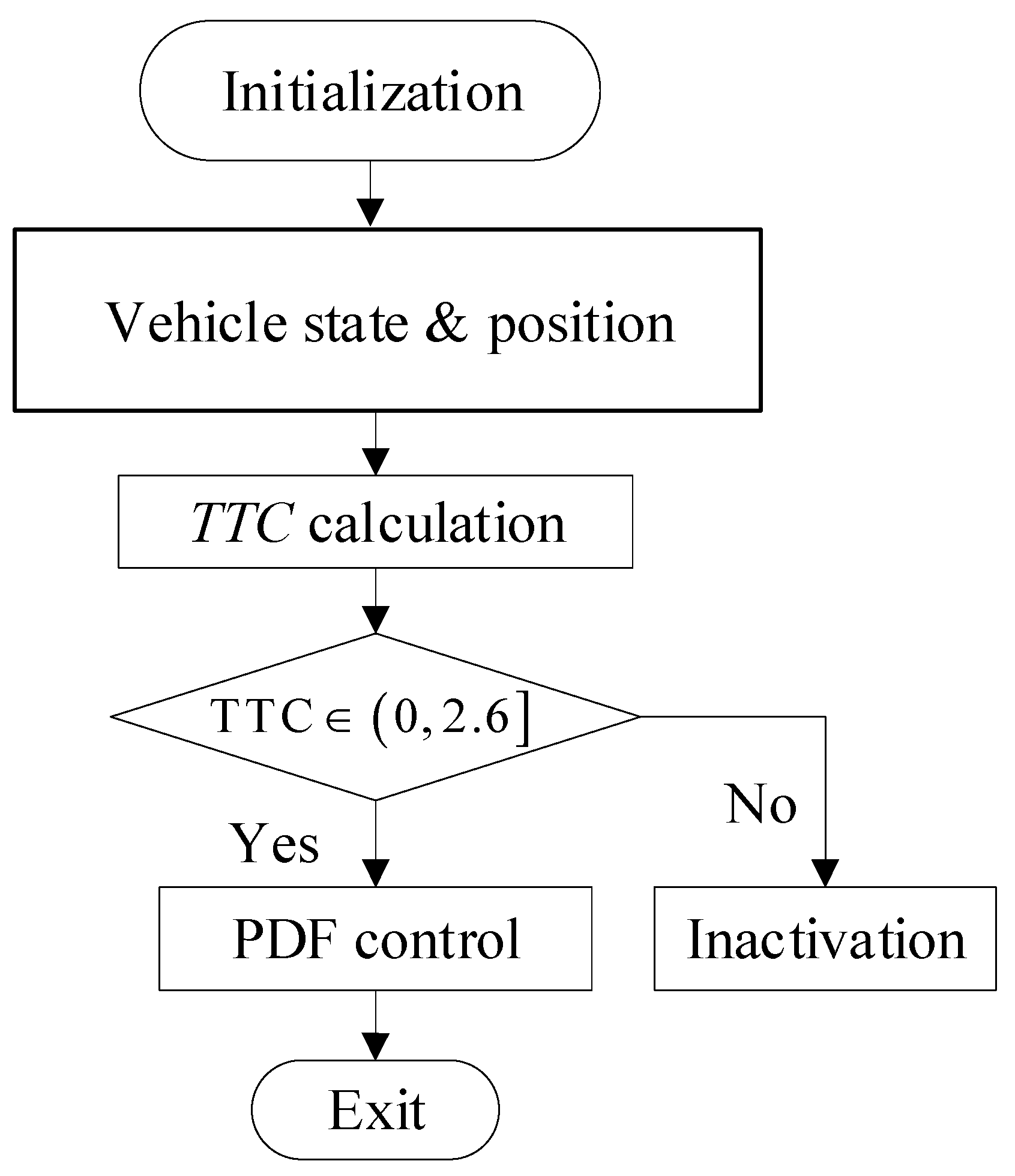
2.3. PDF Control Algorithm
2.3.1. Judgment of Initial Braking Time
2.3.2. Deceleration Control
2.4. Proposed Control Algorithm
3. Simulation and Analysis
3.1. Test Scenarios
3.2. Test Results
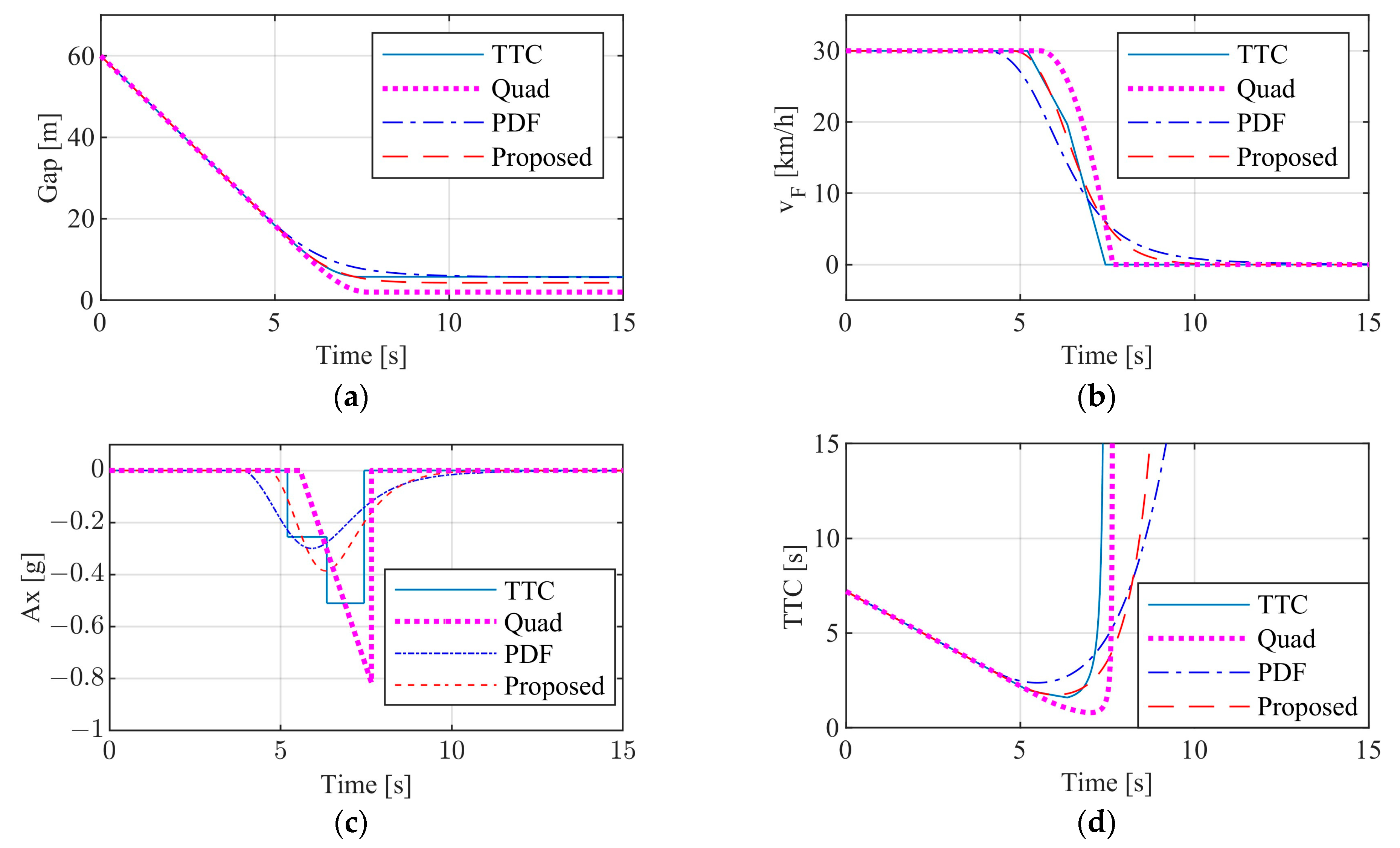
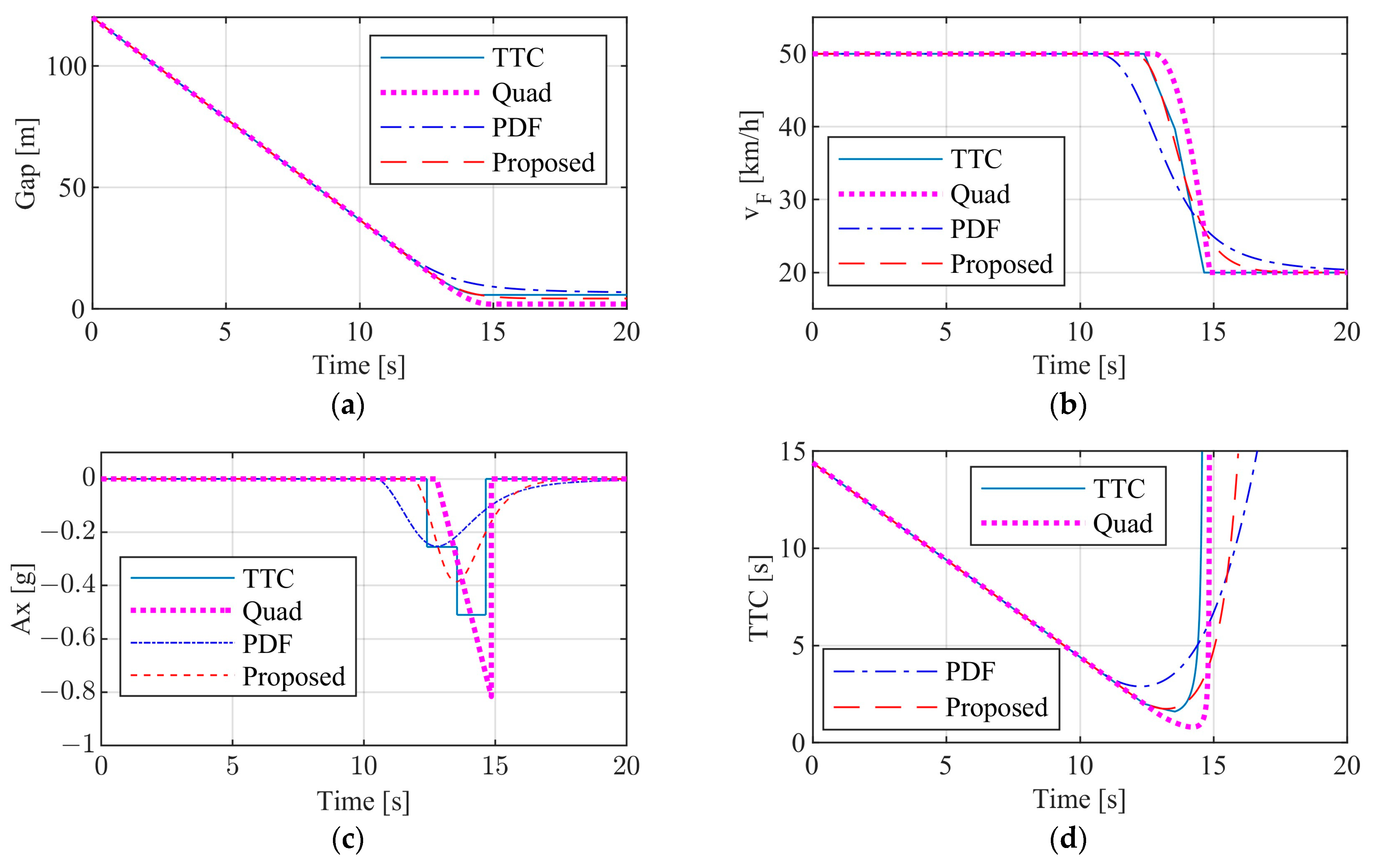
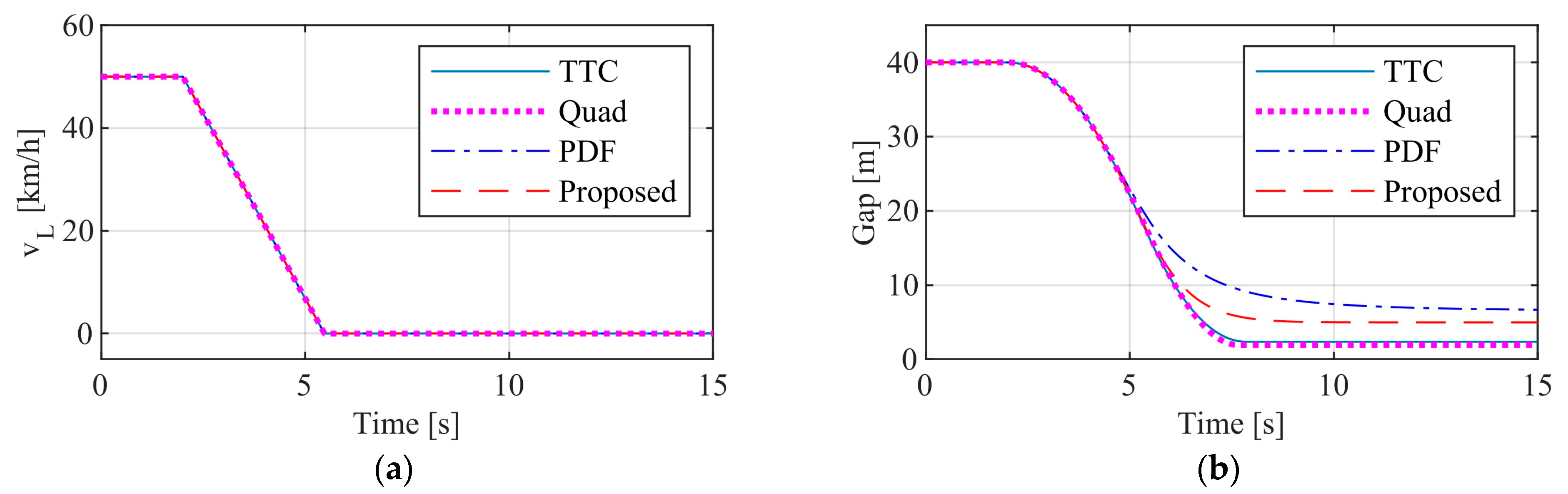
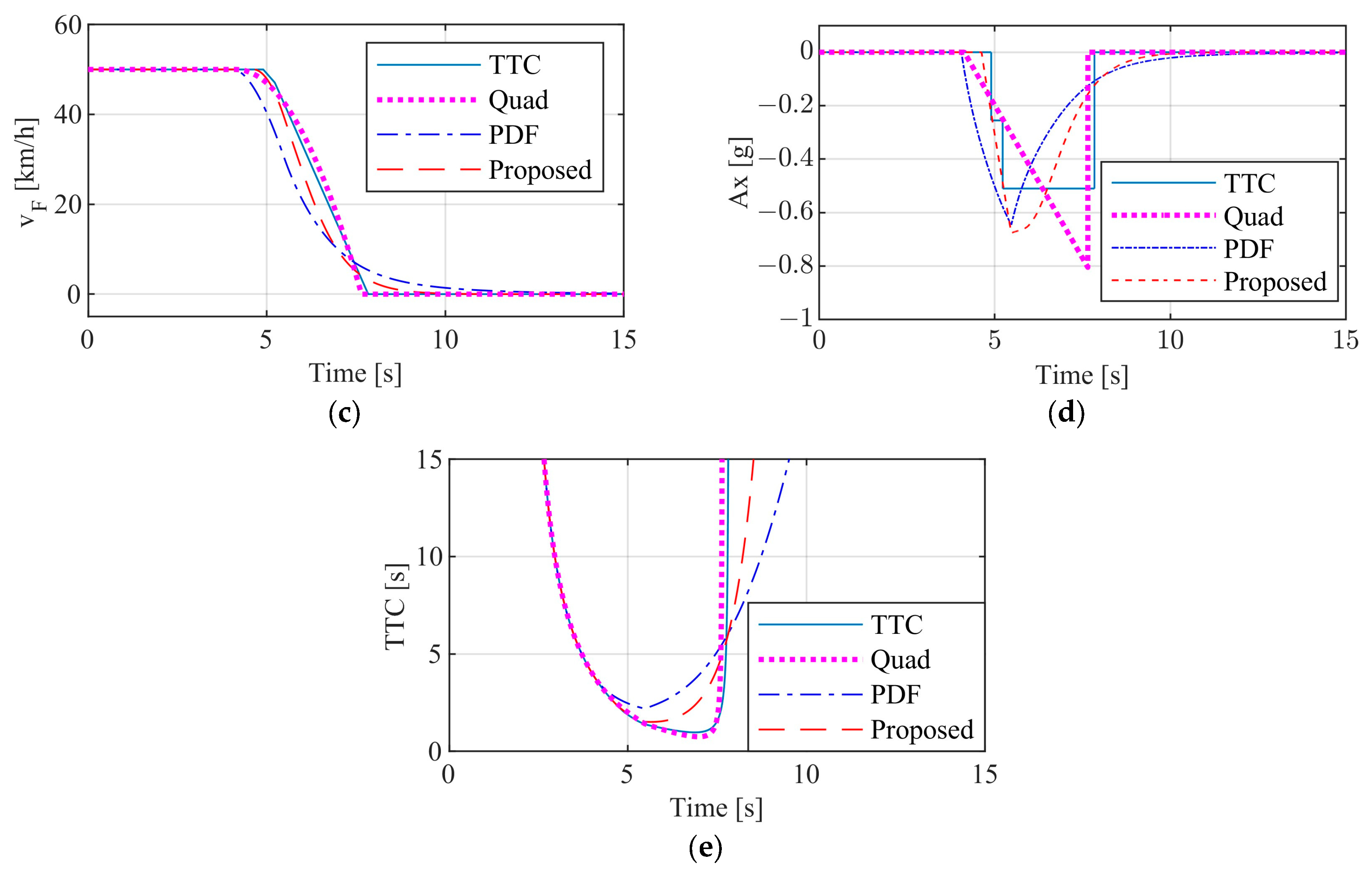
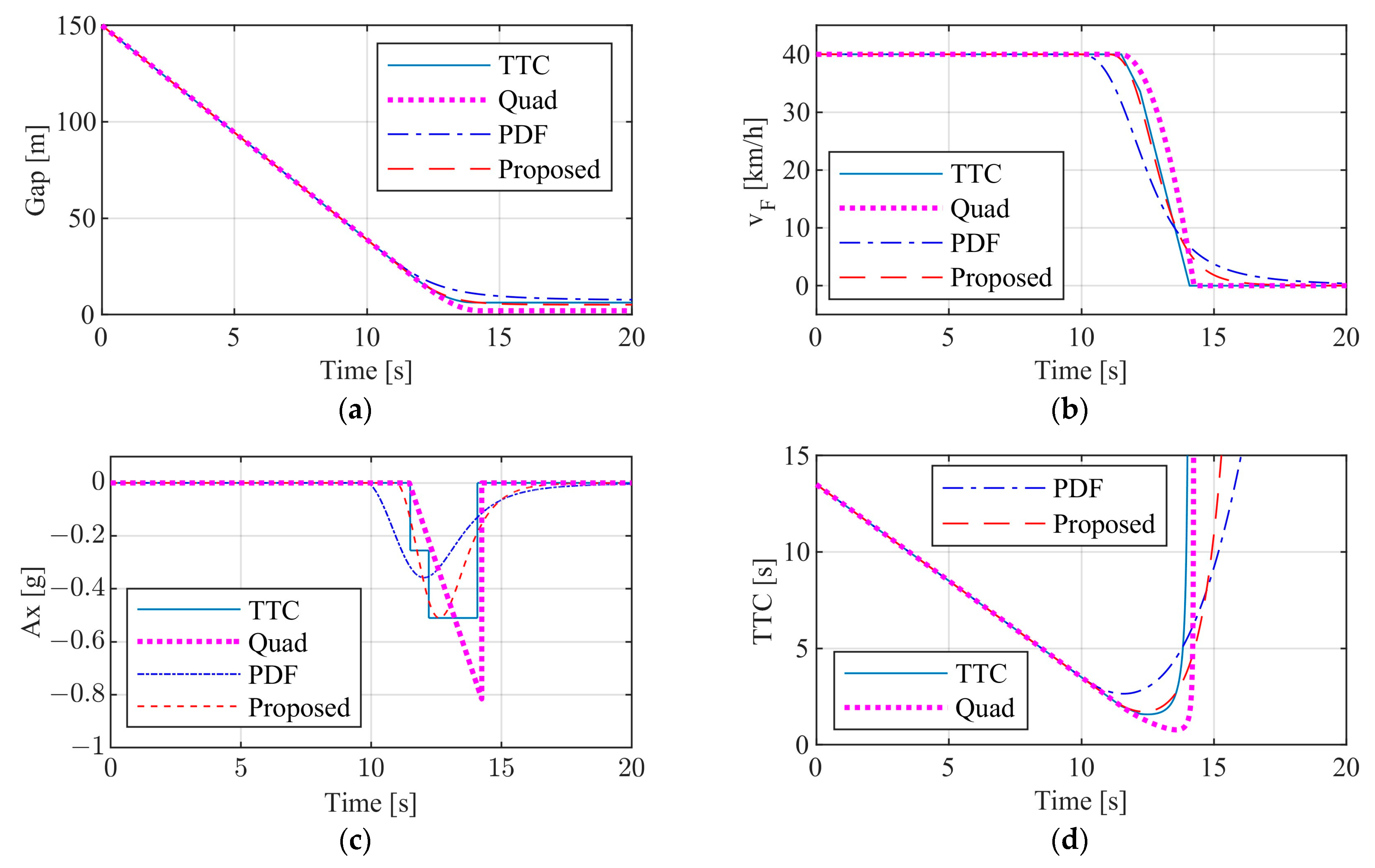
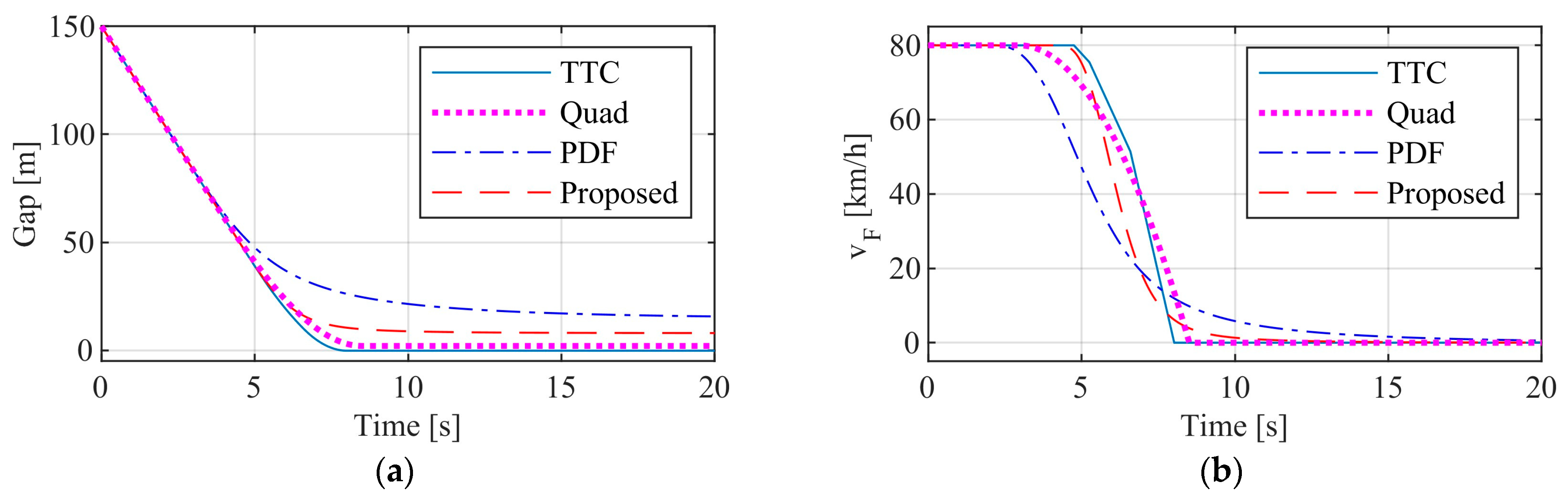
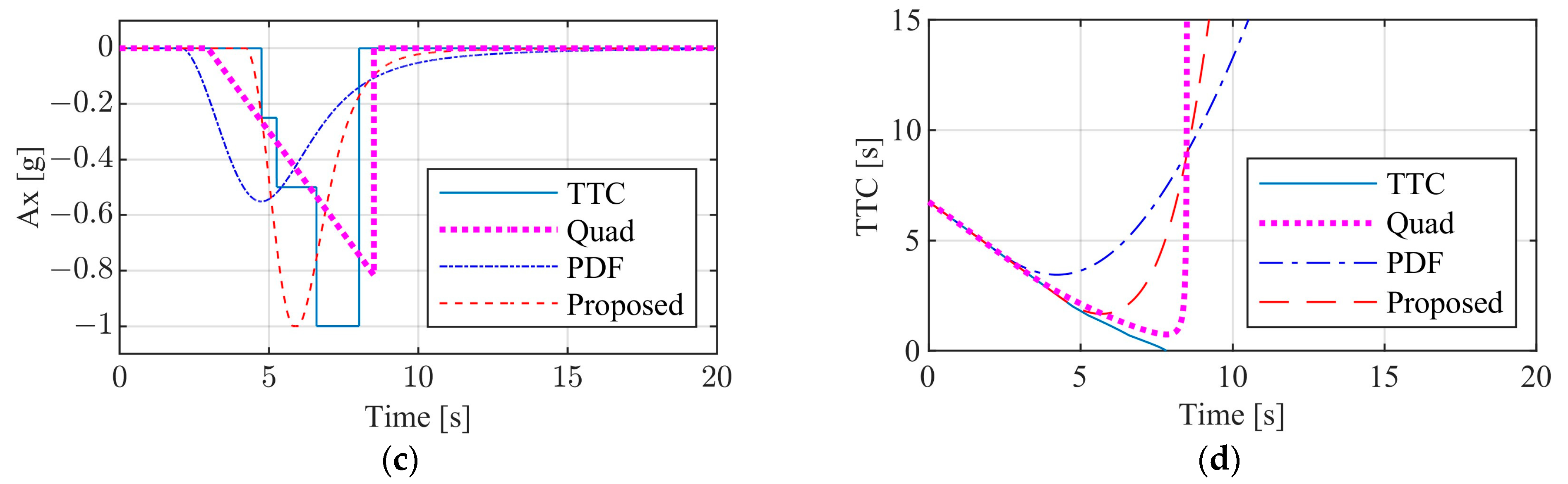
3.2.1. Test Results of Passenger Car
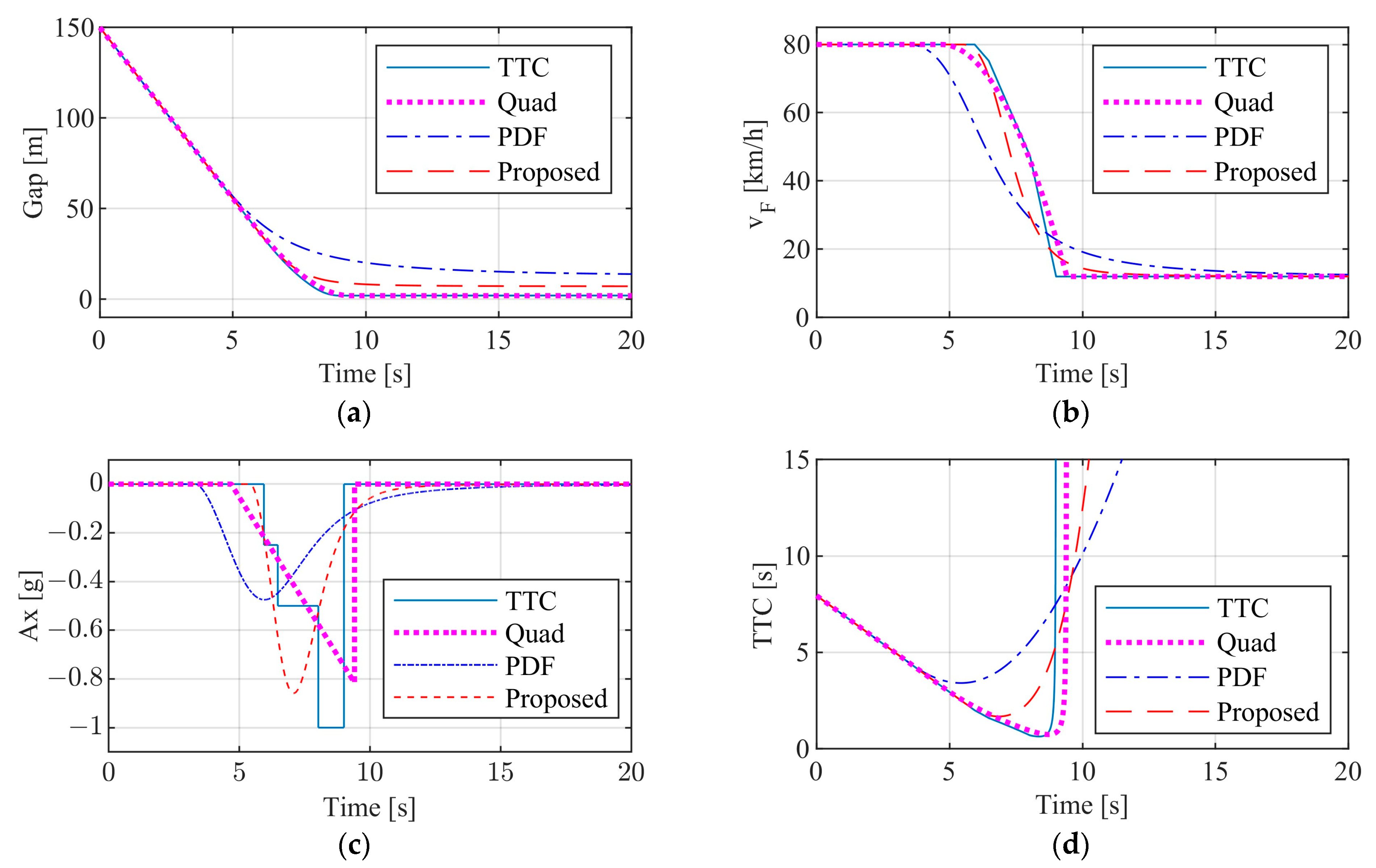
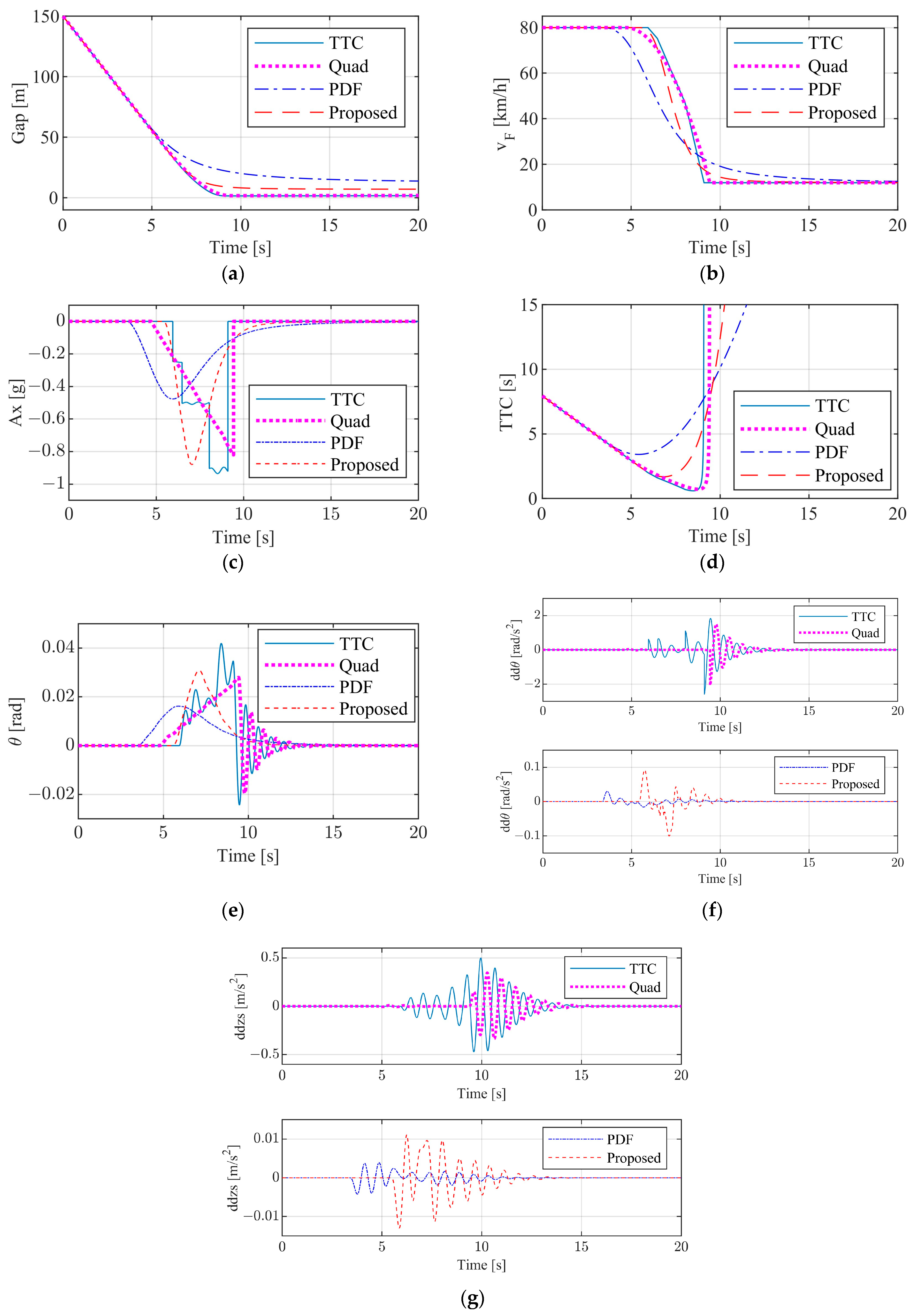
3.2.2. Test Results of Commercial Vehicle
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AEB | Automatic emergency braking |
| TTC | Time to collision |
| THW | Time-headway |
| CCRs | Car-to-Car Rear stationary |
| CCRm | Car-to-Car Rear moving |
| CCRb | Car-to-Car Rear braking |
| Professional driver fitting | |
| DOF | Degrees of freedom |
References
- Cicchino, J.B. Effectiveness of forward collision warning and autonomous emergency braking systems in reducing front-to-rear crash rates. Accid. Anal. Prev. 2017, 99, 142–152. [Google Scholar] [CrossRef] [PubMed]
- Cicchino, J.B. Effects of automatic emergency braking systems on pedestrian crash risk. Accid. Anal. Prev. 2022, 172, 106686. [Google Scholar] [CrossRef] [PubMed]
- Fildes, B.N. Safety Benefits of Automatic Emergency Braking Systems in France; SAE Technical Paper 2012-01-0273; SAE: Warrendale, PA, USA, 2012. [Google Scholar]
- Fildes, B.N.; Keall, M.; Bos, N. Effectiveness of low speed autonomous emergency braking in real-world rear-end crashes. Accid. Anal. Prev. 2015, 81, 24–29. [Google Scholar] [CrossRef] [PubMed]
- Kusano, K.D.; Gabler, H. Safety benefits of forward collision warning, brake assist, and autonomous braking systems in rear-end collisions. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1546–1555. [Google Scholar] [CrossRef]
- Lubbe, N.; Davidsson, J. Drivers’ comfort boundaries in pedestrian crossings: A study in driver braking characteristics as a function of pedestrian walking speed. Saf. Sci. 2015, 75, 100–106. [Google Scholar] [CrossRef]
- Sidorenko, G.; Thunberg, J.; Sjöberg, K. Safety of automatic emergency braking in platooning. IEEE Trans. Veh. Technol. 2022, 71, 2319–2332. [Google Scholar] [CrossRef]
- Doi, A.; Butsuen, T.; Niibe, T. Development of a rear-end collision avoidance system with automatic brake control. JSAE Rev. 1994, 15, 335–340. [Google Scholar] [CrossRef]
- Seiler, P.; Song, B.; Hedrick, J.K. Development of a collision avoidance system. SAE Trans. 1998, 107, 1334–1340. [Google Scholar]
- Moon, S.; Yi, K. Human driving data-based design of a vehicle adaptive cruise control algorithm. Veh. Syst. Dyn. 2008, 46, 661–690. [Google Scholar] [CrossRef]
- Horst, R. Time-to-collision as a cue for decision-making in braking. Vis. Veh. 1991, 3, 19–26. [Google Scholar]
- Hoffmann, E.R.; Mortimer, R.G. Drivers’ estimates of time to collision. Accid. Anal. Prev. 1994, 26, 511–520. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Yang, X.; Liu, X. Hierarchic braking strategy for active collision avoidance and its verification based on driver’s characteristics. Automot. Eng. 2019, 41, 298–306. [Google Scholar]
- Zhao, M.; Wang, H.; Chen, J. Method to optimize key parameters and effectiveness evaluation of the AEB system based on rear-end collision accidents. SAE Int. J. Passeng. Cars—Electron. Electr. Syst. 2017, 10, 310–317. [Google Scholar] [CrossRef]
- Kondoh, T.; Yamamura, T.; Kitazaki, S. Identification of visual cues and quantification of drivers’ perception of proximity risk to the lead vehicle in car-following situations. J. Mech. Syst. Transp. Logist. 2008, 1, 170–180. [Google Scholar] [CrossRef]
- Evans, B.L.; Waard, D.D.; Brookhuis, K.A. That’s close enough—A threshold effect of time headway on the experience of risk, task difficulty, effort, and comfort. Accid. Anal. Prev. 2010, 42, 1926–1933. [Google Scholar] [CrossRef]
- Zavareh, M.F.; Mamdoohi, A.R.; Nordfjærn, T. The effects of indicating rear-end collision risk via variable message Signs on traffic behavior. Transp. Res. Part F Traffic Psychol. Behav. 2017, 46, 524–536. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, M.; Chen, M. Drivers’ rear end collision avoidance behaviors under different levels of situational urgency. Transp. Res. Part C 2016, 71, 419–433. [Google Scholar] [CrossRef]
- Winsum, W.; Heino, A. Choice of time-headway in car-following and the role of time-to-collision information in Braking. Ergonomics 1996, 39, 579–592. [Google Scholar] [CrossRef]
- Xiong, X.; Wang, M.; Cai, Y. A forward collision avoidance algorithm based on driver braking behavior. Accid. Anal. Prev. 2019, 129, 30–43. [Google Scholar] [CrossRef]
- Wada, T.; Doi, S.; Tsuru, N. Characterization of expert drivers’ last-second braking and its application to a collision avoidance system. IEEE Trans. Intell. Transp. Syst. 2010, 11, 413–422. [Google Scholar] [CrossRef]
- Rani, M.F.H.; Bakar, S.A.; Hashim, M. Calculating the brake-application time of AEB system by considering maximum deceleration rate during a primary accident in Penang’s urban road. J. Soc. Automot. Eng. Malays. 2019, 3, 320–332. [Google Scholar] [CrossRef]
- GB/T 39901-2021; Performance Requirements and Test Methods for Advanced Emergency Braking System (AEBS) of Passenger Cars. Standards Press of China: Beijing, China, 2021.
- JT/T 1242-2019; Performance Requirements and Test Procedures for Advanced Emergency Braking System of Commercial Vehicle. Standards Press of China: Beijing, China, 2019.
- Lai, F.; Jiang, C. Establishment and simulation analysis of 18 DOF unified dynamics model of automobile chassis. Int. J. Control Autom. Syst. 2021, 19, 2323–2342. [Google Scholar] [CrossRef]

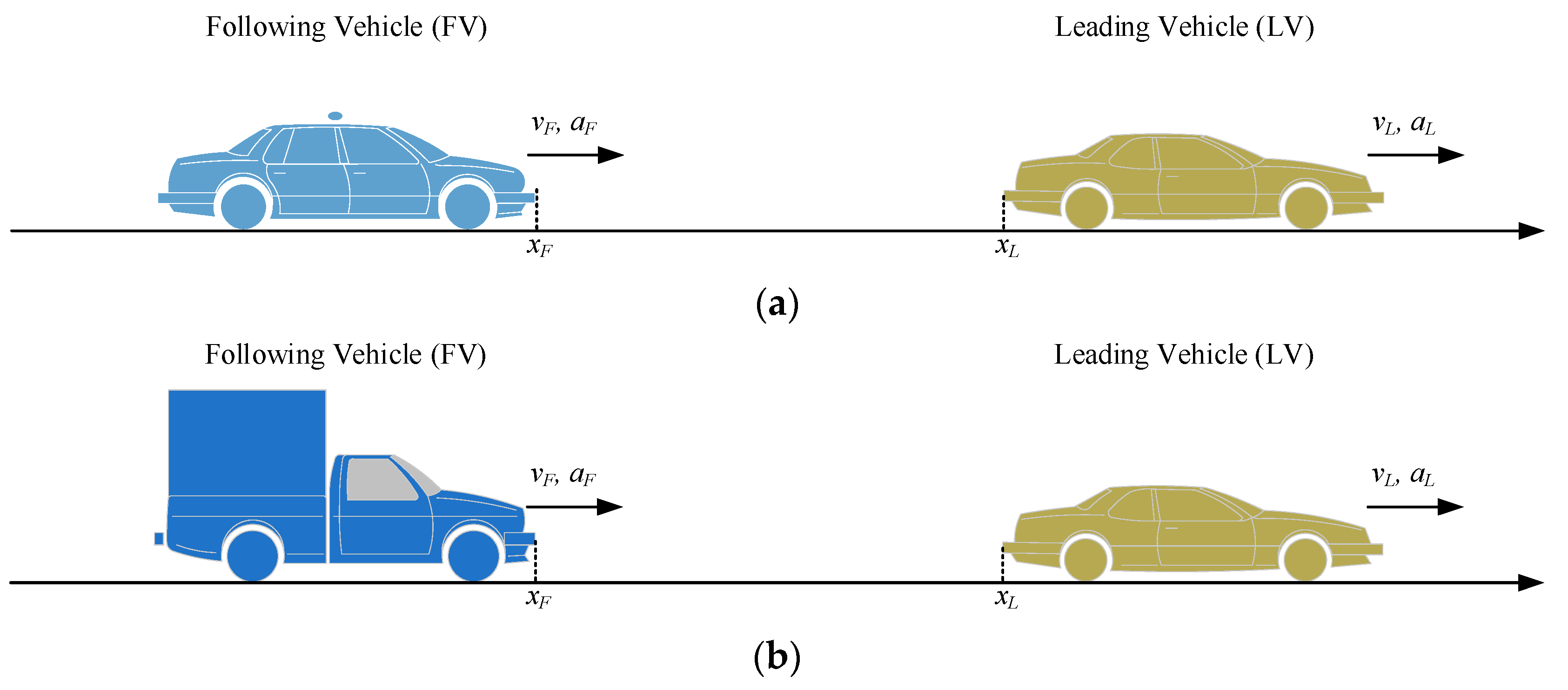
| Test Scenarios | vF (km/h) | vL (km/h) | aL (m/s2) | xr (m) |
|---|---|---|---|---|
| CCRs | 30 | 0 | 0 | 60 |
| CCRm | 50 | 20 | 0 | 120 |
| CCRb | 50 | 50 | −4 | 40 |
| Test Scenarios | vF (km/h) | vL (km/h) | aL (m/s2) | xr (m) |
|---|---|---|---|---|
| CCRs | 40 | 0 | 0 | 150 |
| CCRs | 80 | 0 | 0 | 150 |
| CCRm | 80 | 12 | 0 | 150 |
| Symbol | Parameter Description | Value | Unit |
|---|---|---|---|
| M | Mass of the car model | 1494.7 | kg |
| Ms | Sprung mass | 1374 | kg |
| Mu1j (j = l; r) | Front unsprung mass | 29.3 | kg |
| Mu2j (j = l; r) | Rear unsprung mass | 26.2 | kg |
| L1 | Distance from the body center of gravity to the front axle | 1.356 | m |
| L2 | Distance from the body center of gravity to the rear axle | 0.995 | m |
| h | Height from mass center of gravity to the roll axis | 0.6 | m |
| Iyy | Pitch moment of inertia of sprung mass | 2350 | kg·m2 |
| Ixx | Roll moment of inertia of sprung mass | 1100 | kg·m2 |
| Izz | Yaw moment of inertia of sprung mass | 2465 | kg·m2 |
| Ks1j (j = l; r) | Front suspension stiffness | 25,000 | N/m |
| Cs1j (j = l; r) | Front suspension damping | 4167 | N·s/m |
| Ks2j (j = l; r) | Rear suspension stiffness | 26,000 | N/m |
| Cs2j (j = l; r) | Rear suspension damping | 4000 | N·s/m |
| Kt1j (j = l; r) | Front tire vertical stiffness | 219,090 | N/m |
| Kt2j (j = l; r) | Rear tire vertical stiffness | 221,090 | N/m |
| Kα1j (j = l; r) | Front tire lateral stiffness | −20,000 | N/rad |
| Kα2j (j = l; r) | Rear tire lateral stiffness | −37,000 | N/rad |
| dT | Track width | 1.307 | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, F.; Liu, J.; Hu, Y. An Automatic Emergency Braking Control Method for Improving Ride Comfort. World Electr. Veh. J. 2024, 15, 259. https://doi.org/10.3390/wevj15060259
Lai F, Liu J, Hu Y. An Automatic Emergency Braking Control Method for Improving Ride Comfort. World Electric Vehicle Journal. 2024; 15(6):259. https://doi.org/10.3390/wevj15060259
Chicago/Turabian StyleLai, Fei, Junbo Liu, and Yuanzhi Hu. 2024. "An Automatic Emergency Braking Control Method for Improving Ride Comfort" World Electric Vehicle Journal 15, no. 6: 259. https://doi.org/10.3390/wevj15060259
APA StyleLai, F., Liu, J., & Hu, Y. (2024). An Automatic Emergency Braking Control Method for Improving Ride Comfort. World Electric Vehicle Journal, 15(6), 259. https://doi.org/10.3390/wevj15060259






