Harmonic Resonance Mechanisms and Influencing Factors of Distributed Energy Grid-Connected Systems
Abstract
:1. Introduction
2. Impedance Modeling Analysis of GFL Inverter
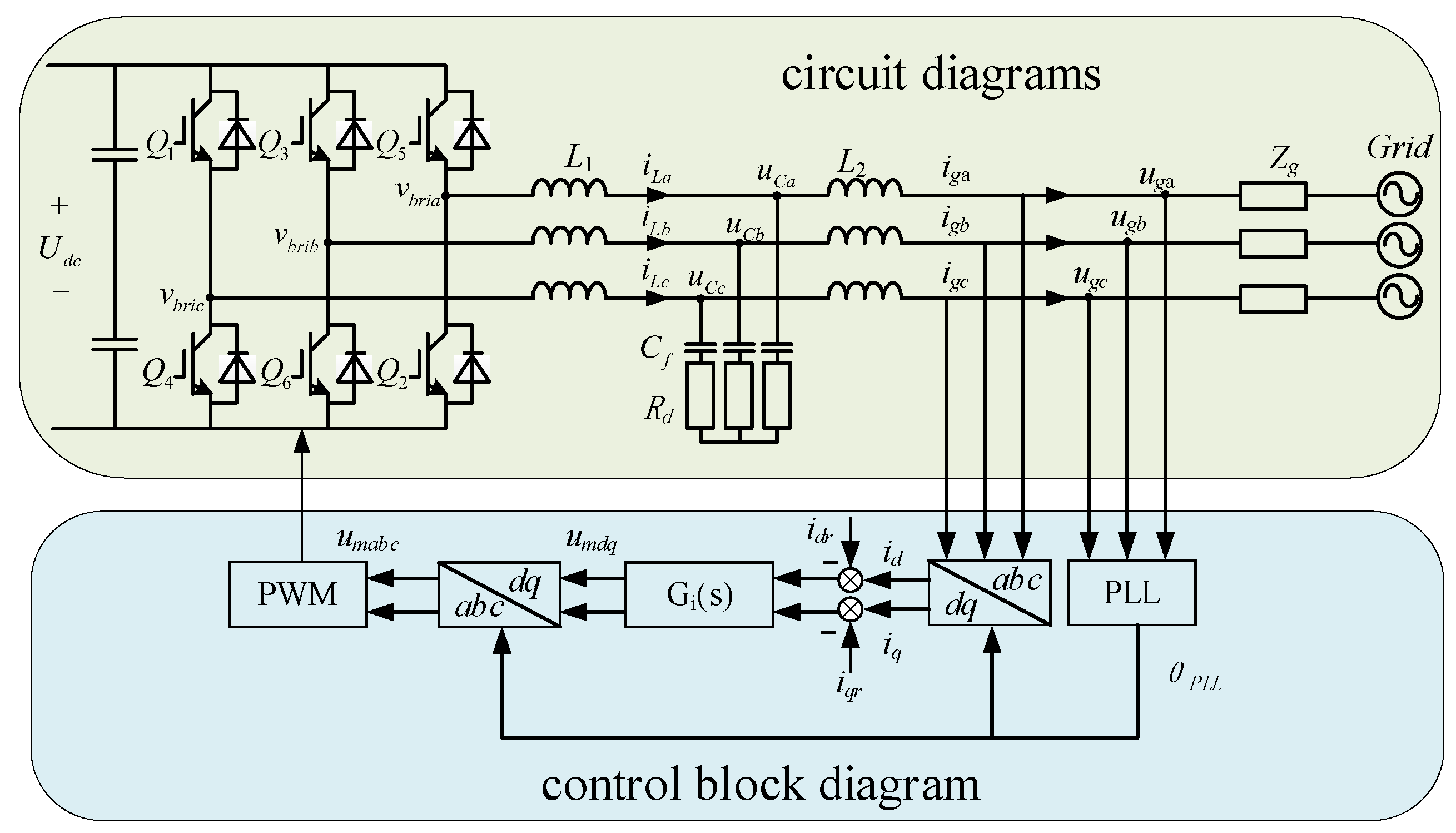
2.1. Typical GFL Inverter Impedance Modeling
2.2. Stability Analysis
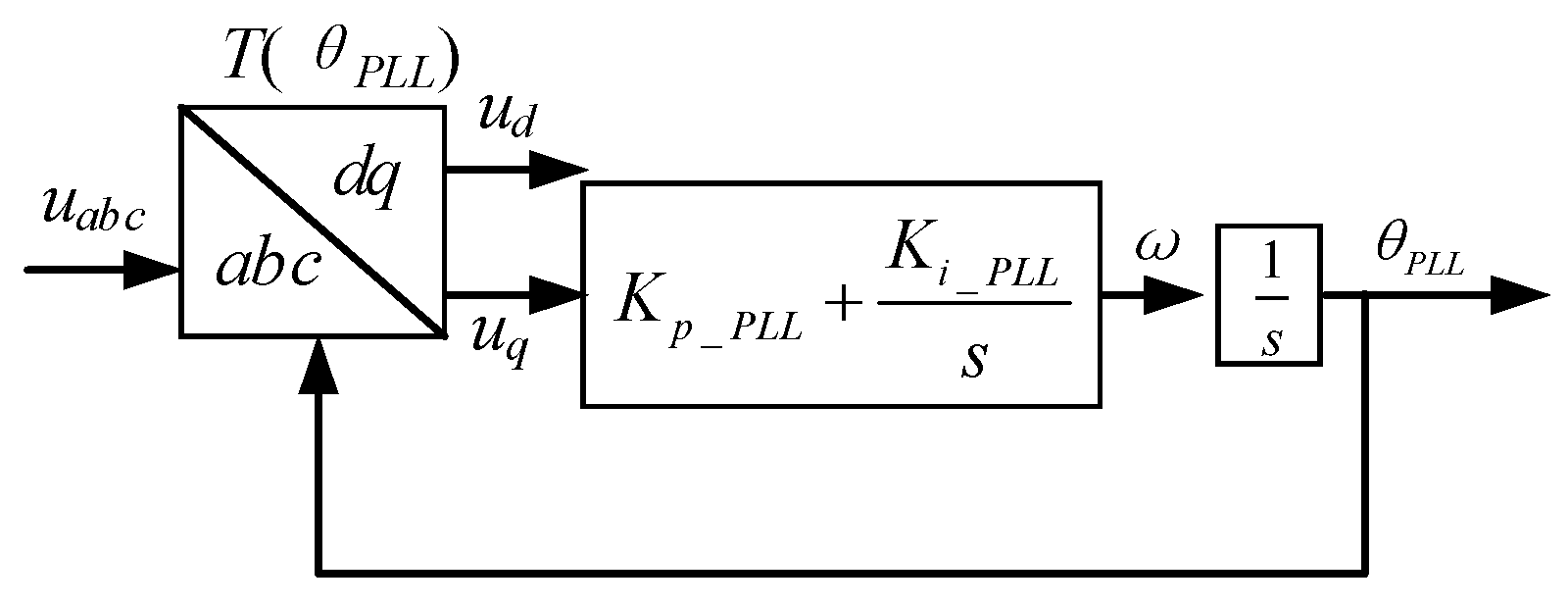
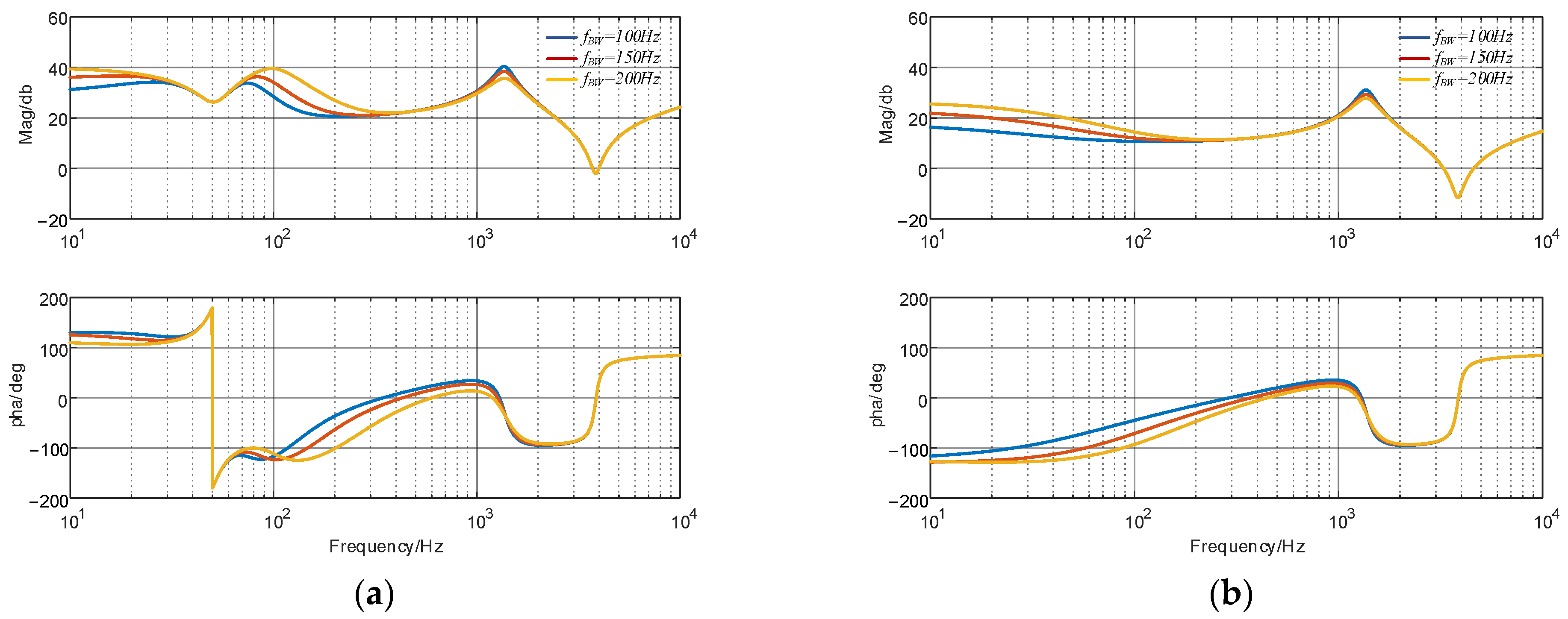
2.3. Influence of PLL Bandwidth on GFL Impedance Curve
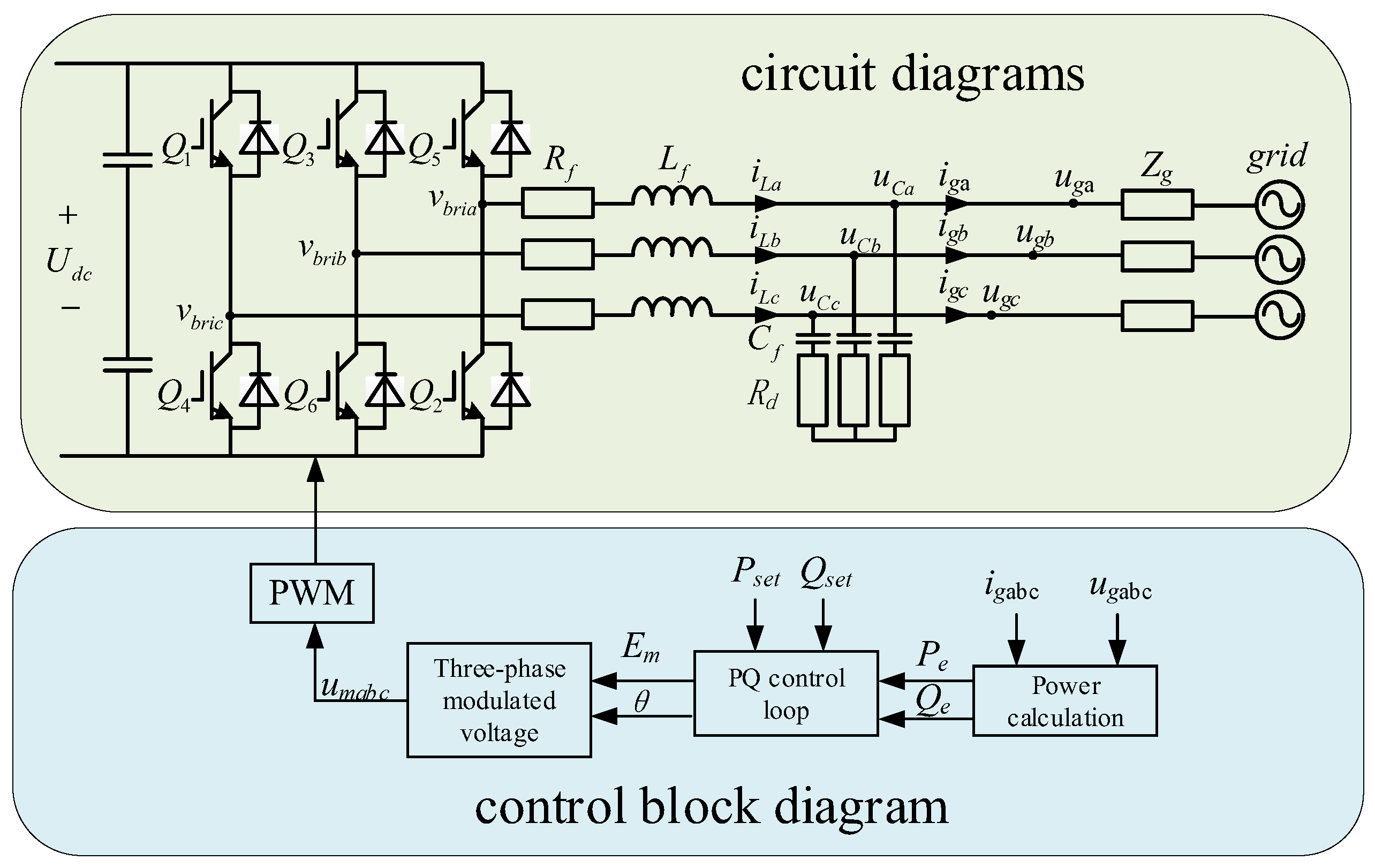
3. Impedance Modeling Analysis of GFM Inverter
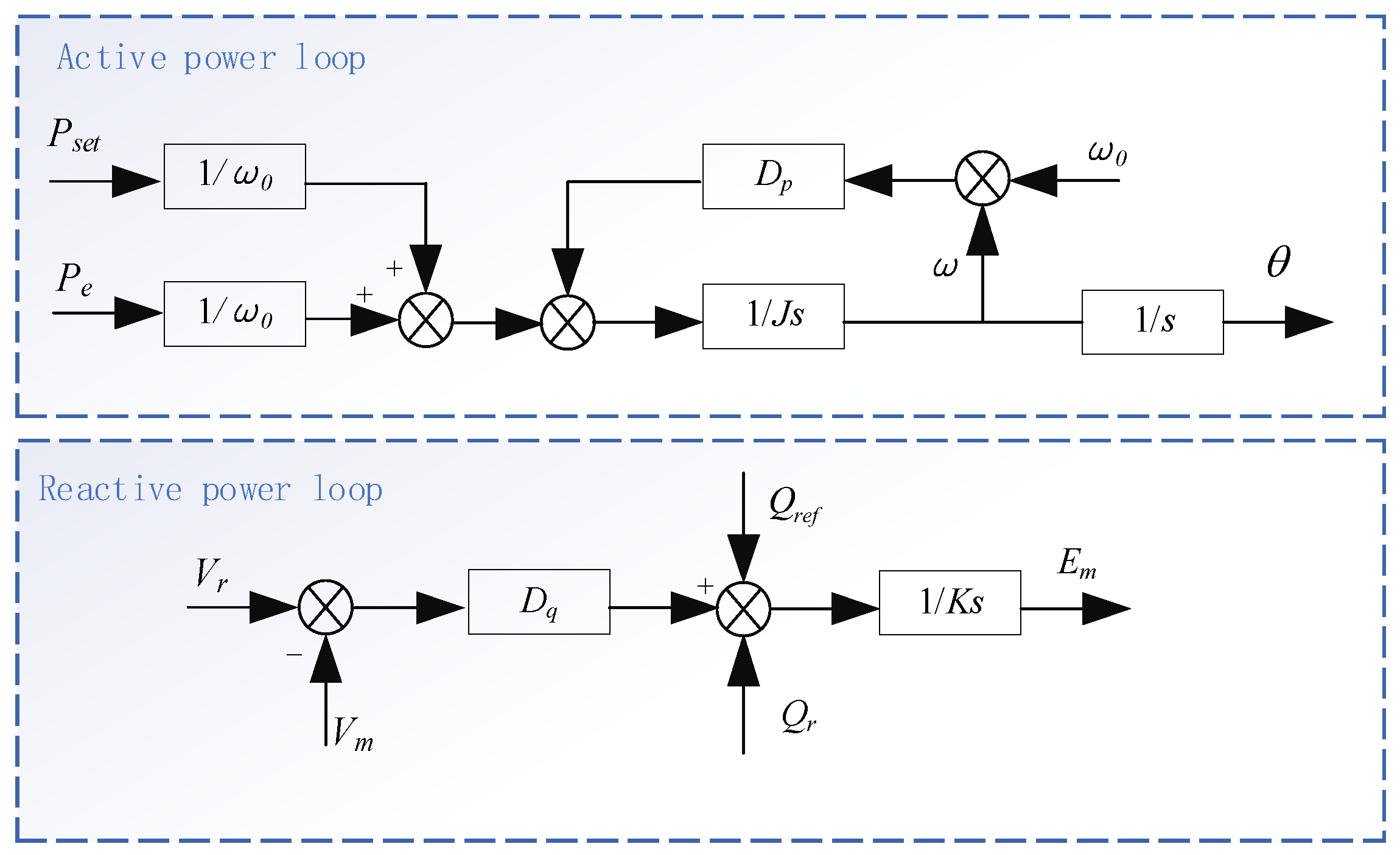
3.1. Typical GFM Inverter Impedance Modeling
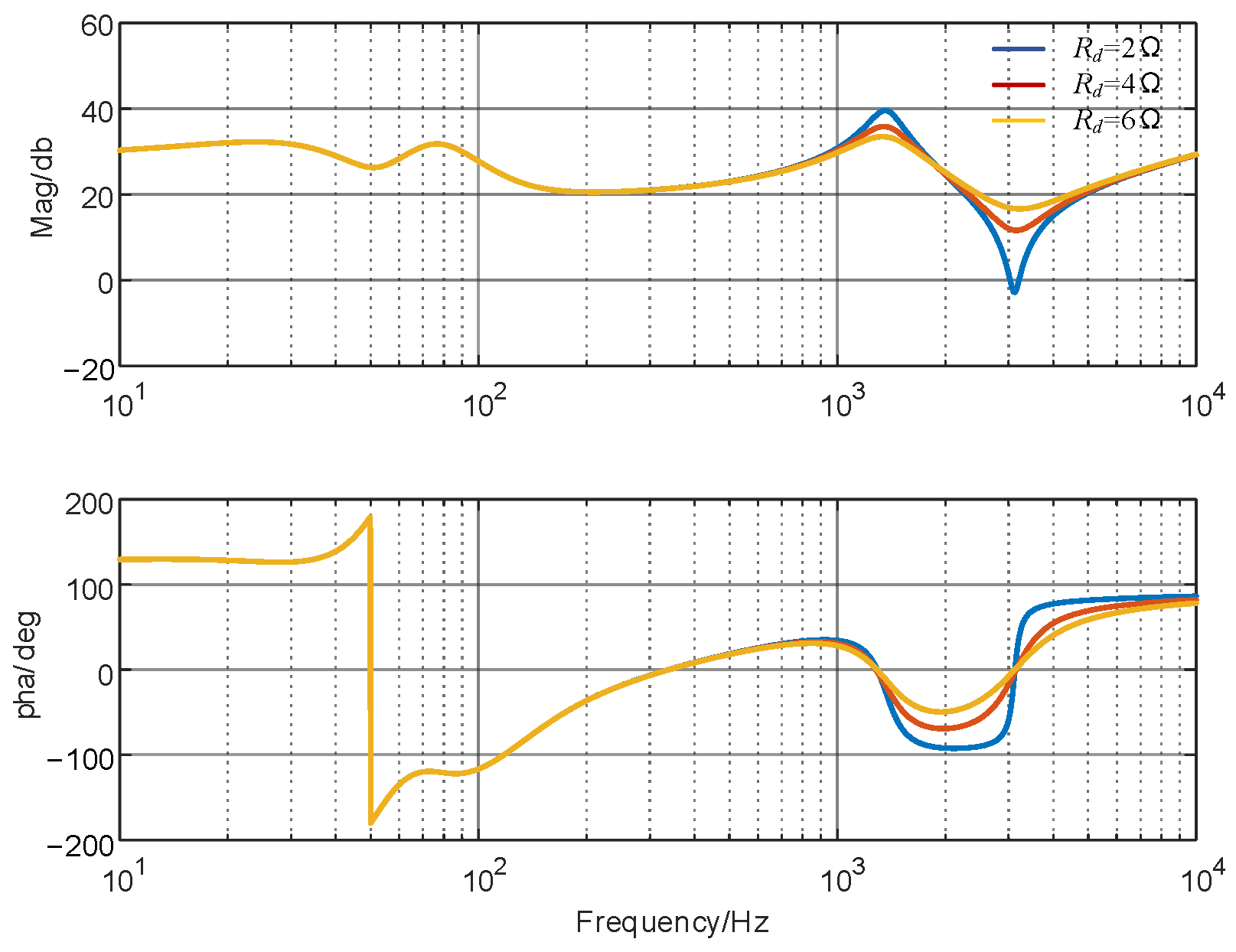
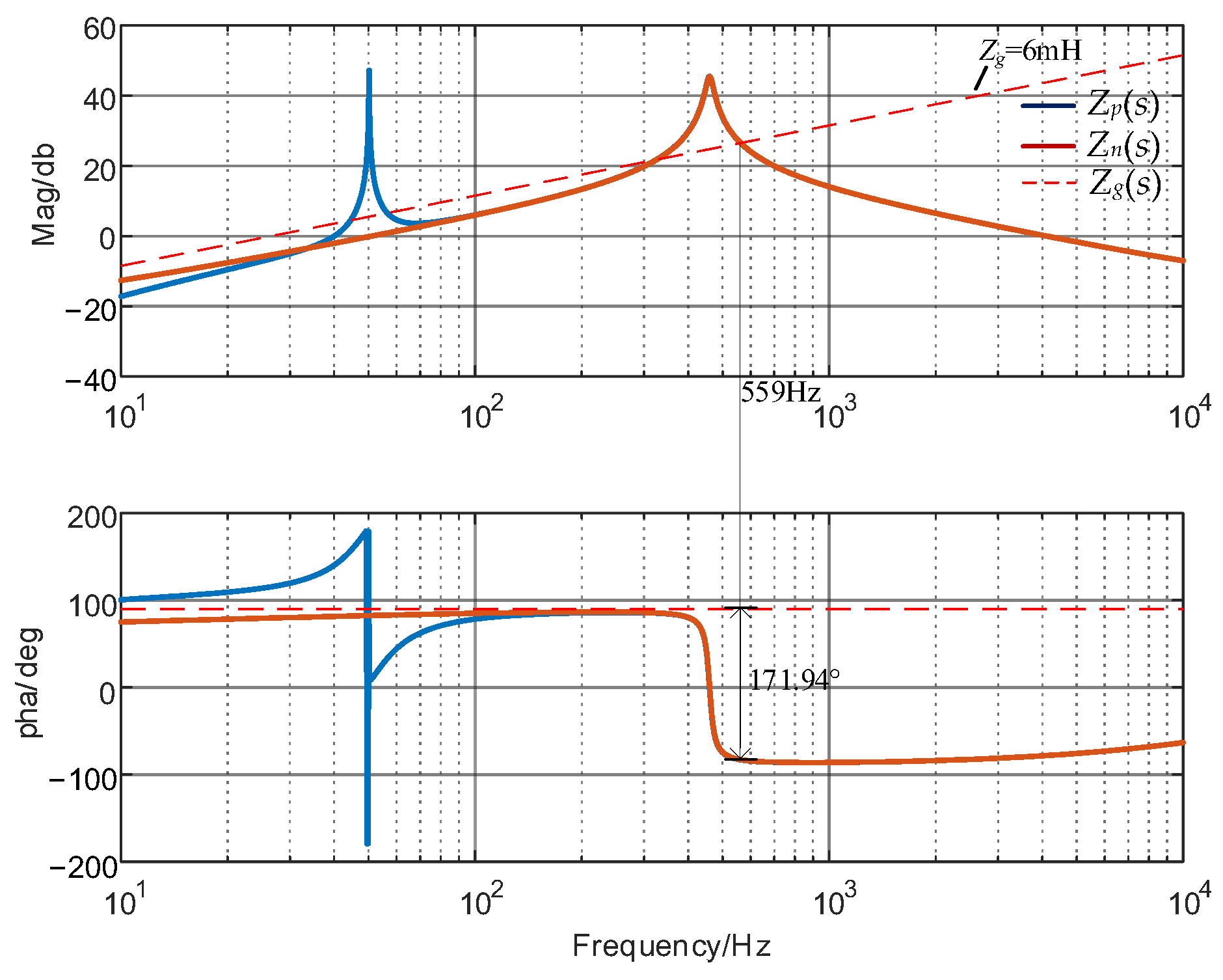
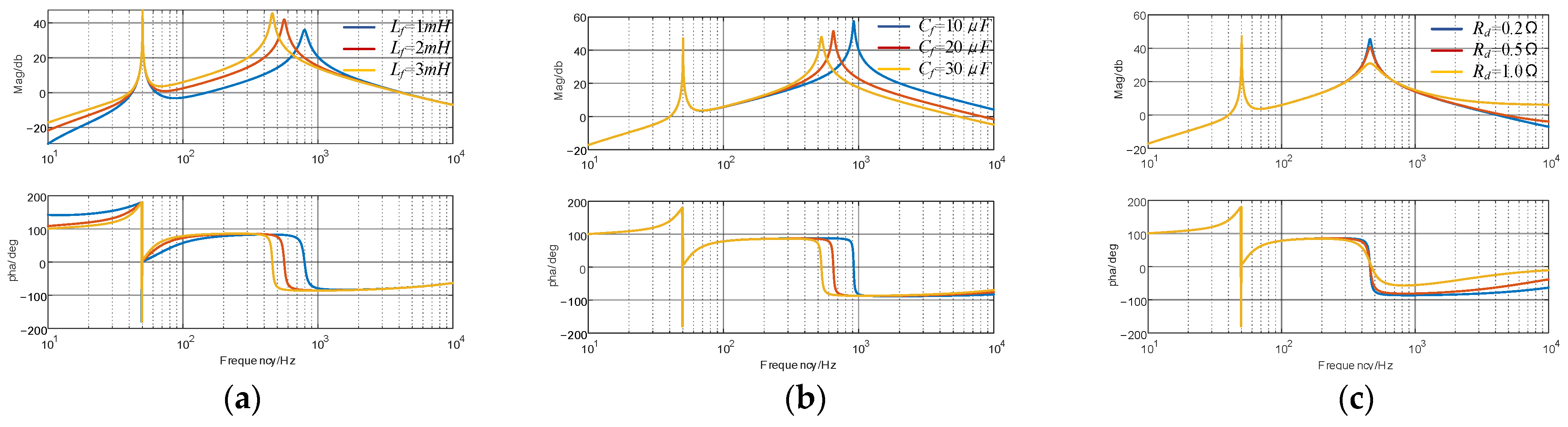
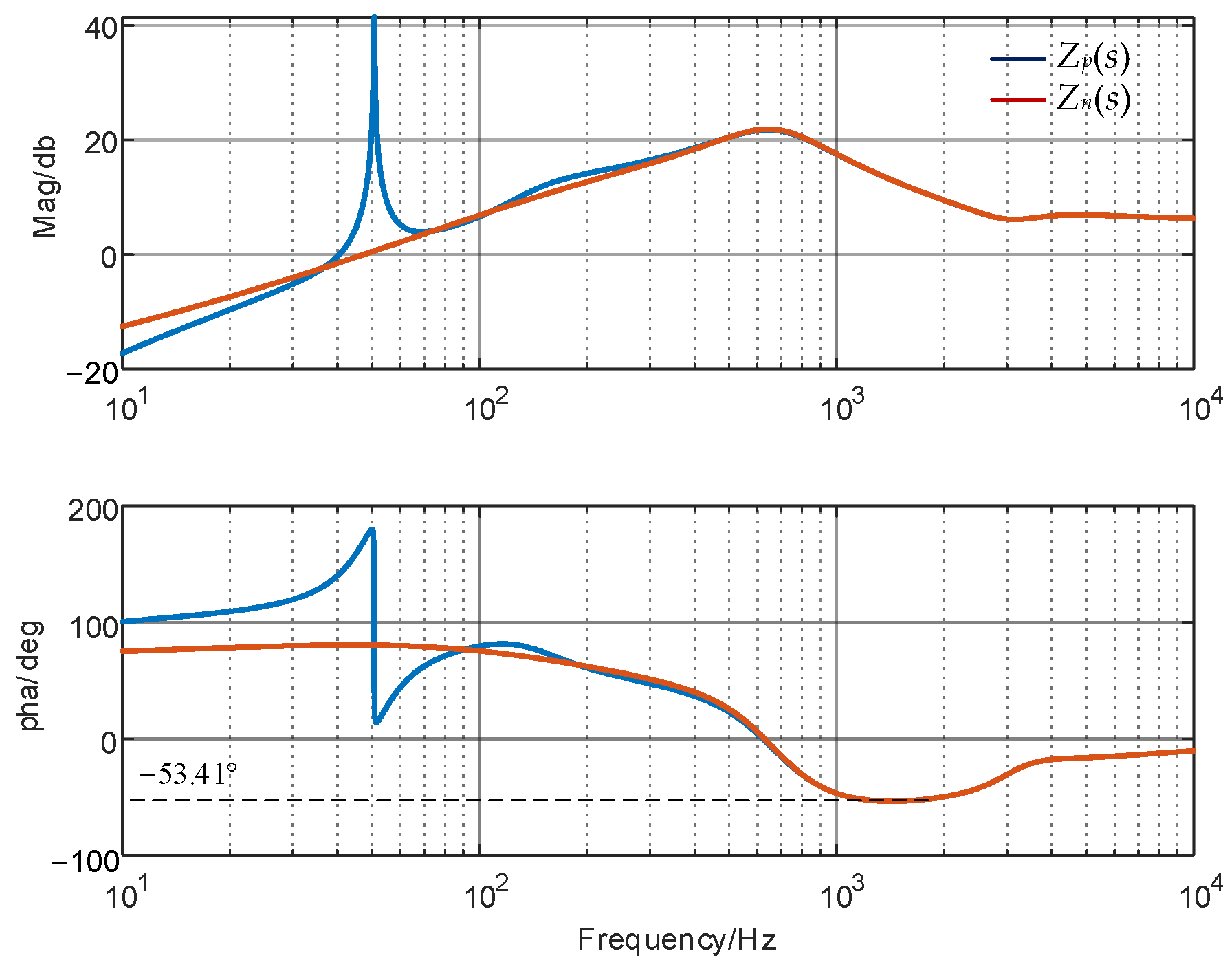
3.2. Influence of Parameters on GFM Inverter Impedance Curve
4. Analysis of Concurrent Grid Integration of Inverters and Electric Vehicles
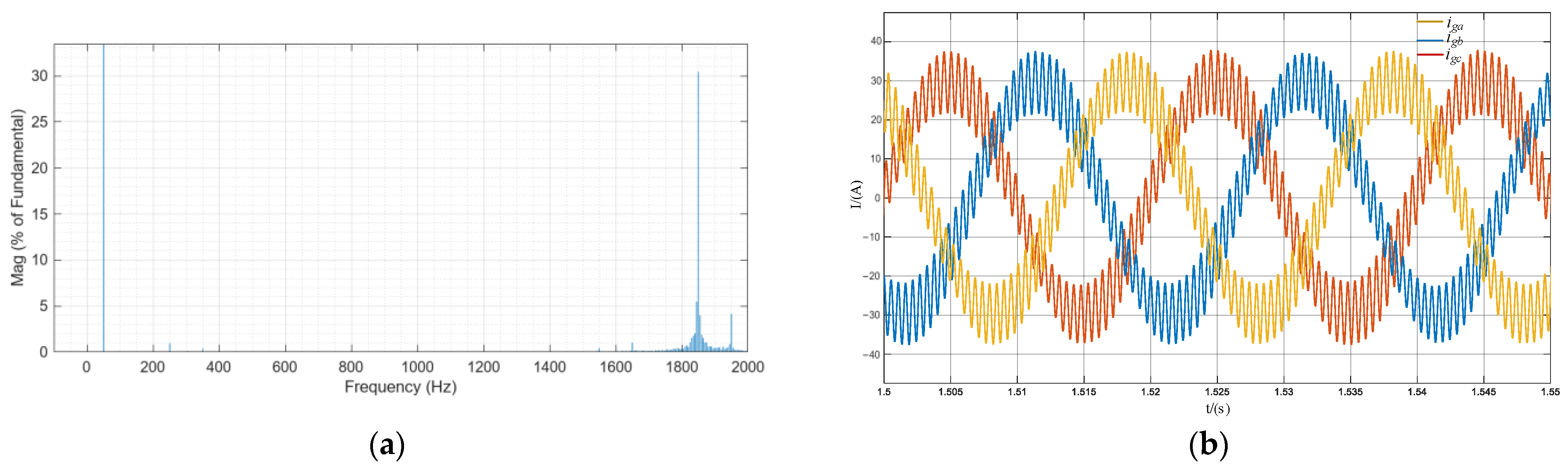
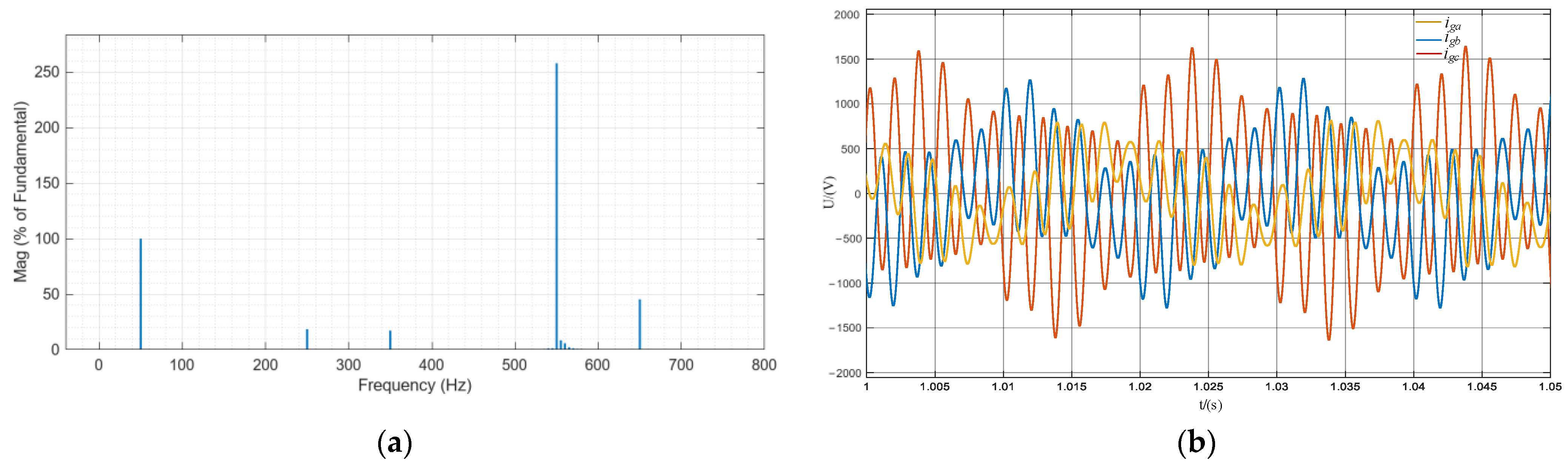
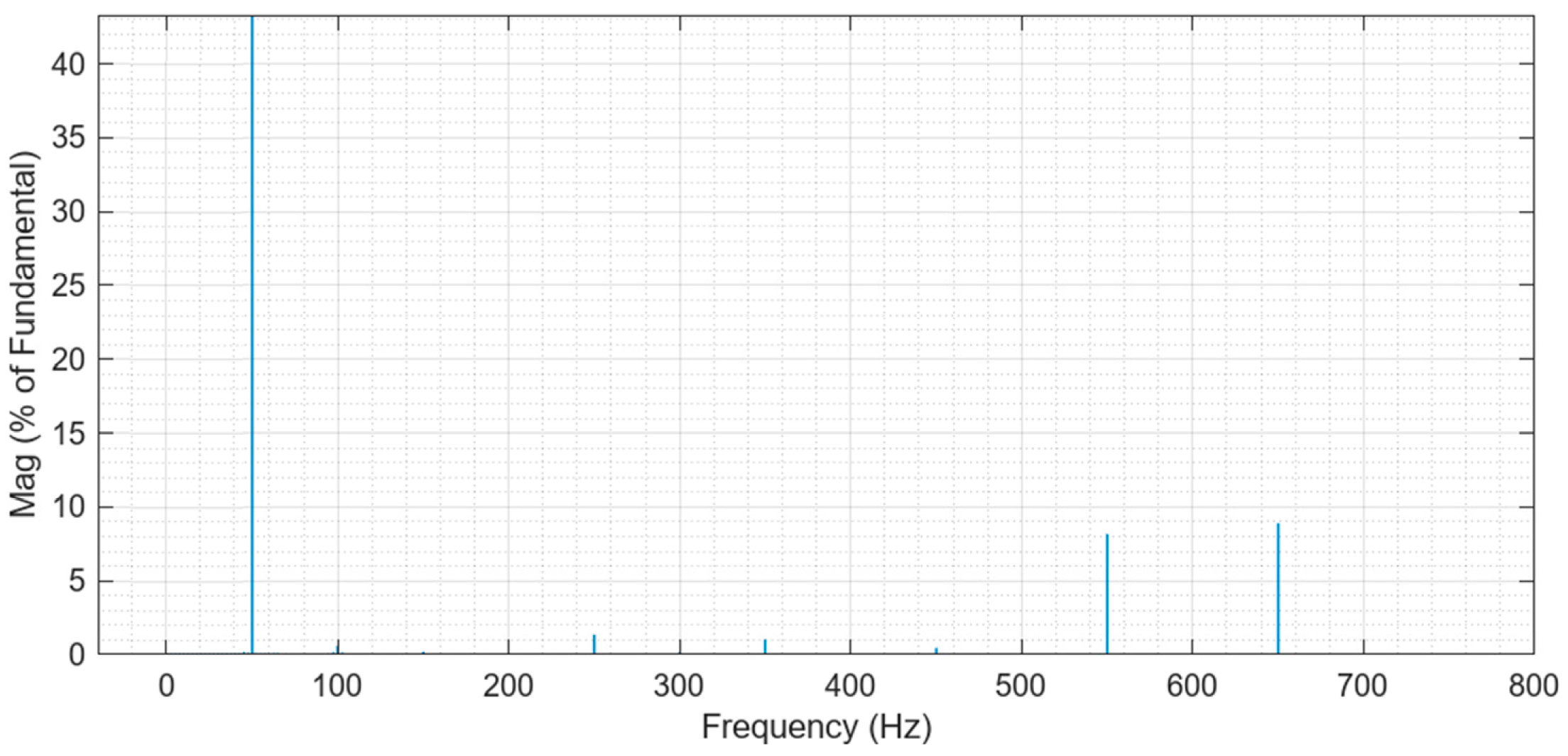
5. Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, Z.; Tang, J.; Buticchi, G.; Liserre, M. Stabilization of Distribution Grids With High Penetration of Renewables: The Path From Decentralized Control to a Centralized One. IEEE Ind. Electron. Mag. 2024, 18, 17–31. [Google Scholar] [CrossRef]
- Wu, W.; Liu, Y.; He, Y.; Chung, H.S.H.; Liserre, M.; Blaabjerg, F. Damping Methods for Resonances Caused by LCL-Filter-Based Current-Controlled Grid-Tied Power Inverters: An Overview. IEEE Trans. Ind. Electron. 2017, 64, 7402–7413. [Google Scholar] [CrossRef]
- Alawasa, K.M.; Mohamed, Y.A.-R.I. A Simple Approach to Damp SSR in Series-Compensated Systems via Reshaping the Output Admittance of a Nearby VSC-Based System. IEEE Trans. Ind. Electron. 2015, 62, 2673–2682. [Google Scholar] [CrossRef]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, X.; Chen, L.; Min, Y.; Li, G.; Wang, L.; Zhang, Y. A Strictly Sufficient Stability Criterion for Grid-Connected Converters Based on Impedance Models and Gershgorin’s Theorem. IEEE Trans. Power Deliv. 2020, 35, 1606–1609. [Google Scholar] [CrossRef]
- Kroutikova, N.; Hernandez-Aramburo, C.A.; Green, T.C. State-space model of grid-connected inverters under current control mode. IET Electr. Power Appl. 2007, 1, 329–338. [Google Scholar] [CrossRef]
- Kwon, J.; Wang, X.; Bak, C.L.; Blaabjerg, F. The modeling and harmonic coupling analysis of multiple-parallel connected inverter using harmonic state space (HSS). In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Rygg, A.; Molinas, M. Apparent impedance analysis: A small-signal method for stability analysis of power electronic-based systems. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1474–1486. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Blaabjerg, F.; Chen, Z. Harmonic Instability Assessment Using State-Space Modeling and Participation Analysis in Inverter-Fed Power Systems. IEEE Trans. Ind. Electron. 2016, 64, 806–816. [Google Scholar] [CrossRef]
- Gui, Y.; Zheng, J.; Liu, Z.; Gou, Y.; Ding, Y. Improved Impedance Stability Analysis of Power Electronic System Considering Harmonic Source. In Proceedings of the 2022 5th International Conference on Renewable Energy and Power Engineering (REPE), Beijing, China, 28–30 September 2022. [Google Scholar]
- Sun, J. Small-signal methods for electric ship power systems. In Proceedings of the 2009 IEEE Electric Ship Technologies Symposium, Baltimore, MD, USA, 20–22 April 2009. [Google Scholar]
- Cespedes, M.; Sun, J. Impedance Modeling and Analysis of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2014, 29, 1254–1261. [Google Scholar] [CrossRef]
- Fang, T.; Shen, S.; Zhang, L.; Jin, Y.; Huang, C. Capacitor Current Feedback With Phase-Lead Compensator to Eliminate Resonant Frequency Forbidden Region for LCL-Type Grid-Connected Inverter in Weak Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5581–5596. [Google Scholar] [CrossRef]
- Nishida, K.; Ahmed, T.; Nakaoka, M. A Novel Finite-Time Settling Control Algorithm Designed for Grid-Connected Three-Phase Inverter With an LCL-Type Filter. IEEE Trans. Ind. Appl. 2014, 50, 2005–2020. [Google Scholar] [CrossRef]
- Yu, Y.; Li, H.; Li, Z. Impedance modeling and stability analysis of LCL-type grid-connected inverters with different current sampling schemes. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016. [Google Scholar]
- Wu, W.; Zhou, L.; Chen, Y.; Luo, A.; Dong, Y.; Zhou, X.; Xu, Q.; Yang, L.; Guerrero, J.M. Sequence-Impedance-Based Stability Comparison Between VSGs and Traditional Grid-Connected Inverters. IEEE Trans. Power Electron. 2019, 34, 46–52. [Google Scholar] [CrossRef]
- Lou, G.; Yang, Q.; Gu, W.; Zhang, J. An improved control strategy of virtual synchronous generator under symmetrical grid voltage sag. Int. J. Electr. Power Energy Syst. 2020, 121, 106093. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, J.; Chen, X. Impedance Modeling and Stability Analysis of Weak-Grid Interfaced Single-Phase VSG. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019. [Google Scholar]
- Zhu, D.; Zhou, S.; Zou, X.; Kang, Y. Improved Design of PLL Controller for LCL-Type Grid-Connected Converter in Weak Grid. IEEE Trans. Power Electron. 2020, 35, 4715–4727. [Google Scholar] [CrossRef]
- Wang, K.; Yuan, X.; Li, S.; Wu, X. Stability-Margin-Oriented Key Parameter Design for Voltage-Source Rectifiers in Weak Power Grids With Inductive Impedance. IEEE Open J. Ind. Electron. Soc. 2021, 2, 511–527. [Google Scholar] [CrossRef]
- Gonzalez-Espin, F.; Figueres, E.; Garcera, G. An Adaptive Synchronous-Reference-Frame Phase-Locked Loop for Power Quality Improvement in a Polluted Utility Grid. IEEE Trans. Ind. Electron. 2012, 59, 2718–2731. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, B.; Deng, J. Multi-objective optimization strategy for distribution network considering V2G-enabled electric vehicles in building integrated energy system. Prot. Control. Mod. Power Syst. 2020, 5, 1–8. [Google Scholar] [CrossRef]
- Lan, D.; Wu, Y.; Soeiro, T.B.; Granello, P.; Qin, Z.; Bauer, P. 12-pulse Rectifier with DC-Side Buck Converter for Electric Vehicle Fast Charging. In Proceedings of the IECON 2022–48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022. [Google Scholar]


| System Parameters | Values |
|---|---|
| Grid Phase Voltage Peak (V1) | 311 V |
| DC Voltage (Vdc) | 700 V |
| Inverter Rated Current (I) | 30 A |
| Phase-Locked Loop Coefficients (Kp_PLL, Ki_PLL) | 2.4, 929.4 |
| Inductance on the Inverter Side (L1) | 2 mH |
| Inductance on the Grid Side (L2) | 0.5 mH |
| Filter Capacitor (Cf) | 6.8 μF |
| Series Damping Resistor (Rd) | 2 Ω |
| Switching Frequency (fs) | 10 kHz |
| Sampling Frequency (fsw) | 20 kHz |
| System Parameters | Values |
|---|---|
| Grid Phase Voltage Peak (V1) | 311 V |
| Virtual Inertia (J) | 0.02 |
| Droop Coefficient (Dp) | 10 |
| Excitation Controller Integral Coefficient (K) | 6 |
| Voltage Regulation Coefficient (Dq) | 200 |
| DC Voltage (Vdc) | 700 V |
| Inverter Power (P) | 10 kW |
| Inductor’s Series Resistor (Rf) | 0.2 Ω |
| Filter Inductor (Lf) | 3 mH |
| Filter Capacitor (Cf) | 40 μF |
| Capacitor’s Series Resistor (Rd) | 0.2 Ω |
| Switching Frequency (fs) | 10 kHz |
| Sampling Frequency (fsw) | 20 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Li, Z.; Lu, S.; Xu, T.; Zhang, Z.; Quan, X. Harmonic Resonance Mechanisms and Influencing Factors of Distributed Energy Grid-Connected Systems. World Electr. Veh. J. 2024, 15, 287. https://doi.org/10.3390/wevj15070287
Xu M, Li Z, Lu S, Xu T, Zhang Z, Quan X. Harmonic Resonance Mechanisms and Influencing Factors of Distributed Energy Grid-Connected Systems. World Electric Vehicle Journal. 2024; 15(7):287. https://doi.org/10.3390/wevj15070287
Chicago/Turabian StyleXu, Minrui, Zhixin Li, Shufeng Lu, Tianyang Xu, Zhanqi Zhang, and Xiangjun Quan. 2024. "Harmonic Resonance Mechanisms and Influencing Factors of Distributed Energy Grid-Connected Systems" World Electric Vehicle Journal 15, no. 7: 287. https://doi.org/10.3390/wevj15070287
APA StyleXu, M., Li, Z., Lu, S., Xu, T., Zhang, Z., & Quan, X. (2024). Harmonic Resonance Mechanisms and Influencing Factors of Distributed Energy Grid-Connected Systems. World Electric Vehicle Journal, 15(7), 287. https://doi.org/10.3390/wevj15070287






