Abstract
The accuracy and real-time performance of 3D object detection are key factors limiting its widespread application. While cameras capture detailed color and texture features, they lack depth information compared to LiDAR. Multimodal detection combining both can improve results but incurs significant computational overhead, affecting real-time performance. To address these challenges, this paper presents a real-time multimodal fusion model called Fast Transfusion that combines the benefits of LiDAR and camera sensors and reduces the computational burden of their fusion. Specifically, our Fast Transfusion method uses QConv (Quick Convolution) to replace the convolutional backbones compared to other models. QConv concentrates the convolution operations at the feature map center, where the most information resides, to expedite inference. It also utilizes deformable convolution to better match the actual shapes of detected objects, enhancing accuracy. And the model incorporates EH Decoder (Efficient and Hybrid Decoder) which decouples multiscale fusion into intra-scale interaction and cross-scale fusion, efficiently decoding and integrating features extracted from multimodal data. Furthermore, our proposed semi-dynamic query selection refines the initialization of object queries. On the KITTI 3D object detection dataset, our proposed approach reduced the inference time by 36 ms and improved 3D AP by 1.81% compared to state-of-the-art methods.
1. Introduction
Three-dimensional object detection as cutting-edge computer vision technology seeks to accurately identify and categorize objects within a three-dimensional space. The applications of 3D object detection are diverse. For instance, in autonomous driving [1,2], it is imperative to identify the location and category of various objects. In Augmented Reality (AR), enhanced scene recognition and understanding are required [3]. Furthermore, for tasks such as robotic object manipulation, knowledge of the object’s location and category is necessary. And 3D object detection techniques are recently gaining popularity due to the necessity of object shape and orientation estimation in real-world space [4]. Nowadays, it is seeing advancements through LiDAR sensors [5], which offer reliable object localization under varying lighting conditions by capturing depth as point clouds [6]. Despite progress, LiDAR-based detection performance diminishes for distant objects due to sparse sampling density [7]. Contrarily, color image sensors furnish high-resolution sampling and abundant contextual data, thus compensating for the LiDAR limitations. The amalgamation of RGB image and LiDAR data typically enhances 3D detection performance [8].
Current LiDAR–camera fusion methodologies can be broadly classified into three categories: result level, proposal level, and point level. Result-level techniques [9], such as FPointNet [10] and RoarNet [11], leverage pre-existing 2D detectors to initiate 3D proposals, subsequently employing a PointNet for object localization. Proposal-level fusion techniques, including MV3D [12] and AVOD [13], execute fusion at the region proposal level by implementing RoIPool in each modality for shared proposals. However, these coarse-grained fusion techniques have demonstrated suboptimal results due to the high level of background noise typically present in rectangular regions of interest (RoIs). Recently, most approaches have attempted point-level fusion, yielding promising results. These methods initially establish a firm association between LiDAR points and image pixels based on calibration matrices, and subsequently augment LiDAR features with the segmentation scores or CNN features of the associated pixels through point-wise concatenation. Similarly, some studies first project a point cloud onto the bird’s eye view (BEV) plane and then fuse the image features with the BEV pixels [14]. Transfusion [1] as one of the state-of-the-art techniques is one of the best studies that uses two transformer decoder layers as the detection head. It is to reposition the focus of the fusion process, from hard association to soft association, leading to robustness against degenerated image quality and sensor misalignment.
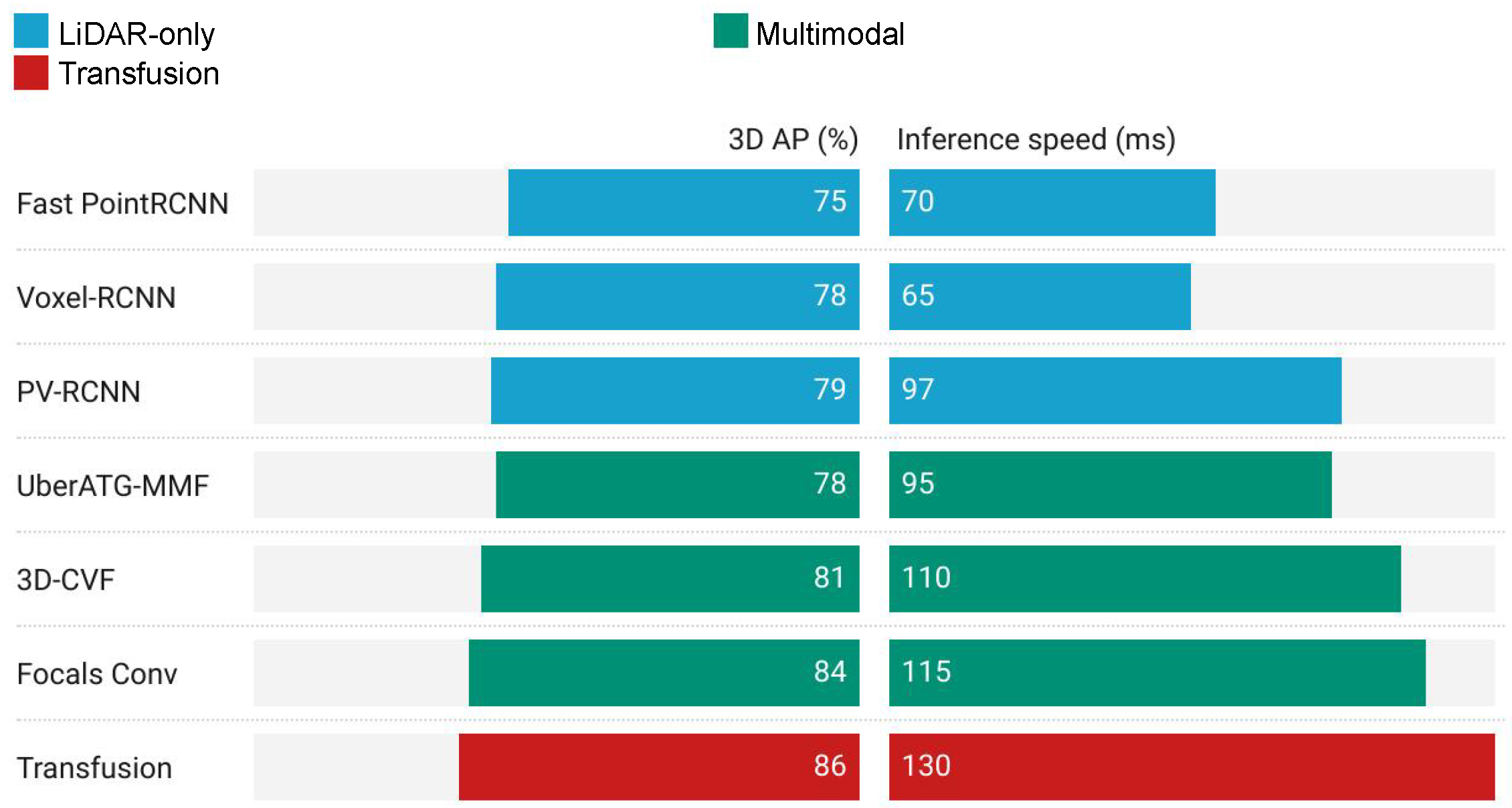
Despite Transfusion’s superior detection accuracy compared to other models, it suffers from longer inference durations as shown in Figure 1. It is because Transfusion grapples with three principal challenges that impede its wider adoption. Firstly, the model’s backbone is unoptimized, resulting in inefficient feature extraction. Secondly, the traditional decoder’s multiscale feature fusion mechanism also imposes significant computational overhead. At last, Transfusion’s design includes queries that are inherently difficult to optimize, slowing down the inference speed of the model. As a result, Transfusion becomes the computational bottleneck of the model due to the high computational cost. What is obvious is that multimodal models outperform LiDAR-only models in terms of 3D AP; however, they exhibit slower inference speeds, particularly the Transformer-based multimodal model, Transfusion. Despite its superior detection accuracy, Transfusion’s slow inference speed limits its practical utility in future applications.

Figure 1.
Three-dimensional AP and inference time across multiple models in the KITTI. It can be seen that compared with LiDAR-only, multimodal achieves higher accuracy on the basis of sacrificing inference time.
Therefore, this paper proposes Fast Transfusion, which uses three technologies, QConv, EH decoder and semi-dynamic query selection, for lightweight modeling. The method replaces the original convolutional network with the QConv network as the backbone and substitutes the original transformer decoder with the EH decoder, while employing semi-dynamic query selection in place of single dynamic query selection or static query selection. In addition, our proposed detector supports flexible adjustment of the inference speed by using different decoder layers without the need for retraining, which benefits from the design of the decoder in the Transformer architecture and facilitates the practical application of the real-time detector. The main contributions of this paper are as follows:
- We propose a QConv network as the backbone of the model, which uses QConv instead of the basic Conv. The QConv applies filters on only a few input channels while leaving the remaining ones untouched and uses deformable convolution and deformable RoI pooling to accelerate training and inference.
- A novel decoder, EH decoder, is proposed, which decouples the intra-scale interaction and cross-scale fusion of multiscale features to efficiently process features with different scales.
- A semi-dynamic query selection is introduced to boost the quality of the initial bounding box predictions for image fusion. The method lets position queries change dynamically associated with the selected top-K features but leaves the content queries static.
- Our study presents a viable strategy for the real-time application of contemporary end-to-end detectors, enabling the proposed model to adapt inference speed via various decoder layers, sidestepping the retraining requirement, a notable hurdle in current real-time detection systems.
- The method achieves state-of-the-art 3D detection performance on nuScenes and competitive results on Waymo. The method also achieves significant acceleration in inference speed compared to existing models.
2. Related Work
2.1. LiDAR-Based 3D Object Detection
LiDAR-based 3D object detection has garnered considerable attention in recent years, marking significant advancements in the field. According to different implementation routes, 3D detection methods based on LiDAR can be divided into three categories: point cloud methods, voxelization methods, and depth map methods. PointNet [15] and PointNet++ [16] are methods that directly extract features from the point cloud, enabling tasks such as classification and segmentation of the point cloud [17]. Traditional approaches typically involve projecting LiDAR point clouds onto 2D planes, such as a bird’s eye view (BEV) or range view images, to facilitate 3D object detection [18,19]. This methodology, while effective, simplifies the complex spatial relationships inherent within the data. Recent studies have endeavored to process raw point clouds directly, bypassing the need for data quantization, thereby preserving the richness of the spatial information [3,20]. The design of detection heads for these systems often mirrors those used in 2D detection frameworks, relying heavily on anchor boxes to identify object boundaries. However, innovative approaches have emerged, utilizing center-based representations to streamline the 3D detection process. Despite the transformative impact of transformer architectures in 2D detection, their application in 3D object detection, particularly for outdoor environments, has been primarily confined to feature extraction phases [21]. The computational demands of the transformer’s attention mechanism, especially when applied to the voluminous data generated by LiDAR systems, are significant. Therefore, a strategy that can save a substantial amount of computational resources is required.
Addressing these challenges, this paper proposes a novel combination of a QConv backbone for feature extraction and an EH decoder equipped with a concise set of object queries for detection. This hybrid approach significantly reduces the computational burden, making it a viable solution for real-time applications. Nonetheless, it is imperative to acknowledge a persistent challenge: the inherently low scanning resolution of LiDAR systems, especially for distant objects, which exacerbates the issue of data sparsity. Our research proposes an innovative solution [22], the LiDAR–camera fusion method, by integrating RGB image data through attentively associating and fusing the object queries, enhancing the model’s ability to detect and interpret sparse LiDAR data effectively. This strategy not only mitigates the limitations posed by the LiDAR resolution but also enriches the detection framework, offering a more robust and accurate detection system [23].
2.2. Image-Based 3D Object Detection
Addressing image-based 3D object detection methodologies have rapidly evolved, with significant distinctions between monocular and binocular vision techniques. The most direct approach [24] involves employing neural networks to estimate the 3D box parameters [25] from the image directly. These methods draw inspiration from the architectural design of 2D object detection networks such as fast RCNNs [26], which have demonstrated efficacy in facilitating end-to-end training. Monocular vision-based detection systems primarily leverage methodologies that include depth estimation, keypoint detection, and the utilization of CAD-based prior information [27,28,29]. The fundamental challenge with monocular images lies in their intrinsic limitation: they offer only a 2D projection of the 3D world, inherently lacking depth information. This limitation significantly constrains the accuracy and reliability of depth perception and, by extension, the effectiveness of 3D object detection. In contrast, binocular vision-based detection methods attempt to overcome these limitations by exploiting the disparity between two vantage points, simulating human stereoscopic vision to infer depth. This approach has led to the development of innovative frameworks and algorithms aimed at generating more accurate 3D data from binocular images. Noteworthy among these is the 3DOP system [30] proposed by Chen et al., which estimates point clouds from binocular imagery, and the MLF method [31] by Xu and Chen, which calculates parallax maps from binocular images to reconstruct depth maps and point clouds. Additionally, the CGStereo system [32] introduced by Li et al., enhanced with semantic segmentation supervision, significantly advances the precision of foreground depth estimation. Moreover, Chen et al. developed a technique named pseudo-stereo [33], which estimates depth maps from binocular images, and Peng et al. introduced an approach for generating pseudo radar and target-level depth estimation by leveraging the SIDE of dual branch networks [34]. Despite these advancements, the inherent challenge of accurately capturing 3D information from 2D images remains a significant hurdle. It is unrealistic to precisely extract depth and other 3D information from 2D images without relying on additional modalities. Consequently, while these methodologies mark progress in the field, the quest for improving detection accuracy through image-based methods continues to be a complex and evolving challenge [35]. Therefore, as previously mentioned, this paper employs a LiDAR–camera fusion method to address the issue of information deficiency inherent in single-modality approaches.
2.3. Multimodal 3D Object Detection
Visual image-based methods excel in offering rich texture details but fall short in providing depth cues [36]. Conversely, point cloud-based approaches deliver spatial geometric insights yet lack textural context. Texture details are crucial for accurate object detection and classification, whereas depth information is vital for estimating the spatial positioning of objects. Multisensor 3D detection methods enable the integration of information from diverse sensors [37], offering solutions to address challenges encountered in LiDAR and camera-based detection methods [38]. The synergistic combination of image and point cloud features exemplifies the significance of sensor fusion [39], while the integration of multisensor aids in mitigating single-sensor failures and enhancing adaptability across diverse environments. Currently, enhancing overall performance by integrating both image and LiDAR data represents a promising research direction in the domain of multimodal 3D object detection methods [40,41,42].
LiDAR–camera 3D detection has garnered significant attention, attributed to the synergistic qualities of point clouds and images. Initial studies [43,44] primarily employed result-level or proposal-level fusion techniques, characterized by a relatively coarse fusion granularity that did not fully exploit the potential of the two modalities. The advent of PointPainting [45] marked a shift towards point-level fusion methods [46,47], which have demonstrated substantial advantages and encouraging outcomes. However, these approaches are susceptible to sensor misalignment issues caused by rigid point-pixel associations defined by calibration matrices [48]. Furthermore, simplistic point-wise concatenation overlooks the integrity and contextual interplay between modalities, leading to performance deterioration when image features are suboptimal. Recently, the introduction of Transfusion, which is a state-of-the-art technique, has emerged as a more robust and efficacious fusion mechanism, addressing these challenges in LiDAR–camera fusion.
Although Transfusion (SOTA) exhibits superior accuracy in multimodal object detection, its inference speed lags compared to single-modality detection approaches. This discrepancy arises partly due to the inherent computational demands of processing multiple modalities and partly due to inefficiencies within the Transfusion architecture that await optimization.
- Transfusion’s reliance on a conventional convolutional neural network backbone introduces significant computational overhead due to redundancy in feature mapping across channels, and the fixed convolutional structures are naturally limited in capturing geometric transformations, which can also detract from accuracy.
- While the integration of multiscale features in Transfusion enhances performance and convergence speed into the decoder, it simultaneously escalates computational costs. Although the deformable attention mechanism mitigates these costs to some extent, the incorporation of multiscale features into the decoder still imposes a substantial computational burden.
- Although Transfusion improves the initialization of Object Query and extends it to content query and position query (anchor), due to the inconsistent distribution of the classification score and location confidence, some predicted boxes have high scores but are not close to GT boxes, which results in boxes with high scores and low IoU scores being selected, while boxes with low scores and high IoU scores are discarded. This impairs the performance of the detector.
Therefore, this paper proposes QConv, EH decoder, and semi-dynamic query selection, three approaches to optimize Transfusion to be Fast Transfusion.
3. Methodology
In this section, we introduce Fast Transfusion, a novel approach tailored for multimodal 3D object detection. Addressing the high computational demands of the original Transfusion model, we propose three key technological advancements: QConv (Quick convolution), EH Decoder (Efficient and Hybrid Decoder), and semi-dynamic query selection.
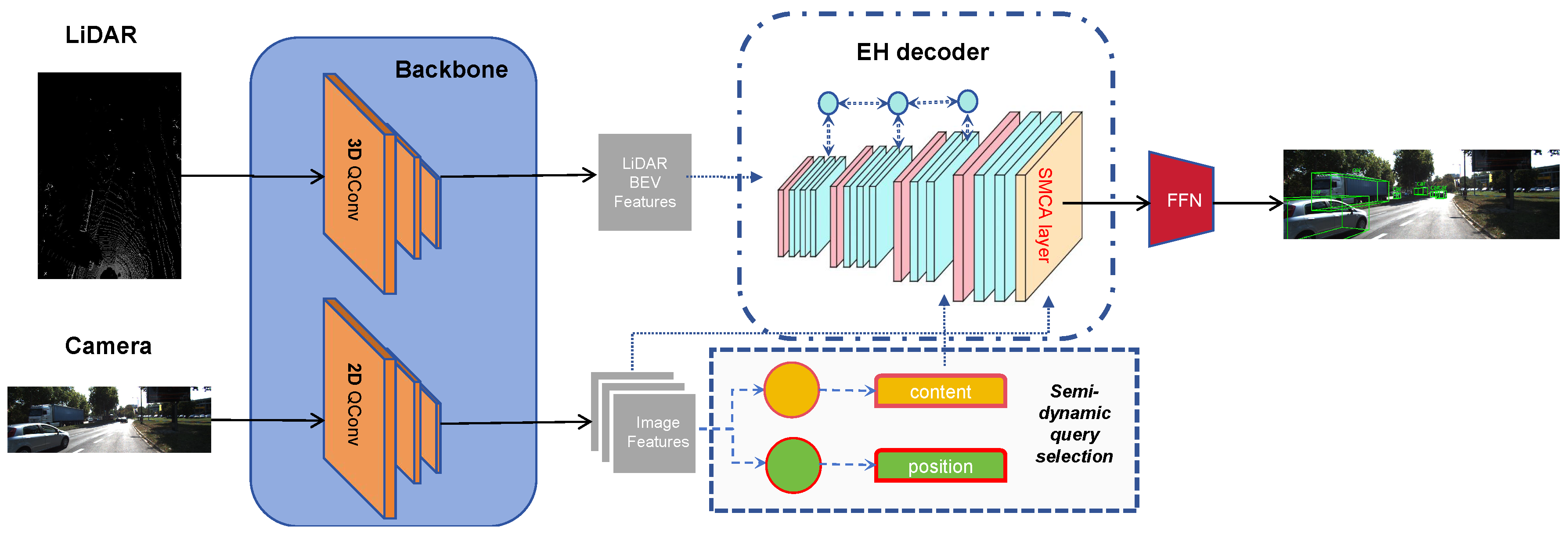
As illustrated in Figure 2, multimodal data first undergo feature extraction through the QConv Network, serving as the backbone. Subsequently, image features are processed via semi-dynamic query selection to complete Query Initialization. Following this, object queries and image features are inputted into the EH Decoder, and through a Feed-Forward Network (FFN), the final prediction output is obtained. By integrating these innovations into our model, Fast Transfusion achieves an optimal balance, significantly enhancing both inference speed and detection accuracy in multimodal 3D object detection tasks. At the same time, we can scale the backbone and decoder of Fast Transfusion using a depth multiplier and a width multiplier. Below, we will first introduce the method of fusing LiDAR and camera data.
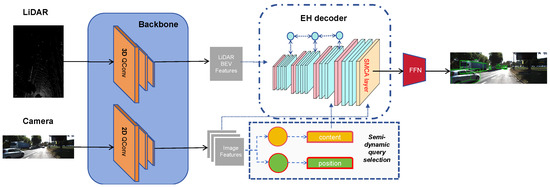
Figure 2.
Overall frame of Fast Transfusion. For semi-dynamic query selection, the yellow means static part and the green means dynamic part. To enhance the robustness of the fusion, the method re-fuses the entirety of the image features with the decoded vectors through the Spatially Modulated Cross Attention (SMCA) module, achieving superior detection performance.
3.1. LiDAR–Camera Fusion
While point-level fusion techniques [14] have demonstrated notable advancements, their effectiveness is significantly constrained by the inherent sparsity of LiDAR points. The scarcity of points per object curtails the ability to harness the comprehensive semantic depth of high-resolution imagery, as each LiDAR point corresponds to a limited set of image features. To circumvent this limitation, our approach eschews the direct correlation of LiDAR points with image pixels. Instead, this paper preserves the entirety of image features within a memory bank, employing a cross-attention mechanism within the transformer decoder as Figure 2. This facilitates a sparse-to-dense, adaptable fusion of features, leveraging the rich contextual information available across modalities. We utilize the feature vectors extracted by (QConv) as the input for the fusion process. And we employ the EH Decoder and semi-dynamic query selection as substitutes for the conventional algorithms in the fusion process, addressing the issue of high computational costs.
3.2. QConv Network
This paper employs the feature vectors extracted by the QConv (Quick convolution) network as inputs for the fusion process. The initial step upon receiving LiDAR and camera data is to extract the pertinent features. Processing these extracted features as opposed to the raw data is more efficient and yields superior results. Our proposed QConv network, serving as the backbone of Fast Transfusion, excels at extracting features from both LiDAR and camera data, surpassing the performance of traditional convolutional neural networks.
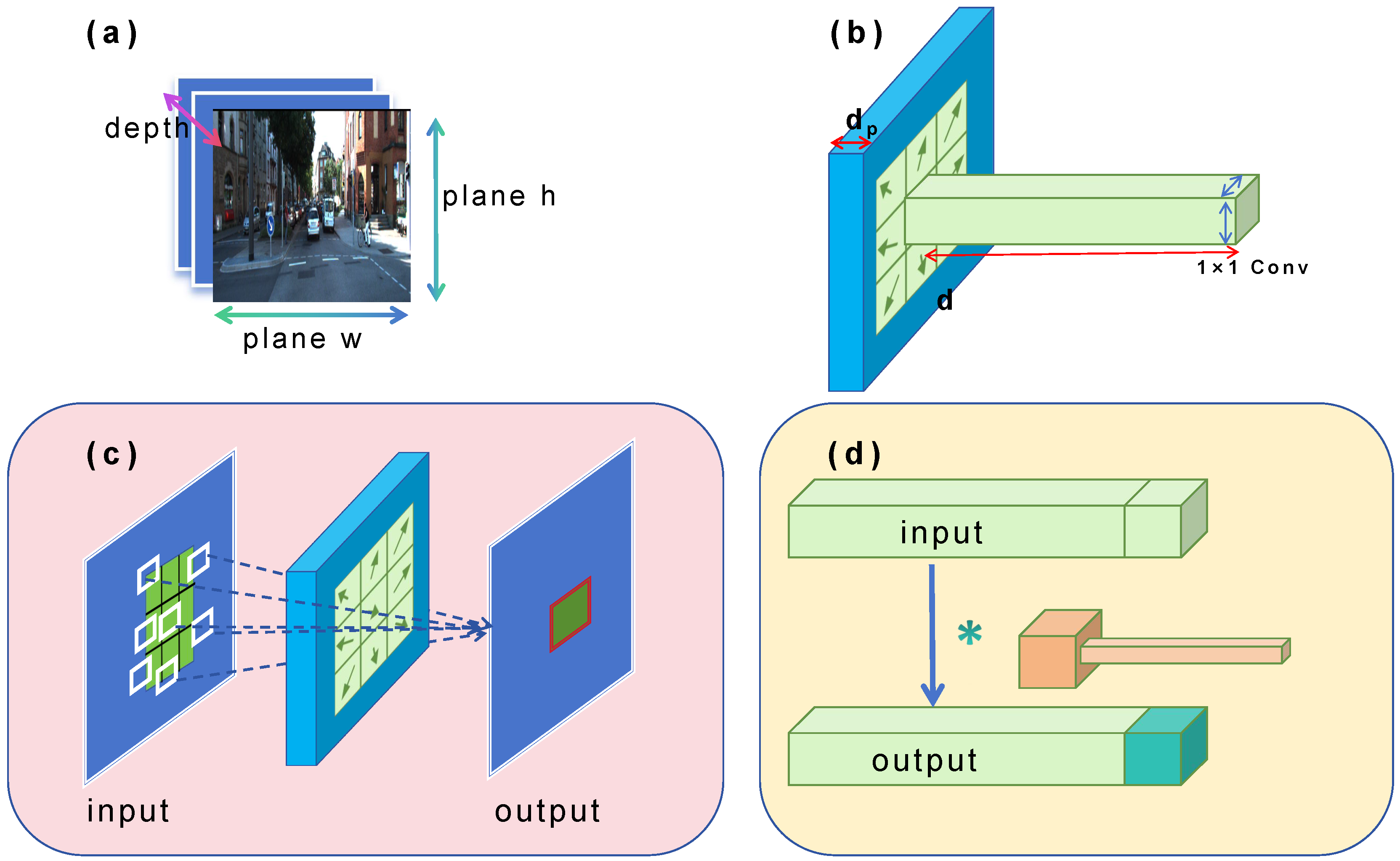
For image data as given in Figure 3a, we consider their three dimensions during feature extraction: the horizontal and vertical coordinates on their plane, and their depth, i.e., the number of channels. This paper optimizes the extraction of features from both the plane and depth of the data separately. The overview of the QConv structure is shown in Figure 3b. Deformable convolution is used in one channel and pointwise convolution in the remaining channels. The deformable convolutional operation optimizes the extraction of planar features as Figure 3c. Convolution operations are no longer limited to regular squares, and each position can be offset, while the partial convolutional operation is designed to optimize the extraction of depth features as shown in Figure 3d. The dark parts are convoluted, while the light parts remain the same. In this way, only a portion of the data is convoluted, which saves a lot of computing resources. Given that the plane and depth are orthogonal in geometric space, the operations performed on them do not interfere with each other. This allows us to fuse the Quick convolutional operations in parallel, achieving comprehensive optimization of feature extraction. The specific steps are as Algorithm 1.
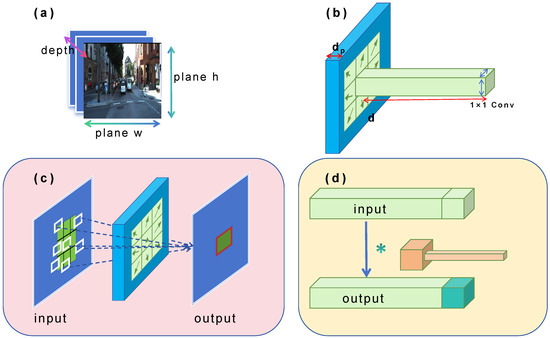
Figure 3.
Workflow of QConv. (a) The input is 3D image data, (b) overview of QConv structure, (c) deformable convolution for the extraction of planar features, (d) partial convolution for the extraction of depth features.
For the extraction of depth features, this paper uses the partial convolutional operation to speed up the process by leveraging the feature maps’ redundancy. The feature maps exhibit considerable redundancy across different channels, a phenomenon widely acknowledged but underutilized in existing literature. To address this efficiently, we introduce a streamlined partial convolution approach designed to simultaneously reduce computational redundancy and minimize memory access. As Figure 3 shows, our method employs a standard convolutional operation on a subset of the input channels to extract spatial features, while leaving the rest untouched. For efficient memory access, either the first or the last consecutive channels are utilized as representatives for the entire feature map computation.
| Algorithm 1 Quick convolution (QConv). |
|
Without loss of generality, we maintain consistency by ensuring that the input and output feature maps contain an equal number of channels d and the plane size of the input and output is the same. For an input , our QConv applies d filters to compute the output . When we calculate only a portion of the channels, that is, , the FLOPs are only
Therefore, with a typical partial ratio , the FLOPs of a partial convolution are only . Note that the method keeps the remaining channels untouched instead of removing them from the feature maps. It is because they are useful for a subsequent pointwise convolution layer, which allows the feature information to flow through all channels. Our architecture integrates a partial convolution layer with a pointwise convolution layer, synergistically enhancing feature extraction efficiency. Their effective receptive field together on the input feature maps looks like a T-shaped Conv, which focuses more on the center position compared to a regular Conv uniformly processing a patch. Despite the reduction in computations, its performance is nearly equivalent to that of a regular convolution because the center position turns out to be the salient position most frequently among the filters. In other words, the center position weighs more than its surrounding neighbors.
Finally, we will delineate how QConv accelerates inference speed during the extraction of depth features. The FLOPs of a QConv are only while the FLOPs of a regular Conv are . Under normal circumstances, is greater than . For example, when and , we take as 1 as usual. Theoretically, the FLOPs of QConv is of the FLOPs of the regular Conv. It means that our QConv is capable of achieving a performance speed that is multiple times faster than that of regular convolution.
For the extraction of planar features, the method employs the deformable convolutional operation to optimize our convolution and pooling processes. The prior implementation of the partial convolutional operation ensures our inference speed, while this adjustment guarantees the precision of our recognition and detection tasks. Given the variance in object scales or deformations at different locations, an adaptive approach to determining scales or receptive field sizes is essential for achieving accurate visual recognition coupled with precise localization. What is more, both modules exhibit lightweight characteristics, introducing a minimal number of parameters and computational overhead for offset learning. They can seamlessly substitute their conventional counterparts in deep CNNs and are amenable to end-to-end training using standard back propagation techniques.
Subsequently, we will explicate the mechanism by which QConv facilitates the free-form deformation of the sampling grid during the extraction of planar features. The regular grid R is augmented with offsets for QConv, while the regular Conv sample using a regular grid R over the input feature map I. As depicted in Figure 3, offsets are derived through the application of a convolutional layer on the identical input feature map. The convolution kernel maintains parity in spatial resolution and dilation with the origin convolutional layer. The resultant offset fields match the spatial resolution of the input feature map. Throughout the training phase, the convolutional kernels tasked with output feature generation and the offsets are learned concurrently. The learning process for the offsets involves the back propagation of gradients via the bilinear operations as follows:
where k is the convolution kernel size and f is top-left corner pixel.The principle of deformable pooling parallels that of convolution, entailing a positional displacement, and thus, is not reiterated further for brevity.
Next, we will integrate these two components into a unified framework. As the partial operation and the deformable operation occupy orthogonal geometric spaces without interference, their integration into QConv merely requires the application of a simple superposition technique. Specifically, in contrast to a regular convolution, our QConv engages only the partial channels of the feature map for deformable convolution. One might question whether this amalgamation of techniques ensures that the computational cost of QConv remains below that of regular convolution. The answer is affirmative. Although the deformable operation slightly increases the computational demand, it remains lightweight, involving only additional additive operations. For instance, with a convolution kernel size of , besides the original 9 multiplications and 9 additions, there are only 9 extra additions. Notably, the computational demand for multiplications significantly surpasses that of additions. Thus, the theoretical FLOPS of QConv are indicated by b, a value close to 1, representing the manageable computational burden introduced by the deformable operation. In total, the FLOPs of QConv are as follows:
Furthermore, not only theoretically but also through experimental validation presented later, the QConv network demonstrates superior performance compared to other models’ backbones.
3.3. EH Decoder
Although the Transformer decoder has demonstrated commendable performance in the domain of object detection, the substantial computational demands of the decoder curtail their practical deployment and hinder the full realization of their advantages, such as the elimination of post-processing steps like non-maximum suppression. Specifically, the incorporation of multiscale features, while beneficial for hastening training convergence and enhancing performance, concurrently augments the sequence length fed into the decoder. Because the increase in accuracy is huge, we cannot just sacrifice it for the sake of inference speed. In the following experiment sections, we also verify the necessity of this mechanism. Consequently, the multiscale feature fusion of the transformer decoder emerges as a computational bottleneck within the model due to its significant computational requirements.
In response, this paper introduce the Enhanced Hybrid (EH) decoder as a substitute for the traditional transformer decoder. This novel approach segregates the interactions within the same scale from the fusion across different scales of multiscale features, thereby enabling the efficient processing of diverse scale features. Upon analyzing the computational redundancies inherent in the multiscale transformer decoder, it becomes evident that the concurrent handling of intra-scale and cross-scale features is computationally onerous. Given that high-level features, rich in semantic content, are derived from lower-level features, engaging in feature interaction across concatenated multiscale features proves to be redundant. Thus, by disentangling the multiscale feature interaction into distinct phases of intra-scale interaction and cross-scale fusion, we significantly diminish the computational overhead while enhancing the decoder’s efficacy.
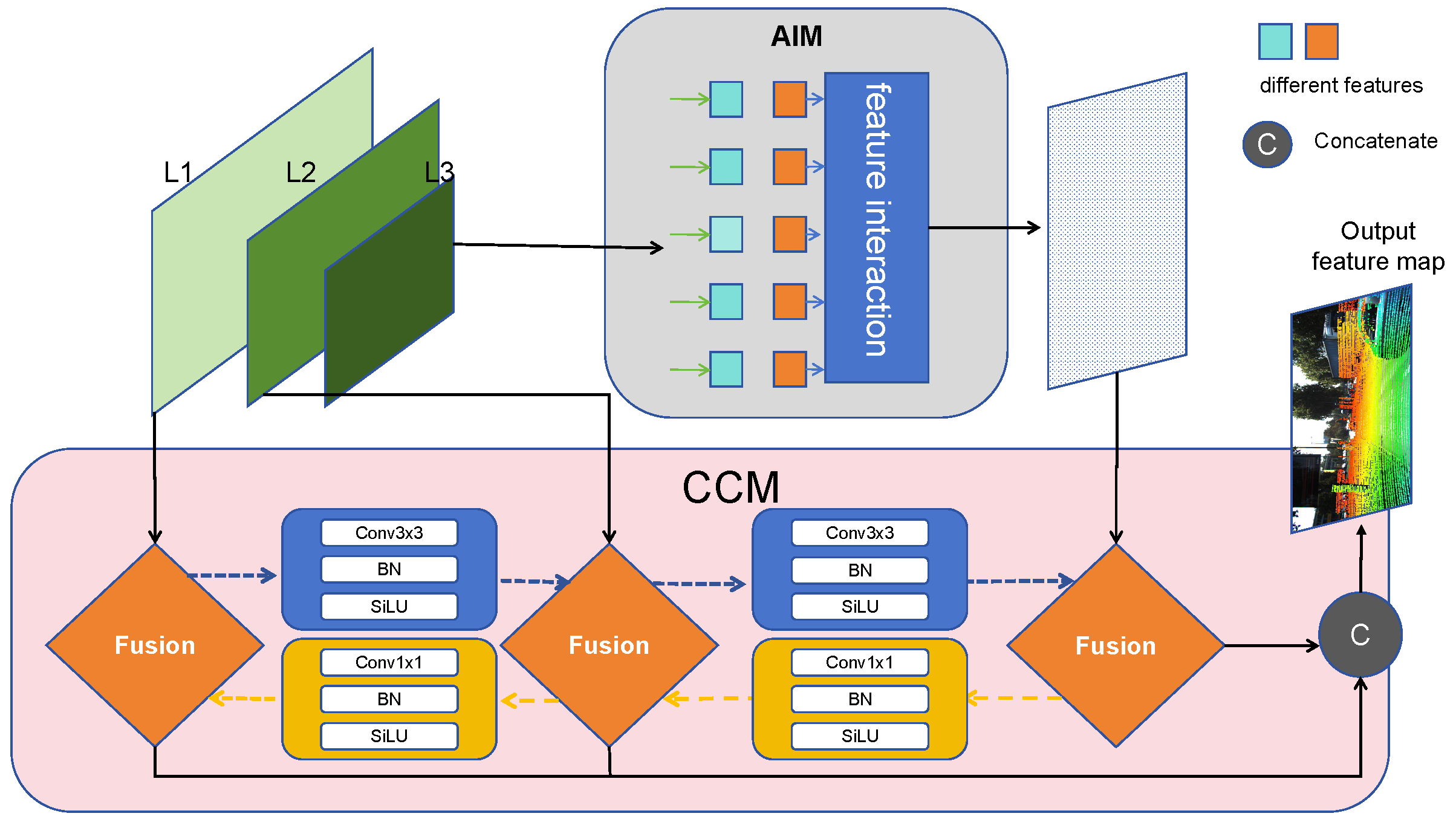
This paper propose a reevaluation of the decoder’s architecture. As depicted in Figure 4, the redesigned decoder is composed of two key modules: the Attention-based Intra-scale feature Interaction Module (AIM) and the CNN-based Cross-scale Feature Fusion Module (CCM). The AIM, refining upon the previous decoder’s approach, solely facilitates intra-scale interaction within last three layers of QConv. This method posits that applying self-attention to high-level features, imbued with dense semantic information, enables the capture of relationships among conceptual entities within images, thereby aiding subsequent modules in object detection and recognition. Conversely, intra-scale interactions among lower-level features are deemed unnecessary due to their semantic paucity and the potential for overlap and confusion with high-level feature interactions. The CCM, also an advancement of the previous decoder, incorporates multiple fusion blocks, consisting of convolutional layers, into the fusion pathway. The specific fusion steps are as shown in Algorithm 2. The primary function of these fusion blocks is to amalgamate adjacent features into a cohesive new feature, thereby streamlining the feature processing landscape.
| Algorithm 2 Fusion algorithm. |
|
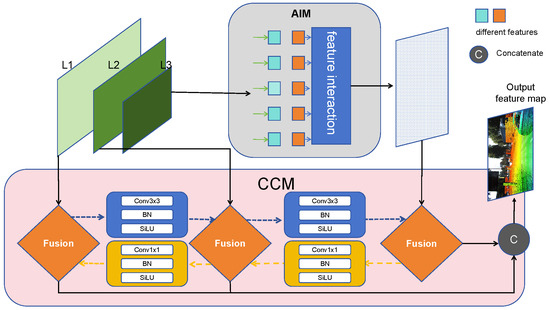
Figure 4.
Overview of EH decoder. The method leverage features of the last three layers of the QConv as the input to the decoder. The EH decoder transforms multiscale features into a sequence of image features through AIM and CCM.
3.4. Semi-Dynamic Query Selection
The concept of Object Query is a pivotal element within the Transformer framework for object detection, representing a vector that denotes the predicted bounding boxes for detected targets. These vectors encapsulate a fusion of content and positional information, where the content information serves to distinguish between different targets, and the positional information describes the location of the targets within the image. The design of Object Query stands as a significant contribution of the Transformer, addressing the issue present in traditional object detection methods that necessitate the pre-definition of anchor boxes. In conventional object detection approaches, the size and position of anchor boxes are pre-specified, potentially resulting in the inadequate coverage of certain targets. By employing Object Query vectors in lieu of anchor boxes, the Transformer facilitates object detection without relying on pre-defined anchor boxes, thereby better accommodating targets of varying sizes and shapes.
Given that Object Query comprises both content and positional information for detected targets, its initialization, or query selection, holds paramount importance. Currently, there are two primary methods for query selection: static query selection, learned from the dataset and independent of input images, remains fixed during inference, thus qualifying as static. However, as static methods do not fully leverage the information from input images, dynamic query selection has been proposed. This approach utilizes dense features extracted from input images to predict categories and bounding boxes, thereby initializing the content and position within the Object Query. Nevertheless, dynamic query selection still possesses shortcomings: the dynamically obtained content query may not be optimal for detection, as these features are unrefined and may harbor ambiguities. For instance, in the case of the “person” category, the selected feature may only encompass a portion of the person or objects surrounding the person, rendering it less precise compared to the static method. Conversely, the position query tends to be more accurate. In light of these considerations, this paper advocates for semi-dynamic query selection, wherein the static part is employed for content query selection, while the dynamic part is utilized for position query selection. In this way, we can make full use of the advantages of both, yielding improved detection performance.
3.5. Scaled Fast Transfusion
To provide a scalable version of Fast Transfusion, this paper simultaneously scales the QConv and the Enhanced Hybrid (EH) decoder using a depth multiplier and a width multiplier. This adjustment results in two variants of Fast Transfusion, differentiated by their parameter counts and frames per second. For QConv, the design of the dynamic network structures enables the adaptation of the network’s depth during both training and inference processes, according to the characteristics of the input data or the requirements of the task at hand. This approach typically employs conditional logic or learning strategies to dynamically determine the engagement of each layer or module. Additionally, network pruning techniques can be leveraged to reduce the complexity and computational demands of the model while maintaining or enhancing its performance.
For the EH decoder, we modulate the depth and width multipliers by altering the number of RepBlocks in the Cross-scale Feature Fusion Module (CCM) and the embedding dimension of the decoder, respectively. Variable-structure decoders allow for the dynamic modification of the decoder’s architecture, enabling the adjustment of the number of parameters or modules in response to the needs of diverse tasks or data attributes. This methodology involves the dynamic addition or removal of neurons, layers, or modules, which is achieved by constraining the number of parameters or the dimension of the encoded space. Such constraints enable the decoder to adaptively adjust within different data distributions or feature spaces. By introducing regularization or sparsity constraints, the decoder is incentivized to exhibit robust performance across various representations of input data, while maintaining model simplicity and generalization capabilities. It is noteworthy that our scaled versions of Fast Transfusion preserve a uniform decoder architecture, which aids in the knowledge distillation from high-precision, large-scale DETR models to lighter detectors. This aspect presents a promising avenue for future exploration.
4. Results and Experiments
4.1. Main Results
The KITTI 3D object detection dataset [35] consists of 7481 and 7518 LiDAR and image frames for training and testing, respectively. Following contemporary methodologies [5,28], we partitioned the training dataset into a training split of 3712 frames and a validation split of 3769 frames. We employed the standard evaluation metric of 3D Average Precision (AP) across 40 recall thresholds (R40), with Intersection over Union (IoU) thresholds set at 0.7, 0.5, and 0.5 for cars, pedestrians, and cyclists, respectively.
We evaluated the performance of our Fast Transfusion model against the original Transfusion model and other prevalent models on the KITTI dataset. Our experimental results confirm that our model not only rectifies the inferential speed limitations of the original model but also enhances detection accuracy. Additionally, we conducted ablation studies to individually assess the contributions of three specific technologies—QConv, the Enhanced Hybrid (EH) decoder, and semi-dynamic query selection. Experiments altering the number of layers in the decoder to modify the model size were also performed. The training and testing of the network were conducted on an NVIDIA GeForce GTX 3080 Ti GPU (NVIDIA, Santa Clara, CA, USA) with 12 GB of memory.
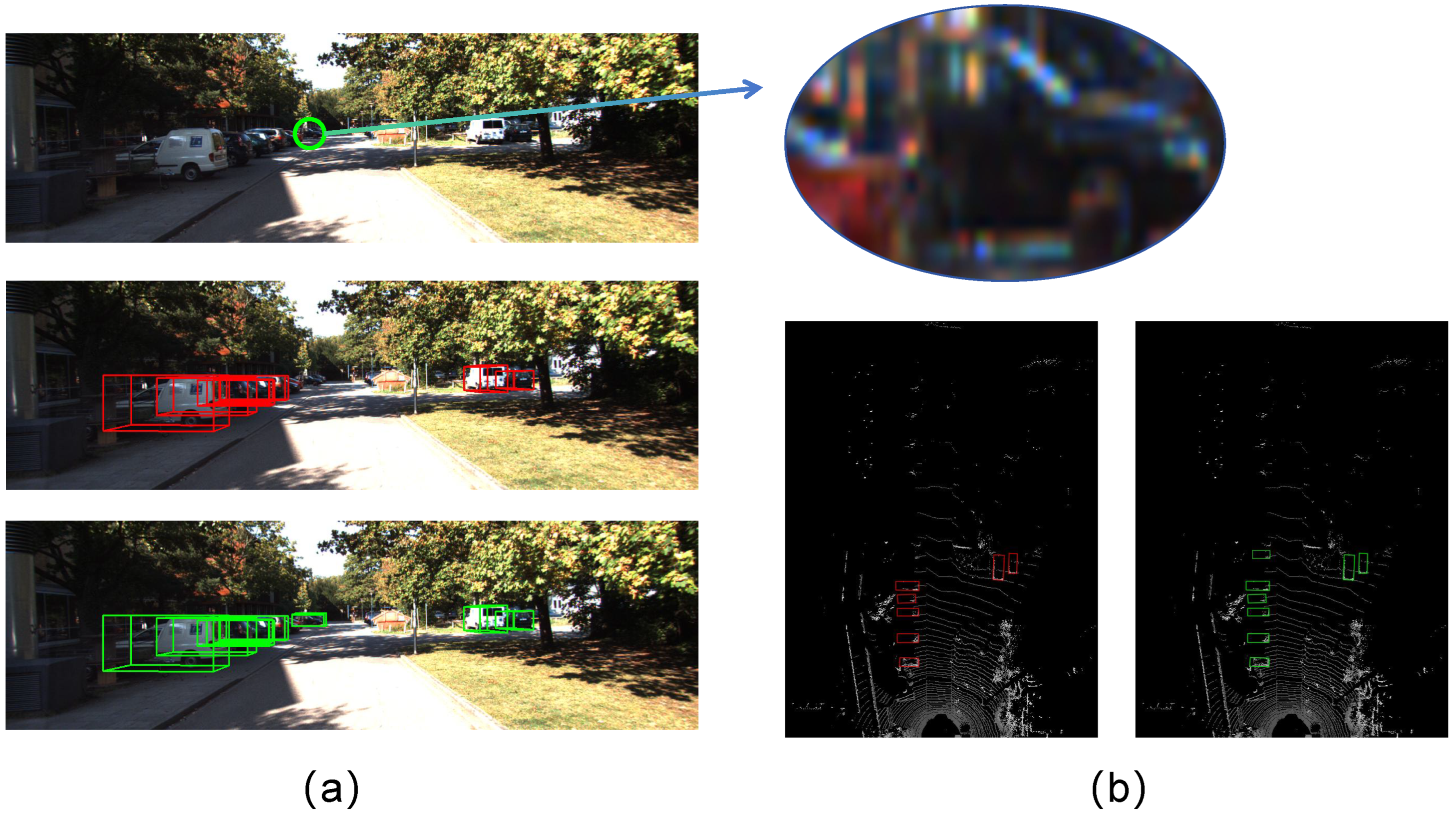
Figure 5 illustrates the input and final detection results for the three target types. (1), (2) and (3) represents three real-life scenes on the street, and they encompass all possible entities on the street, i.e., motorized vehicles, non-motorized vehicles, and pedestrians. Figure 5a,b are the display of these scenes under the camera and LiDAR sensors, and Figure 5c is their detection result. With the above results, it can be seen that our model has excellent detection capabilities for different scenarios and classes.

Figure 5.
Input and test result diagram. (a–c) represent camera input, and LiDAR BEV input and output. (1–3) represent car, pedestrian, and cyclist, the three object classes.
The detection outcomes for small and occluded objects using the baseline and Fast Transfusion methods are presented in Figure 6. We focus on the car class for this demonstration, as issues of small object detection and occlusion are particularly prevalent and pronounced within this category. As depicted in Figure 6, the farthest black car not only occupies few pixels but also has occlusion, which is a great challenge for the object detection task. However, our EH Decoder and query selection can effectively capture small target features and improve the recognition of occluded objects. It can be seen that our model demonstrates superior performance in handling these challenges.
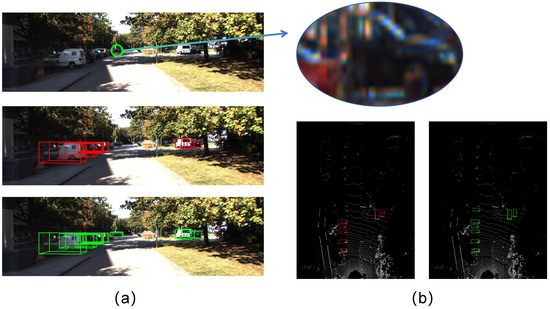
Figure 6.
Comparison of small object detection results. Red is the baseline detection result. Green is our model Fast Transfusion detection result. (a) represents results in real-world scenarios, and (b) represents the results in LiDAR BEV figures.
In the 3D detection category on the KITTI validation set (presented in Table 1), our Fast Transfusion significantly outperformed the baseline detector, Transfusion, and other multimodal detectors, primarily due to the efficient design of our QConv and EH decoder. As can be seen from the table, our model has a shorter inference time than other multimodal models, and the inference time is reduced by 36 ms compared with our baseline Transfusion. While monomodal detectors demonstrate quicker inference times, they fall short in precision compared to our model, positioning our Fast Transfusion as the current state-of-the-art model that aptly balances inferential speed and accuracy. Relative to Transfusion [1], our Fast Transfusion achieved improvements of 1.81%, 0.52%, and 0.75% in 3D AP (R40) in the moderate car category. And for the other two types of pedestrians and cyclists, our model AP has also been improved to varying degrees. These performance gains are largely attributed to the innovations in QConv and semi-dynamic query selection, which effectively address issues stemming from complex data distributions and the initialization of object queries.

Table 1.
The Car, Ped (pedestrian) and Cyc (cyclist) 3D detection results on the KITTI validation set, where the best fully supervised methods are in bold.
4.2. Ablation Study
As shown in Table 2, Table 3 and Table 4, we conducted ablation studies on the KITTI validation dataset to assess the efficacy of each component of the proposed Fast Transfusion method, specifically QConv, the Enhanced Hybrid (EH) decoder, and semi-dynamic query selection. To evaluate the impact of QConv on detection time and accuracy, we compared the original Transfusion model with a version where the backbone was substituted with a QConv network (Transfusion-PD). According to Table 2, the QConv-equipped model outperformed the standard convolutional backbone model in terms of both accuracy and inference time, showing improvements of 3.43%, 4.63%, and 5.58% in 3D AP for the moderate car category, respectively. The inference time was also reduced by 1.2 ms, 1.6 ms, and 1.8 ms. Additionally, we tested the generalizability of our approach across other categories such as pedestrians and cyclists, confirming that QConv effectively addresses complex data distributions while conserving computational resources.

Table 2.
Ablation results on the KITTI validation set by using different backbones based on Transfusion (our baseline).

Table 3.
Ablation results on the KITTI validation set by using different decoders based on Transfusion (our baseline).

Table 4.
Ablation results on the KITTI validation set by using different query selection based on Transfusion (our baseline). Dynamic is baseline and Semi-dyn (semi-dynamic) is our method.
Regarding the effectiveness of the EH decoder, we compared it against a standard decoder utilizing conventional multiscale feature fusion as Table 3. In this table, naive means the naive decoder, which is a decoder without multiscale feature fusion. Standard means standard decoder as our baseline, which is now a commonly used decoder with multiscale feature fusion.
It is shown in Table 3 that the models incorporating the EH decoder demonstrate a 0.84% increase in AP and a reduction of 13 ms in inference time for car class, validating our approach of decoupling the multiscale feature fusion mechanism into AIM and CCM. We also included results from a baseline model without multiscale feature fusion (naive decoder), which showed a significant decrease in accuracy, thereby underscoring the necessity of the multiscale feature fusion mechanism for maintaining performance without compromising significantly on inference speed.
We also compared three query selection strategies, static query selection, dynamic query selection, and our proposed semi-dynamic query selection, to validate the efficacy of our semi-dynamic approach in enhancing performance. According to Table 4, our method showed improvements of 0.34% and 3.22% in Average Precision (AP) over the two prior methods for car class, respectively.
4.3. Experiments on Scaled Fast Transfusion
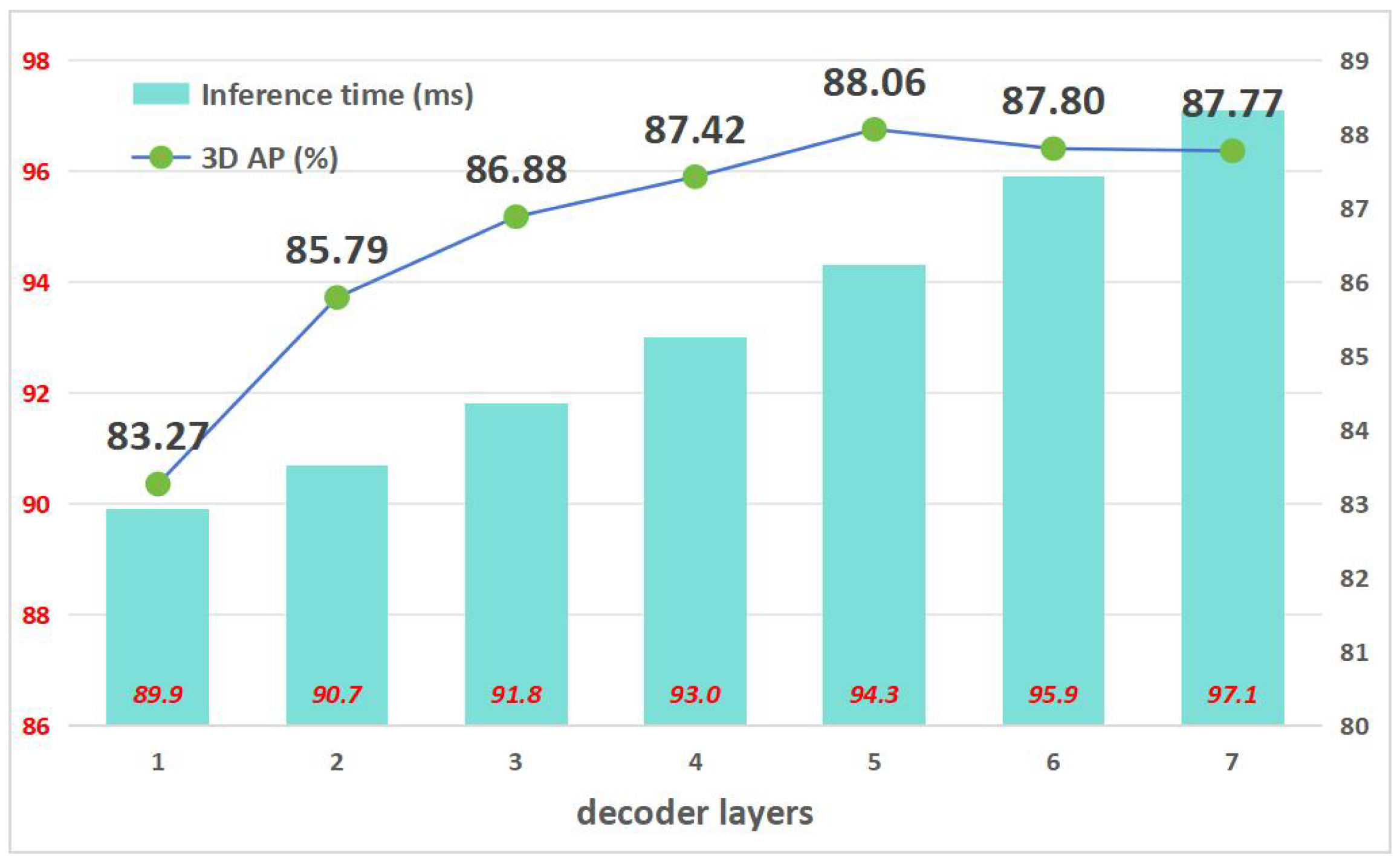
Figure 7 illustrates the accuracy and inference speed associated with each decoder layer of the Fast Transfusion model equipped with varying numbers of decoder layers. Optimal accuracy is attained with a five-layer decoder, achieving a 3D Average Precision (AP) of 88.06%. Our analysis further evaluates the impact of each decoder layer on inference speed, establishing that each layer contributes approximately 1 ms to the total processing time. Additionally, we observe a diminishing discrepancy in accuracy between successive layers as the layer count increases. Specifically, employing a six-layer decoder as opposed to a five-layer decoder results in a marginal loss of 0.26% in AP (from 88.06% to 87.8% AP), while concurrently reducing the latency by 1.6 ms (from 94.3 ms to 95.9 ms).
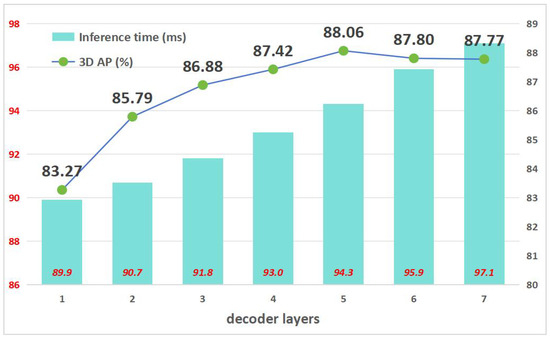
Figure 7.
Results of the ablation study on the number of EH decoder layers. Our model with a five-layer decoder achieved the best performance.
This finding underscores the capability of the Transfusion model to accommodate flexible adjustments in inference speed by selecting different numbers of decoder layers without necessitating retraining for inference purposes. Such flexibility significantly enhances the practical utility of the 3D real-time detector, allowing for tailored performance optimization based on specific operational requirements.
5. Discussion
This paper proposed Fast Transfusion, a novel approach tailored for multimodal 3D object detection. Addressing the high computational demands of the original Transfusion model, the paper proposed three key technological advancements: QConv, EH Decoder and semi-dynamic query selection. The proposed model was investigated and compared with current advanced methods on the KITTI dataset, and the effectiveness of the proposed modules was verified through ablation experiments.
In the 3D detection category on the KITTI dataset, our model has a shorter inference time than other multimodal models, and the inference time is reduced by 36 ms compared with our baseline Transfusion. And our model achieves improvements of 1.81%, 0.52%, and 0.75% in 3D AP (R40) in the moderate car category relative to the baseline. As evidenced by the results, our model outperforms the state-of-the-art (SOTA) in both inference speed and detection accuracy. In terms of inference speed, our designed feature extraction network, QConv, effectively captures essential information while discarding a significant amount of redundant computations. Additionally, our EH decoder leverages a coupling mechanism to substantially reduce the amount of feature interaction computation. In terms of detection accuracy, these performance gains are largely attributed to the innovations in QConv and semi-dynamic query selection, which effectively address issues stemming from complex data distributions and the initialization of object queries.
The detection method employed in this paper falls under the category of multisensor fusion for three-dimensional object detection, which captures a more comprehensive array of feature information, thereby offering superior detection performance compared to single-sensor approaches. The enhanced feature extraction network and decoder significantly reduce the computational load, allowing for faster inference speeds compared to other multimodal detection methods. Additionally, the use of variable convolution and attention mechanisms enables the detection of finer details, providing exceptional performance in detecting distant or small objects. Thus, this method effectively facilitates the three-dimensional detection of small objects. Owing to hardware constraints, our model has not yet been implemented on edge computing devices. Additional validation of the detection accuracy and performance of our method is necessary in real-world scenarios.
6. Conclusions
Three-dimensional object detection functions as a critical upstream subsystem within autonomous driving systems and is integral to the advancement of smart cities. Accurate 3D detection results are essential, allowing vehicles to monitor dynamic objects in their vicinity in real-time, identify potential collision hazards, and enhance safety performance. Consequently, the precision and environmental robustness of 3D object detection algorithms are paramount. In smart cities, autonomous vehicles can engage in intelligent transportation collaboration by sharing data with urban traffic management systems. Utilizing 3D object detection data, vehicles can more effectively communicate with traffic signal systems, road condition monitors, and other infrastructures to collectively optimize traffic flow and reduce congestion.
In this paper, we introduce Fast Transfusion, an advanced model tailored for multimodal 3D object detection. We have designed three key modules—QConv, EH decoder, and semi-dynamic query selection—to enhance the performance of the traditional LiDAR–camera detection model based on the Transformer architecture. These modules address the computational redundancies in convolution operations, complexities in multiscale feature fusion in the Transformer decoder, and limitations of dynamic query selection. Consequently, our model outperforms our baseline on the KITTI dataset. Specifically, the average inference time is reduced by 36 ms, and the detection accuracy as measured by 3D Average Precision at the 40-meter range (3D AP [R40]) is enhanced by 1.81%. Moreover, we facilitate practical application adjustments by allowing modifications to the number of decoder layers to optimize model size. Extensive testing on the KITTI dataset confirms the superiority of our model, while ablation studies validate the effectiveness of the proposed components.
We will further concentrate on deep sensor fusion, investigating more profound strategies for data association and integration, such as methods based on Graph Neural Networks (GNNs), to better comprehend and amalgamate data from diverse sensors. Given the complexity of real-world environments faced by autonomous driving, the generalization capability of the model across various scenarios presents a significant challenge to us. Future research will explore how domain adaptation techniques can enhance the robustness and generalization ability of the model under different conditions.
Author Contributions
Methodology, H.L.; project administration, T.D.; software, H.L.; supervision, T.D.; validation, H.L.; writing—original draft, H.L.; writing—review and editing, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Hengsong Liu and Tongle Duan are employees of the 54th Research Institute of China Electronics Technology Group Corporation. The paper reflects the views of the scientists, and not the company.
Abbreviations
The following abbreviations are used in this manuscript:
| QConv | Quick Convolution |
| EH Decoder | Efficient and Hybrid Decoder |
| AR | Augmented Reality |
| RoI | Regions of Interest |
| BEV | Linear Bird’s Eye View |
| depth, height, width of feature maps | |
| convolution kernel size, top-left corner pixel, partial convolution depth |
References
- Bai, X.; Hu, Z.; Zhu, X.; Huang, Q.; Chen, Y.; Fu, H.; Tai, C.L. Transfusion: Robust lidar-camera fusion for 3d object detection with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1090–1099. [Google Scholar]
- Yang, Z.; Sun, Y.; Liu, S.; Jia, J. 3dssd: Point-based 3d single stage object detector. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11040–11048. [Google Scholar]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. Nuscenes: A multimodal dataset for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11621–11631. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 213–229. [Google Scholar]
- Deng, S.; Liang, Z.; Sun, L.; Jia, K. Vista: Boosting 3d object detection via dual cross-view spatial attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8448–8457. [Google Scholar]
- Shushpanov, I.; Suslov, K.; Ilyushin, P.; Sidorov, D.N. Towards the flexible distribution networks design using the reliability performance metric. Energies 2021, 14, 6193. [Google Scholar] [CrossRef]
- Chen, Q.; Sun, L.; Wang, Z.; Jia, K.; Yuille, A. Object as hotspots: An anchor-free 3d object detection approach via firing of hotspots. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 68–84. [Google Scholar]
- Liang, T.; Xie, H.; Yu, K.; Xia, Z.; Lin, Z.; Wang, Y.; Tang, T.; Wang, B.; Tang, Z. Bevfusion: A simple and robust lidar-camera fusion framework. Adv. Neural Inf. Process. Syst. 2022, 35, 10421–10434. [Google Scholar]
- Contributors, M. MMDetection3D: OpenMMLab Next-Generation Platform for General 3D Object Detection. San Francisco (CA): GitHub. 2020. Available online: https://github.com/open-mmlab/mmdetection (accessed on 16 May 2023).
- Everingham, M.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The pascal visual object classes (voc) challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Fan, L.; Xiong, X.; Wang, F.; Wang, N.; Zhang, Z. Rangedet: In defense of range view for lidar-based 3d object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2918–2927. [Google Scholar]
- Gao, P.; Zheng, M.; Wang, X.; Dai, J.; Li, H. Fast convergence of detr with spatially modulated co-attention. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 3621–3630. [Google Scholar]
- Huang, T.; Liu, Z.; Chen, X.; Bai, X. Epnet: Enhancing point features with image semantics for 3d object detection. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 35–52. [Google Scholar]
- Kim, A.; Ošep, A.; Leal-Taixé, L. Eagermot: 3d multi-object tracking via sensor fusion. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xian, China, 30 May–5 June 2021; pp. 11315–11321. [Google Scholar]
- Zhao, Y.; Luo, S.; Huang, X.; Wei, D. A Multi-Sensor 3D Detection Method for Small Objects. World Electr. Veh. J. 2024, 15, 210. [Google Scholar] [CrossRef]
- Xu, H.; Dong, X.; Wu, W.; Yu, B.; Zhu, H. A two-stage pillar feature-encoding network for pillar-based 3D object detection. World Electr. Veh. J. 2023, 14, 146. [Google Scholar] [CrossRef]
- Wang, L.; Song, Z.; Zhang, X.; Wang, C.; Zhang, G.; Zhu, L.; Li, J.; Liu, H. SAT-GCN: Self-attention graph convolutional network-based 3D object detection for autonomous driving. Knowl.-Based Syst. 2023, 259, 110080. [Google Scholar] [CrossRef]
- Ku, J.; Mozifian, M.; Lee, J.; Harakeh, A.; Waslander, S.L. Joint 3d proposal generation and object detection from view aggregation. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–8. [Google Scholar]
- Yang, Z.; Sun, Y.; Liu, S.; Shen, X.; Jia, J. Std: Sparse-to-dense 3d object detector for point cloud. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1951–1960. [Google Scholar]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Wu, H.; Wen, C.; Shi, S.; Li, X.; Wang, C. Virtual sparse convolution for multimodal 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 21653–21662. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Zhu, B.; Jiang, Z.; Zhou, X.; Li, Z.; Yu, G. Class-balanced grouping and sampling for point cloud 3d object detection. arXiv 2019, arXiv:1908.09492. [Google Scholar]
- Yang, B.; Liang, M.; Urtasun, R. Hdnet: Exploiting hd maps for 3d object detection. In Proceedings of the Conference on Robot Learning, Zurich, Switzerland, 29–31 October 2018; pp. 146–155. [Google Scholar]
- Cao, P.; Chen, H.; Zhang, Y.; Wang, G. Multi-view frustum pointnet for object detection in autonomous driving. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 3896–3899. [Google Scholar]
- Desheng, X.; Youchun, X.; Feng, L.; Shiju, P. Real-time detection of 3D objects based on multi-sensor information fusion. Automot. Eng. 2022, 44, 340. [Google Scholar]
- Wang, C.; Ma, C.; Zhu, M.; Yang, X. Pointaugmenting: Cross-modal augmentation for 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11794–11803. [Google Scholar]
- Guo, Y.; Hu, H. Multi-Layer Fusion 3D Object Detection via Lidar Point Cloud and Camera Image. Appl. Sci. 2024, 14, 1348. [Google Scholar] [CrossRef]
- Karim, T.; Mahayuddin, Z.R.; Hasan, M.K. Singular and Multimodal Techniques of 3D Object Detection: Constraints, Advancements and Research Direction. Appl. Sci. 2023, 13, 13267. [Google Scholar] [CrossRef]
- Wang, D.; Devin, C.; Cai, Q.Z.; Krähenbühl, P.; Darrell, T. Monocular plan view networks for autonomous driving. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 2876–2883. [Google Scholar]
- Wang, H.; Cong, Y.; Litany, O.; Gao, Y.; Guibas, L.J. 3dioumatch: Leveraging iou prediction for semi-supervised 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14615–14624. [Google Scholar]
- Wu, H.; Deng, J.; Wen, C.; Li, X.; Wang, C.; Li, J. CasA: A cascade attention network for 3-D object detection from LiDAR point clouds. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Wu, H.; Wen, C.; Li, W.; Li, X.; Yang, R.; Wang, C. Transformation-equivariant 3d object detection for autonomous driving. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 2795–2802. [Google Scholar]
- Wu, X.; Peng, L.; Yang, H.; Xie, L.; Huang, C.; Deng, C.; Liu, H.; Cai, D. Sparse fuse dense: Towards high quality 3d detection with depth completion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5418–5427. [Google Scholar]
- Chen, J.; Kao, S.h.; He, H.; Zhuo, W.; Wen, S.; Lee, C.H.; Chan, S.H.G. Run, Don’t walk: Chasing higher FLOPS for faster neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 12021–12031. [Google Scholar]
- Zhao, Y.; Lv, W.; Xu, S.; Wei, J.; Wang, G.; Dang, Q.; Liu, Y.; Chen, J. Detrs beat yolos on real-time object detection. arXiv 2023, arXiv:2304.08069. [Google Scholar]
- Brekke, Å.; Vatsendvik, F.; Lindseth, F. Multimodal 3d object detection from simulated pretraining. In Proceedings of the Symposium of the Norwegian AI Society, Trondheim, Norway, 27–28 May 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 102–113. [Google Scholar]
- Liu, Z.; Zhao, X.; Huang, T.; Hu, R.; Zhou, Y.; Bai, X. Tanet: Robust 3d object detection from point clouds with triple attention. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11677–11684. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Yin, T.; Zhou, X.; Krahenbuhl, P. Center-based 3d object detection and tracking. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11784–11793. [Google Scholar]
- Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai, J. Deformable detr: Deformable transformers for end-to-end object detection. arXiv 2020, arXiv:2010.04159. [Google Scholar]
- Zhu, X.; Ma, Y.; Wang, T.; Xu, Y.; Shi, J.; Lin, D. Ssn: Shape signature networks for multi-class object detection from point clouds. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 581–597. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Xu, H.; Liu, F.; Zhou, Q.; Hao, J.; Cao, Z.; Feng, Z.; Ma, L. Semi-supervised 3d object detection via adaptive pseudo-labeling. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 3183–3187. [Google Scholar]
- Xu, Q.; Zhong, Y.; Neumann, U. Behind the curtain: Learning occluded shapes for 3d object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2022; Volume 36, pp. 2893–2901. [Google Scholar]
- Yan, Y.; Mao, Y.; Li, B. Second: Sparsely embedded convolutional detection. Sensors 2018, 18, 3337. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Liu, Z.; Wu, X.; Wang, W.; Qian, W.; He, X.; Cai, D. Graph r-cnn: Towards accurate 3d object detection with semantic-decorated local graph. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 662–679. [Google Scholar]
- Yang, J.; Shi, S.; Wang, Z.; Li, H.; Qi, X. St3d: Self-training for unsupervised domain adaptation on 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 10368–10378. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).