Research on Unbalanced Electromagnetic Force Under Static Eccentricity of the Wheel Hub Motor Based on BP Neural Network
Abstract
:1. Introduction
- (1)
- The analytical model of the unbalanced electromagnetic force of a wheel hub motor is constructed, and its accuracy is verified by finite element modeling of the wheel hub motor. The factors affecting the output characteristics of unbalanced electromagnetic force are discussed, which provides a theoretical basis for the subsequent optimization of the BP neural network of electromagnetic force.
- (2)
- By using the BP neural network to optimize the existing analytical model of unbalanced electromagnetic force, the calculation efficiency of the model is greatly improved on the premise of ensuring the calculation accuracy, thus providing an unbalanced electromagnetic force model that is more suitable for the dynamic simulation of wheel hub direct-drive electric vehicles.
- (3)
- Considering that the unbalanced electromagnetic force is difficult to measure directly through the test, it couples with the vehicle dynamics model, and the correctness of the coupling model is verified by building a test bench, which lays a better foundation for the subsequent research on the vertical vibration effect of wheel hub direct-drive electric vehicles.
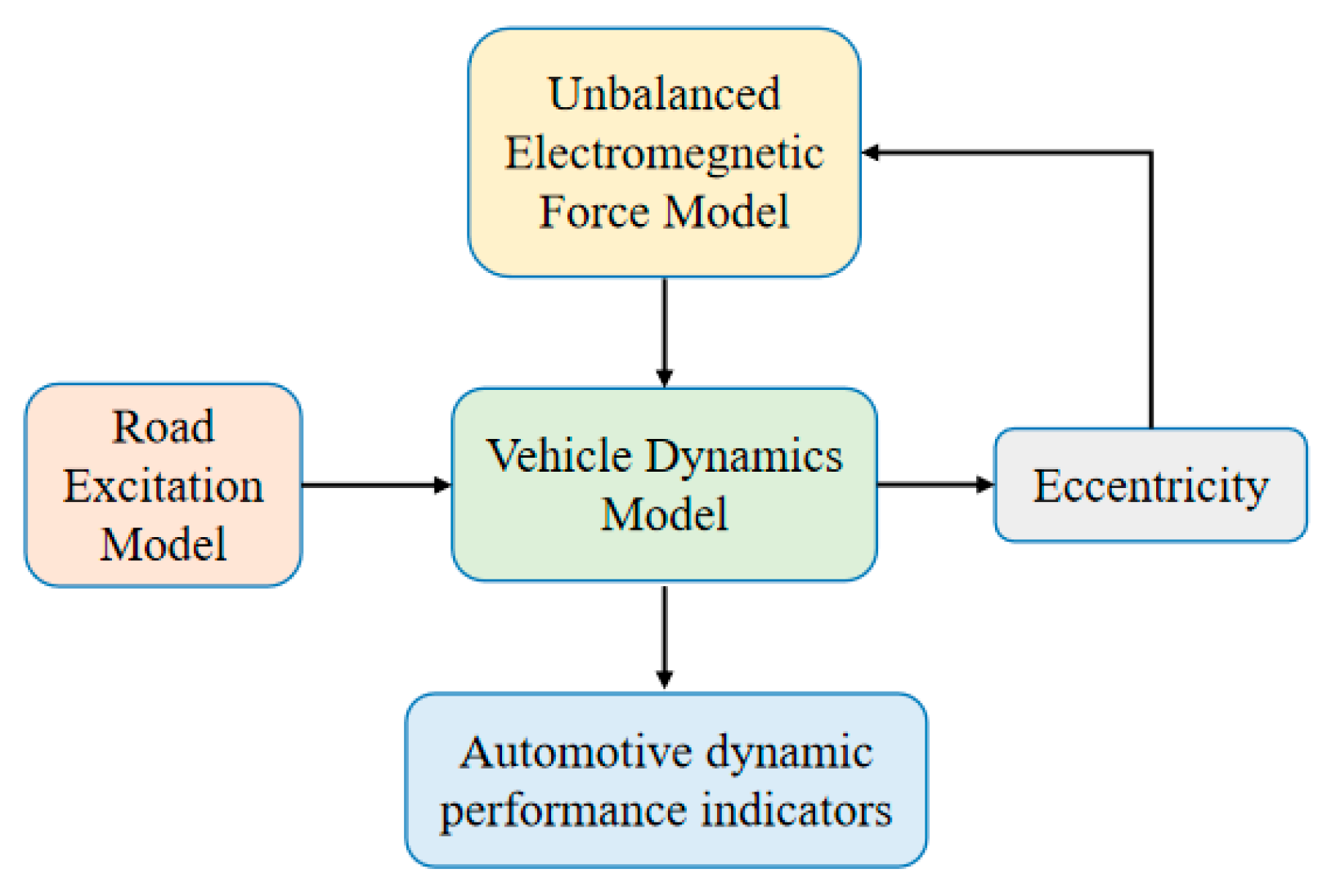
2. Unbalanced Electromagnetic Force Model of Wheel Hub Motor
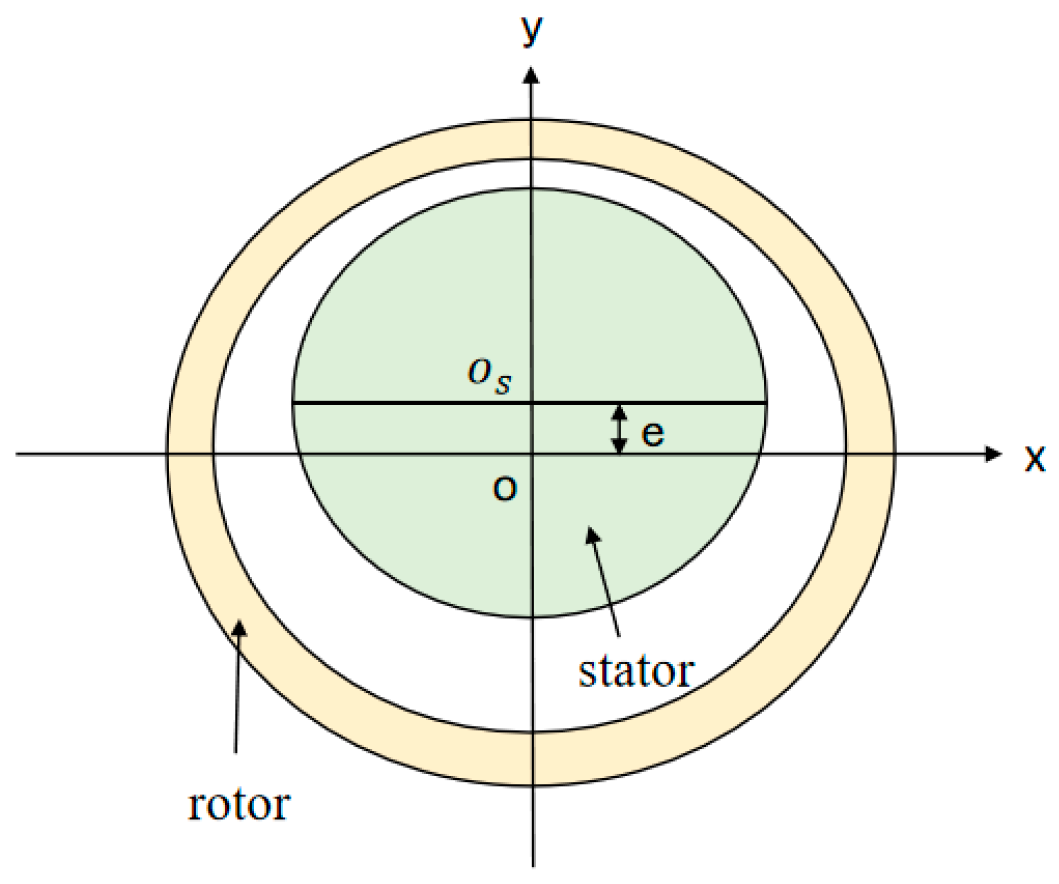
2.1. Wheel Hub Motor Model
2.2. Calculation of Air Gap Magnetic Field of Wheel Hub Motor Without Eccentricity
2.3. Calculation of Air Gap Magnetic Field and Unbalanced Electromagnetic Force of Wheel Hub Motor
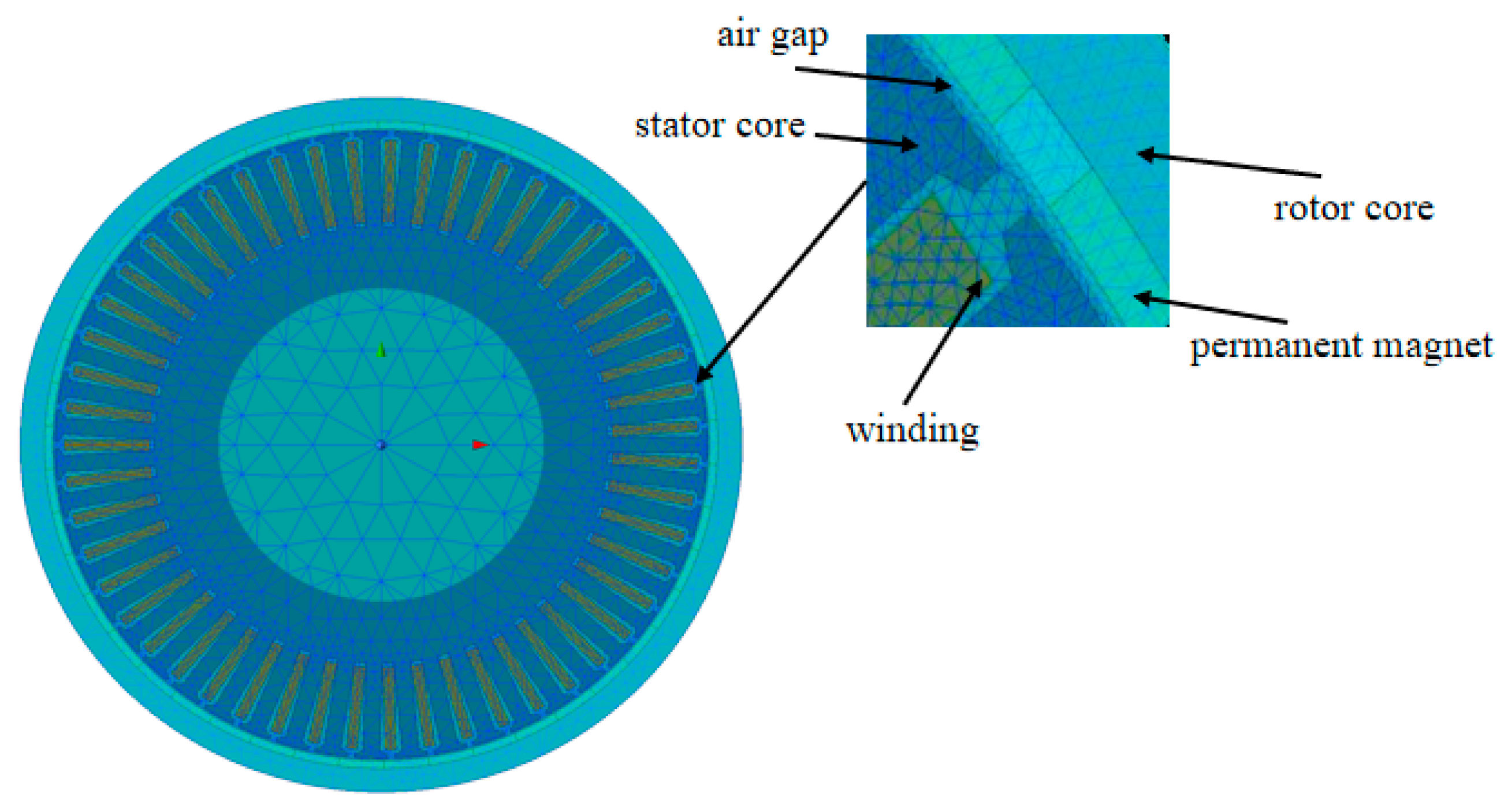
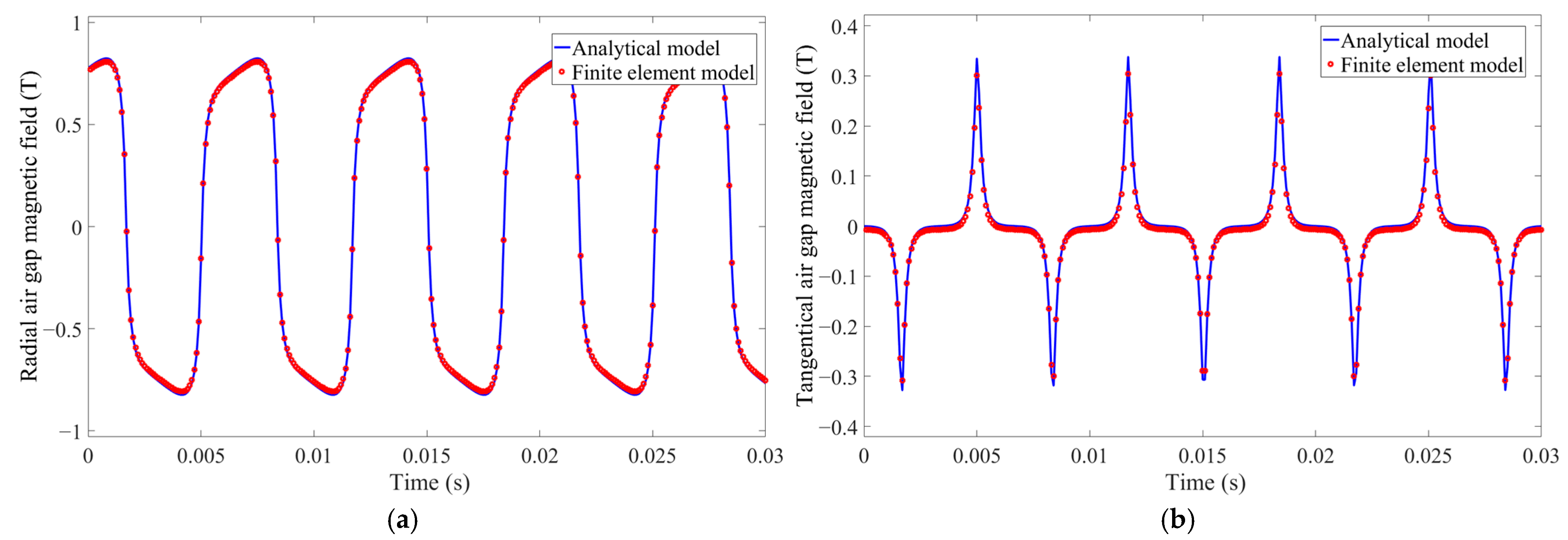
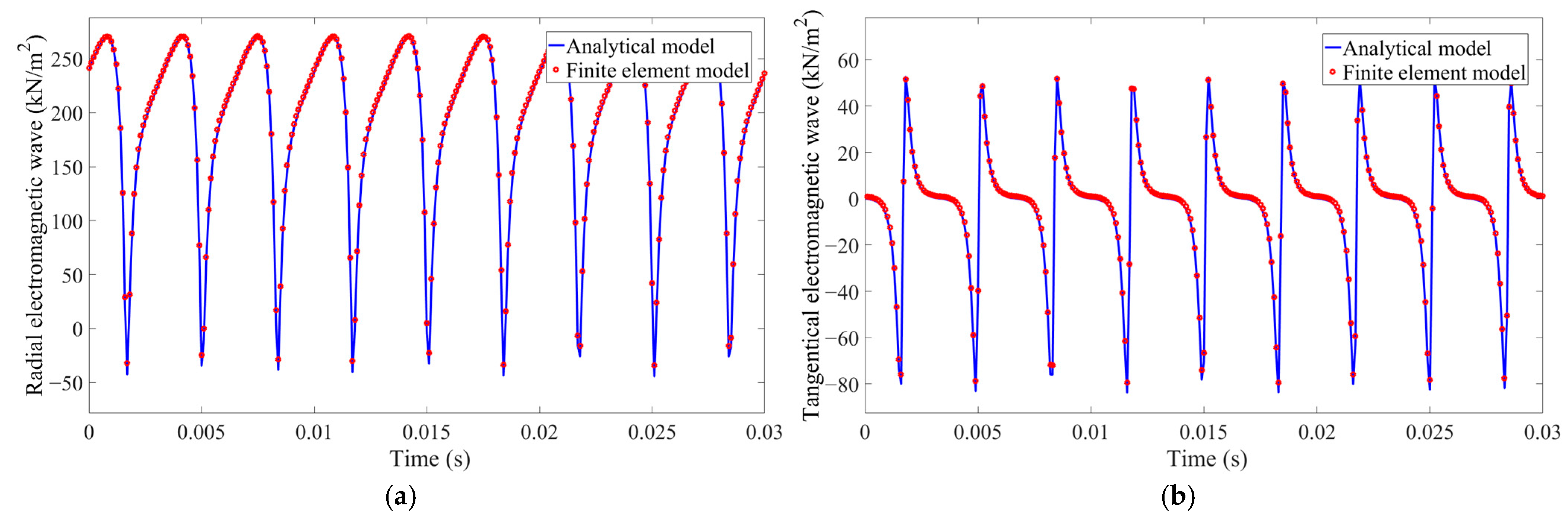
3. Finite Element Verification of Wheel Hub Motor Unbalanced Electromagnetic Force
4. Coupling Model of Unbalanced Electromagnetic Force and Vehicle Dynamics
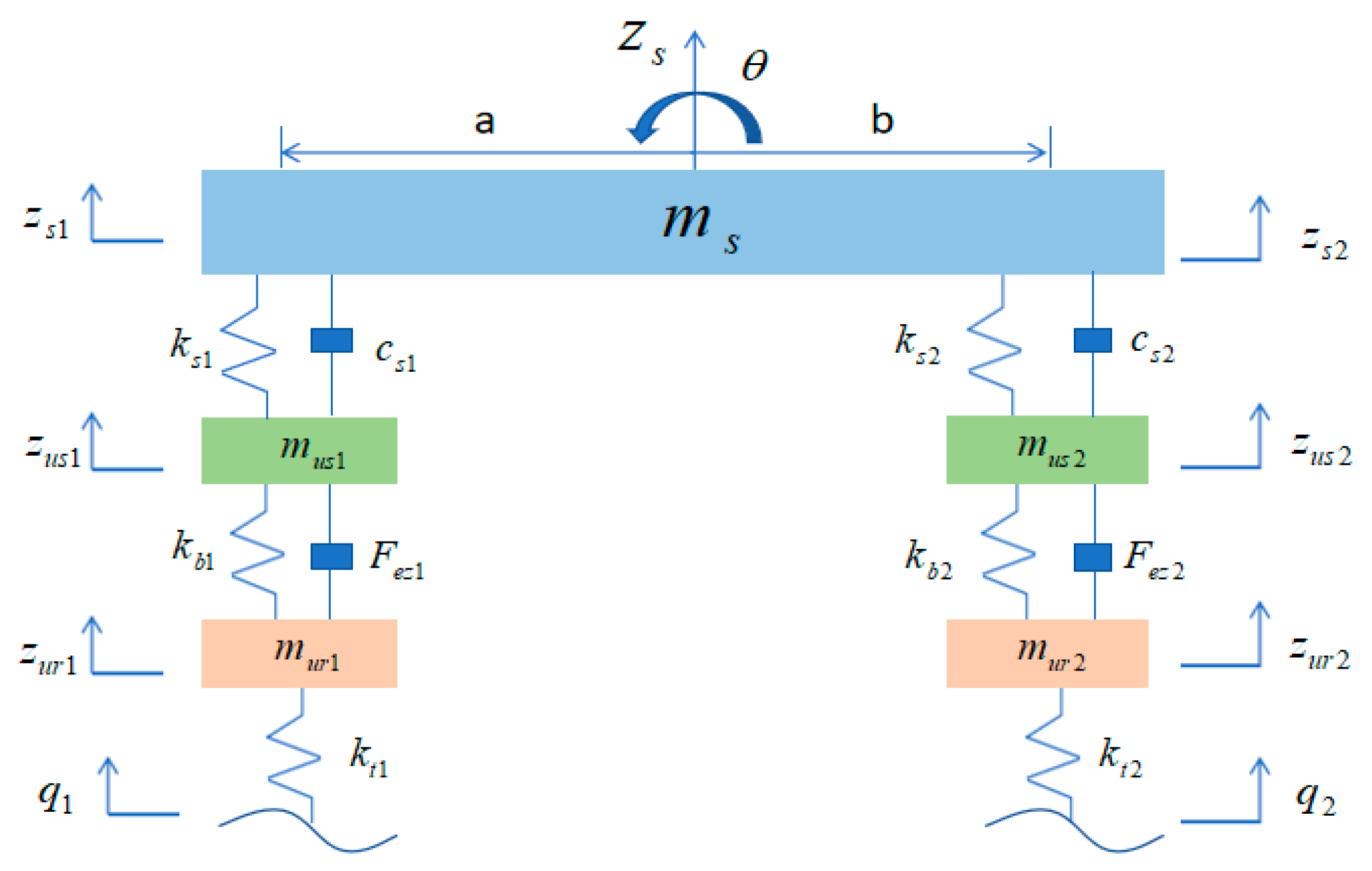
4.1. The Establishment of the Vertical Vehicle Dynamics Model
4.1.1. A 1/2 Vertical Vehicle Dynamics Model
4.1.2. Random Pavement Excitation Model
4.2. The Establishment of BP Neural Network
- (1)
- Parameter Initialization
- (2)
- Selection of Training Samples
- (3)
- Normalization of Data Processing
- (4)
- Selection of Evaluation Indicators
- (5)
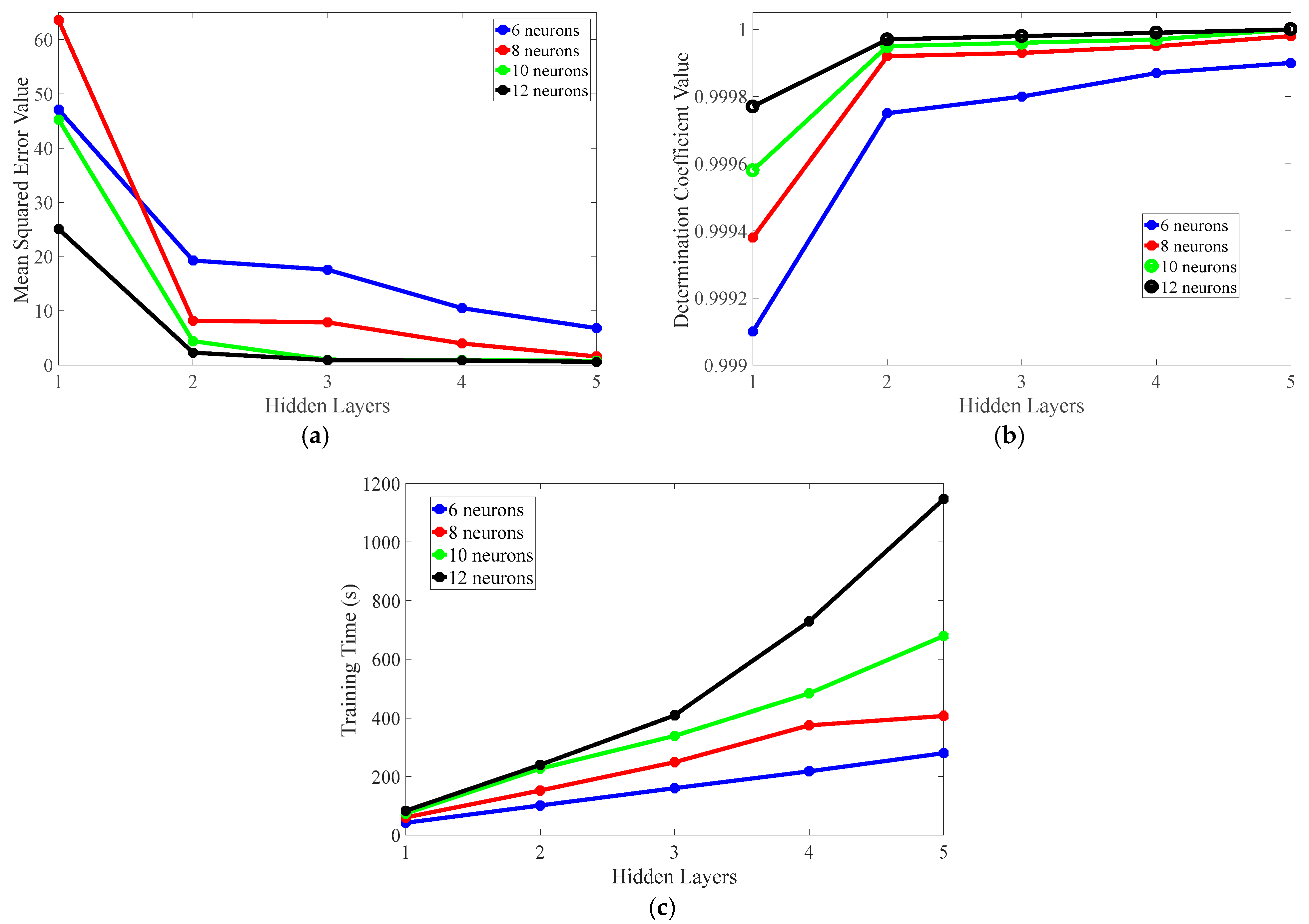
- Determine the Number of Hidden Layers and Neurons of the Neural Network
- (6)
- Selection of Excitation Function
- (7)
- Selection of Training Function
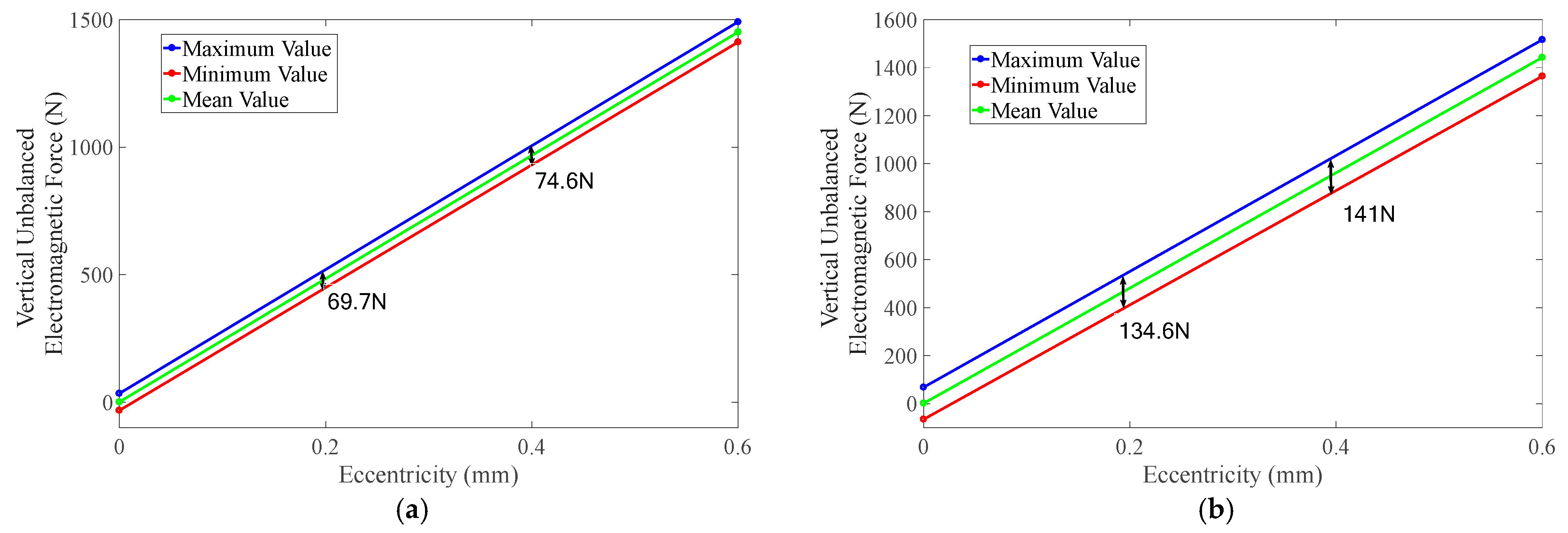
4.3. Optimization Effect Analysis of Unbalanced Electromagnetic Force Model
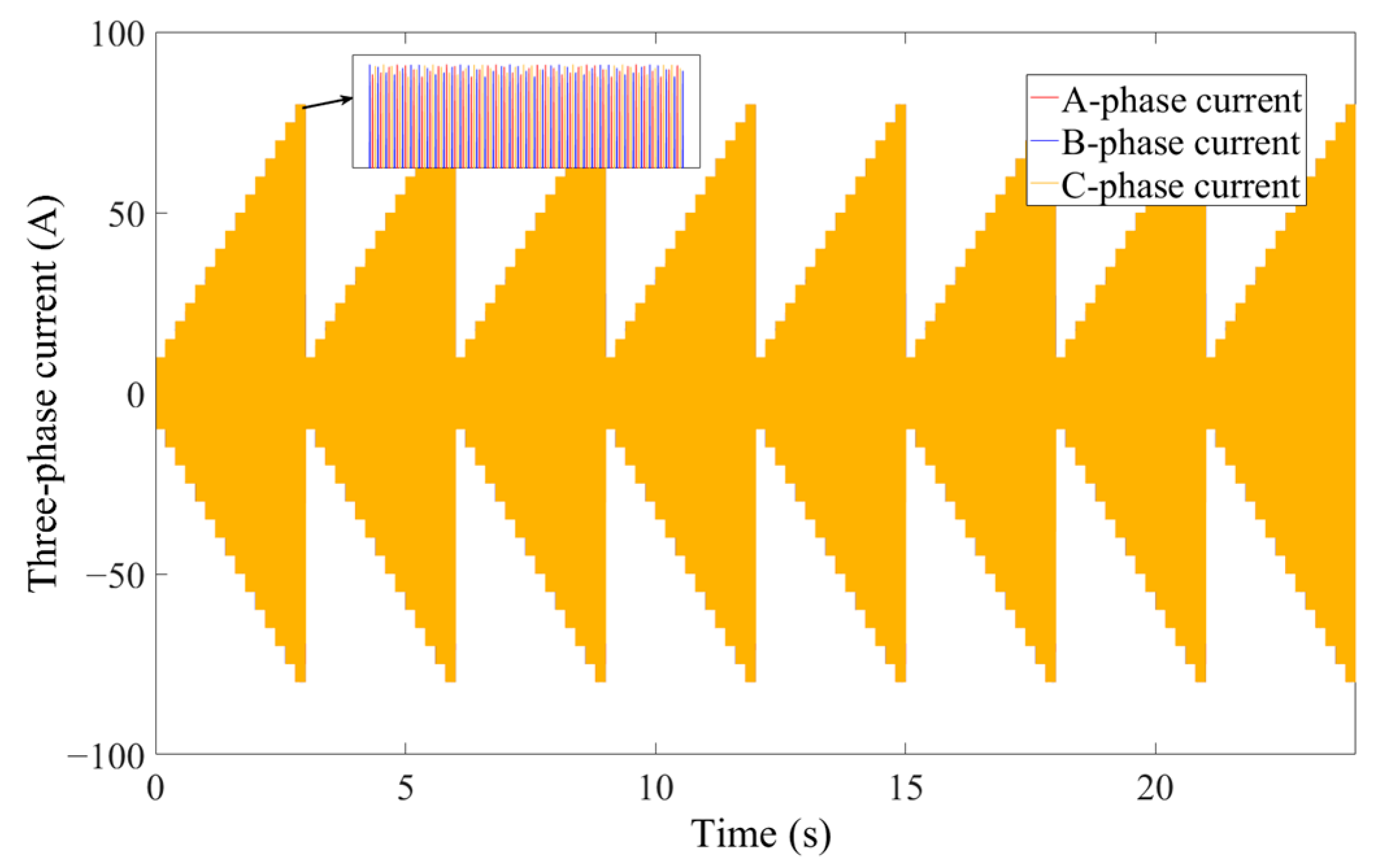
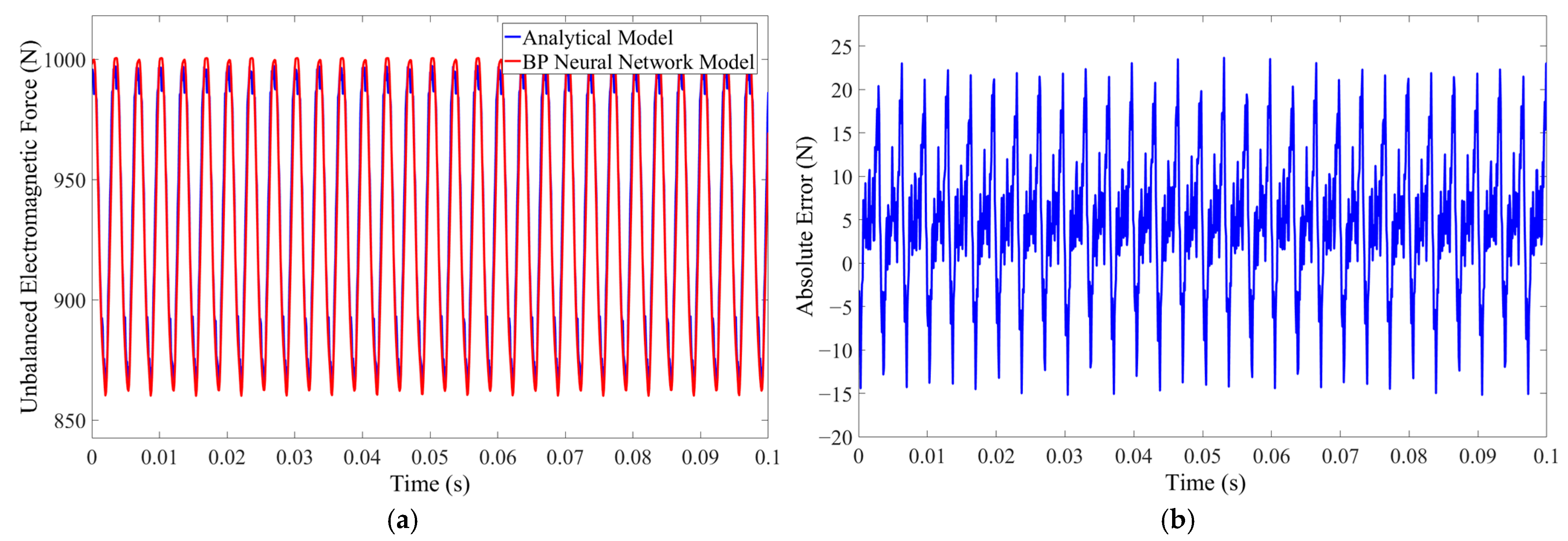
- Simulation of Ideal Uniform Speed of Motor
- 2.
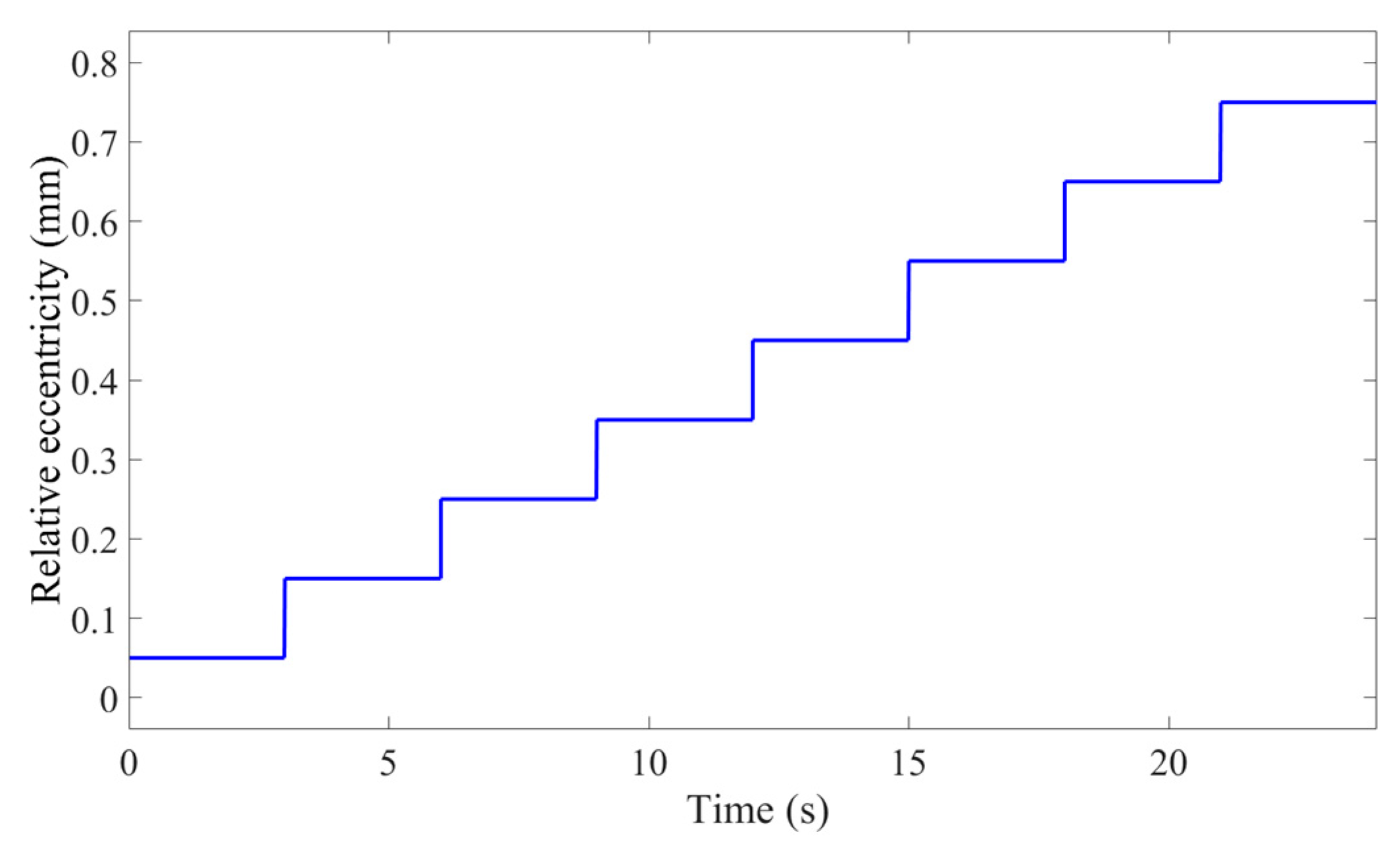
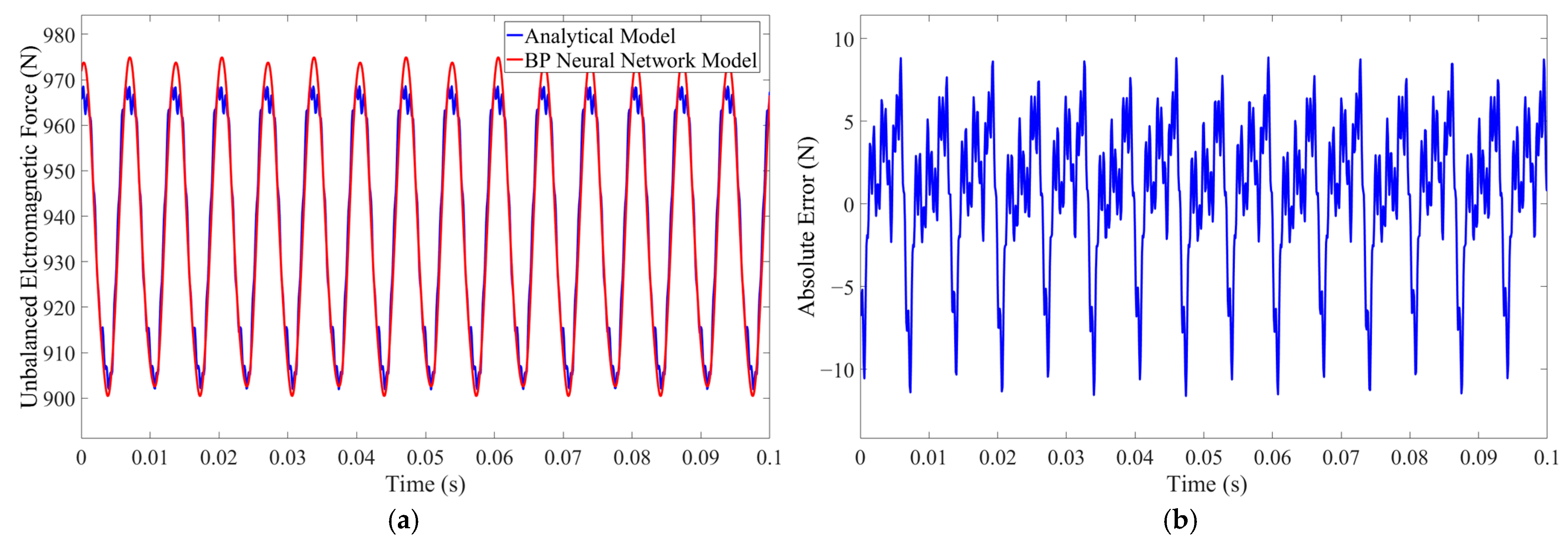
- Simulation of Acceleration and Eccentricity Change
5. Bench Experiment Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Xu, X.; Sun, X.; Jiang, H.; Qu, Y. Research and Development of wheel Motor Drive Technology. Electr. Mach. Control Appl. 2017, 44, 1–7. [Google Scholar]
- Wang, Z.; Ding, X.; Zhang, L. Review on Key Technologies of Anti-skid Control for Vehicle Driven by four-wheel hub Motor. Chin. J. Mech. Eng. 2019, 55, 99–120. [Google Scholar]
- Zhao, Z.; Taghavifar, H.; Du, H.; Qin, Y.; Dong, M.; Gu, L. In-Wheel Motor Vibration Control for Distributed-Driven Electric Vehicles: A Review. IEEE Trans. Transp. Electrif. 2021, 7, 2864–2880. [Google Scholar] [CrossRef]
- Yang, X.; Song, H.; Shen, Y.; Liu, Y. Study on adverse effect suppression of hub motor driven vehicles with inertial suspensions. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 236, 767–779. [Google Scholar] [CrossRef]
- Wang, R.; Jiang, Y.; Ding, R.; Liu, W.; Meng, X.; Sun, Z. Design and experimental verification of self-powered electromagnetic vibration suppression and absorption system for in-wheel motor electric vehicles. J. Vib. Control. 2021, 28, 2544–2555. [Google Scholar] [CrossRef]
- Kartal, E.T.; Arabul, F.K. Effects of air gap eccentricity on different rotor structures for PMSM in electric vehicles. Sci. Rep. 2024, 14, 17335. [Google Scholar] [CrossRef]
- Deng, Z.; Li, X.; Li, X.; Zhao, S.; Wei, H. Mechanism analysis and optimum control of negative airgap eccentricity effect for in-wheel switched reluctance motor driving system. Nonlinear Dyn. 2023, 111, 9075–9093. [Google Scholar] [CrossRef]
- Li, X.; Deng, Z.; Chen, T.; Zhang, Y.; Wei, H. Negative dynamics effect of in-wheel switched reluctance motor with inclined airgap eccentricity on handing stability for electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 238, 3707–3720. [Google Scholar] [CrossRef]
- Zhang, H.; Wan, S.; Zhang, M.; G, J. Analysis on coupled vibration characteristics of electric vehicle’s in-wheel motor with random excitation. J. Mech. Des. 2024, 41, 146–152. [Google Scholar]
- Zhu, Z.Q.; Howe, D.; Bolte, E.; Ackermann, B. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. I. Open-circuit field. IEEE Trans. Magn. 1993, 29, 124–135. [Google Scholar] [CrossRef]
- Zhu, Z.; Howe, D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. II. Armature-reaction field. IEEE Trans. Magn. 1993, 29, 136–142. [Google Scholar] [CrossRef]
- Zhu, Z.; Howe, D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. III. Effect of stator slotting. IEEE Trans. Magn. 1993, 29, 143–151. [Google Scholar] [CrossRef]
- Zhu, Z.; Howe, D. Instantaneous magnetic field distribution in permanent magnet brushless DC motors. IV. Magnetic field on load. IEEE Trans. Magn. 1993, 29, 152–158. [Google Scholar] [CrossRef]
- Sun, J.; Hu, X. Research on Optimization and Control of Vertical Vibration System of Distributed Electric Drive Vehicle. J. Chongqing Univ. Technol. (Nat. Sci.) 2022, 36, 45–52. [Google Scholar]
- Ma, C.; Chen, C.; Li, Q.; Gao, H.; Kang, Q.; Fang, J.; Cui, H.; Teng, K.; Lv, X. Analytical Calculation of No-Load Magnetic Field of External Rotor Permanent Magnet Brushless Direct Current Motor Used as In-Wheel Motor of Electric Vehicle. IEEE Trans. Magn. 2018, 54, 8103106. [Google Scholar] [CrossRef]
- Ma, C.; Cui, H.; Zheng, P.; Zhang, Y.; Gao, H. Influence of static eccentricity on unbalanced magnetic force of external rotor permanent magnet brushless direct current motor used as In-wheel motor. IET Electr. Power Appl. 2019, 13, 538–550. [Google Scholar] [CrossRef]
- Zhang, H.S.; Deng, Z.X.; Yang, M.L.; Zhang, Y.; Tuo, J.Y.; Xu, J. Analytical Prediction of Halbach Array Permanent Magnet Machines Considering Finite Tooth Permeability. IEEE Trans. Magn. 2020, 56, 8101010. [Google Scholar] [CrossRef]
- Zhang, H.S.; Yang, M.L.; Zhang, Y.; Tuo, J.Y.; Luo, S.; Xu, J. Analytical Calculation of Surface-Inset PM In-Wheel Motors and Reduction of Torque Ripple. IEEE Trans. Magn. 2020, 57, 8100211. [Google Scholar] [CrossRef]
- Du, G.; Deng, Z.; Zhang, H.; Yang, M.; Tang, X. Analytical modeling and pole-slot combination of magnetic field in surface-mounted permanent-magnet synchronous motor. J. Chongqing Univ. 2021, 44, 1–13. [Google Scholar]
- Chen, X.; Deng, Z.; Hu, J.; Deng, T. An analytical model of unbalanced magnetic pull for PMSM used in electric vehicle: Numerical and experimental validation. Int. J. Appl. Electromagn. Mech. 2017, 54, 583–596. [Google Scholar] [CrossRef]
- Yang, Z.; Sun, C.; Sun, X.; Sun, Y. An Improved Dynamic Model for Bearingless Induction Motor Considering Rotor Eccentricity and Load Change. IEEE Trans. Ind. Electron. 2021, 69, 3439–3448. [Google Scholar] [CrossRef]
- Deng, Z.; Li, X.; Liu, T.; Zhao, S. Modeling and suppression of unbalanced radial force for in-wheel motor driving system. J. Vib. Control. 2021, 28, 3108–3119. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Cheng, Q.; Yu, Y. Research on GA-LQR Control for Air Suspension Damping of Electric Vehicle with Wheel Motor. J. Chongqing Univ. Technol. 2024, 38, 13–23. [Google Scholar]
- Li, T.; Deng, Z.; Zhang, H.; Lu, P.; Zeng, P. Vertical Dynamics Characteristics of Electromechanical Coupling of Electric Vehicle Driven by hub Motor. J. Chongqing Univ. 2024, 47, 1–17. [Google Scholar]
- Wu, S.; Li, Y. Analysis of Effect of unbalanced electromagnetic Force of Wheel Motor on Vertical Vibration of Vehicle. J. Harbin Univ. Sci. Technol. 2022, 27, 21–28. [Google Scholar]
- Li, J.; Jia, C.; Cheng, L.; Zhao, Q. Influence of eccentricity of wheel motor under Random Road Surface on Ride Comfort of Electric Vehicle. J. Northeast. Univ. (Nat. Sci.) 2022, 43, 1113–1119. [Google Scholar]
- Li, J.; Jia, C.; Cheng, L.; Zhao, Q. Influence of eccentricity of wheel motor under Pulse Road Surface on Ride Comfort of Electric Vehicle. J. Northeast. Univ. (Nat. Sci.) 2022, 12, 321–328. [Google Scholar]
- Yuan, L.; Hu, B.; Wei, K.; Chen, S. Modern Permanent Magnet Synchronous Motor Control Principle and MATLAB Simulation; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2016; pp. 151–165. [Google Scholar]
- Shu, Z.; Liu, L. No-beat Predictive Current Control of Permanent magnet synchronous Motor Based on Parameter Adaptive. Electr. Power Eng. Technol. 2019, 42, 175–184. [Google Scholar]
- Kurihara, N.; Bayless, J.; Chiba, A. Noise and vibration reduction of switched reluctance motor with novel simplified current waveform to reduce force sum variation. In Proceedings of the 2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1794–1800. [Google Scholar]
- Zhang, H.; Wan, S.; Zhang, M. Coupling Vibration Suppression of In-Wheel Motor Electric Vehicle Based on Active Disturbance Rejection Control. Automot. Technol. 2023, 8–14. [Google Scholar]
- Xing, Y.; Li, F. Research on the influence of hidden layers on the prediction accuracy of GA-BP neural network. J. Phys. Conf. Ser. 2020, 1486, 022010. [Google Scholar] [CrossRef]
- He, X.; Zhao, Y.; Cai, C. Random Vibration Analysis of Vehicle-Rail-Bridge System based on SSA-BP Neural Network. J. Railw. Sci. Eng. 2024, 21, 3225–3236. [Google Scholar]
- Zhang, X.; Zhang, R.; Chen, X.; Yang, H.; Yu, D.; Song, Y. Strength evolution prediction of structural concrete in Long Service period based on GA-BP neural network. J. Cent. South Univ. (Nat. Sci.) 2024, 55, 836–850. [Google Scholar]






| Nominal Parameters | Rated Power | Rated Voltage | Equivalent Resistance of the Stator | Three-Phase Winding Self-Inductance | The Moment of Inertia of the Rotor |
|---|---|---|---|---|---|
| Numerical value | 4 kw | 72 V | 0.3 | H |
| Parameter Name | Parameter Symbol | Parameter Value | Unit |
|---|---|---|---|
| Unit motor winding pitch | 0.123 | rad | |
| Number of turns per slot of winding | N | 24 | - |
| Number of slots | 51 | - | |
| Number of poles | 2p | 46 | - |
| Relative permeability of permanent magnet | 1.1 | - | |
| Number of parallel branches | a | 1 | - |
| Polar arc coefficient | 1 | - | |
| Outer diameter of stator core | R | 100 | mm |
| Thickness of permanent magnet | h | 2.5 | mm |
| Radius of permanent magnet | R | 100.8 | mm |
| Axial length of the motor | L | 60 | mm |
| Width of notch | 2.14 | mm | |
| Residual magnetic induction | B | 1.04 | T |
| Notch angle | 0.0214 | rad |
| Physical Quantity | Symbol | Parameter Value | Unit | |
|---|---|---|---|---|
| Quality parameter | Mass of rotor and tire | 17 | kg | |
| Mass of stator and shaft | 22.5 | kg | ||
| Mass of vehicle body | 355 | kg | ||
| Moment of inertia at the center of mass of the car body | J | 1192 | ||
| Stiffness parameter | Tire stiffness | 200,000 | N/m | |
| Motor bearing stiffness | 4,000,000 | N/m | ||
| Suspension stiffness | 15,000/17,000 | N/m | ||
| Damping parameter | Suspension damping | 1450 | N·s/m | |
| Geometric parameter | Distance from front/rear wheels to body center of mass | a/b | 0.795/0.975 | m |
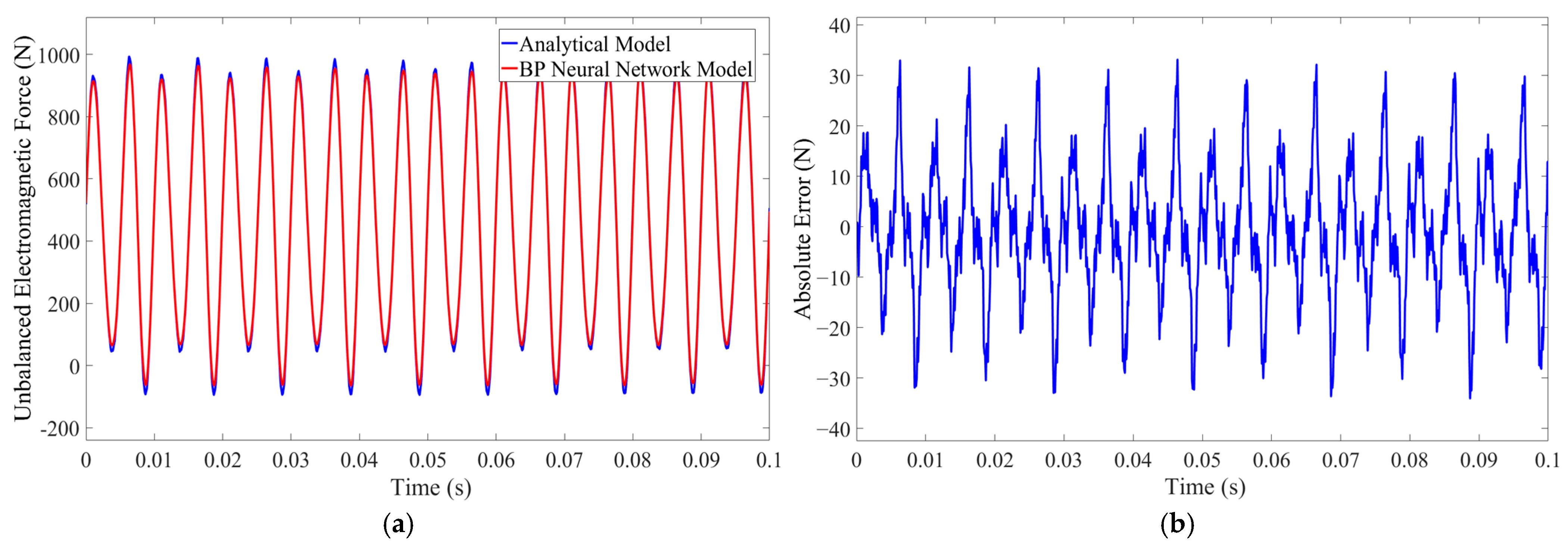
| Working Condition | Analytical Model | BP Neural Network Model | Relative Error of Root Mean Square Value |
|---|---|---|---|
| 390 rpm speed, 40 A phase current amplitude | 937.9 N | 933.3 N | 0.49% |
| 195 rpm speed, 20 A phase current amplitude | 938.3 N | 937.5 N | 0.085% |
| uniform acceleration and variable eccentricity | 574.4 N | 569 N | 0.94% |
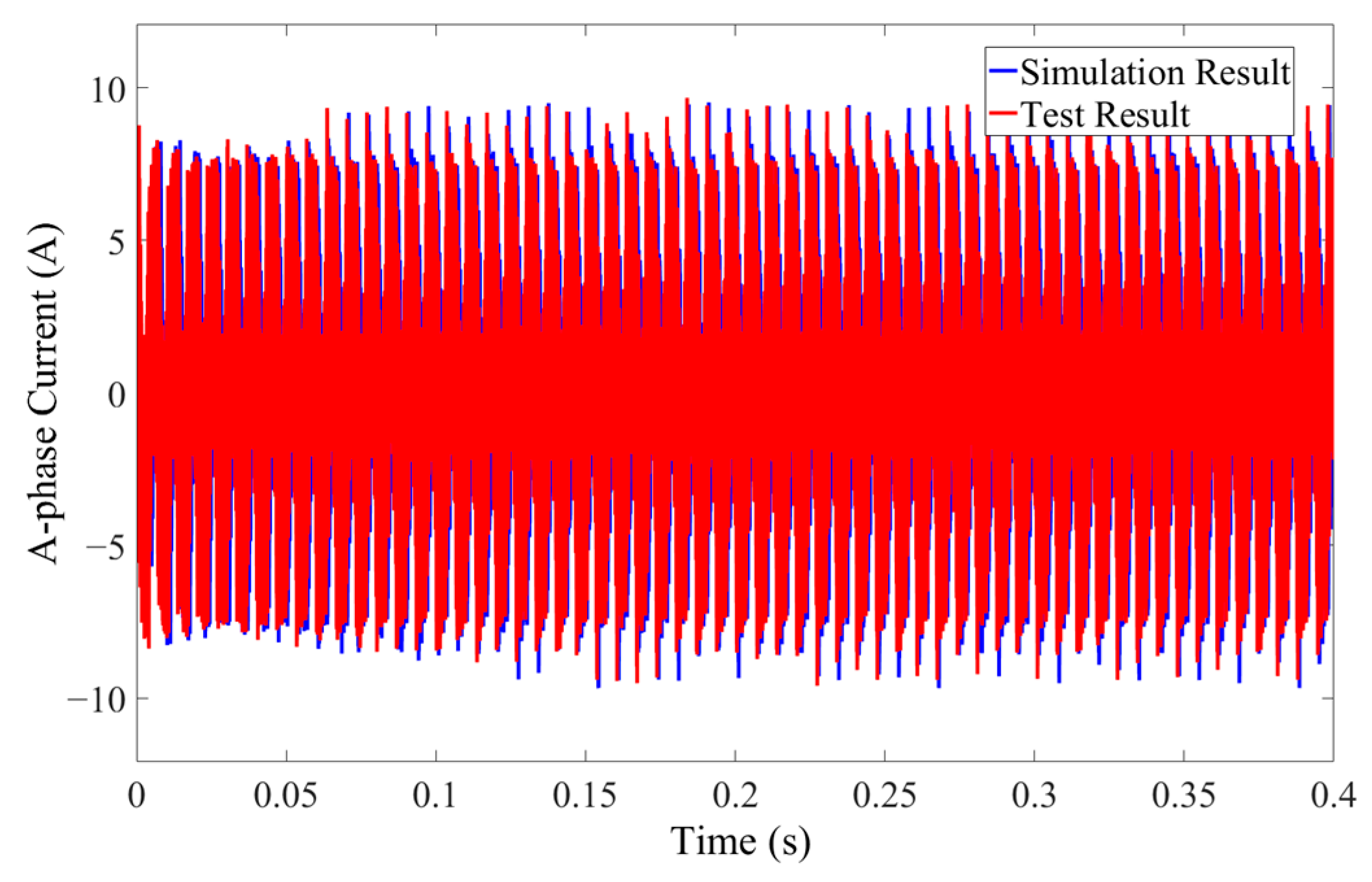
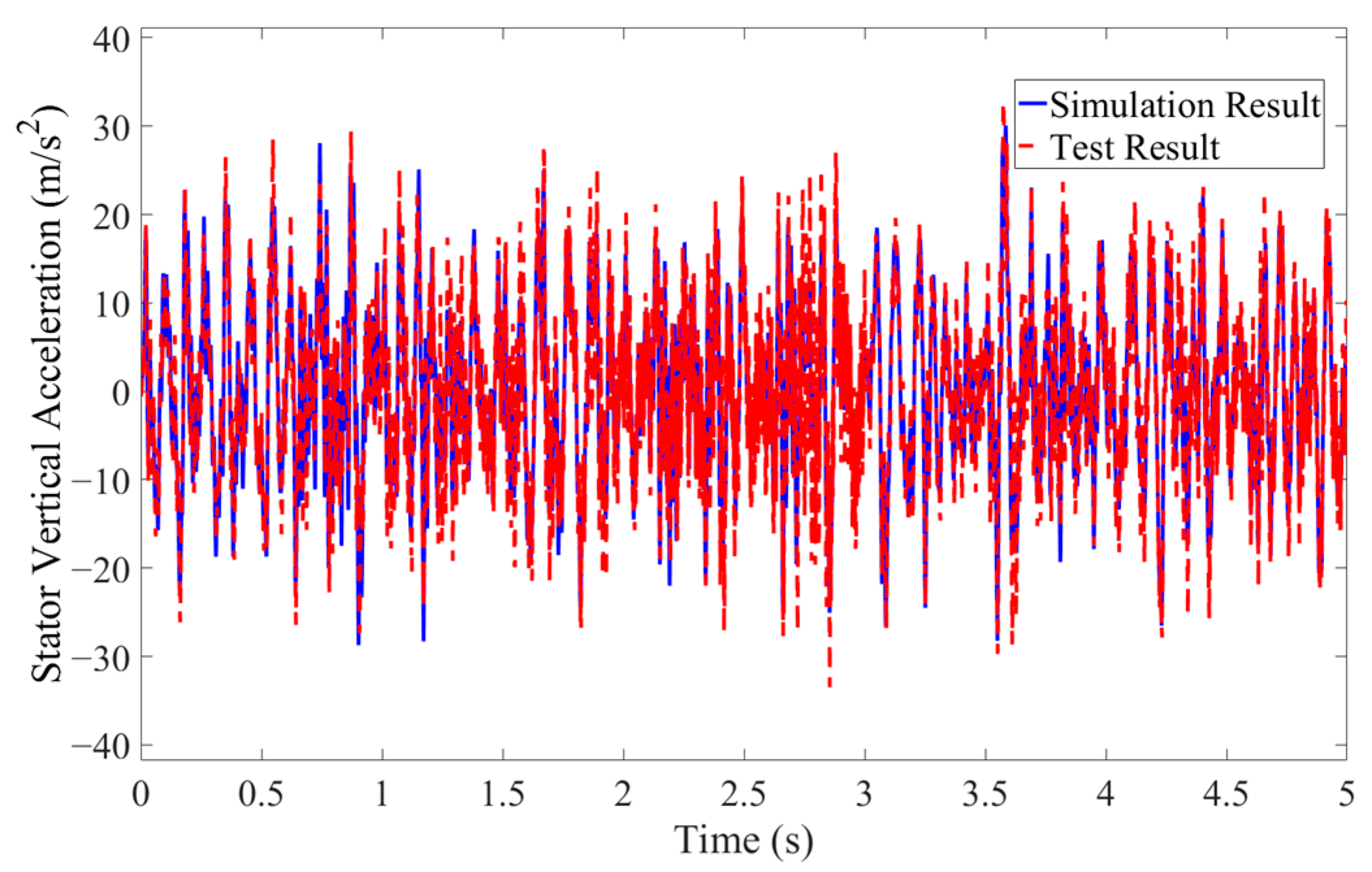
| Comparison Object | Simulation Result | Test Result | Relative Error of Root Mean Square Value |
|---|---|---|---|
| A-phase current | 3.67 A | 3.59 A | 2.18% |
| Stator vertical acceleration | 9.54 m/s2 | 9.78 m/s2 | 2.52% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Zhang, Y.; Ding, R.; Liu, W.; Wang, R. Research on Unbalanced Electromagnetic Force Under Static Eccentricity of the Wheel Hub Motor Based on BP Neural Network. World Electr. Veh. J. 2025, 16, 252. https://doi.org/10.3390/wevj16050252
Meng X, Zhang Y, Ding R, Liu W, Wang R. Research on Unbalanced Electromagnetic Force Under Static Eccentricity of the Wheel Hub Motor Based on BP Neural Network. World Electric Vehicle Journal. 2025; 16(5):252. https://doi.org/10.3390/wevj16050252
Chicago/Turabian StyleMeng, Xiangpeng, Yunquan Zhang, Renkai Ding, Wei Liu, and Ruochen Wang. 2025. "Research on Unbalanced Electromagnetic Force Under Static Eccentricity of the Wheel Hub Motor Based on BP Neural Network" World Electric Vehicle Journal 16, no. 5: 252. https://doi.org/10.3390/wevj16050252
APA StyleMeng, X., Zhang, Y., Ding, R., Liu, W., & Wang, R. (2025). Research on Unbalanced Electromagnetic Force Under Static Eccentricity of the Wheel Hub Motor Based on BP Neural Network. World Electric Vehicle Journal, 16(5), 252. https://doi.org/10.3390/wevj16050252







