Optimal Battery Recycling Strategy for Electric Vehicle under Government Subsidy in China

Abstract

Motivated by the increasing environmental concerns about the used electric vehicle batteries in China, an electric vehicle manufacturer’s battery recycling strategy under government subsidy was studied. A consumer utility function was used to capture consumer environmental awareness associated with battery recycling and the game-theoretical approach was applied to analyze the interaction between the government and the manufacturer. It was found that, with an exogenous government subsidy, the manufacturer either recycles all the batteries, or it does not recycle any batteries if the impact of the recycling scale on costs is unremarkable; otherwise, the manufacturer recycles some used batteries when the benefit from recycling is moderate. Interestingly, an increased subsidy causes the manufacturer’s battery recycling rate to decrease if the subsidy is sufficiently large. When the government subsidy is endogenously, either full recycling, no recycling, or partial recycling can still arise. The optimal battery recycling rate and social welfare are lower in a non-cooperative game than in a cooperative game if the benefit from recycling is relatively low. The main findings were numerically justified with realistic subsidy data in China. The numerical results indicate: (1) the optimal battery recycling rate locates in a closed interval from 0 to 1 given an exogenous or an endogenous government subsidy, and it decreases with the subsidy when the subsidy is not less than 50% of the production cost of electric vehicle; (2) the social welfare first increases to a maximum value and then decreases as the subsidy increases; and (3) the optimal battery recycling rate increases significantly and the social welfare is improved when there is cooperation between the government and the manufacturer.

1. Introduction

With the growing environmental concerns in modern society, electric vehicles (EVs) (mainly battery EVs and plug-in hybrid EVs) have become an increasingly popular transportation option worldwide [1]. In China, the world’s largest electric vehicle (EV) market, the number of EVs sold reached 58,000 in 2017, with an annual growth rate of 72% compared with that in 2017 [2]. The electric vehicle is regarded as one of the most promising alternatives for sustainable transportation [3]. The adoption of EV can address the global issues of climate change and energy shortages; thus, it is vigorously promoted by governments of China through various incentive schemes.

Despite the huge benefits of EV, the adoption of EV may incur additional environmental issues, among which used battery recycling is likely to attract the most concern. The issue of used EV batteries should be paid adequate attentions because, they not only do great harm to the environment, but they also are valuable if dealt with appropriately. In China, there are increasing requirements for EV battery recycling due to the explosive growth of EV use in recent years. According to China Automotive Technology and Research Center (CATRC), the volume of scrapped EV batteries in China is expected to reach 120,000–170,000 tons by 2020. To tackle the challenge, in February 2018, China’s Ministry of Industry and Information Technology issued “interim” rules that hold EV manufacturers responsible for the recovery of the batteries and the establishment of recycling channels [4].

Given the responsibility of battery recycling, an EV manufacturer in China needs to set up facilities to collect and recycle spent batteries and to make decisions regarding battery recycling. Managers of EV manufacturers would be interested in finding the optimal battery recycling decision and understanding how such a decision is affected by various factors. Intuitively, an EV manufacturer’s battery recycling decision is closely related to the costs and revenues from recycling, as well as consumer environmental awareness as it relates to the importance of battery recycling. Furthermore, it may be affected by the government’s incentive schemes; for example, governments of China have been providing a series of subsidies to consumers of EVs in recent years. On the other hand, government policy makers may be interested in how the EV manufacturer’s battery recycling decision impacts social welfare and how to improve social welfare through the provision of appropriate incentive schemes. Therefore, an EV manufacturer’s battery recycling decision and the government’s subsidy decision have a close relationship with each other.

Departing from the above discussions, this study investigated an EV manufacturer’s optimal battery recycling strategy when the government offers a subsidy to consumers of the EV in the presence of environmentally aware consumers. The used batteries are environmentally hazardous and a consumer’s utility of EV consumption is affected by the battery recycling rate due to the consumer environmental awareness. Two cases were considered for this study: one with an exogenous government subsidy and one with an endogenous government subsidy. For the latter case, the government and the manufacturer make decisions in a non-cooperative or a cooperative game to maximize the social welfare and its own profit, respectively. It seems that this study is the first to investigate the interaction between an EV manufacturer’s battery recycling strategy and government subsidy.

This study relates closely to the research stream on EV battery recycling that has attracted considerable interest in recent years. This research stream often concerns the economic impacts of reused EV batteries (e.g., Yano et al. [5], Neubauer and Pesaran [6], Heymans et al. [7], Assunçao et al. [8], and Tang et al. [9]). For example, Neubauer and Pesaran [6] estimated the impacts of the second use of EV batteries on the cost to EV consumers and explored the potential of used EV batteries as grid-based energy storage applications. An economic analysis of the reuse of EV batteries was also conducted by Heymans and Walker [7], who focused on the feasibility and cost savings from repurposing EV battery unit for peak shifting in residential energy storage. Assunçao et al. [8] similarly presented an economic assessment of the reuse of EV batteries in a storage system for the residential sector. Different from these studies, Tang et al. [9] applied a non-cooperative game-theoretical model to explore the impact of sharing business models on economic performance of used EV batteries integrated with distributed PV systems. Their case study shows that sharing business models can reduce electricity expenses of the whole community and improve the NPV of used EV batteries.

The environmental impacts of used EV batteries are also considered by scholars. Using a parameterized life cycle model, Ahmadi et al. [10] analyzed the environmental feasibility of reusing EV batteries and showed that reusing the batteries for off-peak clean electricity storage may achieve a considerable reduction in CO${}_2$ emissions. A follow-up study was conducted by Ahmadi et al. [11], who found that the manufacturing phase of the Li-ion battery would dominate the environmental impacts across the extended life cycle of the battery. The environmental impacts of the used Li-ion battery of EV was also studied by Dunn et al. [12]. They mainly investigated the energy consumed and air emissions generated when recovering the used EV batteries and the effects of closed-loop recycling on environmental impacts. In a recent study, Casals et al. [3] compared different applications of used EV batteries and found that the batteries associated with renewable energy sources in stationary applications can limit the environmental impacts.

Similar to the aforementioned studies, this study also considered the reuse of EV batteries from an economic and environmental perspective. However, none of these studies endogenizes EV manufacturer’s decisions regarding battery recycling by considering the EV manufacturer as an economic subject. In this study, the manufacturer was an independent decision-maker that optimally chooses the battery recycling strategy to maximize its own profit with an exogenous or an endogenous government subsidy. Furthermore, this study incorporated the impact of consumer environmental awareness in the decision process of the players.

Another stream of research related to this study focuses on governmental incentive schemes for sustainable operations and the EV market. An increasing number of studies discuss sustainable operations under governmental incentive policy (e.g., Benjaafar et al. [13], Drake et al. [14], Chen et al. [15], Zhou et al. [16], Wang and Huang [17], Yuan et al. [18], Zhang et al. [19], Tsai and Jhong [20], Siddiqui [21], and Gonseth et al. [22]). Benjaafar et al. [13] highlighted the effect of operational decisions on carbon emissions and the importance of operational models in evaluating the impact of different regulatory policies, such as mandatory emission caps, taxes on carbon emissions, and emission cap and trade. Following the study of Benjaafar et al. [13], Drake et al. [14] investigated the effects of emissions tax and emissions cap-and-trade regulation on a firm’s technology choice and capacity decisions; Chen et al. [15] analyzed the optimal strategies for warehouse management and technology investment under the cap-and-trade emission policy; Zhou et al. [16] focused on how carbon tax policy affects the pricing decisions of supply chain parties and social welfare by incorporating consumer environmental awareness; and Wang and Huang [17] studied the optimal strategies regarding carbon reduction level and online return for a firm that sells green products via an e-commerce platform under carbon tax policy. Unlike these studies, this study focused on the interaction between the government subsidy and an EV manufacturer’s battery recycling strategy.

There is also a growing number of studies that consider governmental incentive schemes for the EV market (e.g., Hao et al. [23], Yang et al. [24], Luo et al. [25], Langbroek et al. [26], Li et al. [27], Huang et al. [28], Guo et al. [29], Shao et al. [30], Zheng et al. [31], and Gu et al. [32]). A few papers apply the game-theoretical approach to study players’ optimal decisions in the EV market. Luo et al. [25] focused on the interaction between an EV manufacturer and a retailer under an exogenous governmental subsidy scheme with both a price discount rate and a subsidy ceiling. Similarly, with the government subsidy scheme exogenously given, Huang et al. [28] studied a cooperative game in which both the retailer and the consumer have some bargaining power in a setting of a fuel-powered automobile supply chain and an electric-and-fuel automobile supply chain competing for consumers. By endogenizing the government’s subsidy choice, Shao et al. [30] developed game-theoretical models to analyze the government’s and the manufacturers’ optimal decisions regarding subsidies and marketing under a monopoly or a duopoly EV market structure; and Zheng et al. [31] assessed how an EV manufacturer’s production and pricing decisions are affected by the government’s subsidy decision from a maximal social welfare perspective.

This study resembles the aforementioned studies since all studies use the game-theoretical approach to investigate the impact of government subsidy on EV manufacturer’s optimal marketing decisions with an exogenous or an endogenous subsidy. However, this study differs significantly in the focus, as it also examined an EV manufacturer’s optimal battery recycling strategy when the government is a non-strategic or a strategic player in the presence of consumer environmental awareness. Notice that none of these studies has considered EV battery recycling except that of Gu et al. [32]. They investigated an EV manufacturer’s optimal production decisions under an exogenous battery recycling rate and government subsidy by applying the classic news vendor model. This study, on the other hand, focused on an EV manufacturer’s battery recycling strategy when the subsidy is exogenously or endogenously determined by the government.

2. Model

This section introduces the model setting and provides the main assumptions. First, this section describes the battery recycling issues and specifies the related costs and revenue. Then, the consumer utility function is proposed. The relationship between consumer utility and battery recycling is characterized. Finally, the decision-making models for different cases are introduced.

This study considered a setting in which a manufacturer produces EVs for end consumers and the government provides a subsidy to consumers for an EV purchase to promote the EV market. The manufacturer is responsible for collecting and recycling used EV batteries. Without loss of generality, it was assumed that one EV unit produces one unit of the used battery. Then, the total recycling quantity of the used batteries equals the market demand of the EV multiplied by the manufacturer’s battery recycling rate. Similar to Gu et al. [32], it was assumed that the manufacturer’s total recycling cost equals the sum of a variable recycling cost associated with the total recycling quantity and a scaling cost depending solely on the battery recycling rate in the recycling process, i.e.,

$$\begin{array}{c}\hfill C_r=A·q·\tau +B·{\tau }^{\alpha },\end{array}$$

(1)

where $C_r$ is the total recycling cost; $\tau$ is the battery recycling rate, $\tau \in [0,1]$; A is the recycling cost of one unit of the EV; q is the market demand (sales volume) of the EV; and B and $\alpha$ are the cost parameters associated with the scale of battery recycling.

It was assumed that the manufacturer can benefit from battery recycling when the used batteries are recovered by the manufacturer for different purposing options (e.g., reuse in a vehicle, stationary energy storage, and metals extraction, as discussed by Ahmadi et al. [11] and Richa et al. [33]), and the manufacturer’s direct revenue from battery recycling is

$$\begin{array}{c}\hfill B_r=r·q·\tau ,\end{array}$$

(2)

where r is the average benefit from recycling one unit of the used battery. Furthermore, it was assumed that the used EV battery is environmentally harmful. The overall environment impacts of the EV batteries, denoted as $E_i$, can be expressed as follows:

$$\begin{array}{c}\hfill E_i=e·(1-\tau )·q,\end{array}$$

(3)

where e is the environmental impact of one unit of the used battery when it is not recycled. The term $(1-\tau )$ denotes the rate of the used batteries that are not recycled.

Consumer Utility Function. It was assumed that that consumers are rational economic subjects and obtain utility from purchasing the EV. A consumer’s net utility depends on the utility from EV consumption, the government subsidy for the EV purchase, and the market price of the EV. It was also assumed that the consumers are environmentally aware and obtain extra utility from an increased battery recycling rate $\tau$. This assumption captures the growing environmental concerns about the used batteries with the explosive development of the EV market in recent years. It follows that a consumer’s net utility is

$$\begin{array}{c}\hfill U_p=(1+k\tau )\theta +s-p\end{array}$$

(4)

when the consumer purchases an EV, and it is

$$\begin{array}{c}\hfill U_n=0\end{array}$$

(5)

without an EV purchase. In the equation of $U_p$, $\theta$ is the consumer’s valuation of the EV, k is the sensitivity of consumer utility to the battery recycling rate (or the degree of consumer environmental awareness), s is the government’s subsidy to the consumer for one unit of EV purchase, and p is the market price of the EV.

The consumers are heterogeneous in their valuations of the EV, and a consumer’s valuation $\theta$ is randomly drawn from a uniform distribution over the interval $[0,1]$ for traceability of the analysis. Similar assumptions are often seen in the literature on the EV market (e.g., Shao et al. [30] and Zheng et al. [31]). In $U_p$, the term $k\tau \theta$ captures the positive effect of the battery recycling rate $\tau$ on consumer utility. The parameter k reflects the sensitivity of consumer utility to the battery recycling rate associated with consumer environmental awareness. It was assumed that $A-r<k<1$ because: (1) the manufacturer would not recycle any batteries if $k\le A-r$; and (2) a consumer’s valuation of the EV most likely dominates the consumers’ utility over environmental awareness. Furthermore, it was assumed that $s\in [0,1]$, which ensures that the government subsidy is no more than a consumer’s maximum valuation.

Demand Model. A consumer can choose to either purchase an EV or remain inactive. The market demand function of the EV can be obtained based on the consumers’ utilities. A consumer purchases an EV if its net utility from a purchase is larger than that without the purchase, and remains inactive if its net utility without the purchase is larger than that with the purchase. In particular, a consumer is indifferent between purchasing an EV and not purchasing it if the consumer has equal net utility with or without a purchase. By equating the utilities $U_p$ and $U_n$, i.e., $U_p=U_n$, it follows that the indifference point of the consumer’s valuation (see Figure 1), denoted as $\widehat{\theta }$, is

$$\begin{array}{c}\hfill \widehat{\theta }=\frac{p-s}{1+ks}.\end{array}$$

(6)

Intuitively, given the market price of the EV, p, $\widehat{\theta }$ is a threshold such that a consumer purchases the EV if $\theta \in [0,\widehat{\theta })$ and remains inactive if $\theta \in (\widehat{\theta },1]$. Therefore, the normalized demand function of the EV is $q=1-\widehat{\theta }$. It follows that

$$\begin{array}{c}\hfill q=1-\frac{p-s}{1+k\tau }.\end{array}$$

(7)

Notice that the above demand function corresponds to the case with deterministic market demand. One can include randomness in the demand model by adding an exogenous random variable to this function following the studies of Mills [34] and Petruzzi and Dada [35], who offered two different ways to capture this issue. The main insights can continue to hold under stochastic market demand.

Decision Making. Two different decision-making models based on the role of the government were considered. First, the manufacturer is the sole decision-maker that makes the optimal decisions regarding the battery recycling rate $\tau$ and the market price and demand, p and q, when the government subsidy s is exogenously given. This indicates that the government may be non-strategic and does not interact with the manufacturer in practice. Second, the government is an independent player that interacts with the manufacturer in a game setting. The game-theoretic approach is often applied to the study of the strategic interaction between the government and the EV manufacturer in the literature (e.g., Huang et al. [28], Shao et al. [30] and Zheng et al. [31]). It was assumed that the government endogenously chooses the subsidy for EV purchases to maximize the social welfare. Social welfare consists of the manufacturer’s profit, the consumer surplus, the overall government subsidy, and the environmental impact of the EV batteries, and it can be written as follows:

$$\begin{array}{c}\hfill W={\mathrm{\Pi }}_m+C_s-S-E_i,\end{array}$$

(8)

where W is social welfare, ${\mathrm{\Pi }}_m$ is the manufacturer’s profit, $C_s$ is the consumer surplus, and S is the overall government subsidy. Two cases, in which the government and the manufacturer move in a non-cooperative or a cooperative game, were considered.

In the non-cooperative game, the two players make their decisions in sequence under a Stackelberg framework. The sequence of events is as follows:

Stage 1.

The government decides on the subsidy s to maximize the social welfare.

Stage 2.

The manufacturer makes the optimal battery recycling and market decisions to maximize its own profit given the government subsidy.

In the cooperative game, the government and the manufacturer move in a centralized way. There is a centralized decision-maker, instead of the government and the manufacturer, who makes all the decisions regarding subsidy, battery recycling rate and market to maximize the social welfare.

3. Decision Analysis

This section analyzes the firms’ optimal decisions in different cases: first, the case in which the government subsidy is exogenously given; and, second, the case in which the subsidy is endogenously determined in a non-cooperative or a cooperative game.

3.1. Exogenous Government Subsidy

This section discusses the manufacturer’s optimal decisions regarding battery recycling and the market when the government subsidy is exogenously given.

Given the government subsidy s, the manufacturer’s profit function is

$$\begin{array}{c}\hfill {\mathrm{\Pi }}_m(s,\tau ,p)=(p-c)q+B_r-C_r.\end{array}$$

(9)

where c is the unit production cost of the EV. Substituting $B_r$ and $C_r$ into ${\mathrm{\Pi }}_m(s,\tau ,p)$, it follows that

$$\begin{array}{c}\hfill {\mathrm{\Pi }}_m(s,\tau ,p)=[p-c+(r-A)\tau ](1-\frac{p-s}{1+k\tau })-B{\tau }^{\alpha }.\end{array}$$

(10)

By solving the equation of the first-order derivative $\partial {\mathrm{\Pi }}_s(\tau ,p)/\partial p=0$, it follows that the optimal market price of the EV is

$$\begin{array}{c}\hfill p^{*}(s,\tau )=\frac{1}{2}[1+c+s+(k-r+A)\tau ].\end{array}$$

(11)

Substituting $p^{*}(s,\tau )$ into Equation (7), the optimal market demand of the EV is

$$\begin{array}{c}\hfill q^{*}(s,\tau )=1-\frac{p^{*}(s,\tau )-s}{1+k\tau }=\frac{1}{2(1+k\tau )}[1-c+s+(k+r-A)\tau ],\end{array}$$

(12)

where $-1+c-(k+r-A)\tau \le s\le 1+c+(k-r+A)\tau$ must hold to ensure that the market demand of the EV $q^{*}(s,\tau )\in [0,1]$ and the boundary value $\widehat{\theta }\in [0,1]$. Notice that $-1+c-(k+r-A)\tau$ may be negative, which implies that the consumers may be willing to pay additional fee to the government for the EV purchase. This case was ignored and only the case with non-negative subsidy was considered.

Substituting $p^{*}(s,\tau )$ and $q^{*}(s,\tau )$ into Equation (10), it follows that the manufacturer’s profit is

$$\begin{array}{c}\hfill {\mathrm{\Pi }}_m(s,\tau )=\frac{1}{4(1+k\tau )}{[1-c+s+(k+r-A)\tau ]}^2-B{\tau }^{\alpha }.\end{array}$$

(13)

Define ${\tau }^{*}(s)$ as the manufacturer’s optimal battery recycling rate, i.e.,

$${\tau }^{*}(s)\in \underset{0\le \tau (s)\le 1}{argmax}{\mathrm{\Pi }}_m(s,\tau ).$$

(14)

Based on ${\tau }^{*}(s)$, the optimal market price $p^{*}(s)$, the optimal market demand $q^{*}(s)$, and the manufacturer’s profit at equilibrium can be derived. The following proposition characterizes the manufacturer’s optimal battery recycling decision. All proofs of the main results are available in the Supplementary Materials.

Proposition 1.

(Manufacturer’s Optimal Recycling Decision under Exogenous Government Subsidy) Suppose that $max\{0,-1+c-(k+r-A)\tau \}\le s\le 1+c+(k-r+A)\tau$ for $\tau \in [0,1]$.

(i) 

When $0\le \alpha \le 1$ or when $\alpha >1$ and $B<{\displaystyle \frac{{[k(s-c)+A-r]}^2}{2\alpha (\alpha -1){\tau }^{\alpha -2}{(1+k\tau )}^3}}$, the optimal battery recycling rate is ${\tau }^{*}(s)=0$ if $k+r-A\le \sqrt{(1+k){(1-c+s)}^2+4(1+k)B}-1+c-s$; otherwise, the optimal battery recycling rate is ${\tau }^{*}(s)=1$.

(ii) 

When $\alpha >1$ and $B>{\displaystyle \frac{{[k(s-c)+A-r]}^2}{2\alpha (\alpha -1){\tau }^{\alpha -2}{(1+k\tau )}^3}}$, there exists a unique optimal battery recycling rate ${\tau }^{*}(s)\in [0,1]$, where ${\tau }^{*}(s)=0$ if $k+r-A<{\displaystyle \frac{k(1+s-c)}{2}}$, ${\tau }^{*}(s)=1$ if $B<{\displaystyle \frac{(1+s-c+k+r-A)[(2+k)(k+r-A)-k(1+s-c)]}{4\alpha {(1+k)}^2}}$, and otherwise ${\tau }^{*}(s)\in (0,1)$ and ${\displaystyle \frac{[1+s-c+(k+r-A){\tau }^{*}(s)][(2+k{\tau }^{*}(s))(k+r-A)-k(1+s-c)]}{4{(1+k)}^2}}-B\alpha {({\tau }^{*}(s))}^{\alpha -1}=0$.

Proposition 1 indicates that the manufacturer either recycles all the batteries or does not recycle any batteries when the impact of the recycling scale on costs is not notable (e.g., the scaling cost parameter $\alpha$ or B is relatively small). Specifically, if the benefit from recycling is small (i.e., $k+r-A\le \sqrt{(1+k){(1-c+s)}^2+4(1+k)B}-1+c-s$), the manufacturer would not collect and recycle any batteries. Otherwise, the manufacturer would collect and recycle all the batteries. When the impact of the recycling scale on costs becomes notable (e.g., $\alpha$ and B are relatively large), the manufacturer may choose to recycle part of the batteries to equalize the marginal benefit and marginal cost of the recycling.

Departing from Proposition 1, the optimal battery recycling rate may be independent of the government subsidy, as described below.

Corollary 1.

Suppose that $B=0$. The optimal battery recycling rate ${\tau }^{*}(s)=0$ if $k+r-A\le (1-c)(\sqrt{1+k}-1)$.

Corollary 1 states that, when the recycling scaling cost parameter is zero, the optimal battery recycling rate always equals zero if the benefit from recycling is sufficiently small, regardless of the size of the subsidy.

The following proposition characterizes the impacts of the government subsidy on the manufacturer’s optimal battery recycling decision. Interestingly, it was found that an increase in the government subsidy causes the optimal battery recycling rate to decrease when the government subsidy is sufficiently large.

Proposition 2.

(Impact of Government Subsidy on the Optimal Recycling Decisions) There exists a threshold $\widehat{s}={\displaystyle \frac{kc+r-A}{k}}$ such that the optimal battery recycling rate ${\tau }^{*}(s)$ is non-decreasing in the subsidy s if $s\le \widehat{s}$, and is non-increasing in the subsidy s if $s\ge \widehat{s}$.

Proposition 2 demonstrates that the government subsidy may have different impacts on the manufacturer’s battery recycling decision, depending on the size of the subsidy. If the subsidy is relatively small ($s\le \widehat{s}$), an increase of the subsidy has a non-decreasing effect on the optimal battery recycling rate. However, if the subsidy is relatively large ($s>\widehat{s}$), an increase of the subsidy leads to a non-increasing optimal battery recycling rate. This result is because an increased subsidy promotes the manufacturer’s market price and demand and hence promotes the manufacturer’s profit, which may consequently lower the manufacturer’s incentive of battery recycling.

Notice that the threshold $\widehat{s}$ decreases (increases) with k when $r-A>0$ ($<0$). This implies that, with $r-A>0$ ($<0$), an increased subsidy is more likely to lower (enhance) the optimal battery recycling rate as the sensitivity of consumer utility to recycling rate due to environmental awareness increases. Meanwhile, the threshold $\widehat{s}$ increases in the production cost c and the net benefit from recycling $r-A$.

3.2. Endogenous Government Subsidy

This section considers that the government is an independent decision-maker and the subsidy is endogenously determined. Both a non-cooperative game, in which the government and the manufacturer make decisions to maximize their own objective functions, and a cooperative game, in which the two players act in a cooperative way, were analyzed.

3.2.1. A Non-Cooperative Game

Recall that, in the non-cooperative game, the government first decides on the subsidy to maximize the social welfare (Stage 1), and then the manufacturer makes the decisions regarding battery recycling and the market (Stage 2) to maximize its own profit.

The dynamic game was solved by backward induction. Let us first consider the manufacturer’s decisions in Stage 2. Intuitively, the manufacturer’s optimal battery recycling and market decisions and optimal profit under an exogenous government subsidy in Section 3.1 apply in this stage. Hence, given the subsidy s in Stage 1, the optimal recycling rate is

$${\tau }^{*}(s)\in \underset{0\le \tau (s)\le 1,}{argmax}{\mathrm{\Pi }}_m(s,\tau ),$$

where ${\mathrm{\Pi }}_m(s,\tau )={\displaystyle \frac{1}{4(1+k\tau )}}{[1-c+s+(k+r-A)\tau ]}^2-B{\tau }^{\alpha }$, and the optimal market price and the optimal market demand are, respectively,

$$\begin{array}{ccc}\hfill p^{*}(s)& =& \frac{1}{2}[1+c+s+(k-r+A){\tau }^{*}(s)],\hfill \\ \hfill q^{*}(s)& =& \frac{1}{2(1+k{\tau }^{*}(s))}[1-c+s+(k+r-A){\tau }^{*}(s)].\hfill \end{array}$$

Then, the government’s decision regarding the subsidy in Stage 1 was analyzed. The government’s objective is to maximize the social welfare W. Based on Section 2, the social welfare depends on the manufacturer’s profit ${\mathrm{\Pi }}_m$, the consumer surplus $C_s$, the overall government subsidy S, and the environmental impact of the EV batteries $E_i$ (refer to Equation (8) in Section 2).

The consumer surplus, which measures all the consumers’ aggregate utilities, can be derived by integrating the consumers’ utilities with respect to the valuation parameter $\theta$ in the EV purchase, i.e.,

$$\begin{array}{c}\hfill C_s(s,{\tau }^{*}(s))={\int }_{\widehat{\theta }}^1{U}_p(\theta )d\theta +{\int }_0^{\widehat{\theta }}{U}_n(\theta )d\theta .\end{array}$$

(15)

Recall that $U_p=(1+k\tau )\theta +s-p$ and $U_n=0$. Given ${\tau }^{*}(s)$ and $p^{*}(s)$, it follows that

$$\begin{array}{c}\hfill C_s(s,{\tau }^{*}(s))=\frac{{(1+s-c+(k+r-A){\tau }^{*}(s))}^2}{8(1+k{\tau }^{*}(s))}.\end{array}$$

(16)

Furthermore, the overall government subsidy equals the product of the subsidy and the market demand, i.e., $S(s)=s·q^{*}(s)=s(1-{\displaystyle \frac{p^{*}(s)-s}{1+k{\tau }^{*}(s)}})$, and the environment impact of the EV batteries is $E_i({\tau }^{*}(s))=e·(1-{\tau }^{*}(s))·q^{*}(s)=e(1-{\tau }^{*}(s))(1-{\displaystyle \frac{p^{*}(s)-s}{1+k{\tau }^{*}(s)}})$. Substituting $p^{*}(s)$, it follows that the social welfare is

$$\begin{array}{c}\hfill W(s,{\tau }^{*}(s))={\mathrm{\Pi }}_m(s,{\tau }^{*}(s))+C_s(s,{\tau }^{*}(s))-S(s)-E_i({\tau }^{*}(s)).\end{array}$$

(17)

Hence,

$$\begin{array}{c}W(s,{\tau }^{*}(s))=\frac{(1+s-c+(k+r-A){\tau }^{*}(s))[3-s-3c+3(k+r-A){\tau }^{*}(s)-4e(1-{\tau }^{*}(s))]}{8(1+k{\tau }^{*}(s))}-B{({\tau }^{*}(s))}^{\alpha }.\end{array}$$

(18)

The superscript “*" is used to represent the optimal solution at equilibrium. Define $s^{*}$ as the government’s optimal choice of the subsidy, i.e.,

$$s^{*}\in \underset{s\ge 0}{argmax}W(s,{\tau }^{*}(s)).$$

(19)

Based on $s^{*}$, the optimal recycling rate ${\tau }^{*}$ can be obtained. Then, the optimal market price $p^{*}$, the optimal market demand $q^{*}$, the manufacturer’s optimal profit ${\mathrm{\Pi }}_m^{*}$, and the optimal social welfare $W^{*}$ at equilibrium can be derived.

Proposition 3.

(Equilibrium Decisions under Endogenous Government Subsidy) Assume that the optimal subsidy is nonnegative in the non-cooperative game.

(i) 

When $0\le \alpha \le 1$ or when B is sufficiently small, the optimal recycling rate ${\tau }^{*}=0$ or ${\tau }^{*}=1$. Specifically, when $B=0$, ${\tau }^{*}=0$ and $s^{*}=1-c-2e$ if $k+r-A<2(1-c-e)(\sqrt{1+k}-1)$, and ${\tau }^{*}=1$ and $s^{*}=1-c+k+r-A$ if $k+r-A>{\displaystyle \frac{2k(1-c)}{1-k+\sqrt{1+k}}}$; otherwise, ${\tau }^{*}=1$ and $s^{*}={\displaystyle \frac{k+r-A}{\sqrt{1+k}-1}}-1+c$.

(ii) 

When $\alpha >1$ and B is sufficiently large, ${\tau }^{*}=0$ and $s^{*}=1-c-2e$ if $r-A\le c+e$, ${\tau }^{*}=1$ and $s^{*}=1-c-2e+k+r-A$ if $B\ge {\displaystyle \frac{(1-c-e+k+r-A)[(2(r-A+k(c+e))-k(k+r-A)]}{2\alpha {(1+k)}^2}}$; otherwise, there exists a unique equilibrium, in which ${\tau }^{*}={\tau }^{*}(s^{*})\in (0,1)$ and $s^{*}\in \underset{s\ge 0}{argmax}W(s,{\tau }^{*}(s))$, if $d^{2}W(s,{\tau }^{*}(s))/d{s}^2<0$, where ${\tau }^{*}(s)\in \underset{0\le \tau (s)\le 1}{argmax}{\displaystyle \frac{1}{4(1+k\tau )}}{[1-c+s+(k+r-A)\tau ]}^2-B{\tau }^{\alpha }$ and $W(s,{\tau }^{*}(s))={\displaystyle \frac{(1+s-c+(k+r-A){\tau }^{*}(s))[3-s-3c+3(k+r-A){\tau }^{*}(s)-4e(1-{\tau }^{*}(s))]}{8(1+k{\tau }^{*}(s))}}-B{({\tau }^{*}(s))}^{\alpha }$.

Proposition 3 summarizes the optimal battery recycling rate and subsidy at equilibrium. Similar to the case with an exogenous government subsidy, given a relatively small $\alpha$, the manufacturer recycles all the batteries if the benefit from recycling (i.e., $k+r-A$) is sufficiently small; otherwise, the manufacturer would recycle all the batteries or not recycle any batteries. The government may have different optimal subsidies given the same optimal recycling rate, depending on the size of the benefit from recycling $k+r-A$. That is, the optimal subsidy may be $s^{*}=1-c+k+r-A$ or $s^{*}={\displaystyle \frac{k+r-A}{\sqrt{1+k}-1}}-1+c$ when the optimal recycling rate equals one. When $\alpha$ is relatively large, it is also possible that the manufacturer recycles all the batteries or does not recycle at all. Furthermore, with a relatively large $\alpha$, a unique equilibrium and partial recycling may arise.

Notice that, in a decentralized system, the social welfare may not be maximized from a systematic perspective, which is discussed in the following section.

3.2.2. A Cooperative Game

This subsection considers a cooperative game in which there is a centralized decision-maker, instead of the government and the manufacturer, who makes decisions to maximize the social welfare. Suppose that the government and the manufacturer reach an agreement prior to cooperation that ensures the manufacturer’s profit in the cooperative game is no less than that in the non-cooperative game. This subsection first analyzes the equilibrium outcomes, and then compares the equilibrium outcomes between the cooperative game and the non-cooperative game.

As mentioned in Section 2, the social welfare consists of the manufacturer’s profit, the consumer surplus, the overall government subsidy, and the environmental impact of the EV batteries. Similar to the derivation process in Section 3.2, the social welfare was obtained as follows:

$$\begin{array}{c}\hfill W(s,\tau ,p)=[p-c-s+(r-A)\tau -e(1-\tau )](1-\frac{p-s}{1+k\tau })+\frac{{(1+s-p+k\tau )}^2}{2(1+k\tau )}-B{\tau }^{\alpha }.\end{array}$$

(20)

By the first-order derivation $\partial W(s,\tau ,p)/\partial p=0$, it follows that the optimal market price of the EV is

$$\begin{array}{c}\hfill p(s,\tau )=s+c-(r-A)\tau +e(1-\tau ),\end{array}$$

and the optimal market demand of the EV is

$$\begin{array}{c}\hfill q(s,\tau )=1-\frac{p^c(s,\tau )-s}{1+k\tau }=\frac{1-c+(k+r-A)\tau -e(1-\tau )}{1+k\tau },\end{array}$$

where $0\le c-(r-A)\tau +e(1-\tau )\le 1+k\tau$ ensures $0\le q^c(s,\tau )\le 1$. Therefore, the social welfare is

$$\begin{array}{c}\hfill W(s,\tau )=\frac{{[1-c+(k+r-A)\tau -e(1-\tau )]}^2}{2(1+k\tau )}-B{\tau }^{\alpha }\end{array}$$

The superscript “c" is used to denote the optimal solution at equilibrium in the cooperative game. Define ${\tau }^c$ as the optimal battery recycling rate at equilibrium, i.e.,

$${\tau }^c\in \underset{0\le \tau \le 1}{argmax}W(s,\tau ).$$

Given ${\tau }^c$, the optimal market price $p^{*}$, the market demand $q^c$, and the optimal social welfare $W^c$ can be then obtained.

Proposition 4.

The optimal market demand of the EV $q^c$ and the optimal social welfare $W^c$ do not depend on the subsidy s; rather, they depend on the battery recycling rate τ. The optimal battery recycling rate ${\tau }^c$ does not depend on the subsidy s.

In a centralized system, the marginal benefit of and the marginal cost of the EV sale must be equal when the social welfare is maximized. To achieve this, the centralized decision-maker should set a market price of the EV that equals the sum of the marginal cost and the subsidy. Hence, the optimal market demand of the EV, and hence the optimal recycling rate and social welfare, are not impacted by the subsidy.

Proposition 5.

(Optimal Recycling Decision in the Cooperative Game) Assume that $0\le c-(r-A)\tau +e(1-\tau )\le 1+k\tau$ for $\tau \in [0,1]$ in a cooperative game.

(i) 

When $0\le \alpha \le 1$ or when $\alpha >1$ and $B<{\displaystyle \frac{{[r-A+kc+(1+k)e]}^2}{\alpha (\alpha -1){\tau }^{\alpha -2}{(1+k\tau )}^3}}$, the optimal battery recycling rate ${\tau }^c=0$ if $k+r-A<\sqrt{(1+k){(1-c-e)}^2+2(1+k)B}-1+c$; otherwise, ${\tau }^c=1$.

(ii) 

When $\alpha >1$ and $B>{\displaystyle \frac{{[r-A+kc+(1+k)e]}^2}{\alpha (\alpha -1){\tau }^{\alpha -2}{(1+k\tau )}^3}}$, there exists a unique optimal battery recycling rate ${\tau }^c\in [0,1]$, where ${\tau }^c=0$ if $k+r-A<k(1-c-e)/2-e$, ${\tau }^c=1$ if $B<{\displaystyle \frac{(1-c+k+r-A-e)[(2+k)(k+r-A+e)-k(1-c-e)]}{2\alpha {(1+k)}^2}}$, and otherwise ${\tau }^c\in (0,1)$ and satisfies ${\partial W(s,\tau )/\partial \tau |}_{\tau ={\tau }^c}=0$.

Proposition 5 describes the optimal decisions regarding battery recycling in the cooperative game. Similar to the non-cooperative game, the optimal recycling rate in the cooperative game may either equal zero or equal one if the scaling cost parameters are relatively small. Furthermore, different recycling decisions with full recycling, no recycling, and partial recycling may arise if the scaling parameters are relatively large.

The equilibrium outcomes between the cooperative game and non-cooperative game were then compared. It was found that the maximal social welfare realized in the cooperative game may not be achieved in the non-cooperative game. The following proposition shows this finding in the case of the scaling parameter $B=0$.

Proposition 6.

(Comparison of Equilibrium Outcomes between Different Game Models) Suppose that $B=0$. When $k+r-A\in ((1-c-e)(\sqrt{1+k}-1)-e,2(1-e-c)(\sqrt{1+k}-1))$, the optimal battery recycling rate, the optimal market demand of the EV, and the optimal social welfare in the non-cooperative game are lower than those in the cooperative game, i.e., ${\tau }^{*}<{\tau }^c$, $q^{*}<q^c$ and $W^{*}<W^c$.

Proposition 6 shows that, compared with that in the cooperative game, the decentralized decision-making may lower the recycling rate and hence lower the market demand and the social welfare. This result stems from the different objectives of the manufacturer and the government in a non-cooperative game. Specifically, when making the battery recycling decision, the manufacturer focuses on the direct benefit from recycling (i.e., $k+r-A$) and does not consider the environment impacts of the used batteries. However, such impacts are taken into consideration in the government’s subsidy decision; hence, an objective conflict arises between the two players in their optimal decisions. Given this case, the manufacturer may choose a recycling rate lower than that in the cooperative game, which consequently may cause the market demand and social welfare to decrease.

Notice that, when $B=0$, the optimal recycling rate equals one in the cooperative game and equals zero in the non-cooperative game if $k+r-A\in [(1-c-e)(\sqrt{1+k}-1)-e,2(1-e-c)(\sqrt{1+k}-1)]$; otherwise, the optimal recycling rate equals one in both the cooperative and non-cooperative games. Therefore, it is more likely that a higher recycling rate arises in the cooperative game than in the non-cooperative game as the benefit from recycling increases. A similar inference may also hold in the case of $B>0$. The analytical solutions for this case are very complex and Section 4 provides the related numerical example.

4. Numerical Experiments

This section highlights the main findings of Section 3 and the applications of the proposed model through numerical analysis. Based on Section 3, this section first characterizes the manufacturer’s optimal battery recycling decision under an exogenous government subsidy and the impacts of the government subsidy on this decision. Then, this section analyzes the government’s and the manufacturer’s optimal decisions in the non-cooperative and the cooperative game, and compares the equilibrium outcomes in the two games.

Suppose that consumers purchase from an EV manufacturer (e.g., Build Your Dreams (BYD)) in the case with an exogenous government subsidy (refer to the model in Section 3.1). The numerical analysis used realistic data of government subsidy for battery EV purchases in China and some data from the existing literature. Some other data were assumed due to issues of availability. Without loss of generality, the manufacturer’s overall market size was assumed to equal one and consumers’ valuation of the EV follows a uniform distribution over the interval $[0,1]$. Then, the data on the unit production cost of the EV, the government subsidy and the market price of the EV should be normalized accordingly with a certain scale. The battery EV with a range of 250–300 km was used as an illustrating example. According to China’s EV subsidy program in 2018 (https://insideevs.com/china-updates-ev-subsidy-program-to-favor-long-range-bevs/), the government subsidy for this category of battery EV is $9731, which consists of $6487 from China’s central government and $3244 from the local government (notice that many local governments in China offer a subsidy to consumers equaling 50% of the central government’s subsidy). Based on the work of Huang et al. [28] and Shao et al. [30], the unit production cost of a battery EV was assumed to be $29,000. Similar to Shao et al. [30], the production cost of the EV c was normalized to a medium value $0.5$ that equals consumers’ average valuation; hence, the conversion scale is ${\displaystyle \frac{1}{58,000}}$ and the actual government subsidy becomes $s={\displaystyle \frac{9731}{58,000}}\approx 0.17$. All of the following values of costs and profits can be similarly converted.

Suppose that $k=0.2$, $A=0.1$, $r=0.05$, $B=0.05$, and $e=0.1$ in the numerical example. If $a=0.5$, then the optimal battery recycling rate ${\tau }^{*}=1$, the optimal market price of the EV $p^{*}=0.91$, the optimal market demand of the EV $q^{*}=0.3417$, and the manufacturer’s optimal profit ${\mathrm{\Pi }}_m^{*}=0.0901$; if $a=2$, then ${\tau }^{*}=27.84\%$, $p=0.8559$, $q=0.3371$, and ${\mathrm{\Pi }}_m^{*}=0.1161$. This supports Proposition 1, according to which the optimal battery recycling rate is either 0 or 1 when $0\le a\le 1$, and could be in between 0 and 1 when $a>1$. Figure 2 graphically illustrates the effects of changes in the government subsidy s on the optimal battery recycling rate ${\tau }^{*}$ for $s\in [0,0.4]$. It is observed that the maximum of the optimal battery recycling rate is ${\tau }_{max}^{*}=28.12\%$; the optimal battery recycling rate ${\tau }^{*}$ is increasing for $s\in [\mathrm{0.0.25}]$ (the respective actual subsidy is located in $[0,14,500]$ by scale conversion), and is decreasing for $s\in [0.25,0.4]$ (the respective actual subsidy is located in $[14,500,24,000]$ by scale conversion). Therefore, the optimal battery recycling rate ${\tau }^{*}$ decreases with the subsidy s when the subsidy s and the production cost of the EV c are comparable (e.g., the subsidy is no less than 50% of the production cost of the EV). Such a change tendency also confirms the result in Proposition 3 that an increased subsidy can lower the manufacturer’s incentive to recycle if the subsidy is sufficiently large. Figure 3 plots the impacts of the degree of consumer environmental awareness (corresponding to the sensitivity of consumer utility to the battery recycling rate, k) on the optimal battery recycling rate ${\tau }^{*}$. It was observed that the optimal battery recycling rate ${\tau }^{*}$ is non-decreasing as the consumers become more environmentally aware with respect to battery recycling.

Now, it comes to the case with an endogenous government subsidy. Assume that $k=0.1$, $A=0.1$, $r=0.05$ and $e=0.1$ when the government and the manufacturer interact non-cooperatively (refer to the model in Section 3.2.1). Then, at equilibrium, the government’s optimal subsidy is $s^{*}=0.55$ and the manufacturer’s optimal battery recycling rate is ${\tau }^{*}=1$ when $B=0$ and $a=2$; and the government’s optimal subsidy is $s^{*}=0.37$ and the manufacturer’s optimal battery recycling rate is ${\tau }^{*}=27.49\%$ when $B=0.05$ and $a=2$. Such equilibrium outcomes are consistent with Proposition 3. To show how the equilibrium outcomes are derived, the effects of changes in the subsidy s on social welfare, the manufacturer’s profit, and battery recycling rate are plotted in Figure 4 and Figure 5.

Figure 4 demonstrates that, with $B=0$ and $a=2$, the social welfare increases with s if $s\le 0.55$ and decreases in s if $s\ge 0.55$. Meanwhile, the manufacturer’s profit always increases with s. Therefore, the government’s optimal subsidy choice is $0.55$. Because the manufacturer’s optimal battery recycling rate equals 1 if $s\in [0,0.61]$ and equals 0 if $s\in [0.61,1]$ (see Figure 5), ${\tau }^{*}=1$ given $s^{*}=0.55$. It follows that the optimal social welfare is $W^{*}=0.1375$ and the manufacturer’s optimal profit is ${\mathrm{\Pi }}_m^{*}=0.275$. In addition, based on $s^{*}$ and ${\tau }^{*}$, the optimal market price of the EV is $p^{*}=1.05$ and the optimal market demand of the EV is $q^{*}=0.5$. When $B=0.05$ and $a=2$, it is similarly show in Figure 5 that the optimal subsidy is $s^{*}=0.284$ and the optimal battery recycling rate is ${\tau }^{*}=4.25\%$; hence, the optimal social welfare is $W^{*}=0.082$ and the manufacturer’s optimal profit is ${\mathrm{\Pi }}_m^{*}=0.1538$. Furthermore, the optimal market price of the EV is $p^{*}=0.8931$ and the optimal market demand of the EV is $q^{*}=0.3914$. Notice that both Figure 4 and Figure 5 show that the social welfare decreases with the subsidy s when the subsidy is sufficiently large. This outcome stems from the fact that a higher subsidy lowers the manufacturer’s incentive to recycle and therefore adversely affects the social welfare when the subsidy is sufficiently high.

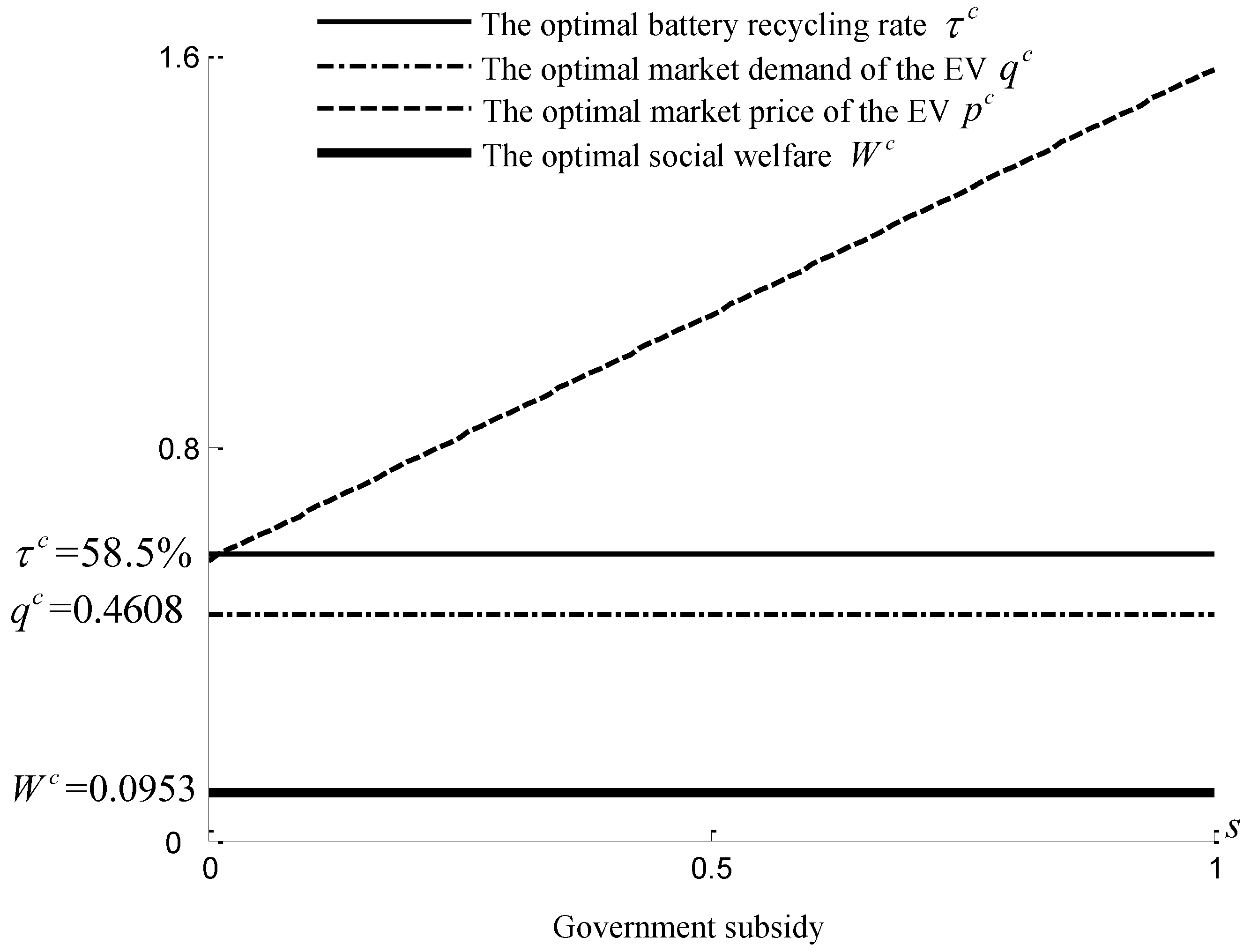
Suppose that the government and the manufacturer make decisions cooperatively (refer to the model in Section 3.2.2). The same parameter setting as in the non-cooperative game was used (i.e., $k=0.1$, $A=0.1$, $r=0.05$, $e=0.1$, $B=0.05$, and $a=2$). Figure 6 plots the impacts of the subsidy on the equilibrium outcomes for $s\in [0,1]$. It is shown that the optimal battery recycling rate ${\tau }^c=58.5\%$, the optimal market demand $q^c=0.4608$, and the optimal social welfare $W^c=0.0953$ always hold as the subsidy s changes, while the market price of the EV increases with the subsidy s. Hence, the major equilibrium outcomes are independent of s in the cooperative game, which supports the results of Proposition 5. By comparison, given the above parameter setting, $W^c=0.0953>0.082=W^{*}$ (i.e., the optimal social welfare increases at a rate of 16.2%), ${\tau }^c=58.5\%>4.25\%={\tau }^{*}$, and $q^c=0.4608>0.3914=q^{*}$. Therefore, the optimal battery recycling rate increases significantly and the optimal social welfare increases at a rate of 16.2% when there is cooperation between the government and the manufacturer. This outcome extends the results of Proposition 6 in the case of $B>0$ and indicates that the two players should work together to improve the social welfare when the decisions regarding battery recycling are incorporated.

5. Conclusions

In China, the recycling of used EV batteries has raised an increasing concern due to the explosive growth of EV utilization in recent years. This study constructed a stylized model to investigate an EV manufacturer’s optimal battery recycling strategy in China when the government offers a subsidy to the EV purchase in the presence of environmentally aware consumers. Two cases were analyzed in this study: first, the one in which the government is non-strategic and the subsidy is exogenously given; and, second, the one in which the government is strategic and interacts with the manufacturer in a non-cooperative or a cooperative game. The manufacturer’s optimal battery recycling decisions and the equilibrium outcomes in different cases were characterized by applying the consumer utility function and the game-theoretical approach. This study contributed to the literature by endogenizing the EV manufacturer’s decisions regarding battery recycling in an EV market under government subsidy.

The analytic results demonstrated that, with an exogenous government subsidy, the manufacturer has different battery recycling strategies depending on the impact of the recycling scale on costs. If such an impact is unremarkable, the manufacturer either recycles all the used batteries or does not recycle any used batteries; otherwise, partial battery recycling arises when the benefit from recycling is moderate. The impacts of government subsidy on the manufacturer’s optimal battery recycling decisions were also characterized. It was found that the optimal battery recycling rate is increasing with the government subsidy if the government subsidy is relatively small. However, the optimal battery recycling rate may be decreasing with the government subsidy if the government subsidy is sufficiently large. This outcome offers an interesting insight that a higher government subsidy does not always result in a greater reduction in the environmental hazard. A similar conclusion was reached by Huang et al. [17] in a setting of a fuel-powered automobile supply chain and an electric-and-fuel automobile supply chain. In this study, the rationale for this outcome is different from that in their study because this study relates this outcome to the impact of government subsidy on the battery recycling decisions.

The analytical results also indicate that, when the subsidy is endogenously chosen and the government and the manufacturer interact in the non-cooperative game, full recycling, no recycling, or partial recycling may also arise, depending on the impact of the recycling scale. Meanwhile, given the same optimal battery recycling rate, the government’s optimal subsidy choice varies with the size of the benefit from recycling. When the government and the manufacturer act in the cooperative game, the optimal battery recycling, market demand, and the social welfare are not impacted by the government subsidy. In particular, it was found that the optimal battery recycling rate may be lower in the non-cooperative game than in the cooperative game because of the conflicting objectives associated with the environmental impacts of the used batteries. Given this case, the social welfare may not be maximized in the non-cooperative game compared with that in the cooperative game. This provides the important insight that cooperation between the government and the EV manufacturer in China can improve the social welfare when the battery recycling decisions are considered.

The analytical results and the models were further examined by numerical experiments with realistic subsidy data in China. The numerical results show that the optimal battery recycling rate varies with the impact of the recycling scale on costs and locates in the closed interval from 0 to 1 in both cases with an exogenous or an endogenous government subsidy. Meanwhile, the optimal battery recycling rate decreases with the government subsidy given certain parameter setting with comparable government subsidy and production cost of the EV (e.g., the government subsidy is not less than 50% of the production cost of the EV). This numerical result may explain why the Chinese government has been cutting the subsidy for EV purchase in recent years. Based on this study, such an initiative of the Chinese government may help promote the manufacturer’s battery recycling incentive; therefore, it may be environmentally friendly and benefit the social welfare in China.

The numerical results also show that, in the non-cooperative game, the social welfare increases first and then decreases as the government subsidy increases, and there exists a unique government subsidy that maximizes the social welfare. Finally, numerical examples were developed to compare the equilibrium outcomes between the two different game models. It was numerically shown that, compared with that in the non-cooperative game, the optimal battery recycling rate increases significantly and the optimal social welfare is improved in the cooperative game.