Toward Supply Chain Sustainability: Governance and Implementation of Joint Sustainability Development
Abstract
:1. Introduction
- How does the impact of manufacturers’ and retailers’ individual sustainability development efforts on consumer demand influence their decisions in terms of pricing (i.e., wholesale and retail prices) and their JSD effort levels?
- How do the revenue sharing arrangements (i.e., partial sharing (unit profit margin sharing without associated fixed costs sharing) and full sharing (unit profit margin and associated fixed costs sharing)) affect manufacturers’ and retailers’ decisions on initiating their JSD?
- Is it possible to identify a particular contractual arrangement (i.e., derivative of revenue sharing) that is preferred by both manufacturer and retailer simultaneously?
2. Literature Review
3. Models and Analyses
3.1. Sequential Game without Sharing Mechanism
3.2. Sequential Game with Partial Sharing Mechanism
- a.
- Bothandare increasing in, when
- b.
- is increasing butis decreasing in, when
- c.
- is decreasing butis increasing in, when
- d.
- Bothandare decreasing in, when,
3.3. Simultaneous Game with Partial Sharing Mechanism
3.4. Sequential Game with Full Sharing Mechanism
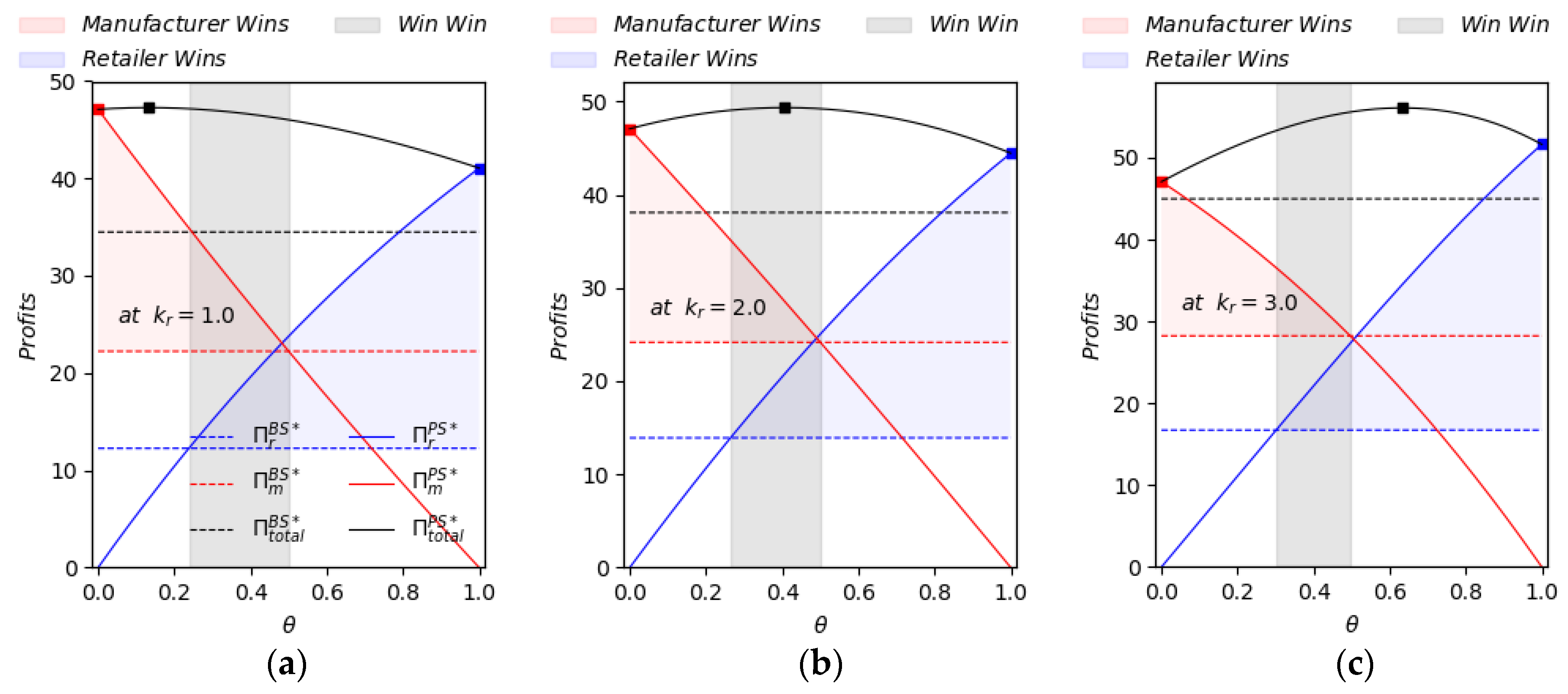
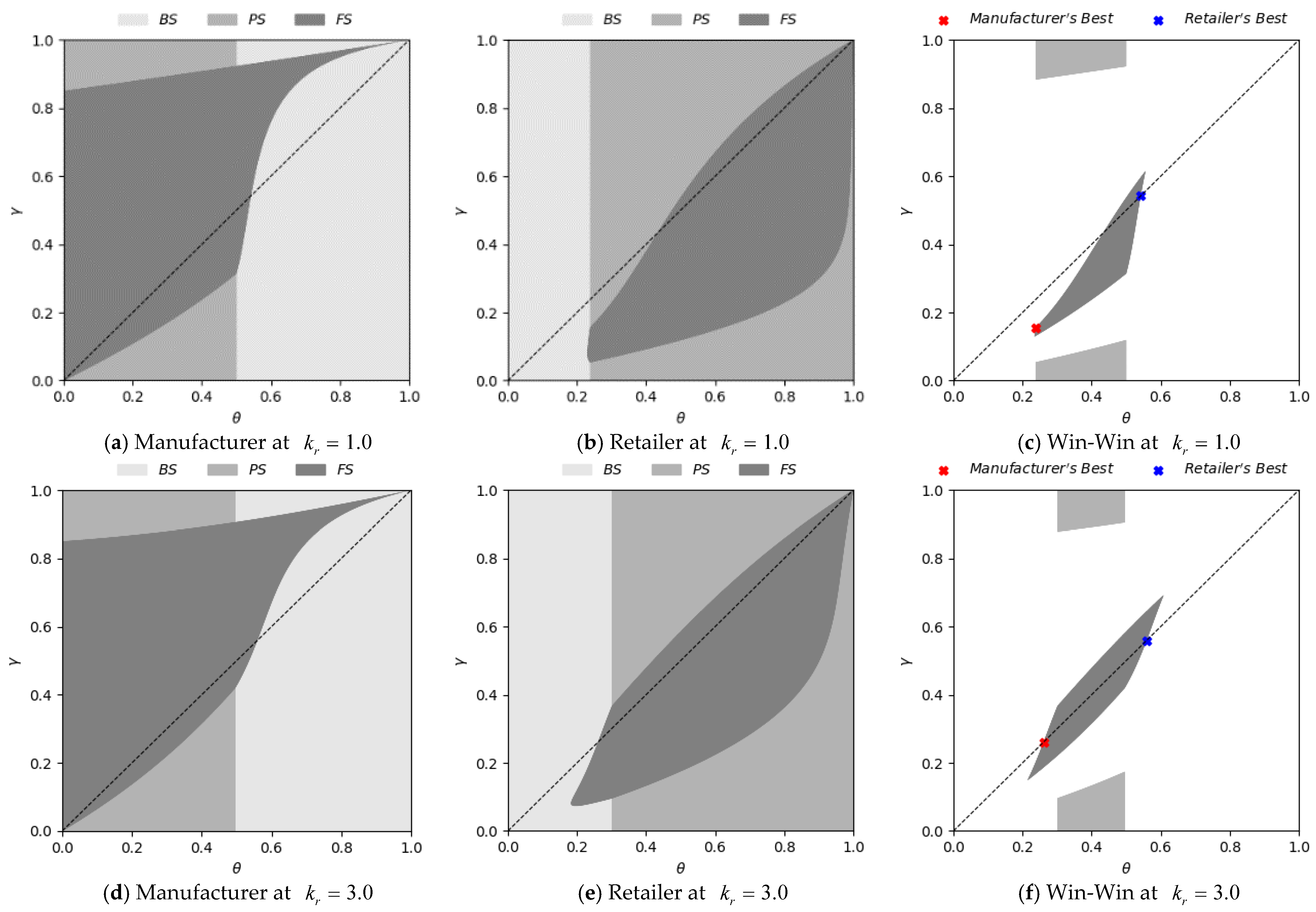
4. Numerical Experiments
5. Conclusions and Implications
Author Contributions
Conflicts of Interest
Appendix A
References
- Alshehhi, A.; Nobanee, H.; Khare, N. The Impact of Sustainability Practices on Corporate Financial Performance: Literature Trends and Future Research Potential. Sustainability 2018, 10, 494. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J. Corporate Sustainability Management and Its Market Benefits. Sustainability 2018, 10, 1455. [Google Scholar] [CrossRef]
- Kuchinka, D.; Balazs, S.; Gavriletea, M.; Djokic, B.-B. Consumer Attitudes toward Sustainable Development and Risk to Brand Loyalty. Sustainability 2018, 10, 997. [Google Scholar] [CrossRef]
- Oroian, C.; Safirescu, C.; Harun, R.; Chiciudean, G.; Arion, F.; Muresan, I.; Bordeanu, B. Consumers’ Attitudes towards Organic Products and Sustainable Development: A Case Study of Romania. Sustainability 2017, 9, 1559. [Google Scholar] [CrossRef]
- JustMeans. Nike’s Yearly CSR Budget is $25 Million but Refuses to Pay $2.2 Million in Severance to Honduran Garment Workers. Available online: http://justmeans.com/blogs/nike-spends-25-million-on-csr-annually-refuses-to-pay-22-million-in-severance-to-honduran (accessed on 14 April 2018).
- Miller, D.; Merrilees, B. Linking retailer corporate brand and environmental sustainability practices. J. Prod. Brand Manag. 2013, 22, 437–443. [Google Scholar] [CrossRef]
- Huffington Post. The Real March Madness: Nike Ditches University Commitments. Available online: https://www.huffingtonpost.com/entry/the-real-march-madness-nike-ditches-university-commitments_us_58deba30e4b0d804fbbb72b7 (accessed on 14 April 2018).
- Human Thread Campaign. Fashion Transparency Index. Available online: http://www.humanthreadcampaign.org/wp-content/uploads/2017/06/FR_FashionTransparencyIndex2017.pdf (accessed on 14 April 2018).
- The Guardian. Walmart Is Slapping Itself on the Back for Sustainability but it still Has a Way to Go. 2015. Available online: https://www.theguardian.com/sustainable-business/2015/nov/18/walmart-climate-change-carbon-emissions-renewabe-energy-environment (accessed on 18 May 2018).
- Govindan, K. Sustainable consumption and production in the food supply chain: A conceptual framework. Int. J. Prod. Econ. 2018, 195, 419–431. [Google Scholar] [CrossRef]
- Grosvold, J.; Hoejmose, S.U.; Roehrich, J.K. Squaring the circle: Management, measurement and performance of sustainability in supply chains. Supply Chain Manag. 2014, 19, 292–305. [Google Scholar] [CrossRef]
- Björklund, M.; Forslund, H.; Isaksson, M.P. Exploring logistics-related environmental sustainability in large retailers. Int. J. Retail Distrib. Manag. 2016, 44, 38–57. [Google Scholar] [CrossRef]
- Hassini, E.; Surti, C.; Searcy, C. A literature review and a case study of sustainable supply chains with a focus on metrics. Int. J. Prod. Econ. 2012, 140, 69–82. [Google Scholar] [CrossRef]
- Narasimhan, R.; Schoenherr, T.; Jacobs, B.W.; Kim, M.K. The financial impact of FSC certification in the United States: A contingency perspective. Decis. Sci. J. 2015, 46, 527–563. [Google Scholar] [CrossRef]
- Kim, Y.H.; Davis, G.F. Challenges for global supply chain sustainability: Evidence from conflict minerals reports. Acad. Manag. J. 2016, 59, 1896–1916. [Google Scholar] [CrossRef]
- Paulraj, A.; Blome, C. Plurality in environmental supply chain mechanisms: Differential effects on triple bottom line outcomes. Int. J. Oper. Prod. Manag. 2017, 37, 1010–1030. [Google Scholar] [CrossRef]
- Mani, V.; Gunasekaran, A.; Delgado, C. Enhancing supply chain performance through supplier social sustainability: An emerging economy perspective. Int. J. Prod. Econ. 2018, 195, 259–272. [Google Scholar] [CrossRef]
- Unruh, G.; Kiron, D.; Kruschwitz, N.; Reeves, M.; Rubel, H.; Zum Felde, A.M. Investing for a sustainable future: Investors care more about sustainability than many executives believe. MIT Sloan Manag. Rev. 2016, 57, 3–28. [Google Scholar]
- Lal, R.; Narasimhan, C. The Inverse Relationship Between Manufacturer and Retailer Margins: A Theory. Mark. Sci. 1996, 15, 132–151. [Google Scholar] [CrossRef]
- Lewis, L.E.; Schmidt, K.; Duvall, M.N. Retailer sustainability and the supply chain. Nat. Resour. Environ. 2012, 26, 18–22. [Google Scholar]
- Lavorata, L. Influence of retailers’ commitment to sustainable development on store image, consumer loyalty and consumer boycotts: Proposal for a model using the theor. J. Retail. Consum. Serv. 2014, 21, 1021–1027. [Google Scholar] [CrossRef]
- He, H.; Li, Y. CSR and Service Brand: The Mediating Effect of Brand Identification and Moderating Effect of Service Quality. J. Bus. Ethics 2011, 100, 673–688. [Google Scholar] [CrossRef]
- Roy, V.; Schoenherr, T.; Parikshit, C. The thematic landscape of literature in sustainable supply chain management (SSCM): A review of the principal facets in SSCM development. Int. J. Oper. Prod. Manag. 2018, 38, 1091–1124. [Google Scholar] [CrossRef]
- Drumwright, M.E. Socially responsible organizational buying: Environmental concern as a noneconomic buying criterion. J. Mark. 1994, 58, 1–19. [Google Scholar] [CrossRef]
- Carter, C.R.; Rogers, D.S. A framework of sustainable supply chain management moving toward new theory. Int. J. Retail Distrib. Manag. 2008, 38, 360–387. [Google Scholar] [CrossRef]
- Golicic, S.L.; Smith, C.D. A Meta-Analysis of Environmentally Sustainable Supply Chain Management Practices and Firm Performance. J. Supply Chain Manag. 2013, 49, 78–95. [Google Scholar] [CrossRef]
- Markman, G.D.; Krause, D. Theory building surrounding sustainable supply chain management: Assessing what we know, exploring where to go. J. Supply Chain Manag. 2016, 52, 3–10. [Google Scholar] [CrossRef]
- Pagell, M.; Shevchenko, A. Why research in sustainable supply chain management should have no future. J. Supply Chain Manag. 2014, 50, 44–55. [Google Scholar] [CrossRef]
- Touboulic, A.; Walker, H. Theories in sustainable supply chain management: A structured literature review. Int. J. Phys. Distrib. Logist. 2015, 45, 16–42. [Google Scholar] [CrossRef]
- Montabon, F.; Pagell, M.; Wu, Z. Making Sustainability Sustainable. J. Supply Chain Manag. 2016, 52, 11–27. [Google Scholar] [CrossRef]
- Cao, M.; Zhang, Q. Supply chain collaboration: Impact on collaborative advantage and firm performance. J. Oper. Manag. 2011, 29, 163–180. [Google Scholar] [CrossRef]
- Fawcett, S.E.; McCarter, M.W.; Fawcett, A.M.; Webb, G.S.; Magnan, G.M. Why supply chain collaboration fails: The socio-structural view of resistance to relational strategies. Supply Chain Manag. 2015, 20, 648–663. [Google Scholar] [CrossRef]
- Touboulic, A.; Walker, H. Love me, love me not: A nuanced view on collaboration in sustainable supply chains. J. Purch. Supply Manag. 2015, 21, 178–191. [Google Scholar] [CrossRef]
- Crespin-Mazet, F.; Dontenwill, E. Sustainable procurement: Building legitimacy in the supply network. J. Purch. Supply Manag. 2012, 18, 207–217. [Google Scholar] [CrossRef]
- Carter, C.R.; Easton, L.P. Sustainable supply chain management: Evolution and future directions. Int. J. Phys. Distrib. Logist. 2011, 41, 46–62. [Google Scholar] [CrossRef]
- Wang, Z.; Huo, B.; Tian, Y.; Hua, Z. Effects of external uncertainties and power on opportunism in supply chains: Evidence from China. Int. J. Prod. Res. 2015, 53, 6294–6307. [Google Scholar] [CrossRef]
- Cheng, J.H.; Sheu, J.B. Inter-organizational relationships and strategy quality in green supply chains—Moderated by opportunistic behavior and dysfunctional conflict. Ind. Mark. Manag. 2012, 41, 563–572. [Google Scholar] [CrossRef]
- Herczeg, G.; Akkerman, R.; Hauschild, M.Z. Supply chain coordination in industrial symbiosis. In Proceedings of the 20th International EurOMA Conference, Dublin, Ireland, 7–12 June 2013. [Google Scholar]
- Cachon, G.P.; Lariviere, M.A. Supply chain coordination with revenue-sharing contracts: Strengths and limitations. Manag. Sci. 2005, 51, 30–44. [Google Scholar] [CrossRef]
- Guo, R.; Lee, H.L.; Swinney, R. Responsible sourcing in supply chains. Manag. Sci. 2015, 62, 2722–2744. [Google Scholar] [CrossRef]
- You, D.; Jiang, K.; Li, Z. Optimal coordination strategy of regional vertical emission abatement collaboration in a low-carbon environment. Sustainability 2018, 10, 571. [Google Scholar] [CrossRef]
- Plambeck, E.L.; Taylor, T.A. Supplier Evasion of a Buyer’s Audit: Implications for Motivating Compliance with Labor and Environmental Standards. Manuf. Serv. Oper. Manag. 2015, 18, 184–197. [Google Scholar] [CrossRef]
- Ahmadi-Javid, A.; Hoseinpour, P. On a cooperative advertising model for a supply chain with one manufacturer and one retailer. Eur. J. Oper. Res. 2012, 219, 458–466. [Google Scholar] [CrossRef]
- Cui, T.H.; Raju, J.S.; Zhang, Z.J. Fairness and channel coordination. Manag. Sci. 2007, 53, 1303–1314. [Google Scholar]
- Dellarocas, C. Double Marginalization in Performance-Based Advertising: Implications and Solutions. Manag. Sci. 2012, 58, 1178–1195. [Google Scholar] [CrossRef]
- Brandenburg, M.; Govindan, K.; Sarkis, J.; Seuring, S. Quantitative models for sustainable supply chain management: Developments and directions. Eur. J. Oper. Res. 2014, 233, 299–312. [Google Scholar] [CrossRef]
- Xiao, T.; Qi, X. Price competition, cost and demand disruptions and coordination of a supply chain with one manufacturer and two competing retailers. Omega 2008, 36, 741–753. [Google Scholar] [CrossRef]
- Orlitzky, M.; Schmidt, F.L.; Rynes, S.L. Corporate social and financial performance: A meta-analysis. Organ. Stud. 2003, 24, 403–441. [Google Scholar] [CrossRef]
- Heese, H.S.; Swaminathan, J.M. Product line design with component commonality and cost-reduction effort. Manuf. Serv. Oper. Manag. 2006, 8, 206–219. [Google Scholar] [CrossRef]
- Tang, S.Y.; Gurnani, H.; Gupta, D. Managing Disruptions in Decentralized Supply Chains with Endogenous Supply Process Reliability. Prod. Oper. Manag. 2014, 23, 1198–1211. [Google Scholar] [CrossRef]
- Yoon, J.; Rosales, C.; Talluri, S. Inter-firm partnerships-strategic alliances in the pharmaceutical industry. Int. J. Prod. Res. 2018, 56, 862–881. [Google Scholar] [CrossRef]
- Ghosh, D.; Shah, J. Supply chain analysis under green sensitive consumer demand and cost sharing contract. Int. J. Prod. Econ. 2015, 164, 319–329. [Google Scholar] [CrossRef]
- Jeuland, A.P.; Shugan, S.M. Managing Channel Profits. Mark. Sci. 2008, 27, 52–69. [Google Scholar] [CrossRef]
- Gerstner, E.; Hess, J.D. Pull promotions and channel coordination. Mark. Sci. 1995, 14, 43–60. [Google Scholar]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Yoon, J.; Kim, M.K.; Sheu, C. Toward Supply Chain Sustainability: Governance and Implementation of Joint Sustainability Development. Sustainability 2018, 10, 1658. https://doi.org/10.3390/su10051658
Xu Y, Yoon J, Kim MK, Sheu C. Toward Supply Chain Sustainability: Governance and Implementation of Joint Sustainability Development. Sustainability. 2018; 10(5):1658. https://doi.org/10.3390/su10051658
Chicago/Turabian StyleXu, Yongmei, Jiho Yoon, Myung Kyo Kim, and Chwen Sheu. 2018. "Toward Supply Chain Sustainability: Governance and Implementation of Joint Sustainability Development" Sustainability 10, no. 5: 1658. https://doi.org/10.3390/su10051658




